Abstract
In the last few decades, various solutions have been proposed to increase the modulation bandwidth and, consequently, the transmission bit-rate of semiconductor lasers. In this manuscript, we discuss a design procedure for a recently proposed laser cavity realized with the monolithic integration of two distributed Bragg reflector (DBR) lasers allowing one to extend the modulation bandwidth. Such an extension is obtained introducing in the dynamic response a photon-photon resonance (PPR) at a frequency higher than the modulation bandwidth of the corresponding single-section laser. Design guidelines will be proposed, and dynamic small and large signal simulations results, calculated using a finite difference traveling wave (FDTW) numerical simulator, will be discussed to confirm the design results. The effectiveness of the design procedure is verified in a structure with PPR frequency at allowing one to obtain an open eye diagram for a non-return-to-zero (NRZ) digital signal up to . Furthermore, the investigation of the rich dynamics of this structure shows that with proper bias conditions, it is possible to obtain also a tunable self-pulsating signal in a frequency range related to the PPR design.
1. Introduction
Semiconductor laser diodes with a wide direct modulation bandwidth represent an important element to fulfill the continuously increasing request for low-cost optical communications systems with a high bit-rate (see, e.g., [1]). Whilst the maximum bit-rate achieved by direct modulated lasers is typically limited by the well-known resonance between carriers and photons (carrier-photon resonance (CPR)) [2], many solutions have been proposed to overcome this restriction; see, for example, [3] for a recent review.
A first mechanism identified to extend the modulation bandwidth is the detuned loading (DL) due to the dispersion effect introduced by a coupled passive cavity [4,5] or by a distributed mirror (DBR [6,7,8] or Distributed Feedback (DFB) [9]) when the lasing mode is properly positioned at a slightly higher wavelength with respect to the minimum threshold gain condition.
A second approach used to extend the lasers dynamic properties is to take advantage, in a properly designed cavity, of the interaction between the lasing mode and an adjacent longitudinal cavity mode. This interaction is made possible by the carrier pulsation introduced by the current modulation applied at the gain section electrode [6,7,10,11,12]. This interaction introduces a resonance in the intensity modulation response at the frequency corresponding to the two cavity modes’ separation; such a resonance is frequently called photon-photon resonance (PPR).
Since the PPR usually occurs at a frequency that is much higher than the CPR frequency, the request for an almost flat modulation response implies the need for a proper cavity design to have the PPR at the correct frequency, allowing one to fill the gap between the PPR and CPR peaks of the modulation response. In this condition of modulation bandwidth extension, it is possible to obtain an open eye diagram of an NRZ signal at a greater bit-rate than in the corresponding single-section DBR laser.
An approach that is frequently used to achieve this condition is the introduction of an external feedback to the laser cavity. On this concept, various cavity designs have been studied and realized as, e.g., the complex cavity injection grating (CCIG) [13,14,15,16], DFB with integrated feedback (IFB-DFB) [17] or single-mode cavity with feedback effects [18,19]. Furthermore, the modulation bandwidth extension can be obtained with the injection-locking of a laser to the optical signal of an external source (see, e.g., [20,21,22]). The modulation bandwidth extension has also been obtained exploiting the coupling between two modes in a waveguide supporting two transverse modes [23] or in coupled vertical-cavity surface-emitting lasers (VCSELs) [24,25]. In all of the previously-cited cases, the bandwidth extension by PPR can be used either (1) to improve the dynamic characteristics of a laser that shows a limited modulation bandwidth because of its non-optimal material [26] or cavity [1] properties or (2) to extend the dynamic properties of a device that already exhibits a good modulation response.
The structure investigated in this manuscript consists of two coupled cavity DBR lasers integrated in a single chip, as shown in Figure 1a. This structure can be seen both as an example of a DBR laser with an external feedback from an active cavity or as an integrated injection-locked DBR laser, as has been already presented in [27,28,29,30] depending on the injection level in the two cavities. In this paper, just for simplicity, we will call the master the unmodulated laser cavity and the slave the other one.
The additional contributions in this paper with respect to the previous ones [27,28,29,30] are: the definition of a design procedure allowing one to determine the cavity parameters necessary to achieve a prescribed PPR frequency (), the validation of the design results by showing the possibility of large signal operation conditions with a clearly open eye diagram at a higher bit-rate with respect to that of the single-cavity configuration and also a more complete mapping of the dynamic characteristic with the demonstration of the existence of conditions of good self-pulsation operation in proper bias conditions.

Figure 1.
(a) Schematics of the coupled-cavity DBR laser. and are the sum of the lengths of the active and phase-control sections of the two laser cavities. The currents () and () are injected in the active (phase-control) sections of the master (left) and slave (right) laser cavities, respectively. (b) Analyzed coupled cavity. The phase tuning sections are replaced by a lumped phase term . The right dashed line indicates the reference plane at which the equivalent reflectivities and are calculated using the transfer matrix method.
The paper is organized as follows: First, in Section 2, we will present the cavity design procedure and the obtained PPR frequency maps as functions of the cavity parameters. In Section 3, the results obtained from the simulations of the small and large signal modulation and of self-pulsation operation will be discussed. Finally, in Section 4, we will draw the conclusions.
2. Design of the Coupled DBR Laser Cavity
For the composite DBR cavity under consideration (Figure 1a), as well as for the other cases of laser cavity referenced in Section 1, a proper choice of the cavity parameters is the essence for the exploitation of the PPR mechanism between the lasing mode and the nearest neighbor with the requested frequency separation.
The need for a design derives from two competing factors: if the cavity length is reduced to avoid the parasitic effect limiting the laser dynamics, the mode separation is then usually too high to obtain a flat dynamic modulation response using the PPR effect. Therefore, careful design of the cavity is needed in order to control the separation between the two modes that must interact to obtain the modulation extension effect.
The precise mode separation can only be obtained from the above-threshold analysis [16,17], but an analysis at the threshold [12,13] allows a good estimation. Thus, the results found at the threshold may be used to design the structure to be analyzed in the above-threshold regime.
2.1. Master and Slave Lasers’ Definition
The first step in the cavity design is the definition of the role of the two lasers. Since we assumed that the slave (right DBR) laser will be modulated, the output power will be therefore extracted from the right mirror. The second assumption is that the master (left DBR) laser has only a small output power on the left side of the cavity in order to maximize its power coupling to the slave laser. Obviously, with these preliminary assumptions, the higher reflectivity at will be the peak reflectivity of the left DBR mirror (), while the lower one will be the peak reflectivity of the right grating (). The peak value of the central mirror reflectivity () will be in between and ; obviously, it will determine the strength of the coupling between the two cavities and, consequently, the frequency splitting between the resonances of the composite cavity.
2.2. Photon-Photon Resonance Frequency Calculation
We are interested in the case where both cavities are above-threshold with independent current injection in the active regions. First, we assume that the active section of the master (left) cavity is at transparency and that there is gain only in the slave (right) cavity. In this condition, we perform a below-threshold analysis, and we search for the threshold condition for the full coupled cavity structure. To emphasize the role of the two cavities in the lasing mode selection, we assume a wavelength-independent gain function. In this condition, we compute at threshold the gain and the frequency of the lasing mode and of its adjacent ones and the round trip gain (RTG) and phase (RTP) function of the full cavity in the frequency range around the grating Bragg condition. The RTG and RTP functions at the lasing condition are expressed as:
where the equivalent reflectivities and are calculated using the transmission matrix approach [2] considering a reference plane placed at the left input of the slave grating (Figure 1b). Details on the calculation of and are presented in Appendix A1.
This threshold analysis allows one to obtain the frequency separation between the lasing and the adjacent modes and also gives preliminary information on the mode competition from the gain margin between the lasing mode and the non-lasing ones.
Examples of RTG and RTP functions around the lasing frequency are reported in Figure 2 for three values of the control phase . In order to qualitatively appreciate the dynamic behavior in the three operation conditions in Figure 2, we present in Figure 3a preview of small signal modulation responses discussed more completely in Section 3 for a suitable choice of the currents injected in the active sections.
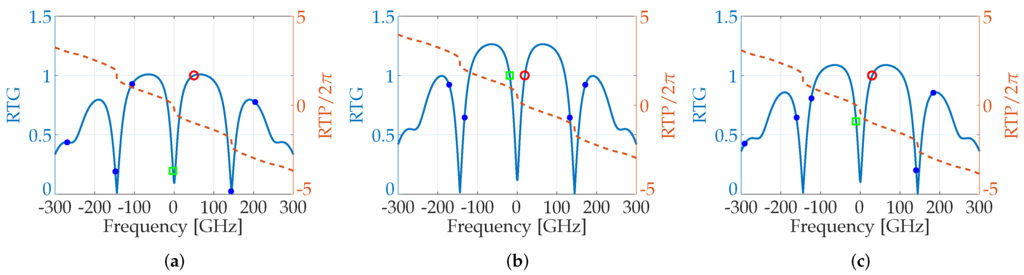
Figure 2.
Round trip gain (RTG) (continuous blue line) and phase (RTP) (dashed red line) functions plots at threshold around the Bragg frequency for three different additional phase shifts in the slave laser cavity. The lasing mode is indicated by the red circle, the closest non-lasing mode by the green square marker and the other non-lasing modes by the blue dots. , , , , . (a) and , (b) and and (c) and .
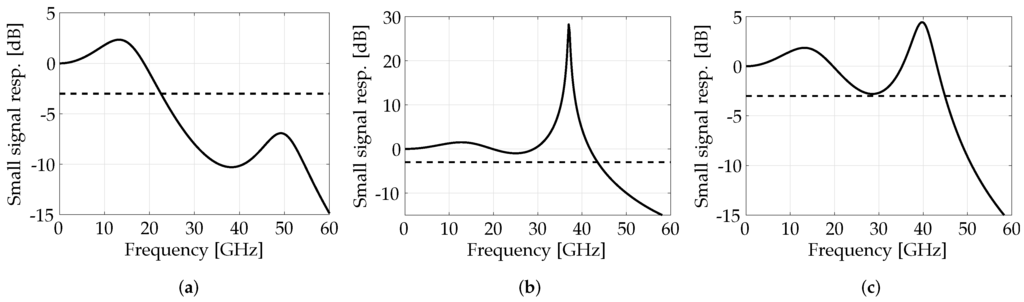
Figure 3.
Examples of small signal modulation responses obtained with the finite difference traveling wave (FDTW) model for cavity parameters and phase tuning used in Figure 2. (a) and , (b) and and (c) and .
When , the lasing mode (red circle) and its closest cavity mode (green square) are separated by 47 (Figure 2a); however, the PPR peak is barely visible in the small signal modulation response (Figure 3a) due to the large gain margin between the lasing mode and the closest one, which is located near the RTG minimum. In this condition, the dB bandwidth only depends on the CPR. When , two modes have RTG , and their frequency separation is (Figure 2b): the corresponding small signal modulation response typically shows a strong peak at the PPR frequency (Figure 3b), indicating that the beating between the two modes generates a self-pulsating output power. While this condition could be useful for radio-frequency (RF) photonics applications, it cannot be employed for direct digital modulation.
In order to obtain a modulation response suitable for digital transmission applications, the correct balancing between PPR frequency and the gain margin of the mode closest to the lasing one must be ensured, as in Figure 2c and in the corresponding Figure 3c, where the dB bandwidth is enhanced up to . With respect to the case with , now, the is increased by 10%, but the PPR peak is strongly reduced. Good large signal operations can be obtained around this phase condition; on the contrary, an excessively large could generate a gap between the CPR and the PPR peaks, again limiting the dB modulation bandwidth. From our experience, a good choice for the in order to maximize the bit rate for digital transmission application is .
2.3. Coupled Cavities’ Design
Different from previous studies [27,28], in our analysis, the distributed characteristics of the DBR mirrors have been considered; therefore, the cavities’ parameters for the laser design are:
- the three DBR mirrors maximum reflectivities (, , ) or the corresponding lengths (, , ); we assumed the coupling coefficient κ to be the same for all of the gratings;
- the right () and left () cavity lengths.
In order to obtain an estimate of the cavity , once the cavity and material parameters have been fixed, we calculate the frequency separation in the condition indicated in Figure 2b. While in this condition, the device could be self-pulsating, in proper operation conditions above-threshold, a small tuning of the cavity modes’ positions will ensure an optimal intensity of the PPR peak with a small increase of , as shown in Figure 2c, producing the extra peak in the small signal modulation response due to PPR, which allows a significant extension of the laser modulation bandwidth [12,16].
In particular, the PPR frequency is computed choosing the value of the lossless left grating reflectivity and assuming the output right facet to be either cleaved, for realization simplicity, or realized with a grating with maximum reflectivity %. Three values of the grating coupling coefficient (, 100, 200 cm−1) were considered, and the waveguides and grating losses were assumed to be 10 cm−1. The remaining cavity parameters (central grating reflectivity and the total master and slave cavity lengths and ) have been varied; for this first analysis, we assume . Results and considerations for different values of the ratio will be reported in the following.
The results of this PPR frequency analysis at threshold have been represented in Figure 4 in which we kept constant the left grating reflectivity %, and we considered as parameters for each figure the coupling coefficient κ. These figures are fundamental to select the structures to consider also on the basis of the available technology for the grating realization and the active material gain characteristics.
In Figure 4, the map is represented both for the case of the cleaved (continuous line) and grating (dashed line) output facet. In the figure, the dotted horizontal lines indicate the number of the cavity modes inside the central reflectivity lobe of the left grating of the master cavity , which is the grating with the largest optical bandwidth (see Figure 1).
This parameter is important because the larger is its value, the greater is the possibility of competition between the lasing mode and the adjacent ones, which can lead to mode jumps when tuning the cavity phase. As can be seen from the maps in Figure 4, can be obtained over a broad range of frequencies, from 10 to . As we predicted, small values are obtained for higher values of the central grating reflectivity due to the weak coupling between the two cavities, while the opposite is obtained for smaller values. Obviously, also the cavity length affects the value of , which decreases for longer cavities because of the reduction of the free spectral range (FSR). The regions in Figure 4’s maps where the constant lines have not been reported indicate operation conditions in which, with the approximation used to generate the maps, the gain margin with respect to the other modes of the cavity is very small or lasing can be found at frequencies strongly shifted from the Bragg condition due to the complexity of the RTG reflectivity curve. The latter behavior is usually due to the higher number of cavity modes inside the main reflectivity lobe of . From our experience [16], in these regions, the extended modulation bandwidth conditions could still be obtained, but they are more sensitive to the cavity parameters. To simplify the reading of the maps, the truncation points have been connected with a thick dash-point blue line. As can be seen, the frequency selection introduced using a Bragg grating at the output facet instead of a cleaved surface allows one to extend the curves over all of the considered parameters’ range.
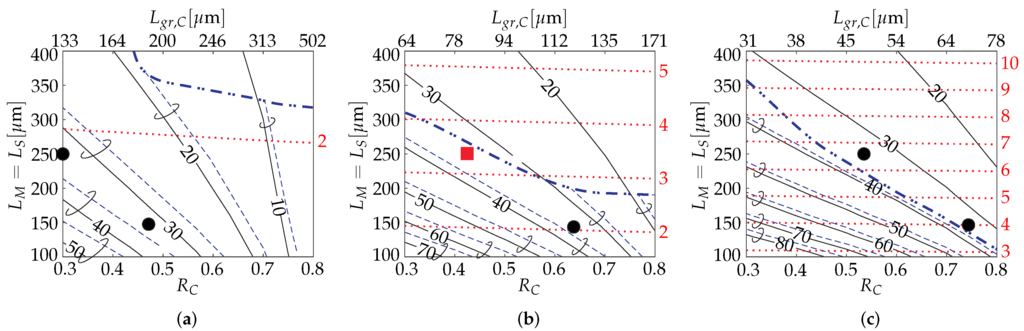
Figure 4.
Coupled cavities DBR laser design maps for equal cavity length (): constant photon-photon resonance (PPR) frequency (in ) curves as functions of the central grating reflectivity () and for the cleaved (dashed lines map) and grating (continuous lines map) right facet with the same maximum reflectivity %. Results are obtained at the laser threshold using the transmission matrix method for a lossless left reflectivity % and with (a), (b) and (c). In the area above the double dotted line, where the dashed constant frequency lines are not reported, the PPR conditions are more critical to be found. The red dotted lines, referring to the right vertical axes, indicate the number of longitudinal modes of the slave cavity inside the reflectivity main lobe of the grating with the largest optical bandwidth. The large markers indicate the structures that we have analyzed in their small and large signal modulation responses; the square marker indicates the structure whose dynamic results have been reported in this paper.
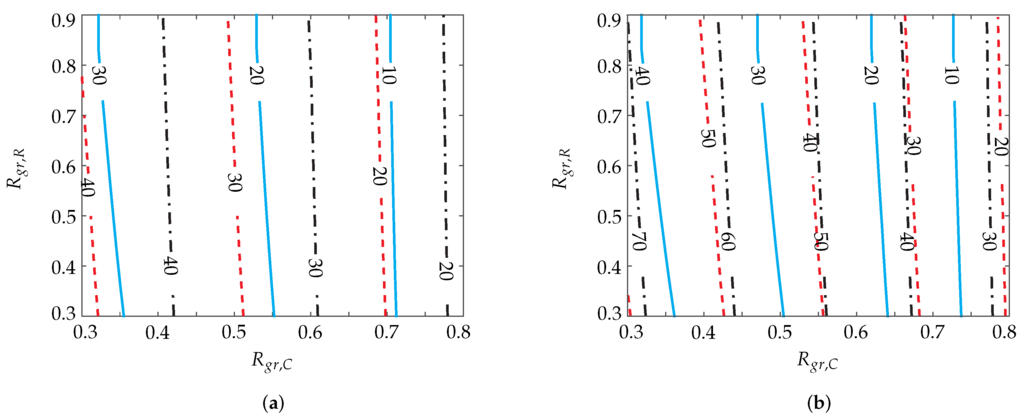
Figure 5.
PPR frequency map as a function of the maximum central grating reflectivity and the maximum right grating reflectivity , for active section lengths (a) and (b). Three values of the grating coupling coefficient are considered: (continuous lines), (dashed lines) and (dashed-dotted lines); the labels on the lines report the PPR frequency. The left grating maximum reflectivity is 90%.
The previous analysis has been repeated also for different lengths of the two sections () while keeping constant the total cavity length; the results show a significant reduction of the PPR frequency and an increase of the area of mode competition as long as the master cavity length is reduced. In the following, we therefore present results only for the case of equal cavity lengths.
To quantitatively highlight the fundamental role of the central grating reflectivity on the , the map in Figure 5 shows its value when and are varied for a constant value of and two values of the cavity lengths and . The estimated values of show a large independence from and a significant dependence on κ due to the change of the effective grating length for a given value.
3. Dynamic Characteristics
Recently, the small signal properties of the two integrated DBR laser structures have been analyzed using composite mode theory [27,28] and also experimentally realized and characterized [28,29] with respect to their small signal modulation response.
In this section, we report the results of the dynamic simulations using our FDTW numerical code [31]. These simulations have as objectives the verification of operation conditions showing the presence of the PPR in the small signal modulation response to confirm the results of the previous static design procedure in Section 2, but they also aim to show the existence of extended modulation bandwidth conditions allowing digital data transmission at a higher bit-rate with respect to one obtainable in single-cavity DBR lasers realized with the same active material.
More details about the implemented FTDW method are presented in Appendix A2.
As highlighted in Figure 2 and in Figure 3, a fine tuning of the longitudinal cavity modes’ position obtained varying the phase is generally required in order to obtain the modulation bandwidth enhancement. In real devices, this tuning is generally accomplished using the phase-control sections currents and (Figure 1a). In the following simulations, for consistency with the presented analysis at threshold and in order to simplify the results interpretations, we simply represented the phase tuning adding a phase to the electric field propagating in the slave laser section (Figure 1b).
We simulated the six laser cavities that we indicated with markers in Figure 4’s maps. We have chosen cavities with a PPR around 35 , and between the various options, we considered the cases with short cavity lengths to limit the parasitic effects. Furthermore, we have decided to operate with cavity parameters granting only a limited number of longitudinal modes in the main reflectivity lobe, allowing the use, for realization simplicity, of an output cleaved facet. The material and the waveguide parameters used in the simulation are reported in Table 1; the values have been chosen in agreement with [27].
For all of the considered structures, when varying the tuning phase, the obtained modulation results present a very similar behavior with respect to the injected currents in the active sections. In the map in Figure 6a, we summarize this behavior as a function of the currents and normalized with respect to the threshold currents and of the master and slave lasers in isolation: the former is composed of the left grating, the master active region and the central grating, while the latter is defined as the central grating, the slave active section and the right cleaved facet.
In the upper part of the map (Region (A)), in the considered structures, we obtained typically self-sustained relaxation oscillations (RO) as described, e.g., in [32] for lasers with feedback. In this region, sinusoidal self-pulsations (SP) can generally be found over wide ranges of the tuning phase when the currents in the two active sections are properly chosen: in the two examples shown in Figure 7, we report two cases of SP found when the two active section currents are the same and for two values of the phase control currents. The phase control allows one to shift the oscillation frequency from a minimum value corresponding to the PPR frequency obtained in the previously-reported design procedure to higher values. The results show in both cases the possibility to obtain a good extinction ratio and narrow RF spectra.
In Region (B), single mode operation has been typically obtained changing the control phase; examples of the corresponding small signal modulation characteristics have been reported in Figure 6b. Obviously, these operation conditions are not suitable for the extended digital modulation we are looking for.
The single mode behavior in continuous wave (CW) is also obtained in Region (D) of higher slave injection current, over a wide range of the control phase; in this region, however, the modulation results shown in Figure 6d clearly show that a large signal modulation bandwidth extension can be obtained for some values of the tuning phase .
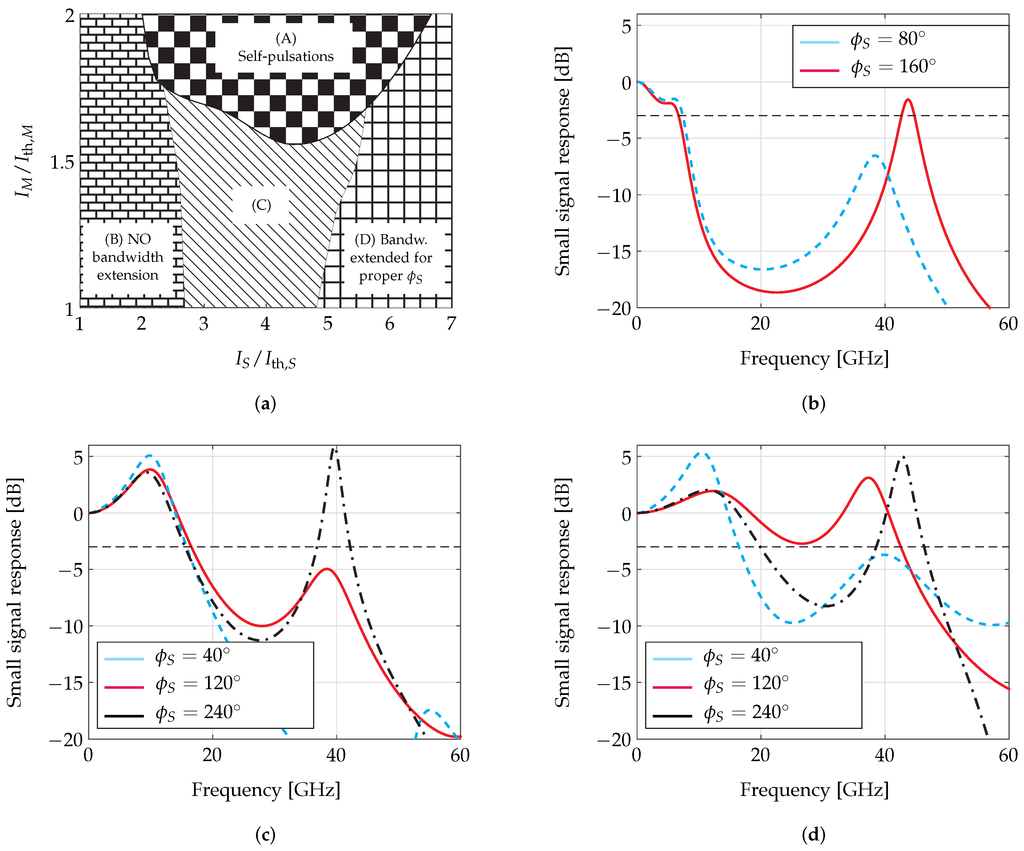
Figure 6.
(a) Map in the normalized master and slave active sections’ current plane indicating the four typical dynamic behaviors found tuning the phase control . Examples of the typical small signal modulation response obtained with different values of in the B, C, D regions are reported in (b,c,d) of this figure for the structure characterized by the red square marker in Figure 4b. The horizontal dashed lines represent the dB level for the modulation response.
In Region (C), the operation condition in between those previously described in Regions (B) and (D) is obtained as shown in Figure 6c. The dashed modulation curve for in Figure 6c represents an operation condition whose response is practically equal to that of a corresponding single-section DBR laser; the effect of the coupled cavity DBR configuration can be directly obtained comparing the other results with this one. Furthermore, we put in evidence that the borders between the various regions are “soft” in the sense that one should consider a gradual transition of the laser behavior from Regions (B), (C) and (D). A sharper transition has been typically found at the borders with Region (A).
We discuss now for brevity only the dynamic simulation results obtained for one of the six structures indicated with markers in Figure 4: the laser cavity indicated with a squared marker in Figure 4b, with , , , , the right facet as cleaved and having a threshold current density . For this laser, we report in detail the results obtained only for bias points in Region (D) of Figure 6a and allowing high speed large signal modulation.
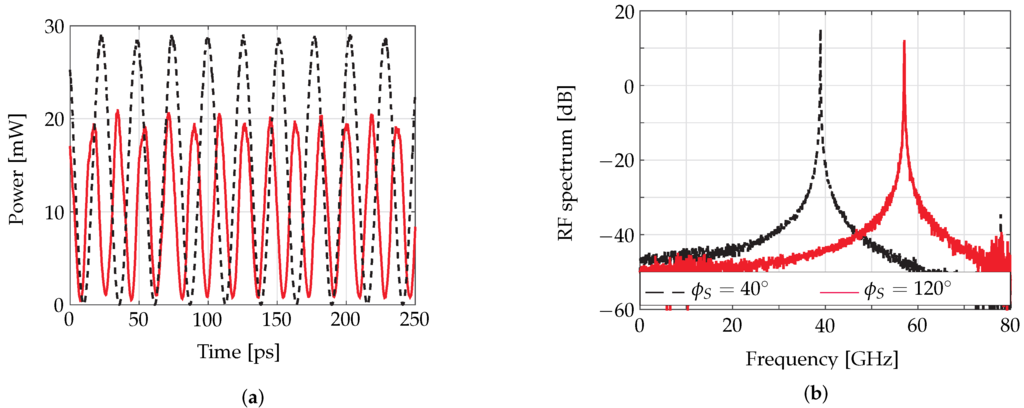
Figure 7.
Two examples of sinusoidal the self-pulsation (SP) operation in Region (A) of Figure 6a for for two different values of : (a) the time domain signals and (b) the corresponding RF spectrum. The dashed black line () is used for the minimum value of the PPR frequency , while the continuous red line () is used for the case .
The small signal modulation results are show in Figure 8’s color map, where the modulation frequency is reported in the abscissa, while the ordinates indicate the static phase change in the slave section used to tune the position of the cavity modes to obtain an operation condition allowing the extension of the modulation bandwidth.
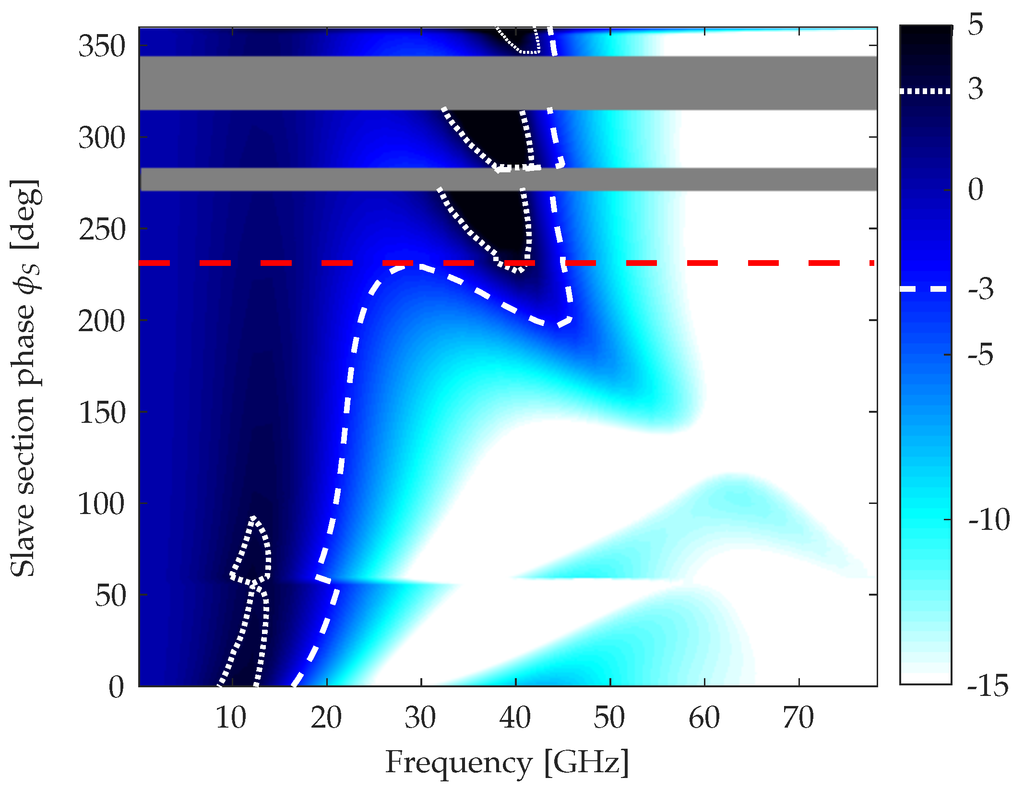
Figure 8.
Modulation response map, in dB, for the device indicated by the red square marker in Figure 4b, with, in the ordinate, the tuning phase shift introduced in the slave optical cavity. The output power is approximately 25 ; , . Contour lines indicate -3 dB (dashed line) and +3 dB (dotted line) levels of the modulation response. The red dashed horizontal line indicates the operation condition chosen for the large signal simulation.
The two gray horizontal strips in the map represent regions with self-sustained RO similar to those in Region (A) shown in Figure 6, but with a smaller extinction ratio corresponding to the presence of a mode in the optical spectrum with a side mode suppression ratio greater than 20 dB. In these operation conditions, the large signal modulation eye diagram is practically close also for a low bit rate. The blue “horn” pointing to the lower part of the map shows the effect of the presence of PPR on the modulation response; for high frequency PPR, the resonance peak is weak and becomes stronger as the mode separation decreases. In the lower part of the map, this effect does not appear, because in this range of phases , the closest side mode is on the shorter wavelength side with respect to the lasing mode: in this condition, the PPR effect does not take place [12].

Table 1.
Main material parameters used for the FDTW simulations.
| Symbol | Description | Value |
|---|---|---|
| Effective refractive index | 3.2 | |
| Group velocity | 8.3 × 107 m/s | |
| Transversal optical confinement factor | 10% | |
| Carrier density at transparency | 1 × 1018 cm−3 | |
| Active region differential gain | 13 × 10−16 cm2 | |
| Material intrinsic losses | 10 cm−1 | |
| Bragg wavelength | 1.550 | |
| Linewidth enhancement factor | 3 | |
| ε | Non-linear gain compression factor | 5 × 10−17 cm3 |
| A | Mono-molecular recombination coefficient | 1.4 ns−1 |
| B | Bi-molecular recombination coefficient | 0.1 cm3 ns−1 |
| C | Auger recombination coefficient | 7.5 cm6 ns−1 |
The horizontal discontinuities appearing in the lower part of the modulation response when varying the tuning phase, as for example at in Figure 8, are associated with longitudinal mode jumps. This behavior highlights the importance of limiting the number of longitudinal modes inside the main lobe of the reflectivity peak.
For the value of the slave cavity phase highlighted by the red dashed horizontal line, where the modulation bandwidth is extended with not a too high resonance peak, the value of the PPR frequency is around 40 , in good agreement with the value used to choose the cavity parameters from the map in Figure 4; this result, valid for all of the simulated devices, confirms the reliability of the proposed design procedure based on the PPR analysis at threshold.
The laser operation condition in Figure 8 was considered for the large signal modulation analysis using an FDTW approach. For this analysis, the master section current was kept constant, and a NRZ pseudo-random bit sequence (PRBS) composed of bits was applied to the slave section, and the slave section phase was set to in order to take advantage of the bandwidth extension provided by the PPR effect.
Results are presented as eye diagrams in Figure 9. For each eye, on the right axes, we report the output power P, while on the left vertical axes, we indicate P normalized with respect to the bit “0” and “1” levels and : . In order to allow for an easy estimation of the eyes opening, in the figure, we also report the limits for optical transmission systems indicated by the IEEE P802.3ba standard [33].
As expected, the results reported in Figure 9a,b show that open eyes can be obtained using a 40 Gbit/s bit-rate when dB (a) and dB (b). Similar results were obtained in a wide range from to of the tuning phase shift . For a large-scale deployment of these devices, a control electronic circuit with a lookup table could be used for the correct selection of the currents in the phase control regions to ensure this extended modulation bandwidth operation.
We then increased the bit-rate and found that, with respect to the considered mask, the upper limit allowed one to obtain an open eye diagram as 60 Gbit/s when operating with dB (c) and 80 Gbit/s when dB (d), which indicates an extension of the modulation frequency well above the CPR frequency. These results were obtained in a significantly reduced range of the tuning phase shift extending from to . The eyes are closed for any value of when higher bit rates are used.
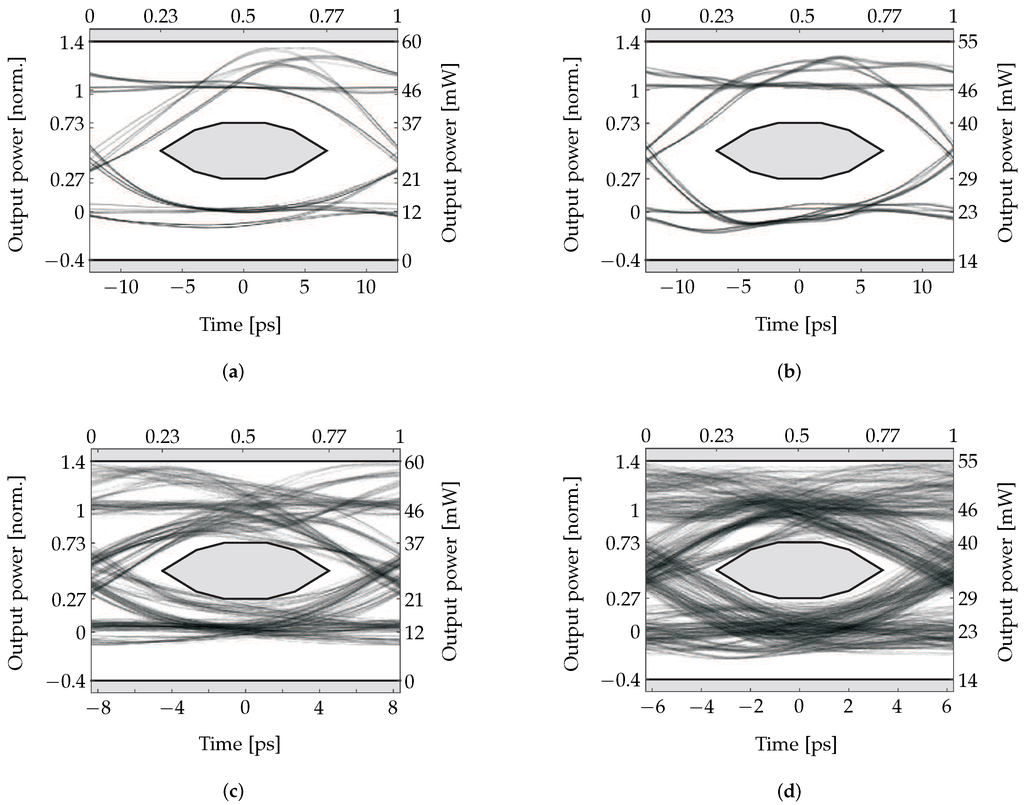
Figure 9.
Eye diagrams for the operation condition considered in Figure 8 using , computed with a bits-long non-return-to-zero (NRZ) pseudo-random bit sequence (PRBS) sequence. The master section current is fixed (), while the slave section current is modulated from (corresponding to the logic “0” level) to (corresponding to the logic “1” level). (a) , , corresponding to a 6 modulation amplitude, with a 40 Gbit/s bitrate, increases to 60 Gbit/s in (c). (b) , , corresponding to a 3 dB modulation amplitude, with a 40 Gbit/s bitrate, increased to 80 Gbit/s in (d).
4. Conclusions
We proposed a design procedure to exploit the PPR effect in an integrated device composed of two mutually-coupled DBR lasers. The design maps, obtained using the transmission matrix method, allow for an optimal combination of the cavity parameters once the required bandwidth extension and the technological aspects have been defined.
A detailed investigation of the dynamics of this structure using an FDTW simulator over a wide range of the bias conditions allows one to obtain a tunable self-pulsating signal with a good extinction ratio and extended modulation conditions in the range of the proposed design procedure. The approach gives the cavity modes’ position, resulting in an increase of the −3 dB modulation bandwidth thanks to the PPR peak appearing close to the design frequency. Finally, the large signal modulations with PRBS signals allowed one to obtain eye diagrams, which are open up to .
Acknowledgments
This work is partially supported by the Sandia LDRD program, funded by the U.S. Department of Energy under Contract No. DE-AC04-94AL85000 and by the EU FP7 project “Development of low-cost technologies for the fabrication of high-performance telecommunication lasers” (DeLight) under Grant 224366.
Author Contributions
W.W.C. proposed the mutually injected DBR lasers device investigated in the paper; P.B. implemented the numerical methods and the analysis tools, and performed the simulations; P.B. and I.M. analyzed the simulation results; P.B., W.W.C. and I.M. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
A1. Transmission Matrix Model
The transmission matrix of a generic passive section with a Bragg grating can be written as [34]:
where , , L is the section length, κ is the grating coupling coefficient, are the intrinsic material losses, is the wavelength dependent effective index and, finally, is the Bragg wavelength.
Finally, the equivalent reflectivity can be evaluated [2] as:
with the transmission matrix of the central grating section and and the complex propagation constants of the master and slave sections, respectively. In Equation (A1), is a phase term included to control in the simulations the effects due to tuning in the slave section, which can be experimentally accomplished with a fine tuning of the passive section current ; is the reflectivity indicated in Figure 1b, being the transmission matrix of the master cavity output grating.
The equivalent reflectivity is simply , with the transmission matrix of the slave cavity output grating.
A2. Finite Difference Traveling Wave Model
In our FDTW model, we just consider the slowly-varying forward () and backward () components of the electric cavity field :
where , and are the pitch, the Bragg wavelength and the effective refractive index of the grating sections, respectively, and .
The electric fields and are normalized in such a way that the photon density is ; in the master and slave regions, they are coupled with the carrier density () rate equation, yielding the system:
where is the group velocity, are the material optical losses, is the spontaneous emission term, is the injected current density, A, B, C are carriers recombination parameters, is the transversal optical confinement factor and ε is the non-linear gain compression factor.
In Equation (A2), the variation of the effective refractive index is represented as , with the linewidth enhancement factor; we consider a linear dependence of the material gain with the carrier density, , with differential gain and carrier density at transparency.
For the gratings regions, we include the coupling between and :
References
- De Valicourt, G.; Levaufre, G.; Pointurier, Y.; Le Liepvre, A.; Antona, J.C.; Jany, C.; Accard, A.; Lelarge, F.; Make, D.; Duan, G.H. Direct Modulation of Hybrid Integrated InP/Si Transmitters for short and long reach access network. J. Lightw. Technol. 2015, 33, 1608–1616. [Google Scholar] [CrossRef]
- Coldren, L.A.; Corzine, S.W.; Maǎnović, M.L. Diode Lasers and Photonic Integrated Circuits; Wiley: New York, NY, USA, 2012. [Google Scholar]
- Montrosset, I.; Bardella, P. Laser dynamics providing enhanced-modulation bandwidth. Proc. SPIE 2014, 9134. [Google Scholar] [CrossRef]
- Vahala, K.; Yariv, A. Detuned loading in coupled cavity semiconductor lasers—effect on quantum noise and dynamics. Appl. Phys. Lett. 1984, 45, 501–503. [Google Scholar] [CrossRef]
- Vahala, K.; Paslaski, J.; Yariv, A. Observation of modulation speed enhancement, frequency modulation suppression, and phase noise reduction by detuned loading in a coupled-cavity semiconductor laser. Appl. Phys. Lett. 1985, 46, 1025–1027. [Google Scholar] [CrossRef]
- Feiste, U. Optimization of modulation bandwidth in DBR lasers with detuned Bragg reflectors. IEEE J. Quant. Electron. 1998, 34, 2371–2379. [Google Scholar] [CrossRef]
- Kjebon, O.; Schatz, R.; Lourdudoss, S.; Nilsson, S.; StAlnacke, B.; Backbom, L. Two–section InGaAsP DBR-lasers at 1.55 μm wavelength with 31 GHz direct modulation bandwidth. In Proceedings of the International Conference on Indium Phosphide and Related Materials, Hyannis, MA, USA, 11–15 May 1997; pp. 665–668.
- Chaciński, M.; Schatz, R. Impact of Losses in the Bragg Section on the Dynamics of Detuned Loaded DBR Lasers. IEEE J. Quant. Electron. 2010, 46, 1360–1367. [Google Scholar] [CrossRef]
- Pan, X.; Olesen, H.; Tromborg, B. Modulation characteristics of tunable DFB/DBR lasers with one or two passive tuning sections. IEEE J. Quant. Electron. 1989, 25, 1254–1260. [Google Scholar] [CrossRef]
- Kjebon, O.; Schatz, R.; Lourdudoss, S.; Nilsson, S.; StAlnacke, B.; Backbom, L. 30 GHz direct modulation bandwidth in detuned loaded InGaAsP DBR lasers at 1.55 μm wavelength. Electron. Lett. 1997, 33, 488–489. [Google Scholar] [CrossRef]
- Bach, L.; Kaiser, W.; Reithmaier, J.P.; Forchel, A.; Berg, T.; Tromborg, B. Enhanced direct–modulated bandwidth of 37 GHz by a multi–section laser with a coupled–cavity–injection–grating design. Electron. Lett. 2003, 39, 1592–1593. [Google Scholar] [CrossRef]
- Bardella, P.; Montrosset, I. A New Design Procedure for DBR Lasers Exploiting the Photon–Photon Resonance to Achieve Extended Modulation Bandwidth. IEEE J. Sel. Top. Quant. Electron. 2013, 19. [Google Scholar] [CrossRef]
- Reithmaier, J.P.; Kaiser, W.; Bach, L.; Forchel, A.; Feies, V.; Gioannini, M.; Montrosset, I.; Berg, T.; Tromborg, B. Modulation speed enhancement by coupling to higher order resonances: a road towards 40 GHz bandwidth lasers on InP. In Proceedings of 2005 International Conference on Indium Phosphide and Related Materials, Glasgow, UK, 8–12 May 2005; pp. 118–123.
- Reithmaier, J.; Bach, L.; Kaiser, W. Multisectional Laser. US Patent 7,570,681, 2009. [Google Scholar]
- Gerschütz, F.; Fischer, M.; Koeth, J.; Krestnikov, I.; Kovsh, A.; Schilling, C.; Kaiser, W.; Höfling, S.; Forchel, A. 1.3 μm Quantum Dot Laser in coupled-cavity-injection-grating design with bandwidth of 20 GHz under direct modulation. Opt. Express 2008, 16, 5596–5601. [Google Scholar] [CrossRef] [PubMed]
- Vallone, M.; Bardella, P.; Montrosset, I. Enhanced Modulation Bandwidth in Complex Cavity Injection Grating Lasers. IEEE J. Quant. Electron. 2011, 47, 1269–1276. [Google Scholar] [CrossRef]
- Radziunas, M.; Glitzky, A.; Bandelow, U.; Wolfrum, M.; Troppenz, U.; Kreissl, J.; Rehbein, W. Improving the Modulation Bandwidth in Semiconductor Lasers by Passive Feedback. IEEE J. Sel. Top. Quant. Electron. 2007, 13, 136–142. [Google Scholar] [CrossRef]
- Morthier, G.; Schatz, R.; Kjebon, O. Extended modulation bandwidth of DBR and external cavity lasers by utilizing a cavity resonance for equalization. IEEE J. Quant. Electron. 2000, 36, 1468–1475. [Google Scholar] [CrossRef]
- Grillot, F.; Wang, C.; Naderi, N.; Even, J. Modulation Properties of Self-Injected Quantum-Dot Semiconductor Diode Lasers. IEEE J. Sel. Top. Quant. Electron. 2013, 19. [Google Scholar] [CrossRef]
- Simpson, T.B.; Liu, J.; Gavrielides, A. Bandwidth enhancement and broadband noise reduction in injection-locked semiconductor lasers. IEEE Photonics Technol. Lett. 1995, 7, 709–711. [Google Scholar] [CrossRef]
- Murakami, A.; Kawashima, K.; Atsuki, K. Cavity resonance shift and bandwidth enhancement in semiconductor lasers with strong light injection. IEEE J. Quant. Electron. 2003, 39, 1196–1204. [Google Scholar] [CrossRef]
- Lau, E.; Wong, L.J.; Wu, M. Enhanced Modulation Characteristics of Optical Injection-Locked Lasers: A Tutorial. IEEE J. Sel. Top. Quant. Electron. 2009, 15, 618–633. [Google Scholar] [CrossRef]
- Enard, A.; Resneau, P.; Calligaro, M.; Parillaud, O.; Krakowski, M.; Vallone, M.; Bardella, P.; Montrosset, I. Mode locking and bandwidth enhancement in single section ridge laser with two spatial modes. In Proceedings of the 22nd IEEE International Semiconductor Laser Conference (ISLC), Kyoto, Japan, 26–30 September 2010; pp. 113–114.
- Dalir, H.; Koyama, F. High-speed operation of bow-tie-shaped oxide aperture VCSELs with photon–photon resonance. Appl. Phys. Express 2014, 7. [Google Scholar] [CrossRef]
- Dalir, H.; Koyama, F. Highly stable operations of transverse-coupled cavity VCSELs with enhanced modulation bandwidth. Electron. Lett. 2014, 50, 823–824. [Google Scholar] [CrossRef]
- Gerschütz, F.; Fischer, M.; Koeth, J.; Krestnikov, I.; Kovsh, A.; Schilling, C.; Kaiser, W.; Höfling, S.; Forchel, A. 1.3 μm Quantum Dot Laser in coupled-cavity-injection-grating design with bandwidth of 20 GHz under direct modulation. Opt. Express 2008, 16, 5596–5601. [Google Scholar] [CrossRef] [PubMed]
- Chow, W.; Yang, Z.; Vawter, G.; Skogen, E. Modulation response improvement with isolator-free injection-locking. IEEE Photonics Technol. Lett. 2009, 21, 839–841. [Google Scholar] [CrossRef]
- Yang, Z.; Tauke-Pedretti, A.; Vawter, G.; Chow, W. Mechanism for Modulation Response Improvement in Mutually Injection-Locked Semiconductor Lasers. IEEE J. Quant. Electron. 2011, 47, 300–305. [Google Scholar] [CrossRef]
- Tauke-Pedretti, A.; Vawter, G.; Skogen, E.; Peake, G.; Overberg, M.; Alford, C.; Chow, W.; Yang, Z.; Torres, D.; Cajas, F. Mutual Injection Locking of Monolithically Integrated Coupled-Cavity DBR Lasers. IEEE Photonics Technol. Lett. 2011, 23, 908–910. [Google Scholar] [CrossRef]
- Tauke-Pedretti, A.; Skogen, E.; Vawter, G.; Chow, W. Mutually Injection Locked Lasers for Enhanced Frequency Eesponse. US Patent 8,687,665, 2014. [Google Scholar]
- Bardella, P.; Montrosset, I. Analysis of self-pulsating three–section DBR lasers. IEEE J. Sel. Top. Quant. Electron. 2005, 11, 361–366. [Google Scholar] [CrossRef]
- Mork, J.; Tromborg, B.; Mark, J. Chaos in semiconductor lasers with optical feedback: Theory and experiment. IEEE J. Quant. Electron. 1992, 28, 93–108. [Google Scholar] [CrossRef]
- 802.3-2008 IEEE Standard for Information Technology-Specific Requirements-Part 3: Carrier Sense Multiple Access with Collision Detection (CMSA/CD) Access Method and Physical Layer Specifications. Available online: http://ieeexplore.ieee.org/servlet/opac?punumber=4726157 (accessed on 29 December 2015).
- Bonello, R.; Montrosset, I. Analysis of multisection and multielectrode semiconductor lasers. J. Lightw. Technol. 1992, 10, 1890–1900. [Google Scholar] [CrossRef]
- Kim, B.S.; Chung, Y.; Lee, J.S. An efficient split-step time-domain dynamic modeling of DFB/DBR laser diodes. IEEE J. Quantum Electron. 2000, 36, 787–794. [Google Scholar]
- Jones, D.J.; Zhang, L.; Carroll, J.; Marcenac, D.D. Dynamics of monolithic passively mode-locked semiconductor lasers. IEEE J. Quantum Electron. 1995, 31, 1051–1058. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).