1. Introduction
In the last fifteen years, intense efforts have been devoted to the investigation of man-made artificial materials or metamaterials [
1,
2]. Metamaterials are attractive because they possess a rich variety of electromagnetic constitutive parameters, such as electric permittivity, magnetic permeability, and bianisotropy, all of which can be tailored by their geometry [
3,
4,
5]. For example, metamaterials have made transformation optics possible by providing a blueprint for the realization of anisotropic, inhomogeneous, and graded electromagnetic properties [
6,
7]. To date, almost all metamaterials investigated have been periodic. Indeed, periodicity not only simplifies the simulation of metamaterials but also their fabrication. However, at optical frequencies, current top-down fabrication technologies, such as electron-beam lithography, are very costly, intrinsically planar, and not compatible with large scale-devices. Bottom-up fabrication technologies could alleviate part of this problem but suffer from limitations of their own, namely the absence of long-range order [
8], even though they’ve made strides in recent years [
9]. Therefore, to leverage bottom-up fabrication technologies and go towards three-dimensional, large-scale devices, it is necessary to develop novel tools for a thorough understanding of disordered metamaterials [
10,
11].
Metamaterials electromagnetic properties have most often been investigated using parameter retrieval,
i.e., they were computed from reflection and transmission coefficients of periodic arrays [
12]. However, this approach is no longer possible for disordered metamaterials. To overcome this difficulty, another approach to metamaterials is needed. For instance, metamaterials can be seen as a collection of essential building blocks, also referred to as meta-atoms, which support different multipoles: electric dipoles, magnetic dipoles, as well as higher-order multipoles [
13]. From this perspective, it is the induction of this microscopic polarization and magnetization that gives rise to macroscopic effective properties, such as electric permittivity, magnetic permeability, or bianisotropy [
14]. Then, a natural and versatile method of considering the electromagnetic properties of disordered metamaterials consists of computing the intrinsic multipoles of meta-atoms and complement those with a mixing law [
15]. Investigations of individual meta-atoms thus represent a required stepping stone towards the engineering of disordered metamaterials.
Split-ring resonators are one of the essential building blocks of metamaterials. They have been used in the first experimental demonstrations to obtain negative permeability and negative index and, more recently, in magnetic resonance imaging and cloaking [
16,
17]. The first investigations of one-gap split-ring resonators were essentially focused on their fundamental resonance due to their resonant magnetic response. It was referred to as an LC resonance, in analogy with electrical engineering practice, because the gap and ring were seen as a capacitance (C) and inductance (L), respectively [
18]. With the transition to optics, however, it was soon realized that all resonances can be interpreted within the unified framework of plasmonic, standing-wave resonances [
19,
20]. In such models, split-rings are essentially viewed as thin plasmonic films that are truncated into a wire and bent into a split-ring [
21]. Other investigations focused on the properties of multi-gap split-ring resonators and their coupling effects [
22], most notably to extend the operating range of one-gap split-rings because of its saturation-imposed limits at optical frequencies [
23]. A similar plasmonic, standing-wave picture was shown to apply to multi-gap split-rings as well [
24]. In addition, it was recently shown that one-gap split-ring resonators are possible platforms for the realization of random metamaterials with a negative index due to the inherent superposition of their intrinsic electric and magnetic dipoles [
25].
In this paper, we go one step further and investigate the multipoles of split-ring resonators with an odd or even number of gaps (from one to four gaps) and show that electric and magnetic dipoles are always degenerate in the odd case, while that is only accidentally true in the even case. We present extensive numerical evidence to support this claim, namely multipole coefficients of individual split-ring resonators retrieved from full-wave simulations, and thus shed light on the effective properties of disordered metamaterials.
3. From 1-SRR to 4-SRR
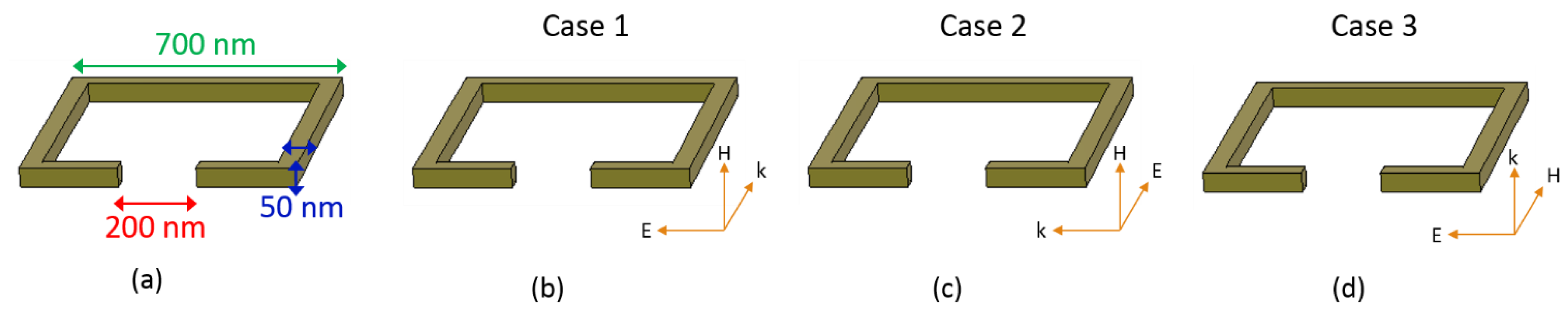
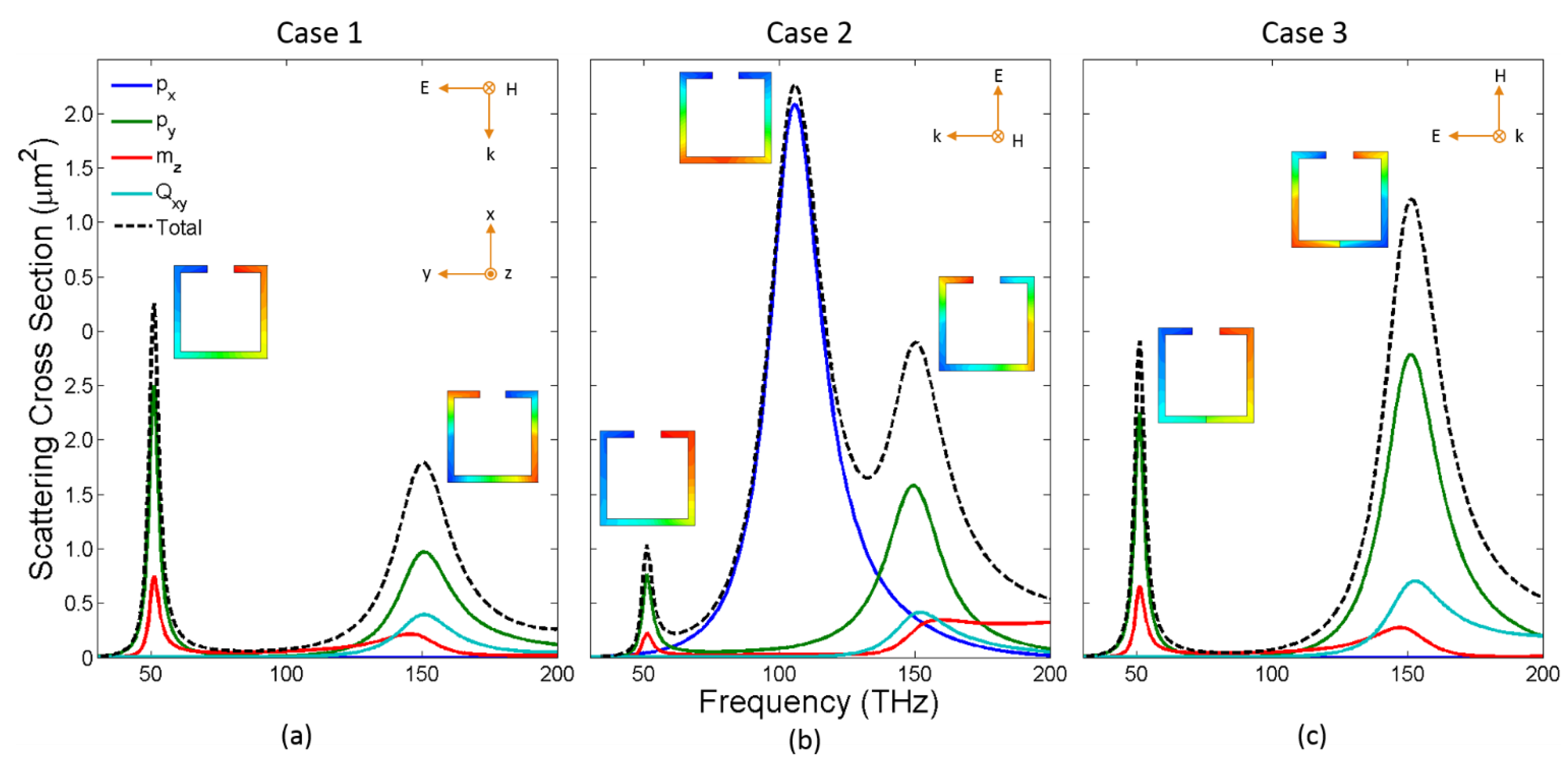
We plot in
Figure 2 the different scattering cross-sections (electric dipole, magnetic dipole, electric quadrupole, and total) of the 1-SRR for the three different cases defined in
Figure 1. In case 1, only modes that are even with respect to the
xy-plane and odd with respect to the
xz-plane can be excited. In case 2, only the former symmetry holds true, while in case 3, only the latter symmetry holds true. Due to these symmetry constraints, the electric dipole,
px, cannot be excited in cases 1 and 3. As can be seen in
Figure 2, in all three cases there are two resonances that are always excited (f
1 = 51 THz, f
3 = 151 THz) while in the second case there is also an additional resonance (f
2 = 106 THz). Resonance 2 is due to the excitation of the electric dipole,
px. Resonances 1 and 3 can be excited either by the electric field along the gap, or the magnetic field normal to the plane of SRR, or a combination of both, and yield both an electric dipole,
py, and a magnetic dipole,
mz, response. In addition, resonance 3 shows an in-plane quadrupole,
Qxy, response. Surprisingly, when both fields are present with the right polarization (case 1), their effects do cumulate for resonance 1 but not for resonance 3. This would seem to indicate that case 3 is the most favorable to multipole overlap but, in a planar configuration, the magnetic dipole,
mz, does not radiate in the direction of propagation, thus making case 1 the preferred illumination scenario.
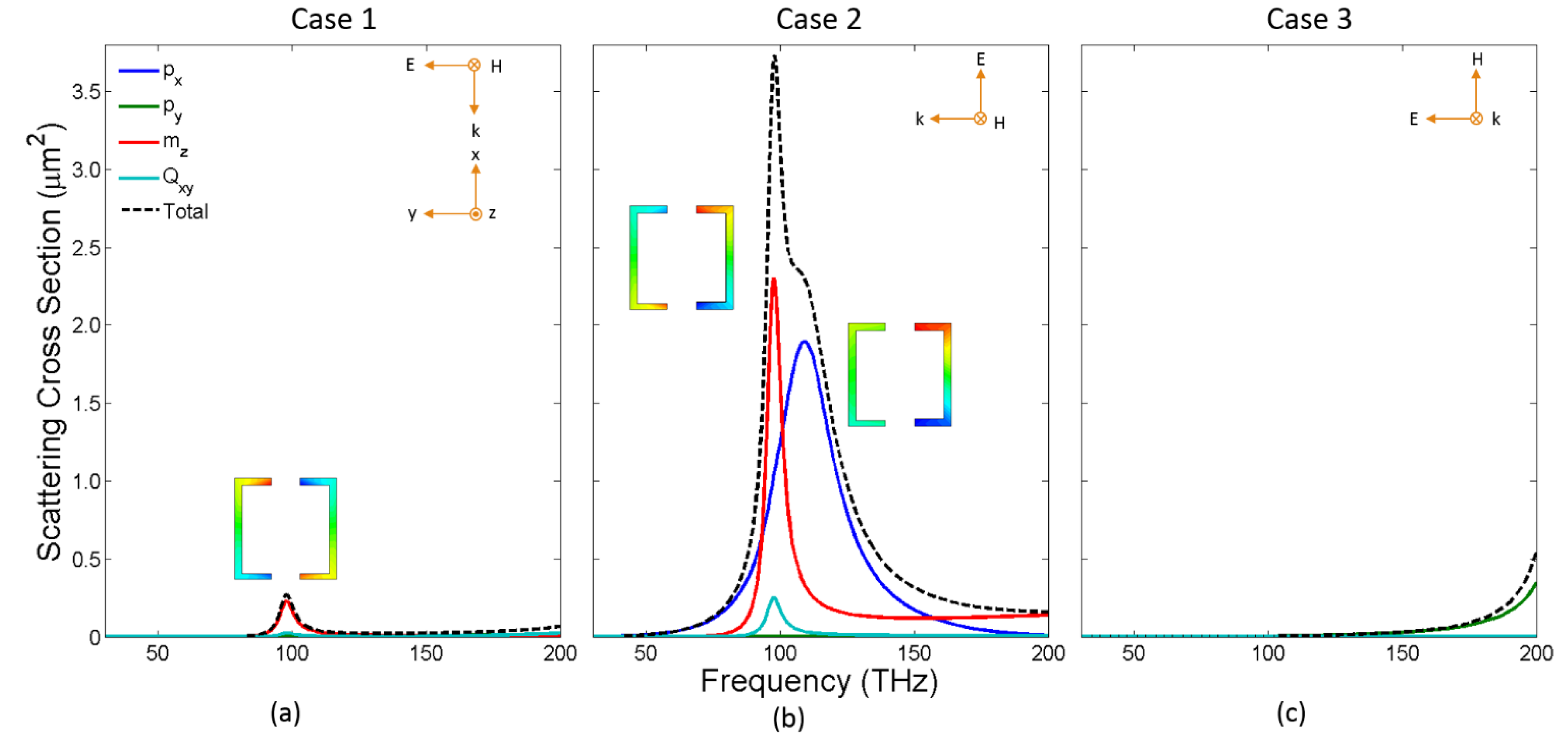
We plot in
Figure 3, the scattering cross-sections of the 2-SRR (even) for the three different cases defined in
Figure 1. We highlight that all further additions of gaps carry the same dimensions of
G = 200 nm centered along a given side of the starting square split-ring (see
Figure 1a). In case 1, only modes that are even with respect to the
xy-plane and odd with respect to the
xz-plane can be excited. In case 2, only modes that are even with respect to the
xy-plane and odd with respect to the
yz-plane can be excited. In case 3, only modes that are even with respect to the
yz-plane and odd with respect to the
xz-plane can be excited. Due to these symmetry constraints, the electric dipole,
px, cannot be excited in cases 1 and 3, the electric dipole,
py, cannot be excited in case 2, and the magnetic dipole,
mz, and electric quadrupole,
Qxy, cannot be excited in case 3. As a result, there can only be an overlap between the electric dipole,
py, and the magnetic dipole,
mz, in case 1. However, as can be seen from
Figure 3, both modes are only weakly excited in this case (f
1 = 98 THz). Unlike the 1-SRR, in case 2, the 2-SRR has a small overlap between the electric dipole,
px, and the magnetic dipole,
mz, (f
1 = 98 THz, f
2 = 106 THz), which could prove useful in the design of novel metamaterials. This overlap is not due to symmetry but rather to the specific dimensions of the 2-SRR considered here and, hence, is accidental. For the 2-SRR, case 2 is the preferred illumination scenario.
Figure 2.
Multipolar decomposition of the scattering cross-section, for a 1-SRR between 30 THz and 200 THz, into the lowest order multipoles; (a) Case 1: electric field in-plane and along the gap, magnetic field out-of-plane; two resonances are observed at f1 = 51 THz and f3 = 151 THz (b) Case 2: electric field in-plane and normal to the gap, magnetic field out-of-plane; three resonances are observed, those observed in case 1 plus another one at f2 = 106 THz due to the excitation of the electric dipole, px (c) Case 3: electric and magnetic fields in-plane, along the gap and normal to it, respectively; two resonances are observed, just as in Case 1. The resonances excited in Case 1 and 3 yield both an electric dipole, py, and a magnetic dipole, mz, response. Resonance 3 also shows an in-plane quadrupole, Qxy, response in all cases. Insets show the real part of Ez at the corresponding resonance frequencies using a rainbow colormap (min in blue, zero in green, and max in red).
Figure 2.
Multipolar decomposition of the scattering cross-section, for a 1-SRR between 30 THz and 200 THz, into the lowest order multipoles; (a) Case 1: electric field in-plane and along the gap, magnetic field out-of-plane; two resonances are observed at f1 = 51 THz and f3 = 151 THz (b) Case 2: electric field in-plane and normal to the gap, magnetic field out-of-plane; three resonances are observed, those observed in case 1 plus another one at f2 = 106 THz due to the excitation of the electric dipole, px (c) Case 3: electric and magnetic fields in-plane, along the gap and normal to it, respectively; two resonances are observed, just as in Case 1. The resonances excited in Case 1 and 3 yield both an electric dipole, py, and a magnetic dipole, mz, response. Resonance 3 also shows an in-plane quadrupole, Qxy, response in all cases. Insets show the real part of Ez at the corresponding resonance frequencies using a rainbow colormap (min in blue, zero in green, and max in red).
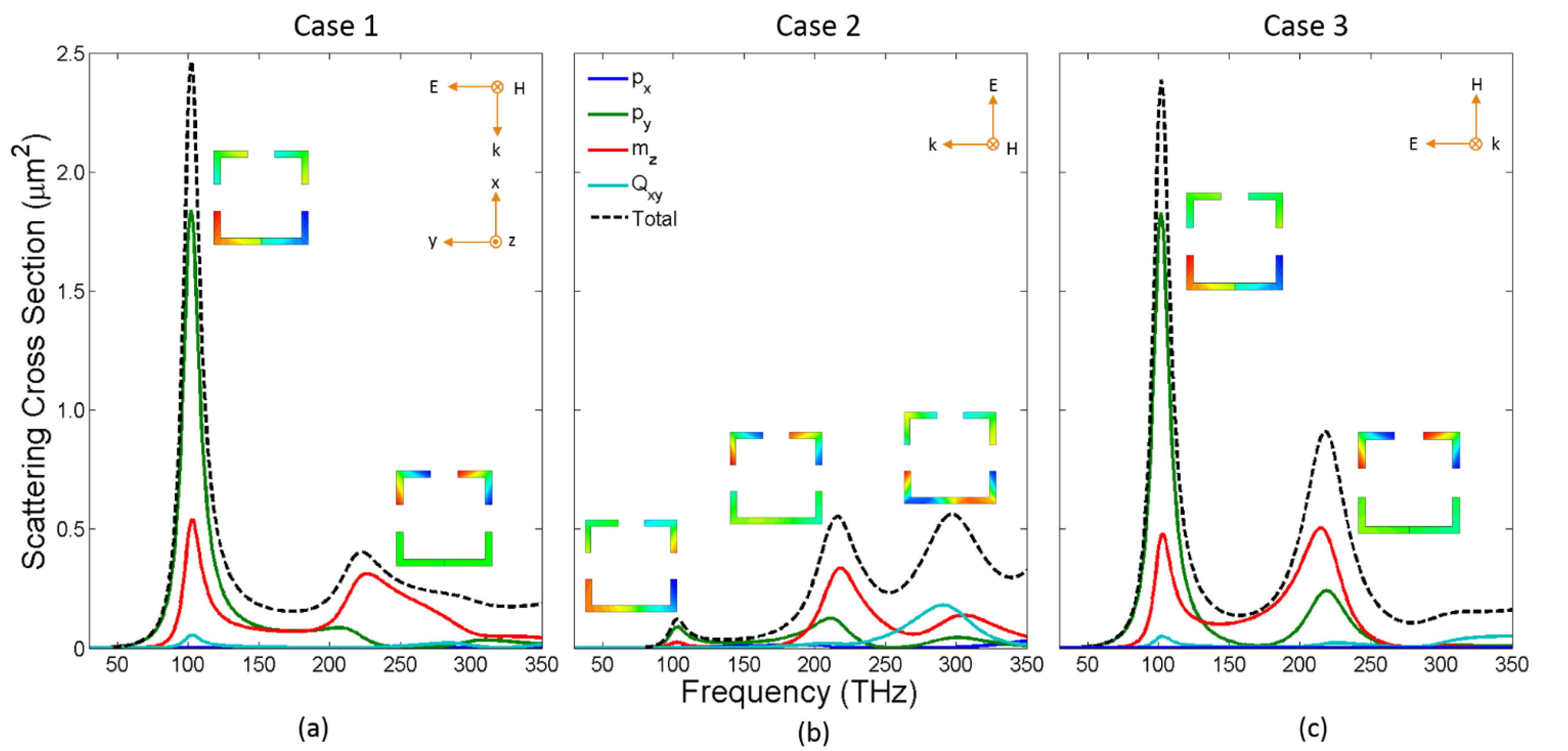
In
Figure 4, we plot the scattering cross-sections of the 3-SRR (odd) for the three cases defined in
Figure 1. The 3-SRR has exactly the same symmetry properties as the 1-SRR, thus exactly the same multipoles are forbidden or allowed. As can be seen in
Figure 4, in all three cases there are two resonances that are always excited (f
1 = 121 THz, f
2 = 219 THz) and, similar to the 1-SRR, when both fields are present with the right polarization (case 1), their effects do cumulate for resonance 1 but not for resonance 2. Furthermore, just as for the 1-SRR, the planar configuration of case 3 is not suitable for multipole overlap as it suffers from a lack of radiation along the direction of propagation. A notable difference for the 3-SRR is that resonance 2 has a much less prominent electric quadrupole,
Qxy, than the 1-SRR. Overall, the 3-SRR is very similar to the 1-SRR, e.g., case 1 is the preferred illumination scenario, with the only important difference being that its resonances occur at higher frequencies.
Figure 3.
Multipolar decomposition of the scattering cross-section, for a 2-SRR between 30 THz and 200 THz, into the lowest order multipoles; (a) Case 1: electric field in-plane and along the gaps, magnetic field out-of-plane; one resonance is observed at f1 = 98 THz. Weak excitation of electric dipole, py, and the magnetic dipole, mz observed. (b) Case 2: electric field in-plane and normal to the gaps, magnetic field out-of-plane; two resonances are observed, that observed in case 1 plus another one at f2 = 106 THz. Small overlap between the electric dipole, px, and the magnetic dipole, mz observed. (c) Case 3: electric and magnetic fields in-plane, along the gaps and normal to them, respectively; no resonances are observed. Insets show the real part of Ez at the corresponding resonance frequencies using a rainbow colormap (min in blue, zero in green, and max in red).
Figure 3.
Multipolar decomposition of the scattering cross-section, for a 2-SRR between 30 THz and 200 THz, into the lowest order multipoles; (a) Case 1: electric field in-plane and along the gaps, magnetic field out-of-plane; one resonance is observed at f1 = 98 THz. Weak excitation of electric dipole, py, and the magnetic dipole, mz observed. (b) Case 2: electric field in-plane and normal to the gaps, magnetic field out-of-plane; two resonances are observed, that observed in case 1 plus another one at f2 = 106 THz. Small overlap between the electric dipole, px, and the magnetic dipole, mz observed. (c) Case 3: electric and magnetic fields in-plane, along the gaps and normal to them, respectively; no resonances are observed. Insets show the real part of Ez at the corresponding resonance frequencies using a rainbow colormap (min in blue, zero in green, and max in red).
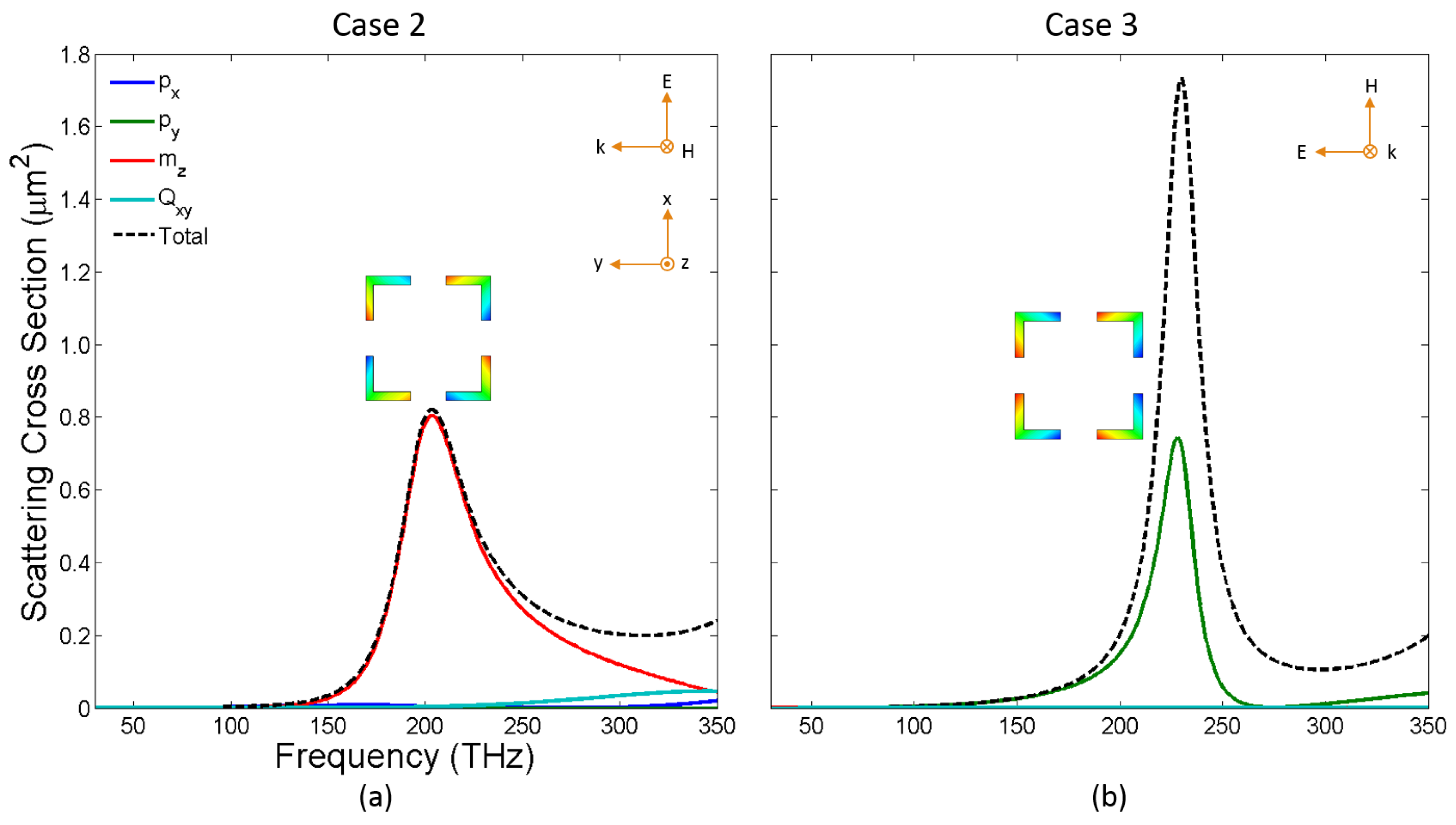
In
Figure 5, we plot the scattering cross-sections of the 4-SRR (even) for the three cases defined in
Figure 1. For this case, case 1 and case 2 are identical due to the symmetry of the 4-SRR and are referred to from here on as case 2. In case 2, only modes that are even with respect to the
xy-plane and odd with respect to the
yz-plane can be excited. In case 3, only modes that are even with respect to the
yz-plane and odd with respect to the
xz-plane can be excited. Due to these symmetry constraints, the electric dipole,
px, cannot be excited in case 3, the electric dipole,
py, cannot be excited in case 2, the magnetic dipole,
mz, and the electric quadrupole,
Qxy, cannot be excited in case 3. As a result, there can only be an overlap between the electric dipole,
px, and the magnetic dipole,
mz, in case 2. However, as can be seen from
Figure 5, only the magnetic dipole,
mz, is strongly excited in this case (f
1=203 THz). For the 4-SRR, there is thus no preferred illumination scenario.
Figure 4.
Multipolar decomposition of the scattering cross-section, for a 3-SRR between 30 THz and 350 THz, into the lowest order multipoles; (a) Case 1: electric field in-plane and along the single gap, magnetic field out-of-plane; two resonances are observed at f1 = 121 THz and f2 = 219 THz (b) Case 2: electric field in-plane and normal to the single gap, magnetic field out-of-plane; three resonances are observed, those observed in case 1 plus another one at f3 = 297 THz (c) Case 3: electric and magnetic fields in-plane, along the single gap and normal to it, respectively; two resonances are observed, just as in case 1. The resonances excited in Case 1 and 3 yield both an electric dipole, py, and a magnetic dipole, mz, response similar to the 1-SRR. Insets show the real part of Ez at the corresponding resonance frequencies using a rainbow colormap (min in blue, zero in green, and max in red).
Figure 4.
Multipolar decomposition of the scattering cross-section, for a 3-SRR between 30 THz and 350 THz, into the lowest order multipoles; (a) Case 1: electric field in-plane and along the single gap, magnetic field out-of-plane; two resonances are observed at f1 = 121 THz and f2 = 219 THz (b) Case 2: electric field in-plane and normal to the single gap, magnetic field out-of-plane; three resonances are observed, those observed in case 1 plus another one at f3 = 297 THz (c) Case 3: electric and magnetic fields in-plane, along the single gap and normal to it, respectively; two resonances are observed, just as in case 1. The resonances excited in Case 1 and 3 yield both an electric dipole, py, and a magnetic dipole, mz, response similar to the 1-SRR. Insets show the real part of Ez at the corresponding resonance frequencies using a rainbow colormap (min in blue, zero in green, and max in red).
Figure 2,
Figure 3,
Figure 4 and
Figure 5 help us paint a portrait of the rich multipolar response of SRRs to electromagnetic radiation. For odd-gap rings (2N + 1-SRR), the fundamental resonance exhibits strong and overlapping electric and magnetic dipole responses regardless of the illumination, while for even-gap rings (2N-SRR), it exhibits a strong magnetic dipole response when the magnetic field is out-of-plane. Hence, the parity of the rings plays a crucial role in SRR’s electromagnetic response, with analogous resonances for the odd-gap rings and even-gap rings.
We have shown that the planar configuration of SRRs, which is the one currently amenable to fabrication in the optical range, is not the best for multipole overlap. This highlights the need to move away from periodic, top-down structures and towards random, bottom-up ones. We note that this can also be achieved using dielectric nanoparticles, such as disk or ring resonators [
28]. Moreover, we also note that recent works have extended investigations of randomness to the field of metasurfaces [
29,
30].
Figure 5.
Multipolar decomposition of the scattering cross-section, for a 4-SRR between 30 THz and 350 THz, into the lowest order multipoles; (a) Case 2: electric field in-plane, magnetic field out-of-plane; one resonance is observed at f1 = 203 THz. Strong magnetic dipole, mz, excitation is observed. (b) Case 3: electric and magnetic fields in-plane; one resonance is observed at f2 = 230 THz. Only electric dipole, py, excitation is observed. Insets show the real part of Ez at the corresponding resonance frequencies using a rainbow colormap (min in blue, zero in green, and max in red).
Figure 5.
Multipolar decomposition of the scattering cross-section, for a 4-SRR between 30 THz and 350 THz, into the lowest order multipoles; (a) Case 2: electric field in-plane, magnetic field out-of-plane; one resonance is observed at f1 = 203 THz. Strong magnetic dipole, mz, excitation is observed. (b) Case 3: electric and magnetic fields in-plane; one resonance is observed at f2 = 230 THz. Only electric dipole, py, excitation is observed. Insets show the real part of Ez at the corresponding resonance frequencies using a rainbow colormap (min in blue, zero in green, and max in red).