Dynamics of a Low-Dimensional Model for Short Pulse Mode Locking
Abstract
:1. Introduction
2. Governing Equations and Reduced Models
2.1. Short Pulse Equation
2.2. Alternative Formulations of Short Pulse Dynamics
2.3. Short Pulse Master Mode Locking Equation
2.4. Reduced Model
3. Phase-Plane Analysis and Stability of Mode Locking
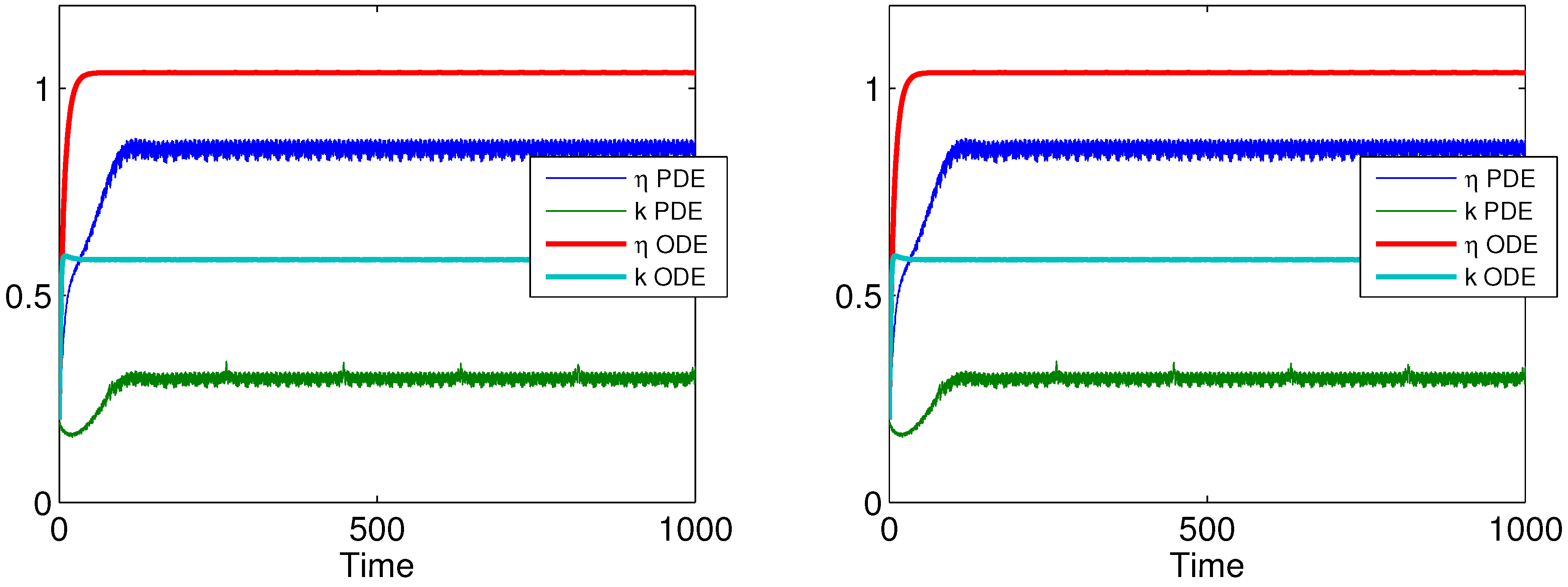
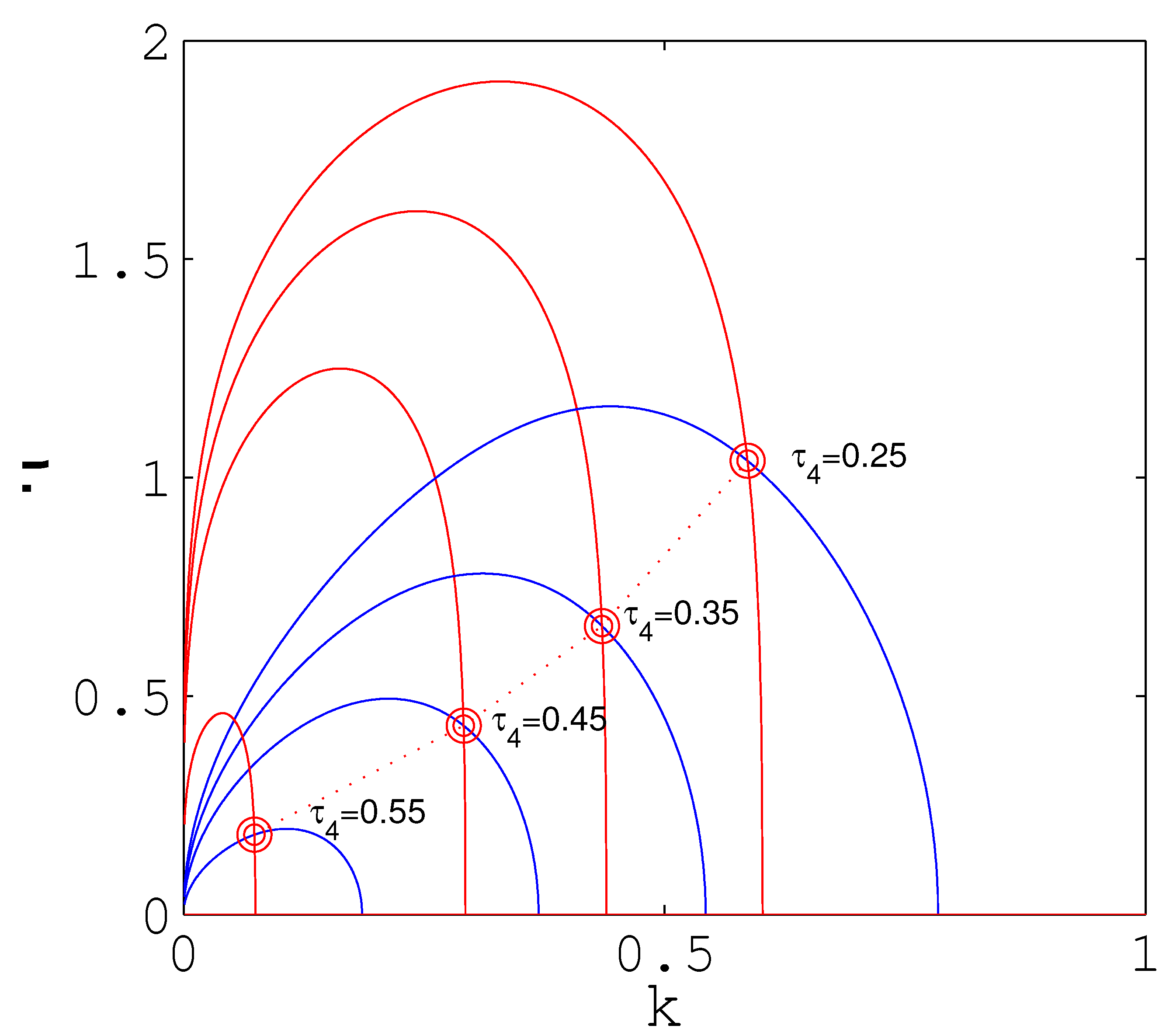
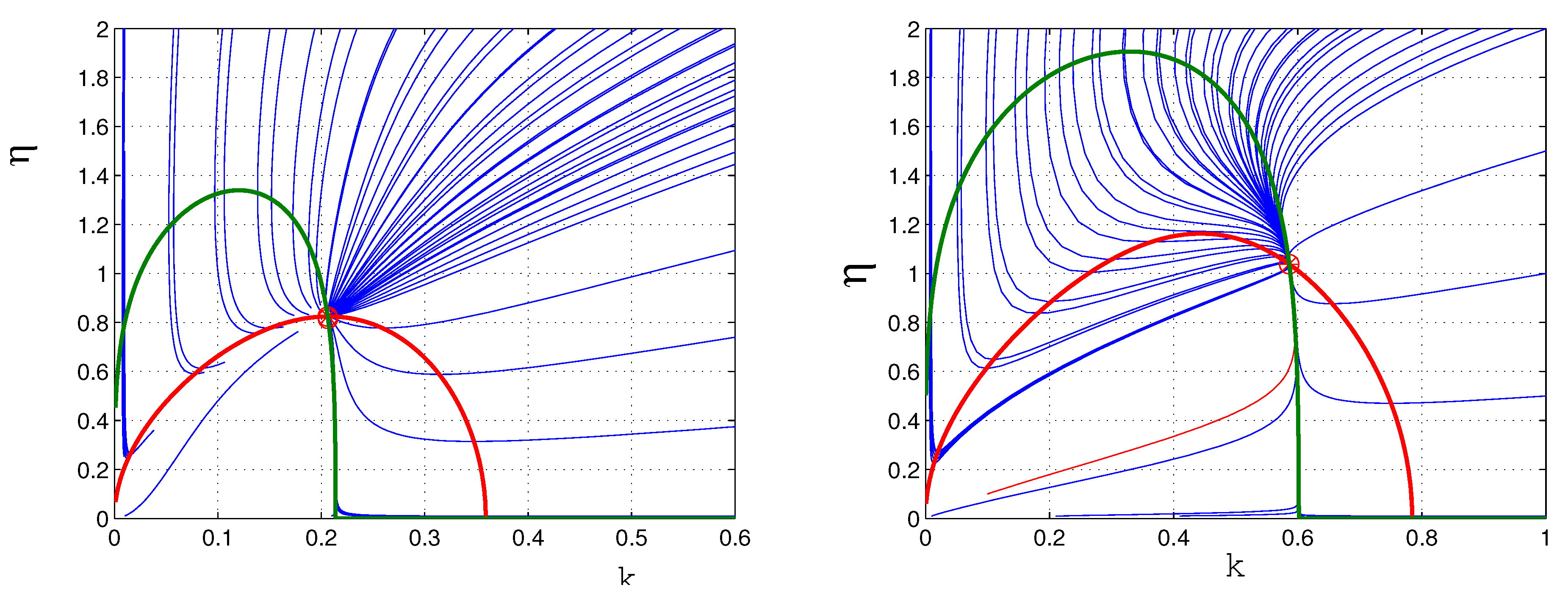
3.1. Nullclines and Fixed Points
3.2. Stability
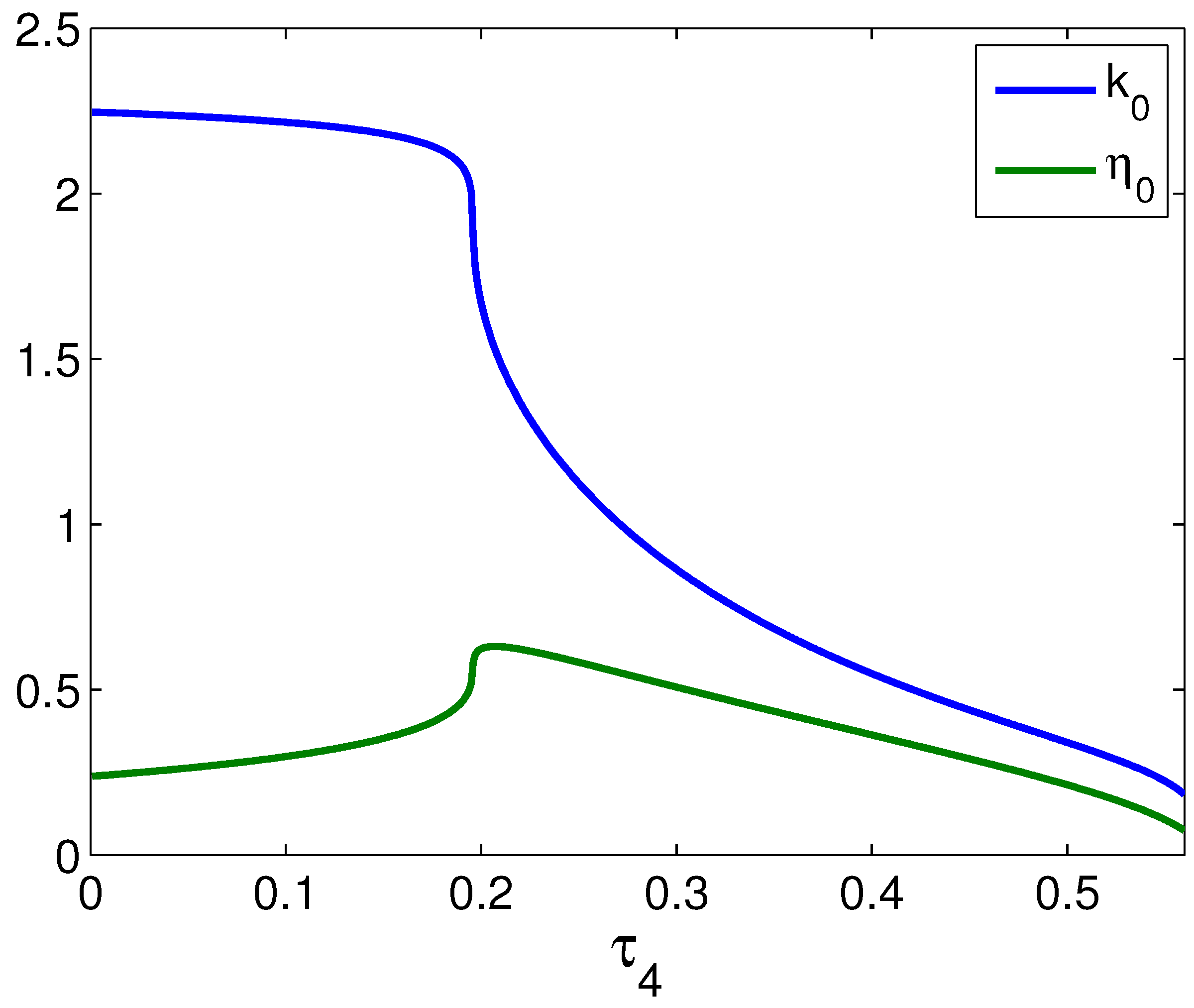
4. Bifurcations in the SPE Mode Locking Model
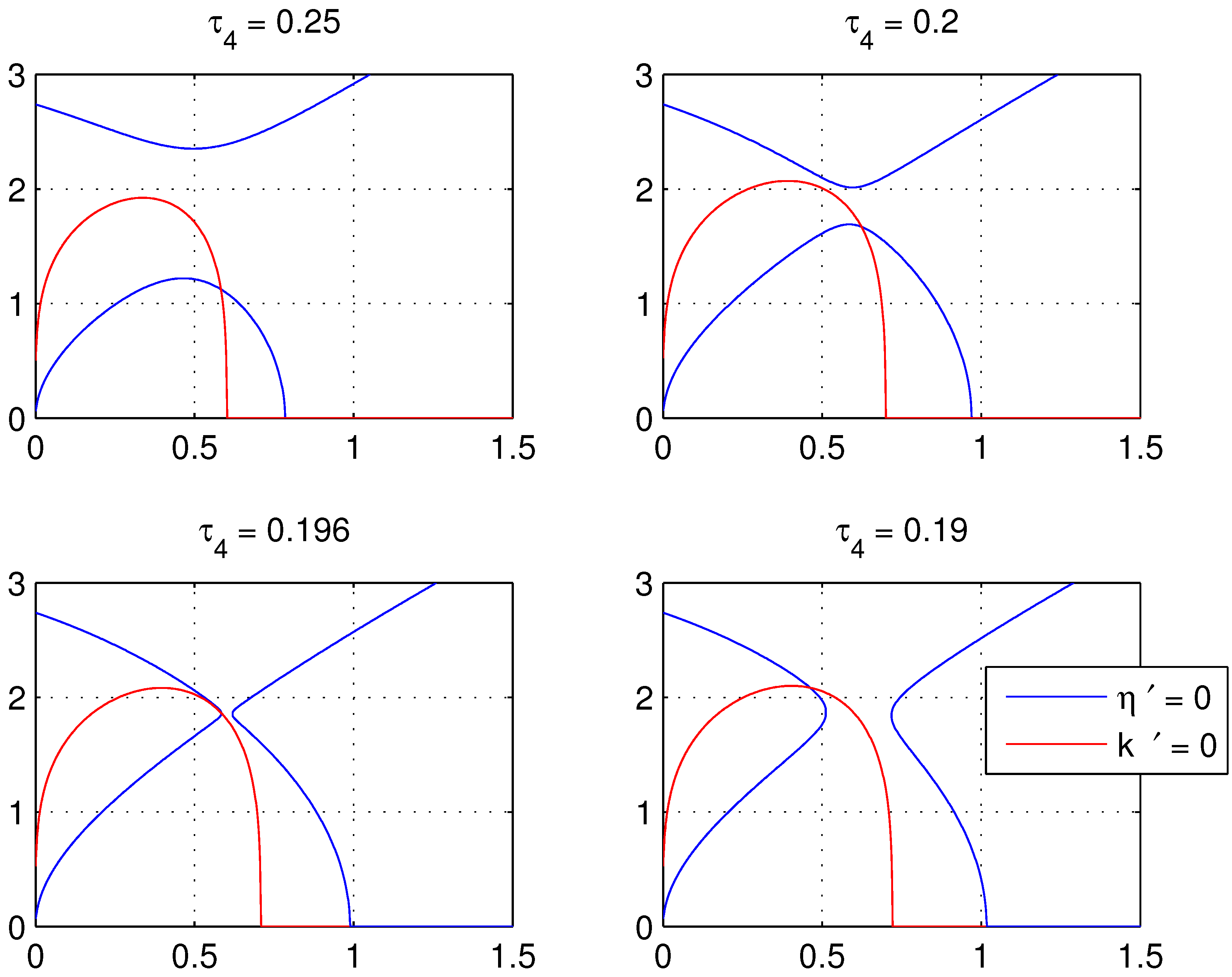
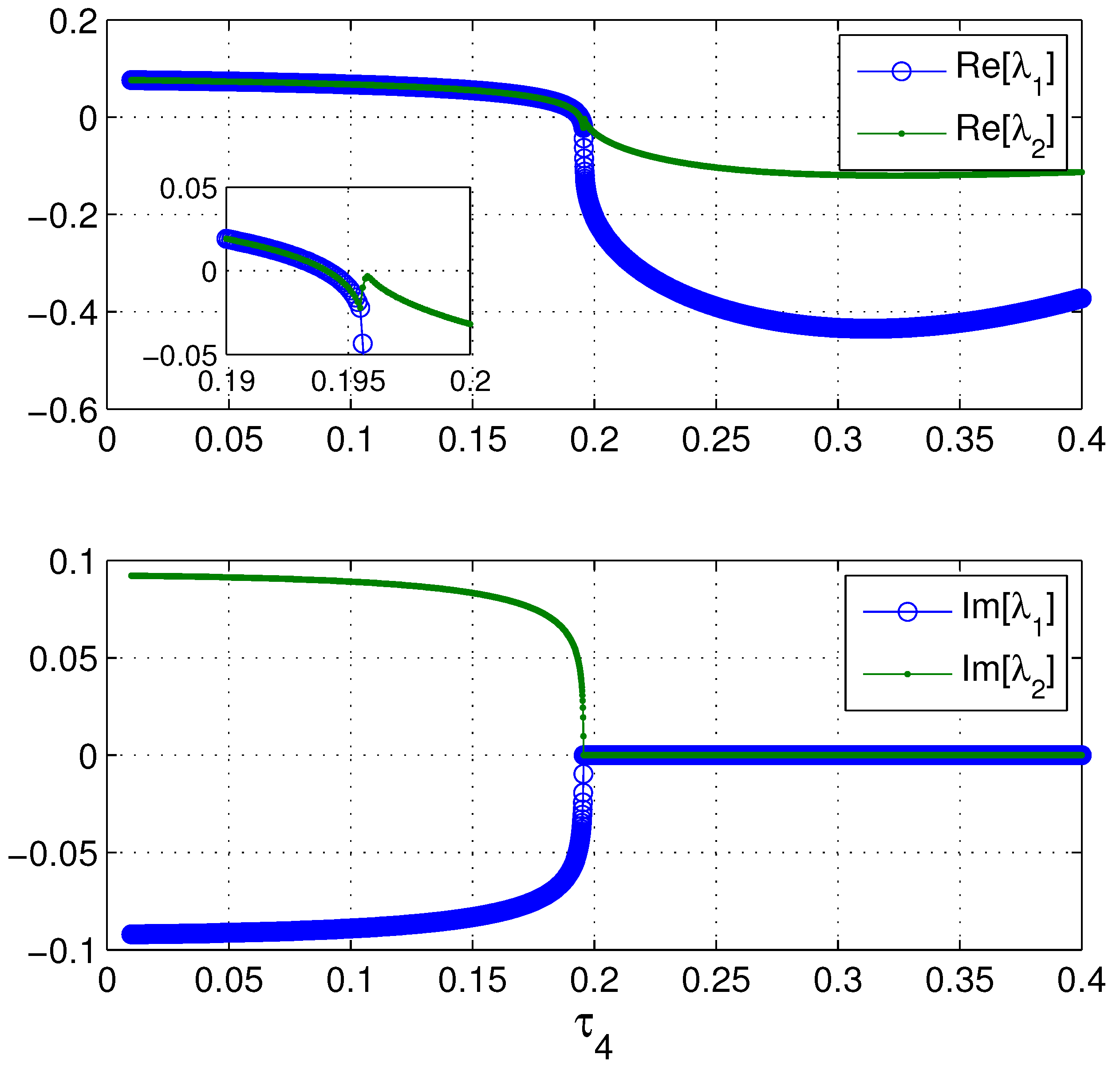
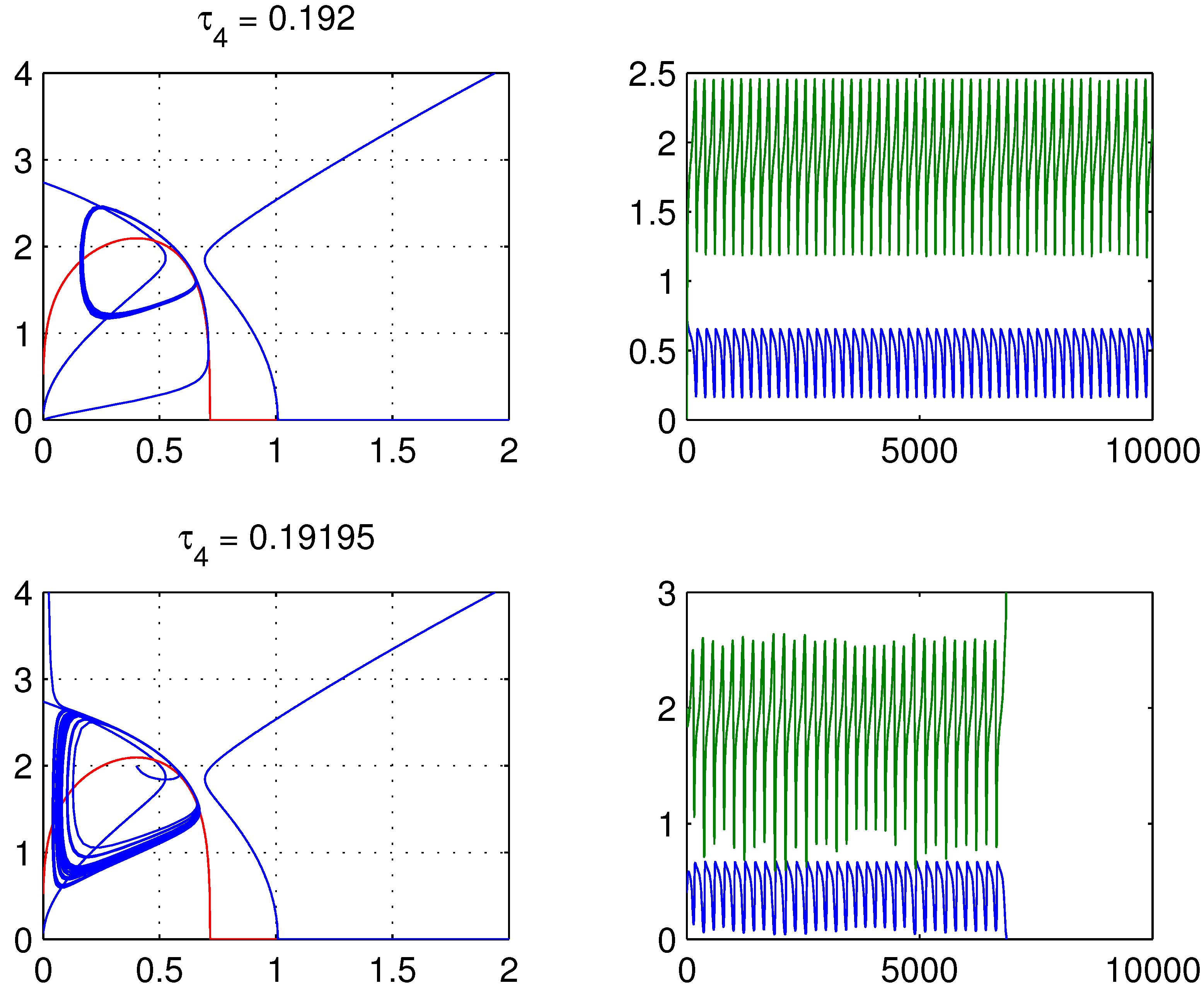
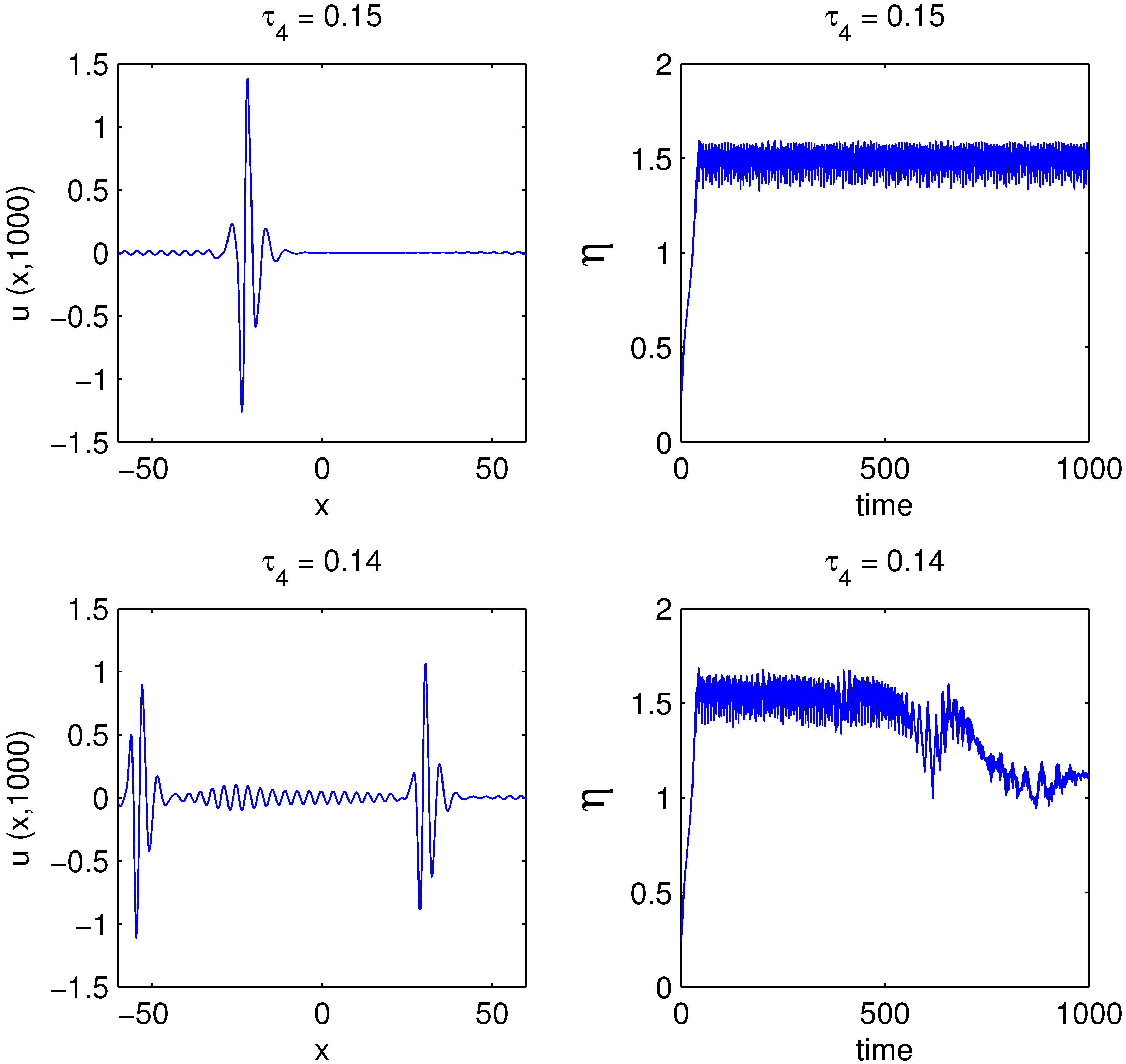
5. Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Backus, S.; Durfee, C.G.; Murname, M.M.; Kapteyn, H.C. High power ultrafast lasers. Rev. Sci. Instrum. 1998, 69, 1207–1233. [Google Scholar] [CrossRef]
- Spielmann, C.; Curley, P.F.; Brabec, T.; Krausz, F. Ultrabroadband femtosecond lasers. IEEE J. Quantum Electron. 1994, 1100, 1100–1114. [Google Scholar] [CrossRef]
- Sutter, D.H.; Jung, I.D.; Kärtner, F.X.; Matuschek, N.; Morier-Genoud, F.; Scheuer, V.; Tilsch, M.; Tschudi, T.; Keller, U. Self-starting 6.5-fs pulses from a Ti:Sapphire laser using a semiconductor saturable absorber and double-chirped mirrors. IEEE J. Sel. Top. Quantum Electron. 1998, 4, 169–178. [Google Scholar] [CrossRef]
- Ell, R.; Angelow, G.; Seitz, W.; Lederer, M.J.; Huber, H.; Kopf, D.; Birge, J.R.; Kärtner, F.X. Quasi-synchronous pumping of modelocked few-cycle Titanium Sapphire lasers. Opt. Express 2005, 13, 9292–9298. [Google Scholar] [CrossRef] [PubMed]
- Kärtner, F.X.; Morgner, U.; Ell, R.; Schibli, T.; Fujimoto, J.G.; Ippen, E.P.; Scheuer, V.; Angelow, G.; Tschudi, T. Ultrabroadband Double-Chirped Mirror Pairs for Generation of Octave Spectra. J. Opt. Soc. Am. B 2001, 19, 382–385. [Google Scholar] [CrossRef]
- Keller, U. Ultrafast solid-state lasers. Progr. Opt. 2004, 46, 1–115. [Google Scholar]
- Hentschel, M.; Kienberger, R.; Spielmann, Ch.; Reider, G.A.; Milosevic, N.; Brabec, T.; Corkum, P.; Heinzmann, U.; Drescher, M.; Krausz, F. Attosecond metrology. Nature 2001, 414, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Schafer, K.; Gaarde, M.; Heinrich, A.; Biegert, J.; Keller, U. Strong Field Quantum Path Control Using Attosecond Pulse Trains. Phys. Rev. Lett. 2004, 92, 023003. [Google Scholar] [CrossRef] [PubMed]
- Silberberg, Y. Physics at the attosecond frontier. Nature 2001, 414, 494–495. [Google Scholar] [CrossRef] [PubMed]
- Scrinzi, A.; Ivanov, M.Y.; Kienberger, R.; Villeneuve, D.M. Attosecond physics. J. Phys. B At. Mol. Opt. Phys. 2006, 39, R1–R37. [Google Scholar] [CrossRef]
- Cundiff, S.T. Attosecond Physics: Better by half. Nature Phys. 2007, 3, 16–18. [Google Scholar] [CrossRef]
- Cundiff, S.T. Femtosecond comb technology. J. Korean Phys. Soc. 2006, 48, 1181–1187. [Google Scholar]
- Cundiff, S.T.; Ye, S.J.; Hall, J. Rulers of light. Sci Am. 2008, 298, 74–81. [Google Scholar] [CrossRef] [PubMed]
- Haus, H.A. Mode-Locking of Lasers. IEEE J. Sel. Top. Quant. Elec. 2000, 6, 1173–1185. [Google Scholar] [CrossRef]
- Kutz, J.N. Mode-locked soliton lasers. SIAM Rev. 2006, 48, 629–678. [Google Scholar] [CrossRef]
- Haus, H.A.; Fujimoto, J.G.; Ippen, E.P. Structures for additive pulse mode locking. J. Opt. Soc. Am. B 1991, 8, 2068–2076. [Google Scholar] [CrossRef]
- Schafer, T.; Wayne, C.E. Propagation of ultra-short optical pulses in cubic nonlinear media. Phys. D 2004, 196, 90–105. [Google Scholar] [CrossRef]
- Chung, Y.; Jones, C.K.R.; Schafer, T. Ultra-short pulses in linear and nonlinear media. Nonlinearity 2005, 18, 1351–1374. [Google Scholar] [CrossRef]
- Amiranashvili, Sh.; Vladimirov, A.G.; Bandelow, U. Solitary-wave solutions for few-cycle optical pulses. Phys. Rev. A 2008, 77, 063821. [Google Scholar] [CrossRef]
- Pietrzyk, M.; Kanattsikov, I.; Bandelow, U. On the propagation of vector ultra-short pulses. JNMP 2008, 15, 162–170. [Google Scholar] [CrossRef]
- Farnum, E.; Kutz, J.N. Master mode-locking theory for few-femtosecond pulses. Opt. Lett. 2010, 35, 3033–3035. [Google Scholar] [CrossRef] [PubMed]
- Farnum, E.; Kutz, J.N. Mode Locking in the Few-Femtosecond Regime Using Waveguide Arrays and the Coupled Short-Pulse Equations. IEEE J. Sel. Top. Quantum Electron. 2012, 18, 113–118. [Google Scholar] [CrossRef]
- Elgin, J. Perturbations of optical solitons. Phys. Rev. A 1993, 47, 4331–4341. [Google Scholar] [CrossRef] [PubMed]
- Kaup, D.J. Perturbation theory for solitons in optical fibers. Phys. Rev. A 1990, 42, 5689–5694. [Google Scholar] [CrossRef] [PubMed]
- Gordon, J.P.; Haus, H.A. Random walk of coherently amplified solitons in optical fiber transmission. Opt. Lett. 1986, 11, 665–667. [Google Scholar] [CrossRef] [PubMed]
- Gordon, J.P. Theory of the soliton self-frequency shift. Opt. Lett. 1986, 11, 662–664. [Google Scholar] [CrossRef] [PubMed]
- Kapitula, T.; Kutz, J.N.; Sandstede, B. Stability of Pulses in the Master-Modelocking Equation. J. Opt. Soc. Am. B 2002, 19, 740–746. [Google Scholar] [CrossRef]
- Gordon, J.P. Dispersive perturbations of solitons of the nonlinear Schrödinger equation. J. Opt. Soc. Am. B 1992, 9, 91–97. [Google Scholar] [CrossRef]
- Mamyshev, P.V.; Mollenauer, L.F. Soliton collisions in wavelength-division-multiplexed dispersion-managed systems. Opt. Lett. 1999, 24, 448–450. [Google Scholar] [CrossRef] [PubMed]
- Mamyshev, P.V.; Mollenauer, L.F. Pseudo-phase-matched four-wave mixing in soliton wavelength-division multiplexing transmission. Opt. Lett. 1996, 21, 396–398. [Google Scholar] [CrossRef] [PubMed]
- Farnum, E.; Kutz, J.N. Short-pulse perturbation theory. J. Opt. Soc. Am. B 2013, 30, 2191–2198. [Google Scholar] [CrossRef]
- Sakovich, A.; Sakovich, S. The short pulse equation is integrable. J. Phys. Soc. Jpn. 2005, 74, 239–241. [Google Scholar] [CrossRef]
- Sakovich, A.; Sakovich, S. Solitary wave solutions of the short pulse equation. J. Phys. A 2006, 39, 361–367. [Google Scholar] [CrossRef]
- Brabec, T.; Krausz, F. Nonlinear optical pulse propagation in the single-cycle regime. Phys. Rev. Lett. 1997, 78, 3282. [Google Scholar] [CrossRef]
- Porras, M.A. Propagation of single-cycle pulsed light beams in dispersive media. Phys. Rev. A 1999, 60, 5069. [Google Scholar] [CrossRef]
- Kolesik, M.; Moloney, J.V.; Mlejnek, M. Unidirectional Optical Pulse Propagation Equation. Phys. Rev. Lett. 2002, 89, 283902. [Google Scholar] [CrossRef]
- Kolesik, M.; Moloney, J.V. Nonlinear optical pulse propagation simulation: From Maxwell's to unidirectional equations. Phys. Rev. E 2004, 70, 036604. [Google Scholar] [CrossRef]
- Leblond, H.; Sanchez, F. Models for optical solitons in the two-cycle regime. Phys. Rev. A 2003, 67, 013804. [Google Scholar] [CrossRef]
- Rosanov, N.N.; Kozlov, V.V.; Wabnitz, S. Maxwell-Drude-Bloch dissipative few-cycle optical solitons. Phys. Rev. A 2010, 81, 043815. [Google Scholar] [CrossRef]
- Bondeson, A.; Lisak, M.; Anderson, D. Soliton Perturbations: A Variational Principle for the Soliton Parameters. Phys. Scr. 1979, 20, 479. [Google Scholar] [CrossRef]
- Bale, B.; Kutz, J.N. Variational method for mode-locked lasers. J. Opt. Soc. Am. B 2008, 25, 1193–1202. [Google Scholar] [CrossRef]
- Brunelli, J.C. The bi-Hamiltonian structure of the short pulse equation. Phys. Lett. A 2006, 353, 475–478. [Google Scholar] [CrossRef]
- Feng, L.; Ding, E.; Kutz, J.N.; Wai, P.K.A. Dual transmission filters for enhanced energy in mode-locked fiber lasers. Opt. Express 2011, 19, 23408–23419. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Kutz, J.N. High-energy mode-locked fiber lasers using multiple transmission filters and a genetic algorithm. Opt. Express 2013, 21, 6526–6537. [Google Scholar] [CrossRef] [PubMed]
- Namiki, S.; Ippen, E.P.; Haus, H.A.; Yu, C.X. Energy rate equations for mode-locked lasers. J. Opt. Soc. Am. B 1997, 14, 2099–2111. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farnum, E.D.; Kutz, J.N. Dynamics of a Low-Dimensional Model for Short Pulse Mode Locking. Photonics 2015, 2, 865-882. https://doi.org/10.3390/photonics2030865
Farnum ED, Kutz JN. Dynamics of a Low-Dimensional Model for Short Pulse Mode Locking. Photonics. 2015; 2(3):865-882. https://doi.org/10.3390/photonics2030865
Chicago/Turabian StyleFarnum, Edward D., and J. Nathan Kutz. 2015. "Dynamics of a Low-Dimensional Model for Short Pulse Mode Locking" Photonics 2, no. 3: 865-882. https://doi.org/10.3390/photonics2030865
APA StyleFarnum, E. D., & Kutz, J. N. (2015). Dynamics of a Low-Dimensional Model for Short Pulse Mode Locking. Photonics, 2(3), 865-882. https://doi.org/10.3390/photonics2030865



