3.1. Numerical Examples
In order to validate the theory on an explicit example, we have considered a quantum dot whose fluorescence is enhanced by a golden sphere of diameter
nm located at a distance
nm from one another. Exact simulations for this case were done in [
32] using the semi-classical model. The Drude-like model for the complex permittivity of gold corresponds to [
33]. The radiating system is located in the liquid host
. The single quantum dot emits at
nm. This wavelength nearly coincides with the plasmon resonance of the metal sphere in the liquid, which holds at
nm.
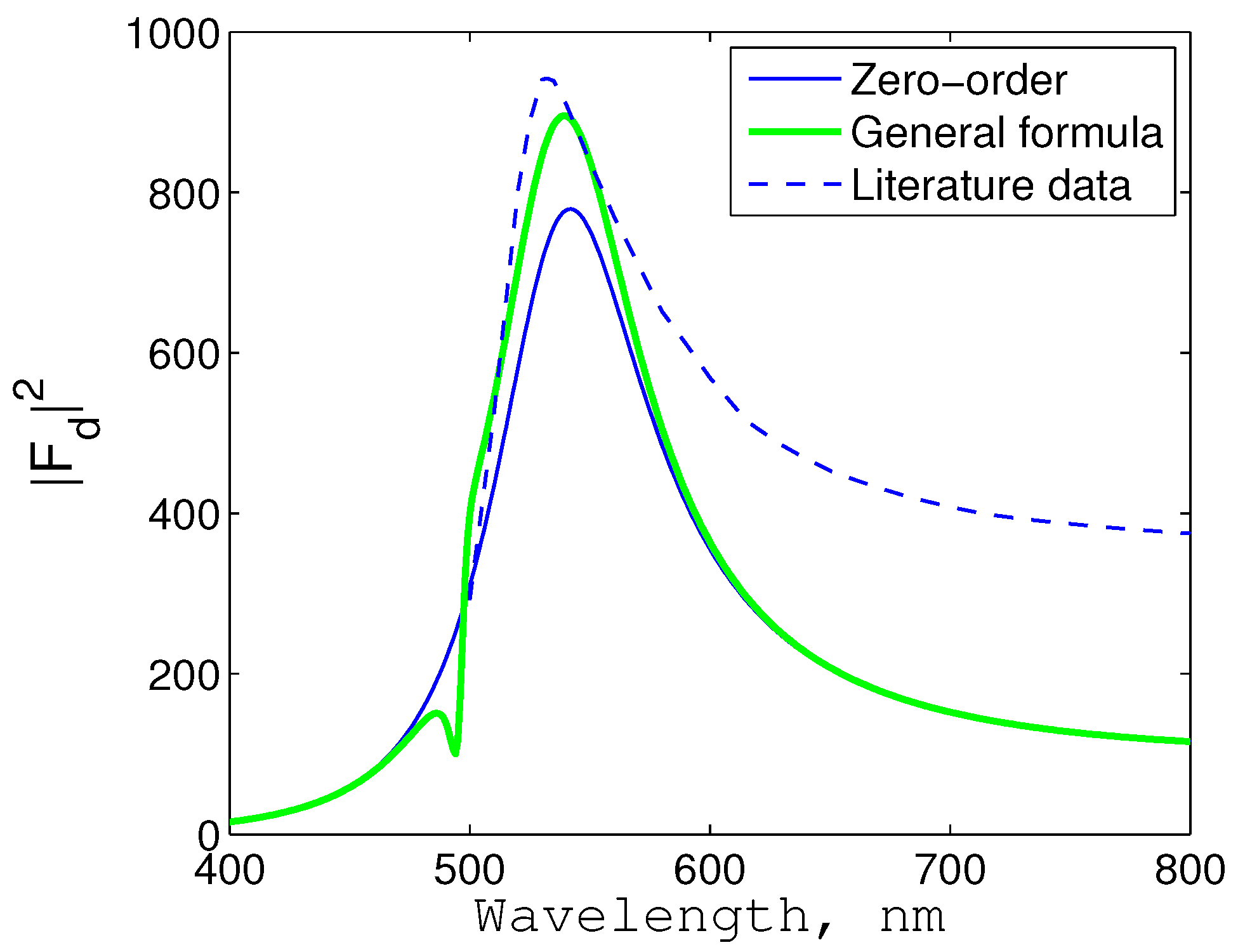
Figure 4.
Fluorescence spectrum of a quantum dot coupled to a golden nanosphere normalized to that of the single quantum dot. Thin line: zero-order model [
23]. Dashed line: exact simulations of the semiclassical model [
32]. Thick line: our general Formula (
33).
Figure 4.
Fluorescence spectrum of a quantum dot coupled to a golden nanosphere normalized to that of the single quantum dot. Thin line: zero-order model [
23]. Dashed line: exact simulations of the semiclassical model [
32]. Thick line: our general Formula (
33).
The fluorescence spectrum calculated in [
32] was normalized to the radiated power of the single QE. In fact, in Figure 1 of [
32], the authors show the radiative and non-radiative parts of the Purcell factor (they call them the normalized radiative and non-radiative decay rates) in a broad range of wavelength (500–900 nm). The sum of these two factors in accordance with [
23] gives the total frequency-dependent Purcell factor,
i.e., in our notations representing the value
. These numerical data were compared with
calculated using the zero-order approximation Equation (
32) and using the final Equation (
33). The polarizability
of the metal nanosphere was calculated taking into account the dissipation Equation (like in [
23]). The results are shown in
Figure 4. For the decay factor of the quantum dot, we used the lossless approximation Equation (
31).
Within the plasmon resonance band, the zero-order model represented by a thin solid curve is in rather good agreement with the exact calculations (dashed curve). The error becomes more significant beyond the resonance. Here, we concentrate on the high-frequency edge of the resonance band where the zero-order model predicts the Lorentzian shape for the spectrum, whereas the dashed curve clearly has a huge non-Lorentzian slope. The comparison with the result of Equation (
33) shows the reason for this strong non-symmetry of the spectral line. Extending the range of wavelengths to 400–500 nm (in [
32], calculations are done for 500–900 nm), we can see the typical feature of the Fano resonance with the dip at 500 nm. Clearly, the inexact coincidence of the plasmon resonance and the emission frequency together with the difference in decay rates obviously result in this type of resonance. In general, the behavior of the thick curve in the resonance band fits the exact data much better: the error for the maximal value of
reduces from 12% (thin Curve 1) to 4% (thick curve).
Calculating parameters
and
with the use of Equation (
35), we saw that this system in our terminology corresponds to the case of IMC. This is the most difficult case, when the hybridization does not result in the Rabi splitting, but results in the strong distortion of the spectral shape compared to the usual Lorentzian line. This distortion is the Fano resonance.
Notice that the model developed in this paper does not imply obviously the condition of the exact resonance. This condition was used only to simplify the comparison of our model with previous analytical models. In fact, our circuit model allows (at least approximately) predictions of fluorescence spectra in the practical case when the resonance of the nanosystem is approximate. Our Equation (
33) does not require the exact resonance. The polarizabilities of the quantum dot
and that of the NA
may be calculated using Equations (
25) and (
26) also beyond the exact resonance. We may put different resonant frequencies
and
into Equations (
25) and (
26), and nothing will change in our model. The relative difference
is sufficient to produce the noticeable Fano resonance: a narrow spectral hole near the rather broad maximum. Of course, the Lorentzian line results from the zero-order approximation (the same Equation (
33) with the substitution
).
We do not know exactly the reasons for the disagreement between the exact dashed curve and our theoretical thick curve at wavelengths 600–800 nm where the quasi-static dipole model is expected to work better than in the resonance band. Most probably, this disagreement is related to dissipative losses in the quantum dot, which were fully neglected in our calculations. These losses may enlarge the low-frequency part of the resonance band. Furthermore, the value
d, which determines the static polarizability
of the QE, is not exactly known, since it is not given in [
32]. We found this
d using a fitting procedure. The thick curve in
Figure 4 corresponds to
D, when the numerical deviation from the dashed curve is minimal over the resonance band
500–600 nm. Slightly larger values of
d correspond to a much larger maximum of
; slightly smaller values correspond to a much broader resonance band. This value
D for a two-level nanocrystal quantum dot is realistic. In accordance with [
34], the estimation of the transition dipole moment is as follows:
, where
e is the electron charge and
is the relative permittivity of the quantum dot semiconductor at the emission frequency. This formula gives for the InSb quantum dot the value
D,
i.e., the value of the same order of magnitude as that given by our numerical fitting.
In [
16], one notices that the Fano resonance occurs in the extinction spectra, even if the resonances of the QE and NA coincide. The strong asymmetry of the frequency dependence inherent to the Fano resonance becomes possible because the shape of the Lorentzian spectral line is not perfectly symmetric with respect to
. Therefore, even for the exact resonance, the Fano spectral hole may result from the interference of the very tiny resonance band of a quantum dot compared to that of the plasmon resonance of an NA. The condition of the Fano resonance in this case is a sufficient value of the resonant polarizability of the QE. In [
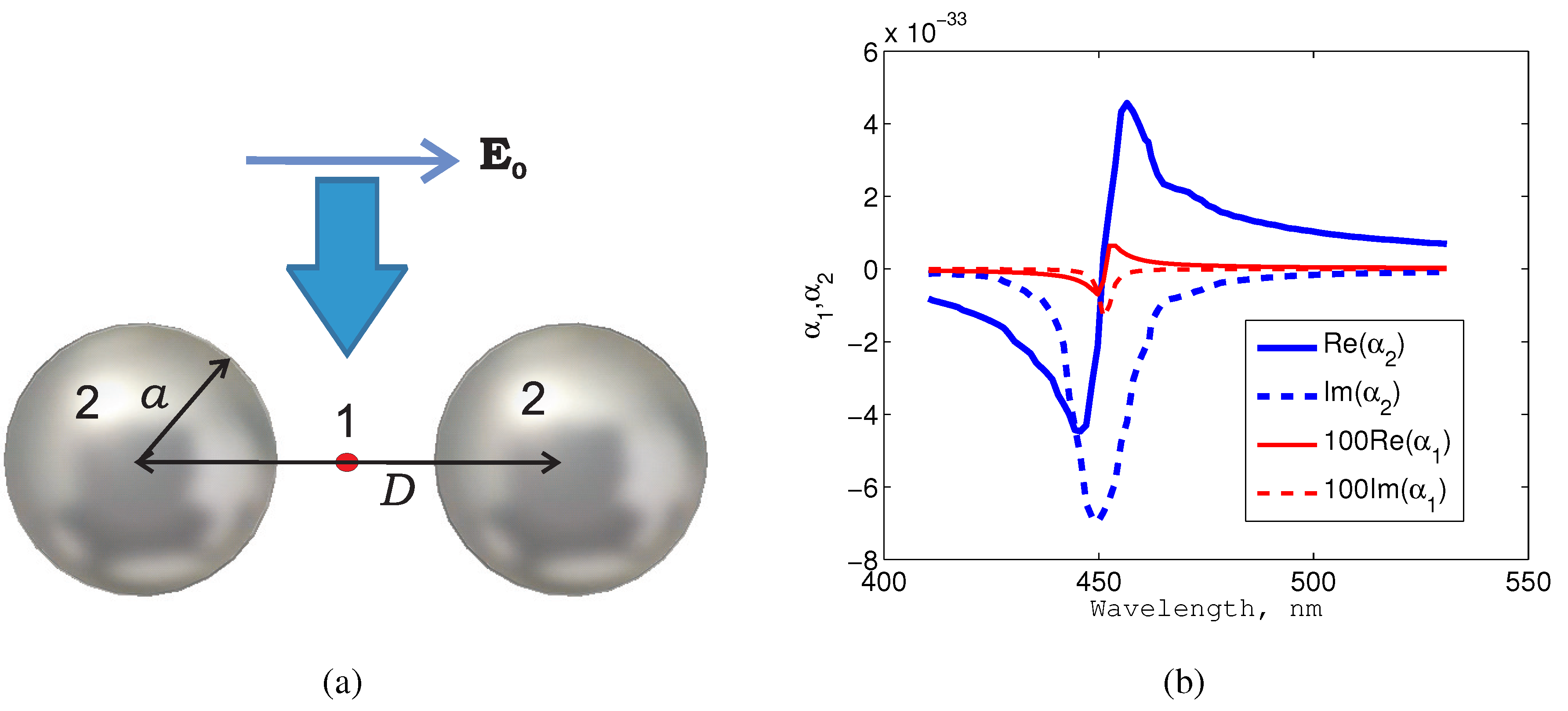
16], one calculates the extinction cross-section of the structure depicted in
Figure 5a. A quantum dot located at the center of a plasmonic dimer of Ag nanospheres is illuminated symmetrically by a plane wave, whereas the whole nanosystem is placed in the host
. In Figure 3b of [
16], the evolution of the extinction cross-section (ECS) is presented when the transition dipole moment
d varies from zero to
, where
nm. In all cases, QE 1 and NA 2 have their individual resonances at the same wavelength
450 nm. The complex permittivity of silver is taken from [
35].
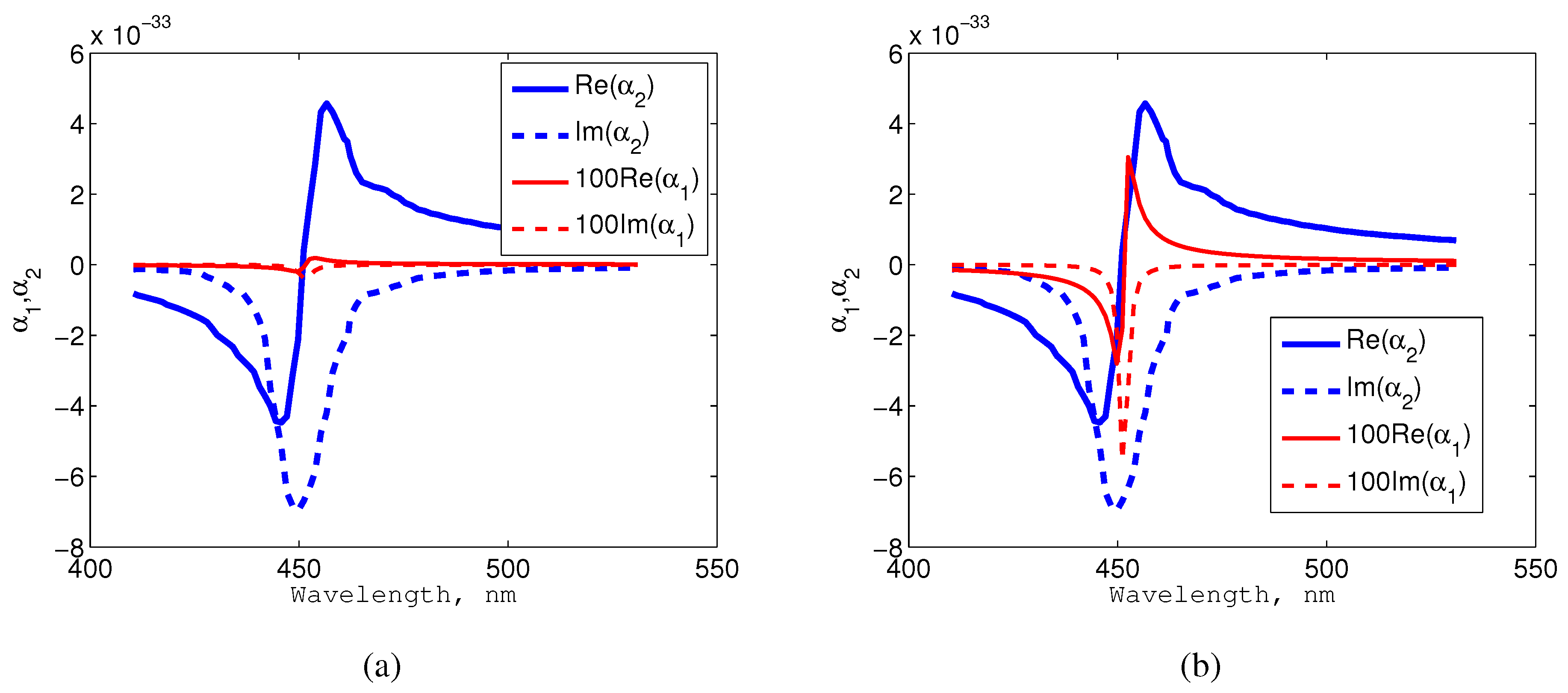
Figure 5.
(a) Sketch of the simulated nanosystem, where nm, nm; (b) complex polarizabilities of Elements 1 and 2 illuminated separately for the case nm. Polarizability is calculated analytically, and is simulated numerically using the CST software.
Figure 5.
(a) Sketch of the simulated nanosystem, where nm, nm; (b) complex polarizabilities of Elements 1 and 2 illuminated separately for the case nm. Polarizability is calculated analytically, and is simulated numerically using the CST software.
The spectra of ECS in semiclassical calculations of [
16] were normalized to the maxima of these spectrum for every value of
d. We have performed similar calculations and compared the evolution of spectra
versus d with the numerical data of [
16]. Let us consider the single QE 1, with polarizability
illuminated by a plane wave. Then, its individual dipole moment equals
. Now, let us illuminate the nanosystem, as is shown in
Figure 5a. Then, the total dipole moment of the system
, where
and
are interaction fields expressed through the interaction constant
. In the case of the dimer, this constant is not so simple to calculate analytically, because the coupling field
is now produced by two nanospheres, which are additionally mutually coupled with one another. This coupling though basically dipoles is not exactly that of two point dipoles located at their centers. The coupling of silver nanospheres also qualitatively modifies the frequency dependence of the individual polarizability of the dimer compared to that of a single sphere. Therefore, we performed exact numerical simulations of both
and
. Using the CST software, we have calculated the dipole moment of the NA 2, integrating its polarization currents, and found the complex value
. In the same simulation project, the value
was found as
, where the field
(
is the total electric field at the center of the dimer). The polarizabilities
for different values of
d were found using Equation (
26), neglecting the dissipation in the QE. In
Figure 5b, we depict
(analytically calculated) and
(numerically simulated) for the realistic case
nm (then
D), which may correspond to a quantum dot of a radius of 2 nm [
16]. The resonance band of this QE turns out to be ten-times narrower than that of the NA, and the resonant value of
is lower than that of
by three orders of magnitude. However, we will see below that in combination with the plasmonic dimer, it is enough for the Rabi splitting.
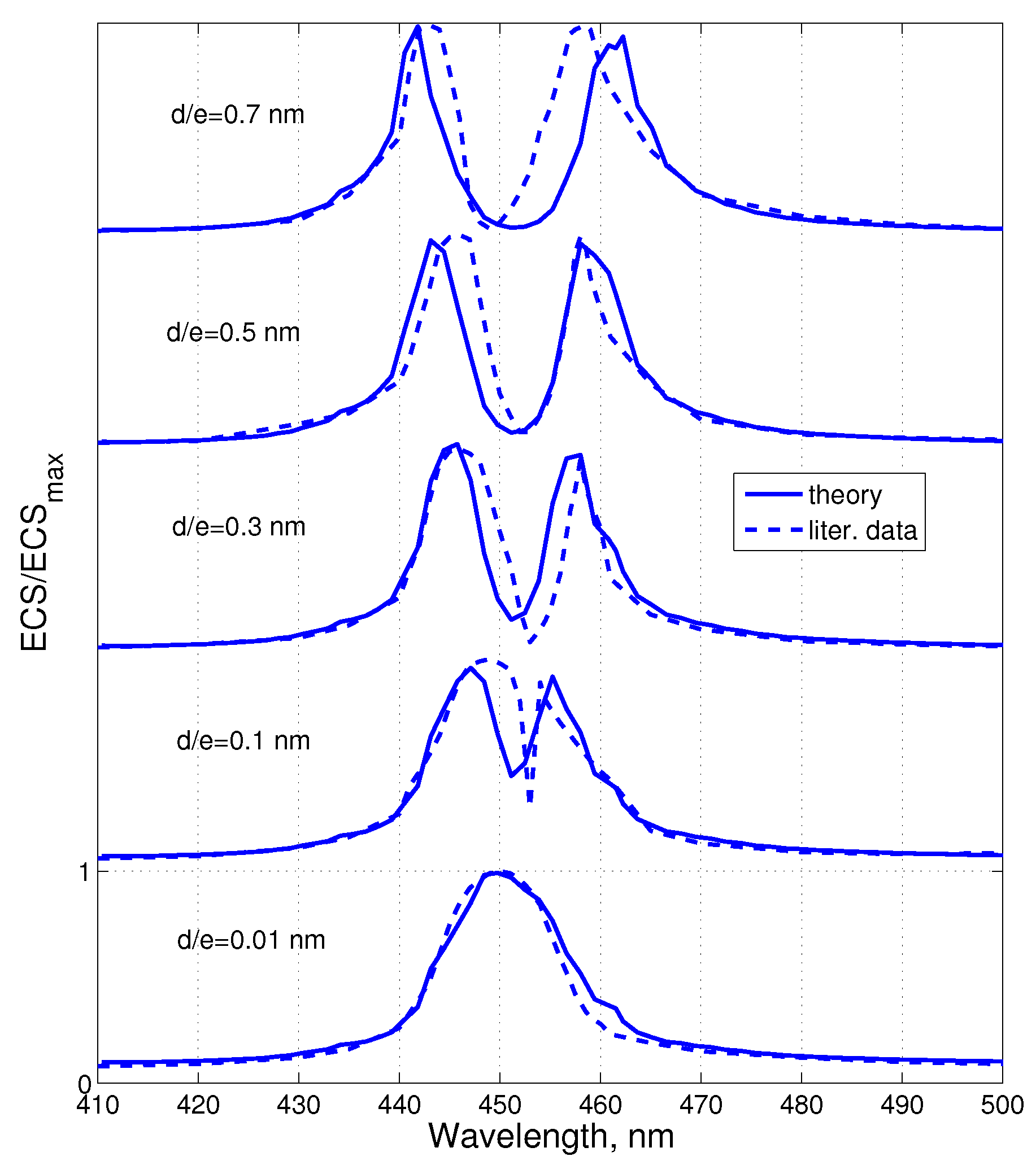
Figure 6.
Normalized extinction cross-sections
versus wavelength for five values of the transition dipole moment: solid curves: Equation (
33); dashed ones: data from [
16].
Figure 6.
Normalized extinction cross-sections
versus wavelength for five values of the transition dipole moment: solid curves: Equation (
33); dashed ones: data from [
16].
Once we know values
and
, we may find
and, applying the same speculations as above, derive
, where Equation (
33) still holds for
. This allows us to study the evolution of extinction spectra
versus because (see, e.g., [
27]):
The results for
are presented in
Figure 6. The qualitative agreement holds until
nm, and this agreement is sufficient in order to claim that our approximate analytical model is quantitatively adequate. The spectral hole at 452–454 nm appears when
nm, and this is clearly the Fano resonance and not the Rabi splitting, as is noticed in [
16]. In the classification of the present paper, this case is referred to as SEFC/IMC. The corresponding plot of polarizabilities is shown in
Figure 7a. The Fano modification of the spectrum occurs when the resonant polarizability of the QE is smaller than that of the NA by four orders of magnitude.
Figure 7.
Complex polarizabilities of Elements 1 and 2 illuminated separately: (a) nm; (b) nm.
Figure 7.
Complex polarizabilities of Elements 1 and 2 illuminated separately: (a) nm; (b) nm.
When
nm, the spectrum of ECS in
Figure 6 combines the features of the Fano resonance and Rabi oscillations. The cases
and
nm clearly correspond to the Rabi splitting. However, all values of
B in the range 0.1–0.7 nm still correspond to the case we called SEFC/IMC. Polarizabilities
and
for the case
nm are depicted in
Figure 7b. The resonant value of
is here lower than that of
by two orders of magnitude. This polarizability of the QE is still insufficient to implement the regime of SMC. The relative Rabi splitting is in this case equal 3.5%. This splitting is not yet accompanied by the damping of radiation, which is still enhanced.
Really, for the case nm, we obtained the values and , respectively, at hybridized resonance wavelengths and 462 nm. At both of these wavelengths, the value is nearly equal to 2% of the resonant value . Therefore, at and 462 nm is only slightly smaller than the value at the individual resonance of the QE. Respectively, the overall extinction of the nanosystem is not suppressed compared to the single QE in spite of the noticeable Rabi splitting. The same refers to the overall fluorescence. This is still the regime SEFC IMC in our classification.
Higher values of
d (for which there are no data in [
16]) in our calculations may correspond to stronger Rabi splitting and to a more noticeable decrease of the overall fluorescence compared to that of the single QE. The value
nm corresponds to the relative Rabi splitting 5% and to the decrease of
by one order of magnitude compared to
. The same damping level obviously refers to the fluorescence. This regime would correspond to SMC,
i.e., non-radiative Rabi oscillations or fluorescence quenching.
3.2. Discussion
Above, we have presented an express-analysis of our formulas based on the equivalent circuits of two coupled antennas, which quantitatively describe the quantum emitter and the plasmonic nanoparticle forming the plasmon-enhanced fluorescence system. This express-analysis is validated via the comparison of the present model with the literature data. We think that our analysis is helpful for studying the plasmon-enhanced fluorescence by newcomers and may be also useful for experienced researchers working in the field.
Its main educational merit is the simple deterministic model of Rabi oscillations and fluorescence quenching. Both of these effects (especially the second one) are still considered by the majority of researchers as quantum effects. In our deep conviction, the nature of these effects is as classical as that of the Purcell effect. Even the fluorescence quenching effects is simply a classical non-radiative coupling of two dipole antennas, which may happen even for collinear dipoles due to hybridization of their resonances. In this regime, QE and NA mutually suppress their radiation resistances. Of course, the semiclassical model and even the purely quantum model also correctly describe these effects. However, they hardly bring anything qualitatively new. The role of the quantum theory is two-fold: it is capable of properly describing the nonlinear effects, which we ignore, and of properly determining the bounds of validity for the classical model (mainly concerning the pumping level).
In the modern literature, our point of view can be met. Classical interpretation of Rabi oscillations is quite popular, and corresponding works have been already mentioned above. The quenching in plasmon-enhanced fluorescence is seldom treated as a classical effect. One of these rare works is [
10], where this effect was claimed to be classical. If we accept this point of view, the following question arises: does the fluorescence quench for sufficiently strong mutual coupling of two dipoles or does this obviously implies high-order multipoles? In [
29] (where the fluorescence quenching is also claimed to be a classical effect), the quenching arises due to the coupling of a quantum dot to high-order multipole modes excited in the NA. These modes, in accordance with [
29], receive all of the near-field power from the QE and dissipate it, because higher multipoles radiate weakly. If the dipole mode is induced in the NA, this, in accordance with [
29], results in the high Purcell factor, and the fluorescence quenches only if high-order modes dominate.
We disagree with this claim. In our model, the quenching nicely occurs within the framework of the dipole model. In this model, it occurs not for all QEs. However, all QEs possessing the SEFC must experience the quenching when they approach too closely to the NA, and the mutual coupling becomes strong. The quenching mainly results from the strong detuning, which obviously accompanies the strong hybridization of the resonance. At frequencies located too far from , the resonance magnitude of the dipole moments of both NA and QE is small compared to the case of the individual resonances. Moreover, their dipole moments at these frequencies turn out to be out-of phase, and the total dipole moment is smaller than their arithmetic sum. This regime is called in the antenna theory either the non-radiative coupling regime or the dark mode regime and is known for two dipole antennas.
As for the multipole modes of NAs, they may be noticeable for NAs more complex than the single metal nanosphere or dimer of nanospheres. However, we believe that for any mode, it is possible to build its equivalent circuit and to reveal the same effects that we have analyzed for the dipole modes of Objects 1 and 2. The enhancement due to the Purcell effect and the quenching due to the hybridization may hold for the near-field interaction of any multipole moments. For the simple-shape structures, like in Figure 1, these fine effects may provide correction terms to the factors obtained within the framework of the dipole model.
To conclude this discussion, let us notice that our model is applicable even to so-called spacers [
30]. The spacer is a generator of localized surface plasmon excited by the fluorescence of a QE (or several QEs). The feedback is offered by the strong near-field mutual coupling of the QE and the Ag or Au nanoparticle. Our system in the case of SMC becomes the spacer on the condition of the very high pumping. Then, the nonlinear instability is developed, and the system passes the generation threshold,
i.e., the coherent plasmon arises in the NA. Though this coupling is non-radiative, the dipole moment of the system in the over-threshold regime is not fully suppressed, and the spacer emits a small amount of coherent light. The coherency of this light can be seen from the dramatic squeezing of the Lorentzian line of radiation centered at the plasmon resonance. The linewidth becomes by one order of magnitude narrower than that described by the Lorentzian damping factor
Equation (
25). Before the regime, when the plasmon and its radiation become coherent, the transition process occurs. This process is non-linear, and this non-linearity restricts the oscillation amplitude.
At first glance, our linear model, which implies modest pumping of the QE, has nothing to do with this regime. However, in [
17], it was shown that the transition regime in any spacer starts from non-radiative (fluorescence quenching holds!) Rabi oscillations. In accordance with the semiclassical theory of [
17], these oscillations occur in the background of the modulation instability and represent an initial process of the over-threshold dynamics of the spacer. After some dozens of Rabi periods, the non-linear auto-oscillations competing with this linear process [
31] replace non-radiative Rabi oscillations, and the transition regime continues towards the steady regime. If there were no fluorescence quenching, the power absorbed from pumping would be radiated, and auto-oscillations could not develop.
Finally, let us try to guess why the model of the fluorescence quenching presented in this paper has not been published before. This seems strange, because the explanation in terms of the suppressed dipole moment
is simplest. The dipoles of QE and NA, which are strongly mutually coupled, suppress one another; their mutual resistances compensate the radiation resistances, and the mode of their oscillation is dark. Probably, it was not understood earlier because the dipole moments of the QE and NA are collinear. In both optical and radio communities, there is conviction that the coupling of collinear dipoles is constructive for radiation (whereas the coupling of two parallel dipoles is destructive). Really, a high Purcell is known for the case when the dipoles of our system are collinear. High Raman gain is known for a molecule emitting the Raman radiation enhanced by a collinear dipole of the plasmonic nanoparticle. Parallel components of the dipole moment interact destructively; both Purcell and Raman gains for parallel dipoles are smaller than unity. In the theory of wire antennas [
25], it is stated that, unlike two parallel dipoles, a collinear passive wire enhances the radiation of the active one. However, in the antenna theory, resonant collinear wire dipoles are never strongly coupled. Their centers are always distanced from one another at least by the total length of two arms. As for the molecule in the scheme of surface-enhanced Raman scattering, it is also never strongly coupled to the plasmonic particles, because it is not resonant. Its Raman radiation is emitted at different frequencies. Therefore, the destructive mutual coupling of two collinear resonant dipoles making their total dipole moment close to zero has not been sufficiently studied. The radio analogue of the non-radiative Rabi oscillations can be imaged as a coaxial system of active and passive wire antennas both performed as helices with resonant total length and a very small height to allow the strong mutual coupling. Such systems can be definitely used for wireless power transfer.