Tailoring Effective Media by Mie Resonances of Radially-Anisotropic Cylinders
Abstract
:1. Introduction
2. Scattering from an RA Cylinder
2.1. Full-Wave Solution
2.2. Asymptotes of the Scattering Coefficients
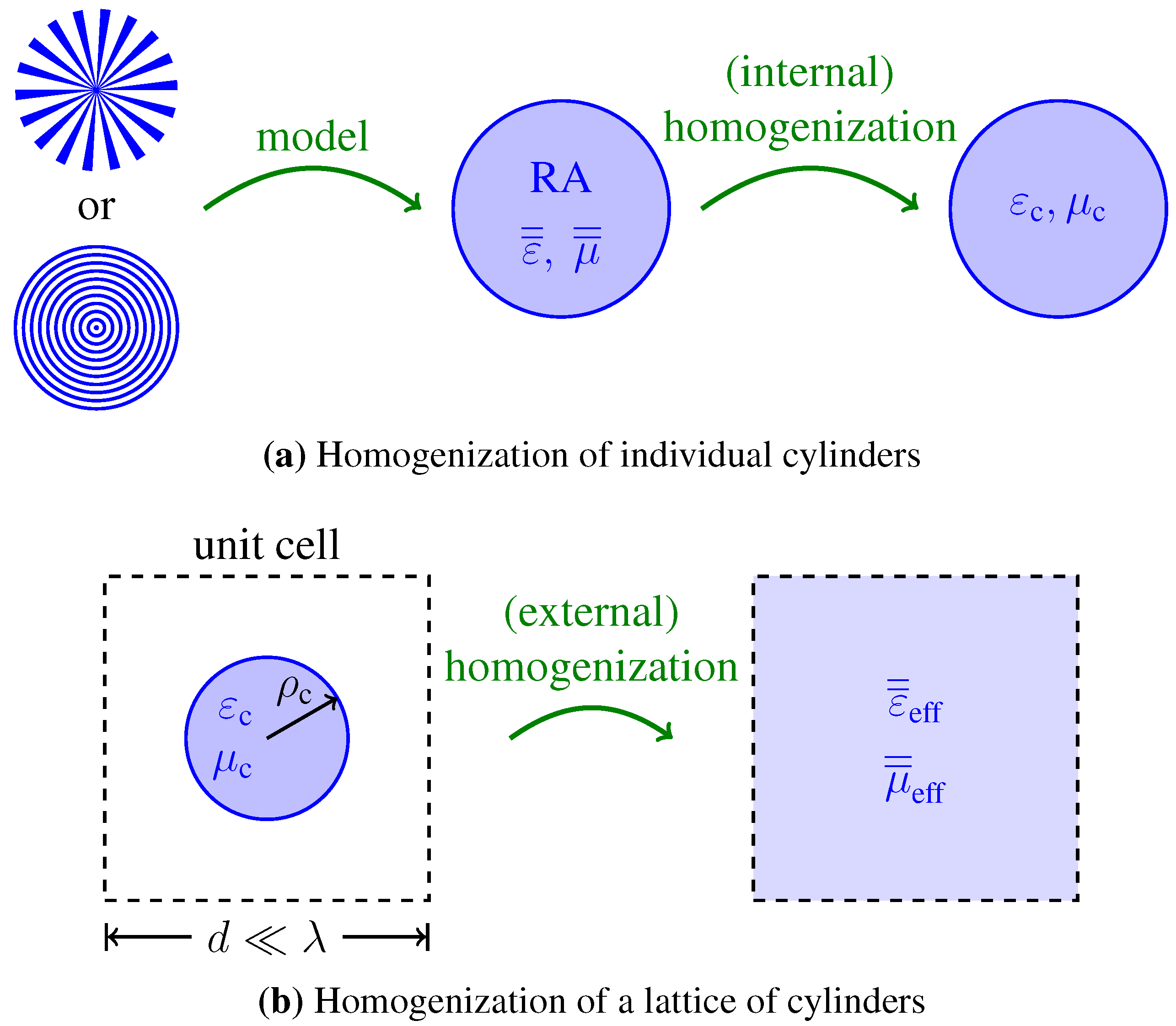
3. Homogenization Approach for RA Cylinders
3.1. Homogenization of an Individual Cylinder
3.2. Homogenization of Composite Media Consisting of RA Cylinders
3.3. Artificial Magnetism from All-Dielectric RA Cylinders
3.4. Double-Negative Response from Magnetodielectric RA Cylinders
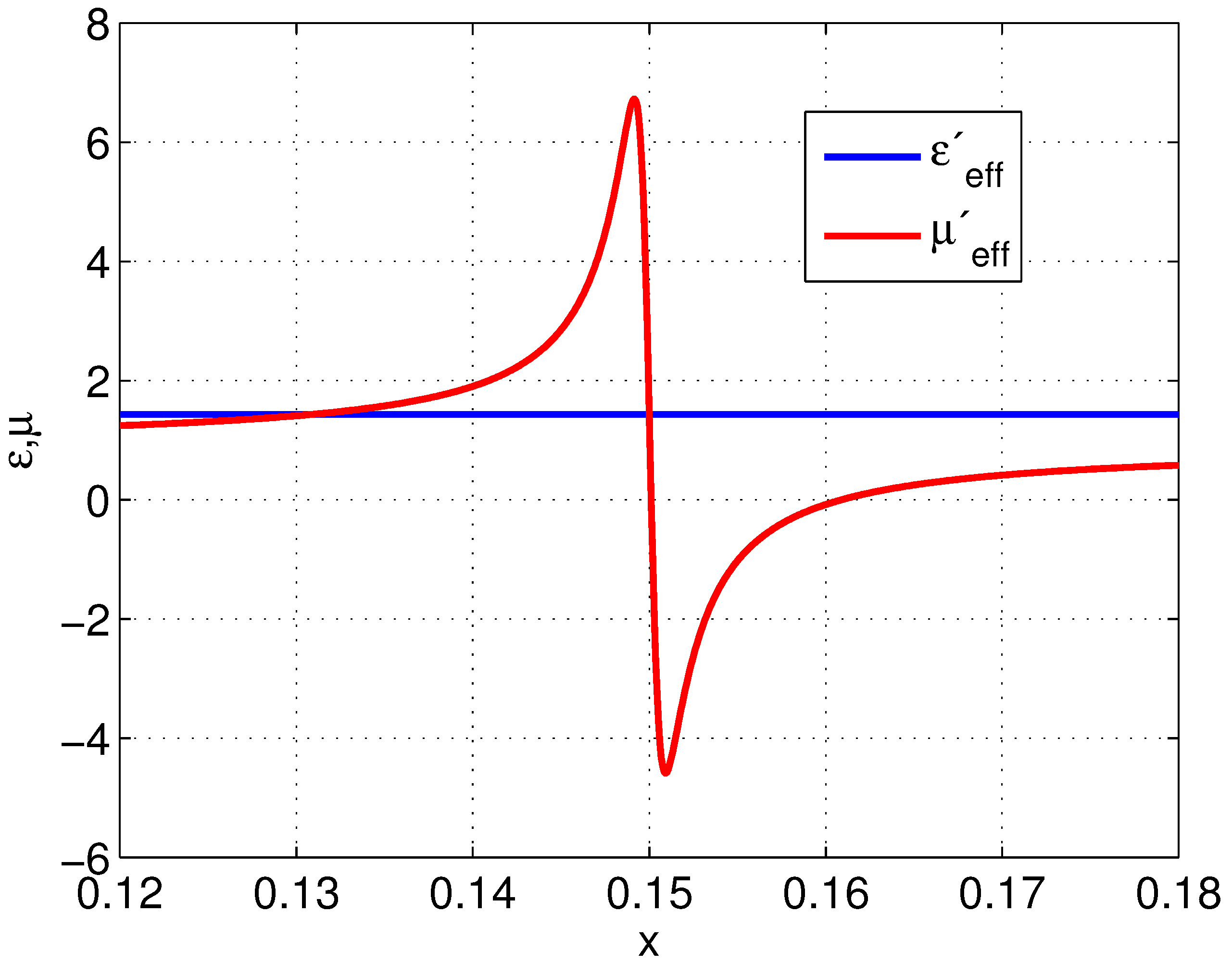
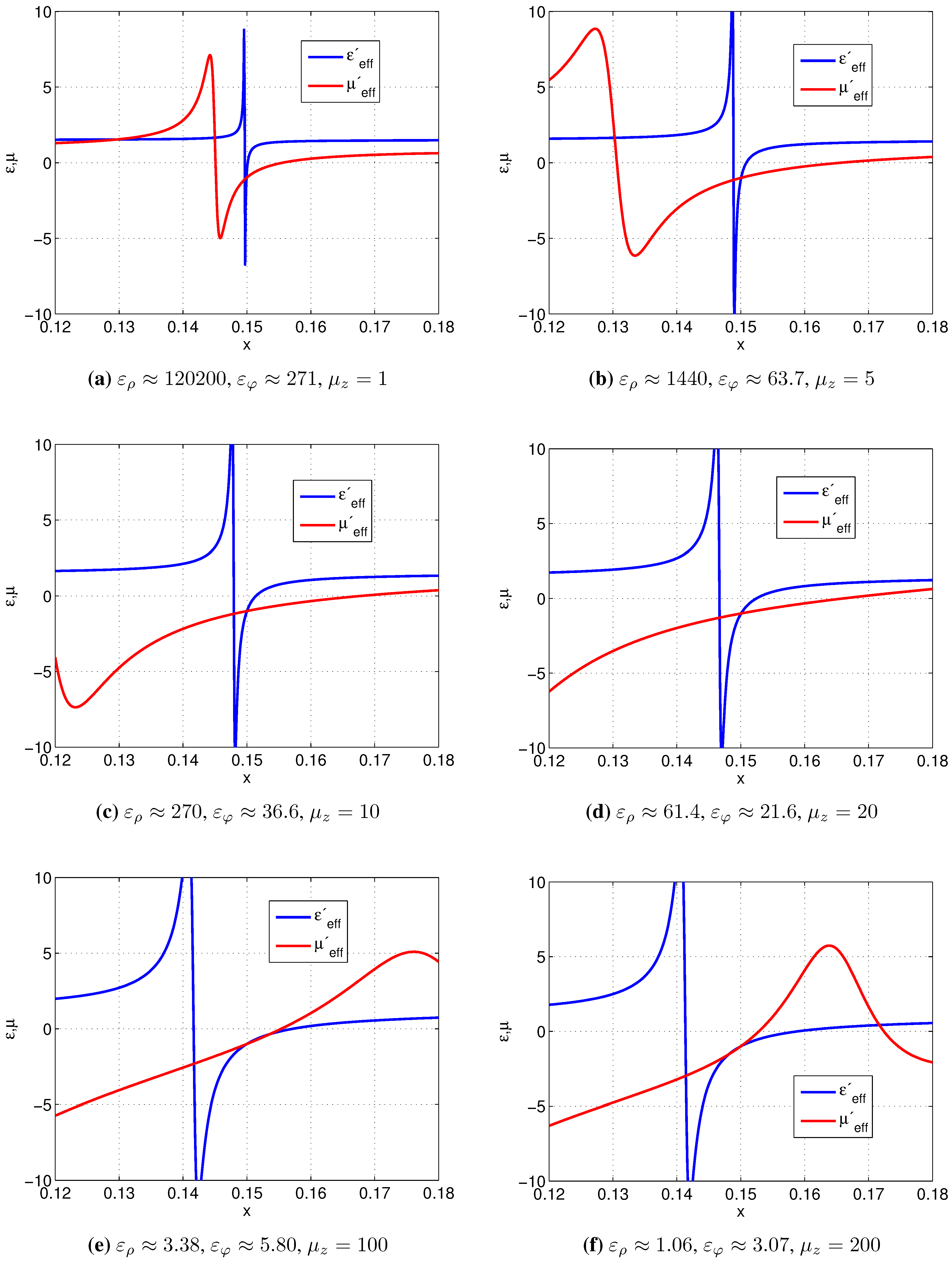
3.5. Effects of Different Design Parameters
3.6. Omittance of Losses
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Engheta, N.; Ziolkowski, R.W. Metamaterials: Physics and Engineering Explorations; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ϵ and μ. Sov. Phys. Uspekhi 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism for conductors and enhanced nonlinear phenomena. IEEE Trans. Microwave Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- O’Brien, S.; Pendry, J.B. Photonic band-gap effects and magnetic activity in dielectric composites. J. Phys. Condens. Matter 2002, 14, 4035–4044. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhou, J.; Zhang, F.; Lippens, D. Mie resonance-based dielectric metamaterials. Mat. Today 2009, 12, 60–69. [Google Scholar] [CrossRef]
- Ueda, T.; Itoh, T. Mu-negative, double-negative, and composite right/left handed metamaterials based on dielectric resonators. IEICE Electron. Exp. 2012, 9, 65–80. [Google Scholar] [CrossRef]
- Van de Hulst, H.C. Light Scattering by Small Particles; Dover: New York, NY, USA, 1981. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Monticone, F.; Alù, A. The quest for optical magnetism: From split-ring resonators to plasmonic nanoparticles and nanoclusters. J. Mater. Chem. C 2014, 2, 9059–9072. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Fu, Y.H.; Zhang, J.B.; Luk’yanchuk, B. Magnetic light. Sci. Rep. 2012, 2, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Ginn, J.C.; Brener, I.; Peters, D.W.; Wendt, J.R.; Stevens, J.O.; Hines, P.F.; Basilio, L.I.; Warne, L.K.; Ihlefeld, J.F.; Clem, P.G.; et al. Realizing optical magnetism from dielectric metamaterials. Phys. Rev. Lett. 2012, 108. 097402:1–5. [Google Scholar] [CrossRef]
- Gans, R.; Happel, H. Zur Optik kolloidaler Metallösungen. Ann. Phys. (Leipzig) 1909, 334, 277–300. [Google Scholar] [CrossRef]
- Stratton, J.A. The effect of rain and fog on the propagation of very short radio waves. Proc. IRE 1930, 18, 1064–1074. [Google Scholar] [CrossRef]
- Lewin, L. The electrical constants of a material loaded with spherical particles. Proc. Inst. Elec. Eng. 1947, 94, 65–68. [Google Scholar]
- Waterman, P.C.; Pedersen, N.E. Electromagnetic scattering by periodic arrays of particles. J. Appl. Phys. 1986, 59, 2609–2618. [Google Scholar] [CrossRef]
- Grimes, C.A.; Grimes, D.M. Permeability and permittivity spectra of granular materials. Phys. Rev. B 1991, 43, 10780–10788. [Google Scholar] [CrossRef]
- Holloway, C.L.; Kuester, E.F.; Baker-Jarvis, J.; Kabos, P. A double negative (DNG) composite medium composed of magnetodielectric spherical particles embedded in a matrix. IEEE Trans. Antennas. Propag. 2003, 51, 2596–2603. [Google Scholar] [CrossRef]
- Wheeler, M.S.; Aitchison, J.S.; Mojahedi, M. Three-dimensional array of dielectric spheres with an isotropic negative permeability at infrared frequencies. Phys. Rev. B 2005, 72. 193103:1–4. [Google Scholar] [CrossRef]
- Wheeler, M.S.; Aitchison, J.S.; Mojahedi, M. Coated nonmagnetic spheres with a negative index of refraction at infrared frequencies. Phys. Rev. B 2006, 73. 045105:1–7. [Google Scholar] [CrossRef]
- Jylhä, L.; Kolmakov, I.; Maslovski, S.; Tretyakov, S. Modeling of isotropic backward-wave materials composed of resonant spheres. J. Appl. Phys. 2006, 99. 043102:1–7. [Google Scholar] [CrossRef]
- Vendik, I.; Vendik, O.; Kolmakov, I.; Odit, M. Modelling of isotropic double negative media for microwave applications. Opto-Electron. Rev. 2006, 14, 179–186. [Google Scholar] [CrossRef]
- Chern, R.-L.; Liu, X.X. Effective parameters and quasi-static resonances for periodic arrays of dielectric spheres. J. Opt. Soc. Am. B 2010, 27, 488–497. [Google Scholar] [CrossRef]
- Kuester, E.F.; Memić, N.; Shen, S.; Scher, A.; Kim, S.; Kumley, K.; Loui, H. A negative refrective index metamaterial based on a cubic array of layered nonmagnetic spherical particles. Prog. Electromagn. Res. B 2011, 33, 175–202. [Google Scholar] [CrossRef]
- Liu, L.Y.; Yang, D.P.; Zhou, Y.M.; Zhou, J. Artificial isotropic magnetism and negative refraction of metamaterial consisting of dielectric spherical shells. Appl. Phys. A 2014, 117, 747–753. [Google Scholar] [CrossRef]
- Schuller, J.A.; Zia, R.; Taubner, T.; Brongersma, M.L. Dielectric metamaterials based on electric and magnetic resonances of silicon carbide particles. Phys. Rev. Lett. 2007, 99. 107401:1–4. [Google Scholar] [CrossRef]
- Vynck, K.; Felbacq, D.; Centeno, E.; Căbuz, A.I.; Cassagne, D.; Guizal, B. All-Dielectric rod-type metamaterials at optical frequencies. Phys. Rev. Lett. 2009, 102. 133901:1–4. [Google Scholar] [CrossRef]
- Chern, R.-L.; Chen, Y.T. Effective parameters for photonic crystals with large dielectric contrast. Phys. Rev. B 2009, 80. 075118:1–9. [Google Scholar] [CrossRef]
- Townsend, S.; Zhou, S.; Li, Q. Multiscale metamaterials: a new route to isotropic double-negative behaviour at visible frequencies. Opt. Express 2014, 22, 21929–21937. [Google Scholar] [CrossRef] [PubMed]
- Kallos, E.; Chremmos, I.; Yannopapas, V. Resonance properties of optical all-dielectric metamaterials using two-dimensional multipole expansion. Phys. Rev. B 2012, 86. 245108:1–10. [Google Scholar] [CrossRef]
- Strickland, D.; Ayón, A.; Alù, A. Dynamic polarizability tensor for circular cylinders. Phys. Rev. B 2015, 91. 085104:1–10. [Google Scholar] [CrossRef]
- Dirksen, A.; Arslanagic, S.; Breinbjerg, O. Resonances and dipole moments in dielectric, magnetic and magnetodielectric cylinders – an overview. Appl. Phys. A 2011, 103, 789–793. [Google Scholar] [CrossRef]
- Bouchitté, G.; Felbacq, D. Homogenization near resonances and artificial magnetism from dielectrics. C. R. Acad. Sci. Paris Ser. I 2004, 339, 377–382. [Google Scholar] [CrossRef]
- Peng, L.; Ran, L.; Chen, H.; Zhang, H.; Kong, J.A.; Grzegorczyk, T.M. Experimental observation of left-handed behavior in an array of standard dielectric resonators. Phys. Rev. Lett. 2007, 98. 157403:1–4. [Google Scholar] [CrossRef]
- Valdivia-Valero, F.J.; Nieto-Vesperinas, M. Composites of resonant dielectric rods: A test of their behavior as metamaterial refractive elements. Photonics Nanostruct. 2012, 10, 423–434. [Google Scholar] [CrossRef]
- Němec, H.; Kužel, P.; Kadlec, F.; Kadlec, C.; Yahiaoui, R.; Mounaix, P. Tunable terahertz metamaterials with negative permeability. Phys. Rev. B 2009, 79. 241108(R):1–4. [Google Scholar] [CrossRef]
- Kang, L.; Lippens, D. Mie resonance based left-handed metamaterial in the visible frequency range. Phys. Rev. B 2011, 83. 195125:1–6. [Google Scholar] [CrossRef]
- Yu, X.; Gao, L. Nonlinear dielectric response in partially resonant composites with radial dielectric anisotropy. Phys. Lett. A 2006, 359, 516–522. [Google Scholar] [CrossRef]
- Kettunen, H.; Wallén, H.; Sihvola, A. Cloaking and magnifying using radial anisotropy. J. Appl. Phys. 2013, 114. 044110:1–9. [Google Scholar] [CrossRef]
- Ni, Y.; Gao, L.; Qiu, C.-W. Achieving invisibility of homogeneous cylindrically anisotropic cylinders. Plasmonics 2010, 5, 251–258. [Google Scholar] [CrossRef]
- Jin, Y.W.; Gao, D.L.; Gao, L. Plasmonic resonant light scattering by a cylinder with radial anisotropy. Prog. Electromagn. Res. 2010, 106, 335–347. [Google Scholar] [CrossRef]
- Chen, H.L.; Gao, L. Anomalous electromagnetic scattering from radially anisotropic nanowires. Phys. Rev. A 2012, 86. 033825:1–8. [Google Scholar] [CrossRef]
- Gao, L.; Fung, T.H.; Yu, K.W.; Qiu, C.W. Electromagnetic transparency by coated spheres with radial anisotropy. Phys. Rev. E 2008, 78. 046609:1–11. [Google Scholar] [CrossRef]
- Wallén, H.; Kettunen, H.; Sihvola, A. Anomalous absorption, plasmonic resonances, and invisibility of radially anisotropic spheres. Radio Sci. 2015, 50, 18–28. [Google Scholar] [CrossRef]
- Ishii, S.; Inoue, S.-I.; Otomo, A. Electric and magnetic resonances in strongly anisotropic particles. J. Opt. Soc. Am. B 2014, 31, 218–222. [Google Scholar] [CrossRef]
- Mangini, F.; Tedeschi, N.; Frezza, F.; Sihvola, A. Homogenization of a multilayer sphere as a radial uniaxial sphere: Features and limits. J. Electromagnet. Wave. 2014, 28, 916–931. [Google Scholar] [CrossRef]
- Lindell, I.V. Methods for Electromagnetic Field Analysis, 2nd ed.; IEEE: New York, NY, USA, 1995. [Google Scholar]
- Sihvola, A. Electromagnetic Mixing Formulas and Applications; IEEE: London, UK, 1999. [Google Scholar]
- Shen, J.T.; Platzman, P.M. Near field imaging with negative dielectric constant lenses. Appl. Phys. Lett. 2002, 80, 3286–3288. [Google Scholar] [CrossRef]
- Smith, D.R.; Schurig, D.; Rosenbluth, M.; Schultz, S.; Ramakrishna, S.A.; Pendry, J.B. Limitations on subdiffraction imaging with a negative refractive index slab. Appl. Phys. Lett. 2003, 82, 1506–1508. [Google Scholar] [CrossRef]
- Podolskiy, V.A.; Narimanov, E.E. Near-sighted superlens. Opt. Lett. 2005, 30, 75–77. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kettunen, H.; Wallén, H.; Sihvola, A. Tailoring Effective Media by Mie Resonances of Radially-Anisotropic Cylinders. Photonics 2015, 2, 509-526. https://doi.org/10.3390/photonics2020509
Kettunen H, Wallén H, Sihvola A. Tailoring Effective Media by Mie Resonances of Radially-Anisotropic Cylinders. Photonics. 2015; 2(2):509-526. https://doi.org/10.3390/photonics2020509
Chicago/Turabian StyleKettunen, Henrik, Henrik Wallén, and Ari Sihvola. 2015. "Tailoring Effective Media by Mie Resonances of Radially-Anisotropic Cylinders" Photonics 2, no. 2: 509-526. https://doi.org/10.3390/photonics2020509
APA StyleKettunen, H., Wallén, H., & Sihvola, A. (2015). Tailoring Effective Media by Mie Resonances of Radially-Anisotropic Cylinders. Photonics, 2(2), 509-526. https://doi.org/10.3390/photonics2020509




