1. Introduction
X-ray and extreme ultraviolet (EUV) radiation acts on core electronic states inducing resonant transitions to valence states and ionization. The strongly bound core-level electrons involved are highly confined at certain atoms within a compound giving rise to the element sensitivity in x-ray spectroscopy. Short pulses in the extreme ultraviolet and x-ray spectral ranges become more available due to progress in free electron lasers [
1,
2,
3,
4] and an increased availability of high harmonic sources [
5,
6]. The high local sensitivity of x-rays and EUV light has helped to probe ultrafast photoinduced dynamics as can be exemplified on charge transfer phenomena in transition metal complexes [
7], photoinduced phase transitions [
8,
9], magnetic phenomena [
10], as well as internal conversion in nucleobases [
11].
Using short wavelength pulses for the excitation of the quantum system will allow direct creation of localized valence-electron wavepackets which could be probed with high local fidelity by further x-ray interactions [
12,
13,
14,
15,
16]. The theoretical description of nonlinear x-ray spectroscopy is already well advanced [
14], its experimental realization is, however, far from trivial. The first stimulated signals at free electron lasers [
17,
18] have been recently demonstrated and the field is moving towards more complex nonlinear multi-pulse schemes [
19]. Nonlinear spectroscopy in the optical domain became feasible with the advent of high intensity laser sources rendering the intrinsically weak nonlinear signals measurable. Compared to the optical domain, nonlinear x-ray methods will cause damage of the sample via valence ionization. Thus any nonlinear signal will compete with the sample damage at the high x-ray power needed for nonlinear spectroscopy. As a consequence, the x-ray intensity needs to be kept low, which in turn decreases the nonlinear signal.
Heterodyning by a phase stable reference electric field is a well known technique to amplify weak nonlinear responses which is successfully used in the infrared and optical domain [
20,
21]. The generation of a reference field however, is much more difficult in the extreme ultraviolet and x-ray range because of a lack of suitable beamsplitters. In addition, phase stability over different optical paths is much more demanding for the few nm EUV and x-ray wavelengths compared to several 100 nm in the optical range.
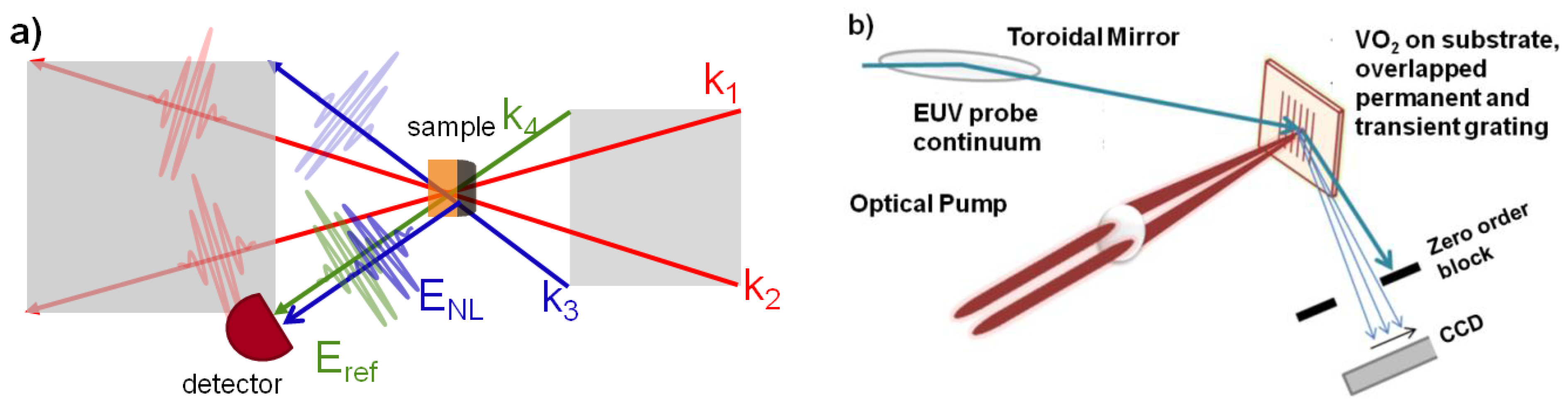
In this paper we address these problems by presenting a new scheme for the generation of a phase stable reference electric field at the position of the sample. The latter is periodically structured in the form of a grating to steer a reference beam in the direction of the nonlinear sample response. The relative phase of the reference and nonlinear beam can be altered by translating the permanent grating with respect to the incoming beams. We show a first demonstration of the heterodyning scheme for transient grating experiment on VO2. The transient grating is induced by two infrared beams and probed by extreme ultraviolet light in the region of 3d metal M-edges.
2. Experimental Section
The optical diagram for transient grating spectroscopy is shown in
Figure 1. Two pulses under different directions given by the wavevectors k
1 and k
2 hit the sample at the same time. Due to the angle between the two pulses, they create an interference pattern which becomes translated into a periodic modulation of the sample optical properties in form of a grating. For pulses with wavelength λ
0 and relative angle θ, the grating period is d
0 = λ
0/(2sin(θ/2)). A pulse in direction k
3 hits the sample after a time delay and scatters from the transient grating generated by pulses 1 and 2 giving rise to a pulse propagating in direction k
4. For a thick sample leading to Bragg reflection, the scattered wavevector needs to fulfill the relation k
4 = k
1 − k
2 + k
3 [
22]. For a thin grating, as applies to the experiment described later, phase matching is less confined and the usual grating diffraction condition applies. If the beam 3 hits the grating under an angle α, the diffracted beam 4 can be observed under an angle β
m (m being the order of the diffraction), if the following condition is fulfilled sin(β
m + α) − sin α = mλ
3/d
0 = mk
12sin(θ/2)/k
3. In a heterodyne experiment, the electric field from the nonlinear interaction E
NL is superimposed with a stronger reference field E
ref on a detector measuring the intensity of the superimposed electric fields:
The interference term shows the multiplication and thus amplification of the weak signal, ENL by the stronger one, Eref. The relative phase Δϕ of the two fields is changed experimentally to deduce the amplitude of ENL via the phase dependent intensity. The reference field is always split off the probe pulse before the interaction with the sample by means of a beamsplitter and needs to be recombined with the nonlinear response via a phase stable optical reference path. As mentioned in the introduction, beamsplitting and phase stability requirements are hard to fulfill for short wavelengths in the extreme ultraviolet and soft x-ray regions.
A solution to this problem is splitting of the probe pulse at the sample by using a permanent grating with the same periodicity as the transient grating. This permanent grating deflects a reference field into direction k
4 even in the absence of a transient grating. As the transient signal is superimposed, reference and nonlinear signal will interfere and since both are generated at the same spot of only one optical element, the fields are phase locked. The relative phase between reference and nonlinear signal Δϕ can be tuned by translating the permanent grating under the transient grating in the direction perpendicular to the grating lines. This technique is well known from Moire interferometry [
23]. Half a linespace translation of the permanent grating (with respect to the transient grating of beams 1 and 2) results in a phase shift of π. At typical linespacings of a several µm, this control can be implemented with high accuracy and stability as a relatively large grating shift translates into small shifts in the relative phase. This technique does not add additional detrimental intensity for the measurement, beam 3 is already needed to create the nonlinear signal. The intensity of beam 3 can be kept low from the heterodyning perspective, since the diffracted reference intensity scales linearly with the intensity of beam 3.
Figure 1.
(a) General transient grating scheme. Pulses 1 and 2 hit the sample simultaneously with different wavevectors k1 and k2, thus creating a transient grating. Pulse 3 propagating in direction k3 scatters from the sample in direction k4 creating the transient grating response ENL. A reference field Eref in direction k4 is used to create a heterodyne signal on the detector. Usually this field is created in front of the sample using beamsplitting optics and appropriate delays. In our case, the sample is structured in form of a permanent grating such that part of pulse 3 is scattered in direction k4 even in the absence of pulses 1 and 2. This self referencing field is automatically phase locked to the nonlinear transient grating response; (b) Realization of the transient grating scheme in a reflective geometry for grazing incidence of the probe pulse required by the short wavelength of the probe continuum.
Figure 1.
(a) General transient grating scheme. Pulses 1 and 2 hit the sample simultaneously with different wavevectors k1 and k2, thus creating a transient grating. Pulse 3 propagating in direction k3 scatters from the sample in direction k4 creating the transient grating response ENL. A reference field Eref in direction k4 is used to create a heterodyne signal on the detector. Usually this field is created in front of the sample using beamsplitting optics and appropriate delays. In our case, the sample is structured in form of a permanent grating such that part of pulse 3 is scattered in direction k4 even in the absence of pulses 1 and 2. This self referencing field is automatically phase locked to the nonlinear transient grating response; (b) Realization of the transient grating scheme in a reflective geometry for grazing incidence of the probe pulse required by the short wavelength of the probe continuum.
We demonstrate the feasibility of this technique using our transient grating setup as described in detail in [
24]. In short, the beam of an 800 nm, 30 fs 1 kHz Ti:Sapphire laser is split into three pulses. Two are generating a transient grating with a period around 15 µm on a 100 nm thick VO
2 sample grown on an Al
2O
3(10
10) substrate. The VO
2 film was grown by pulsed laser deposition technique (PLD), epitaxially oriented with the c-axis of the rutile phase pointing out of the plane of the substrate. For the experiment described here, a broadband EUV pulse was produced by high harmonic generation in Ne gas. The high harmonics are refocused with a toroidal mirror, hitting the VO
2 sample surface at a grazing angle of 22° before reaching the focus at a cooled CCD detector. The temporal overlap of the grating and probe pulses was independently calibrated by a cross correlation measurement using a nonlinear crystal at the sample position. To achieve that, the EUV pulse was substituted by its generating infrared pulse by means of removing an infrared blocking Al filter [
24]. The time delay between the two pulses forming the grating and the EUV probe pulse was set to approximately 6 ps. The permanent grating that creates the reference field in the heterodyne scheme was imprinted by overexposure of the VO
2 sample with the 800 nm transient grating optical pulses. In this case, a destructive laser fluence above 30 mJ/cm
2 was applied, while the fluence used to generate the transient grating response was about half this value, remaining below the damage threshold. After overexposure we clearly observed the creation of a permanent grating leading to spectrally dispersed EUV light on the detector even in the absence of a transient grating. The Masciovecchio group at FERMI also observed heterodyned signals by damage induced permanent gratings, in their case by overexposure with extreme ultraviolet light [
25].
3. Results and Discussion
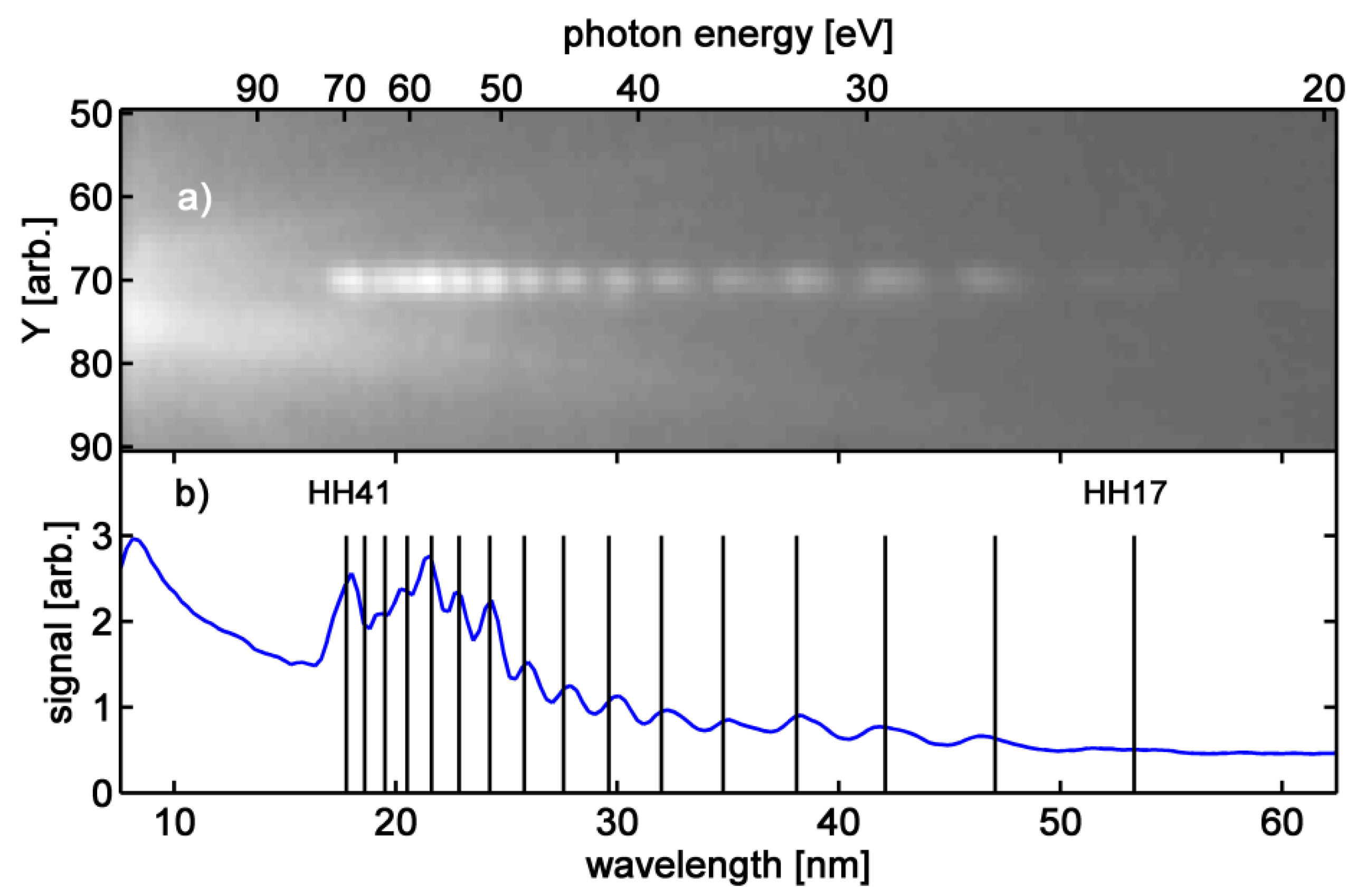
Figure 2a shows the raw image of diffracted light from the permanent grating in the VO
2 sample. The different odd harmonics of our 800 nm Ti:Sapphire fundamental are clearly distinguishable. Despite blocking the zero order we still observe some diffuse scattering into our region of interest on the detector. We used the harmonics to calibrate the wavelength scale of our detector.
Figure 2b shows the different harmonics plotted together with the expected wavelength of odd harmonics from order 17 to 41. The fit describes the data well. The width of the harmonics is dominated by the spectral resolution of the grating. The harmonics have a linewidth around 0.5 nm in the region of 40 nm [
26], much narrower than the several nm linewidth observed in
Figure 2. This is consistent with the low line density of this grating. The signal strength increases from long to short wavelength, which is a general trend observed for harmonics of Ne [
26].
Figure 2.
(a) Diffracted signal from the permanent grating on a logarithmic gray scale. The x axis is calibrated in terms of wavelength, the y axis is the orthogonal dimension of the CCD chip. Different odd harmonics of the 800 nm Ti:Sapph laser can be clearly distinguished. The background at short wavelength is due to scattering of zero order light; (b) Integration of the signal shown in (a) over a window of around the spectral trace. The predicted position of the different odd harmonics from order 17 to 41 was used to calibrate the spectrum.
Figure 2.
(a) Diffracted signal from the permanent grating on a logarithmic gray scale. The x axis is calibrated in terms of wavelength, the y axis is the orthogonal dimension of the CCD chip. Different odd harmonics of the 800 nm Ti:Sapph laser can be clearly distinguished. The background at short wavelength is due to scattering of zero order light; (b) Integration of the signal shown in (a) over a window of around the spectral trace. The predicted position of the different odd harmonics from order 17 to 41 was used to calibrate the spectrum.
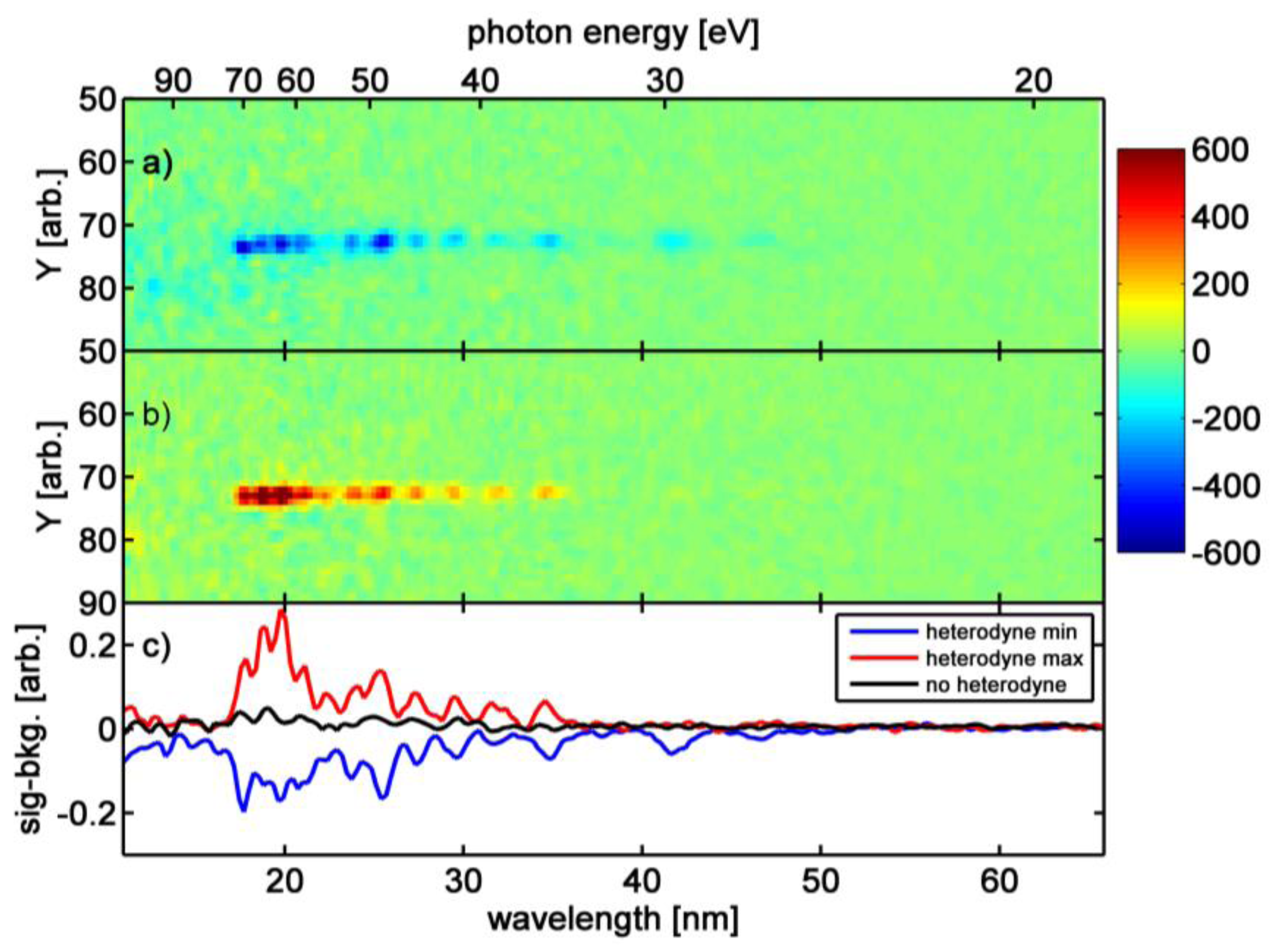
Figure 3a shows a difference plot obtained by subtracting the diffraction image of the unpumped sample (containing a permanent but no transient grating) from the pumped sample diffraction (containing both the transient as well as the permanent grating). The negative signal, also shown as a projection by the blue line in
Figure 3c, is clearly visible. This negative signal can only be explained by an interference of reference and nonlinear signal of two coherent signals from the permanent and transient grating. We further analyze the data to find the relative phase among the signals that must be between π/2 and 3π/2 to result in destructive interference in Equation (1). Each difference image in
Figure 3a,b was acquired for 2.5 s, using consecutive images recorded with and without the pump beams. The minima and maxima of the heterodyne signal (
Figure 3a,b, respectively) were recorded approximately 3 h apart. In addition to the opposite sign due to the heterodyning effect, one observes that the spectral shape of the blue and red curves in
Figure 3c is different. The time between the acquisition of those two spectra was several hours. During this time, the beam pointing and energy of the infrared beam generating the EUV pulse change slightly. This results in observable changes in the EUV spectrum, which is generated in a highly nonlinear process.
Figure 3.
(
a) Difference image of signal without transient grating minus transient grating diffraction. The blue color at the position of the harmonic trace from
Figure 2 clearly indicates a negative difference signal due to heterodyning. The red harmonics in (
b) show a constructive interference due to the heterodyne term. Integrated signals are shown in (
c) together with a measurement that shows no heterodyne contribution due to absence of the permanent grating on a fresh sample spot.
Figure 3.
(
a) Difference image of signal without transient grating minus transient grating diffraction. The blue color at the position of the harmonic trace from
Figure 2 clearly indicates a negative difference signal due to heterodyning. The red harmonics in (
b) show a constructive interference due to the heterodyne term. Integrated signals are shown in (
c) together with a measurement that shows no heterodyne contribution due to absence of the permanent grating on a fresh sample spot.
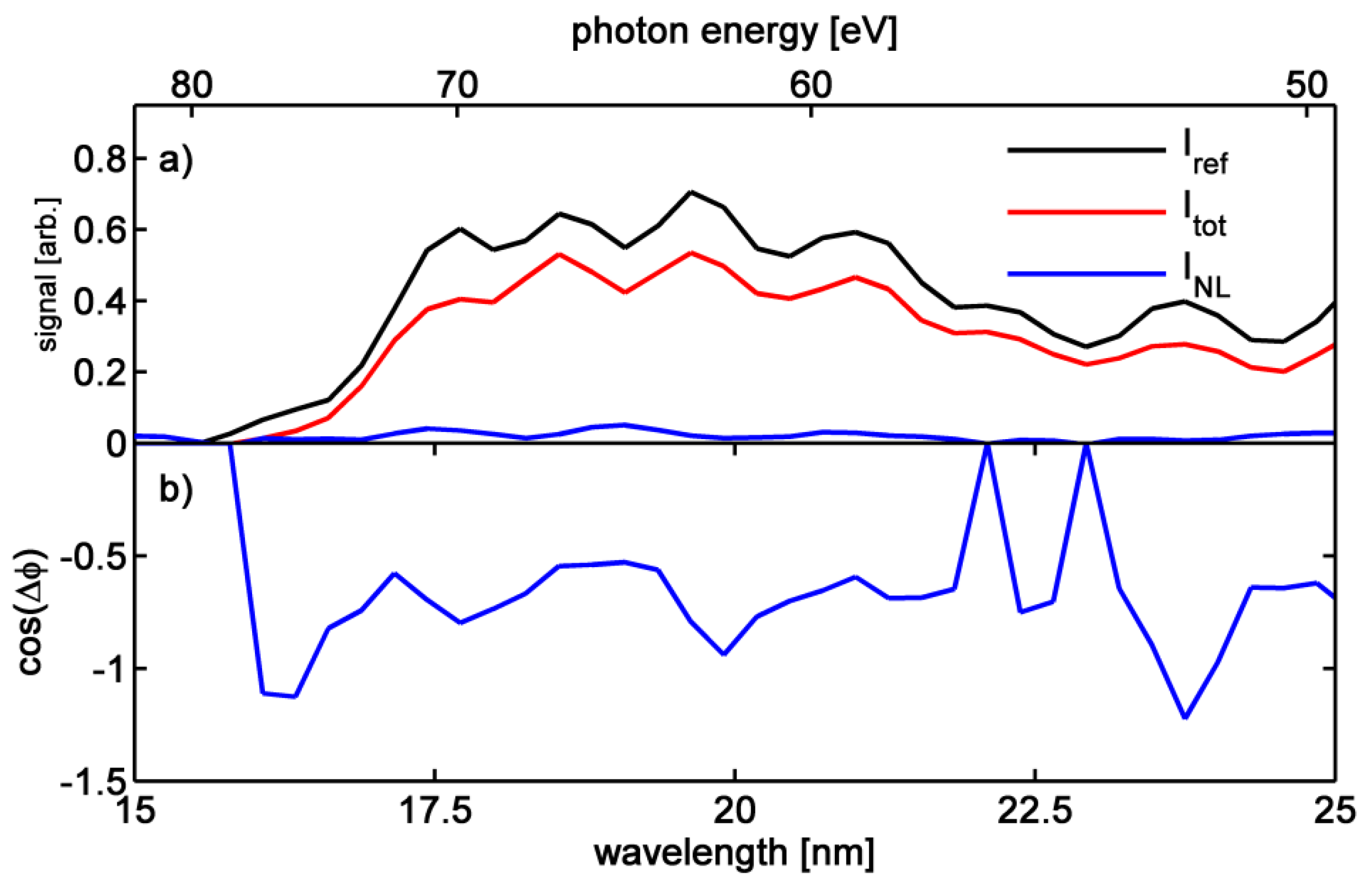
Figure 4a shows the measured intensities of the permanent grating (I
ref) and the total diffraction with permanent and transient grating (I
tot). They are deduced by subtracting a fitted decaying scattering background to the original data. The scattered background hits the camera under an angle that is different from the diffracted signal. This results in fast spatial fringes that will average out the heterodyne contribution with the background. The intensity diffracted from only the transient grating (I
NL) is directly measured by translating the sample macroscopically to drive the permanent grating out of the beam.
Instead of using active phase control to deduce I
NL, we show a retrieval of the phase using the measured, comparatively weak I
NL. For this purpose, we use Equation (1) and set |E
ref + E
NL|
2 = I
tot. We obtain the value of the phase cosine shown in
Figure 4b by cos(Δϕ)=(I
tot − I
NL − I
ref)/√(I
NLI
ref); all intensities are measured by the CCD. We clearly observe the negative sign of this term for the data in
Figure 3a. The average value of cos(Δϕ) is around −0.75, which corresponds to a relative phase between reference and nonlinear signal of about 0.77 π. For relatively high nonlinear signals I
NL, the error in this quantity due to shot noise is about 20%, which seems to describe the fluctuations with wavelength well. If the nonlinear signal however is close to zero, the error of an individual point in
Figure 4b is dominated by the division with that small nonlinear signal leading to a much larger error. With active phase control, this uncertainty will be eliminated and the heterodyned signal will be used to reconstruct I
NL with high fidelity.
Figure 4.
(
a) Intensities of the permanent grating (I
ref), the total diffraction with permanent and transient grating (I
tot) are deduced from the raw scattering images as in
Figure 2 by subtracting an exponential fit to account for the scattering background. The intensity of the transient grating only (I
NL) is directly measured by driving the permanent grating out of the beam. The heterodyned signal I
tot is about one order of magnitude larger than the nonlinear signal; (
b) Using Equation (1) we calculate the value for cos(Δϕ), showing the negative interference.
Figure 4.
(
a) Intensities of the permanent grating (I
ref), the total diffraction with permanent and transient grating (I
tot) are deduced from the raw scattering images as in
Figure 2 by subtracting an exponential fit to account for the scattering background. The intensity of the transient grating only (I
NL) is directly measured by driving the permanent grating out of the beam. The heterodyned signal I
tot is about one order of magnitude larger than the nonlinear signal; (
b) Using Equation (1) we calculate the value for cos(Δϕ), showing the negative interference.
The positive difference signal shown in
Figure 3b and its projection is the red line in
Figure 3c. Comparing it with the pure nonlinear signal without permanent grating (black curve in
Figure 3c) demonstrates that a constructive interference must take place. We repeat the analysis of the destructive interference and now obtain a relative phase of π/3. Our scans were taken without actively controlling the relative phase, however a thermal drift shifts the permanent and transient grating with respect to each other resulting in the observed modulation. We performed many of those scans presented in
Figure 3 and analyzed in
Figure 4. Neighboring scans delivered very similar phases however over the timescale of many hours the phase was slowly drifting. We are thus certain, that the phase drifts during a single scan are negligible. In future we will first stabilize the relative phase and then modulate it by a translating actuator on the permanent grating. Further reduction of the noise in the heterodyne signal can be obtained by lock-in detection with chopped transient grating beams, which leads to a more accurate value for the reference field.
4. Conclusions
We have demonstrated a new self-referencing technique for heterodyning transient grating signals. The method makes use of a permanent grating matching the line spacing of the transient grating for the creation of the reference field. The relative phase among the two can be changed by a relative translation of permanent and transient grating in the direction orthogonal to the grating lines. The method is well suited for short wavelength in the EUV and x-ray region, where amplitude beamsplitters are not easily available and where the short wavelength requires extreme accuracy for the phase -stabilization of different beampaths.
The enormous advantage in this technique is that controlling the phase of a few nanometer wavelength pulses is accomplished by translating a grating by parts of its grating constants, which can be well into the 100 nm to micron range. Here the grating was conveniently written by the laser pulses but one can also produce structured samples. The sample to be studied needs to be attached on a permanent grating. However the permanent grating can be produced from materials different than the one studied in the nonlinear experiment. Conveniently, one would attach the sample onto a prefabricated and completely characterized grating of a given diffraction efficiency, blaze and periodicity. Grating optics are extremely well developed in the extreme ultraviolet and x-ray domain. This scheme makes use of the available technology to overcome the much harder technological problem of beamsplitters.
We have demonstrated the technique for a transient grating on VO2 and observe constructive as well as destructive interference signals as temperature drifts change the translation of permanent and transient grating. The implementation for free electron lasers will need to be critically tested in the future. For seeded lasers, like FERMI in Trieste, the implementation might be very similar because the noise characteristics of the source are similar to a Ti:Sapph laser system. For lasers starting from noise by self-amplified spontaneous emission however, the noise characteristics are dramatically different. Single shot reference spectra of the diffracting beam will most likely be needed to normalize heterodyned signals.