On the Importance of Electron Beam Brightness in High Gain Free Electron Lasers
Abstract
:1. Introduction
2. Merit Functions of High Gain Free Electron Lasers
3. Approaches to FEL Linac-Driver Design
3.1. Pulse Length-Driven Approach
3.2. Wavelength-Driven Approach (with Some Wavelength Tuning)
3.3. Cost-Driven Approach
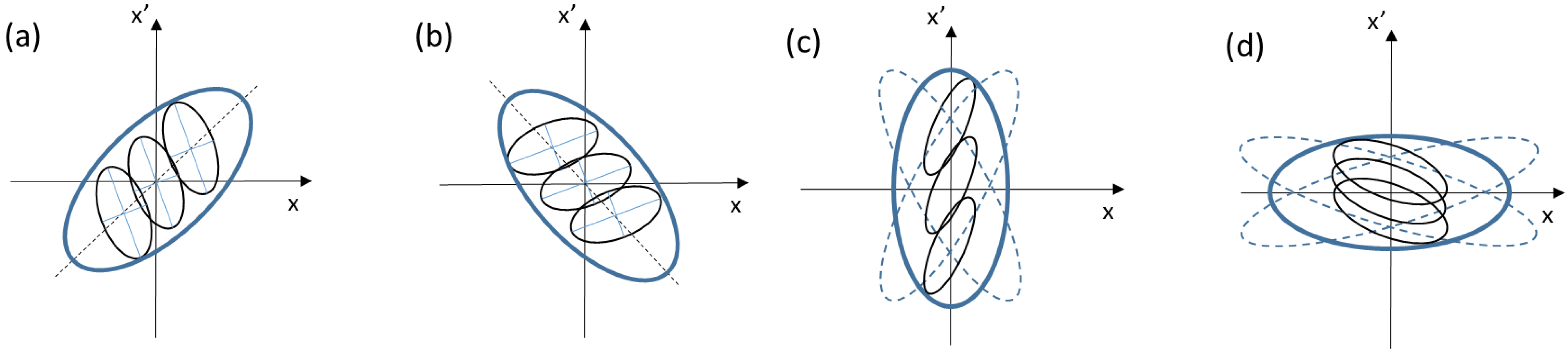
4. Six-Dimensional Electron Beam Brightness
4.1. Definition
4.2. Scaling Laws
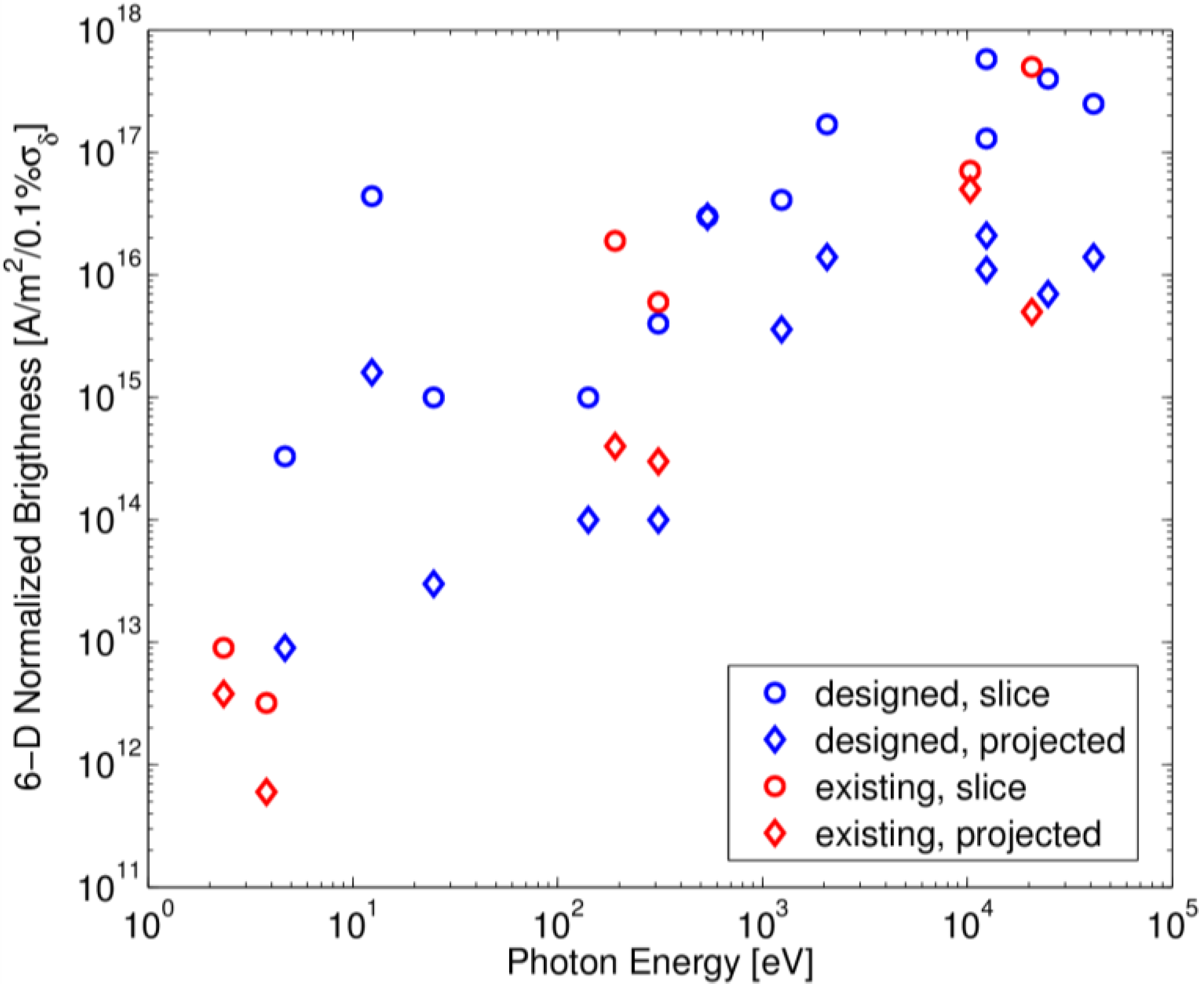
5. Gain Length and Electron Beam Slice Parameters
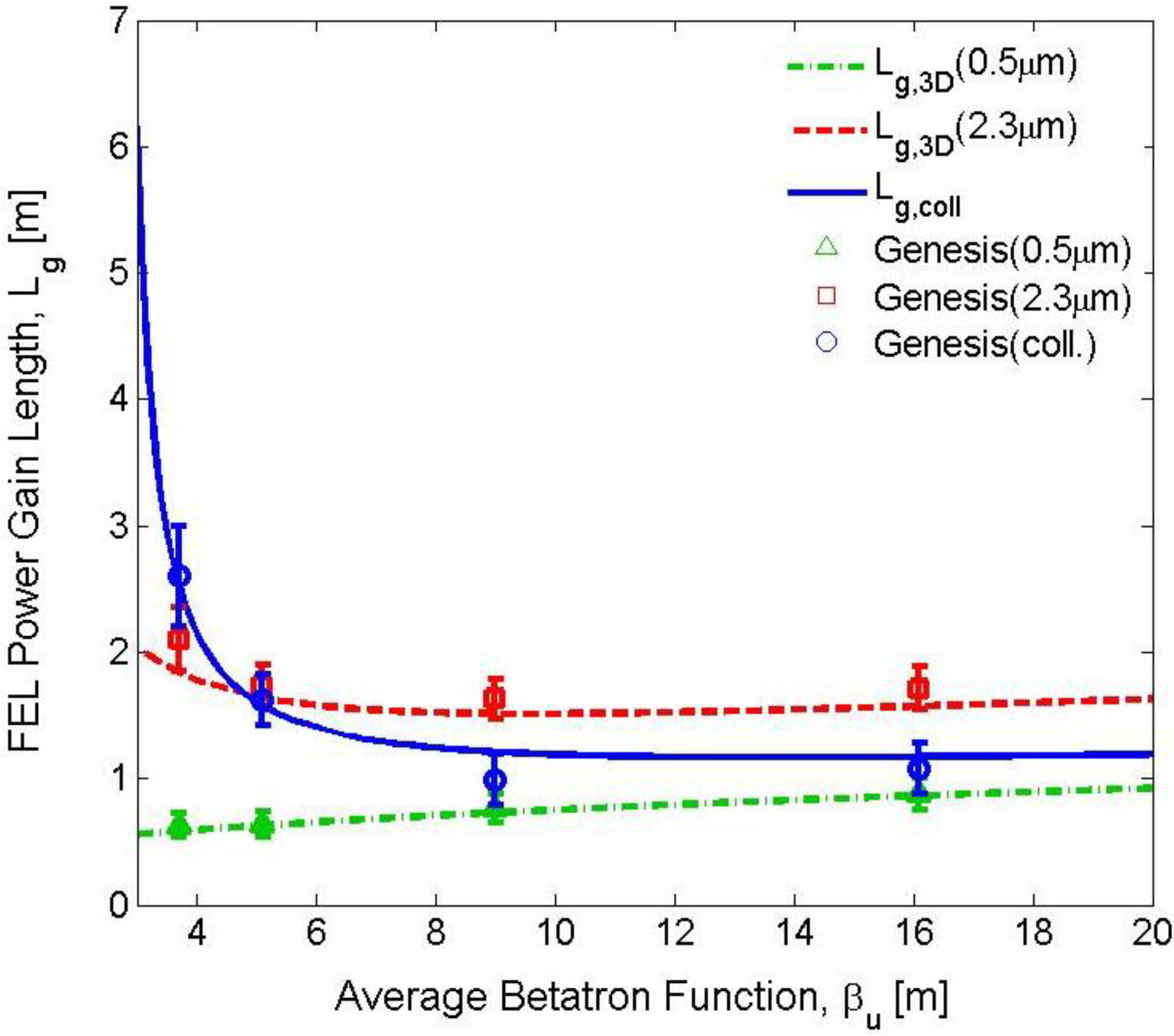
5.1. Three-Dimensional Gain Length
| Parameter | Value | Unit |
|---|---|---|
| Energy | 2.8 | GeV |
| Peak Current | 2.5 | kA |
| Norm. Trasv. Emittance, rms | 2.0 | μm rad |
| Energy Spread, rms | 1.0 | MeV |
| Undulator RMS Parameter, K | 1 | |
| Undulator Type | Planar | |
| Undulator Period Length | 20 | mm |
| Fundamental Wavelength | 1.0 | nm |
5.2. Gain Length and Electron Beam Brightness
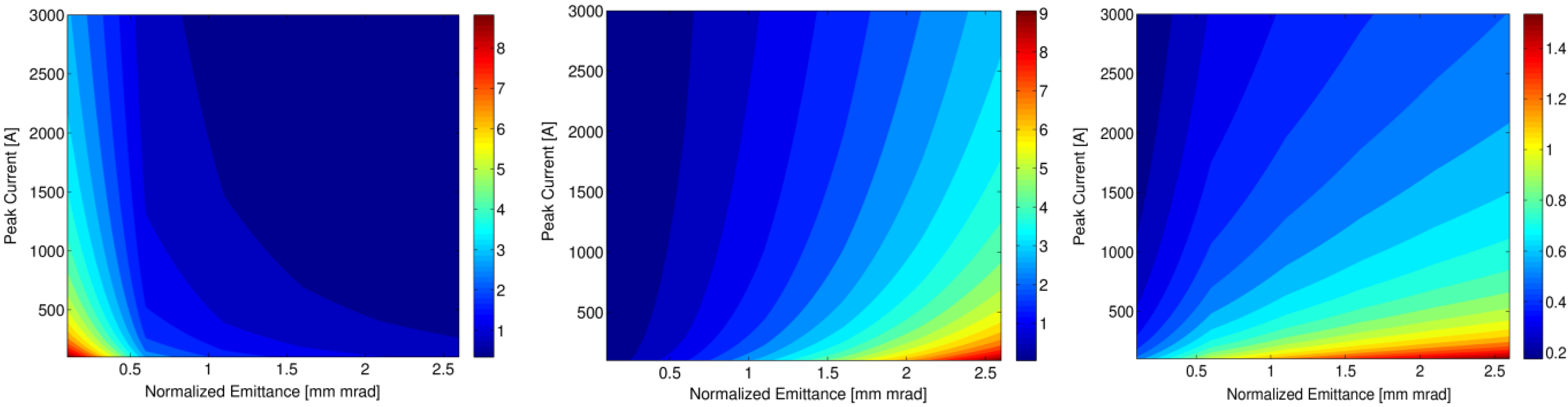
6. Importance of Electron Beam Projected Emittance
6.1. Considerations for FEL Operation
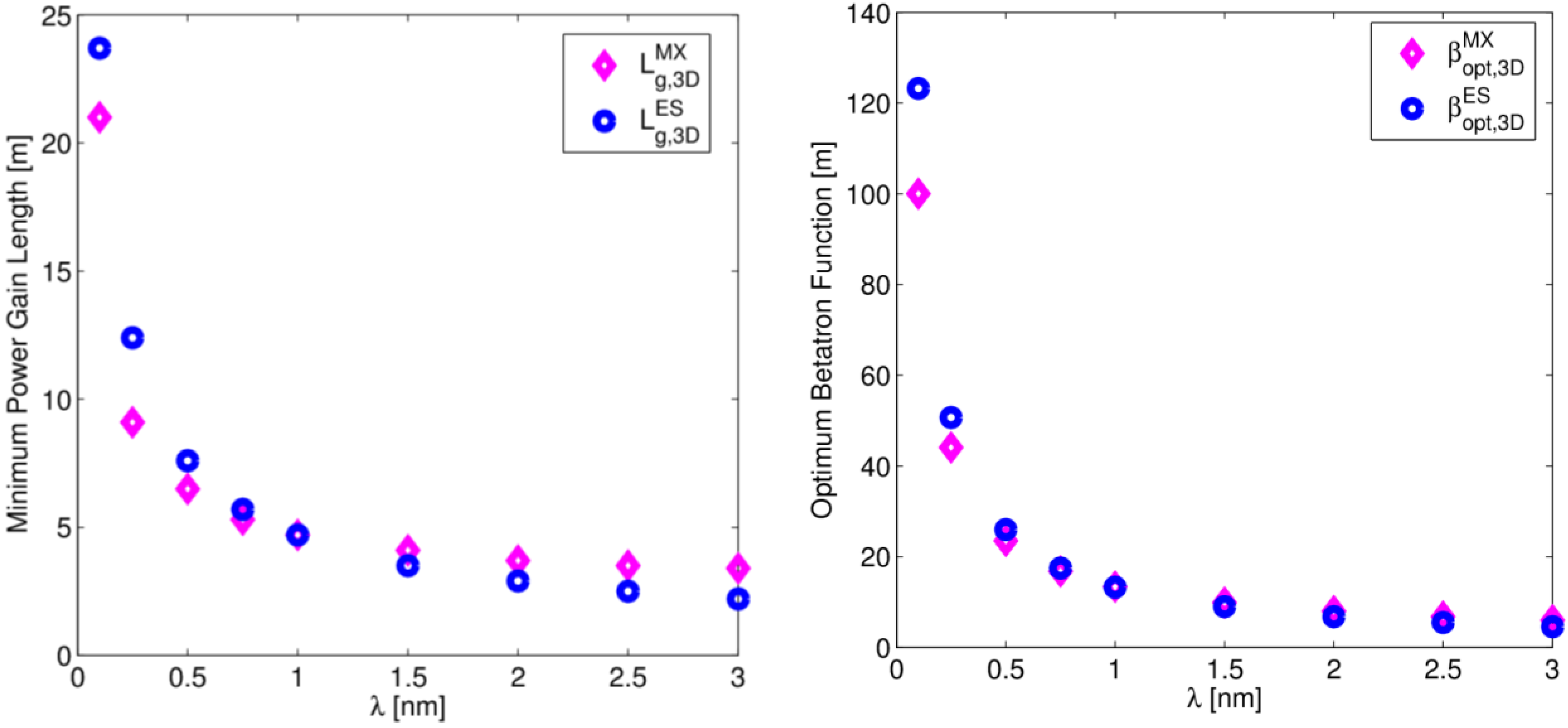
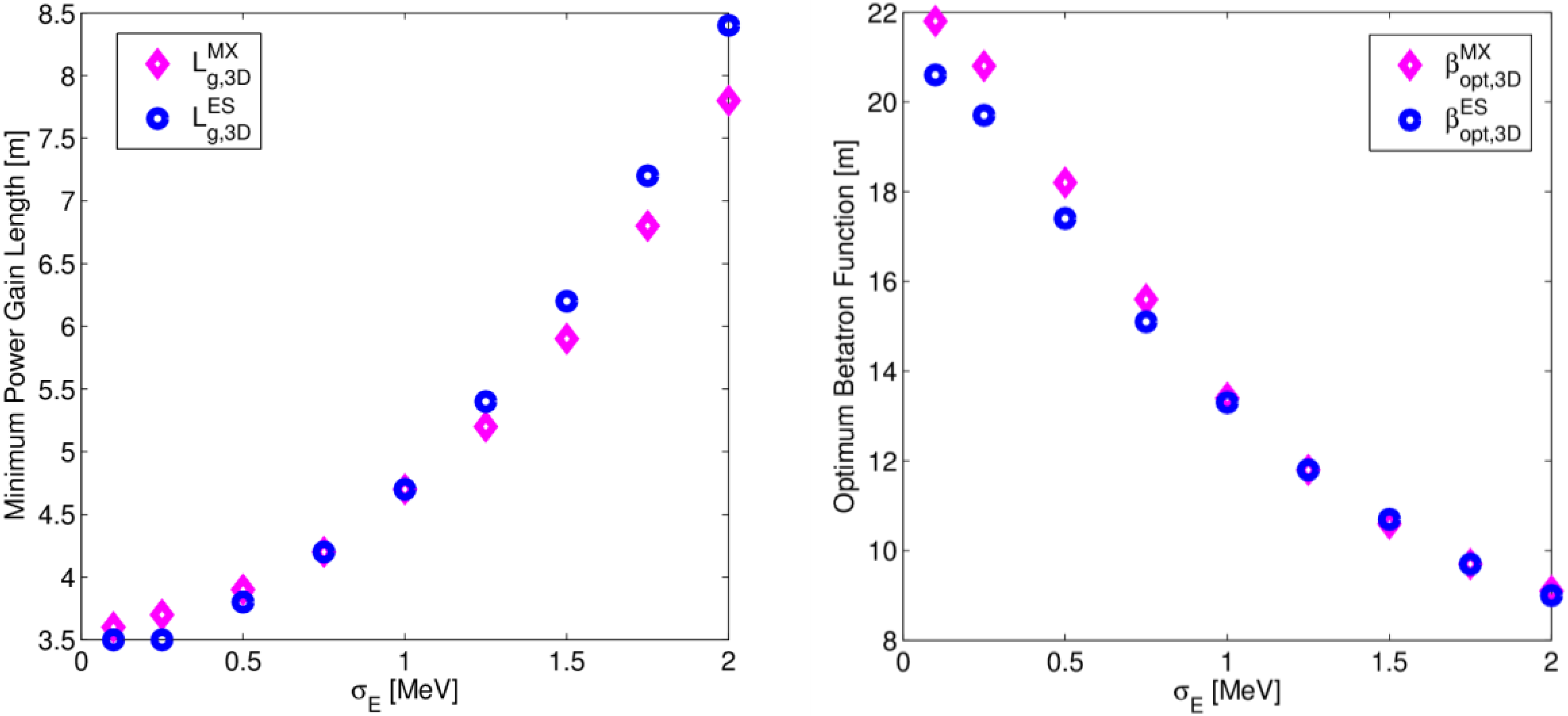
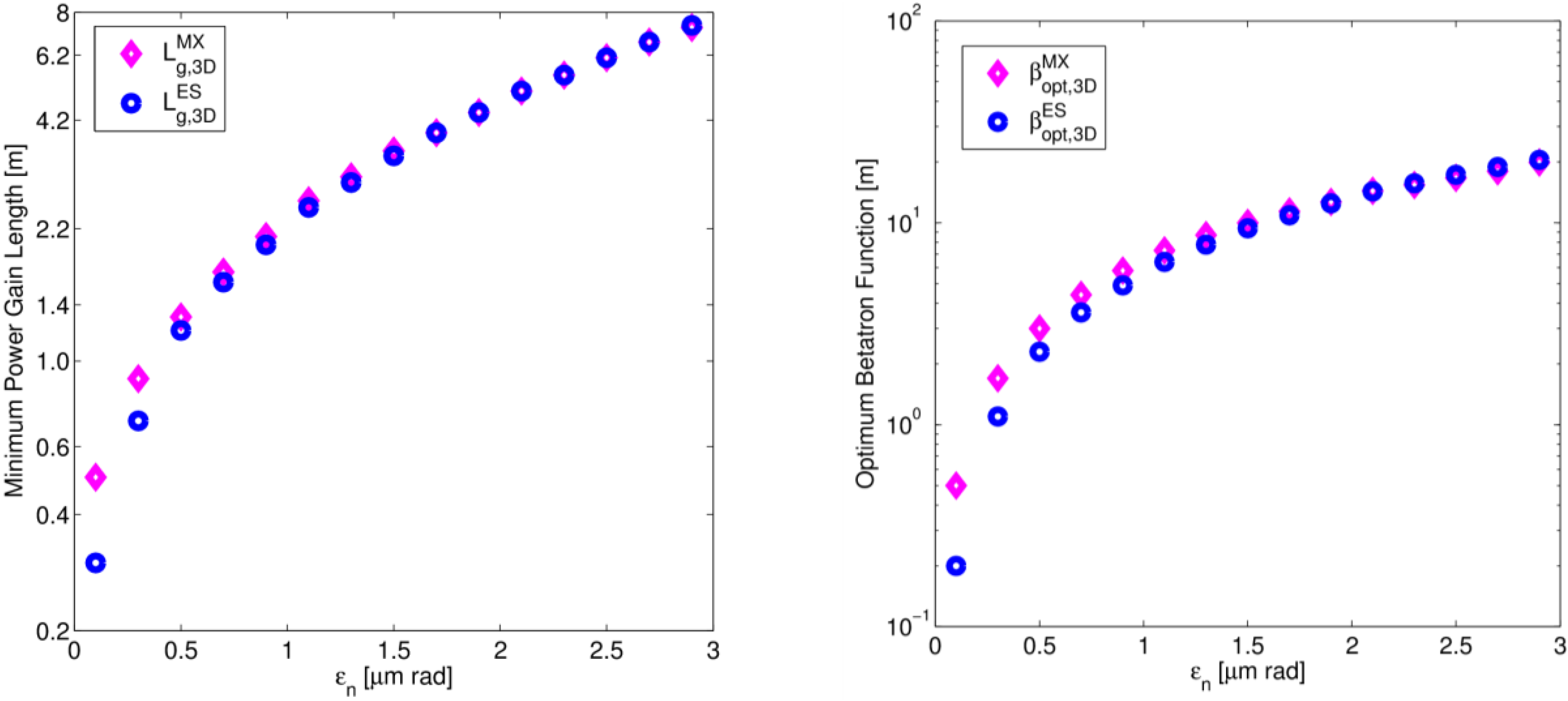
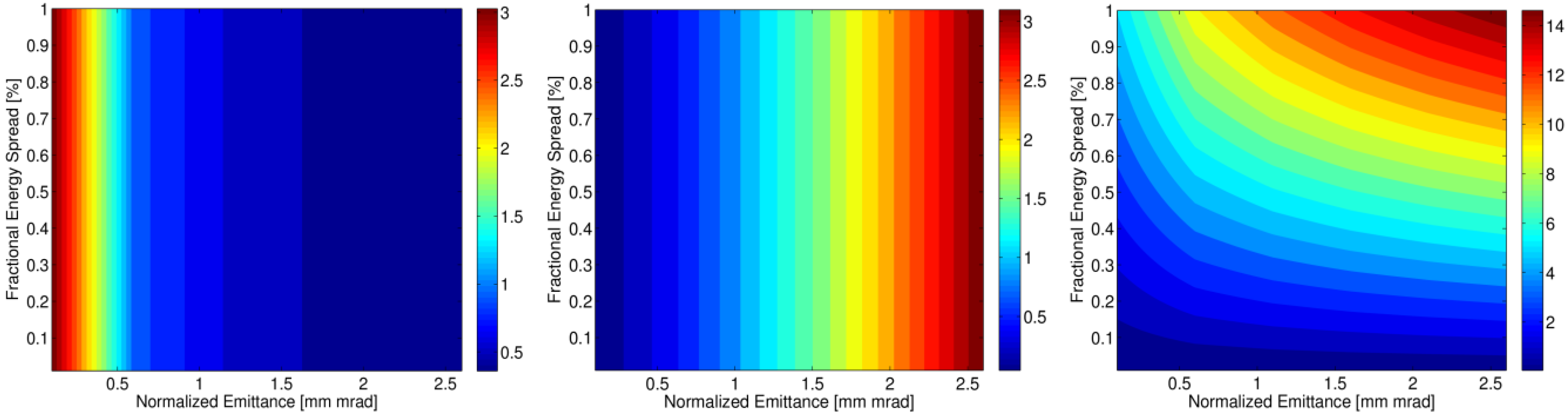
6.2. 3-D Gain Length Including Projected Emittance
6.3. Optimization Study
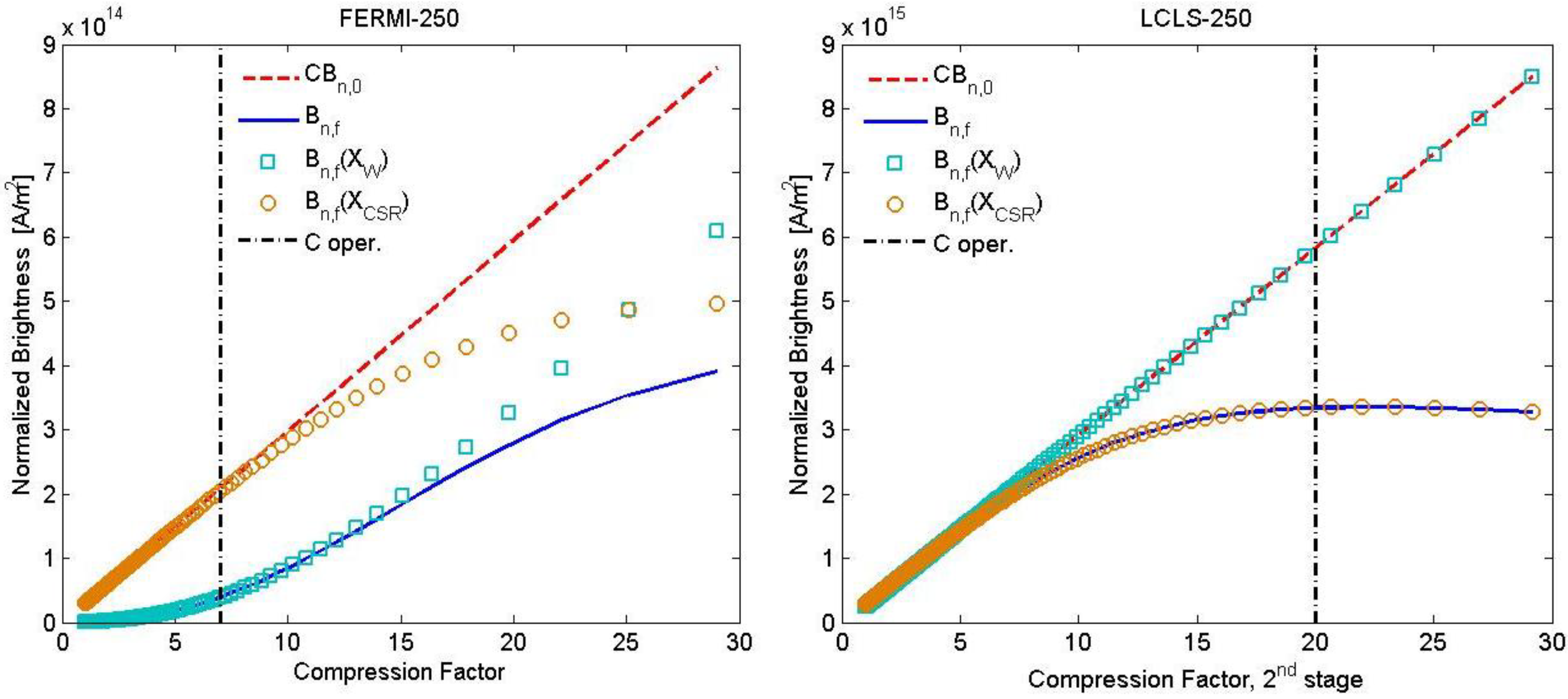
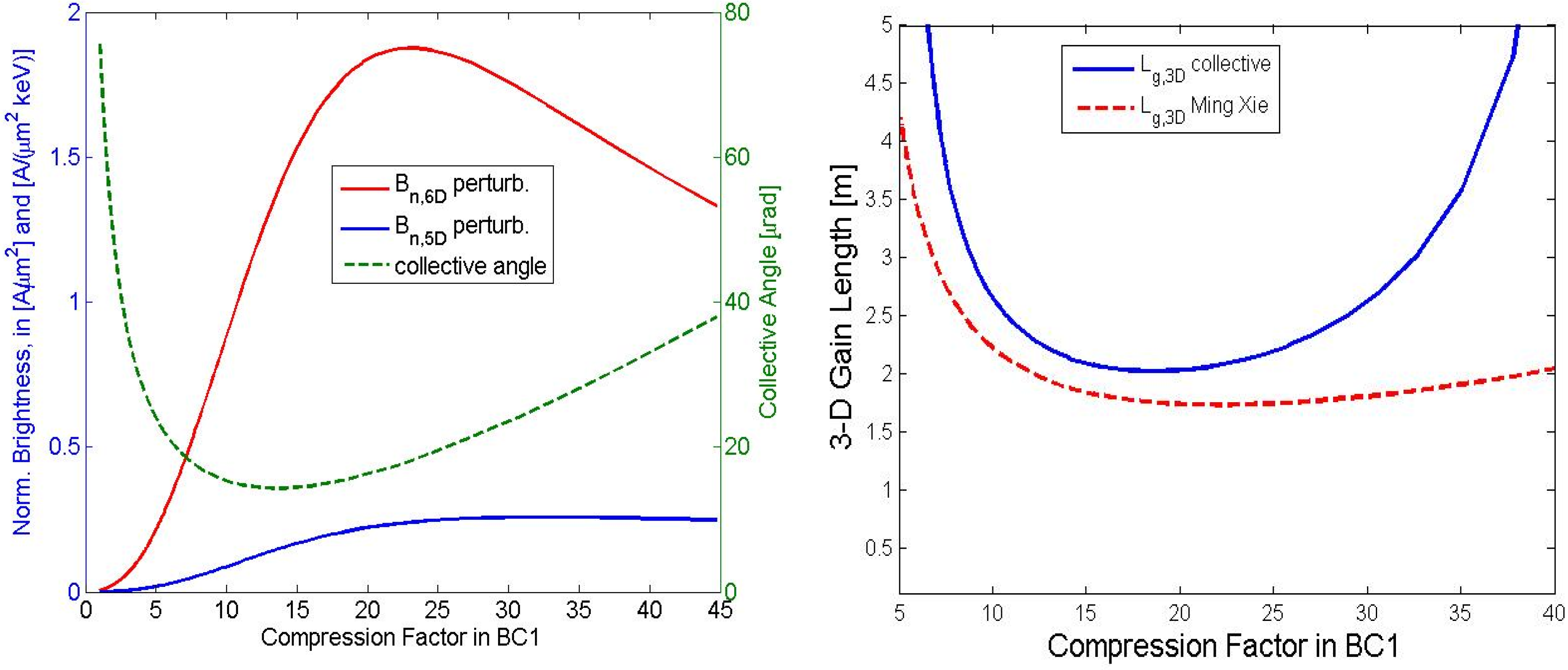
7. Conclusions
Acknowledgments
Conflict of Interest
References
- Madey, J.M.J. Stimulated Emission of Bremsstrahlung in a Periodic Magnetic Field. J. Appl. Phys. 1971, 42. [Google Scholar] [CrossRef]
- Madey, J.M.J.; Schwetman, M.A.; Fairbank, W.M. A Free Electron Laser. IEEE Trans. Nucl. Sci. 1973, 20, 980–983. [Google Scholar] [CrossRef]
- Madey, J.M.J. Wilson Prize article: From vacuum tubes to lasers and back again. Phys. Rev. Spe. Top. Accel. Beams 2014, 17, 074901. [Google Scholar] [CrossRef]
- Bonifacio, R.; Casagrande, F.; Cerchioni, G.; De Salvo Souza, L.; Pierini, P.; Piovella, N. Physics of the High-Gain FEL and Superradiance. La Rivista del Nuovo Cimento 1990, 13, 1–69. [Google Scholar] [CrossRef]
- Schmüser, P.; Dohlus, M.; Rossbach, J. Ultraviolet and Soft X-Ray Free-Electron Lasers. Spring. Tract. Mod. Phys. 2008. [Google Scholar] [CrossRef]
- Saldin, E.L.; Scheidmiller, E.A.; Yurkov, M.V. The Physics of Free Electron Lasers; Springer: New York, NY, USA, 2000. [Google Scholar]
- McNeil, B.W.J.; Thompson, N.R. X-ray free-electron lasers. Nat. Photonics 2012, 239, 814–821. [Google Scholar]
- Pellegrini, C. The history of free-electron lasers. Eur. Phys. J. H 2010, 37, 659–708. [Google Scholar] [CrossRef]
- Huang, Z.; Kim, K.-J. Review of x-ray free-electron laser theory. Phys. Rev. Spe. Top. Accel. Beams 2007, 10, 034801. [Google Scholar] [CrossRef]
- Yu, L.H.; Babzien, M.; Ben-Zvi, I.; DiMauro, L.F.; Doyuran, A.; Graves, W.; Johnson, E.; Krinsky, S.; Malone, R.; Pogorelsky, I.; et al. High-gain harmonic-generation free-electron laser. Science 2000, 37, 932–934. [Google Scholar] [CrossRef]
- Ackermann, W.; Asova, G.; Ayvazyan, V.; Azima, A.; Baboi, N.; Bähr, J.; Balandin, V.; Beutner, B.; Brandt, A.; Brinkmann, R.; et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photon. 2007, 1, 336–342. [Google Scholar] [CrossRef] [Green Version]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.-J.; et al. First lasing and operation of an angstrom-wavelength free-electron laser. Nat. Photon. 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Ishikawa, T.; Aoyagi, H.; Asaka, T.; Asano, Y.; Azumi, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; Furukawa, Y.; et al. A compact X-ray free-electron laser emitting in the sub-angstrom region. Nat. Photon. 2012, 6, 540–544. [Google Scholar] [CrossRef]
- Amann, J.; Berg, W.; Blank, V.; Decker, F.-J.; Ding, Y.; Emma, P.; Feng, Y.; Frisch, J.; Fritz, D.; Hastings, J.; et al. Demonstration of self-seeding in a hard X-ray free-electron laser. Nat. Photon. 2012, 6, 693–698. [Google Scholar] [CrossRef]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photon. 2012, 6, 699–704. [Google Scholar] [CrossRef]
- Allaria, E.; Castronovo, D.; Cinquegrana, P.; Craievich, P.; Dal Forno, M.; Danailov, M.; D’Auria, G.; Demidovich, A.; De Ninno, G.; Di Mitri, S.; et al. Two-stage seeded soft-X-ray free-electron laser. Nat. Photon. 2013, 7, 913–918. [Google Scholar] [CrossRef]
- Kondratenko, A.M.; Saldin, E.L. Generation of coherent radiation by a relativistic electron beam in an undulator. Partic. Accel. 1980, 10, 207–216. [Google Scholar]
- Sprangle, P.; Tang, C.-M.; Manheimer, W.M. Nonlinear theory of free-electron lasers and efficiency enhancement. Phys. Rev. A 1980, 21, 302–318. [Google Scholar] [CrossRef]
- Haus, H. Noise in free-electron laser amplifier. IEEE J. Quant. Electron. 1981, 17, 1427–1435. [Google Scholar] [CrossRef]
- Bonifacio, R.; Pellegrini, C.; Narducci, L.M. Collective instabilities and high-gain regime in a free-electron laser. Opt. Commun. 1984, 50, 373–378. [Google Scholar] [CrossRef]
- Kroll, N.M.; McMullin, W.A. Stimulated emission from relativistic electron passing through a spatially periodic transverse magnetic field. Phys. Rev. A 1978. [Google Scholar] [CrossRef]
- Gover, A.; Livni, Z. Operation Regimes of Cerenkov-Smith-Purcell Free Electron Lasers and T.W. Amplifiers. Opt. Commun. 1978, 26, 375–380. [Google Scholar] [CrossRef]
- Shih, C.C.; Yariv, A. Inclusion of space-charge effects with Maxwell’s equations in the single-particle analysis of free-electron lasers. IEEE J. Quant. Electron. 1981, 17, 1387–1394. [Google Scholar] [CrossRef]
- Dattoli, G.; Marino, A.; Renieri, A.; Romanelli, F. Progress in the Hamiltonian picture of the free-electron laser. IEEE J. Quant. Electron. 1981, 17, 1371–1387. [Google Scholar] [CrossRef]
- Pierce, J.R. Traveling-Wave Tubes; Van Nostrand Company, Inc.: New York, NY, USA, 1950. [Google Scholar]
- Colson, W.B. The nonlinear wave equation for higher harmonics in free-electron laser. IEEE J. Quant. Electron. 1981, 17, 1417–1427. [Google Scholar] [CrossRef]
- Bonifacio, R.; McNeil, B.W.; Pierini, P. Superradiance in the high-gain free-electron laser. Phys. Rev. A 1989, 40, 4467–4475. [Google Scholar] [CrossRef] [PubMed]
- Murphy, J.; Pellegrini, C.; Bonifacio, R. Collective instability of a free electron laser including space charge and harmonics. Opt. Commun. 1985, 53, 197–202. [Google Scholar] [CrossRef]
- Murphy, J.; Pellegrini, C. Generation of High Intensity Coherent Radiation in the Soft X-ray and VUV Region. In Proceedings of the International Conference on Quantum Electronics, San Diego, CA, USA, June 1984.
- Kim, K.-J. Brightness, coherence and propagation characteristics of synchrotron radiation. Nucl. Instrum. Meth. Phys. Res. A 1986, 246, 71–76. [Google Scholar] [CrossRef]
- Leujeune, C.; Aubert, J. Emittance and Brightness: Definitions and Measurements; Academic Press, Inc.: Paris, France, 1980; pp. 159–259. [Google Scholar]
- Barletta, W.A.; Sessler, A.M.; Yu, L.-H. Physically transparent formulation of a free-electron laser in the linear gain regime. Nucl. Instrum. Meth. Phys. Res. A 1993, 331, 491–495. [Google Scholar] [CrossRef]
- Yu, L.-H. Generation of intense UV radiation by subharmonically seeded single-pass free-electron lasers. Phys. Rev. A 1991, 44, 5178–5193. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.H.; Di Mauro, L.; Doyuran, A.; Graves, W.S.; Johnson, E.D.; Heese, R.; Krinsky, S.; Loos, H.; Murphy, J.B.; Rakowsky, G.; et al. First ultraviolet high-gain harmonic-generation free-electron laser. Phys. Rev. Lett. 2003, 91, 074801. [Google Scholar] [CrossRef]
- Labat, M.; Bellaveglia, M.; Bougeard, M.; Carré, B.; Ciocci, F.; Chiadroni, E.; Cianchi, A.; Couprie, M.E.; Cultrera, L.; Del Franco, M.; et al. High-gain harmonic-generation free-electron laser seeded by harmonics generated in gas. Phys. Rev. Lett. 2011, 107, 224801. [Google Scholar] [CrossRef]
- Giannessi, L.; Bellaveglia, M.; Chiadroni, E.; Cianchi, A.; Couprie, M.E.; Del Franco, M.; Di Pirro, G.; Ferrario, M.; Gatti, G.; Labat, M.; et al. Superradiant cascade in a seeded free-electron laser. Phys. Rev. Lett. 2013, 110, 044801. [Google Scholar] [CrossRef]
- Liu, B.; Li, W.B.; Chen, J.H.; Chen, Z.H.; Deng, H.X.; Ding, J.G.; Fan, Y.; Fang, G.P.; Feng, C.; Feng, L.; et al. Demonstration of a widely-tunable and fully-coherent high-gain harmonic-generation free-electron laser. Phys. Rev. Spe. Top. Accel. Beams 2013, 16, 020704. [Google Scholar] [CrossRef]
- Dowell, D. The Limits of Beam Brightness from Photocathode RF Guns. In Proceedings of the 32th International Free Electron Laser Conference, Malmö, Sweden, 23–27 August 2010.
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M. Longitudinal space charge-driven microbunching instability in the TESLA Test Facility linac. Nucl. Instr. Meth. Phys. Res. A 2004, 528, 355–359. [Google Scholar] [CrossRef]
- Huang, Z.; Brachmann, A.; Decker, F.-J.; Ding, Y.; Dowell, D.; Emma, P.; Frisch, J.; Gilevich, S.; Hays, G.; Hering, Ph.; et al. Measurements of the linac coherent light source laser heater and its impact on the x-ray free-electron laser performance. Phys. Rev. Spe. Top. Accel. Beams 2010, 13, 020703. [Google Scholar] [CrossRef]
- Spampinati, S; Allaria, E.; Badano, L.; Bassanese, S.; Biedron, S.; Castronovo, D.; Craievich, P.; Danailov, M.B.; Demidovich, A.; De Ninno, G.; et al. Laser heater commissioning at an externally seeded free-electron laser. Phys. Rev. Spe. Top. Accel. Beams 2014, 17, 120705. [Google Scholar] [CrossRef]
- Hüning, M.; Schlarb, H. Measurement of the beam energy spread in the TTF photo-injector. In Proceedings of the 2003 Particle Accelerator Conference, Portland, OR, USA, 12–16 May 2003.
- Clarke, J.A. The Science and Technology of Undulators and Wigglers; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Bahrdt, J.; Ivanyushenkov, Y. Short Period Undulators for Storage Rings and Free Electron Lasers. J. Phys. 2013, 425, 032001. [Google Scholar]
- Shumail, M.; Bowden, G.; Chang, C.; Neilson, J.; Tantawi, S. Beam dynamics studies of a helical X-band RF undulator. AIP Conf. Proc. 2012, 1507, 752–756. [Google Scholar]
- Chang, C.; Liang, J.; Hei, D.; Becker, M.F.; Tang, K.; Feng, Y.; Yakimenko, V.; Pellegrini, C.; Wu, J. High-brightness X-ray free-electron laser with an optical undulator by pulse shaping. Opt. Express 2013, 21, 32013–32018. [Google Scholar] [CrossRef] [PubMed]
- Petrillo, V.; Serafini, L.; Tomassini, P. Ultrahigh brightness electron beams by plasma-based injectors for driving all-optical free-electron lasers. Phys. Rev. Spe. Top. Accel. Beams 2008, 11, 070703. [Google Scholar] [CrossRef]
- Di Mitri, S.; Spampinati, S. Estimate of free electron laser gain length in the presence of electron beam collective effects. Phys. Rev. Spe. Top. Accel. Beams 2014, 17, 110702. [Google Scholar] [CrossRef]
- Di Mitri, S.; Cornacchia, M. Electron beam brightness in linac drivers for free-electron-lasers. Phys. Rep. 2014, 539, 1–48. [Google Scholar] [CrossRef]
- Pellegrini, C. Progress towards a Soft X-ray FEL. Nucl. Instrum. Meth. Phys. Res. A 1988, 272, 364–367. [Google Scholar] [CrossRef]
- Yu, L.-H.; Krinsky, S.; Gluckstern, R.L. Calculation of universal scaling function for free-electron-laser gain. Phys. Rev. Lett. 1990, 64. [Google Scholar] [CrossRef]
- Chin, Y-H.; Kim, K.-J.; Xie, M. Three-dimensional free electron laser dispersion relation including betatron oscillations. Nucl. Instrum. Meth. Phys. Res. A 1992, 318, 481–488. [Google Scholar] [CrossRef]
- Xie, M. Design optimization for an x-ray free electron laser driven by SLAC linac. In Proceedings of the 16th IEEE Particle Accelerator Conference, Dallas, TX, USA, 1–5 May 1995; pp. 183–185.
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. Design Formulas for VUV and X-Ray FELs. In Proceedings of the 26th International Free Electron Laser Conference, Trieste, Italy, 3 September 2004.
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. The general solution of the eigenvalue problem for a high-gain FEL. Nucl. Instrum. Meth. Phys. Res. A 2001, 475, 86–91. [Google Scholar] [CrossRef]
- Tanaka, T.; Kitamura, H.; Shintake, T. Consideration on the BPM alignment tolerance in X-ray FELs. Nucl. Instrum. Meth. Phys. Res. A 2004, 528, 172–178. [Google Scholar] [CrossRef]
- Chae, Y.-V.; Lumpkin, A.H.; Erdmann, M.; Lewellen, J.W.; Milton, S.V. An Experimental Study of the Beam-Steering Effect on the FEL Gain at LEUTL’s Segmented Undulators. In Proceedings of the 11th International Free Electron Laser Conference, Trieste, Italy, 3 September 2004.
- Di Mitri, S. Maximum brightness of linac-driven electron beams in the presence of collective effects. Phys. Rev. Spe. Top. Accel. Beams 2011, 16, 050701. [Google Scholar] [CrossRef]
- Guetg, M.W.; Beutner, B.; Prat, E.; Reiche, S. Optimization of free electron laser performance by dispersion-based beam-tilt correction. Phys. Rev. Spe. Top. Accel. Beams 2015, 18, 030701. [Google Scholar] [CrossRef]
- Freund, H.P.; O’Shea, P.G. The effect of a matched electron beam on high-gain free-electron-laser amplifier performance. Phys. Rev. Lett. 1998, 80. [Google Scholar] [CrossRef]
- Reiche, S. Compensation of FEL gain reduction by emittance effects in a strong focusing lattice. Nucl. Instr. Meth. Phys. Res. A 2000, 445, 90–94. [Google Scholar] [CrossRef]
- Geloni, G.; Kocharyan, V.; Saldin, E.L. The effects of betatron motion on the preservation of FEL microbunching. DESY 11–081. 2011. Available online: http://arxiv.org/abs/1105.3878v1 (accessed on 19 May 2011).
- Minty, M.G.; Zimmermann, F. Beam Techniques–Beam Control and Manipulation; Report No. SLAC-R-621; SLAC: Stanford, CA, USA, 2003. [Google Scholar]
- Chao, A.W.; Tigner, M. Handbook of Accelerator Physics and Engineering, 3rd ed.; World Scientific: Singapore, 2006. [Google Scholar]
- Reiche, S.; Goldammer, K.; Musumeci, P. Recent Upgrade to the Free-electron Laser Code Genesis 1.3. In Proceedings of the 22nd Particle Accelerator Conference, Albuquerque, NM, USA, 25–29 June 2007.
- Di Mitri, S.; Allaria, E.; Appio, R.; Badano, L.; De Ninno, G.; Castronovo, D.; Cornacchia, M.; Craievich, P.; Ferry, S.; Frolich, L.; et al. Recent Commissioning Experience on the FERMI@Elettra First Bunch Compressor Area: Investigations of Beam Dynamics, Modeling and Control Software. In Proceedings of the 32nd International Free Electron Laser Conference, Malmö, Sweden, 23–27 August 2010.
- Ding, Y.; Brachmann, A.; Decker, F.-J.; Dowell, D.; Emma, P.; Frisch, J.; Gilevich, S.; Hays, G.; Hering, Ph.; Huang, Z.; et al. Measurements and Simulations of Ultralow Emittance and Ultrashort Electron Beams in the Linac Coherent Light Source. Phys. Rev. Lett. 2009, 102, 254801. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Mitri, S. On the Importance of Electron Beam Brightness in High Gain Free Electron Lasers. Photonics 2015, 2, 317-341. https://doi.org/10.3390/photonics2020317
Di Mitri S. On the Importance of Electron Beam Brightness in High Gain Free Electron Lasers. Photonics. 2015; 2(2):317-341. https://doi.org/10.3390/photonics2020317
Chicago/Turabian StyleDi Mitri, Simone. 2015. "On the Importance of Electron Beam Brightness in High Gain Free Electron Lasers" Photonics 2, no. 2: 317-341. https://doi.org/10.3390/photonics2020317
APA StyleDi Mitri, S. (2015). On the Importance of Electron Beam Brightness in High Gain Free Electron Lasers. Photonics, 2(2), 317-341. https://doi.org/10.3390/photonics2020317





