Towards Realistic Simulations of Macromolecules Irradiated under the Conditions of Coherent Diffraction Imaging with an X-ray Free-Electron Laser
Abstract
:1. Introduction
2. Unsolved Issues and Challenges for Simulations of Single Non-Periodic Objects
2.1. Contribution of Inelastic Scattering Background to the Total Scattering Signal
2.2. Realistic Particle Size
2.3. Effect of Interparticle Correlations
2.4. Effect of Pulse Duration for Pulses below 10 fs
2.5. Strongly Non-Equilibrium Evolution of Electron Distribution during Femtosecond Pulse

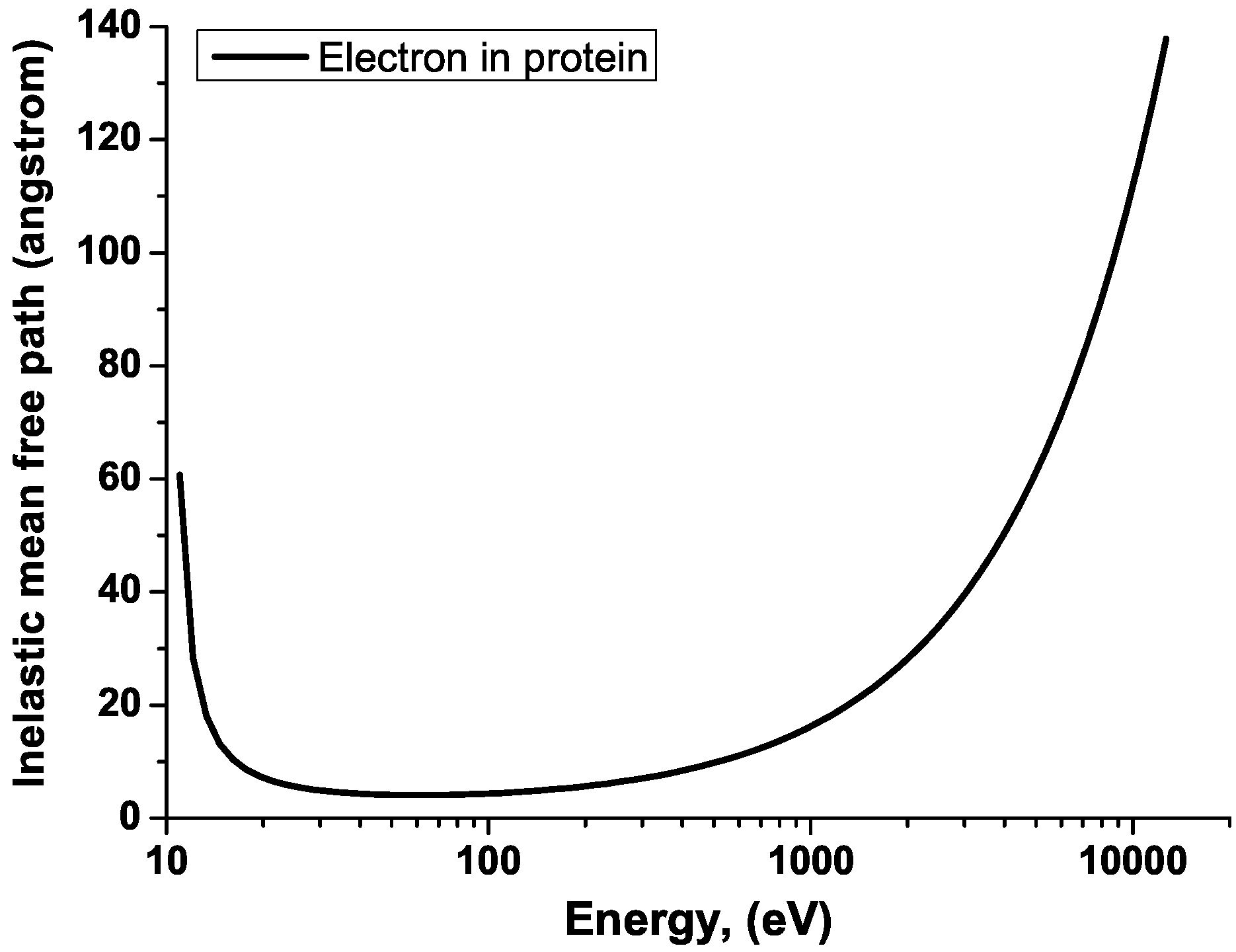
2.6. Effect of Chemical Environment and Plasma Screening on Ionization Dynamics
3. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Neutze, R.; Wouts, R.; van der Spoel, D.; Weckert, E.; Hajdu, J. Potential for biomolecular imaging with femtosecond X-ray pulses. Nature 2000, 406, 752–757. [Google Scholar] [CrossRef] [PubMed]
- Jurek, Z.; Faigel, G.; Tegze, M. Dynamics in a cluster under the influence of intense femtosecond hard X-ray pulses. Eur. Phys. J. D 2004, 29, 217–229. [Google Scholar] [CrossRef]
- Jurek, Z.; Oszlányi, G.; Faigel, G. Imaging atom clusters by hard X-ray free-electron lasers. Europhys. Lett. 2004, 65, 491. [Google Scholar] [CrossRef]
- Hau-Riege, S.P.; London, R.A.; Szöke, A. Dynamics of biological molecules irradiated by short X-ray pulses. Phys. Rev. E 2004, 69, 051906. [Google Scholar] [CrossRef]
- Hau-Riege, S.P.; London, R.A.; Huldt, G.; Chapman, H.N. Pulse requirements for X-ray diffraction imaging of single biological molecules. Phys. Rev. E 2005, 71, 061919. [Google Scholar] [CrossRef]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.J.; et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Ishikawa, T.; Aoyagi, H.; Asaka, T.; Asano, Y.; Azumi, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; Furukawa, Y.; et al. A compact X-ray free-electron laser emitting in the sub-angstrom region. Nat. Photonics 2012, 6, 540–544. [Google Scholar] [CrossRef]
- Altarelli, M.; Brinkmann, R.; Chergui, M.; Decking, W.; Dobson, B.; Dusterer, S.; Grubel, G.; Graeff, W.; Graafsma, H.; Hajdu, J.; et al. The European X-Ray Free-Electron Laser Technical Design Report, DESY Report 2006-097 07/2007. 2007.
- Chapman, H.; Barty, A.; Bogan, M.J.; Boutet, S.; Frank, M.; Hau-Riege, S.P.; Marchesini, S.; Woods, B.W.; Bajt, S.; Benner, W.H. Femtosecond diffractive imaging with a soft-X-ray free-electron laser. Nat. Phys. 2006, 2, 839–843. [Google Scholar] [CrossRef]
- Bogan, M.J.; Benner, W.H.; Boutet, S.; Rohner, U.; Frank, M.; Barty, A.; Seibert, M.M.; Maia, F.; Marchesini, S.; Bajt, S.; et al. Single Particle X-ray Diffractive Imaging. Nano Lett. 2008, 8, 310–316. [Google Scholar] [CrossRef] [PubMed]
- Seibert, M.M.; Ekeberg, T.; Maia, F.R.N.C.; Svenda, M.; Andreasson, J.; Joensson, O.; Odic, D.; Iwan, B.; Rocker, A.; Westphal, D.; et al. Single mimivirus particles intercepted and imaged with an X-ray laser. Nature 2011, 470, 78–U86. [Google Scholar] [CrossRef] [PubMed]
- Barty, A.; Caleman, C.; Aquila, A.; Timneanu, N.; Lomb, L.; White, T.A.; Andreasson, J.; Arnlund, D.; Bajt, S.; Barends, T.R.M.; et al. Self-terminating diffraction gates femtosecond X-ray nanocrystallography measurements. Nat. Photonics 2012, 6, 35–40. [Google Scholar] [CrossRef] [PubMed]
- Lomb, L.; Barends, T.R.M.; Kassemeyer, S.; Aquila, A.; Epp, S.W.; Erk, B.; Foucar, L.; Hartmann, R.; Rudek, B.; Rolles, D.; et al. Radiation damage in protein serial femtosecond crystallography using an X-ray free-electron laser. Phys. Rew. B 2011, 84, 214111. [Google Scholar] [CrossRef] [PubMed]
- Boutet, S.; Lomb, L.; Williams, G.J.; Barends, T.R.M.; Aquila, A.; Doak, R.B.; Weierstall, U.; DePonte, D.P.; Steinbrener, J.; Shoeman, R.L.; et al. High-Resolution Protein Structure Determination by Serial Femtosecond Crystallography. Science 2012, 337, 362–364. [Google Scholar] [CrossRef] [PubMed]
- Chapman, H.N.; Fromme, P.; Barty, A.; White, T.A.; Kirian, R.A.; Aquila, A.; Hunter, M.S.; Schulz, J.; DePonte, D.P.; Weierstall, U.; et al. Femtosecond X-ray protein nanocrystallography. Nature 2011, 470, 73–U81. [Google Scholar] [CrossRef] [PubMed]
- Tenboer, J.; Basu, S.; Zatsepin, N.; Pande, K.; Milathianaki, D.; Frank, M.; Hunter, M.; Boutet, S.; Williams, G.J.; Koglin, J.E.; et al. Time-resolved serial crystallography captures high-resolution intermediates of photoactive yellow protein. Science 2014, 346, 1242–1246. [Google Scholar] [CrossRef] [PubMed]
- Schropp, A.; Schroer, C.G. Dose requirements for resolving a given feature in an object by coherent X-ray diffraction imaging. New J. Phys. 2010, 12, 035016. [Google Scholar] [CrossRef]
- Fratalocchi, A.; Ruocco, G. Single-Molecule Imaging with X-Ray Free-Electron Lasers: Dream or Reality? Phys. Rew. Lett. 2011, 106, 105504. [Google Scholar] [CrossRef]
- Quiney, H.M.; Nugent, K.A. Biomolecular imaging and electronic damage using X-ray free-electron lasers. Nat. Phys. 2011, 7, 142–146. [Google Scholar] [CrossRef]
- Ziaja, B.; Chapman, H.N.; Faeustlin, R.; Hau-Riege, S.; Jurek, Z.; Martin, A.V.; Toleikis, S.; Wang, F.; Weckert, E.; Santra, R. Limitations of coherent diffractive imaging of single objects due to their damage by intense X-ray radiation. New J. Phys. 2012, 14, 115015. [Google Scholar] [CrossRef]
- Lorenz, U.; Kabachnik, N.M.; Weckert, E.; Vartanyants, I.A. Impact of ultrafast electronic damage in single-particle X-ray imaging experiments. Phys. Rew. E 2012, 86, 051911. [Google Scholar] [CrossRef]
- Van Hove, L. Correlations in Space and Time and Born Approximation Scattering in Systems of Interacting Particles. Phys. Rev. 1954, 95, 249. [Google Scholar] [CrossRef]
- Hubbell, J.H.; Veigele, W.J.; Briggs, E.A.; Brown, R.T.; Cromer, D.T.; Howerton, R.J. Atomic form factors, incoherent scattering functions, and photon scattering cross sections. J. Phys. Chem. Ref. Data 1975, 4, 471. [Google Scholar] [CrossRef]
- Slowik, J.M.; Son, S.K.; Dixit, G.; Jurek, Z.; Santra, R. Incoherent X-ray scattering in single molecule imaging. New J. Phys. 2014. [Google Scholar] [CrossRef]
- Son, S.-K.; Santra, R. XATOM: An integrated toolkit for x-ray and atomic physics. In The Hamburg Centre for Ultrafast Imaging International Symposium 2013, Hamburg, Germany, 13–15 November 2013.
- Jurek, Z.; Thiele, R.; Ziaja, B.; Santra, R. Effect of two-particle correlations on X-ray coherent diffractive imaging studies performed with continuum models. Phys. Rev. E 2012, 86, 036411. [Google Scholar] [CrossRef]
- Dixit, G.; Vendrell, O.; Santra, R. Imaging Electronic Quantum Motion with Light. Avaiable online: http://www.pnas.org/content/109/29/11636.full (accessed on 25 February 2015).
- Dixit, G.; Slowik, J.M.; Santra, R. Theory of time-resolved nonresonant X-ray scattering for imaging ultrafast coherent electron motion. Phys. Rev. A 2014, 89, 043409. [Google Scholar] [CrossRef]
- Vrakking, M.J.; Elsaesser, T. X-Ray photonics: X-rays inspire electron movies. Nat. Photonics 2012, 6, 645–647. [Google Scholar] [CrossRef]
- Huldt, G.; Szõke, A.; Hajdu, J. Diffraction imaging of single particles and biomolecules. J. Struct. Biol. 2003, 144, 219–227. [Google Scholar] [CrossRef] [PubMed]
- Bortel, G.; Faigel, G. Classification of continuous diffraction patterns: A numerical study. J. Struct. Biol. 2007, 158, 10–18. [Google Scholar] [CrossRef] [PubMed]
- Shneerson, V.L.; Ourmazd, A.; Saldin, D.K. Crystallography without crystals. I. The common-line method for assembling a three-dimensional diffraction volume from single-particle scattering. Acta Cryst. A 2008, 64, 303. [Google Scholar] [CrossRef] [PubMed]
- Bortel, G.; Faigel, G.; Tegze, M. Classification and averaging of random orientation single macromolecular diffraction patterns at atomic resolution. J. Struct. Biol. 2009, 166, 226–233. [Google Scholar] [CrossRef] [PubMed]
- Bortel, G.; Tegze, M. Common arc method for diffraction pattern orientation. Acta Crystallogr. Sect. A 2011, 67, 533–543. [Google Scholar] [CrossRef] [PubMed]
- Loh, N.T.D.; Elser, V. Reconstruction algorithm for single-particle diffraction imaging experiments. Phys. Rev. E 2009, 80, 026705. [Google Scholar] [CrossRef]
- Fung, R.; Shneerson, V.; Saldin, D.K.; Ourmazd, A. Structure from fleeting illumination of faint spinning objects in flight. Nat. Phys. 2009, 5, 64. [Google Scholar] [CrossRef]
- Tegze, M.; Bortel, G. Selection and orientation of different particles in single particle imaging. J. Struct. Biol. 2013, 183, 389–393. [Google Scholar] [CrossRef] [PubMed]
- Hosseinizadeh, A.; Schwander, P.; Dashti, A.; Fung, R.; D’Souza, R.M.; Ourmazd, A. High-resolution structure of viruses from random diffraction snapshots. Philos. Trans. R Soc. Lond. B Biol. Sci. 2014. [Google Scholar] [CrossRef] [PubMed]
- Loh, N.D.; Bogan, M.J.; Elser, V.; Barty, A.; Boutet, S.; Bajt, S.; Hajdu, J.; Ekeberg, T.; Maia, F.R.N.C.; Schulz, J.; et al. Cryptotomography: Reconstructing 3D Fourier Intensities from Randomly Oriented Single-Shot Diffraction Patterns. Phys. Rev. Lett. 2010, 104, 225501. [Google Scholar] [CrossRef] [PubMed]
- Mancuso, A. Conceptual Design Report Scientific Instrument Single Particles, Clusters, and Biomolecules (SPB). European XFEL, XFEL.EU TR-2011-007. 2012. [Google Scholar]
- Ziaja, B.; de Castro, A.R.B.; Weckert, E.; Möller, T. Modelling dynamics of samples exposed to free-electron-laser radiation with Boltzmann equations. Eur. Phys. J. D 2006, 40, 465–480. [Google Scholar] [CrossRef]
- Hau-Riege, S.P.; London, R.A.; Szoke, A. Dynamics of biological molecules irradiated by short X-ray pulses. Phys. Rev. E 2004, 69, 051906. [Google Scholar] [CrossRef]
- Murphy, B.; Osipov, T.; Jurek, Z.; Fang, L.; Son, S.K.; Mucke, M.; Eland, J.; Zhaunerchyk, V.; Feifel, R.; Avaldi, L.; et al. Femtosecond X-ray-induced explosion of C60 at extreme intensity. Nat. Commun. 2014. [Google Scholar] [CrossRef] [PubMed]
- Tachibana, T.; Jurek, Z.; Fukuzawa, H.; Motomura, K.; Nagaya, K.; Wada, S.; Johnsson, P.; Siano, M.; Mondal, S.; Ito, Y.; et al. Nanoplasma formation by high intensity hard X-rays. submitted.
- Jurek, Z.; Ziaja, B.; Santra, R. Applicability of the classical molecular dynamics method to study X-ray irradiated molecular systems. J. Phys. B 2014, 47, 124036. [Google Scholar] [CrossRef]
- Son, S.K.; Young, L.; Santra, R. Impact of hollow-atom formation on coherent X-ray scattering at high intensity. Phys. Rev. A 2011, 83, 033402. [Google Scholar] [CrossRef]
- Perkins, S.T. Tables and Graphs of Atomic Subshell and Relaxation Data Derived from the LLNL Evaluated Atomic Data Library (EADL). Z=1–100; UCRL-50400-V-30; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1991. [Google Scholar]
- Hau-Riege, S.P. Photoelectron Dynamics in X-Ray Free-Electron-Laser Diffractive Imaging of Biological Samples. Phys. Rev. Lett. 2012, 108, 238101. [Google Scholar] [CrossRef] [PubMed]
- Ziaja, B.; Wabnitz, H.; Wang, F.; Weckert, E.; Möller, T. Energetics, Ionization, and Expansion Dynamics of Atomic Clusters Irradiated with Short Intense Vacuum-Ultraviolet Pulses. Phys. Rev. Lett. 2009, 102, 205002. [Google Scholar] [CrossRef] [PubMed]
- Ziaja, B.; London, R.A.; Hajdu, J. Unified model of secondary electron cascades in diamond. J. Appl. Phys. 2005, 97, 064905. [Google Scholar] [CrossRef]
- Chapman, H.N.; Caleman, C.; Timneanu, N. Diffraction before destruction. Philos. Trans. R Soc. Lond. B Biol. Sci. 2014, 369. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3954–3967. [Google Scholar] [CrossRef] [PubMed]
- Vinko, S.; Ciricosta, O.; Cho, B.; Engelhorn, K.; Chung, H.K.; Brown, C.; Burian, T.; Chalupský, J.; Falcone, R.; Graves, C.; et al. Creation and diagnosis of a solid-density plasma with an X-ray free-electron laser. Nature 2012, 482, 59–62. [Google Scholar] [CrossRef] [PubMed]
- Ciricosta, O.; Vinko, S.M.; Chung, H.K.; Cho, B.I.; Brown, C.R.D.; Burian, T.; Chalupský, J.; Engelhorn, K.; Falcone, R.W.; Graves, C.; et al. Direct Measurements of the Ionization Potential Depression in a Dense Plasma. Phys. Rev. Lett. 2012, 109, 065002. [Google Scholar] [CrossRef] [PubMed]
- Cho, B.I.; Engelhorn, K.; Vinko, S.M.; Chung, H.K.; Ciricosta, O.; Rackstraw, D.S.; Falcone, R.W.; Brown, C.R.D.; Burian, T.; Chalupský, J.; et al. Resonant Kα Spectroscopy of Solid-Density Aluminum Plasmas. Phys. Rev. Lett. 2012, 109, 245003. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.C.; Pyatt, K.D. Lowering of Ionization Potentials in Plasmas. Astrophys. J. 1966, 144, 1203–1211. [Google Scholar] [CrossRef]
- Son, S.K.; Thiele, R.; Jurek, Z.; Ziaja, B.; Santra, R. Quantum-Mechanical Calculation of Ionization-Potential Lowering in Dense Plasmas. Phys. Rev. X 2014, 4, 031004. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziaja, B.; Jurek, Z.; Medvedev, N.; Saxena, V.; Son, S.-K.; Santra, R. Towards Realistic Simulations of Macromolecules Irradiated under the Conditions of Coherent Diffraction Imaging with an X-ray Free-Electron Laser. Photonics 2015, 2, 256-269. https://doi.org/10.3390/photonics2010256
Ziaja B, Jurek Z, Medvedev N, Saxena V, Son S-K, Santra R. Towards Realistic Simulations of Macromolecules Irradiated under the Conditions of Coherent Diffraction Imaging with an X-ray Free-Electron Laser. Photonics. 2015; 2(1):256-269. https://doi.org/10.3390/photonics2010256
Chicago/Turabian StyleZiaja, Beata, Zoltan Jurek, Nikita Medvedev, Vikrant Saxena, Sang-Kil Son, and Robin Santra. 2015. "Towards Realistic Simulations of Macromolecules Irradiated under the Conditions of Coherent Diffraction Imaging with an X-ray Free-Electron Laser" Photonics 2, no. 1: 256-269. https://doi.org/10.3390/photonics2010256
APA StyleZiaja, B., Jurek, Z., Medvedev, N., Saxena, V., Son, S.-K., & Santra, R. (2015). Towards Realistic Simulations of Macromolecules Irradiated under the Conditions of Coherent Diffraction Imaging with an X-ray Free-Electron Laser. Photonics, 2(1), 256-269. https://doi.org/10.3390/photonics2010256



