Photo-Ionization of Noble Gases: A Demonstration of Hybrid Coupled Channels Approach

Abstract

We present here an application of the recently developed hybrid coupled channels approach to study photo-ionization of noble gas atoms: Neon and Argon. We first compute multi-photon ionization rates and cross-sections for these inert gas atoms with our approach and compare them with reliable data available from R-matrix Floquet theory. The good agreement between coupled channels and R-matrix Floquet theory show that our method treats multi-electron systems on par with the well established R-matrix theory. We then apply the time dependent surface flux (tSURFF) method with our approach to compute total and angle resolved photo-electron spectra from Argon with linearly and circularly polarized 12 nm wavelength laser fields, a typical wavelength available from Free Electron Lasers (FELs).

1. Introduction

Photo-ionization has been a useful tool in understanding electronic structure of materials for several decades. The availability of highly tunable, high photon flux sources like FELs and synchrotron has deepened our dependence on photo-ionization experiments by providing very accurate structural information [1]. Noble gas atoms are chemically inert due to their closed shell electronic configuration. This makes them attractive systems for experimental studies. In the field of strong field physics, they have been extensively used to study ionization properties and core-hole dynamics, and they were used in proof of principle experiments to demonstrate time resolved electron spectroscopy. Krypton atoms were used in [2] to demonstrate that attosecond transient absorption spectroscopy can be used to observe real time motion of valence electrons. The presence of cooper minimum in high harmonic spectra from Argon is considered as a proof that high harmonic generation carries the electronic structural information in it and has attracted many photo-ionization studies, for example [3,4]. Inert gas atoms like helium and neon have also been widely used to investigate double ionization [1], a process that can be used to understand electron correlation in photo-emission. Using attosecond streaking, time delays in photo-emission from Neon were measured in [5]. It was experimentally found that the 2s and 2p electrons are emitted with a relative time delay of 20 as. This remains an unexplained result to date. The closest theoretical estimate so far has been from the R-matrix theory that predicts around 10 as [6] for the time delay. The difficulty in producing accurate theoretical estimates stems from the difficulties in numerical treatment of many body problem.

In the theoretical domain, the major road block in understanding these photo-ionization processes is the multi-dimensionality of the wavefunction which leads to a very unfavorable scaling of numerical solvers for the time dependent Schrödinger equation (TDSE). In the weak field regime, it may be possible to use perturbation theory to compute the ionization properties. In [7], multi-photon perturbation theory was used to compute two, three and four photon ionization cross-sections of helium. However, in [8] it has been shown that even in the “perturbative” regime, resonances in helium can lead to non-perturbative effects in photo-ionization, pointing to the limits of applicability of multi-photon perturbation theory. Multi-photon perturbation theory is also limited in its application to multi-electron systems as computing the multi-electron scattering states and the whole set of intermediate states involved in a multi-photon ionization process can be an impractical task. Therefore, one resorts to numerical solutions of the TDSE even in the perturbative regime.

As a full dimensional numerical solution for multi-electron TDSE is not feasible, several methods have been developed in the past decade that only use a part of the Hilbert space that is seemingly important for the ionization process. Some of them include multi-configuration time dependent hartree-fock method [9], time dependent Configuration Interaction method [10], time dependent restricted-active-space configuration-interaction method [11], time dependent R-matrix method [12] and coupled channels method [13]. However, in terms of multi-photon ionization of atoms, R-matrix theory is the main source of available theoretical data. There have been many studies on multi-photon ionization of noble gas atoms performed using R-matrix theory, for example [12,14,15].

We recently developed a hybrid coupled channels method [16] to study photo-ionization of multi-electron systems. The method combines multi-electron bound states from quantum chemistry and one-electron numerical basis sets to construct N-electron wavefunctions that are used as basis functions to solve the TDSE. This method in conjunction with the time dependent surface flux method [17,18] can compute accurate single photo-electron spectra. We present here an application of our method to study photo-ionization from noble gas atoms-Neon and Argon. We compute multi-photon ionization rates and cross-sections and compare them with reliable data available from the R-matrix Floquet approach. We find that our results are in good agreement with the R-matrix Floquet (RMF) calculations. This shows that our method treats ionization of multi-electron systems on par with the well established R-matrix theory. We then compute photo-electron spectra from Argon with linearly and circularly polarized 12 nm wavelength laser fields. The results presented here are the first steps to computing photo-electron spectra at long wavelengths that are currently inaccessible from any theoretical approach that considers multi-electron effects.

2. Hybrid Coupled Channels Method

We solve the N-electron TDSE:

$$i\frac{\partial \Psi }{\partial t}=\widehat{H}\Psi$$

(1)

in dipole approximation using a hybrid anti-symmetrized coupled channels (haCC) basis composed of multi-electron states from quantum chemistry and a numerical one-electron basis. We refer the reader to [16] for an elaborate description of the approach and present here the salient features of the method. We discretize the N-electron wavefunction as:

$$|\Psi \left(t\right)\rangle \approx \sum _{\mathcal{I}}|\mathcal{I}\rangle C_{\mathcal{I}}\left(t\right)+|\mathcal{G}\rangle C_{\mathcal{G}}\left(t\right)$$

(2)

where

$$|\mathcal{I}\rangle =\mathcal{A}[|i\rangle |I\rangle ]$$

(3)

Here, $\mathcal{A}$ indicates anti-symmetrization, $C_{\mathcal{G}}$ and $C_{\mathcal{I}}$ are the time dependent coefficients, $|i\rangle$ represents a numerical one-electron basis and $|I\rangle$ are (N-1) electron wavefunctions which are chosen to be the eigen states of the single ionic hamiltonian obtained from the Multi-Reference Configuration Interaction Singles Doubles (MR-CISD) [19] level of quantum chemistry. $|\mathcal{G}\rangle$ is chosen as the ground state of the N-electron system, also obtained from MR-CISD level of quantum chemistry. As correlated states need many ionic states to be correctly represented, we include the ground state explicitly in the basis for the sake of efficiency. We use COLUMBUS [19] quantum chemistry code to compute these states. The basis is suitable to study single ionization problems, and it can represent an active electron in a polarizable core. By active electron we mean, the basis set representing this electron is flexible enough to represent bound as well as continuum states. The active electron is represented using a high order finite element basis, $|f_i\left(r\right)\rangle$, for the radial coordinate and spherical harmonics, $Y_{l_i{m}_i}$, for the angular coordinates.

$$|i\left(\overrightarrow{r}\right)\rangle =|f_i\left(r\right)\rangle |Y_{l_i{m}_i}(\Omega )\rangle$$

(4)

Using basis Equation (2) with TDSE Equation (1) leads to a set of coupled ordinary differential equations for the time dependent coefficients:

$$\begin{array}{c}\hfill i\left[\langle \mathcal{G}|\mathcal{G}\rangle \frac{d{C}_{\mathcal{G}}}{dt}+\langle \mathcal{G}|\mathcal{I}\rangle \frac{d{C}_{\mathcal{I}}}{dt}\right]=\langle \mathcal{G}|\widehat{H}|\mathcal{G}\rangle C_{\mathcal{G}}+\langle \mathcal{G}|\widehat{H}|\mathcal{I}\rangle C_{\mathcal{I}}\end{array}$$

(5)

$$\begin{array}{c}\hfill i\left[\langle \mathcal{I}|\mathcal{G}\rangle \frac{d{C}_{\mathcal{G}}}{dt}+\langle \mathcal{I}|\mathcal{I}\rangle \frac{d{C}_{\mathcal{I}}}{dt}\right]=\langle \mathcal{I}|\widehat{H}|\mathcal{G}\rangle C_{\mathcal{G}}+\langle \mathcal{I}|\widehat{H}|\mathcal{I}\rangle C_{\mathcal{I}}.\end{array}$$

(6)

We solve them with an explicit fourth order Runge-Kutta solver with an automatic step size controller. A mixed gauge representation of the dipole operator is used for the reasons discussed in [20]. To absorb the wavefunction at the box boundaries we use infinite range Exterior Complex scaling (irECS) [21]. Finally, we employ the time dependent surface flux (tSURFF) method [17,18] to compute photo-electron spectra.

One of the main advantages of a coupled channels ansatz is that the time propagation scales quadratically with the number of ionic channels included and is independent of the number of electrons. In our haCC scheme, the ionic states are directly read from the output of a quantum chemistry calculation. This gives us the flexibility to treat ionic states at different levels of quantum chemistry. Any coupled channels scheme based only on ionic bound state channels also suffers from several limitations. The description of polarization of the ionic core is incomplete without the ionic continuum. The quantum chemistry ionic states based on gaussian orbitals will not have the exact asymptotic behavior. These limitations can lead to certain inaccuracies in our calculations. However, the high dimensionality of the multi-electron wavefunction limits us to go beyond these kind of approximations and all multi-electron TDSE solvers suffer from these kind of limitations.

3. Results

3.1. One- and Two-Photon Cross-Sections of Neon

In this section, we compute the one- and the two-photon ionization cross-sections of Neon and compare them with the results from experiments and the R-matrix theory. We use in our Neon basis four ionic states-the three fold degenerate $1s^{2}2s^{2}2p^5$ state and the $1s^{2}2s2p^6$ state. This implies that we have four possible ionization channels:

$$\begin{array}{cc}\hfill 1s^{2}2s^{2}2p^6& \to 1s^{2}2s^{2}2p^5+e^{-}\hfill \\ & \to 1s^{2}2s2p^6+e^{-}\hfill \end{array}$$

(7)

The configurations used to represent the states are only symbolic and as we compute them using Configuration Interaction theory [19], each multi-electron state is composed of several configurations. In our time dependent approach we compute cross-sections using Equation (51) in [12]:

$${\sigma }^{\left(n\right)}={\left(8\pi \alpha \right)}^n{\left(\frac{3.5\times {10}^{16}}{I}\right)}^n{\omega }^n\Gamma a_0^{2n}{t}_0^{n-1}$$

(8)

where ${\sigma }^{\left(n\right)}$ is the n photon ionization cross-section in units $c{m}^{2n}/s^{n-1}$, I is the intensity in $W/c{m}^2$, ω is the laser frequency in a.u, α is the fine structure constant and $a_0$, $t_0$ are atomic units of length and time respectively in cms. Γ is the total ionization rate in a.u. which is computed in a time dependent approach by monitoring the rate at which the norm of the wavefunction in a certain inner region drops. We use for our computations a 150-cycle continuous wave laser pulse with a 3-cycle ${cos}^2$ ramp up and ramp down and with an intensity of ${10}^{12}W/c{m}^2$. Calculations were performed with a simulation volume radius of up to 100 a.u. and an angular momentum expansion of upto $L_{max}=6$ for the active electron basis.

Figure 1 shows one-photon ionization cross-sections from Neon in the photon energy range 50–125 eV with haCC and from experimental results published in [22]. We find a very good agreement between the experimental results and our calculations.

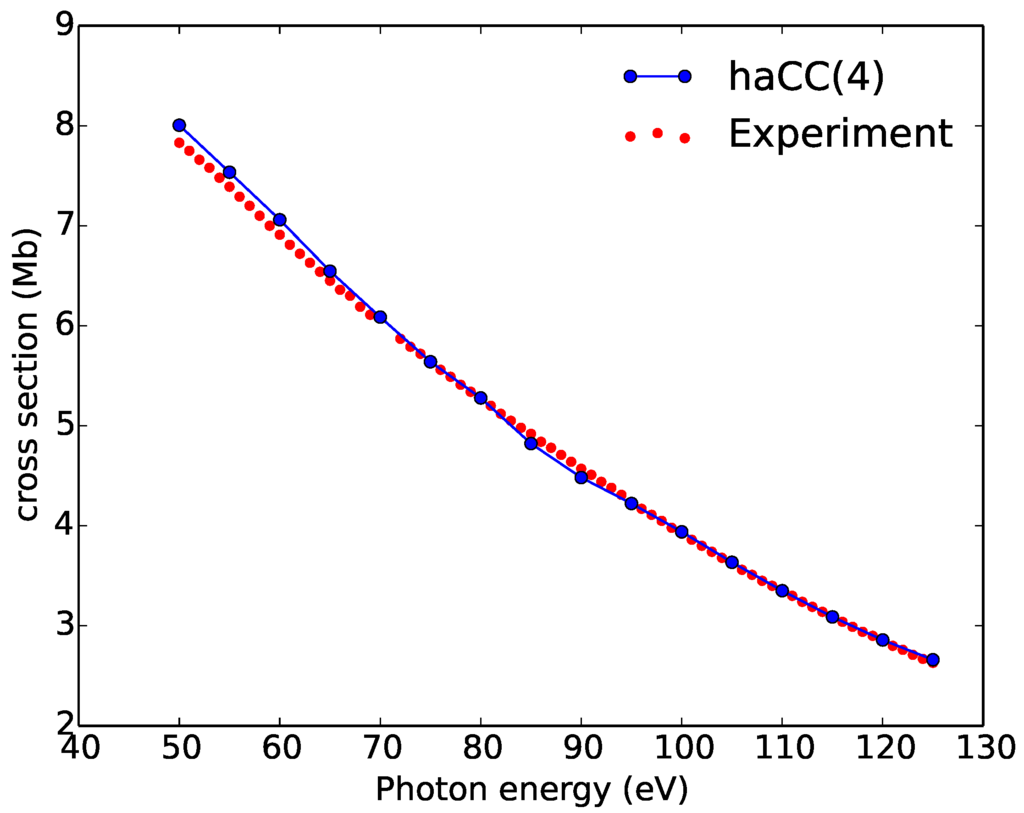
Figure 1. One-photon ionization cross-sections of Neon as a function of photon energy from haCC and from experiments [22]. haCC(4): Ionic basis consists of both $1s^{2}2s^{2}2p^5$ states and $1s^{2}2s2p^6$ state.

Figure 1. One-photon ionization cross-sections of Neon as a function of photon energy from haCC and from experiments [22]. haCC(4): Ionic basis consists of both $1s^{2}2s^{2}2p^5$ states and $1s^{2}2s2p^6$ state.

Figure 2 shows two-photon cross-sections from Neon with haCC, RMF and time dependent R-matrix (TDRM) methods. haCC(3) indicates computations with only the $1s^{2}2s^{2}2p^5$ ionic states and haCC(4) indicates computations including both the $1s^{2}2s^{2}2p^5$ states and the $1s^{2}2s2p^6$ state. Firstly, we find that haCC(3) and haCC(4) calculations give identical results. This is consistent with the knowledge that the $1s^{2}2s2p^6$ ionization channel is strongly closed [14]. Hence, there is no influence of this state on the two-photon cross-sections.

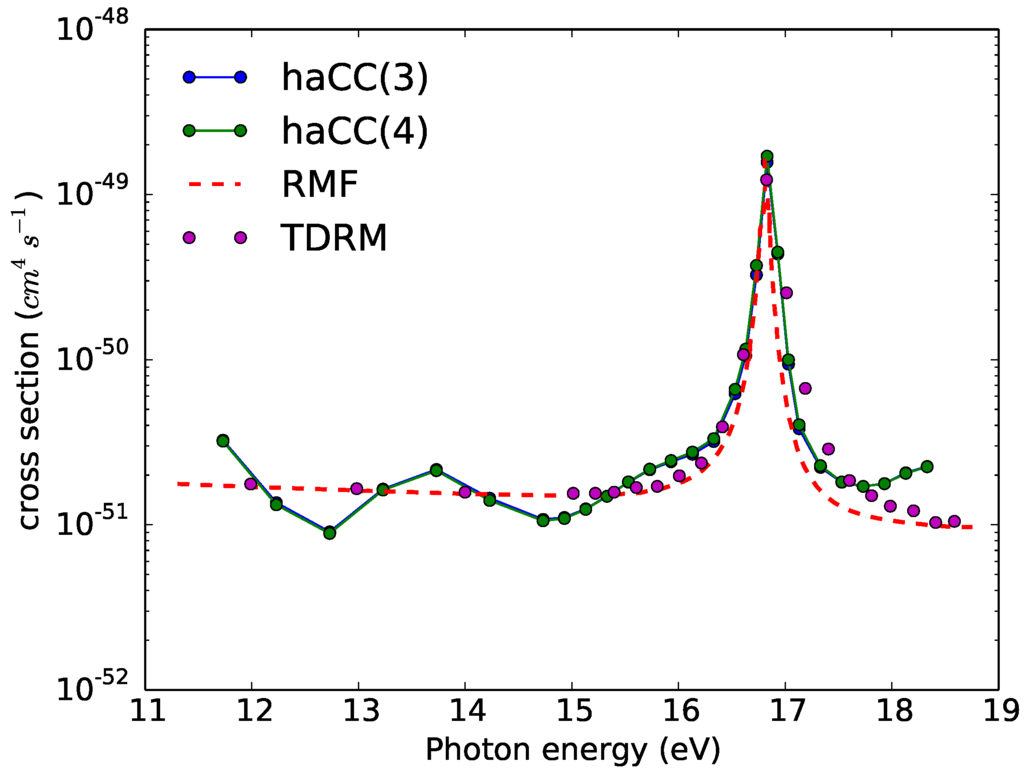
Figure 2. Two photon ionization cross-sections of Neon as a function of photon energy. The RMF and the TDRM results are from [12]. haCC(3): Ionic basis consists of only $1s^{2}2s^{2}2p^5$ states. haCC(4): Ionic basis consists of both $1s^{2}2s^{2}2p^5$ states and $1s^{2}2s2p^6$ state. The results from haCC(3) and haCC(4) are superposed.

Figure 2. Two photon ionization cross-sections of Neon as a function of photon energy. The RMF and the TDRM results are from [12]. haCC(3): Ionic basis consists of only $1s^{2}2s^{2}2p^5$ states. haCC(4): Ionic basis consists of both $1s^{2}2s^{2}2p^5$ states and $1s^{2}2s2p^6$ state. The results from haCC(3) and haCC(4) are superposed.

The R-matrix calculations [12] and haCC calculations have an overall good agreement. The resonance structure at 16.83 eV photon energy corresponds to the $1s^{2}2s^{2}2p^{5}3s$ state [12]. The peak heights of the resonant structure in all the computations agree very well. The peak is broader in the haCC and TDRM results compared to the RMF results. A contribution to this width is from the finite bandwidth of the laser pulse. In principle, the RMF results are exactly comparable to a result from a time dependent method only in the continuous wave limit. There is also an additional oscillation in the haCC cross-sections which is not present in the R-matrix results. This oscillation is stable with respect to the variation of the active electron discretization parameters. By construction haCC does not include any double continuum, which, if in turn included in R-matrix, could be one possible source of the differences. Other possible sources may be in the description of the atomic structure. The TDRM calculations in [12] were performed with a 20 a.u. inner region, $L_{max}=5$ angular momentum expansion and 60 continuum functions per each angular momentum of the continuum electron. In general, a numerical discretization of the continuum as used in haCC yields more accurate results compared to the spectral descritization of the continuum used in [12]. A more exact definition of the discretization used for the calculations in [12] would be needed for an analysis of these differences. Apart from these minor differences, it should be emphasized that this agreement is achieved without any adjustment of parameters, which provides for a quantitative confirmation of all the results.

3.2. Five-Photon Ionization Rates from Argon

In this section, we compute the five-photon ionization rates from Argon and compare them with RMF calculations at laser intensity ${10}^{13}W/c{m}^2$. We use in our Argon basis four ionic states-the three fold degenerate $\left[Ne\right]3s^{2}3p^5$ state and the $\left[Ne\right]3s3p^6$ state. This implies we have four possible ionization channels:

$$\begin{array}{cc}\hfill \left[Ne\right]3s^{2}3p^6& \to \left[Ne\right]3s^{2}3p^5+e^{-}\hfill \\ & \to \left[Ne\right]3s3p^6+e^{-}\hfill \end{array}$$

(9)

Again here, the configurations used to represent the states are only symbolic and in practice we use configuration interaction theory to treat them.

Figure 3 shows the five-photon ionization rates from haCC computations and RMF theory [14]. We use a simulation volume radius of 40 a.u. and an angular momentum expansion up to $L_{max}=9$ for the active electron basis. The ionization rates are computed by monitoring the rate at which the norm of the wavefunction in the simulation box drops. We use continuous wave laser pulses with ramp up and ramp down for our calculations. Hence, the rate at which the norm of the wavefunction drops reaches a steady state for any given simulation box size. We find that our haCC computations are in very good agreement with the RMF results. Both the approaches produce the two resonances $3p^{5}4p{}^{1}S$ at 364 nm and $3p^{5}4p{}^{1}D$ at 370 nm. The resonant structures are broader with the haCC method due to the finite bandwidth of the laser pulse.

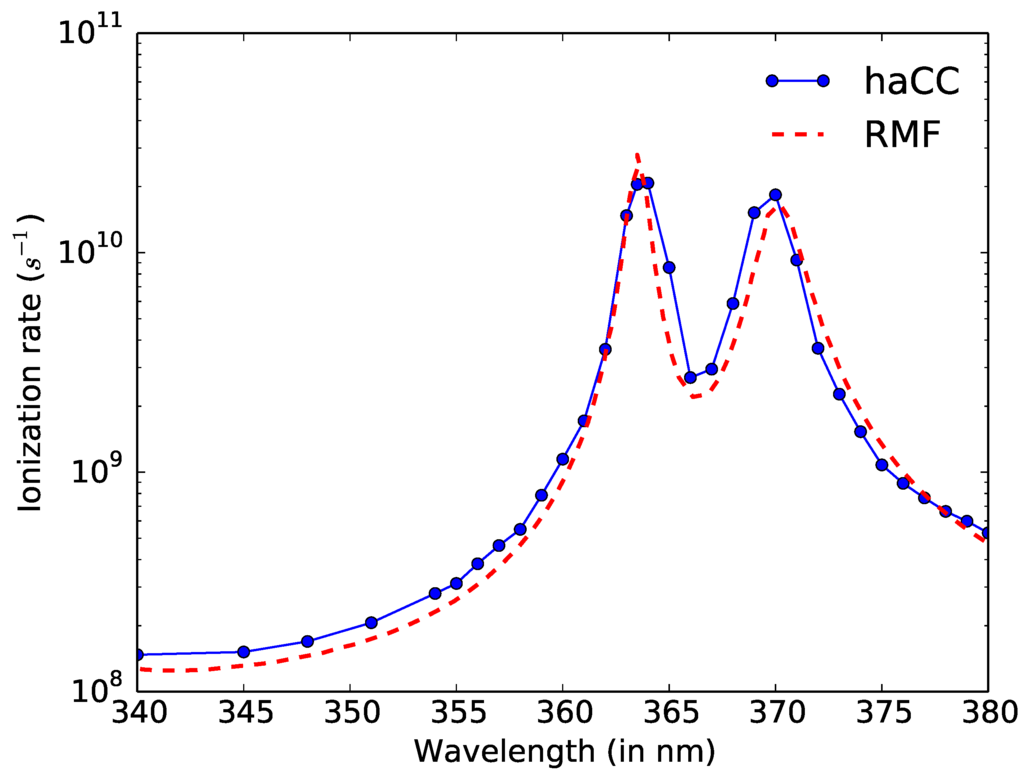
Figure 3. Five-photon ionization rates as a function of wavelength. The peak intensity of the laser fields used is ${10}^{13}W/c{m}^2$. The RMF results are from [14].

Figure 3. Five-photon ionization rates as a function of wavelength. The peak intensity of the laser fields used is ${10}^{13}W/c{m}^2$. The RMF results are from [14].

3.3. Photo-Electron Spectra from Argon with 12 nm Wavelength Laser Fields

As photo-electron spectra is a typical quantity measured in photo-ionization experiments such as with FELs, we present as a demonstration, photo-electron spectra from Argon at a typical wavelength produced at FELs, 12 nm ($\hslash \omega \approx$ 105 eV). This wavelength has been of experimental interest and also attracted theoretical attention recently [23].

Figure 4 shows total photo-electron spectra from Argon with linearly and circularly polarized 12 nm wavelength laser pulses. The exact pulse parameters are in the figure caption. The pulse shape used is

$$A_{z/x}\left(t\right)=A_{0z/x}{cos}^2\left(\frac{\pi t}{2cT}\right)sin(\frac{2\pi t}{T}+\beta )$$

(10)

where $A_{0z/x}$ is the peak vector potential of the z component or the x component, T is the single cycle duration, c is the number of laser cycles and β is the carrier envelope phase. Here, the $xz$ plane is the polarization plane for the circularly polarized laser pulses.

Figure 4 shows the one- and two-photon ionization peaks. The two peak structure in the spectrum is a result of ionization to two different channels. Single photon ionization to $\left[Ne\right]3s^{2}3p^5$ is the dominant ionization process with these pulse parameters. Single photon ionization is a linear process and ionization with circular polarization can be understood as a simple sum of ionization from two perpendicular linear polarized laser fields. The single photon peaks with circular polarization are twice as large as the single photon peaks with linear polarization, supporting this fact.

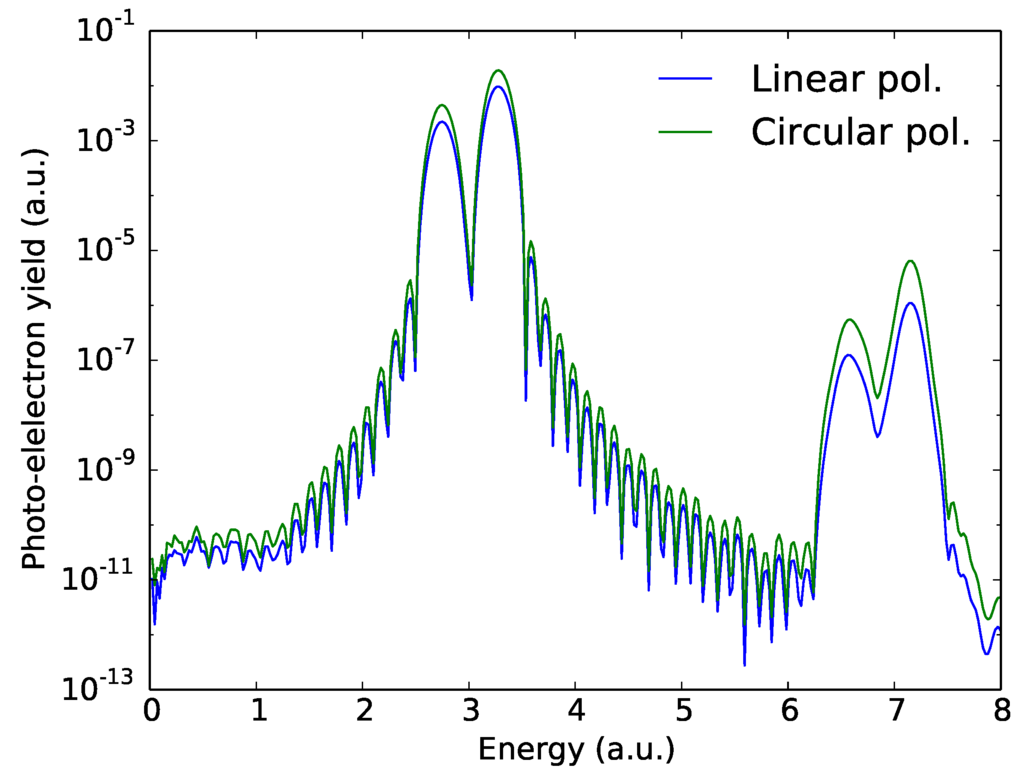
Figure 4. Total photo-electron spectra from Argon with linearly and circulary polarized 15 cycle, 12 nm wavelength, ${cos}^2$ envelope laser pulses with a peak intensity of $9\times {10}^{13}W/c{m}^2$. The figure shows the one- and two-photon ionization peaks.

Figure 4. Total photo-electron spectra from Argon with linearly and circulary polarized 15 cycle, 12 nm wavelength, ${cos}^2$ envelope laser pulses with a peak intensity of $9\times {10}^{13}W/c{m}^2$. The figure shows the one- and two-photon ionization peaks.

Figure 5 shows the partial wave decomposition and angle resolved spectra corresponding to the single photon ionization peaks with linear polarization. The partial wave decomposition shows the typical dipole selection rules. The spectra corresponding to the $\left[Ne\right]3s3p^6$ ionization channel, which is the inner structure in the angle resolved spectra, has a node in the plane perpendicular to the laser polarization. In order to ionize into this channel, the s electron is ionized to a $l=1$ continuum, resulting in the node. The outer structure, corresponding to ionization to $\left[Ne\right]3s^{2}3p^5$ channels, is a superposition of s and d waves.

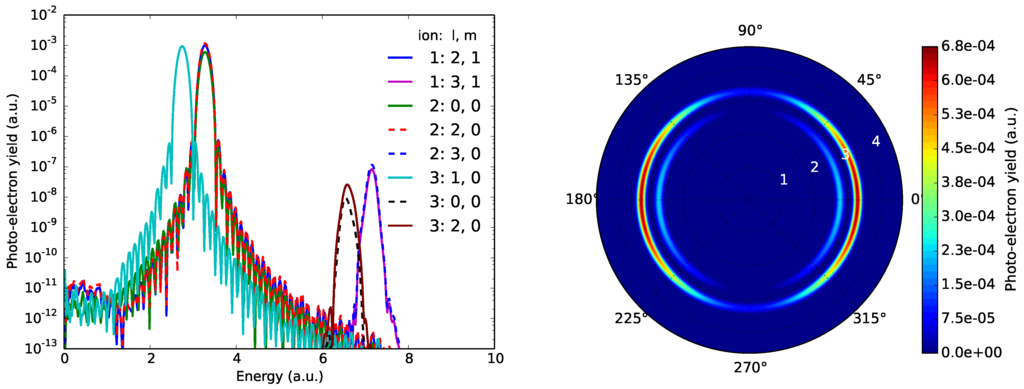
Figure 5. Resolving photo-electron spectra from Argon with linearly polarized 12 nm wavelength laser fields. Left figure: dominant partial waves in the ionic channels 1:$\left[Ne\right]3s^{2}3p_x^{2}3p_{y}3p_z^2$, 2:$\left[Ne\right]3s^{2}3p_x^{2}3p_y^{2}3p_z$, 3:$\left[Ne\right]3s3p^6$. The channel 2 is dominated by the s-d superposition. Right figure: Angle resolved spectra corresponding to the one-photon ionization double peak in Figure 4. The angle is defined with respect to the laser polarization direction.

Figure 5. Resolving photo-electron spectra from Argon with linearly polarized 12 nm wavelength laser fields. Left figure: dominant partial waves in the ionic channels 1:$\left[Ne\right]3s^{2}3p_x^{2}3p_{y}3p_z^2$, 2:$\left[Ne\right]3s^{2}3p_x^{2}3p_y^{2}3p_z$, 3:$\left[Ne\right]3s3p^6$. The channel 2 is dominated by the s-d superposition. Right figure: Angle resolved spectra corresponding to the one-photon ionization double peak in Figure 4. The angle is defined with respect to the laser polarization direction.

With circular polarization, the photo-emission is nearly uniform in all the directions in the plane of laser polarization and its a sum of dipole emissions into all the directions.

4. Conclusions

The hybrid coupled channels technique has been shown to be a promising tool in studying single ionization dynamics of multi-electron systems in [16]. The applications of this method presented here strengthens this observation. The applications considered here are computation of multi-photon cross-sections, ionization rates and fully differential photo-electron spectra of inert gas atoms. We computed one- and two-photon cross-sections from Neon and five-photon ionization rates from Argon. The good agreement between the haCC results and RMF results shows that haCC can treat multi-electron systems on par with the well established multi-electron theories. However, the haCC approach promises to reach a step ahead of the other multi-electron theories in terms of flexibility that it possesses due to a direct interface to state of the art quantum chemistry and its compatibility with the efficient tSURFF spectra method. haCC can be used to compute photo-electron spectra from multi-electron systems at long wavelengths which has not been accessible from any multi-electron methods so far. As a first step in this direction, we presented total and angle resolved photo-electron spectra from Argon at an XUV wavelength.