Abstract
Two-center electron interference in molecular attosecond photoionization processes is investigated from numerical solutions of time-dependent Schrödinger equations. Both symmetric H and nonsymmetric HHe one electron diatomic systems are ionized by intense attosecond circularly polarized XUV laser pulses. Photoionization of these molecular ions shows signature of interference with double peaks (minima) in molecular attosecond photoelectron energy spectra (MAPES) at critical angles between the molecular axis and the photoelectron momentum . The interferences are shown to be a function of the symmetry of electronic states and the interference patterns are sensitive to the molecular orientation and pulse polarization. Such sensitivity offers possibility for imaging of molecular structure and orbitals.
1. Introduction
Recent advances in the synthesis and characterization of ultrashort intense laser pulses allow for investigating laser-matter interaction into a new regime of highly nonlinear nonperturbative response, leading to a new science, attosecond science [1,2,3]. To date the shortest linearly polarized single pulse with duration of 67 as (1 as = s) has been produced from high-order harmonic generation (HHG) with a few cycle intense IR laser field in atoms [4]. With a mid-infrared femtosecond laser HHG spectra of very high order (1.6 keV) can also be generated thus allowing for the generation of pulses as short as few attoseconds [5]. By the superposition of multiple harmonics from HHG, zeptosecond pulses can be predicted as well [6]. Such ultrafast pulses thus offer a new tool to observe pure electronic quantum effects without interference from nuclear motion [7], and allowing in particular through attosecond imaging the creation of electron movies [8]. Attosecond pulses therefore allow one to separate electronic and nuclear effects due to the different time scales of attosecond for electron motion and femtosecond for nuclear motion.
The interference of electron waves emitted coherently from the two atoms in a diatomic molecule was first predicted by Cohen and Fano [9] and Kaplan and Markin [10] more than fourty years ago in perturbative single photon ionization. This can be regarded as a molecular Young’s double-slit experiment, since the wavefunctions are described by a linear combination of the orbitals of the two separated atoms. Such an interference model has been extended to nonperturbative photoionization with few-cycle intense laser pulses [11,12]. Thus one can envisage the emergence of a new science, laser induced electron diffraction (LIED) [11,12,13] as a new method for measuring molecular electronic structure and electron motion for different fixed nuclear configurations. This will be most useful to study molecular, chemical and biochemical processes since electron structure and transfer is fundamental to these processes [14]. In recent years such interference has been investigated extensively [15,16,17,18,19,20,21,22,23,24], where a laser induced rescattering mechanism occurs through recombination with the parent ion [25,26,27] or with neighboring ions [28,29] with electron wavelengths controlled by the laser intensity through laser induced ponderomotive energies. Molecular interference effects can be observed in measurements of molecular above-threshold ionization (MATI) spectra which have been well established both experimentally and theoretically, e.g., [30,31]. Novel destructive interferences in angular high-order MATI spectra of a diatomic molecule involving four geometric orbits have also been found experimentally and confirmed theoretically based on molecular strong field approximation (MSFA) simulations for the suppressed ionization of the O molecule [31]. Such electron destructive interference with minima in MATI has also been investigated with circularly polarized infrared (IR) laser pulses [32,33]. It has been shown that the symmetry of the electronic state and the molecular internuclear distance for both homonuclear and heteronuclear molecules determine the localization of the interference minimum in MATI spectra [33]. Interference structure of MATI versus above-threshold detachment has also been compared [34]. We have also investigated previously the two-center interference effects in MATI angular distributions of H at both equilibrium and extended internuclear distance for both linear and circular polarizations in IR [35] and XUV [36] regimes. In all previous work, nuclear motion has been neglected.
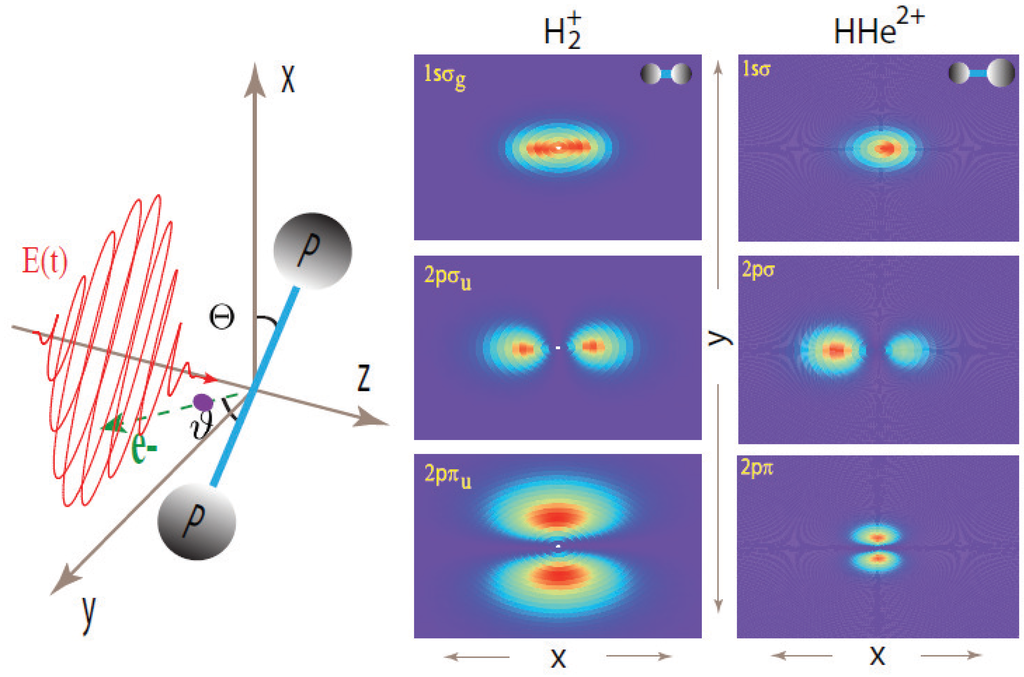
Figure 1.
Left column: Schematic illustration of the photoionization process in an oriented molecular ion by circularly polarized attosecond XUV laser pulses propagating along the z axis, perpendicular to the () plane. Θ is the orientation angle between the molecular internuclear R axis and the x axis, and the green dashed line () indicates the direction of the photoelectron with an ejected angle ϑ with respect to the molecular internuclear R axis in the molecular and laser polarization () plane. 3D plots of initial wavefunction densities for the three lowest electronic states of the x oriented () molecular ions at a.u.: (middle column) the H , , and states, and (right column) the HHe , , and states. Adapted from [24].
In this paper we review the two-center electron interference in single electron circular polarization XUV photoionization. We simulate angle dependent molecular attosecond photoelectron energy spectra (MAPES) with intense circularly polarized attosecond XUV laser pulses for different electronic states of oriented diatomic molecules H and HHe as schematically illustrated in Figure 1. It is found that at a critical angle between the ionized electron momentum and the molecular internuclear axis the MAPES exhibit doublets due to two-center destructive interferences. Such interference is shown to be strongly influenced by the pulse polarization and molecular orientation due to the nonspherical molecular Coulomb potential. Simulations are performed by solving numerically the corresponding three-dimensional (3D) time-dependent Schrödinger equation (TDSE) for static nuclei [49]. We use a 3D model, restricting the electron motion in a plane with static nuclei to describe these attosecond photoionization processes, thus enabling to go beyond perturbation theory and independent of gauge transformations [53]. Many methods have been proposed for describing attosecond electron dynamics, eg, attosecond preturbation theory (APT) [54], strong field approximation (SFA) [55], and time-dependent density functional theory (TDDFT) [56]. However in these simulation methods the effects of intermediate electronic states can not be exactly described. Such a fixed nuclei approach is appropriate due to the longer femtosecond (fs) time scale of nuclear motions. XUV ultrashort laser pulses with frequency (, the molecular ionization potential) and intensity W/cm are used in the present simulations.
The paper is arranged as follows: In Section 2, we derive the two center interference model in molecular attosecond photoionization. In Section 3, We briefly describe the computational methods for time-dependent quantum electron wave packet calculations from the corresponding TDSEs. The numerical results of the electron interference in MAPES by intense ultrashort circularly polarized XUV laser fields for the H and HHe are shown in Section 4. Effects of pulse ellipticity, molecular orientation, and pulse intensity are discussed. Finally, we summarize our findings in Section 5. Throughout this paper, atomic units (a.u.) are used unless otherwise stated.
2. Two-Center Interference Models
We first derive the two center interference model in MAPES. According to the attosecond perturbative theory developed recently by Starace and coworkers [54], the differential probability for ionization with momentum into the solid angle and the energy interval is given in the electric dipole approximation (to the first order in the laser intensity)
where in a.u.. and are the final continuum and initial electronic states, respectively. is an energy Fourier transform of the ionizing pulse
and is the eigenenergy of the initial electronic state. From Equation (1) one sees that the photoelectron distribution is the product of an electronic Franck-Condon factor (photoionization amplitude) and the pulse spectral width . Then Equation (1) can be written as
with
and is the shape of the pulse in frequency domain, where is the pulse maximum amplitude. We see that the MAPES strongly depend of the bandwidth of the laser pulse . The relation of the photoelectron momentum and the angle between the momentum and the molecular axis is determined by the transition amplitude , and the pulse bandwidth determines the shape of the photoelectron energy spectra.
Taking into account an impulsive field model [57], the wavefunction in momentum space right after the pulse is given by,
where is the wavefunction of the initial electronic state in momentum space. Transforming the wavefunction to coordinate space, we then get
The transition amplitude to a continuum state can be expressed as
For the initial ground electronic states of H at internuclear distance , the corresponding wavefunction is expressed as . i.e., linear combinations of hydrogenic 1s orbital located at . Then the transition amplitude , i.e., the momentum distribution of photoelectron in Equation (7) can be written as,
is the laser polarization vector and the unit vector . For the first excited electronic state with wavefunction , the corresponding distributions exhibit a strong phase difference as
For the second excited electronic states, the momentum distribution then can be expressed as,
where the wavefunction is taken to be a linear combination of the hydrogenic orbitals, i.e.,
For a nonsymmetric molecular ion HHe, the momentum distribution is [58]
where and and and denote the atomic orbital of hydrogen and helium respectively. and are coefficients of the orbitals. From Equations (8)–(12) one can see that the effect of the delta pulse is to shift the total momentum distribution by the total amplitude of the field vector .
In the present work we can use the interference model in Equations (8)–(12) with for both H and HHe since the chosen intensities produce negligible ponderomotive energies , at intensity W/cm ( a.u.) and frequency a.u. (wavelength nm). The Stark potential energy term is therefore negligible compared to the momentum term .
For the state of H at internuclear distance R, Equation (8) yields constructive interference at the condition , , and destructive case at . Similar results are obtained for the state of H in Equation (10) and nonsymmetric HHe in Equation (12) since the distribution amplitude is a cosine function of p and R. For the excited state the constructive and destructive interference processes are predicted at and . For the cases of constructive interference multiple angle nodes appear in photoelectron distributions at certain kinetic energy, i.e., LIED [11], whereas minima appear for destructive interference patterns [24].
3. Numerical methods
To simulate the interference effects described in Section 2, we consider oriented diatomic molecular ions, symmetric H and nonsymmetric HHe, interacting with an ultrashort (attosecond) intense laser pulse. The corresponding TDSE with static nuclei in cylindrical coordinates is written as,
where the field-molecule Hamiltonian is and with (, ). The plane is defined by the molecular internuclear axis and the laser polarization. is the molecular two-center Coulomb potential. The molecular kinetic energy term (Laplacian) is (in a.u.)
The 3D electron-nuclear potential is written as,
and are the charges of the nuclei. For H, and and for HHe, and and and , where is the internuclear distance. Θ is the molecular orientation angle between the molecular R axis and the x axis, Figure 1. A regularization parameter is used to remove the singularity in the Coulomb potential in Equation (15), allowing the accurate reproduction of the electronic state potential energies of H [45]. Removing the Coulomb singularity allows for using efficient split operator methods to solve the TDSE, Equation (13) as described below. The field-molecule interaction is treated in the length gauge with a laser field propagating along the z axis (Figure 1), with the form
ϵ is the pulse ellipticity with for circular polarization and for linear polarization. A temporal slowly varying envelope , with one optical cycle (o.c.) period and total duration is adopted. Thus we do not need to consider effects of pulse carrier envelope phase (CEP).
We solve numerically the 3D TDSE in Equation (13) by a five-point finite difference method and fast Fourier transform technique combined with high-order split-operator methods [45,59]. The time step is fixed at a.u. (1 a.u.=24 as) thus allowing maximum to consider an energy spectrum of 100 a.u.. The spatial discretization is a.u. (1 a.u.=1 , Bohr radius) for a maximum momentum spectrum a.u. and energy a.u. for radial grid sizes a.u., a.u., and angle grid size radian. To prevent unphysical effects due to the reflection of the electron wave packet from the boundary, we multiply by a absorbing “mask function" with the form
where a.u. and a.u..
For an intense laser pulse, a quite large grid range must be used to obtain via Fourier transform the high energy of the ejected electron in the ionization spectra. In the present work we use an efficient method by calculating a radial flux (electron current density) to describe the ionization spectra, where the high kinetic energy of the ionized electron can be accurately calculated. At an asymptotic point a.u, the electron wave function generates the flux in the molecular and laser polarization () plane before the grid absorption at the boundary. For attosecond photoionization processes, the laser duration as is very short. At the large asymptotic point , the angular flux distributions can be ignored, i.e., . As a result we only need to consider the radial part of the electronic flux along the radial direction, . The time-independent energy-resolved angular differential yield (photoelectron spectra) is obtained by a Fourier transform from the exact time dependent functions [44]:
where is the time after the pulse switches off. (in a.u.) is the kinetic energy of an ionized electron with wave vector (in a.u.), is the momentum of a photoelectron of wavelength . Since only the radial electronic flux is taken into account, we can also define θ as the angle between the photoelectron momentum and the x axis. For the case of x oriented molecular photoionization, the angles θ and ϑ are same, i.e., . With the transformation and , we then obtain the 2D momentum distributions of photoelectrons from Equation (18).
4. Numerical Results and Discussions
In this section we simulate two-center interference patterns in MAPES of oriented H and HHe by circularly polarized attosecond XUV laser pulses. It should be noted that the pulse duration is important. One can only observe the interference minima in MAPES with sufficient broad spectral width from short duration pulses. Therefore in the present work we adopt attosecond XUV pulses with durations of few hundred attoseconds ( as). A further advantage is that this corresponds to “frozen" nuclei, thus allowing to neglect nuclear motion. Results show that due to effects of the nonspherical molecular Coulomb potential, the photoelectron distributions are strongly modified by the laser fields when compared to atomic distributions. The interference pattern is also sensitive to the polarization of the driving pulses. In these simulations, the Keldysh parameter [60] indicates a multi-photon ionization process regime [2]. The quiver or ponderomotive energies of the free electron a.u., thus effects of laser induced Stark shifts can be ignored. We choose a single photon ionization energy, , to eliminate the effects of resonant intermediate electronic bound states. High-order MATI spectra can also be observed in XUV laser fields but the spectrum intensity decreases rapidly as the photoelectron kinetic energy increases [61]. Therefore in the present work we only show the interference patterns in the first order MATI spectra, i.e., with strong ionization signal intensity.
As illustrated in Figure 1, the laser pulse propagates along the z axis, perpendicular to the polarization () plane. It is to be noted that the distance covered by light in 1 as is 0.3 nm = 5.67 a.u.. The total pulse durations chosen (Figure 1) are as, much larger than the traversal time of a single photon across a molecule. As a result the photoelectron is ejected in the molecular and laser polarization () plane with an angle ϑ between the momentum and the molecular axis.
4.1. Interference Patterns in MAPES of H
We consider first the interference effect in single photon () molecular ionization processes for the three lowest electronic states of the x oriented molecular ion H, the , the , and the electronic states, illustrated in Figure 1. Figure 2 shows angle dependent MAPES around the three critical interference angle predicted from Equations (8)–(10) for intensity W/cm circularly polarized attosecond XUV laser pulses. According to Equations (8)–(10) at , the pulse wavelengths and durations are chosen respectively as (a) nm and as, (b) nm and as, and (c) nm and as. The corresponding wavelengths and momenta of continuum electrons are a.u. ( a.u.), 1.4 a.u. (4.49 a.u.), and 2.77 a.u. (2.27 a.u.), as listed in Table 1.
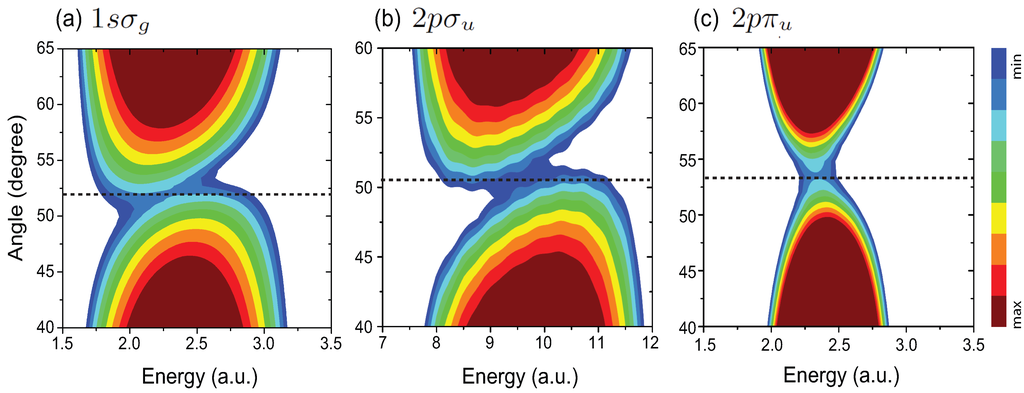
Figure 2.
Angle θ resolved MAPES in (a) the , (b) the , and (c) the electronic states of the x oriented molecular ion H at a.u. with intense intensity W/cm circularly polarized attosecond XUV laser pulses. The corresponding pulse wavelengths and durations are respectively (a) nm and as, (b) nm and as, and (c) nm and as. Dashed lines denote the critical angles . Signal intensities of the ionization spectra are on a logarithmic scale in arbitrary units. Adapted from [24].
From Figure 2a and b we see that the MAPES split into two separate sub-peaks around the critical angles and . According to the interference model in Equations (8) and (9), such doublets in MAPES mainly results from effects of destructive interference of electron wave packet emitted separately from the two nuclear centers. For the state, the critical angle is predicted at from Equation (10). However in the angle resolved MAPES in Figure 2c we note that no doublet (minimum) is induced and only one single peak appears. From Equations (10) and (11) since the wavefunction is a linear combination of the hydrogenic orbitals, i.e., and , this process is actually a four “center" electron interference, i.e., the ionization from the hydrogenic orbitals . The photoelectron distributions are a superposition of these ionization components. Alternatively, the state in Equation (11) corresponds to a simple circular orbital of the electron around the R axis. Consequently, the interference minima in MAPES predicted in Equation (10) are absent.
To illustrate the effects of multiple centers, in Figure 3 we show results in the H excited electronic state with attosecond XUV laser pulses for both the linear x parallel and y perpendicular (to the molecular internuclear R axis) polarization ionizations. The laser parameters are the same as in Figure 2c, except the laser polarization. For the linear y perpendicular polarization ionization in Figure 3b, results are similar to those in Figure 2c for the circular polarization process. We see that in Figure 3b at a critical angle the doublet disappears as well. This absence of the interference patterns confirms the effects of the four “center” interference. However, it is found that for the linear x parallel polarization ionization in Figure 3a the interference patterns with doublets at a critical angle are produced again. This is similar to those for the and electronic states in Figure 2a and b. Due to the strongly asymmetric Coulomb force, the orientation ionization probabilities from the two nuclear centers are spatially asymmetric, and the two-center interference can not be efficiently induced. We attribute this doublet structure in MAPES in Figure 3a to the interference resulting from an up-down two “center” ionization, as illustrated in Figure 1. For the hydrogenic orbital , the corresponding electron density distributions are localized perpendicular to the molecular internuclear R axis. An interference between the two electron wave packets ionized separately from the orbitals and at the right nuclear center is induced, thus leading to the doublet at the critical angle as shown in Figure 3a.
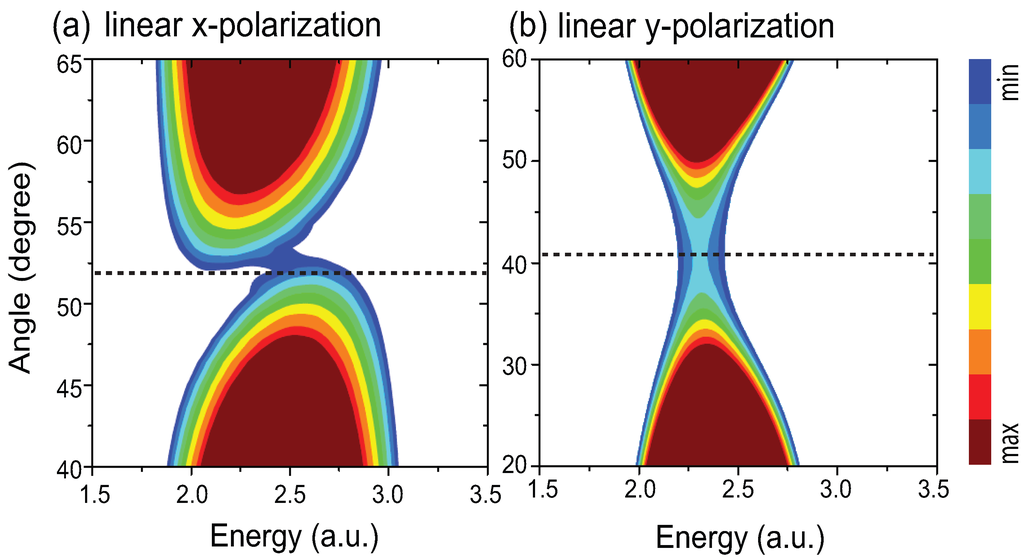
Figure 3.
Angle θ resolved MAPES for the x oriented () H excited state at equilibrium with intensity W/cm, wavelength nm and duration as XUV laser pulses for (a, left column) linear x parallel polarization, and (b, right column) linear y perpendicular (to molecular internuclear R axis) polarization ionizations. Dashed lines denote the critical angles . Signal intensities of the ionization spectra are on a logarithmic scale in arbitrary units. Adapted from [24].

Table 1.
Momenta p and wavelengths of a photoelectron calculated by and for different electronic states of the molecular ions H and HHe at a.u. by varying the wavelength λ (angular frequency ω) of XUV laser pulses.
| XUV Pulses | Photoelectron | |||
| λ | ω | p | ||
| H ( | 12.5 nm | 3.65 a.u. | 2.26 a.u. | 2.78 a.u. |
| H ( | 19.5 nm | 2.34 a.u. | 1.57 a.u. | 4.0 a.u. |
| H ( | 3.75 nm | 12.1 a.u. | 4.70 a.u. | 1.34 a.u. |
| H ( | 4.25 nm | 10.7 a.u. | 4.49 a.u. | 1.4 a.u. |
| H ( | 15.0 nm | 3.0 a.u. | 2.27 a.u. | 2.77 a.u. |
| HHe ( | 10.0 nm | 4.56 a.u. | 2.22 a.u. | 2.83 a.u. |
| HHe ( | 12.0 nm | 3.8 a.u. | 2.21 a.u. | 2.84 a.u. |
| HHe ( | 12.5 nm | 3.65 a.u. | 2.26 a.u. | 2.78 a.u. |
In Figure 2 we note that the interference critical is slightly bigger than the theoretical predictions in Equations (8)–(10), i.e., there is an angle shift . In a left-handed circularly polarized laser field, photoelectron angular distributions exhibit an anticlockwise rotation with respect to the molecular axes due to effects of the nonspherical molecular Coulomb potential [49,50,51,52]. Therefore the critical angle shifts as well following the polarization of the laser field.
4.2. Interference in Nonsymmetric HHe
We next present the two-center interference of electron wave packets for a nonsymmetric molecular ion HHe. Figure 4 illustrates the angle resolved MAPES for the ground state, the first excited state, and the second excited electronics state of the x oriented molecular ion HHe at internuclear distance a.u. with intense W/cm circularly polarized attosecond XUV laser pulses at nm and as, panel (a), nm and as, panel (b), nm and as, panel (c). With such pulses the critical angle is predicted at since the interference model follows the from in Equation (12). The molecular ionization potential energies for the three lowest electronic states are respectively, 2.1 a.u., 1.36 a.u., and 1.1 a.u.. The corresponding photoelectron de Broglie wavelengths are listed in Table 1.
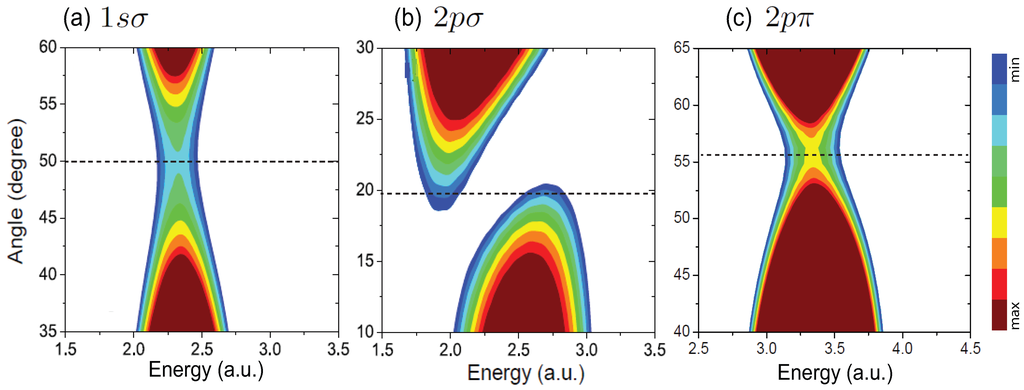
Figure 4.
Angle θ resolved MAPES in (a) the , (b) the , and (c) the electronic states of the x oriented molecular ion HHe at a.u. with intensity W/cm circularly polarized attosecond XUV laser pulses. The corresponding pulse wavelengths and durations are respectively (a) nm and as, (b) nm and as, and (c) nm and as. Dashed lines denote the critical angles . Signal intensities of the ionization spectra are on a logarithmic scale in arbitrary units. Adapted from [24].
For the ground electronic state, the initial electron density distribution is mainly localized on the He ion, i.e., . Then the interference term is approximately proportional to . In Figure 4a one sees that for the ground state around the predicted critical angle the interference patterns with doublets in MAPES disappear. The localized electron density distribution results in a strong spatial asymmetry of photonionization but no efficient interference. Such absence of the interference doublet has also been observed in MATI spectra of the heteronuclear molecule CO with circularly polarized IR laser pulses [33]. Nevertheless, a shift of the critical angle is obtained due to the rotation of circular polarization angular distributions. Again for the state in Figure 4c one sees that there is no interference minimum in MAPES at the angle , similar as the state of H in Figure 2c. The initial electron density distributions are mainly localized on the center He and perpendicular to the molecular R axis with no interference minimum.
However for the excited HHe state at small internuclear distance a.u., the total electron density is delocalized on H and He (Figure 1) and the corresponding ionization probabilities from each center are comparable, [62]. The free-electron wave packets are of comparable density at the two nuclear centers and can interfere. As a result, doublets in the MAPES are produced. Comparing with results of H in Figure 2, angular distributions of HHe exhibit a bigger angle shift at the critical angle in Figure 4b, arising from the asymmetry of the initial atomic orbitals of hydrogen and helium, and the effects of the molecular permanent dipole, as reported recently in both MATI [47] and HHG [64] for asymmetric molecules.
4.3. Interference patterns in elliptical polarization ionization
In elliptical polarization ionization processes, the interference patterns can also be produced. In Figure 5(c–f) we illustrate angle and energy resolved photoelectron distributions in the state and the state by elliptically polarized attosecond XUV laser pulses with ellipticities [panels (a) and (c)] and 0.3 [panels (b) and (d)]. The other laser parameters are the same as those used in Figure 2a and b. The simulation results also give destructive interference patterns with a double peak structure at a critical angle . However, the critical angle and the corresponding angle shift show a sensitivity to the pulse ellipticity ϵ. From Figure 5 we see that for the state, the critical angle increases gradually with decrease of the pulse ellipticity ϵ. In Figure 5a with ellipticity , the critical angle is and with ellipticity , in Figure 5b, i.e., the critical angle difference increases with decrease of ellipticity ϵ. For the state, one sees that the critical angle decreases from at , Figure 5c to at , Figure 5d.
Decreasing ellipticity of pulses leads to a change of the rotation of the photoelectron angular distribution, i.e., a shift of the critical interference angle . As reported previously [50], rotations of angular distributions is sensitive to the ellipticity of pulses. With left-handed elliptically polarized laser pulses, decreasing the pulse ellipticity, i.e., field strength , the asymmetry between the parallel and perpendicular (to the molecular axis) polarization ionization probabilities increases. Since the angular distribution is determined by the symmetry of the initial electronic state, for the state the angular distributions are mainly localized along the molecular internuclear R axis [, Equation (8)], i.e., the parallel ionization dominates, whereas for the state the perpendicular ionization distribution dominates [, Equation (9)]. Therefore decreasing the pulse ellipticity ϵ () leads to different changes of the critical interference angle shift for the state and the state. The dependence of the rotation angle on the pulse ellipticity ϵ is also a function of the symmetry of the electronic state [50]. For the state the angular distribution rotation with respect to the perpendicular y polarization axis increases. As a result the critical angle difference increases in an anticlockwise direction, in Figure 5a and b. However, for the state the rotation angle with respect to the parallel polarization (the molecular R axis) clockwise decreases, giving rise to a decrease of the critical angle . Therefore, the critical angle shift decreases gradually as shown in Figure 5c and d.
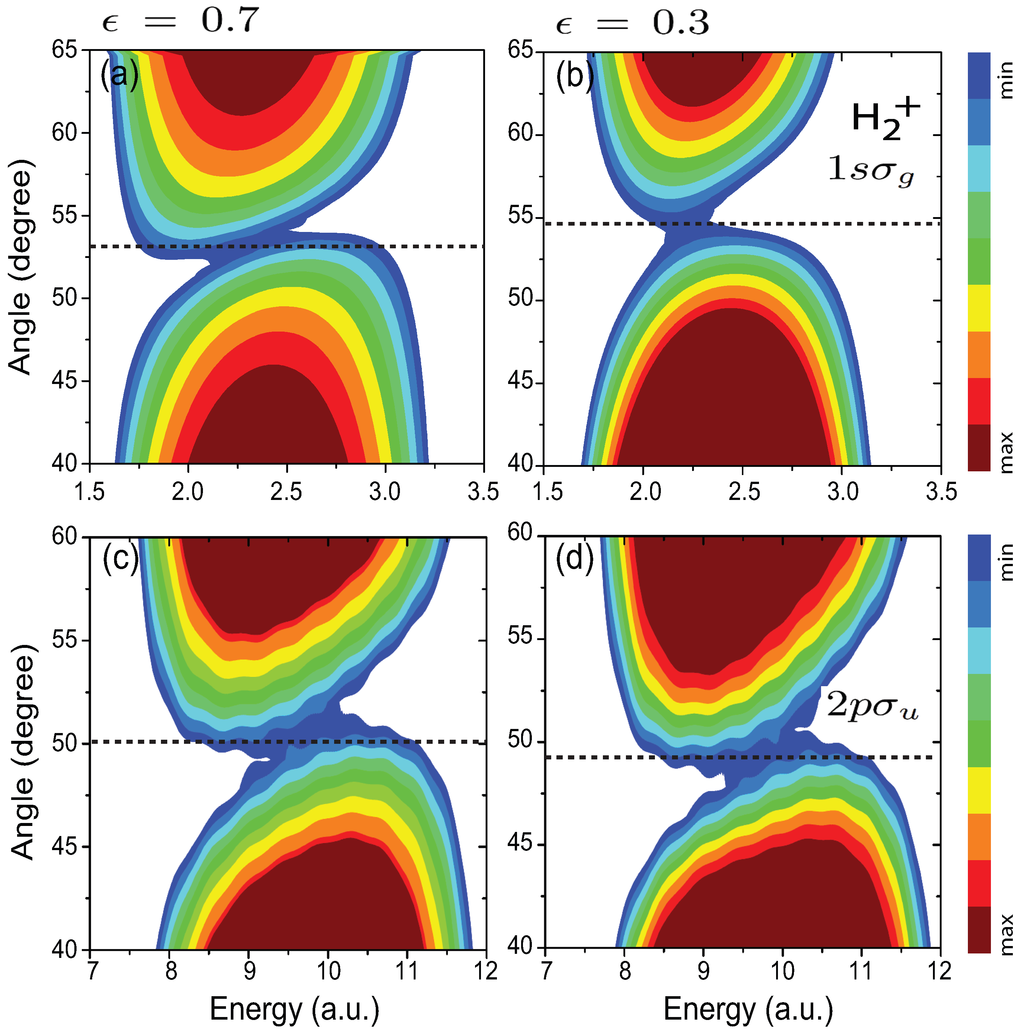
Figure 5.
Angle resolved MAPES from the state (a,b, upper row) and the state (c,d, bottom row) of x-oriented H with intense W/cm attosecond elliptically polarized laser pulses with ellipticities (a,c, left column) and (b,d, right column) . Laser wavelengths and duration are respectively (a,b) nm and as, and (c,d) nm and as. Dashed lines denote the critical angles . Signal intensities of the ionization spectra are on a logarithmic scale in arbitrary units. Adapted from [24].
For the ionization with an elliptically polarized laser pulse in the ground electronic state in Figure 5b, the destructive interference pattern with doublets in angular distributions nearly disappears at the critical angle . This absence of the interference doublets mainly comes from the spatial asymmetry of ionization probabilities from the two nuclear centers. The difference between the state and the state, [Figure 5b vs Figure 5d] is due to the dependence of the photoelectron kinetic energies on the interference. These are also we will discuss below.
4.4. Effects of Molecular Orientation Θ on Interference Patterns
In Figure 3 one sees that in linear polarization ionization processes the interference patterns are critically sensitive to the polarization direction of the ionizing laser pulse and in Figure 5b the interference doublet is absent at . Due to the nonspherical molecular Coulomb potential a spatial asymmetry of the ionization probability from the multiply centers can be induced. Such sensitivity to the pulse polarization also reflects the density distributions of the initial electron state. Therefore we illustrate below the effects of molecular orientation on the two center interference in the electronic state of H.
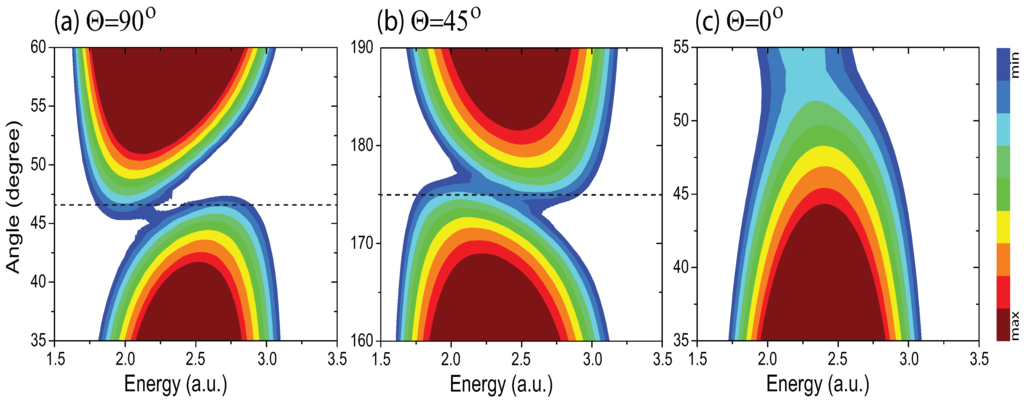
Figure 6.
MAPES of equilibrium H state at orientation angles (a) , (b) , and (c) with intense W/cm and nm linearly x polarized attosecond XUV laser pulses. Signal intensities of the ionization spectra are on a logarithmic scale in arbitrary units.
We present results of MAPES in Figure 6 at three different molecular orientation angles, (a) , (b) , and (c) in the H state by a linearly x-polarized attosecond XUV laser pulse with intensity W/cm and wavelength nm, and durations as. From Equation (8) the interference minimum is predicted at . However one sees that interference patterns and the critical angles are strongly dependent on the molecular orientation angle Θ.
For these linear polarization ionization processes, the dominant ionization is along the x polarization axis, where the density is maximum, i.e., along the bond. It has been recently found that high frequency imaging of polyatomics through photoelectron angular distributions occurs mainly from bond direction of ionized electron [63]. The electron is initially localized on the two nuclei, and then ionized to the continuum by the field. Therefore, the orientation ionization probabilities from the two-centers are influenced by the asymmetric Coulomb force and the polarization direction of the driving pulses. As the molecular R axis rotates with respect to the x polarization axis, the two center interferences becomes weak. Results in Figure 6a at the y oriented molecular angle exhibit a clear interference patterns with deep minima in MAPES at (), in good agrement with the prediction in Equation (8). However at one sees that the amplitude of the interference patterns in MAPES decreases. At angle () strong asymmetric sub-peaks are obtained as illustrated in Figure 6b. Due to the asymmetric Coulomb force, spatial asymmetry of the ionization probability from the left ion and the right ion is induced following the x polarization. For the ionized electron with the ejection angle the ionization from the left center dominates. The asymmetry therefore leads to a decrease of the electron interference. Rotating the molecular R axis further the asymmetry between the two center photoionization increases as well. At the ionization mainly comes from one center. The strongly asymmetric amplitudes of the two outgoing electron wave packets can not trigger sufficiently an efficient interference to produce a minimum in the energy spectra around the critical angle predicted from Equation (8). Therefore only one broad peak is obtained in MAPES in Figure 6c. For the ionization at , the asymmetric Coulomb force essentially does not influence the molecular ionization. Therefore, as shown in Figure 6a a pronounced interference pattern at () is observed. Of note is that due to the asymmetric ionization from the two nuclear center the numerical results of the critical angle shift slightly comparing to the predictions in Equation (8).
It is also found that the dependence of the interference patterns on the molecular orientation is a function of the photoelectron kinetic energies. In Figure 7 we compare the results at different photoelectron kinetic energies for the ground state. Figure 7a shows MAPES at in the state with intensity W/cm linearly polarized attosecond XUV laser pulses. The pulse duration is 20.4 a.u.=493.7 as. The molecular axis is oriented along the x polarization axis, i.e., . The corresponding momentum of the ionized electron is a.u. (Table 1). According to the two-center ionization model in Equation (8), destructive interference patterns with minima in MAPES should be expected at . It is, however, found that in Figure 7a spectrum splitting and minima are absent again and the energy spectra only exhibit a single peak around the photoelectron energy 1.24 a.u., the same as Figure 6c. For comparison, in Figure 7b, we also display the corresponding results for a higher frequency laser pulse. The laser wavelength nm ( a.u.) and duration as are adopted. With such laser pulses, the momentum of the ionized electron is a.u.=0.25 nm (), as listed in Table 1. Contrary to the previous result () in Figure 7a, the expected double peak structure predicted in Equation (8) is now obtained due to the two-center destructive interference.
The absence of the doublet in MAPES for the state in Figure 7a mainly results from the asymmetric ionization for the two centers and the molecular Coulomb potential, the same as Figure 6c. At such low kinetic energies ( a.u. a.u.) the two outgoing electron wave packets from the two nuclei do not match each other in amplitude. Efficient destructive interference can not be induced, therefore leading to a single peak in MAPES. For the higher energy photoelectron, effects of Coulomb potential on the electron interference can be ignored. For , the spatial asymmetry of the two-center ionization is weak. Therefore, in Figure 7b where a.u. , we observe interference patterns in the MAPES only at . Similar processes have also been predicted in the rotation of molecular circular polarization photoelectron angular distributions in MATI for H [49], and the rotation angle arising from the Coulomb effects is absent in the high kinetic energy region (). The dependence on the photoelectron kinetic energy of the interference patterns confirms the effects of the spatial orientation asymmetry of the two center photionization as functions of angle. Similar dependence of molecular orientation should occur for nonsymmetric HHe.
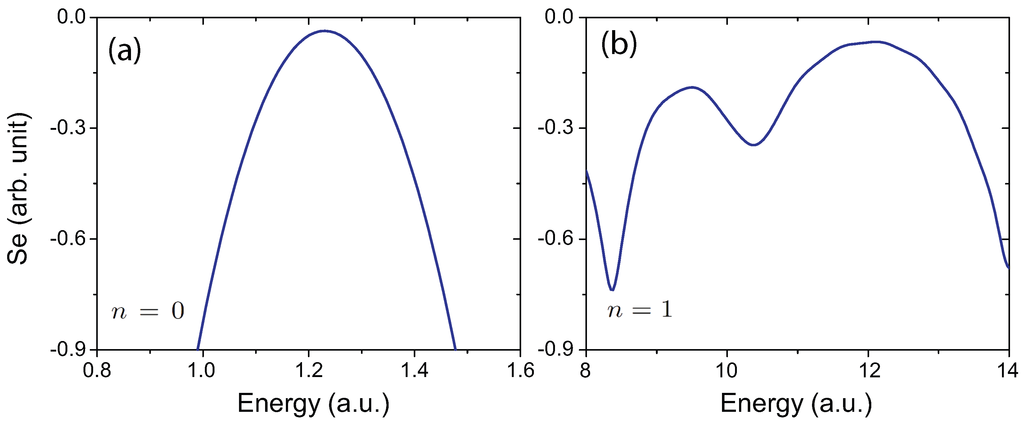
Figure 7.
MAPES at a critical angle (forward scattering) of the ejected electron (along the molecular axis) in the H ground state at equilibrium with molecular orientation angle at the intense intensity W/cm and wavelengths (a) nm and (b) nm linearly polarized attosecond XUV laser pulses. The corresponding electron wavelengths are 4.0 a.u. and 1.34 a.u., respectively, as listed in Table 1, leading to the destructive interference models and predicted in Equation (8). Signal intensities of the ionization spectra are on a logarithmic scale in arbitrary units.
4.5. Influence of the Pulse Intensity
Finally we display the influence of the pulse intensity on the interference. It is found that in circular polarization ionization processes with , the pulse intensity plays a minor role in the multi-photon regime. We also use H to illustrate such influence of pulse intensity. Figure 8 shows angular MAPES for the three lowest , , and electronic states of x oriented H () with weaker circularly polarized attosecond XUV laser pulses at intensity W/cm ( a.u.). The other parameters are the same as in Figure 2. Interference patterns with doublets are observed again. Comparing with Figure 2 with the stronger intensity W/cm laser pulses, one sees that for the three cases similar MAPES are obtained. The interference patterns are shown to be insensitive to the pulse intensity in circular polarization molecular ionization processes. For circular polarization multi-photon ionization processes, decreasing the pulse intensity results in suppression of the ionization rate from both nuclear centers. As shown previously, the rotation angle of photoelectron distributions does not depend on the pulse intensity but relies mainly on the symmetry of the initial electronic state [50,52]. Altering the pulse intensity does not result in a change of the critical angle . Moreover from Equations (8)–(10) one sees that the interference patters are mainly determined by the symmetry of the electronic states.
Of note is that in the tunnelling ionization regime , the pulse intensity plays an essential role in the two-center interference processes [32,33]. In an IR laser field, an inner Coulomb barrier emerges between the two nuclear centers. The molecular potential is then a function of the field amplitude. For example for a parallel x polarization ionization, the dressed potential can be expressed as . The electron then ionizes by tunnelling through the the inner barrier. As a result a spatial asymmetry of the ionization probability between the two centers is induced as well. Increasing the pulse intensity () suppresses the inner Coulomb barrier, thus reducing the spatial asymmetry of the ionization [65]. Consequently, the interference patterns have a strong dependence on the laser pulse intensity, whereas in multi-photon ionization processes with XUV pulses barrier effects are absent. The pulse intensity (in)dependence indicates the different regimes of molecular ionization by intense IR and XUV pulses, tunnelling vs multi-photon.
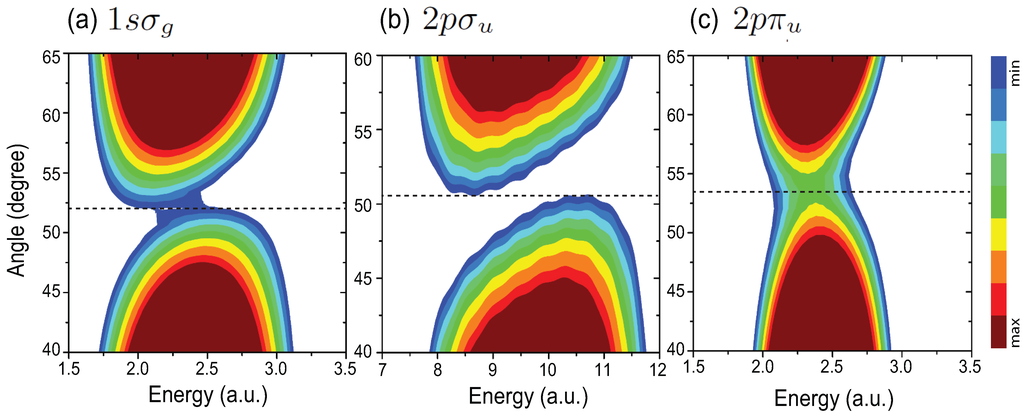
Figure 8.
Angle θ resolved MAPES in (a) the state, (b) the , and (c) electronic states of the x oriented molecular ion H at a.u. with weaker circularly polarized attosecond XUV laser pulses at intensity W/cm ( a.u.). The corresponding pulse wavelengths and durations are respectively (a) nm and as, (b) nm and as, and (c) nm and as. Dashed lines denote the critical angles . Signal intensities of the ionization spectra are on a logarithmic scale in arbitrary units.
5. Summary
Photoelectron angle resolved energy distributions of oriented symmetric H and nonsymmetric HHe single electron molecular ion have been investigated by intense circularly polarized attosecond XUV laser pulses with high frequency . Simulations from numerical solutions of the corresponding TDSEs show that at critical angles of the ejected electrons with respect to the molecular internuclear R axis, photoelectron energy spectra exhibit a doublet structure in molecular circular polarization ionization processes. We attribute these minima to effects of the destructive interference between the electron wave packets ionized separately from the two nuclear centers.
In this article, we first review the two center electron interference patterns with different molecular symmetric orbitals. We derive the exactly solvable photoionization model using a linearly polarized δ-function pulse which has previously been used successfully to describe LIED [11]. The minima and the critical angle in MAPES satisfy the relations in Equations (8)–(12). The interference patterns show strong dependence of the symmetry. It is also found that the molecular Coulomb potential plays an essential role in the two-center interference. For circular polarization ionization processes, photoelectron angular distributions also rotate with respect to the molecular symmetry axes. As a result an angle shift is induced related to the predictions of the interference model in Equations (8)–(12). The shift (rotation) of the interference minima is also sensitive to the symmetry of the initial electronic states and the ellipticity of the ionizing pulse.
The new results dealing with interference from molecular orbitals are i) the independence on the pulse intensity and ii) the dependence on the molecular orientation.
(i) We find that the same interference patterns are obtained by varying the pulse intensity . Such a results is important for intense attosecond XUV ionization processes. The theoretical model in Equations (8)–(12) also confirms numerical results that in high frequency ionization processes the interference patterns are mainly determined by the pulse frequency ω, i.e., the kinetic energy p of the photoelectron.
(ii) It is also found that the interference minima are strongly influenced by the the molecular orientation. This mainly results from a spatial orientation asymmetry of the two outgoing electrons from the two nuclear centers due to effects of the molecular Coulomb potential. At high photoelectron kinetic energy , absence of such interference occurs due to decreasing Coulomb potential effects.
In summary, in this work we present two center interference patterns for oriented H by attosecond XUV laser pulses. The interference minimum in photoelectron angle-energy spectra is shown to be (in)sensitive to molecular orbitals, pulse intensities and molecular orientation. Thus these interference patterns allow for imaging intramolecular structure and orbital symmetry by intense ultrashort circularly polarized attosecond XUV laser pulses.
Acknowledgments
We thank Xue-Bin Bian (WIPM, Wuhan) for helpful discussion. The authors also thank RQCHP and Compute Canada for access to massively parallel computer clusters and NSERC, FQRNT for financial support in ultrafast science program.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Corkum, P.B.; Krausz, F. Attosecond science. Nature Phys. 2007, 3, 381–387. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Chang, Z.; Corkum, P. Attosecond photon sources: the first decade and beyond. J. Opt. Soc. Am. B 2010, 27, B9–B17. [Google Scholar] [CrossRef]
- Zhao, K.; Zhang, Q.; Chini, M.; Wu, Y.; Wang, X.; Chang, Z. Tailoring a 67 attosecond pulse through advantageous phase-mismatch. Opt. Lett. 2012, 37, 3891–3893. [Google Scholar] [CrossRef] [PubMed]
- Popmintchev, T.; Chen, M.-C.; Popmintchev, D.; Arpin, P.; Brown, S.; Ališauskas, S.; Andriukaitis, G.; Balčiunas, T.; Mücke, O.D.; Pugzlys, A.; Baltuška, A.; Shim, B.; Schrauth, S.E.; Gaeta, A.; Hernández-García, C.; Plaja, L.; Becker, A.; Jaron-Becker, A.; Murnane, M.M.; Kapteyn, H.C. Bright coherent ultrahigh harmonics in the keV x-ray regime from mid-infrared femtosecond lasers. Science 2012, 336, 1287–1291. [Google Scholar]
- Hernández-García, C.; Pérez-Hernández, J.A.; Popmintchev, T.; Murnane, M.M.; Kapteyn, H.C.; Jaron-Becker, A.; Becker, A.; Plaja, L. Zeptosecond high harmonic keV X-ray waveforms driven by mid-infrared laser pulses. Phys. Rev. Lett. 2013, 111, 033002. [Google Scholar] [CrossRef] [PubMed]
- Bandrauk, A.D.; Chelkowski, S.; Diestler, D.J.; Manz, J.; Yuan, K.-J. Quantum-mechanical models for photo-ionization: Uni-directional electron re-scattering by a laser pulse. Int. J. Mass Spectrom. 2008, 277, 189–196. [Google Scholar] [CrossRef]
- Vrakking, M. Chemical physics: Electronic movies. Nature 2009, 460, 960. [Google Scholar] [CrossRef] [PubMed]
- Cohen, H.D.; Fano, U. Interference in the photo-ionization of molecules. Phys. Rev. 1966, 150, 30. [Google Scholar] [CrossRef]
- Kaplan, I.G.; Markin, A.P. Interference phenomena in photoionization of molecules. Sov. Phys. Dokl. 1969, 14, 36. [Google Scholar]
- Zuo, T.; Bandrauk, A.D.; Corkum, P.B. Laser-induced electron diffraction: A new tool for probing ultrafast molecular dynamics. Chem. Phys. Lett. 1996, 259, 313. [Google Scholar] [CrossRef]
- Hu, S.X.; Collins, L.A. Imaging molecular structures by electron diffraction using an intense few-cycle pulse. Phys. Rev. Lett. 2005, 94, 073004. [Google Scholar] [PubMed]
- Meckel, M.; Comtois, D.; Zeidler, D.; Staudte, A.; Pavicic, D.; Bandulet, H.C.; Pépin, H.; Kieffer, J.C.; Dörner, R.; Villeneuve, D.M.; Corkum, P.B. Laser-induced electron tunneling and diffraction. Science 2008, 320, 1478. [Google Scholar] [CrossRef] [PubMed]
- Matta, C.F.; Boyd, R.J. The Quantum Theory of Atoms in Molecules; Wiley-VCH: New York, NY, USA, 2009. [Google Scholar]
- Lein, M.; Marangos, J.P.; Knight, P.L. Electron diffraction in above-threshold ionization of molecules. Phys. Rev. A 2002, 66, 051404(R). [Google Scholar] [CrossRef]
- Spanner, M.; Smirnova, O.; Corkum, P.B.; Ivanov, M.Y. Reading diffraction images in strong field ionization of diatomic molecules. J. Phys. B 2004, 37, L243. [Google Scholar] [CrossRef]
- Kamta, G.L.; Bandrauk, A.D. Orbital symmetry and interference effects in molecular high-order harmonic generation. Phys. Rev. A 2009, 80, 041403(R). [Google Scholar]
- Picón, A.; Bahabad, A.; Kapteyn, H.C.; Murnane, M.M.; Becker, A. Two-center interferences in photoionization of a dissociating H molecule. Phys. Rev. A 2009, 83, 013414. [Google Scholar] [CrossRef]
- Peters, M.; Nguyen-Dang, T.T.; Cornaggia, C.; Saugout, S.; Charron, E.; Keller, A.; Atabek, O. Ultrafast molecular imaging by laser-induced electron diffraction. Phys. Rev. A 2011, 83, 051403(R). [Google Scholar] [CrossRef]
- Canton, S.E.; Plésiat, E.; Bozek, J.D.; Rude, B.S.; Decleva, P.; Martín, F. Direct observation of Young’s double-slit interferences in vibrationally resolved photoionization of diatomic molecules. Proc. Natl. Acad. Sci. USA 2011, 108, 7302. [Google Scholar] [CrossRef]
- Blaga, C.I.; Xu, J.; DiChiara, A.D.; Sistrunk, E.; Zhang, K.; Miller, T.; Agostini, P.; DiMauro, L.F.; Lin, C.D. Imaging ultrafast molecular dynamics with laser-induced electron diffraction. Nature 2012, 483, 194. [Google Scholar] [CrossRef] [PubMed]
- Bian, X.B.; Bandrauk, A.D. Attosecond time-resolved imaging of molecular structure by photoelectron holography. Phys. Rev. Lett. 2012, 108, 263003. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.; DuToit, R.C.; Bartschat, K. Photoionization of the H ion by ultrashort elliptically polarized laser pulses. Phys. Rev. A 2013, 87, 053410. [Google Scholar] [CrossRef]
- Yuan, K.J.; Bian, X.B.; Bandrauk, A.D. Two-center interference in molecular photoelectron energy spectra with intense attosecond circularly polarized XUV laser pulses. Phys. Rev. A 2014, 90, 023407. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [PubMed]
- Lewenstein, M.; Balcou, Ph.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef] [PubMed]
- Bandrauk, A.D.; Chelkowski, S.; Goudreau, S. Control of harmonic generation using two-colour femtosecond-attosecond laser fields: quantum and classical perspectives. J. Mod. Opt. 2005, 52, 411–428. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Chelkowski, S.; Yu, H.; Constant, E. Enhanced harmonic generation in extended molecular systems by two-color excitation. Phys. Rev. A 1997, 56, R2537–R2540. [Google Scholar] [CrossRef]
- Moreno, P.; Plaja, L.; Roso, L. Ultrahigh harmonic generation from diatomic molecular ions in highly excited vibrational states. Phys. Rev. A 1997, 55, R1593–R1596. [Google Scholar] [CrossRef]
- Hetzheim, H.; Figueira de Morisson Faria, C.; Becker, W. Interference effects in above-threshold ionization from diatomic molecules: Determining the internuclear separation. Phys. Rev. A 2007, 76, 023418. [Google Scholar] [CrossRef]
- Okunishi, M.; Itaya, R.; Shimada, K.; Prümper, G.; Ueda, K.; Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Two-source double-slit interference in angle-resolved high-energy above-threshold ionization spectra of diatoms. Phys. Rev. Lett. 2009, 103, 043001. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Zhang, X.; Xu, Y.; Ma, H.; Yang, J. Two-center interference in photoionization of H in circularly polarized laser fields. J. Opt. Sco. Am. B 2012, 29, 2124. [Google Scholar] [CrossRef]
- Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Molecular above-threshold ionization with a circularly polarized laser field. Eurp. Phys. J. D 2013, 67, 61. [Google Scholar] [CrossRef]
- Korneev, P.A.; Popruzhenko, S.V.; Goreslavski, S.P.; Becker, W.; Paulus, G.G.; Fetić, B.; Milošević, D.B. Interference structure of above-threshold ionization versus above-threshold detachment. New J. Phys. 2012, 14, 055019. [Google Scholar] [CrossRef]
- Yuan, K.J.; Bandrauk, A.D. Angle-dependent molecular above-threshold ionization with ultrashort intense linearly and circularly polarized laser pulses. Phys. Rev. A 2011, 84, 013426. [Google Scholar] [CrossRef]
- Yuan, K.J.; Lu, H.Z.; Bandrauk, A.D. Electron interference in molecular photoionization by attosecond laser pulses. Chem. Phys. Chem. 2013, 14, 1496. [Google Scholar] [CrossRef] [PubMed]
- Milošević, D.B.; Sandner, W. Extreme-ultraviolet harmonic generation near 13 nm with a two-color elliptically polarized laser field. Opt. Lett. 2000, 25, 1532. [Google Scholar] [CrossRef] [PubMed]
- Milošević, D.B.; Becker, W. Attosecond pulse trains with unusual nonlinear polarization. Phys. Rev. A 2000, 62, 011403(R). [Google Scholar] [CrossRef]
- Fleischer, A.; Kfir, O.; Diskin, T.; Sidorenko, P.; Cohen, O. Spin angular momentum and tunable polarization in high-harmonic generation. Nature Photonics 2014, 8, 543. [Google Scholar] [CrossRef]
- Yuan, K.-J.; Bandrauk, A.D. Circularly polarized attosecond pulses from molecular high-order harmonic generation by ultrashort intense bichromatic circularly and linearly polarized laser pulses. J. Phys. B 2012, 45, 074001. [Google Scholar] [CrossRef]
- Yuan, K.-J.; Bandrauk, A.D. Single circularly polarized attosecond pulse generation by intense few cycle elliptically polarized laser pulses and terahertz fields from molecular media. Phys. Rev. Lett. 2013, 110, 023003. [Google Scholar] [CrossRef] [PubMed]
- Yuan, K.-J.; Bandrauk, A.D. Generation of circularly polarized attosecond pulses by intense ultrashort laser pulses from extended asymmetric molecular ions. Phys. Rev. A 2011, 84, 023410. [Google Scholar] [CrossRef]
- Horner, D.A.; Miyabe, S.; Rescigno, T.N.; McCurdy, C.W.; Morales, F.; Martín, F. Classical two-slit interference effects in double photoionization of molecular hydrogen at high energies. Phys. Rev. Lett. 2008, 101, 183002. [Google Scholar] [CrossRef] [PubMed]
- Yuan, K.-J.; Lu, H.Z.; Bandrauk, A.D. Laser-induced electron diffraction in H2 with linear and circular polarization ultrashort XUV laser pulses. Phys. Rev. A 2009, 80, 061403(R). [Google Scholar] [CrossRef]
- Yuan, K.-J.; Lu, H.Z.; Bandrauk, A.D. Linear- and circular-polarization photoionization angular distributions in H2 and H by attosecond xuv laser pulses. Phys. Rev. A 2011, 83, 043418. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, Y.; Liao, Q.; Lu, P. Imaging molecular structures with high-energy photoelectrons produced by extreme ultraviolet pulses. J. Opt. Soc. Am. B 2012, 29, 734. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Q.; Hong, W.; Lu, P.; Xu, Z. Molecular orbital imaging via above-threshold ionization with circularly polarized pulses. Opt. Express 2011, 19, 13722. [Google Scholar] [CrossRef] [PubMed]
- Akoury, D.; Kreidi, K.; Jahnke, T.; Weber, T.; Staudte, A.; Schöffler, M.; Neumann, N.; Titze, J.; Schmidt, L.P.H.; Czasch, A.; et al. The Simplest Double Slit: Interference and Entanglement in Double Photoionization of H2. Science 2007, 318, 949–952. [Google Scholar] [CrossRef] [PubMed]
- Yuan, K.J.; Bandrauk, A.D. Molecular above-threshold-ionization angular distributions with intense circularly polarized attosecond XUV laser pulses. Phys. Rev. A 2012, 85, 053419. [Google Scholar] [CrossRef]
- Yuan, K.J.; Chelkowski, S.; Bandrauk, A.D. Rotations of molecular photoelectron angular distributions with intense ultrashort circularly polarized attosecond laser pulses. J. Chem. Phys. 2013, 138, 134316. [Google Scholar] [CrossRef] [PubMed]
- Yuan, K.J.; Chelkowski, S.; Bandrauk, A.D. Molecular photoelectron angular distributions with intense attosecond circularly polarized UV laser pulses. Chem. Phys. Lett. 2014, 592, 334. [Google Scholar] [CrossRef]
- Yuan, K.J.; Chelkowski, S.; Bandrauk, A.D. Rotations of molecular photoelectron angular distributions in above threshold ionization of H by intense circularly polarized attosecond UV laser pulses. J. Phys. B 2014, 47, 204009. [Google Scholar] [CrossRef]
- Lagmago Kamta, G.; Bandrauk, A.D. Three-dimensional time-profile analysis of high-order harmonic generation in molecules: Nuclear interferences in H. Phys. Rev. A 2005, 71, 053407. [Google Scholar] [CrossRef]
- Pronin, E.A.; Starace, A.F.; Frolov, M.V.; Manakov, N.L. Perturbation theory analysis of attosecond photoionization. Phys. Rev. A 2009, 80, 063403. [Google Scholar] [CrossRef]
- Odžak, S.; Milošević, D.B. Interference effects in high-order harmonic generation by homonuclear diatomic molecules. Phys. Rev. A 2009, 79, 023414. [Google Scholar] [CrossRef]
- Marques, M.A.L.; Maitra, N.T.; Nogueira, F.M.S.; Gross, E.K.U.; Rubio, A. Fundamentals of Time-Dependent Density Functional Theory; Springer: Berlin, Germany, 2012. [Google Scholar]
- Girardeau, M.D.; Kim, K.G.; Widmayer, C.C. Theory of atomic excitation and ionization by ultrashort laser pulses. Phys. Rev. A 1992, 46, 5932. [Google Scholar] [CrossRef] [PubMed]
- Yuan, K.J.; Bandrauk, A.D. Photoelectron angular distributions of H and HHe by intense circularly polarized extreme ultraviolet laser pulses. J. Phys. B 2012, 45, 105601. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Shen, H. Exponential split operator methods for solving coupled time-dependent Schrödinger equations. J. Chem. Phys. 1993, 99, 1185. [Google Scholar] [CrossRef]
- Keldysh, L.V. Ionization in the field of a strong electromagnetic wave. Sov. Phys. JETP 1965, 20, 1307. [Google Scholar]
- Yuan, K.J.; Bandrauk, A.D. Molecular above threshold ionization angular distributions with attosecond bichrimatic intense xuv laser pulses. Phys. Rev. A 2012, 85, 013413. [Google Scholar] [CrossRef]
- Bian, X.B.; Bandrauk, A.D. Multichannel molecular high-order harmonic generation from asymmetric diatomic molecules. Phys. Rev. Lett. 2010, 105, 093903. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.B.; Trevisan, C.S.; Schöffler, M.S.; Jahnke, T.; Bocharova, I.; Kim, H.; Ulrich, B.; Wallauer, R.; Sturm, F.; Rescigno, T.N.; et al. Imaging polyatomic molecules in three dimensions using molecular frame photoelectron angular distributions. Phys. Rev. Lett. 2012, 108, 233002. [Google Scholar] [CrossRef] [PubMed]
- Etches, A.; Gaarde, M.B.; Madsen, L.B. Two-center minima in harmonic spectra from aligned polar molecules. Phys. Rev. A 2011, 84, 023418. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Chelkowski, S.; Yuan, K.J. Controlling electron collisions-recollisions with ultrashort intense laser pulses-from femto to attosecond science. Int. Rev. At. Mol. Phys. 2011, 2, 1–23. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).