1. Introduction and Wavefront Preservation
In terms of optics, what really matters when you have an ultra-intense, ultra-short, and fully-coherent source? Well, the easy answer is, survive the power/fluence and preserve the unique source characteristics: easy to say, but not to achieve.
Let us start with some basic concepts that arise infrequently with UV optics for Synchrotron Radiation sources but appear more often in the Laser world.
The most challenging task for an optic dealing with coherent sources is the preservation of the wavefront. There are two main factors that can alter the wavefront, and reduce the intensity of the beam: Limited mirror acceptance and mirror shape errors. The wish maximize flux collection is obvious, but having to deal with a fully-coherent beam is more challenging. In fact, if one considers the acceptance from a geometrical point of view, this very seriously underestimates the effect on the wavefront. In fact, the mirrors act as slits, and there is a diffraction effect that can introduce periodic structure in an unfocused beam, as well as side-diffraction lobes in a focused beam. However, the most detrimental effect, as well as the most complicated to handle, is the effect of figure or shape errors on both focused and unfocused beams. To quantify this effect, one often uses the Strehl Ratio [
1]. The Strehl Ratio (SR) represents the ratio between the obtained or simulated peak intensity and what is available from a perfect optical system. It therefore has numerical values between 0 and 1. Usually, an optical system is considered “good” if the SR is ≥ 0.8 (Maréchal Criterion [
2]). This is actually only a useful criterion if the optical system always delivers light at a focus. Away from the focus, we need a tougher criterion. To understand what is needed, let us see how the SR is defined:
where φ is the phase error introduced by the non-ideal optics on the wavefront. The phase error φ is wavelength (λ) dependent and, for the purpose of this discussion, due to some imperfection of the mirror surface, e.g., shape errors. In the case of a reflecting, normal-incidence optic, with defects of an rms amplitude error δ, φ = 2δ/λ. In the case of a grazing incidence mirror, with rms shape deviation from the desired profile δh and grazing angle-of-incidence θ, the phase error introduced on the wavefront is:
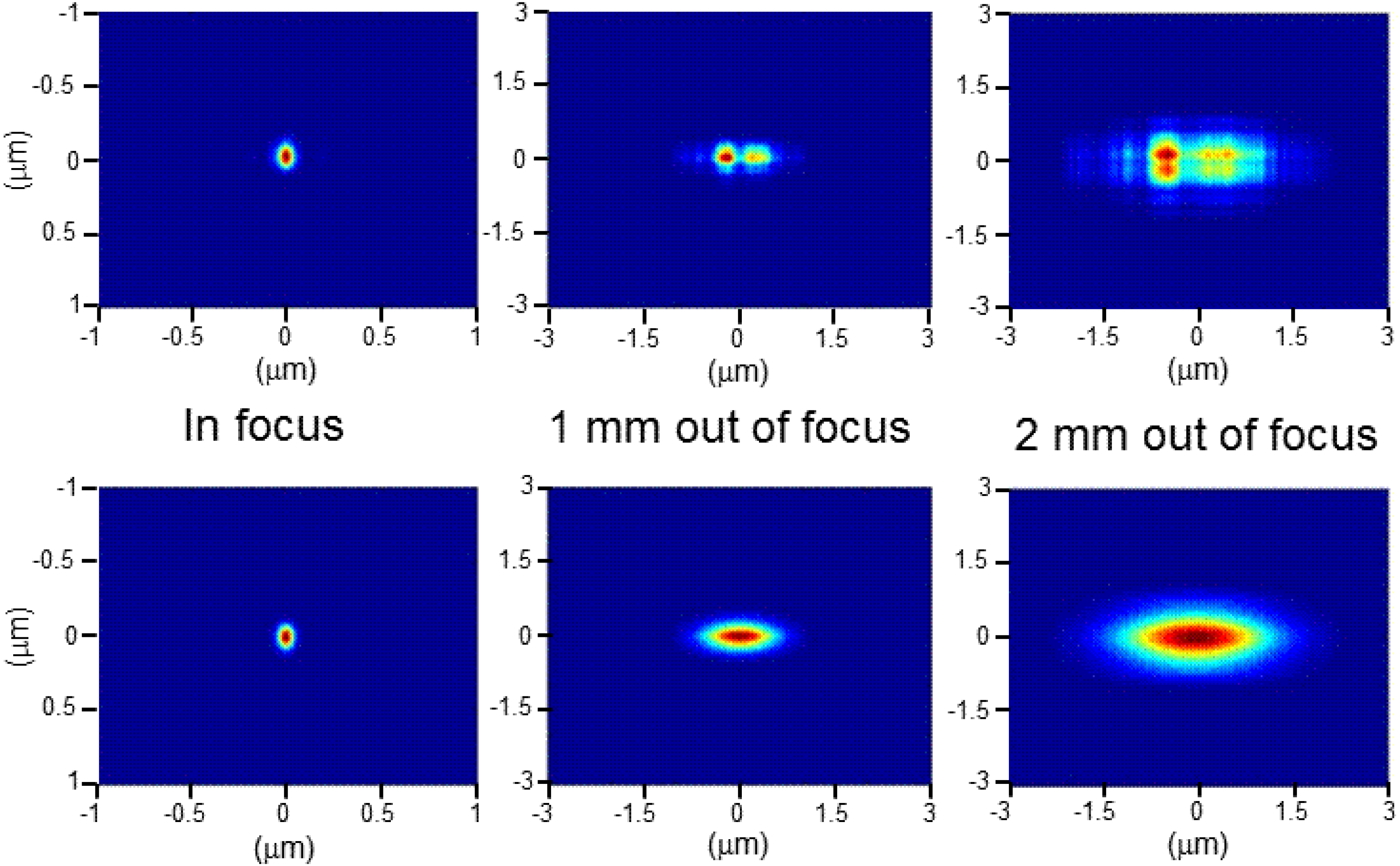
Now, a SR of 0.8 results from an rms phase variation (and therefore reflection amplitude variation) of ~7% (from Equation (1)). If we consider a plane wave reflected by the mirror, and measure the intensity of the unfocussed reflected beam, we will find an rms difference in intensity (proportional to the square of the amplitude) of ~13%. This means that if one is using the beam away from the focus, for instance for imaging or coherent diffraction experiments, the sample will be illuminated in a non-uniform way, even up to 40%–50% (e.g., the peak to valley intensity variation can be easily 5 or more times larger than the rms variation). This is, of course, unacceptable for experiments requiring a “uniform” illuminating beam. For most cases, when a uniform beam is necessary, a required SR of 0.97 is a good assumption (see
Figure 1 for a further explanation of this statement).
It is often difficult to define what is really needed, and sometimes, the state-of-the-art or the cost of the optics could be the limiting factor. What one really needs are two things, a very low residual rms shape error and the absence of high-frequency errors on the mirrors. If the first statement is obvious, the second needs some explanation. High frequency shape errors can have large amplitude but, being of short period, produce a limited increase in the rms value. The overall SR is determined by the rms shape errors but the profile of the intensity variation out-of-focus is mainly determined by the P-V shape errors.
As an example, let us consider a system of four mirrors with 2° grazing-incidence angle, and wavelengths of 10 and 5 nm. A SR of 0.8 requires shape errors of 5 and 2.5 nm rms respectively. A SR of 0.97 would require shape errors as low as 2 and 1 nm rms.
Figure 1.
Effect of mirror shape errors on the spot in-focus and away from the focus. The three upper pictures are for a system of four mirrors, with a combined Strehl ratio of 0.8. The lower three figures are for a Strehl Ratio (SR) of 0.97.
Figure 1.
Effect of mirror shape errors on the spot in-focus and away from the focus. The three upper pictures are for a system of four mirrors, with a combined Strehl ratio of 0.8. The lower three figures are for a Strehl Ratio (SR) of 0.97.
These numbers can be derived from Equation (2). In a system of N consecutive mirrors, with the same angle-of-incidence and with similar, uncorrelated rms shape errors, the shape error can be calculated from:
Shape errors of the order of 1 nm rms are very challenging, in particular for long mirrors. To simplify, slightly, the manufacturing process, the optics could be specified based on the real footprint of the beam on the mirror itself. For instance, let us consider the case of the FERMI@Elettra FEL [
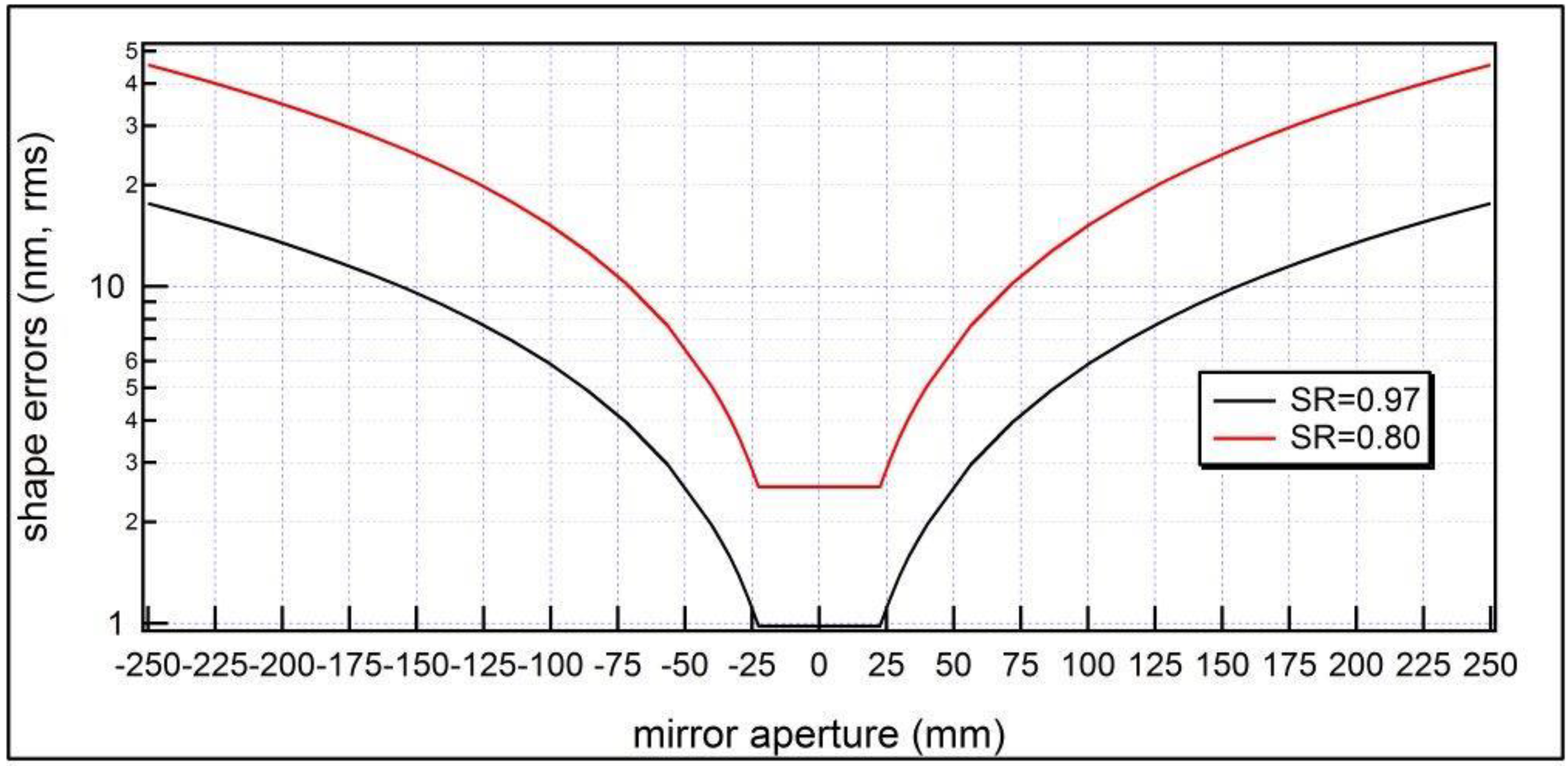
3], the free electron laser source located in Trieste, Italy. This source delivers photons in the wavelength range from 100 to 5 nm (and even lower wavelengths). The beam is diffraction limited, and therefore the divergence, and consequently the footprint of the beam on the mirror surface, changes by a factor of 20 over the wavelength range. Since the tightest specification is required for the shortest wavelengths, the best way to specify a mirror, and have a vendor able to make it, is to request the shape errors as a function of the aperture of the mirror (
Figure 2).
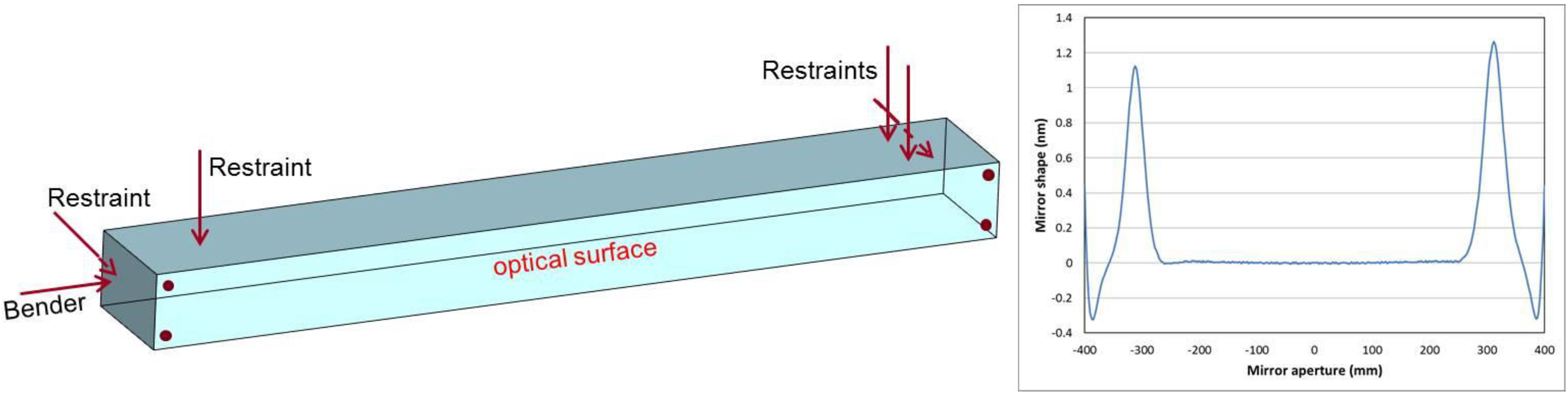
For practically, one is interested in having the central part of the mirror polished to a certain level of shape error, and the rest with lower and lower requirements are acceptable. This is the way to specify the mirrors. To clarify, since most of the incident beam intensity is contained in 2xFWHM, the aperture of the mirror associated with a particular wavelength can be taken as 2 FWHM. Of course, such a mirror profile must be preserved once installed, and that makes the situation even more complicated. Nevertheless, the peculiar characteristics of the source give us further aid. Since the deformation of the mirror bulk is mainly concentrated where the mirror restraints are located, and since the longer wavelengths, having the largest footprint, require lower tolerances, the holder for these mirrors can be designed with the restraints as far as possible from the central part of the mirror. Such a solution is adopted by LCLS for their 1 m long mirrors [
4] and is shown in
Figure 3.
Figure 2.
A possible way to specify shape errors on a mirror, when dealing with preservation of the wavefront. Since the source is diffraction limited, and the SR is dependent on wavelength, it is better to not over-specify the mirror, but require only the figure errors needed for a given length.
Figure 2.
A possible way to specify shape errors on a mirror, when dealing with preservation of the wavefront. Since the source is diffraction limited, and the SR is dependent on wavelength, it is better to not over-specify the mirror, but require only the figure errors needed for a given length.
Figure 3.
A schematic illustration (left) of how a mirror holder should be made for a horizontally deflecting mirror. All of the restraints must be as far as possible from the central part of the mirrors to avoid induce of deformation where the most demanding shape errors are required. The right panel shows the calculated induced deformation for such a holder on a 1 m long silicon mirror.
Figure 3.
A schematic illustration (left) of how a mirror holder should be made for a horizontally deflecting mirror. All of the restraints must be as far as possible from the central part of the mirrors to avoid induce of deformation where the most demanding shape errors are required. The right panel shows the calculated induced deformation for such a holder on a 1 m long silicon mirror.
Since such specifications are rarely met by polishing only, one alternative approach is to use adaptive optics. The idea is to have a number of actuators shaping the mirror surface to compensate most of the errors due to polishing, thermal and mechanical deformations. Several approaches were used in the past, most of them based on the use of piezo actuators. A non-exhaustive list of such projects is listed in the reference section [
5,
6,
7,
8].
2. Damage of Optical Coatings
The other main problem related to an ultra-intense and ultra-short-pulse source is potential damage to the optical surface. Practically, when a mirror is designed for such service, one cannot freely choose the coating and angle-of-incidence, according to the usual paradigm to maximize reflectivity and acceptance, and maybe cut off photon energies above a certain value. Actually, the best coating candidate is one having a large penetration depth, which is usually associated with a lower reflectivity. In fact, the damage threshold for heavy metal coatings, often used in Synchrotron Radiation user facilities is lower than that for light materials like Be, C or compounds like B4C and SiC, which have the further advantage that the absorbed incident energy is distributed among more atoms than occurs in single-component coating.
If we consider a mirror working below the critical angle, too optimistically called the “total external reflection mode”, the non-reflected part of the beam penetrates by 1/
e into the mirror a distance
d equal to [
9]:
with
where δ and β are the unit decrements of the real part and imaginary part of the refractive index
n = 1−δ−iβ.
Now, if one considers an incoming, normal-incidence peak power density
Pd and a reflectivity
R, for a material with an atomic density (number of atoms per unit volume) ρ
atm, the absorbed dose per atom
Datm is:
As a rule of thumb, that is usually very optimistic, an atom cannot absorb more than 1 eV. Studies on several materials set the limit as low as 0.7 eV/atom in grazing incidence for Pt [
10] and 0.3 eV/atom on Si. The best way to avoid damage is therefore to minimize the absorbed power as much as possible. Of course, a better reflectivity helps considerably, but from Equation (6), the penetration depth and the atomic density play an important role. The absolute best material is, in fact, one having a large penetration depth and several atoms among which to distribute the absorbed power. A heavy metal has a large atomic density but the penetration depth is usually very small. A very light material could have a large penetration depth but few atoms among which to distribute the power. Even if the second case is usually preferable to the first one, the best compromise is the use of compound coatings. Materials like MgF
2, B
4C, SiC or other borides or silicate compounds, are an excellent solution. The reflectivity in the UV, once the absorption edges are avoided, is quite good for grazing incidence and the penetration depth reasonably high. However, even if in the SXR, above the Carbon edge, most of these compounds can be used, trying to work in large UV regions, like from 50 to 5 nm wavelengths, is almost impossible. In fact, all of them, excluding carbon, have absorption edges in this region. Therefore, many studies on the damage of carbon and on silicon, as backup solutions, were performed at the beginning of the XUV FEL era [
11,
12,
13]. High density carbon, in particular, has the double advantage of a slightly higher reflectivity and atomic density. Diamond-like carbon would be the best solution but, at the moment, there are no providers able to coat mirrors with such a high-density material.
A multi-coating mirror, e.g., with different single layer reflective stripes in the sagittal direction, is also a valid option, if the expected power density delivered by the source comes close to the damage limit (calculated or estimated) for one coating over part of the desired photon wavelength range. Nevertheless, since several tabletop lasers and FELs are now operating, the best thing to do is test the optics by simulating the desired operation condition. This is routinely made, for instance, at LCLS where each new coatings must go through a series of tests, the most important of which is the damage threshold measurement. However, since the beamtime on an FEL is so precious, and tests are not always possible, the second best option is to have a very large safety margin, for example, 10 or more, between the expected power adsorbed per atom and the calculated (or estimated) damage threshold.
3. Beam Stretching
The last problem, or main difference with respect standard UV optics, is related to the temporal stretch of the beam in presence of diffractive elements like gratings or multilayers. The simple fact that different photons travelling different paths can produce a temporal elongation of the beam that, if not compensated, can drastically elongate the beam.
Diffraction gratings are the most common dispersive element in the UV or XUV range. An FEL source is usually quite monochromatic and a tabletop laser is even better. Nevertheless, there are situations in which a grating is still needed. We will not discuss the case of gratings used in diagnostics (see for instance [
14]), e.g., to measure the spectral profile of a source, since, in this case, one is not interested in preserving the beam temporal profile. Nevertheless, some issues described here can be applicable to the diagnostic case too.
The grating is, as is well known, a diffractive element able to separate different photon wavelengths. An extensive description of the use of gratings in monochromators can be found in [
15]. For the purpose of the discussion here, we report only two formulas; the one related to the dispersion is:
where α and β are the incidence and diffraction angles (with respect the grating normal), and
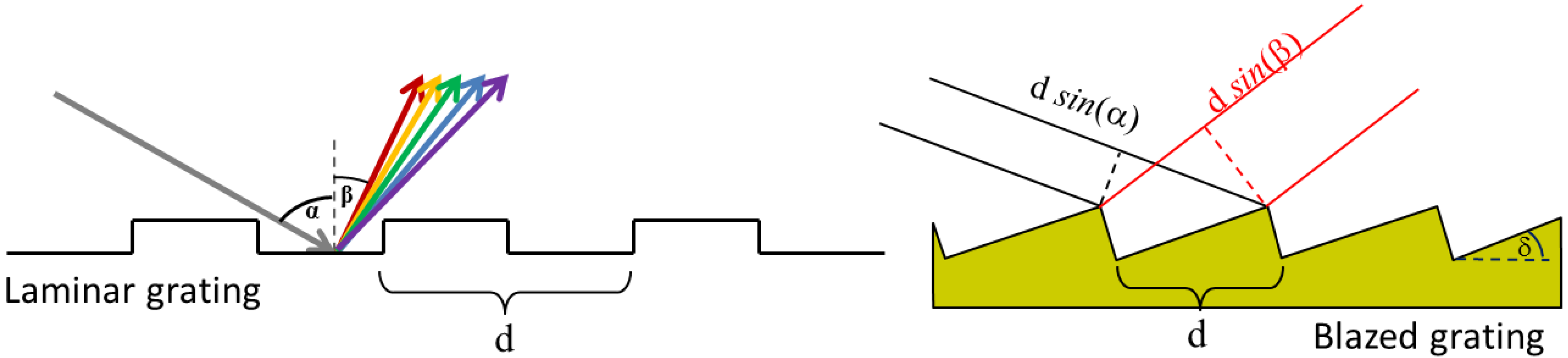
d is the grating groove spacing (often denoted as d-spacing, equal to 1/D where D is the grating groove density), λ is the photon wavelength (see
Figure 4 for details) and
n the diffraction order. From this equation, one can derive the expected resolving power (R = λ/∆λ) of a grating. In a monochromator, in fact, one needs to disperse the radiation and focus it. In the focal position, all the energies are present but spatially separated. To select only the desired one, it is necessary to use a slit having an aperture, ideally, as large as the focal dimension of the beam from the monochromator in the dispersive direction. Calling this aperture
s, the contribution of the exit slit to the resolving power is:
Figure 4.
Profile of diffraction gratings: (Left) Laminar (or lamellar) grating, α and β are the angle of incidence and diffraction respectively, d is the grating period; (Right) Blaze (or blazed) grating, δ is the blaze angle. The light is diffracted in a direction where the difference in path between two rays arriving on the grating with a separation distance d, is equal to a multiple of the wavelength.
Figure 4.
Profile of diffraction gratings: (Left) Laminar (or lamellar) grating, α and β are the angle of incidence and diffraction respectively, d is the grating period; (Right) Blaze (or blazed) grating, δ is the blaze angle. The light is diffracted in a direction where the difference in path between two rays arriving on the grating with a separation distance d, is equal to a multiple of the wavelength.
This is not the final description of how the radiation is dispersed; one must consider the source dimension, the system aberrations and the grating figure errors. However, there is another contribution to the resolution R, actually the most natural one, that is not always considered into the Synchrotron Radiation sources’ monochromators. This is very important for ultra-short sources, in particular, in the presence of very narrow divergence, and is:
where N is the number of illuminated grooves. From basic principles, considering the grating as a series of slits, this is the maximum resolution one can have. Any other terms can only reduce it (this is in principle valid for any contribution).
Now, from
Figure 4 and Equation (7), one can think of the grating as a system where two different rays arriving at the grating surface one d-spacing apart, are diffracted in a direction at which the difference in path between the two rays is equal to a multiple
n of the wavelength λ. Moreover, this obvious statement has an important implication to the preservation of the temporal structure of the beam.
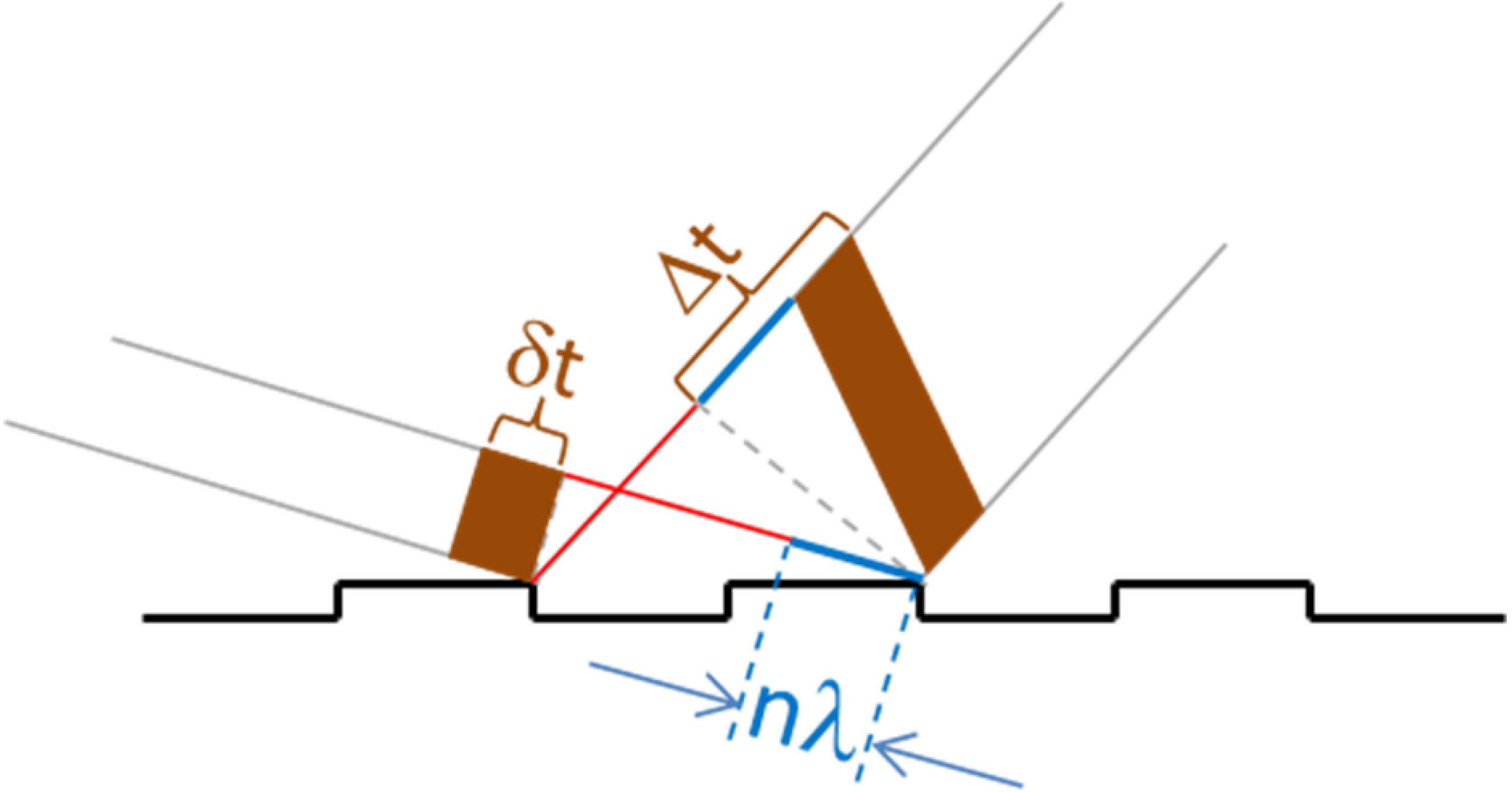
In fact, a path difference of
nλ, equivalent of several nanometers in the UV region, also produce a difference in time between the two rays, equivalent to
nλ/c, with c being the speed of light (
Figure 5). This looks like a very small number, actually it is, but if the total number of illuminated grooves is N, the difference in time between the two outermost rays is:
In the case of a 10 nm wavelength, a groove density as low as 200 L/mm, and a footprint of the order of 50 mm FWHM, that is actually quite small, the difference in time is already of the order of 300 fs. This is acceptable in some cases but not in most.
However, of course, it depends mostly on the required resolution. In fact, the beam cannot be shorter, in time, than the transform limit of its energy bandwidth. Therefore, the ideal case, for a monochromator, is to be fully transform limited. Moreover, this can be achieved in a simple way; all the contributions to the final resolution have to be negligible with respect the contribution due to the number of illuminated grooves. In this case, the beam exiting from the monochromator will be fully transform limited. If this is the case, there are no further actions to take, but if not, two more options can be taken. The first one has very low efficiency and is based on the use of a double monochromator to compensate the stretch due to the first monochromator [
16]. This solution preserves the time duration but is, of course, inefficient. The total transmission of a double monochromator can easily be below 1%.
Figure 5.
Pictorial description of the temporal elongation induced by a grating. The incoming beam has temporal duration δt. The difference in path between the rays must be a multiple of the wavelength. Therefore, different parts of the photon bunch travel different path lengths. As a result, the length of the beam, after diffraction from a single groove is ∆t.
Figure 5.
Pictorial description of the temporal elongation induced by a grating. The incoming beam has temporal duration δt. The difference in path between the rays must be a multiple of the wavelength. Therefore, different parts of the photon bunch travel different path lengths. As a result, the length of the beam, after diffraction from a single groove is ∆t.
A different approach is the use of a grating in conical diffraction. In this configuration the gratings line are parallel to the beam and not perpendicular. The efficiency can be as high as 50% and, more important, the number of illuminated grooves is lower. Of course, the ultimate resolution is also lower than in the standard configuration, but, properly designed, can produce a transform-limited monochromatic beam. The disadvantage of the conical configuration is the mechanical complexity of the system. For further details, the article by Frassetto et al. in this same issue provides interesting reading about monochromators in conical diffraction mounting.
The last issue, about the grating, is the damage. We have described the damage mechanism on mirror in the second section of this article. As mentioned, to avoid damage on the optical surface, it is important to have good reflectivity, a distribution of the power over the mirror surface (e.g., shallow angle of incidence) and a resistant coating. The first two requirements are not necessary satisfied in a grating. In fact, the usual groove profiles for grating in the UV and SXR are blazed and laminar (
Figure 4). In the case of a laminar grating, the beam hits the walls of the grating at almost normal incidence (
Figure 4 left). In this case, there is a very high power density deposited on these walls, and it can easily overcome the damage limit. In the case of a blazed grating (
Figure 4 right) the power density can be handled by reducing at minimum the blaze angle δ, and rounding the tips of the grooves. The reduction of the blaze angle is important to distribute the power. Nevertheless, there are very few manufacturers in the world able to make this angle below 1–2°. The smoothness of the sharp tip of the blaze grating grove is probably an easier process but, again, is something needing careful optimization of the ruling process. Overall, this is something that must be considered when a grating is ordered. Some unpublished tests performed at different facilities, proved the dangerousness of using laminar gratings above certain fluence. To estimate the power absorbed by a blazed grating on its facets, a good estimation is to simulate a mirror with an angle of incidence as large as the angle of incidence on the grating faced (e.g., the angle of incidence on the grating plus the blaze angle). This approximates quite well the absorbed power. In fact, the reflectivity of a mirror at this angle is not far from the total efficiency of a grating considering all the diffraction orders. Nevertheless, as mentioned, on the groove tip, the energy is confined in a smaller volume. Therefore, an extra safety margin must be kept when dealing with gratings. An example on the use of diffraction gratings on an FEL facility and on the problem of handling the damage of it is reported in [
10].