Performance Analysis of Polarization Modulated DirectDetection Optical CDMA Systems over Turbulent FSO LinksModeled by the Gamma-Gamma Distribution

Abstract

This paper proposes a theoretical study to characterize the transmission of optical code division multiple access (CDMA) systems deploying polarization shift keying (PolSK) over a free space optical (FSO) link under the impact of atmospheric turbulence. In our analysis, a novel transceiver architecture for atmospheric OCDMA FSO systems based on polarization modulation with direct detection is proposed and discussed. A detailed analytical model for PolSK-OCDMA systems over a turbulent FSO link is provided. Further, we derive a closed-form bit error ratio (BER) and outage probability expressions, taking into account the multiple-access interference (MAI), optical noise and the atmospheric turbulence effect on the FSO link modeled by the Gamma-Gamma distribution. Finally, the results of this study show the most significant parameters that degrade the transmission performance of the PolSK-OCDMA signal over FSO links and indicate that the proposed approach offers improved bit error ratio (BER) performances compared to the on-off-keying (OOK) modulation scheme in the presence of turbulence.

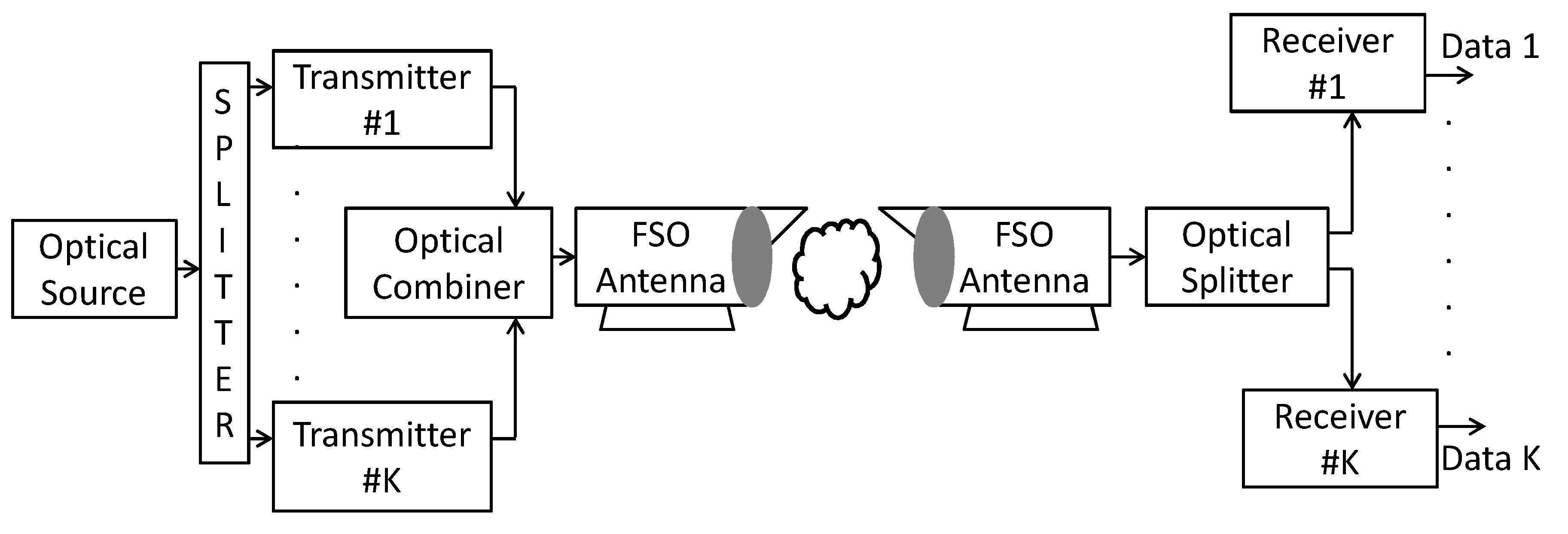
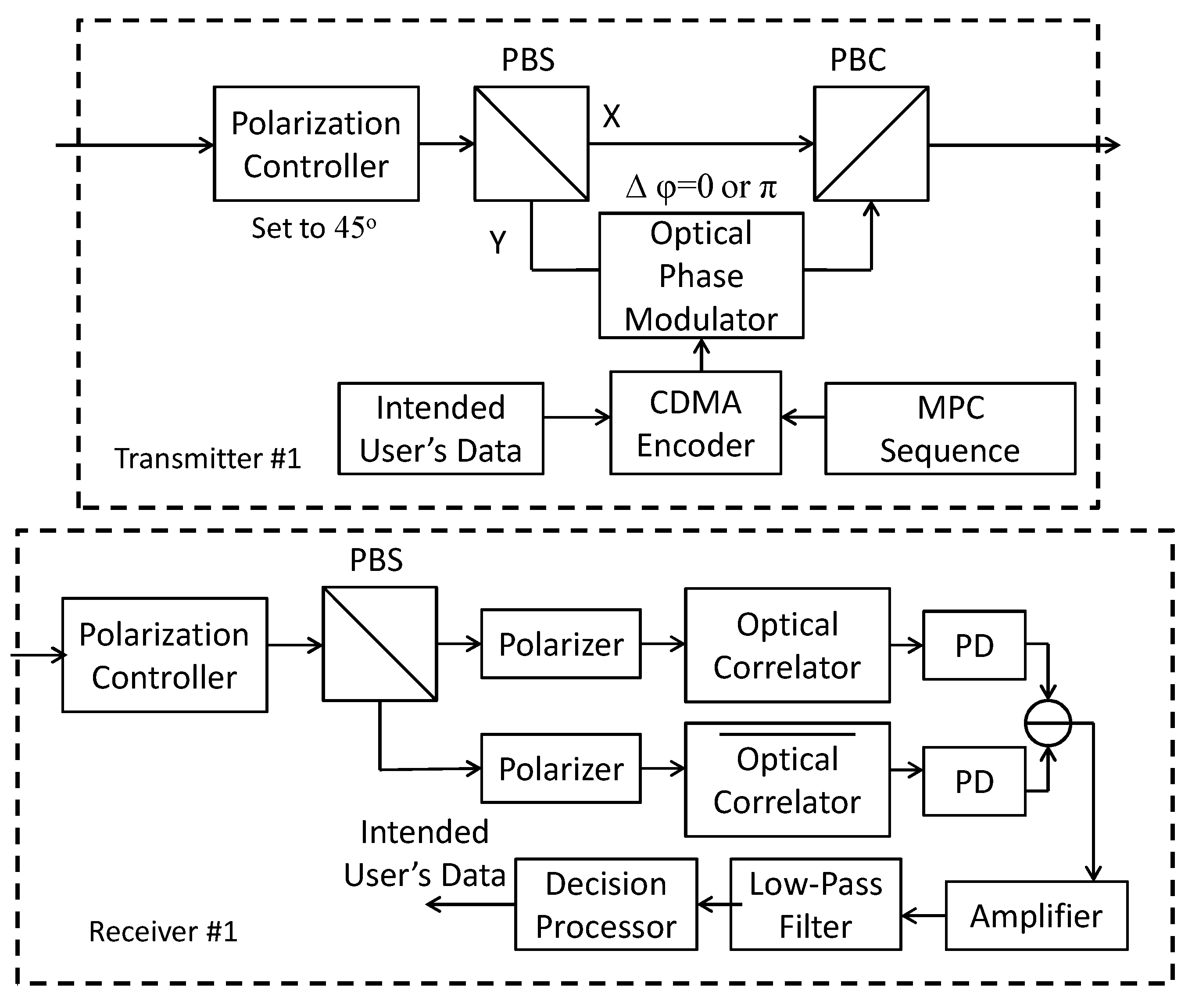
1. Introduction

Free space optical (FSO) communication, a cost-effective and highly secured technique using a wide bandwidth on an unregulated spectrum technique, has received growing attention with recent commercialization successes. It is considered an attractive solution to the last mile problem of bridging the gap between the end user and the backbone construction. In regard to the FSO system model, however, a significant influence factor is the turbulence-induced channel fading, which impairs the quality of the received signal and link performance improvement [1]. Therefore, it is imperative to apply efficient techniques to mitigate the channel fading caused by the atmospheric turbulence. In recent years, many researchers have studied the effects of atmospheric turbulence on FSO communications. A number of turbulence mitigation methods for FSO systems have been proposed, such as diversity techniques, adaptive optical technology, robust modulation techniques, etc.

Traditionally, modulation schemes, in particular based on intensity modulation/direction detection (IM/DD), for FSO systems have been wildly reported, such as amplitude shift keying (ASK), etc. However, the performance of the ASK scheme is highly sensitive to the turbulence fluctuation and modulation index; thus, the adaptive detection technique is required at the receiver to improve the link performance [2,3]. This would mean the requirement of the knowledge of the channel characteristic, which adds to the system complexity [3]. Different from IM-based modulation schemes, polarization shift keying (PolSK) was proposed as an alternative modulation technique to both envelop- and phase-based modulation schemes [4]. Under this technique, information is encoded as different states of polarization (SOPs) of the laser source by an external modulator (i.e., a Mach–Zehnder modulator) [5]. For an optical beam, polarization states are the most stable properties compared with the amplitude and phase when propagating though a turbulent channel [6]. Various PolSK schemes have been proposed for FSO transmission systems [5,6,7]. In [8], it is shown that the binary PolSK modulation scheme offers improved link performance in terms of the peak optical power by about 3 dB compared to the ASK scheme. However, most of the PolSK schemes proposed so far are based on single user access without interference distortion in the FSO link. In this paper, a novel transceiver architecture based on the PolSK scheme with a multiplexing transmission technique has been proposed to mitigate the channel fading, as well as to enhance the system capacity in FSO communication systems.

Optical code division multiplexing access (OCDMA) is a technology to realize multiplexing transmission and multiple access, which supports high-speed and large capacity communication in optical fiber networks. At the same time, the OCDMA technique has also drawn a lot of attention in optical wireless communications. In [9], the authors reported for the first time the experimental performance of OCDMA transmission over 160-m FSO links and 20-km optical fiber links, showing that the OCDMA signals can be utilized in an FSO communication system. Furthermore, the use of OCDMA schemes as a countermeasure for the mitigation of turbulence has been considered in [10,11], in which the transmission performance of OCDMA signals influenced by atmospheric turbulence and multiple-access interference (MAI) was thoroughly discussed. However, in most of the previous literature [10,12,13], FSO links only can be used to transmit the OCDMA signal based on intensity modulation through free space, and no systematic study of a cost-effective all-optical CDMA-FSO system with external modulation has been carried out. Therefore, such a study will be important in designing and optimizing methods to enhance the performance of the OCDMA FSO systems in operation environments, combining the advantages of high transmission capacity enabled by multiplexing transmission technology and the efficiency of a robust modulation scheme for the mitigation of channel fading.

The advantages of combining PolSK and OCDMA in optical fiber networks were already reported in [14,15], where the fiber dispersion and noise are the important impairment factors. However, no complete study providing an analytical model for PolSK-modulated OCDMA systems over an FSO link has been proposed so far to our knowledge. Therefore, the goal of this paper is to analyze and explore the potential of a PolSK-OCDMA FSO system for use in high performance, high speed optical wireless transmission. Firstly, in this paper, we develop a framework for a PolSK-modulated OCDMA signal over a direct detection FSO link modeled by the Gamma-Gamma distribution. Then, we investigate and evaluate the impact of optical scintillation and MAI on the transmission performance of the PolSK-OCDMA FSO link, in terms of the bit error ratio (BER), as well as the outage probability in the case of the plane-wave model. Furthermore, the numerical results show that the transmission performance of the proposed system is highly sensitive to atmospheric turbulence, received optical power and multiple-access interference. For comparison, the OOK and PolSK for the OCDMA-FSO link performance have also been presented. Our theoretical study provides an all-optical CDMA-FSO system structure based on the PolSK scheme, which takes into account the significant influence factors on transmission performance, especially when a large number of active users share the same turbulence channel.

The remainder of the paper is organized as follows. In Section 2, we introduce the statistical modeling for the atmospheric turbulence. In Section 3, we present the mathematical modeling for the transmission of the OCMDA signal over the FSO link based on the PolSK modulation. The analytical results are shown and discussed in Section 4. Section 5 concludes the paper.

2. Atmospheric Turbulence Channel

In the FSO channel, the main effect of atmospheric turbulence is irradiance fluctuations, known as the optical scintillation, resulting in refraction index random variations due to inhomogeneities in temperature and pressure changes [1]. The optical scintillation can deteriorate the quality of the received signal and cause fluctuations in both the intensity and the phase of the received signal when an optical wave propagates through the atmospheric FSO link. Different probability density functions (pdfs) have been proposed for the intensity variation of the received signal of the FSO link. Based on previous studies, we have surmised that the Gamma-Gamma distribution model can be used to analyze the scintillation of atmospheric turbulence in all of the turbulence strength regimes.

The Gamma-Gamma model describes both small-scale and large-scale atmospheric fluctuations and factorizes the irradiance as the product of two independent random processes, each having a gamma pdf and defined as [1]:

$$P{\left(X\right)}_{G-G}=\frac{2{\left(\alpha \beta \right)}^{\frac{\alpha +\beta }{2}}}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{X}^{{}^{\frac{\alpha +\beta }{2}-1}}{K}_{\alpha -\beta }\left(2\sqrt{\alpha \beta X}\right),X>0$$

(1)

where $\Gamma (.)$ is the Gamma function, $K_n(.)$ is the modified Bessel function of the second kind of order n and α and β are the statistically independent unit mean random variable fluctuation caused by small-scale and large-scale turbulence eddies and defined for the plane-wave with aperture averaging (AA) as:

$$\alpha ={\left\{exp\left[\frac{0.49{\sigma }^2}{{\left(1+0.18d^2+0.56{\sigma }^{12/5}\right)}^{-7/6}}\right]-1\right\}}^{-1}$$

(2)

$$\beta ={\left\{exp\left[\frac{0.51{\sigma }^2{\left(1+0.69{\sigma }^{12/5}\right)}^{-5/6}}{\left(1+0.9d^2+0.62d^2{\sigma }^{12/5}\right)}\right]-1\right\}}^{-1}$$

(3)

where ${\sigma }^2$ is the Rytov variance and d is the receiver aperture, ${\sigma }^2=1.23w^{7/6}{C}_n^2{L}^{11/6}$ and $d={(w{D}^2/4L)}^{1/2}$, D is the receiver aperture diameter, the optical wave number is represented by w, the quantity $C_n^2$ is the index of the refraction structure constant and L is the propagation distance. We denote $X=I/〈I〉$; I is a random variable of the signal current, and the symbol $〈.〉$ denotes the average over scintillation. The scintillation index can be expressed as ${\sigma }_I^2=1/\alpha +1/\beta +1/\alpha \beta$.

3. PolSK-OCDMA Signal Transmission over an Atmospheric FSO Link

The focus of this section is to establish an analytical model that is able to characterize the polarization-modulated optical CDMA signal propagation through a turbulent FSO link. We consider the effect of multiple-access interference (MAI) within multiple users; the degradation of transmission performance due to optical scintillation caused by the turbulence channel. The transceiver structure for the proposed direct detection PolSK-OCDMA FSO system is shown in Figure 1. In terms of optical signature sequences, we employ modified prime codes (MPCs) with the auto-correlation and cross-correlation value bounded by one in this analysis. The modified prime code is characterized by its code length $F=p^2$; the code weight $W=p$. The cardinality of MPC is defined $p^2$, and the p is a prime number [4,16].

Figure 1. Block diagram of PolSK-OCDMA systems over turbulent FSO links.

Figure 1. Block diagram of PolSK-OCDMA systems over turbulent FSO links.

3.1. Analysis of the PolSK-OCDMA System Model

A laser beam with a fully polarized SOP generated by a laser diode and propagating along the z-axis will have the transversal electric field components as:

$$E_x\left(t\right)=A_x\left(t\right)exp\left[j\left({\omega }_{s}t+{\phi }_x\right)\right]$$

(4)

$$E_y\left(t\right)=A_y\left(t\right)exp\left[j\left({\omega }_{s}t+{\phi }_y\right)\right]$$

(5)

where $E_0\left(t\right)=E_x\left(t\right)\widehat{x}+E_y\left(t\right)\widehat{y}$ can be expressed as the electromagnetic field vector before the external modulation, $A_x\left(t\right)=Acos\theta$ is the amplitude of the x-component, $A_y\left(t\right)=Asin\theta$ is the amplitude of the y-component and ${\phi }_x$ and ${\phi }_x$ are the phase of the x-component and y-component, respectively. The ${\omega }_s$ is the optical frequency. Then, we assume for simplicity that the laser beam is set to be linearly polarized at an angle of $\pi /4(\theta ={45}^0)$ with respect to the transmitter reference axis by the polarization controller (PC). The linearly polarized beam is divided into horizontal and vertical SOPs with equal amplitude ($A_x=A_y$) and zero phase difference $(\Delta \phi ={\phi }_y-{\phi }_x=0)$ at the output of the polarization beam splitter (PBS). Then, the SOP of the input beam is switched between two orthogonal states by the optical phase modulator, which refer to $0^0$ to ${180}^0$ $(\Delta \phi =0or\Delta \phi =\pi )$. The N times per bit is according to the modified prime code mapping the optical signal into CDMA format. Then, the emitted PolSK-modulated optical field at the polarization beam combiner (PBC) output can be expressed as:

$$E_{T.k}\left(t\right)=\sqrt{\frac{P_t}{2}}exp\left[j\left({\omega }_{s}t+{\phi }_s\right)\right]\left\{\widehat{x}+exp\left(j\Delta \phi S_k\left(t\right)\right)\widehat{y}\right\}$$

(6)

where $S_k\left(t\right)$ is the CDMA signal encoded by the modified prime code of the k-th user and $P_t$ is the transmitted optical power. Hence, the combined total of the transmitted signals at the optical combiner output is as $S_{CDMA}\left(t\right)={\sum }_{k=1}^K{S}_k(t-{\tau }_k)={\sum }_{k=1}^K{d}_k(t-{\tau }_k)c_k(t-{\tau }_k)$, and the ${\tau }_k$, $0\le {\tau }_k\le T_s$ is the time delay of the k-th user; and $d_k\left(t\right)={\sum }_{i=0}^{M-1}{d}_{k,i}{P}_T(t-i{T}_s)$ and $c_k\left(t\right)={\sum }_{i=0}^{N-1}{d}_{k,i}{P}_T(t-i{T}_c)$ are the intended user data signal with M bits. The prime code sequence signal has N chips and $d_k\left(t\right)$, $c_k\left(t\right)\in \left\{0,1\right\}$, where $P_T$ denotes a unity rectangular pulse of width T, and $T_s$ and $T_c$ are the symbol duration and chip duration, $F=p^2=T_s/T_c$. By using the Jones notation [17,18], the electrical field can be represented by the vector of the Jones matrix, $J={\left[\begin{array}{cc}{E}_x& E_y\end{array}\right]}^T$, and two SOPs represented by $J_H$ and $J_Y$ are orthogonal if their inner product is zero [19]. In the PolSK modulation scheme, the binary bits map into the Jones vectors when the angle of one polarization component is switched relative to the other between two angles [4]. Thus, for a K-user PolSK-OCDMA system with the first user as the desired one, the k-th user SOP-encoded OCDMA signal can be written as:

$$J_k\left(t\right)=\left\{\begin{array}{cc}{J}^0\hfill & \text{if}{d}_k\left(t\right)XOR{c}_k\left(t\right)=0(\Delta \phi =0)symbol”0”\hfill \\ J^1\hfill & \text{if}{d}_k\left(t\right)XOR{c}_k\left(t\right)=1(\Delta \phi =\pi )symbol”1”\hfill \end{array}\right.$$

(7)

where $XOR$ denotes the exclusive disjunction operation. Thus, the emitted optical signal is represented by the Jones vector, $J^0=\frac{1}{\sqrt{2}}{\left[11\right]}^T$ and $J^1=\frac{1}{\sqrt{2}}{[-11]}^T$ [14,15]. Furthermore, we have:

$$Q=\left[\begin{array}{cc}{J}^0& J^1\end{array}\right]$$

(8)

where Q is a complex Jones matrix with a unit determinant.

Then, each user modulated signal is combined together by the optical combiner and transmitted through the turbulent FSO channel. Consequently, the optical signal suffers from several impairments, such as polarization fluctuation, channel attenuation, such as beam divergence, and channel fading, due to the optical scintillation.

Moreover, the received composite signal by the Jones vector plus additive white Gaussian noise (AWGN) at the single receiver after splitter can be defined as:

$$J_r(t,X)={\left[\begin{array}{cc}{E}_{r.x}& E_{r.y}\end{array}\right]}^T=J_1(t,X)+\sum _{k=2}^K{J}_k(t,X)+J_{FSO}\left(t\right)$$

(9)

where the first and second elements are the represented data from the intended user and interference by other users, and $J_{FSO}\left(t\right)$ is the Jones vector of AWGN. X quantifies the variation of signal fading, as mentioned earlier, and its pdf $P{\left(X\right)}_{G-G}$ is defined by Equation (1). In this work, as shown in Figure 2, the SOP fluctuation due to the turbulence is compensated by the polarization controller, whose function is to ensure that the received signal at the receiver side has the same SOP reference axis as reported in [20]. Then, the received composite signal passes through the PBS and is divided into upper and lower branches. In this proposed architecture, the polarizer device can be used as a polarization rotator by $\pi /4$ with the polarization filter, in order to align the SOP to the reference axis. The function of the rotator’s output by the Jones vector is given as $J_R^z(t,X)=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ -1& 1\end{array}\right]J_r^z(t,X)$, and $z\in \left\{0,1\right\}$ denotes the upper (x-component) or lower branch (y-component) [19]. Hence, the polarization filter of each branch will only allow the optical beam matched with its axis to pass. Here, the polarizer produces only the x-polarization corresponding to the first elements of the Jones vector; thus, the function of each polarizer output is given as $J_P^z(t,X)={\left[\begin{array}{cc}{E}_{RX}^z& 0\end{array}\right]}^T=\frac{1}{\sqrt{2}}\left\{E_{r.x}^z+E_{r.y}^z\right\}$ [4]. At last, the optical signal of each branch is correlated through the optical correlator. If a signal with the correct codeword arrives, the optical correlator is tuned to the intended user’s assigned spreading code to de-spread the CDMA-encode signals, and thus, the auto-correlation function achieves a high peak value. However, on the contrary, for an incorrect codeword, a cross-correlation is generated and creates the MAI [16].

Figure 2. Block diagram of the PolSK-OCDMA system transceiver structure.

Figure 2. Block diagram of the PolSK-OCDMA system transceiver structure.

Now, we establish the mathematical model and analysis of the PolSK-OCDMA signal processing. Firstly, in the presence of turbulence, the received composite PolSK modulated OCDMA signal for a single receiver is as follows: [4,15]

$$E_R(t,X)=Re\left\{E_0\left(t\right)e^{j({\omega }_{s}t+{\phi }_r)}\sum _{k=1}^{K}Q\left[\begin{array}{c}{d}_k\left(t\right)\\ 1-d_k\left(t\right)\end{array}\right]P_T(t-k{T}_S)c_k\left(t\right)\right\}$$

(10)

where $E_R(t,X)$ is proportional to variable X and has the same statistical model, $Re(.)$ denotes the real part of complex $E_R(t,X)$ and ${\phi }_r$ is the phase of the received optical field. Because both of the orthogonal components (x-, y-component) are assumed as being equally amplitude and channel attenuated, this neglects the loss of orthogonality due to atmospheric turbulence. Thus, the k-th user of the received PolSK modulated OCDMA signal after polarizer for the upper (x-component) and lower branch (y-component) is as follow [4]:

$$E_{R.x.k}^0(t,X)=\left[\frac{E_{x.k}+E_{y.k}}{2}+\sum _{k=1}^K{d}_k\left(t\right)c_k\left(t\right)\frac{E_{x.k}-E_{y.k}}{2}{P}_T(t-k{T}_S)\right]cos\left({\omega }_{s}t+{\phi }_{x.k}\right)$$

(11)

$$E_{R.y.k}^1(t,X)=\left[\frac{E_{x.k}-E_{y.k}}{2}+\sum _{k=1}^K{d}_k\left(t\right)c_k\left(t\right)\frac{E_{x.k}+E_{y.k}}{2}{P}_T(t-k{T}_S)\right]cos\left({\omega }_{s}t+{\phi }_{y.k}\right)$$

(12)

where orthogonal components of the k-th user as $E_{x.k}=J^0{d}_k\left(t\right)c_k\left(t\right)E_0\left(t\right)$ and $E_{y.k}=J^1(1-d_k\left(t\right))c_k\left(t\right)E_0\left(t\right)$ are based on Equations (4), (5) and (8), ${\phi }_{x.k}$ and ${\phi }_{y.k}$ represent the phase of the received optical field for each component. In this analysis, a simple structure for the OCDMA receiver was proposed by using the optical correlator. The optical correlator correlates the arriving signals by pre-reserving the intended user’s assigned spreading code to de-spread the encoded signals [21]. Moreover, as shown in Figure 2, the optical correlator in the lower branch is set up with complement of the code (phase shift of π). Then, the signals are received by the balanced detector to generate differential current ready for extraction in the decision processor. The total current in the upper branch at a certain symbol duration $T_s$ can be expressed as (see Equation (11)):

$$\begin{array}{cc}\hfill I_{R.x}^0=& \rho X{\int }_{t=0}^{T_s}\sum _{n=1}^N\left\{\frac{c\left(n{T}_c\right)+1}{2}\left[\sum _{k=1}^K\left(\frac{E_{x.k}+E_{y.k}}{2}\right.\right.\right.\hfill \\ \hfill +& \left.{\left.\left.d_k\left(t\right)c_k(t-n{T}_c)\frac{E_{x.k}-E_{y.k}}{2}\right)cos({\omega }_{s}t+{\phi }_x)\right]}^2\right\}dt\hfill \end{array}$$

(13)

where ρ is the photo-detector responsivity and $c_k(t-n{T}_c)$ is the n-th chip of the assigned spreading code of the k-th user. Then, the total current in the upper branch [19]:

$$I_{R.x}^0=\frac{\rho X}{4}\sum _{n=1}^N\left\{\frac{c\left(n{T}_c\right)+1}{2}\left[\sum _{k=1}^K\left(E_{x.k}^2+E_{y.k}^2+d_k\left(t\right)c_k(t-n{T}_c)\left(E_{x.k}^2-E_{y.k}^2\right)\right)\right]\right\}+n_0\left(t\right)$$

(14)

Similarly, the total current of the lower branch (y-component) can be derived as [19]:

$$I_{R.y}^1=\frac{\rho X}{4}\sum _{n=1}^N\left\{\frac{1-c\left(n{T}_c\right)}{2}\left[\sum _{k=1}^K\left(E_{x.k}^2+E_{y.k}^2+d_k\left(t\right)c_k(t-n{T}_c)\left(E_{x.k}^2-E_{y.k}^2\right)\right)\right]\right\}+n_1\left(t\right)$$

(15)

In Equations (14) and (15), the $n_0\left(t\right)$ and $n_1\left(t\right)$ represent the filtered Gaussian noise. Thus, the differential current generated at the output balanced detector $I_{diff}$ is derived as:

$$\begin{array}{cc}\hfill I_{diff}(t,X)=& I_{R.x}^0-I_{R.y}^1\hfill \\ \hfill =& \frac{\rho X}{4}\sum _{n=1}^{N}c\left(n{T}_c\right)\sum _{k=1}^K\left(E_{x.k}^2+E_{y.k}^2+d_k\left(t\right)c_k(t-n{T}_c)\left(E_{x.k}^2-E_{y.k}^2\right)\right)+n_{opt}\left(t\right)\hfill \end{array}$$

(16)

where noise $n_{opt}\left(t\right)$ includes the thermal noise, shot noise and relative intensity noise ($RIN$) processes. In this analysis, we consider the first user as the intended user; thus, Equation (16) can be modified as follows:

$$\begin{array}{cc}\hfill I_{diff}(t,X)=& \left[\frac{\rho X}{4}\sum _{n=1}^{N}c\left(n{T}_c\right)\left(E_{x.k}^2+E_{y.k}^2\right)+\frac{\rho X}{4}\sum _{n=1}^{N}c\left(n{T}_c\right)d_1\left(t\right)c_1(t-n{T}_c)\left(E_{x.1}^2-E_{y.1}^2\right)\right.\hfill \\ \hfill +& \left.\frac{\rho X}{4}\sum _{n=1}^N\sum _{k=2}^{K}c\left(n{T}_c\right)d_k\left(t\right)c_k(t-n{T}_c)\left(E_{x.k}^2-E_{y.k}^2\right)\right]+n_{opt}\left(t\right)\hfill \end{array}$$

(17)

where $I_{diff}$ consists of DC current removed in the balanced detector, the second term representing the desired user data with the assigned spreading code auto-correlation and polarization and the third term denoting the interference caused by other users.

3.2. Signal-to-Noise Ratio and Bit Error Ratio Analysis

In this subsection, we derive the expressions of the signal-to-noise ratio (SNR) and bit error ratio (BER), the analysis of which considers the effect of scintillation and MAI within the CDMA users in the presence of atmospheric turbulence. For the direct detection FSO system, the received optical power at a single receiver in the presence of turbulence can be written as:

$$P_{r.FSO}\left(t\right)=X·P_{r.0}\left(t\right)+n_{FSO}\left(t\right)$$

(18)

where $P_{r.0}\left(t\right)$ characterize the received optical power with link losses in the absence turbulence and $n_{FSO}\left(t\right)$ characterizes the AWGN. FSO link losses $L_{FSO}\left(dB\right)=L_{Geo}+L_{weather}+L_{point}+L_{vis}$, and $L_{Geo}$ is geometrical loss; $L_{weather}$ is the FSO channel loss due to weather conditions (i.e., rain); $L_{vis}$ is the attenuation caused by channel scattering with low-visibility; $L_{point}$ is the point loss due to the pointing error between the transmitter and receiver antennas [12]. Thus, we consider the SNR calculation for the proposed system, i.e., ${\tau }_k=0$, and the FSO noise, i.e., background light interference, can be bandpass filtered at the output of the photo-detectors (PDs). Then, the output $Z(t,X)$ of the matched filter after the low-pass filter (LPF) is given by:

$$\begin{array}{cc}\hfill Z(t,X)=& {\int }_{t=0}^{T_s}i(t,X)\sum _{n=1}^{N}c\left(n{T}_c\right)dt\hfill \\ \hfill =& S(t,X)+I_{MAI}(t,X)+n_{opt}\left(t\right)\hfill \end{array}$$

(19)

defining $i(t,X)=\rho P_{RX}{\sum }_{k=1}^K{S}_k\left(t\right)+n_{opt}\left(t\right)$ as the output current of PDs with the distortion component and $P_{RX}=P_{r.0}X$ characterizing the received optical power over the scintillation, $S(t,X)$ and $I_{MAI}(t,X)$ denote the signal from the desired user and the interference component. The $n_{opt}\left(t\right)$ includes the amplifier thermal noise and shot noise of both PDs, as well as the relative intensity noise ($RIN$). In addition, after code de-spreading, the in-phase assigned sequence contributes average power to either PD, whereas the MAI contributes average optical power (i.e., (K-1) users) to each PD [22]. Then, $n_{opt}\left(t\right)$ is the AWGN with a double-sided power spectral density of $N_0/2$ and can be expressed by:

$$\begin{array}{cc}\hfill N_0=& N_{shot}+N_{th}+N_{RIN}\hfill \\ \hfill =& 2q\left(P_{RX}\rho \right)+\frac{4K_B{T}_{abs}{F}_e}{R_L}+\left(RIN\right){\left(P_{RX}\rho \right)}^2\hfill \end{array}$$

(20)

where q is the electron charge, $K_B$ is Boltzmann’s constant, $F_e$ is the noise factor, $T_{abs}$ is the absolute temperature and $R_L$ is the PD load resistance. Hence, the system signal-to-noise ratio in the presence of turbulence based on Equations (17), (19) and (20) can be expressed as [4,15]:

$$\begin{array}{cc}\hfill SNR(K,X^2)=& \frac{S{\left(t,X\right)}^2}{{\sigma }_{I_{MAI}}^2+{\sigma }_{n_{opt}}^2}\hfill \\ \hfill =& \frac{{\left[\frac{\rho X}{4}{\sum }_{n=1}^{N}c\left(n{T}_c\right)d_1\left(t\right)c_1(t-n{T}_c)\left(E_{x.1}^2-E_{y.1}^2\right)\right]}^2}{{\left[\frac{\rho X}{4}{\sum }_{n=1}^N{\sum }_{k=2}^{K}c\left(n{T}_c\right)d_k\left(t\right)c_k(t-n{T}_c)\left(E_{x.k}^2-E_{y.k}^2\right)\right]}^2+N_{0}B}\hfill \end{array}$$

(21)

where $B=1/T_s$ is the bandwidth required to pass the signal without distortion. Based on the MPC properties, the equation denotes the auto-correlation as ${\sum }_{n=1}^{N}c\left(n{T}_c\right)c_1(t-n{T}_c)=p$. In the meantime, the equation ${\sum }_{n=1}^{N}c\left(n{T}_c\right)c_k(t-n{T}_c)={\lambda }_c$ represents the MPC cross-correlation value. According to the theory of MPC properties, the cross-correlation value is either $zero$ or $one$, depending on whether the codes are in the same group or different groups, while only the $one$ can cause the interference, which is among the intended user and $(p^2-p)$ users from the different groups (whole sequences $p^2$, sequences from the same group of the intend user p) [16]. Defining the cross-correlation values as uniformly distributed among interfering users, the pdf of variable ${\lambda }_c$ is defined as $P\left({\lambda }_c\right)=k/p^2-p$, and k is the number of actively involved users in the transmission. Thus, Equation (21) can be modified as:

$$SNR(K,X^2)=\left(\frac{1}{{\left(\frac{K(K-1)}{(p^2-p)p}\right)}^2+\frac{16N_{0}B}{{\left(\rho ·X·p·d_1\left(t\right)(E_{x.1}^2-E_{y.1}^2)\right)}^2}}\right)$$

(22)

When K= 1, Equation (22) denotes the single-user SNR without MAI.

In this analysis, we evaluate the transmission performance of the PolSK-modulated OCDMA signal over the atmospheric FSO link. It is important to determine the scintillation effects on the system performance. The unconditional error probability for binary PolSK modulation in the presence of turbulence is given by averaging the conditional error probability over the Gamma-Gamma distribution, as given by:

$$〈P_e^{BPolSK}\left(K\right)〉={\int }_0^{\infty }{P}_e^{BPolSK}\left(K\right)P{\left(X\right)}_{G-G}dX$$

(23)

where $P_e^{BPolSK}\left(K\right)$=$\frac{1}{2}exp\left(\frac{-SNR(K,X^2)}{2}\right)$ is the conditional error probability based on the binary PolSK modulation in the presence of turbulence [17,23].

In order to solve the integral of Equation (23), we assume that $SNR(K,X^2)$ can be approximated by averaging the noises and interference power over scintillation, i.e., $SNR(K,X^2)\approx 〈S{(t,X)}^2〉X^2/〈{\sigma }_{I_{MAI}}^2〉+〈{\sigma }_{n_{opt}}^2〉\approx 〈SNR(K,X^2)〉X^2$ [24]. To further simplify it, $exp(.)$ and $K_n(.)$ (see [25], Equations (11) and (14)) are rewritten in terms of Meijer’s G-function $G_{p,q}^{m,n}(.)$ (see [26], Equation (9.301)). A close-form error probability for the proposed system becomes:

$$〈P_e^{BPolSK}\left(K\right)〉=\frac{2^{\alpha +\beta -1}}{8\pi \Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{G}_{4,1}^{1,4}\left(\frac{8〈SNR(K,X^2)〉}{{\left(\alpha \beta \right)}^2}|\begin{array}{cccc}\frac{1-\alpha }{2},& \frac{2-\alpha }{2},& \frac{1-\beta }{2},& \frac{2-\beta }{2}\\ & 0& \end{array}\right)$$

(24)

3.3. Outage Probability Analysis

The outage probability is an effective way to evaluate the degradation of OCDMA signals due to the presence of atmospheric turbulence. It is defined as the probability that the instantaneous SNR falls below a threshold value of SNR, which represents a specified value of the SNR above which the quality of the FSO link is satisfactory. The outage probability for a given threshold $SN{R}_{th}$ is defined as [24]:

$$P_{out}\left(SN{R}_{th}\right)=P_r(SNR(K,X^2)<SN{R}_{th})=P_r\left(X^2〈SNR(K,X^2)〉<SN{R}_{th}\right)$$

(25)

we assume a constant $C_{th}$ as a ratio $C_{th}={\left(SN{R}_{th}/〈SNR(K,X^2)〉\right)}^{1/2}$; thus, the outage probability can be expressed as:

$$\begin{array}{cc}\hfill P_{out}\left(SN{R}_{th}\right)=& {\int }_0^{C_{th}}{P}_X{\left(X\right)}_{G-G}dX\hfill \\ \hfill =& {\int }_0^{C_{th}}\frac{2{\left(\alpha \beta \right)}^{\frac{\alpha +\beta }{2}}}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{X}^{{}^{\frac{\alpha +\beta }{2}-1}}{K}_{\alpha -\beta }\left(2\sqrt{\alpha \beta X}\right)dX\hfill \end{array}$$

(26)

Using the above(see [25,26]), a closed-form solution for the outage probability is obtained as:

$$P_{out}\left(SN{R}_{th}\right)=\frac{{\left(\alpha \beta \right)}^{\frac{\alpha +\beta }{2}}}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{C}_{th}{G}_{1,3}^{2,1}\left(\alpha \beta C_{th}|\begin{array}{ccc}& 1-\frac{\alpha -\beta }{2}& \\ \frac{\alpha -\beta }{2},& \frac{\beta -\alpha }{2},& \frac{\alpha +\beta }{2}\end{array}\right)$$

(27)

4. Numerical Results and Discussion

In this section, we evaluate the optical scintillation and MAI effects on both the BER and outage probability, taking into account the overall performance of the PolSK-OCDMA signals over the turbulent FSO link. The main simulation parameters used in the numerical calculation are shown in Table 1.

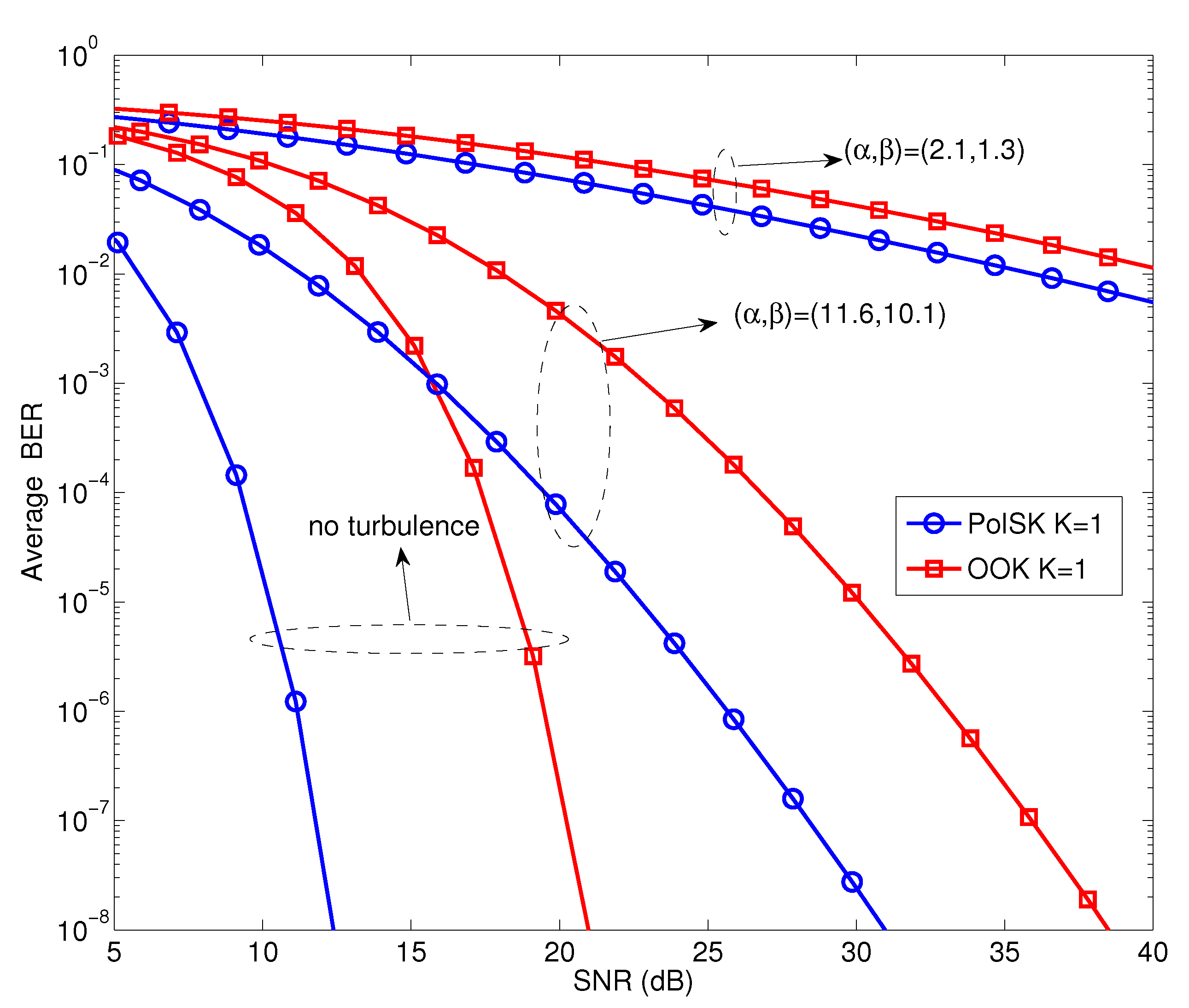
Since the behavior of the OOK-modulated OCDMA FSO system has already been investigated in several works [12,13], we prefer to evaluate the error probability of PolSK modulation to compare it with the OOK scheme under the same OCDMA FSO link conditions. The mathematical model of the error probability for the OOK-based OCDMA FSO system with a fixed threshold has already been evaluated in [23,27]. Figure 3 depicts the error probability against the normalized electric SNR for PolSK and OOK (with a fixed threshold of 0.5) schemes in a turbulent OCDMA FSO link when the number of active users $K=1$ (no multiple-access interference). It is observed that the average BER performance deteriorates with the turbulence level, with OOK displaying the worst case scenario. For a BER of ${10}^{-6}$ and scintillation parameters $\alpha =11.6,\beta =10.1$ as a weak turbulent regime, the SNR for PolSK and OOK are about 24.5 dB and 33 dB, respectively. When the scintillation parameters are changed to $\alpha =2.1,\beta =1.3$ as a strong turbulent regime, a lower SNR is required for PolSK compared with OOK at the same average BER level. Therefore, based on these numerical results illustrated in this plot, we can determine that the information encoded in the intensity of the carrier signal is much more prone to turbulence-induced fluctuation. In other words, PolSK offers improved BER performance compared to OOK across all turbulence regimes.

Table 1. Numerical parameters. PD, photo-detector; PBS, polarization beam splitter; PBC, polarization beam combiner.

Parameters	Value
Link distance L	1000 m
Channel bandwidth B	2 GHz
Operating wavelength λ	1550 nm
Aperture diameter D	100 mm
Coupling losses $L_{point}$	3 dB
Beam divergence Θ	±0.75 rmad
Relative intensity noise $RIN$	−130 dB/Hz
Absolute temperature $T_{abs}$	300 k
PD responsivity ρ	0.9 A/W
Electron charge q	$1.602\times {10}^{19}$ C
Noise figure $F_e$	2 dB
PBS/PBC loss	2 dB
Atmospheric attenuation $L_{vis}$	1 dB
Geometrical loss $L_{Geo}$	1 dB

Table 1. Numerical parameters. PD, photo-detector; PBS, polarization beam splitter; PBC, polarization beam combiner.

Parameters	Value
Link distance L	1000 m
Channel bandwidth B	2 GHz
Operating wavelength λ	1550 nm
Aperture diameter D	100 mm
Coupling losses $L_{point}$	3 dB
Beam divergence Θ	±0.75 rmad
Relative intensity noise $RIN$	−130 dB/Hz
Absolute temperature $T_{abs}$	300 k
PD responsivity ρ	0.9 A/W
Electron charge q	$1.602\times {10}^{19}$ C
Noise figure $F_e$	2 dB
PBS/PBC loss	2 dB
Atmospheric attenuation $L_{vis}$	1 dB
Geometrical loss $L_{Geo}$	1 dB

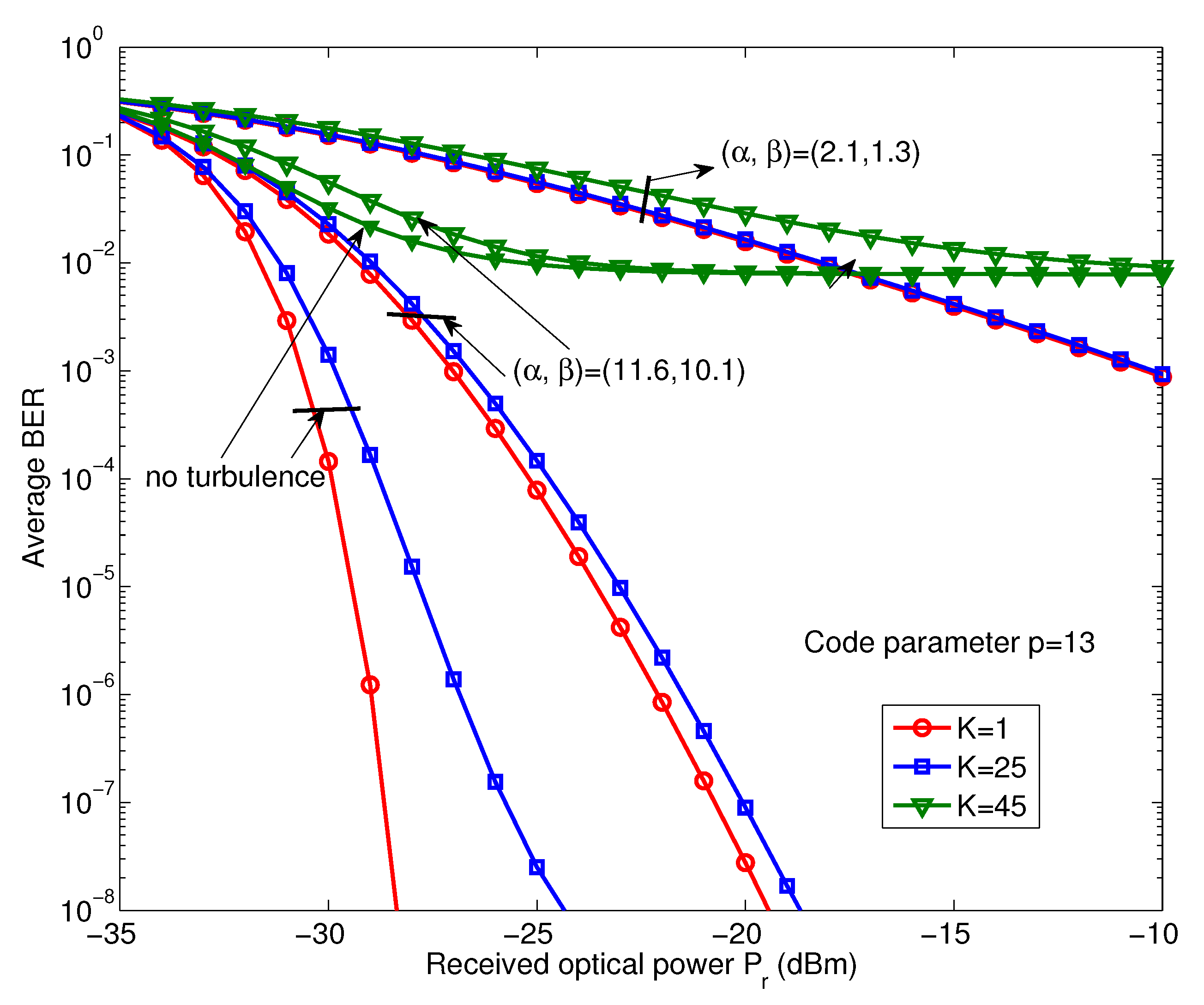
To assess the efficiency of the technique proposed in this work, Figure 4 shows the variation of average BER performance versus received optical power $P_r$ in the turbulence channel. In this case, the number of simultaneous active users is $p^2-p$ in the total of the interfering users when the prime number is given a fixed value $p=13$. The effect of the atmospheric turbulence on the received average BER is obvious. The transmission performance of the system deteriorates as the scintillation index increases. For example, a single active user system with average BER =${10}^{-3}$, $P_r=-30$ dBm, without turbulence outperforms the weak turbulence $(\alpha ,\beta )$ = $(11.6,10.1)$ and strong turbulence $(\alpha ,\beta )$ = $(2.1,1.3)$ by approximately 4 dBm and 20 dBm, respectively. Furthermore, three cases of the number of simultaneous active users have been considered, represented by K= 1, K= 25 and K= 45 as a single user, 15% and 30% of the full-load of active users in the proposed system. As is apparent from graph, the analysis shows that the system can support 15% of the active users to provide a high transmission performance, i.e., BER =${10}^{-8}$ with received optical power $P_r=-18$ dBm in the weak turbulence. However, when the system accommodates 30% of all users, the system is unable to guarantee a reliable communication service in the whole of the turbulence strength regime. These results indicate that the system performance is highly sensitive to the atmospheric turbulence and also requires higher received optical power to overcome the BER degradation caused by MAI at the same time.

Figure 3. Comparison of average bit error ratio (BER) performance of the PolSK and OOK schemes against normalized electric SNR in a turbulent OCDMA-FSO link.

Figure 3. Comparison of average bit error ratio (BER) performance of the PolSK and OOK schemes against normalized electric SNR in a turbulent OCDMA-FSO link.

Figure 4. Variation of the average BER performance versus received optical power $P_r$ with single user and multiple users interfering within all of the turbulence regimes.

Figure 4. Variation of the average BER performance versus received optical power $P_r$ with single user and multiple users interfering within all of the turbulence regimes.

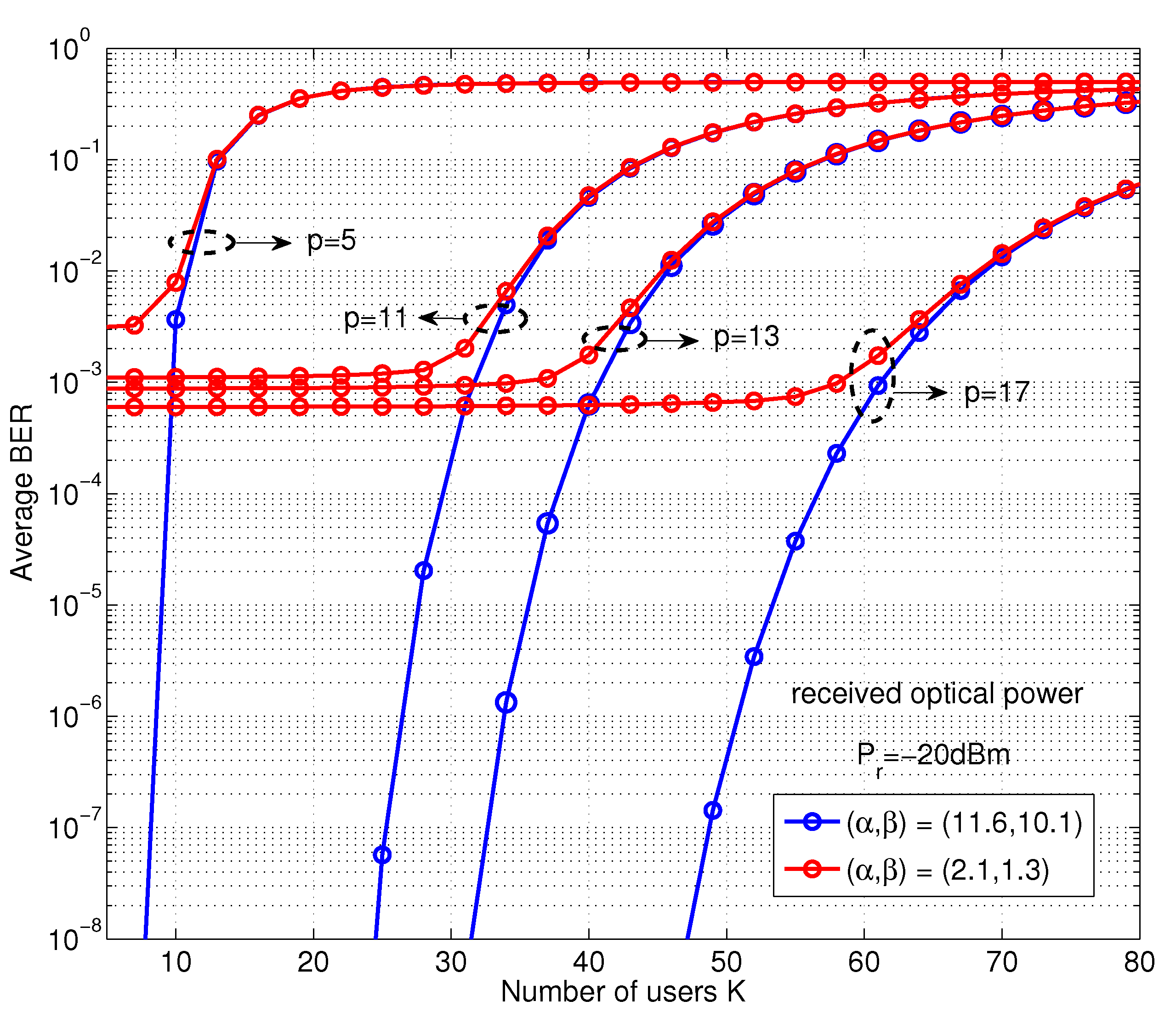
To highlight the impact of MAI on the overall system load performance, we further conduct a study on the averaged BER performance against the number of active users in the turbulence channel and the results, as shown in Figure 5. In this analysis, for the received optical power $P_r=-20$ dBm, the system accommodates the variation number of active users, with prime number parameters ($p=5$, $p=11$, $p=13$, $p=17$) evaluated. According to the theory of the MPC property, the prime code corresponding to the code-set cardinality $p^2$ is the main limiting factor of the number of supporting active users. From the graph, the BER performance improved by p increases due to heavier code weight p and longer code length $p^2$. In fact, the larger of the p is closely related to the higher auto-correlation peaks or lower hit probabilities [16]. Moreover, the BER performance gets worse as K increases with respect to the strong mutual interference and, therefore, is unable to guarantee a reliable communication performance for larger active users, as the previous analysis in Figure 4. In the meantime, under the different turbulence strength regimes, the impact of optical scintillation on the system BER performance is observed, especially when the signal propagates through the strong turbulent channel: $(\alpha ,\beta )$ = $(2.1,1.3)$. These results indicate that the system employed a greater number of users, leading to growing interference. Hence, a larger prime number p can be adopted to guarantee a reliable link performance when the system accommodates a large number of users.

Figure 5. Variation of the average BER performance versus the number of active users K with different prime number p in both the weak and strong turbulence regimes.

Figure 5. Variation of the average BER performance versus the number of active users K with different prime number p in both the weak and strong turbulence regimes.

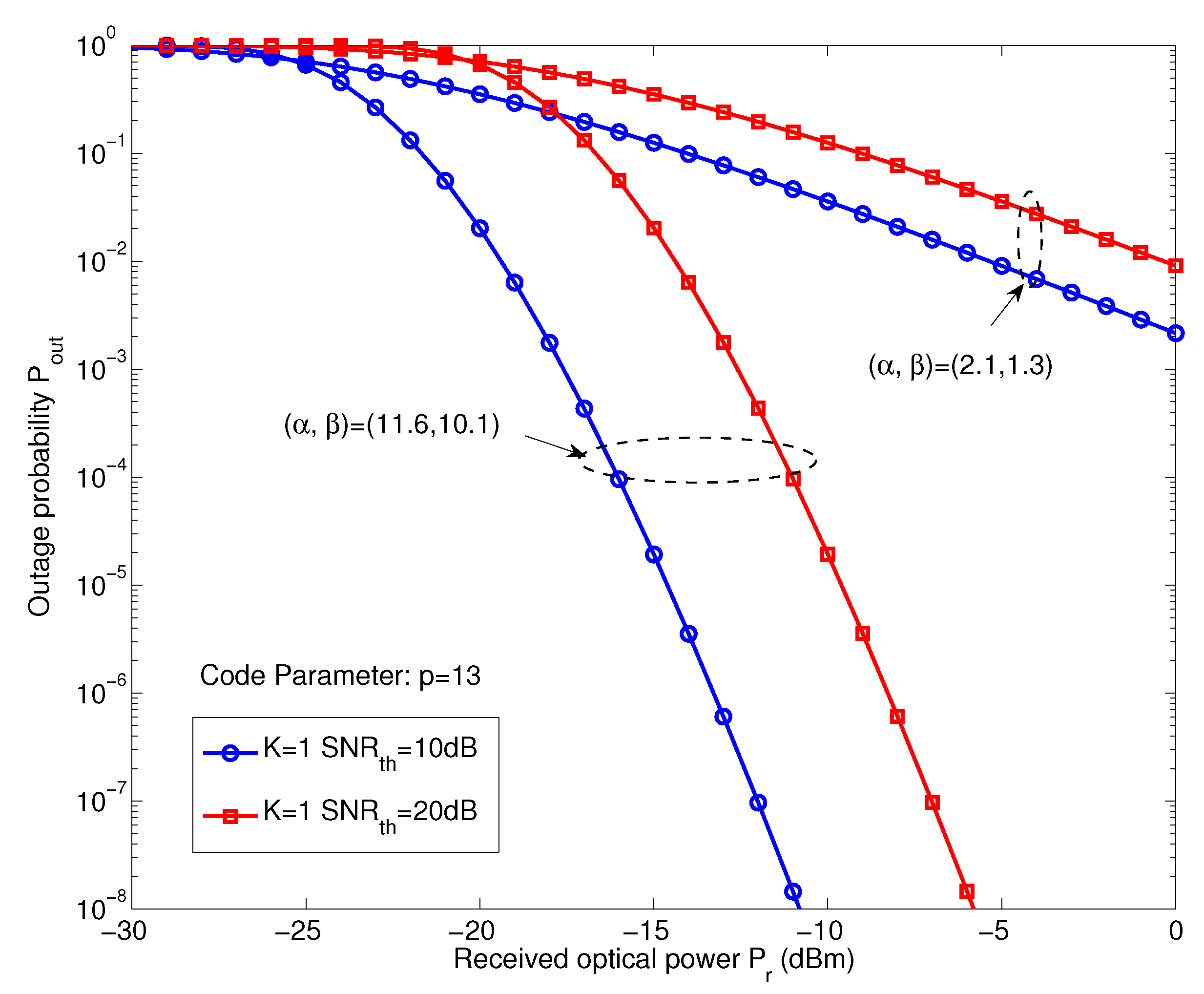
Next, we analyze the system outage probability $P_{out}$ using Equation (26). Figure 6 shows the variation of the outage probability $P_{out}$ versus a single user with different SNR thresholds ($SN{R}_{th}$) in both the weak and strong turbulence regimes. In this analysis, the prime number is $p=13$. Two cases of the SNR threshold level have been considered, $SN{R}_{th}$ = (10 dB, 20 dB), respectively. The system outage probability is similar to the BER performance under the turbulence fluctuation situation. From the Figure 6, we can see clearly that the system outage probability is affected by the atmospheric turbulence and required more received optical power to achieve a better link performance. For example, when the system $P_{out}$ is at ${10}^{-2}$, the received optical power is close to $-19$ dBm in weak turbulence compared to $-5$ dBm in strong turbulence when $SN{R}_{th}=10$ dB. In fact, we found that the system outage probability is also highly dependent on the effect of turbulence fluctuation. Besides, for the received optical power $P_r=-15$ dBm, the outage probability is close to ${10}^{-5}$ and ${10}^{-2}$ for $SN{R}_{th}$ = 10 dB and $SN{R}_{th}=20$ dB, respectively. Note the number of active users $K=1$ in this analysis, which means that the system only suffered from the impact of turbulence fluctuation on the system performance without MAI.

Figure 6. Variation of the outage probability $P_{out}$ versus a single user system with different values of $SN{R}_{th}$ in both the weak and strong turbulence regimes.

Figure 6. Variation of the outage probability $P_{out}$ versus a single user system with different values of $SN{R}_{th}$ in both the weak and strong turbulence regimes.

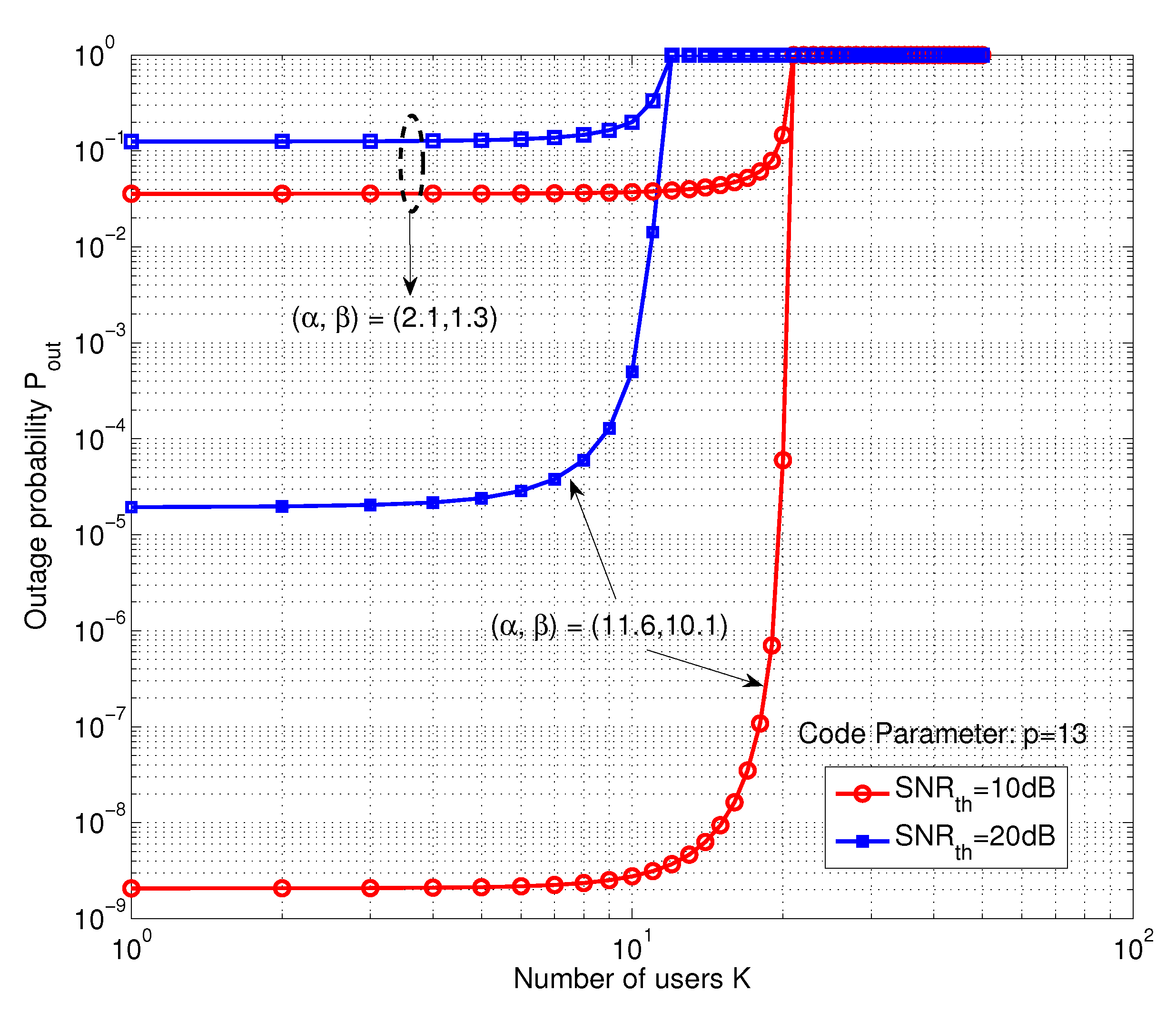
Finally, Figure 7 shows the variation of the outage probability as a function of the number of users K with the SNR threshold level at $SN{R}_{th}$ = (10 dB, 20 dB), a fixed prime parameter $p=13$ in both the weak and strong turbulence regimes. It can be observed that the outage probability gets worse with increasing the number of active users, due to the increase of MAI. In fact, a fixed prime number p restricts the number of supported active users, as well as the system load performance. Because of this limitation factor, in order to tolerate the large number of active users and provide reliable communication service, a longer code is necessary. On the other hand, the graph also shows the impact of atmospheric turbulence on the outage probability performance. For the number of active users $K=20$, the outage probability increases from $P_{out}={10}^{-3}$ to $P_{out}={10}^{-1}$ for the weak turbulence and strong turbulence regime with the same SNR threshold, $SN{R}_{th}=20$ dB.

Figure 7. Variation of the outage probability $P_{out}$ versus the number of active users with different values of $SN{R}_{th}$ in both the weak and strong turbulence regimes.

Figure 7. Variation of the outage probability $P_{out}$ versus the number of active users with different values of $SN{R}_{th}$ in both the weak and strong turbulence regimes.

5. Conclusions

In this paper, we have proposed an analytical model based on polarization modulation to evaluate the performance of optical CDMA signal transmission through an atmospheric FSO link in terms of BER and outage probability. We have presented a mathematical model for characterizing the PolSK-OCDMA signal processing, taking into account the effects of the turbulence fluctuation and MAI on FSO link performance. Different from the optical fiber medium, our analysis results demonstrated that the PolSK-OCDMA FSO system transmission performance is sensitive to the optical scintillation caused by atmospheric turbulence and the received optical power. Moreover, important performance metric parameter, such as the prime number p, have been measured and analyzed to evaluate and quantify the influence of MAI effects on the proposed system. The obtained results indicate that a large number of active users can degrade the system performance due to the effect of MAI, while a larger prime number can potentially improve the overall system performance. Based on a comparison with an OOK performance study in previous work, we also conclude that the choice of PolSK modulation for the design of the FSO system is an optimum method for the mitigation of channel fading.