Design of a Label-Free, Distributed Bragg Grating Resonator Based Dielectric Waveguide Biosensor
Abstract
:1. Introduction
1.1. Background and Motivation
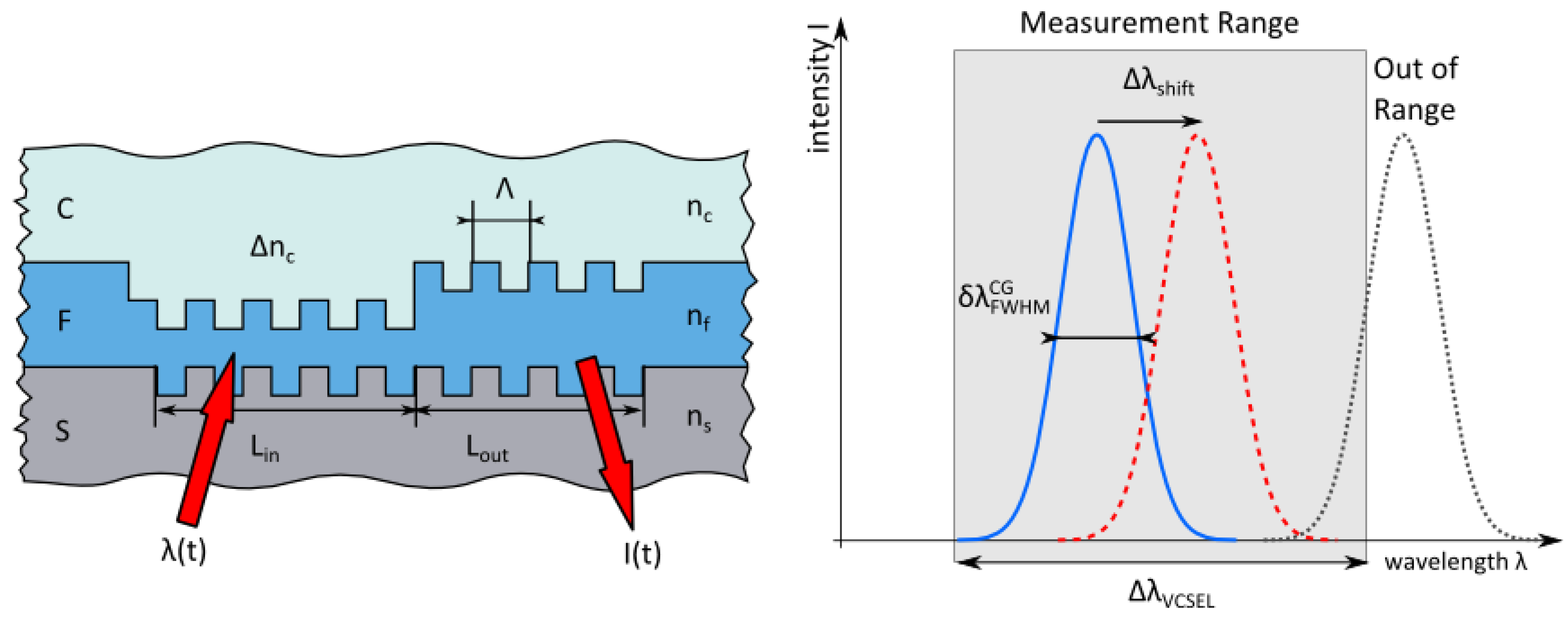
2. Sensor Elements and Design Considerations
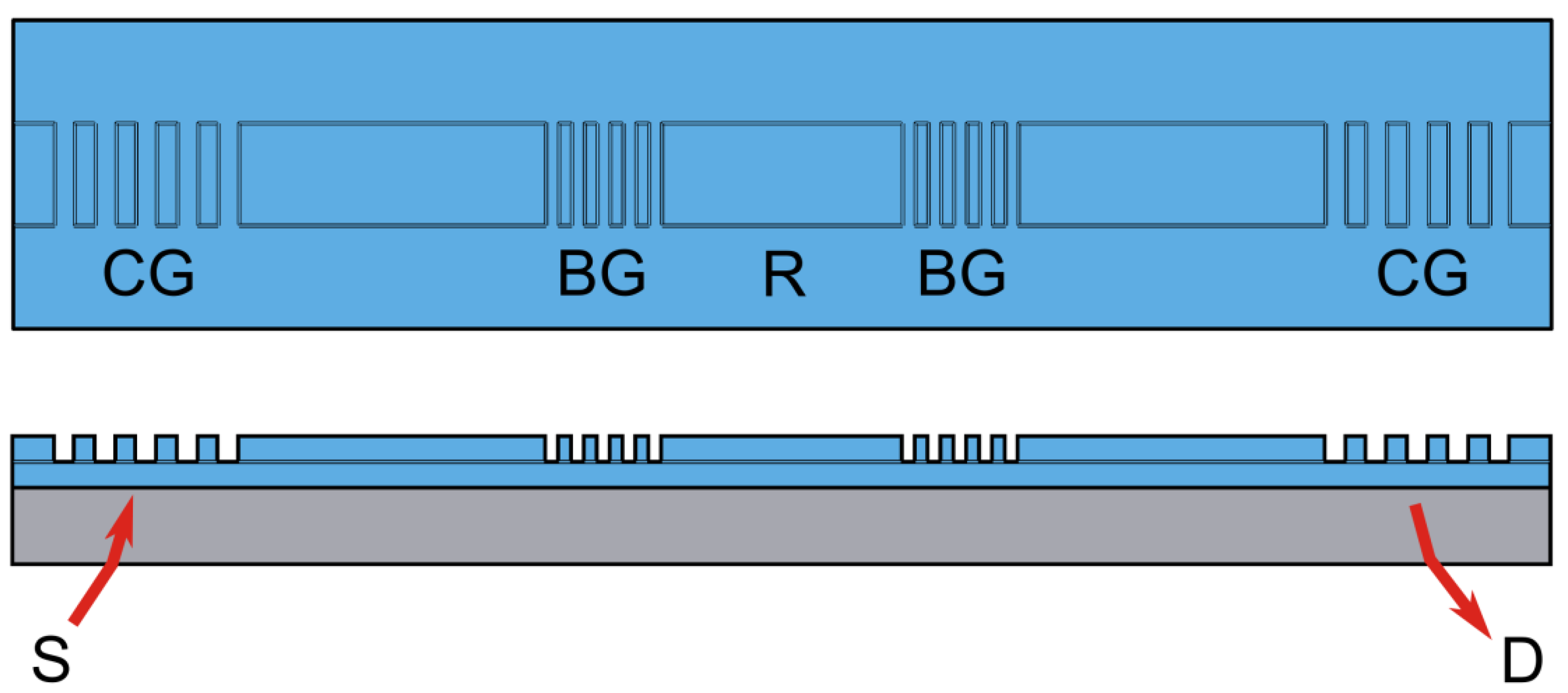
2.1. Bragg grating

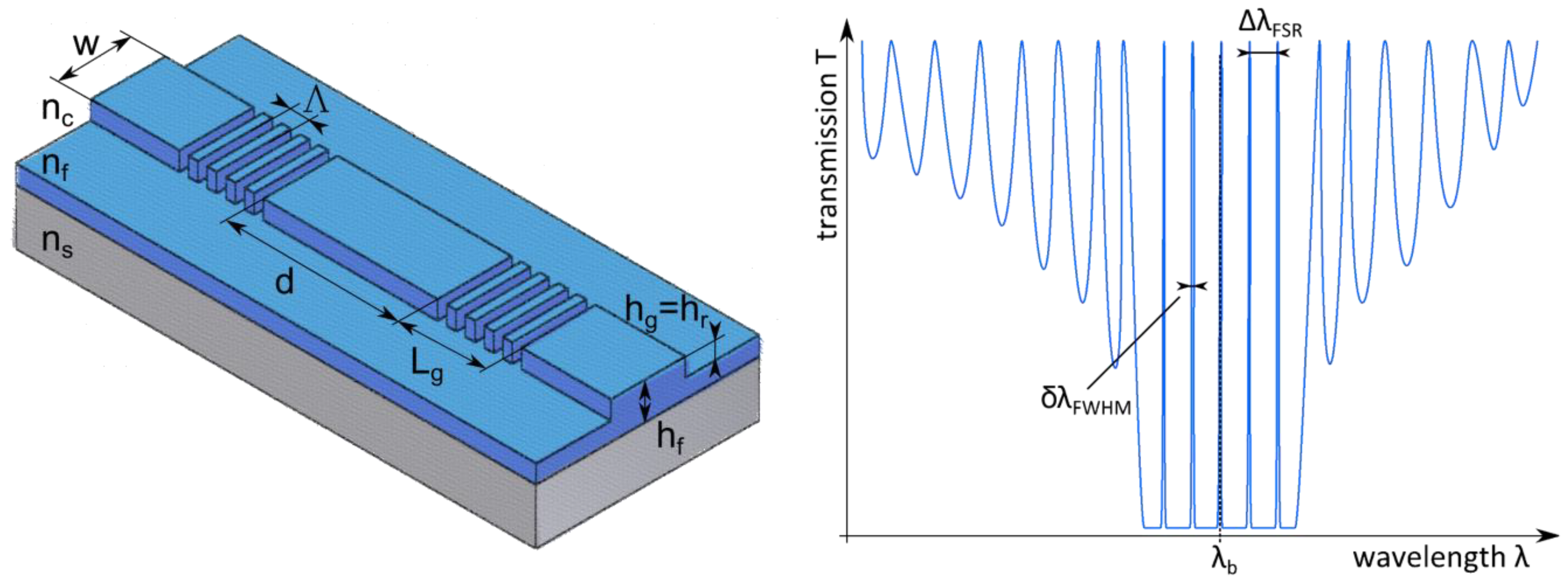
2.2. Fabry-Pérot Resonator
2.3. Sensor Sensitivity
3. Methods
4. Results
4.1. Sensitivity and Figure of Merit
| Parameter | Symbol | BG Reflector | BG Resonator |
|---|---|---|---|
| Rib width | w | 1 µm | 1 µm |
| Rib height | hr | 40 nm | 40 nm |
| Waveguide thickness | hf | 160 nm | 160 nm |
| Grating length | Lg | 100 µm | 2 × 50 µm |
| Grating width | w | 1 µm | 1 µm |
| Grating depth | hg | 40 nm | 40 nm |
| Grating period | Λ | 274.5 nm | 272 nm |
| Resonator length | d | - | 100 µm |
| Refractive index of substrate | ns | 1.5156 | 1.5156 |
| Refractive index of waveguide | nf | 2.097 | 2.097 |
| Refractive index of cover (water) | nc | 1.329 | 1.329 |
| Refractive index change of cover | Δnc | 0.005 | 0.005 |
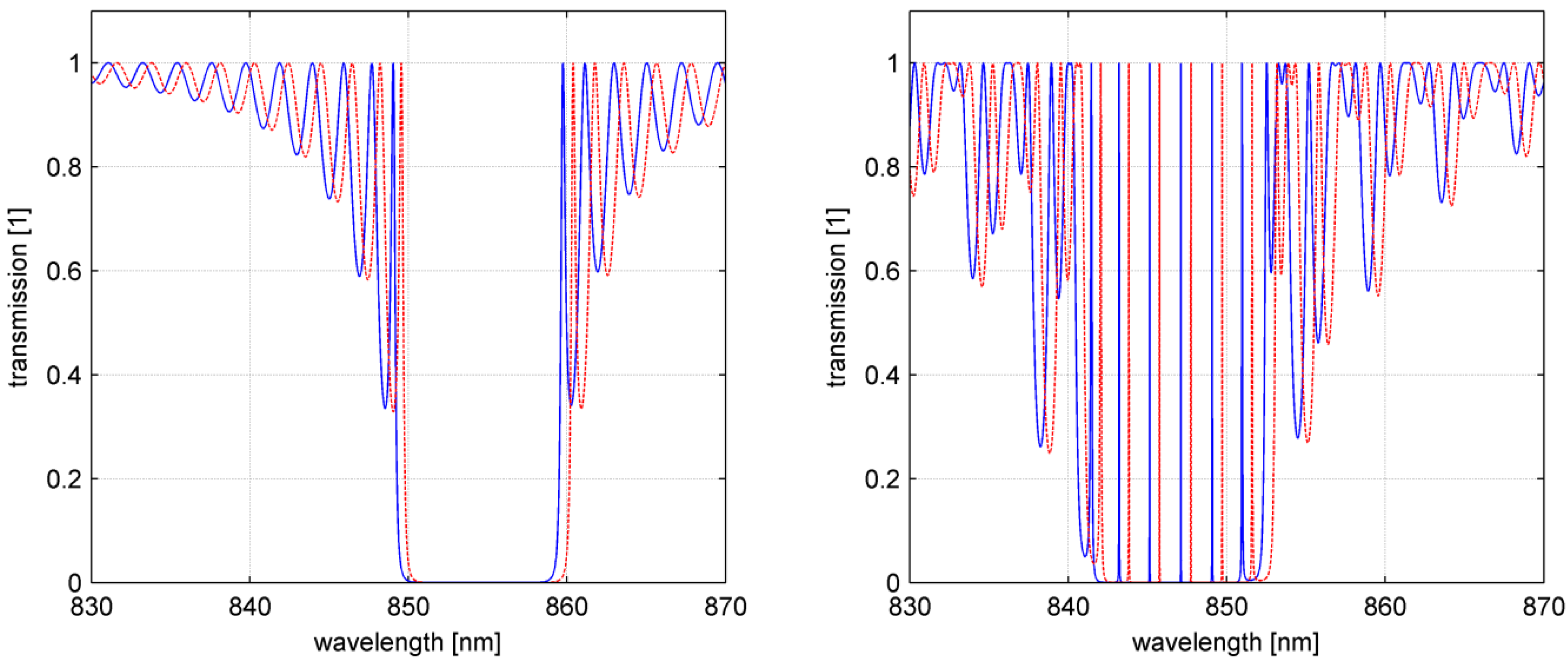
4.2. Measurement Range and Fabrication Tolerances
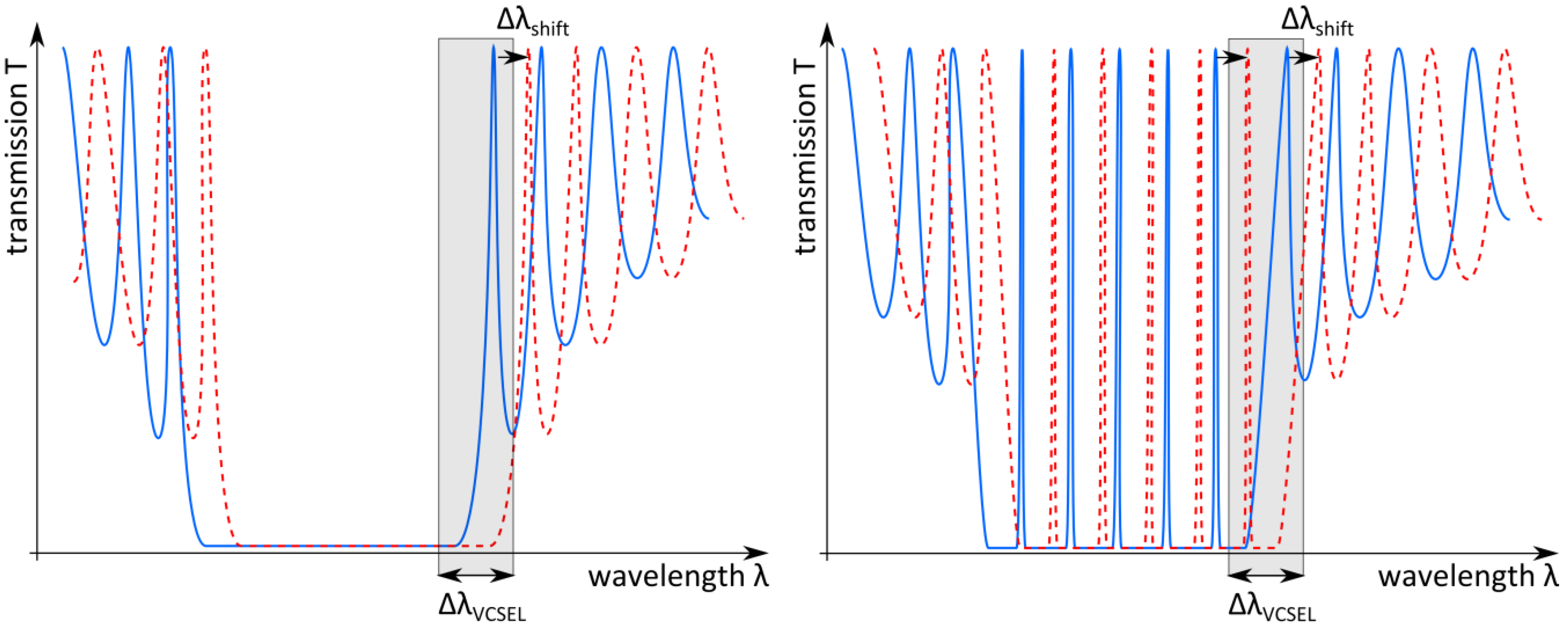
5. Discussion
6. Conclusion
Author Contributions
Acknowledgments
Conflict of Interest
References
- Cooper, M.A. Optical Biosensors in drug discovery. Nat. Rev. Drug Discov. 2002, 1, 515–528. [Google Scholar] [CrossRef]
- Pasche, S.; Wenger, B.; Ischer, R.; Giazzon, M.; Angeloni, S.; Voirin, G. Integrated optical biosensor for in-line monitoring of cell cultures. Biosens. Bioelectron. 2010, 26, 1478–1485. [Google Scholar] [CrossRef] [PubMed]
- Bier, F.F.; Schmid, R.D. Real time analysis of competitive binding using grating coupler immunosensors for pesticide detection. Biosens. Bioelectron. 1994, 9, 125–130. [Google Scholar] [CrossRef]
- Vörös, J.; Graf, R.; Kenausis, G.L.; Bruinink, A.; Mayer, J.; Textor, M.; Wintermantel, E.; Spencer, N.D. Feasibility study of an online toxicological sensor based on the optical waveguide technique. Biosens. Bioelectron. 2000, 15, 423–429. [Google Scholar] [CrossRef] [PubMed]
- Matthew, A. Cooper. In Label-Free Biosensors: Techniques and Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Ciminelli, C.; Campanella, C.M.; Dell’Olio, F.; Campanella, C.E.; Armenise, M.N. Label-free optical resonant sensors for biochemical applications. Prog. Quantum Electron. 2013, 37, 51–107. [Google Scholar] [CrossRef]
- Schmitt, K.; Oehse, K.; Sulz, G.; Hoffmann, C. Evanescent field sensors based on tantalum pentoxide waveguides–a review. Sensors 2008, 8, 711–738. [Google Scholar] [CrossRef]
- Kozma, P.; Kehl, F.; Ehrentreich-Förster, E.; Stamm, C.; Bier, F.F. Integrated planar optical waveguide interferometer biosensors: A comparative review. Biosens. Bioelectron. 2014, 58, 287–307. [Google Scholar] [CrossRef] [PubMed]
- Estevez, M.C.; Alvarez, M.; Lechuga, L.M. Integrated optical devices for lab‐on‐a‐chip biosensing applications. Laser Photon. Rev. 2012, 6, 463–487. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Zhang, D.; Wang, Z.; Huang, Y. Optimizing the quality factor of a wideband guided-mode resonance biosensor. Appl. Phys. A 2014, 117, 553–556. [Google Scholar] [CrossRef]
- Tamir, T. Guided-Wave Optoelectronics; Springer-Verlag: Berlin, Germany, 1988. [Google Scholar]
- Nellen, P.M.; Tiefenthaler, K.; Lukosz, W. Integrated optical input grating couplers as biochemical sensors. Sens. Actuators 1988, 15, 285–295. [Google Scholar] [CrossRef]
- Kunz, R.E.; Dübendorfer, J.; Morf, R.H. Finite grating depth effects for integrated optical sensors with high sensitivity. Biosens. Bioelectron. 1996, 11, 653–667. [Google Scholar] [CrossRef]
- Brazas, J.C.; Li, L. Analysis of input-grating couplers having finite lengths. Appl. Opt. 1995, 34, 3786–3792. [Google Scholar] [CrossRef] [PubMed]
- Norton, S.M.; Erdogan, T.; Morris, G.M. Coupled-mode theory of resonant-grating filters. JOSA A 1997, 14, 629–639. [Google Scholar] [CrossRef]
- Cottier, K.; Wiki, M.; Voirin, G.; Gao, H.; Kunz, R.E. Label-free highly sensitive detection of (small) molecules by wavelength interrogation of integrated optical chips. Sens. Actuators B: Chem. 2003, 91, 241–251. [Google Scholar] [CrossRef]
- Hill, K.O.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Lightwave Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Pham, S.V.; Dijkstra, M.; Hollink, A.J.F.; Kauppinen, L.J.; de Ridder, R.M.; Pollnau, M.; Lambeck, P.V.; Hoekstra, H.J.W.M. On-chip bulk-index concentration and direct, label-free protein sensing utilizing an optical grated-waveguide cavity. Sens. Actuators B: Chem. 2012, 174, 602–608. [Google Scholar] [CrossRef]
- Grieco, A.; Slutsky, B.; Tan, D.T.; Zamek, S.; Nezhad, M.P.; Fainman, Y. Optical bistability in a silicon waveguide distributed Bragg reflector Fabry–Perot resonator. J. Lightwave Technol. 2012, 30, 2352–2355. [Google Scholar] [CrossRef]
- Lee, B. Review of the present status of optical fiber sensors. Optic. Fiber Technol. 2003, 9, 57–79. [Google Scholar] [CrossRef]
- Vaughan, M. The Fabry-Perot Interferometer: History, Theory, Practice and Applications; CRC press: Boca Raton, USA, 1989. [Google Scholar]
- White, I.M.; Fan, X. On the performance quantification of resonant refractive index sensors. Opt. Express 2008, 16, 1020–1028. [Google Scholar] [CrossRef] [PubMed]
- Loock, H.P.; Wentzell, P.D. Detection limits of chemical sensors: Applications and misapplications. Sens. Actuators B: Chem. 2012, 173, 157–163. [Google Scholar] [CrossRef]
- De Vos, K.; Bartolozzi, I.; Schacht, E.; Bienstman, P.; Baets, R. Silicon-on-Insulator microring resonator for sensitive and label-free biosensing. Opt. Express 2007, 15, 7610–7615. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.P. Coupled-mode theory for optical waveguides: An overview. JOSA A 1994, 11, 963–983. [Google Scholar] [CrossRef]
- Hale, G.M.; Querry, M.R. Optical constants of water in the 200-nm to 200-µm wavelength region. Appl. Opt. 1973, 12, 555–563. [Google Scholar] [CrossRef] [PubMed]
- Ganesh, N.; Block, I.D.; Cunningham, B.T. Near ultraviolet-wavelength photonic-crystal biosensor with enhanced surface-to-bulk sensitivity ratio. Appl. Phys. Lett. 2006, 89, 023901. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kehl, F.; Bischof, D.; Michler, M.; Keka, M.; Stanley, R. Design of a Label-Free, Distributed Bragg Grating Resonator Based Dielectric Waveguide Biosensor. Photonics 2015, 2, 124-138. https://doi.org/10.3390/photonics2010124
Kehl F, Bischof D, Michler M, Keka M, Stanley R. Design of a Label-Free, Distributed Bragg Grating Resonator Based Dielectric Waveguide Biosensor. Photonics. 2015; 2(1):124-138. https://doi.org/10.3390/photonics2010124
Chicago/Turabian StyleKehl, Florian, David Bischof, Markus Michler, Mirjad Keka, and Ross Stanley. 2015. "Design of a Label-Free, Distributed Bragg Grating Resonator Based Dielectric Waveguide Biosensor" Photonics 2, no. 1: 124-138. https://doi.org/10.3390/photonics2010124
APA StyleKehl, F., Bischof, D., Michler, M., Keka, M., & Stanley, R. (2015). Design of a Label-Free, Distributed Bragg Grating Resonator Based Dielectric Waveguide Biosensor. Photonics, 2(1), 124-138. https://doi.org/10.3390/photonics2010124





