Autofocusing Method Based on Dynamic Modulation Transfer Function Feedback

Abstract

Accurate measurement of key optical system parameters (such as focal length, distortion, and modulation transfer function (MTF)) depends critically on obtaining sharp images. Conventional autofocus methods are susceptible to noise in complex imaging environments, prone to convergence to local optima, and often exhibit low efficiency. To address these limitations, this paper proposes a high-precision autofocus method based on dynamic MTF feedback. The method employs frequency-domain MTF as a real-time image sharpness metric, enhancing robustness in noisy conditions. For the search mechanism, particle swarm optimization (PSO) is combined with the golden-section search to establish a hybrid optimization framework of “global coarse localization–local fine search,” balancing convergence speed and focusing accuracy. Experimental results show that the proposed method achieves stable and efficient autofocus, providing reliable imaging assurance for high-precision measurement of optical system parameters and demonstrating strong engineering applicability.

1. Introduction

The imaging quality of an optical system is closely dependent on whether it is precisely focused. If the optical focus deviates from the ideal position, defocus will occur, resulting in blurred edges and loss of detail in the image, which severely compromises the reliability of imaging quality assessment. Therefore, achieving rapid and accurate focusing so that the image sensor consistently resides on the optimal focal plane is a critical component of high-precision optical inspection [1,2,3,4,5].

In recent years, autofocus techniques based on digital image processing have attracted considerable attention owing to rapid advances in digital processing and automatic control technologies [6,7,8]. These techniques principally encompass two aspects: image sharpness evaluation functions and the corresponding search strategies [9,10,11]. A reliable evaluation function can faithfully reflect the system’s defocus state and, under no-reference conditions, accurately assess the degree of defocus [12,13,14]. Pan et al. proposed an improved Sobel-operator-based image sharpness evaluation function and a two-stage fast autofocus method that combines coarse and fine focusing with variable step lengths, enhancing the accuracy of the evaluation function and accelerating the search strategy [15]. Hsu and colleagues employed an improved adaptive anisotropic diffusion filter combined with wavelet-based edge detection to perform image smoothing and edge extraction for focus assessment [16]. Xiong et al. combined the Brenner and Roberts functions to propose an autofocus evaluation function adaptable to multi-directional gray-level gradients; by multiplying with the Roberts function, they increased sensitivity to oblique gradients [17]. However, the aforementioned sharpness evaluation algorithms exhibit limited robustness to noise and are sensitive to image disturbances. In many practical scenarios, preprocessing cannot remove all noise from raw images, which substantially degrades the performance of sharpness evaluation functions. With respect to search strategies, hill-climbing algorithms are commonly used but are prone to being trapped by local extrema, and improperly chosen step sizes can prolong search times [18,19]. Lin et al. proposed a strategy combining pre-focusing and final focusing stages, employing different evaluation functions at different stages to shorten focusing time [20]. Jia et al. presented a novel focusing algorithm based on the Laplacian operator together with an improved hill-climbing search; this method integrates local variance information with the Laplacian operator to characterize image sharpness and thus enhance sharpness assessment [21]. Nevertheless, neither approach fully resolves the issue of local extrema. Recently, intelligent optimization methods such as genetic algorithms and simulated annealing have been introduced. Yang Hai et al. established a focus-search model based on simulated annealing theory; through parallel search and probabilistic jump strategies, they improved global optimization capability and, with adaptive step-size adjustment, enhanced focusing efficiency. However, this approach entails substantial computational burden, and a trade-off between real-time performance and accuracy remains necessary [22].

To overcome the aforementioned limitations, this paper proposes a high-precision autofocus method based on dynamic MTF feedback. The method employs dynamically computed real-time MTF as the feedback signal, replacing approaches that rely on precomputed or fixed templates, thereby allowing the quality metric to directly and sensitively reflect the actual defocus state at each iteration and avoiding biases introduced by changes in system state or target variation. On this basis, the method specifically integrates the inherent noise suppression capabilities of the knife-edge technique and frequency-domain analysis, endowing it with robustness in complex imaging environments that is difficult for conventional time-domain gradient methods to match. Furthermore, to fully exploit the advantages of the above evaluation mechanism and to address potential local extrema, a novel “collaborative” hybrid optimization framework is designed: it uses the swarm intelligence of PSO to rapidly identify a trust interval that contains the global optimum, and then applies the golden-section search within that interval to perform an efficient, high-precision deterministic search, effectively balancing convergence speed and the avoidance of premature convergence.

2. Automatic Focus Method Based on Dynamic MTF Feedback

2.1. Image Evaluation Methods

Traditional autofocus techniques that rely on image sharpness evaluation functions, such as gradient-based measures, entropy-based measures, and frequency-domain metrics, have inherent limitations in practical applications [23,24,25,26]. Gradient-based measures (e.g., Sobel, Brenner) are computationally efficient but, under severe defocus or low-contrast conditions, image gradient information becomes weak; their focus evaluation curves therefore flatten or present multiple local extrema, making it difficult to determine the correct focusing direction [27]. Statistical measures such as grayscale entropy are insensitive to changes in grayscale distribution, exhibit low focusing sensitivity, and struggle to achieve precise focus [28]. Frequency-domain methods are more sensitive to image gradient information and offer better noise suppression, making them suitable for optical-system inspection in industrial environments; however, conventional frequency-domain approaches evaluate image quality based on a single spatial- or frequency-domain feature, which limits their accuracy and objectivity [29]. Therefore, this study proposes the use of a dynamic MTF as an image sharpness evaluation metric. By quantifying in the frequency domain, it directly reflects the optical system’s ability to transmit detail at each spatial frequency, thereby providing an accurate characterization of image sharpness. The metric is computed from real-time knife-edge images and exhibits a pronounced unimodal and monotonic behavior in the vicinity of the optimal focus position, offering a well-defined and interference-resistant objective for focus search. Concurrently, its computation inherently suppresses noise, enabling stable and reliable assessment performance in complex imaging environments and furnishing a robust and efficient core criterion for autofocusing systems.

Gray-scale images of an oblique edge target were captured in real time by an image sensor, and an oblique-edge algorithm was employed to compute the optical system’s dynamic MTF values across different spatial frequencies. The computation procedure is shown in Figure 1 [30].

The specific steps are as follows:

• Edge detection: detect prominent edges in the image using the Canny operator;
• Edge Spread Function (ESF) calculation: compute the gradient magnitude along the edge direction to obtain the ESF:

  $$ESF(x)=I(x)$$

  (1)
  Here, I(x) denotes the grayscale value at the edge position, and x is the positional coordinate.
• Line Spread Function (LSF) calculation: differentiate the ESF to obtain the LSF:

  $$LSF(x)={\displaystyle \frac{dESF(x)}{dx}}$$

  (2)
• LSF normalization: normalize the LSF to unit area:

  $$LS{F}_{norm}(x)={\displaystyle \frac{LSF(x)}{{\displaystyle {\int }_{-\infty }^{+\infty }\left|LSF(x)\right|dx}}}$$

  (3)
• Optical Transfer Function (OTF) calculation: perform a Fourier transform on the normalized LSF to obtain the OTF:

  $$OTF(f)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}LS{F}_{norm}(x)e^{-j2\pi fx}dx}$$

  (4)
• MTF calculation: take the modulus of the OTF to obtain the MTF:

  $$MTF(f)=\left|OTF(f)\right|$$

  (5)

2.2. Search Algorithms

To address the inherent shortcomings of traditional hill-climbing methods in autofocus—namely their susceptibility to local extrema and the difficulty of balancing search efficiency with accuracy—this paper proposes a hybrid optimization search strategy. The strategy integrates the global exploration capability of the particle swarm optimization (PSO) algorithm with the local precise-search advantage of the golden-section search. First, PSO is employed to rapidly locate the optimal focus region through population-based parallel search and information-sharing mechanisms, effectively avoiding entrapment in local extrema. Subsequently, the golden-section search is applied within that region to perform an efficient, high-precision local scan that accurately locks onto the optimal focal position. By coordinating “global coarse localization followed by local fine search,” the method significantly accelerates convergence while ensuring the system’s robustness and final focusing accuracy. The overall algorithmic workflow is shown in Figure 2.

The global-best region search procedure of the PSO algorithm is as follows:

• Determine the initial search space for PSO: Based on the designed focal length value f₀ of the tested optical system and the tolerance range δ, provide the possible minimum f_min and maximum f_max of the focal length as the initial search space for PSO: [f_min, f_max]

  f_min = f₀ × (1 − δ)

  (6)

  f_max= f₀ × (1 + δ)

  (7)

  where δ denotes the mechanical adjustment tolerance (typically taken as 0.05–0.1).
• Set the PSO algorithm parameters to include:
  (a) Particle number M: set to 20–50;
  (b) Inertia weight w: initialized at 0.9 and decreased linearly to 0.4;
  (c) Learning factors c₁ and c₂: set to 2;
  (d) Random numbers r₁, r₂: take values in the range 0–1;
  (e) Maximum number of iterations N: set to 50–100 iterations.
• Particle initialization: Particle positions are initialized as $\left\{x_i^0|x_i^0\in [f_{\min },f_{\max }]\right\}$, where $i=1,2,\dots ,M$ denotes the particle index; particle velocities are initialized as $v_i=\left\{v_1^0,v_2^0,\dots ,v_i^0,\dots \right\}=\left\{0,0,\dots ,0,\dots \right\}$
• Calculate particle fitness: compute in real time and record the MTF values of the image at the positions of all particles in the current iteration. Select the MTF value at the Nyquist frequency f_Nyquist as the particle fitness; its calculation function is:

  $$f(x_i^t)=MT{F}_{x_i^t}(f_{Nyquist})$$

  (8)

  $$f_{Nyquist}={\displaystyle \frac{1}{2d}}$$

  (9)
  Here, $x_i^t$ denotes the position of the i-th particle at the t-th iteration, $MT{F}_{x_i^t}(f_{Nyquist})$ is the MTF value of the image at that position under the Nyquist frequency, and d is the pixel size of the image sensor.
• Set the initial individual best ${P_{besti}}^0$ and the global best ${G_{best}}^0$:

  $${P_{besti}}^0=x_i^0$$

  (10)

  $${G_{best}}^0={P_{besti}}^0$$

  (11)
• Iterative update (assuming iteration t to t + 1, where $t=0,1,\dots ,N-1$): after obtaining the fitness values of all particles at the current iteration t + 1, the individual best value ${P_{besti}}^{t+1}$ and the global best value ${G_{best}}^{t+1}$ among particles at iteration t + 1 are identified by comparison and recorded. Their update formulas are as follows:

  $${P_{besti}}^{t+1}=\left\{\begin{array}{l}{x}_i^{t+1},f(x_i^{t+1})\ge f({P_{besti}}^t)\\ {P_{besti}}^t,else\end{array}\right.$$

  (12)

  $${G_{best}}^{t+1}=\left\{\begin{array}{l}{P_{besti}}^{t+1},f({P_{besti}}^{t+1})\ge f({G_{best}}^t)\\ {G_{best}}^t,else\end{array}\right.$$

  (13)
  Here, the fitness value of the current position $x_i^{t+1}$ is compared with the historical best $f(x_i^{t+1})$; if the current one is superior, $f({P_{besti}}^t)$ is updated to the current position; otherwise the original value is retained. Then, all particles, ${P_{besti}}^{t+1}$ are iteratively traversed and the position with the maximum fitness is selected as the new global optimum; if multiple particles share the same optimal fitness value, the position of the first particle is preserved.
• Update particle information: During each iteration, continuously update the velocity and position of the current particles. The update formulas for velocity and position are as follows:

  $$v_i^{t+1}=w{v}_i^t+c_1{r}_1(P_{\mathit{best}}-f_i^t)+c_2{r}_2(G_{\mathit{best}}-f_i^t)$$

  (14)

  $$x_i^{t+1}=x_i^t+v_i^{t+1}$$

  (15)
• Convergence criterion: Terminate when the maximum number of iterations is reached, or when the change in the population best value falls below a threshold (e.g., 1%). Record the optimal interval [f_left, f_right]; the computation is given by the following formula:

  $$f_{left}=G_{best}^t-\epsilon$$

  (16)

  $$f_{right}=G_{best}^t+\epsilon$$

  (17)

  $$\epsilon =k(f_{\max }-f_{\min })$$

  (18)

Here, ε denotes the search step size, and k is an empirical coefficient, typically ranging from 0.1 to 0.3.

The local precise-search procedure of the golden-section algorithm is as follows:

• Interval partitioning: Within the interval [f_left, f_right] produced by PSO, select two points according to the golden ratio:

  $$f_a=f_{\mathit{left}}+0.382\times (f_{\mathit{right}}-f_{\mathit{left}})$$

  (19)

  $$f_b=f_{\mathit{left}}+0.618\times (f_{\mathit{right}}-f_{\mathit{left}})$$

  (20)
• Iteratively narrow the interval: compare the MTF values of the images acquired at the positions f_a and f_b, and retain the interval on the side with the larger MTF value;
• Repeated subdivision of the new point: continue until the interval length is less than the precision threshold, typically set to 0.1% of the focal length range;
• Record the optimal focus position f: compare the MTF values of the images acquired at positions f_a and f_b, and select the position with the higher MTF value as the optimal focus position f.

3. Experimental Validation and Result Analysis

3.1. System Design

Based on autofocus theory, this work establishes an optical imaging autofocus experimental system, whose schematic structural composition is shown in Figure 3. The system comprises five primary modules: a computer with controller, an image-plane analysis unit, a three-axis precision translation stage, a collimated optical system (collimating tube), and a target generator. The target generator produces a knife-edge test pattern that, after collimation by the collimating tube, is imaged onto the sensor plane of the image-plane analysis unit. The image-plane analysis unit acquires images in real time and transmits them to the computer processing module via a data interface. The computer analyzes the spatial intensity distribution of the images and, according to the proposed focusing algorithm, generates control commands that are sent to the drive unit of the three-axis translation stage. That drive unit controls precise displacement of the stage along the system optical axis, thereby adjusting the working distance between the tested optical component and the image-plane analysis unit to achieve focus adjustment. The image-plane analysis unit then acquires images again, forming a closed-loop control sequence of “acquire–analyze–adjust–feedback” until the system reaches optimal imaging performance and the autofocus procedure is completed.

Figure 4 depicts the experimental setup for autofocus in an optical system. The software was executed on a CPU Intel(R) Core(TM) i7-10700 3.4 GHz with 32 GB RAM and Qt 5.14.2.

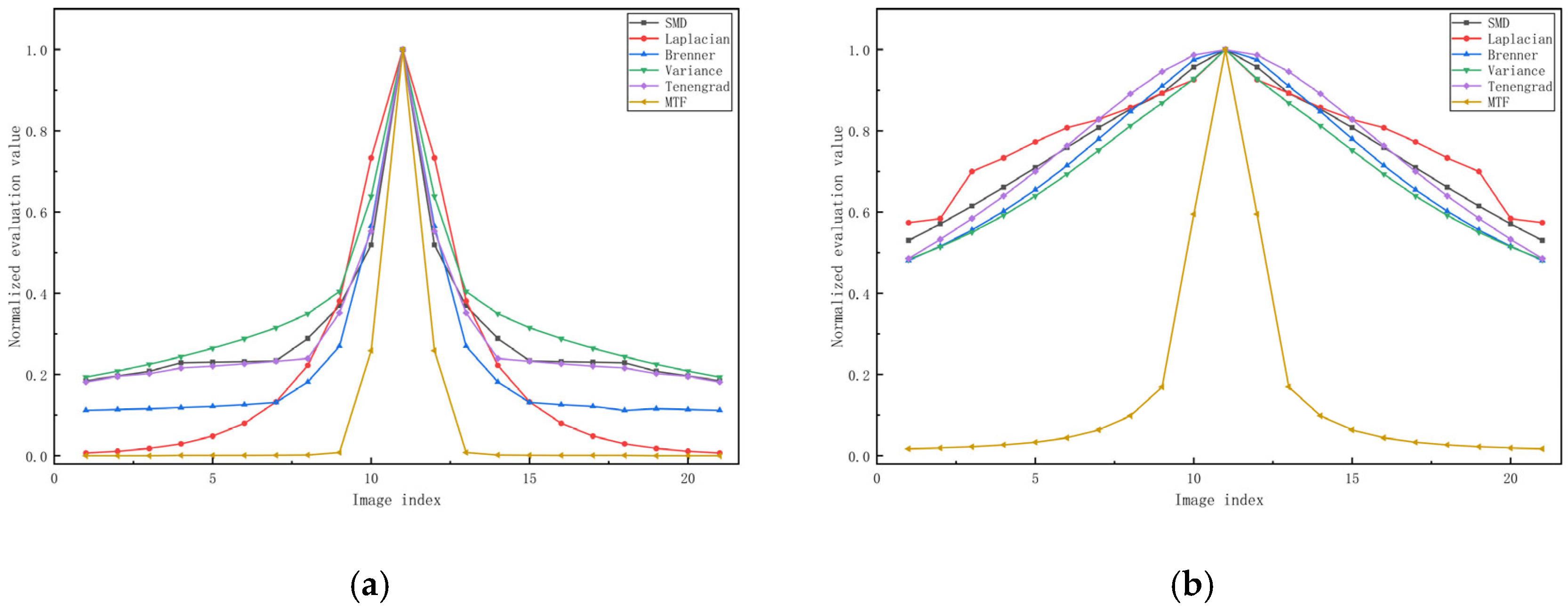
3.2. Image Evaluation Function Experiments

During the autofocus experiments, the camera acquired a total of 20 images within the preset search range using an algorithmic adaptive stepping strategy. Because the target region occupied only a small portion of the image field, the region of interest (ROI) was extracted prior to computing sharpness metrics to improve algorithmic efficiency and responsiveness. To assess the performance of the proposed evaluation method, we compared the MTF-based metric introduced herein with Variance, SMD, Laplacian, Brenner, and Tenengrad functions for image sharpness evaluation [31]. The normalized evaluation curves are shown in Figure 5a. The results indicate that the MTF-based metric substantially outperforms the other methods in terms of sharpness discrimination ratio and exhibits stronger ability to distinguish between in-focus and defocused images.

To further validate the noise robustness of the evaluation algorithm, Gaussian noise with a mean of 0 and a variance of 0.02, as well as salt-and-pepper noise with a noise density of 0.1, were added to the blade-edge target images for testing. Sharpness assessments of the noisy images were conducted using the MTF-based evaluation function and conventional evaluation functions, respectively; the results are shown in Figure 5b. The experiments indicate that, under both types of noise interference, the MTF evaluation curve maintains good monotonicity and stability, demonstrating that the proposed method possesses strong anti-interference capability.

3.3. Repeatability Testing of Autofocus Algorithm

In the repeatability focusing test, to evaluate the stability of the proposed method, ten consecutive repeatability autofocus experiments were performed on the autofocus system, and the axial displacement in each run was recorded as x₁, x₂, …, x₁₀. The corresponding result curves are shown in Figure 6. Based on the measurements, the repeatability error calculated using the formula was better than 0.01, indicating that the proposed method exhibits excellent focusing consistency and measurement reliability, and can meet the repeatability requirements of high-precision optical inspection.

$$\overline{x}=\sqrt{{\displaystyle \frac{1}{n}}}{\displaystyle {\sum }_{i=1}^n{x}_i}$$

(21)

$$\sigma =\sqrt{{\displaystyle \frac{1}{n-1}}}{{\displaystyle {\sum }_{i=1}^n(x_i-\overline{x})}}^2$$

(22)

3.4. Efficiency Experiments of the Autofocus Algorithm

To evaluate the execution efficiency of the proposed method, a comparative experiment against a conventional autofocus approach was conducted; the specific results are presented in

Table 1. Comparison of Autofocus Performance.

Method	Average Focusing Time (ms)	Number of Focusing Failures
Proposed method	4450	0
Traditional Method	8550	8

. The conventional method employed a focus measure based on the Brenner function combined with a hill-climbing search algorithm. Across 30 autofocus tests, the proposed method required an average of 4450 ms, compared with 8550 ms for the conventional method, representing an efficiency improvement of approximately 47.95% and demonstrating superior real-time responsiveness. In addition, the conventional method experienced eight focus failures during testing due to system noise and environmental vibrations, whereas the proposed method achieved successful focus in all tests, indicating greater stability and environmental robustness and thereby confirming its practical value and reliability under complex imaging conditions.

3.5. MTF Measurement Accuracy Experiment

To evaluate the effectiveness of the proposed method in improving MTF measurement accuracy, the MTFs in the meridional and sagittal directions at the best-focus surface were calculated for Optikos’ mid-wave and long-wave standard lenses. In addition, MTF curves were computed for images acquired after autofocus using both the method presented here and the conventional method; the comparison is shown in Figure 7. The comparison indicates that the MTF curves of the mid-wave and long-wave images obtained after autofocus using the proposed method closely match the best-focus MTF curves across the entire spatial frequency range, and perform markedly better than the conventional autofocus method. The deviations between the measured values and the best-focus MTF values are consistently controlled within 0.01. These results directly demonstrate that the autofocus system can operate precisely at the best-focus position, effectively suppressing defocus-induced aberrations and thus enabling MTF measurements to accurately reflect the intrinsic performance of the lens.

3.6. MTF Measurement Repeatability Experiments

To further evaluate the long-term stability of the proposed method in MTF measurement system engineering, repeatability accuracy tests of MTF measurements were conducted on the mid-wave standard lens and the long-wave standard lens developed by Optikos. The best focal plane positions determined for the two lenses were taken as references. The translation stage was moved along the optical axis to shift the system away from the best focal plane by an amount equal to twice the depth of focus, after which the system performed automatic refocusing and the MTFs in the meridional and sagittal directions were computed at the refocused positions. The above procedure was independently repeated nine times; together with the initial measurement this yielded ten sets of MTF data. The standard deviation of the MTF values at each spatial frequency among these ten data sets was then computed according to the following equation $\sigma$.

$$\sigma =\sqrt{{\displaystyle \frac{1}{N-1}}{\displaystyle \sum _{i=1}^N{\left[MT{F}_i(f)-\overline{MTF}(f)\right]}^2}}$$

(23)

where $N=10$ denotes the number of repeated measurements, $MT{F}_i(f)$ denotes the MTF value at frequency f for the i-th measurement, and $\overline{MTF}(f)$ denotes the arithmetic mean of the MTF at frequency N across f measurements. To more rigorously characterize the dispersion of the measurements and to increase the confidence level, a confidence factor of $k=3$ is adopted to compute the repeatability precision $3\sigma$ at each frequency point. The maximum value of $3\sigma$ across all frequency points, denoted $MAX(3\sigma )$, is taken as the final repeatability precision metric for the lens MTF measurement. This metric represents, at a 99.73% confidence level, the maximum possible deviation between a single measurement and the true value, and is a commonly used high-confidence criterion in engineering for assessing measurement system repeatability.

The variation curves of MTF measurement repeatability precision with spatial frequency for the two lenses are shown in Figure 8. The plots indicate that, across the entire tested frequency range (0–100 lp/mm), the repeatability precision for both lenses is maintained within 0.013, outperforming the engineering requirement of 0.02.

The hybrid optimization framework employed in this section addresses challenges at multiple levels through a staged strategy. To mitigate the “directional errors” that cause conventional search methods to become trapped in local optima, a PSO algorithm is incorporated; its population-based parallel exploration and information-sharing mechanisms confer global robustness. To remedy insufficient convergence precision, once PSO has localized a high-quality interval the search switches to the golden-section method for deterministic, high-precision local optimization. For noise suppression, the approach deeply integrates the intrinsic advantages of frequency-domain assessment: through edge fitting, Fourier transformation, and related steps it produces a natural filtering effect against random noise, as validated by quantitative noise experiments (Figure 5b). Throughout the framework, PSO primarily performs global exploration and preliminary localization; its ability to rapidly lock onto potential optimal regions synergizes effectively with the golden-section method’s precise localization, thereby achieving a balance of speed, accuracy, and robustness in complex imaging environments.

4. Conclusions

This study addresses the stringent requirements of imaging sharpness imposed by precise measurement of optical system parameters and proposes an autofocus method based on dynamic MTF feedback. The method employs a real-time computed dynamic MTF as the focus quality metric, replacing conventional time-domain gradient approaches and enabling sensitive, adaptive feedback for defocus states. Furthermore, a hybrid search strategy is developed that synergistically combines particle swarm optimization with the golden-section search; by explicitly partitioning global exploration and local refinement tasks, the approach effectively balances convergence speed and localization accuracy. Experimental results indicate that, compared with conventional approaches, the proposed method reduces focusing time by approximately 47.95%, yields repeatability error better than 0.01, and exhibited no focus failures across all tests, demonstrating superior robustness and consistency. Furthermore, in MTF measurement accuracy and repeatability evaluations, the method limits deviation from theoretical values to within 0.01 and achieves repeatability precision better than 0.013, satisfying high-confidence engineering application requirements. This work not only provides effective autofocus technology to enable automated, high-precision measurement of key optical imaging system parameters but also offers methodological guidance and engineering insights for practical applications in industrial inspection and optical instrument development.