Dynamic Behaviors of Pulsating Noise-like Pulses in an Ultrafast Fiber Laser
Abstract
1. Introduction
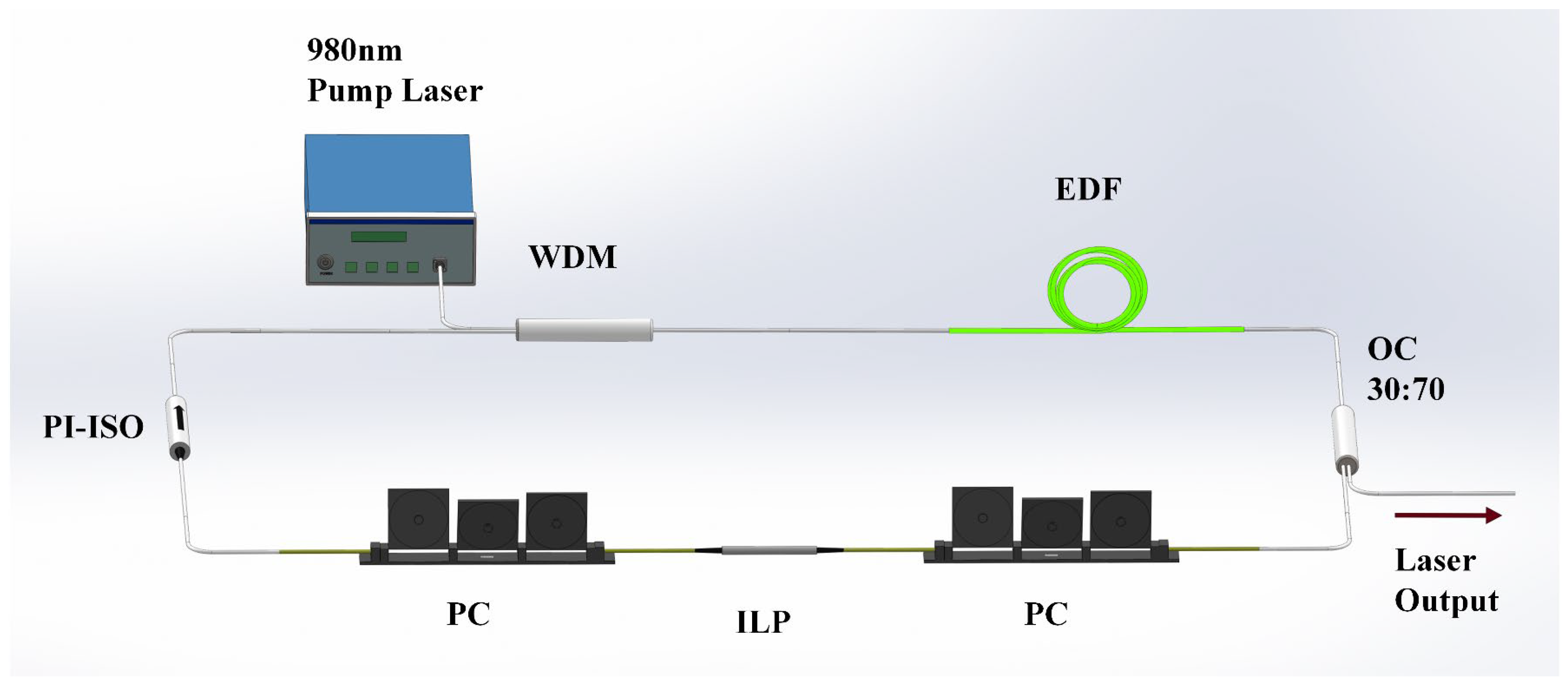
2. Experimental Setup
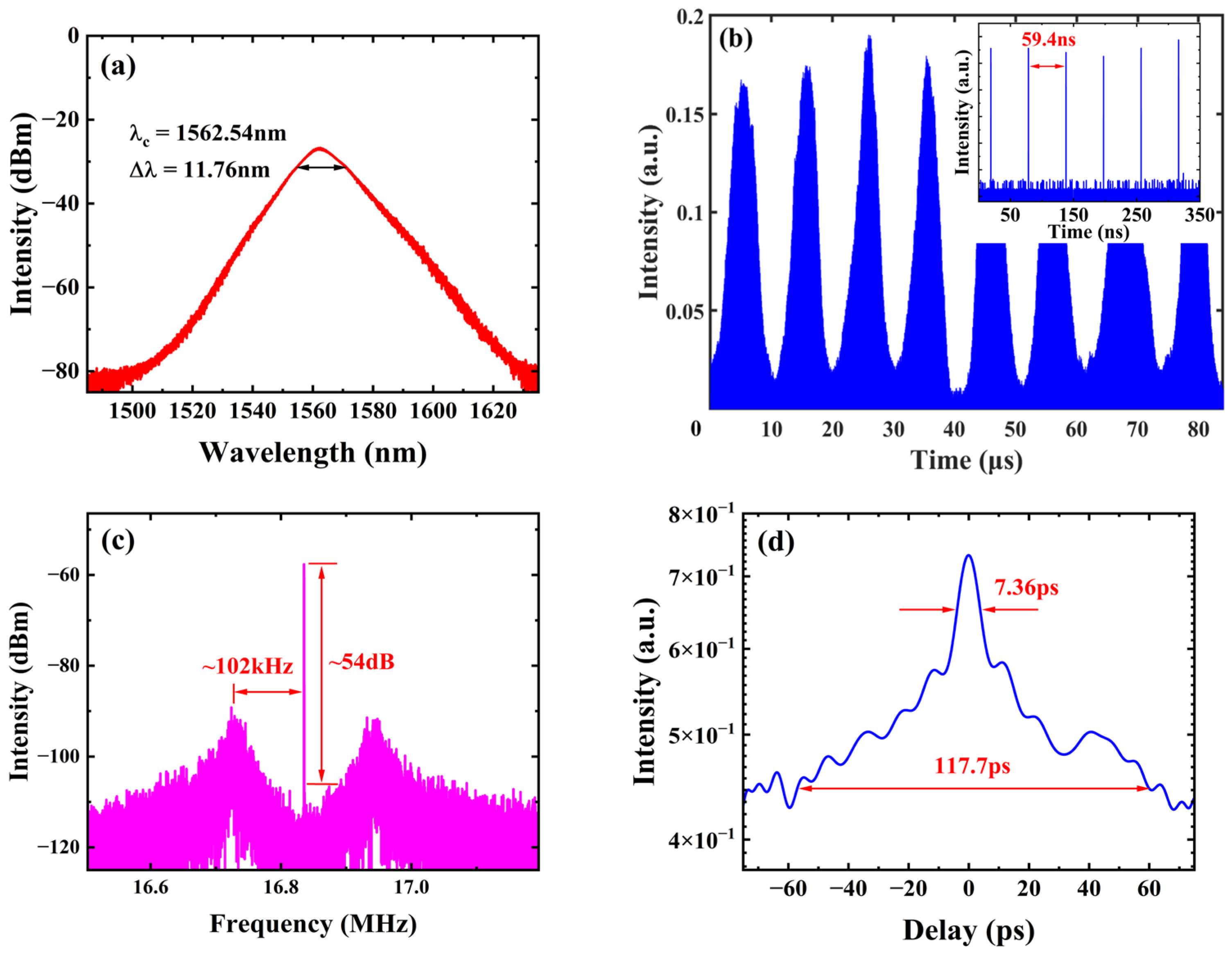
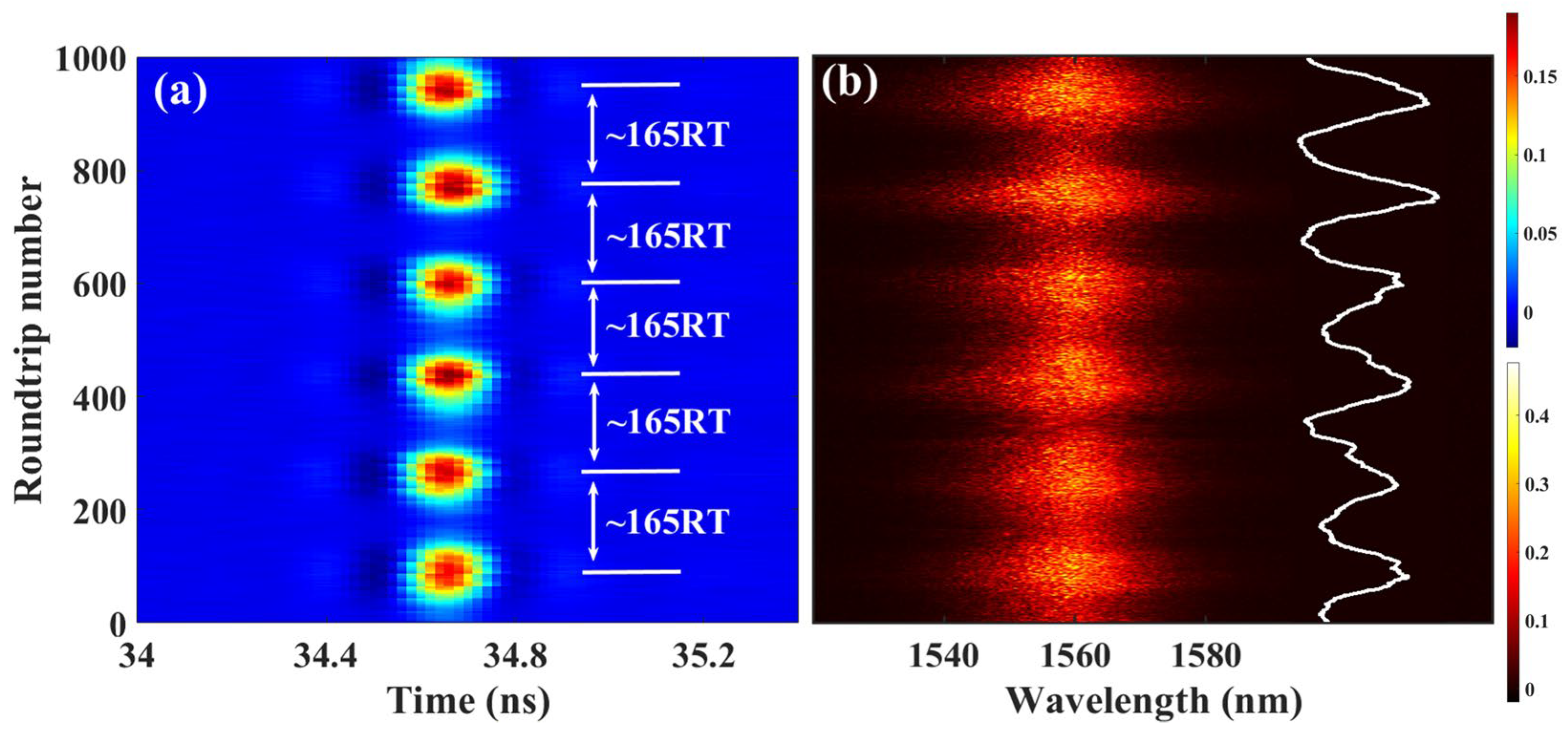
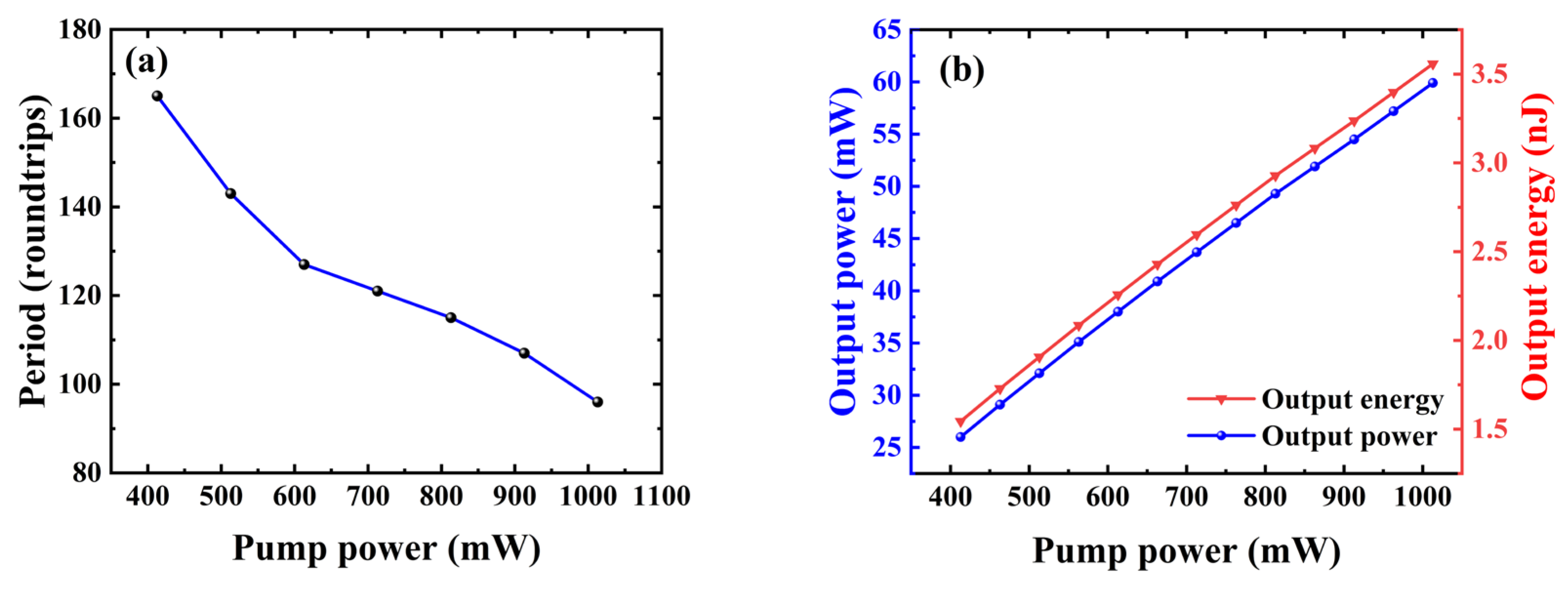
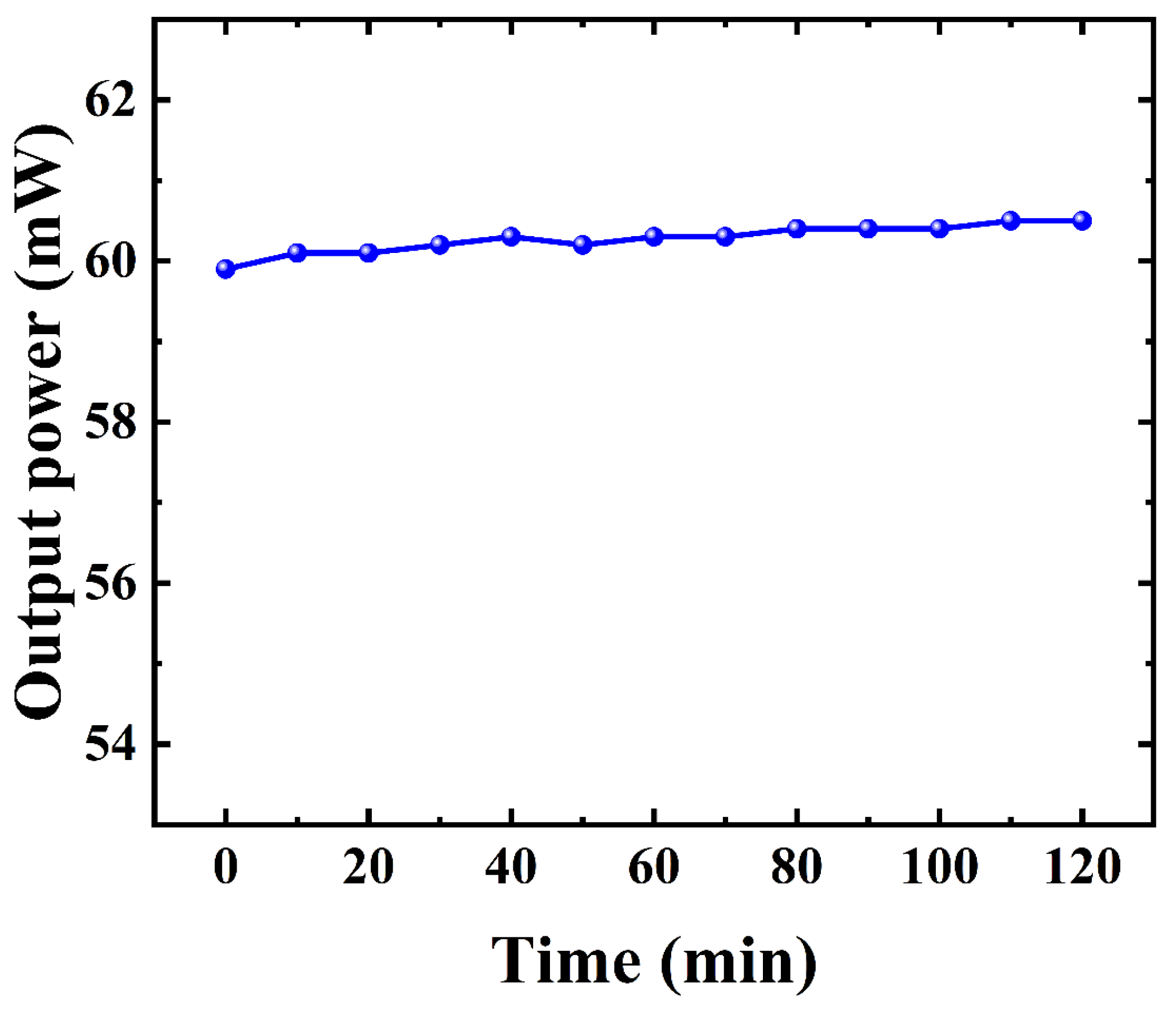
3. Results and Discussion
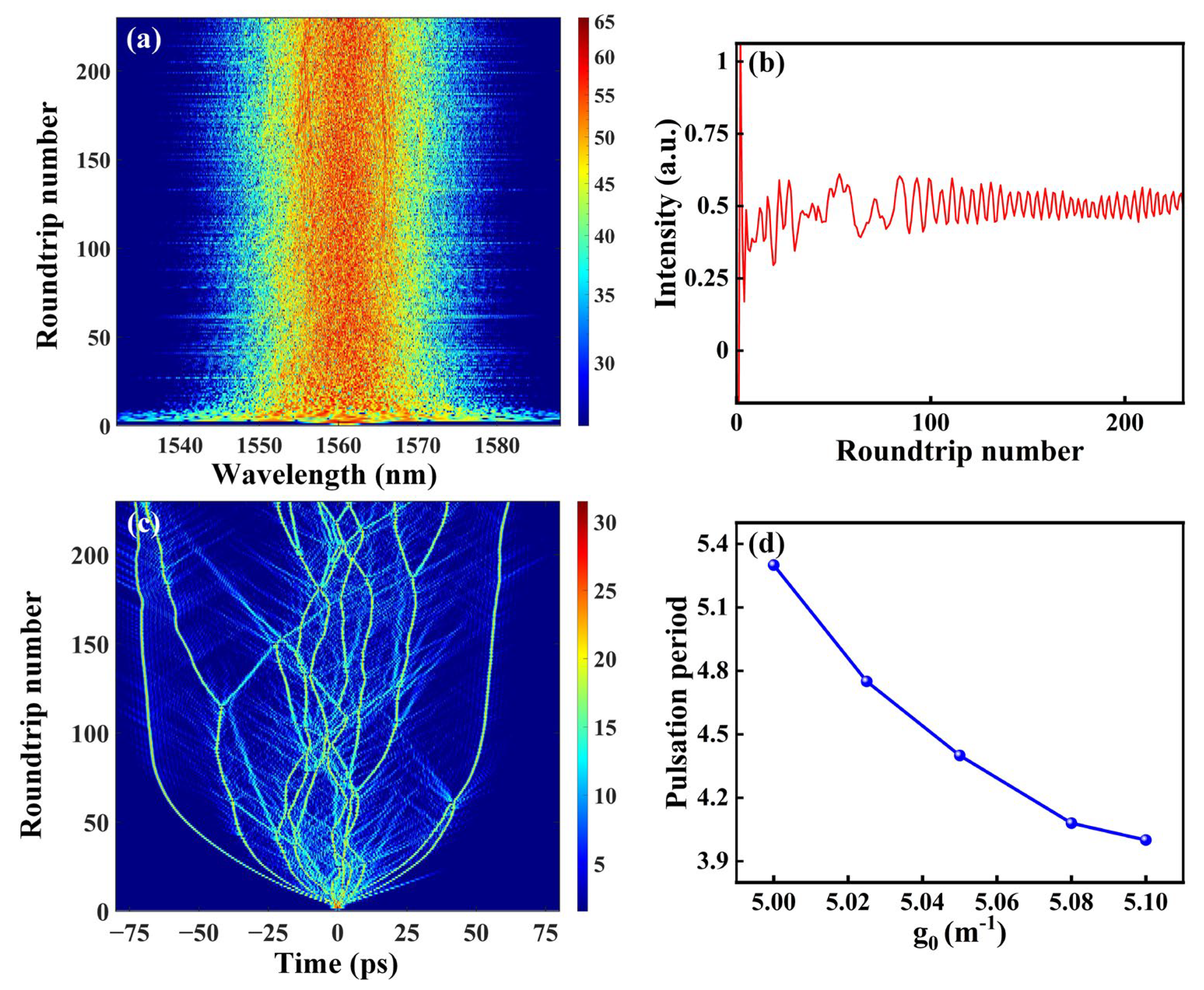
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, G.; Wei, Z. Ultrafast Fiber Lasers: An Expanding Versatile Toolbox. iScience 2020, 23, 101101. [Google Scholar] [CrossRef]
- Fermann, M.E.; Hartl, I. Ultrafast Fibre Lasers. Nat. Photonics 2013, 7, 868–874. [Google Scholar] [CrossRef]
- Ma, J.; Qin, Z.; Xie, G.; Qian, L.; Tang, D. Review of Mid-Infrared Mode-Locked Laser Sources in the 2.0 μm–3.5 μm Spectral Region. Appl. Phys. Rev. 2019, 6, 021317. [Google Scholar] [CrossRef]
- Fermann, M.E.; Hartl, I. Ultrafast Fiber Laser Technology. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 191–206. [Google Scholar] [CrossRef]
- Song, Y.; Shi, X.; Wu, C.; Tang, D.; Zhang, H. Recent Progress of Study on Optical Solitons in Fiber Lasers. Appl. Phys. Rev. 2019, 6, 021313. [Google Scholar] [CrossRef]
- Grelu, P.; Akhmediev, N. Dissipative Solitons for Mode-Locked Lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Mao, D.; Liu, X.; Han, D.; Lu, H. Compact All-Fiber Laser Delivering Conventional and Dissipative Solitons. Opt. Lett. 2013, 38, 3190–3193. [Google Scholar] [CrossRef]
- Liu, M.; Luo, A.-P.; Xu, W.-C.; Luo, Z.-C. Dissipative Rogue Waves Induced by Soliton Explosions in an Ultrafast Fiber Laser. Opt. Lett. 2016, 41, 3912–3915. [Google Scholar] [CrossRef]
- Luo, Z.-C.; Liu, M.; Liu, H.; Zheng, X.-W.; Luo, A.-P.; Zhao, C.-J.; Zhang, H.; Wen, S.-C.; Xu, W.-C. 2 GHz Passively Harmonic Mode-Locked Fiber Laser by a Microfiber-Based Topological Insulator Saturable Absorber. Opt. Lett. 2013, 38, 5212–5215. [Google Scholar] [CrossRef]
- Bale, B.G.; Kieu, K.; Kutz, J.N.; Wise, F. Transition Dynamics for Multi-Pulsing in Mode-Locked Lasers. Opt. Express 2009, 17, 23137–23146. [Google Scholar] [CrossRef]
- Kbashi, H.J.; Sergeyev, S.V.; Araimi, M.A.; Tarasov, N.; Rozhin, A. Vector Soliton Rain. Laser Phys. Lett. 2019, 16, 035103. [Google Scholar] [CrossRef]
- Turnali, A.; Xu, S.; Sander, M.Y. Noise-like Pulse Generation and Amplification from Soliton Pulses. Opt. Express 2022, 30, 13977–13984. [Google Scholar] [CrossRef]
- Chen, H.-J.; Tan, Y.-J.; Long, J.-G.; Chen, W.-C.; Hong, W.-Y.; Cui, H.; Luo, A.-P.; Luo, Z.-C.; Xu, W.-C. Dynamical Diversity of Pulsating Solitons in a Fiber Laser. Opt. Express 2019, 27, 28507–28522. [Google Scholar] [CrossRef]
- Wei, Z.-W.; Liu, M.; Ming, S.-X.; Cui, H.; Luo, A.-P.; Xu, W.-C.; Luo, Z.-C. Exploding Soliton in an Anomalous-Dispersion Fiber Laser. Opt. Lett. 2020, 45, 531–534. [Google Scholar] [CrossRef]
- Runge, A.F.J.; Broderick, N.G.R.; Erkintalo, M. Observation of Soliton Explosions in a Passively Mode-Locked Fiber Laser. Optica 2015, 2, 36–39. [Google Scholar] [CrossRef]
- Wei, Z.-W.; Liu, M.; Ming, S.-X.; Luo, A.-P.; Xu, W.-C.; Luo, Z.-C. Pulsating Soliton with Chaotic Behavior in a Fiber Laser. Opt. Lett. 2018, 43, 5965–5968. [Google Scholar] [CrossRef]
- Peng, J.; Boscolo, S.; Zhao, Z.; Zeng, H. Breathing Dissipative Solitons in Mode-Locked Fiber Lasers. Sci. Adv. 2019, 5, eaax1110. [Google Scholar] [CrossRef]
- He, R.; Wang, Z.; Liu, Y.; Wang, Z.; Liang, H.; Han, S.; He, J. Dynamic Evolution of Pulsating Solitons in a Dissipative System with the Gain Saturation Effect. Opt. Express 2018, 26, 33116–33128. [Google Scholar] [CrossRef]
- Chang, W.; Soto-Crespo, J.M.; Vouzas, P.; Akhmediev, N. Extreme Soliton Pulsations in Dissipative Systems. Phys. Rev. E 2015, 92, 022926. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Wang, Z.; Yue, Y.; He, J.; Mao, B.; He, R.; Hu, J. Transient Behaviors of Pure Soliton Pulsations and Soliton Explosion in an L-Band Normal-Dispersion Mode-Locked Fiber Laser. Opt. Express 2019, 27, 17729–17742. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, X.; Li, T.; Yang, J.; Liu, J.; Zheng, Z. Generation and Observation of Ultrafast Spectro-Temporal Dynamics of Different Pulsating Solitons from a Fiber Laser. Opt. Express 2020, 28, 14127–14133. [Google Scholar] [CrossRef]
- Ji, Y.; Yang, Y.; Song, Y.; Wang, K.; Du, G.; Liu, J.; Tang, D.; Wang, Z. Dynamics of Pulsating Solitons with Chaotic Behaviors from a 1.7 μm Ultrafast Fiber Laser. Chaos Solitons Fractals 2024, 187, 115379. [Google Scholar] [CrossRef]
- Soto-Crespo, J.M.; Grelu, P.; Akhmediev, N.; Devine, N. Soliton Complexes in Dissipative Systems: Vibrating, Shaking, and Mixed Soliton Pairs. Phys. Rev. E 2007, 75, 016613. [Google Scholar] [CrossRef] [PubMed]
- Chang, W.; Ankiewicz, A.; Akhmediev, N.; Soto-Crespo, J.M. Creeping Solitons in Dissipative Systems and Their Bifurcations. Phys. Rev. E 2007, 76, 016607. [Google Scholar] [CrossRef] [PubMed]
- Akhmediev, N.; Soto-Crespo, J.M.; Town, G. Pulsating Solitons, Chaotic Solitons, Period Doubling, and Pulse Coexistence in Mode-Locked Lasers: Complex Ginzburg-Landau Equation Approach. Phys. Rev. E 2001, 63, 056602. [Google Scholar] [CrossRef]
- Chen, T.-H.; Lin, Y.-H.; Cheng, C.-H.; Tsai, C.-T.; Chi, Y.-C.; Lin, G.-R. Unintentional Polarization Dependent Pulsewidth of Graphene Mode-Locked Er-Doped Fiber Lasers. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 50–59. [Google Scholar] [CrossRef]
- Runge, A.F.J.; Hudson, D.D.; Tam, K.K.K.; de Sterke, C.M.; Blanco-Redondo, A. The Pure-Quartic Soliton Laser. Nat. Photonics 2020, 14, 492–497. [Google Scholar] [CrossRef]
- Runge, A.F.J.; Aguergaray, C.; Broderick, N.G.R.; Erkintalo, M. Coherence and Shot-to-Shot Spectral Fluctuations in Noise-like Ultrafast Fiber Lasers. Opt. Lett. 2013, 38, 4327–4330. [Google Scholar] [CrossRef]
- Man, W.S.; Tam, H.Y.; Demokan, M.S.; Wai, P.K.A.; Tang, D.Y. Mechanism of Intrinsic Wavelength Tuning and Sideband Asymmetry in a Passively Mode-Locked Soliton Fiber Ring Laser. J. Opt. Soc. Am. B 2000, 17, 28–33. [Google Scholar] [CrossRef]
- Jeong, Y.; Vazquez-Zuniga, L.A.; Lee, S.; Kwon, Y. On the Formation of Noise-like Pulses in Fiber Ring Cavity Configurations. Opt. Fiber Technol. 2014, 20, 575–592. [Google Scholar] [CrossRef]
- Luo, A.-P.; Luo, Z.-C.; Liu, H.; Zheng, X.-W.; Ning, Q.-Y.; Zhao, N.; Chen, W.-C.; Xu, W.-C. Noise-like Pulse Trapping in a Figure-Eight Fiber Laser. Opt. Express 2015, 23, 10421–10427. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Yang, K.; Tsia, K.K.; Zeng, H.; Wong, K.K.Y. Intelligent Soliton Molecules Control in an Ultrafast Thulium Fiber Laser. Adv. Photonics Nexus 2025, 4, 016012. [Google Scholar] [CrossRef]
- Wang, X.; Li, K.; Lu, M.; Fan, Y.; Fu, M.; Xu, A.; Li, S. Pulsating Dynamics of Noise-like Pulses in a Fiber Laser with Nonlinear Optical Loop Mirror. Laser Phys. Lett. 2024, 21, 085102. [Google Scholar] [CrossRef]
- Han, Y.; Gao, B.; Wu, G.; Huo, J.-Y.; Wen, H.-L.; Li, Y.-Y.; Liu, L.; Ma, C.-Y. Creeping and Erupting Dynamics in a Pure-Quartic Soliton Fiber Laser. Opt. Express 2023, 31, 1787–1798. [Google Scholar] [CrossRef]
- Tang, D.Y.; Zhao, L.M.; Zhao, B.; Liu, A.Q. Mechanism of Multisoliton Formation and Soliton Energy Quantization in Passively Mode-Locked Fiber Lasers. Phys. Rev. A 2005, 72, 043816. [Google Scholar] [CrossRef]
- Liu, J.; Li, M.; He, J.; Song, Y.; Wang, Z. Noisy Soliton Pulsation and Its Dynamics in a Mid-Infrared Ultrafast Fiber Laser. Chaos Solitons Fractals 2023, 177, 114199. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Song, Y.; Liu, J.; Zhang, H. Generation and Pulsating Behaviors of Loosely Bound Solitons in a Passively Mode-Locked Fiber Laser. Phys. Rev. A 2020, 101, 013825. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Tang, P.; Zhu, J.; Zhou, Z.; Wu, H.; Wang, Z. Dynamic Behaviors of Pulsating Noise-like Pulses in an Ultrafast Fiber Laser. Photonics 2025, 12, 937. https://doi.org/10.3390/photonics12090937
Zhang L, Tang P, Zhu J, Zhou Z, Wu H, Wang Z. Dynamic Behaviors of Pulsating Noise-like Pulses in an Ultrafast Fiber Laser. Photonics. 2025; 12(9):937. https://doi.org/10.3390/photonics12090937
Chicago/Turabian StyleZhang, Lei, Pinghua Tang, Jinhai Zhu, Zexin Zhou, Haitao Wu, and Zhenhong Wang. 2025. "Dynamic Behaviors of Pulsating Noise-like Pulses in an Ultrafast Fiber Laser" Photonics 12, no. 9: 937. https://doi.org/10.3390/photonics12090937
APA StyleZhang, L., Tang, P., Zhu, J., Zhou, Z., Wu, H., & Wang, Z. (2025). Dynamic Behaviors of Pulsating Noise-like Pulses in an Ultrafast Fiber Laser. Photonics, 12(9), 937. https://doi.org/10.3390/photonics12090937



