Analysis of Radiative Transfer Characteristics of a Spherical Continuous-Spectrum Light Source Under Rainfall Conditions

Abstract

The current research on light transmission under rainfall conditions primarily focuses on monochromatic converging light sources, and the related conclusions cannot be directly applied to spherical continuous-spectrum light sources (SCLSs). Based on the Lorenz–Mie scattering method, this study calculated the optical parameters of Gamma-distributed rainfall across three rainfall types and four intensity levels. A numerical algorithm model for radiative transfer under rainfall conditions was established for SCLSs. The effects of rainfall type, rainfall intensity, and light wavelength on radiative transfer were analyzed. Key conclusions include the following: when rainfall intensity is below moderate, the type of rainfall can be disregarded. However, for heavy to torrential rain, distinct differences between stratiform and non-stratiform rainfall must be considered. The attenuation caused by rainfall intensity does not increase linearly. Specifically, attenuation during moderate rain is lower than that in light rain, while heavy and torrential rain exhibit greater attenuation than both light and moderate rain. Wavelength bands significantly influence radiative transfer. Efforts to optimize the attenuation of radiative energy by rainfall should focus on the primary energy bands where most energy is concentrated. These findings highlight the importance of considering rainfall classification, nonlinear attenuation mechanisms, and wavelength-specific characteristics when evaluating radiative transfer under varying rainfall conditions.

1. Introduction

Rainfall constitutes a common phenomenon in the atmospheric environment and has a significant impact on light transmission [1]. Quantitative studies on the effects of rainfall on light transmission play a critical role in analyzing the spatial distribution patterns of light transmission parameters and assessing the transmission properties and radiative effects of light. Particularly for thermal radiation energy transfer under fire or petrochemical explosion conditions, accurate calculation of the spatial distribution of radiation energy provides critical references for thermal radiation protection.

Rainfall exhibits obvious spectral differences to light transmission due to the distinct optical parameters of raindrop particles. Currently, most studies on light transmission in rainfall within the visible and near-infrared wavelength ranges focus primarily on monochromatic converging light sources such as lasers. For example, T. S. Chu et al. [2] conducted extensive experimental observations on common laser wavelengths (0.63 μm, 3.5 μm, and 10.6 μm) under rainy conditions. Under equivalent rainfall conditions, they found that the attenuation of 0.63 μm laser light was approximately 40% lower than that of 10.6 μm light, attributing this disparity to the forward scattering effect of raindrops. Meanwhile, Guo Jing et al. [3] theoretically demonstrated that rainfall exhibits weaker absorption of 532 nm laser light compared to 1064 nm laser light, resulting in higher transmittance for the former. Liu Xichuan et al. [4] investigated the transmission of 0.63 μm and 1.3 μm lasers in rainfall and concluded that these two wavelengths experience similar effects under rainy conditions. Martin Grabner et al. [5] studied the impact of rainfall on several characteristic laser wavelengths (0.55 μm, 0.85 μm, 1.55 μm, and 10.5 μm), observing that attenuation at 10.6 μm exceeded that of visible and near-infrared lasers. They also noted significant differences in scattering mechanisms (multiple vs. single scattering effects) across various wavelengths. Collectively, these findings reveal that rainfall induces significantly different attenuation effects on lasers of varying wavelengths.

Rainfall intensity is a critical parameter influencing light transmission. However, due to varying application requirements and modeling methodologies, existing studies on the effects of rainfall intensity on light transmission yield conflicting conclusions. Wan Ziao et al. [6], utilizing raindrop scattering characteristics and the Marshall–Palmer (MP) raindrop size distribution (RSD), analyzed the attenuation of a 1.55 μm laser in rainfall. Their results indicated that the attenuation coefficient of laser propagation increases rapidly with escalating rainfall rates. Liu Xichuan et al. [4] proposed that stronger rainfall intensifies scattering effects, thereby exacerbating attenuation of laser transmission. Guo Pengfei et al. [7] developed a rainfall-attenuation model for laser radar through numerical simulations and experimental validation, establishing an inverse relationship between the intensity of radar echo and rainfall intensity, implying that attenuation increases proportionally with rainfall strength. In contrast, Ke Xizheng et al. [8] observed experimentally that laser intensity attenuation was greater in light or drizzle conditions compared to heavy rain. This phenomenon was attributed to two factors: firstly, large raindrops exhibit weaker scattering intensities across all directions compared to smaller droplets, and secondly, forward scattering intensities increase with increasing droplet radius. This suggests that, in light rain or drizzle, the high concentration of small droplets with strong forward scattering may cause greater attenuation by obstructing the laser path, while larger droplets in heavy rain—despite stronger individual scattering—induce lower overall attenuation due to their lower density. Zhu Yaolin et al. [9] further investigated this contradiction using the Mie scattering theory and the Weibull RSD to analyze the impacts of raindrop sizes on 532 nm laser transmission. They concluded that in light rain, weaker forward scattering by small droplets leads to relatively lower attenuation, but in moderate and heavy rain, strong forward scattering effects dominate, significantly increasing attenuation.

For applications in thermal radiation protection, the light source can be modeled as a spherical continuous-spectrum light source (SCLS). Unlike monochromatic convergent sources, the radiant energy from an SCLS diffuses radially and spans a broad spectral range. Consequently, its behavior cannot be directly analyzed using principles derived from monochromatic light properties. Therefore, it is necessary to study radiation transmission, which provides theoretical guidance for thermal radiation protection.

2. Rainfall Model

2.1. Rainfall Intensity

Rainfall intensity refers to the precipitation flux density through a horizontal plane, typically expressed in millimeters per hour (mm/h). In practical applications, a classification method is employed to categorize rainfall into four grades—light rain, moderate rain, heavy rain, and torrential rain—to simplify descriptions and facilitate studies of general rainfall patterns. The specific criteria for these classifications vary depending on the operational objectives. In optical propagation applications, the focus is on instantaneous rainfall intensity, and the criteria of corresponding rainfall grade is as follows: light rain—≤2.5 mm/h; moderate rain—2.6~8.0 mm/h; heavy rain—8.1–15.9 mm/h; and torrential rain—≥16.0 mm/h [10].

2.2. Raindrop Size Distribution (RSD)

Typically, the shape of raindrops as they fall through the air is determined by their size. When the radius of a raindrop is less than 140 μm, it can be approximated as spherical. As its size increases, the raindrop gradually transitions to an ellipsoid and then adopts a flattened, pancake-like shape. When the radius exceeds 5 mm, the raindrop undergoes breakup [11]. Consequently, precipitation involves a heterogeneous mixture of raindrops of varying sizes.

The RSD (units in m⁻³·mm⁻¹) describes the variation in the number concentration of raindrops as a function of their diameter. This distribution is influenced by geographical location, cloud type, and atmospheric conditions. Researchers have developed multiple RSD models based on observational data, including the Laws–Parsons (L-P) distribution, Gamma distribution [12], Marshall–Palmer (M-P) distribution, log-normal distribution, Joss–Waldvogel distribution, and Weibull distribution. Among these, the Gamma distribution demonstrates strong versatility, accurately fitting diverse precipitation spectra and aligning well with the precipitation patterns observed in China [13,14]. Thus, this study employs the Gamma distribution to model the RSD, with its mathematical formulation given as

$$\mathrm{N}\left(\mathrm{D}\right)={\mathrm{N}}_0{\mathrm{D}}^{\mathsf{\mu }}{\mathrm{e}}^{-\mathsf{\lambda }\mathrm{D}}$$

(1)

Here, D denotes the raindrop diameter (mm), ${\mathrm{N}}_0$ represents the concentration parameter (m⁻³⋅mm⁻¹), λ is the scale parameter (mm⁻¹), and μ is the shape factor (dimensionless), which is a function of rainfall intensity R (mm/h).

Based on the formation mechanisms of rain clouds, rainfall is categorized into stratiform rain, convective rain, and mixed rain. The parameters of the RSDs for these rainfall types [14] are presented in

Table 1. Parameters for RSD of different rainfall types.

Rainfall Type	N0 (R) (m−3·mm−1)	λ (R) (mm−1)	μm
Stratiform rain	2.1 × 104 R−0.384	5.38 R−0.186	2.93
Convective rain	0.4 × 103 R−0.384	1.74 R−0.186	0.91
Mixed rain	2.3 × 103 R−0.384	3.42 R−0.186	1.88

.

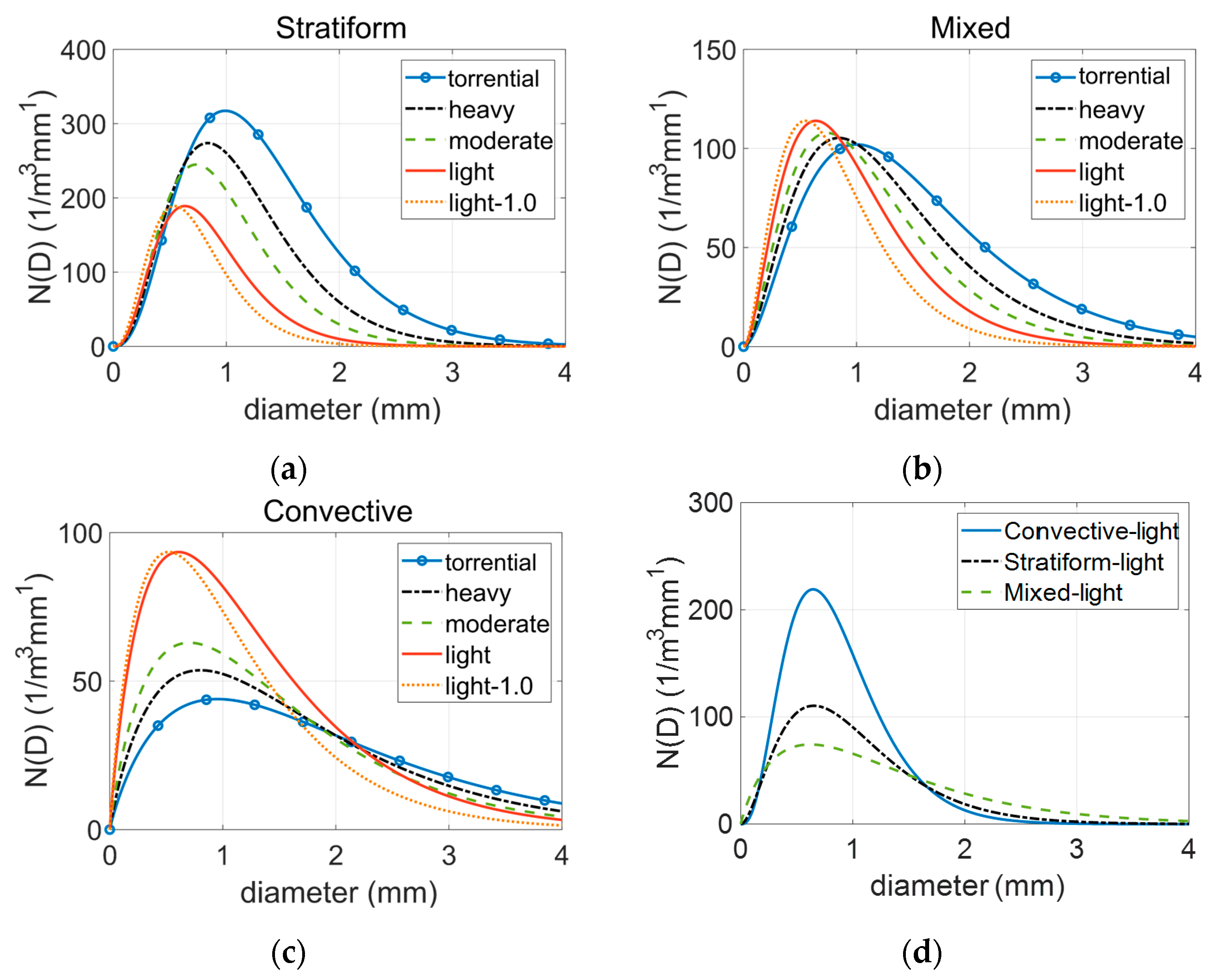
Figure 1 presents a comparative analysis of RSDs under varying rainfall intensities and rain types. Since the rainfall intensity corresponding to each rainfall grade spans a range, this study adopts fixed values for operational convenience: light rain (2.5 mm/h), moderate rain (5 mm/h), heavy rain (10 mm/h), and torrential rain (25 mm/h). In subsequent data analyses, some studies assign light rain a value of 1.0 mm/h. To ensure comparability, the RSD for this case is also provided in the figure and denoted as “light-1.0”. In the figure, “Convective-light” denotes convective rainfall with light intensity, while “Stratiform-light” and “Mixed-light” indicate stratiform rainfall and mixed rainfall, respectively, both at the light rainfall level.

When rainfall intensity is kept constant, convective rain exhibits the widest range of droplet sizes, with the highest concentration of medium-to-large-sized droplets. Stratiform rain shows the narrowest size distribution, characterized by a peak concentration of smaller droplets. Mixed rain occupies an intermediate position between the two in terms of droplet size distribution characteristics. For a fixed rain type, the number concentration of droplets at all size scales increases with rising rainfall intensity, indicating greater precipitation activity. Simultaneously, the central diameter of the raindrop increases gradually as rainfall intensity intensifies, reflecting a shift toward larger droplet dominance in heavier rainfall conditions.

2.3. Rainfall Optical Parameters

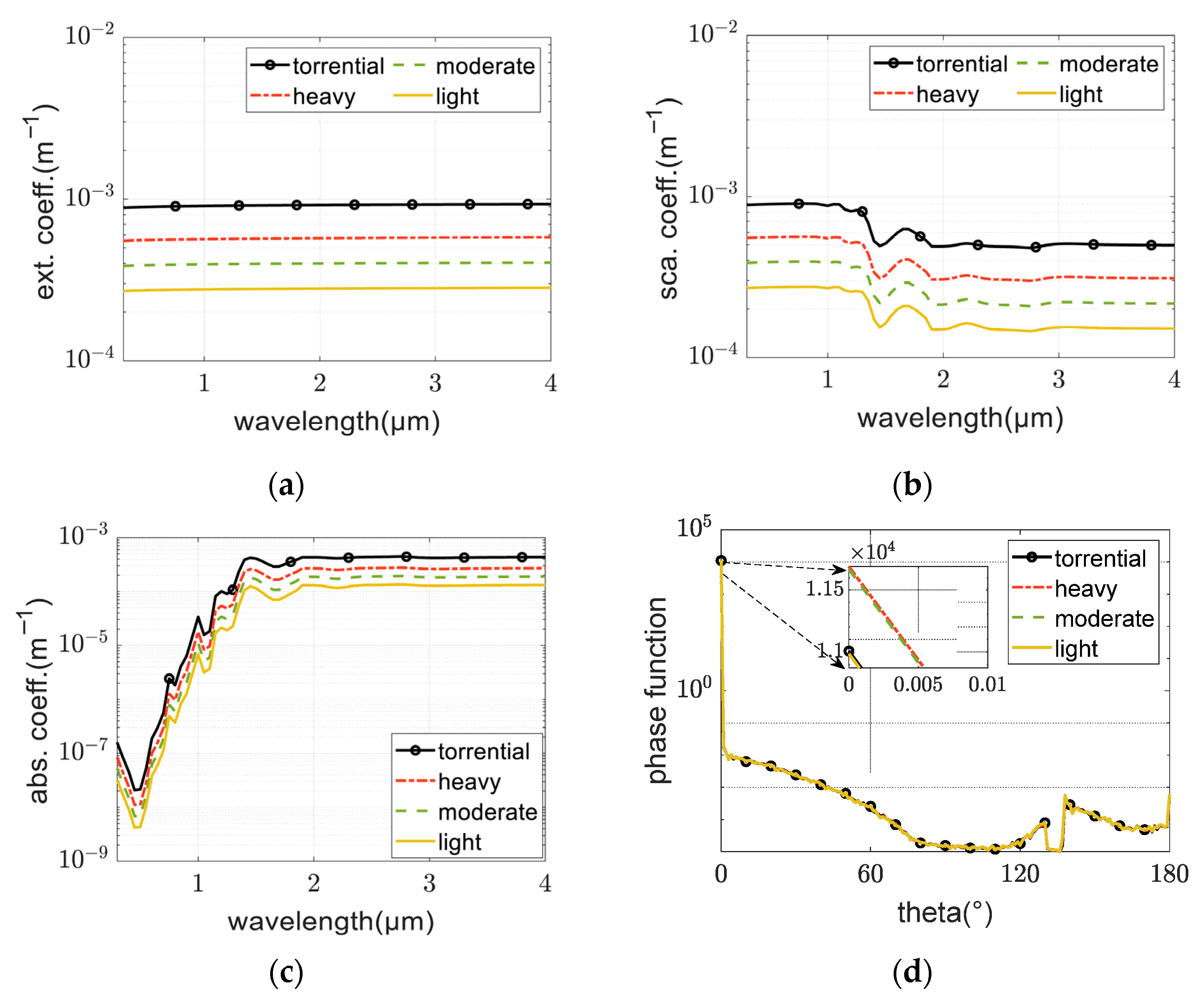
The absorption coefficient, scattering coefficient, and scattering phase function for different rainfall types were calculated using the Lorenz–Mie scattering computational method [15]. For the visible and near-infrared spectrum, the refractive index of raindrops is obtained with reference to Segelstein D. J. [16]. Figure 2 presents the optical parameter results for stratiform rain under varying intensities. The results for other rainfall types exhibit similar characteristics but are omitted due to space limitations. As shown in the figure, within the visible (VIS) and near-infrared (NIR) bands (0.4–1.5 µm), the extinction coefficient, scattering coefficient, and absorption coefficient all increase with rising rainfall intensity when the incident wavelength is kept constant. For a fixed rainfall intensity, the extinction coefficient increases gradually with longer wavelengths, the scattering coefficient decreases with increasing wavelength, and the absorption coefficient increases with increasing wavelength.

In the ultraviolet (UV) and visible bands (0.4–0.7 µm), absorption coefficients range between approximately ${10}^{-9} \mathrm{and} {10}^{-6} {\mathrm{m}}^{-1}$, whereas in the infrared band, absorption coefficients fall between approximately ${10}^{-5} \mathrm{and} {10}^{-3} {\mathrm{m}}^{-1}$, with the latter exhibiting three to four orders of magnitude higher absorption than the former.

Figure 2d illustrates scattering phase functions for stratiform rain at a 0.55 µm wavelength across varying intensities. Due to the large size of raindrops relative to this wavelength, all rain intensities exhibit pronounced forward scattering dominance, with scattering intensity at 0° exceeding that at other angles by approximately ${10}^4$ orders of magnitude. Comparing 0° phase functions among rainfall intensities, moderate and heavy rain exhibit stronger forward scattering compared to light and torrential rain.

3. Algorithm for Radiative Transfer (RT) of SCLS

There are two primary approaches for solving light radiative transfer in the atmosphere, i.e., numerical solutions of the radiative transfer equation (RTE), which, despite high precision, often involve complex computations and limited flexibility in scenarios with complex boundaries or radiation sources [17], and Monte Carlo (MC) statistical methods, which are straightforward and highly adaptable. These have been widely applied to radiative transfer problems in the atmosphere [18,19], aquatic environments [20], vegetation canopies [21,22,23], and space media [24,25]. Given this versatility, the MC method is adopted here to simulate radiative transfer under SCLS.

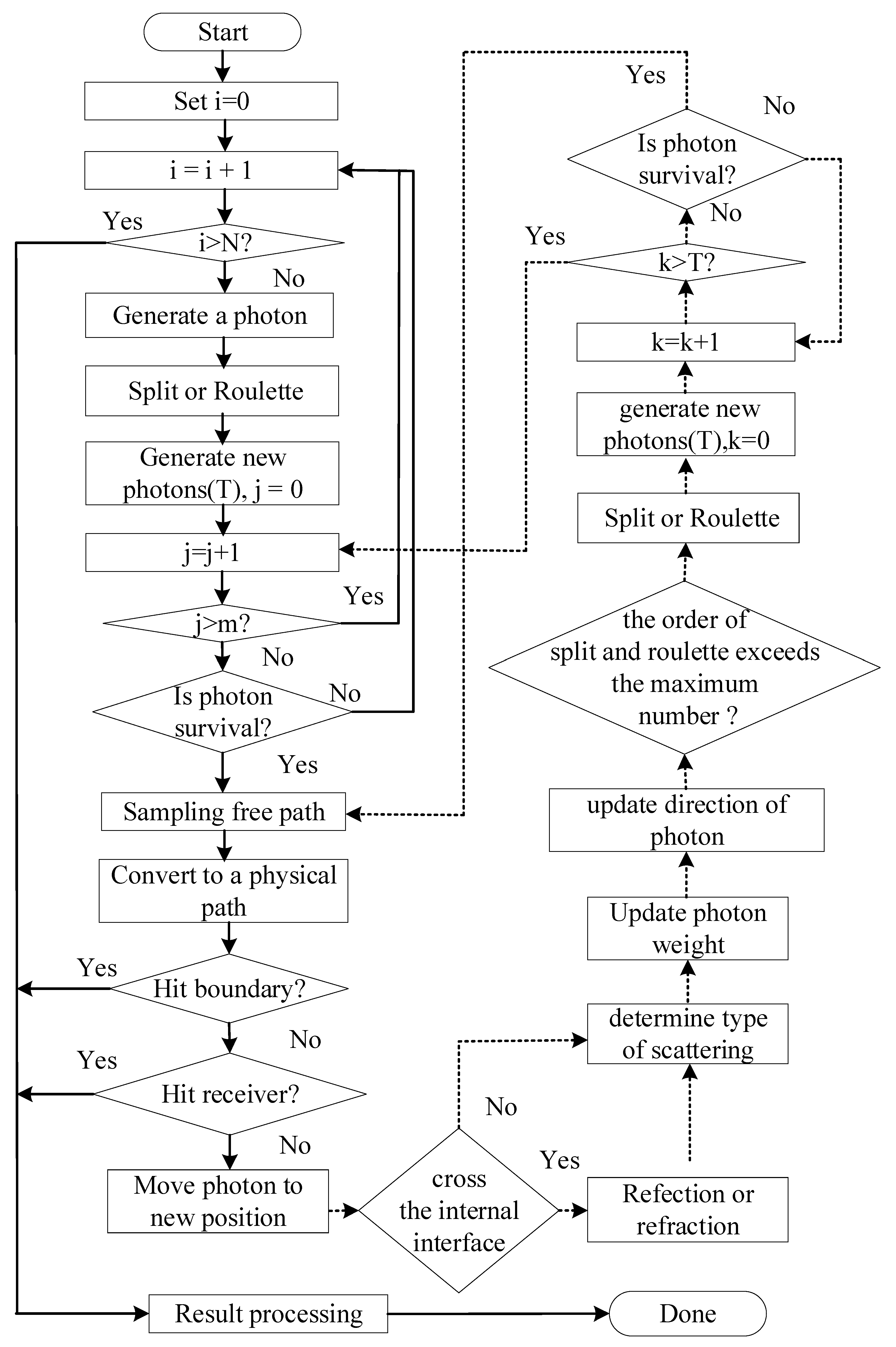
The computational workflow for SCLS radiative transfer based on the MC method is outlined in Figure 3. It comprises five core components: photon generation, photon propagation, photon termination, result statistics, and optimization algorithms. While the fundamental principles of photon propagation, tracking, and statistical analysis are well-established within MC algorithms, this study focuses on SCLS, a scenario with unique characteristics. We therefore provide details on two specialized aspects, namely photon generation methodologies tailored to SCLS and optimization algorithms integrated into the radiative transfer process to enhance computational efficiency and accuracy.

3.1. Photon Generation

The SCLS is modeled as a finite-sized sphere satisfying the blackbody assumption in the MC framework. Radiative energy is abstracted into photons with the following initial parameters: position $l_0\left(x_0,y_0,z_0\right)$, direction $d_0(n_x,n_y,n_z)$, initial radiance $P\left(\lambda \right)$, initial weight $w_0$, and wavelength λ. Typically, the initial weight $w_0$ is set to 1, while other parameters are generated via a multi-step sampling approach.

3.1.1. Initial Position Sampling

A local Cartesian coordinate system is established with the sphere’s center as the origin. For a spherical source with radius $r$, uniformly distributed random numbers ${\eta }_0$ and ${\eta }_1$ within [0, 1] are sampled. The position coordinates $p_0(x_0,y_0,z_0)$ are calculated using Formula (2).

$$\left\{\begin{array}{l}{x}_0=rsin \theta cos \phi \\ y_0=rsin \theta sin \phi \\ z_0=rcos\end{array}\right. \theta where \begin{array}{l}\theta ={\mathit{cos}}^{-1}(1-2{\eta }_0)\\ \phi =2\pi {\eta }_1\end{array}$$

(2)

3.1.2. Initial Direction Sampling

The spherical source’s local coordinate system is defined such that the z-axis aligns with the vector from the sphere’s center to the photon’s initial position $p_0$, and two random numbers ${\eta }_2$ and ${\eta }_3$ are uniformly sampled within [0, 1]. The photon’s direction vector $d_0(n_x,n_y,n_z)$ in the local coordinate system is then determined via Formula (3) [26].

$$\left\{\begin{array}{l}{n}_x=sin \theta cos \phi \\ n_y=sin \theta sin \phi \\ n_z=cos \theta \end{array}\right. where \begin{array}{l}\theta ={\mathit{sin}}^{-1}\left({\eta }_2\right)\\ \phi =2\pi {\eta }_3\end{array}$$

(3)

3.1.3. Photon Wavelength Sampling

Since the optical properties of the transmitting medium are usually spectrally selective when the radiation energy is transmitted in the atmospheric environment, the wavelength of the photons must be sampled according to the spectral characteristics of the spherical source. The wavelength of the photons must be sampled according to the spectral characteristics of the spherical source.

Let $P_{total}$ denote the total radiative power of the SCLS over the wavelength range ${\lambda }_{min}$ to ${\lambda }_{max}$ and $N$ denote the total number of photons to be tracked. The source’s spectral radiance distribution is denoted as $f\left(\lambda \right)$, and its cumulative distribution function (CDF) $F\left(\eta \right)$ is computed. A random number ${\eta }_4\in [0,1]$ is sampled. The photon’s wavelength $\lambda$ and associated radiance $P\left(\lambda \right)$ are calculated by Formulas (4) and (5).

$${\lambda }_s={\lambda }_{min}+F\left({\eta }_4\right)({\lambda }_{max}-{\lambda }_{min})$$

(4)

$$P\left({\lambda }_s\right)={\displaystyle \frac{({\lambda }_{max}-{\lambda }_{min})f\left({\lambda }_s\right)}{{\int }_{{\lambda }_{min}}^{{\lambda }_{max}}f\left(\lambda \right)d\lambda }} {\displaystyle \frac{P_{total}}{N}}$$

(5)

3.2. Optimization Algorithm

To address the issue of a slow convergence speed in MC tracking for SCLS, where emitted photons propagate in dispersed directions across large-scale spaces, this study proposes a strategy to identify photon contributions based on their movement direction. By prioritizing high-contribution photons heading toward the receiver and reducing the tracking of those moving away, the efficiency of the simulation is enhanced. Two optimization algorithms are employed to achieve this objective: geometric splitting and the roulette strategy.

3.2.1. Photon Splitting Algorithm

First, the cosine of the angle between the photon’s motion direction $d(n_x,n_y,n_z)$ and the normal vector $n(n_{x2},n_{y2},n_{z2})$ of the receiver plane is calculated by $cos \theta$. If cos θ > 0, the photon is heading toward the receiver, indicating a high likelihood of contributing to the calculation results. A geometric splitting strategy is then applied.

Subsequently, the splitting multiplier $m$ is determined. By calculating the angle $\phi$ between the photon’s motion direction and the line connecting its current position to the receiver’s target point, a weighting factor is derived. Specifically, the splitter multiplier is given by

$$m=\mathit{round}(M·|\mathit{cos}\phi \left|\right)$$

(6)

where $cos \phi$ reflects the degree of alignment between the photon’s path and the target direction; a larger $cos \phi$ signifies a higher alignment and thus a greater contribution to the result. Here, $M$ denotes the user-defined maximum splitting multiplier.

Finally, the photon is split into $m$ copies. To ensure unbiased results, each replicated photon is assigned a reduced weight $w_{n+1} = w_n/m$. The splitting counter is incremented, while the photon’s position, direction, and other parameters remain unchanged.

3.2.2. Roulette Strategy

For photons traveling away from the receiver ($cos \theta \le 0$), their contribution probability is low. To maintain simulation accuracy without bias, the roulette strategy decides whether to terminate such photons.

A random number $\mathsf{\varsigma }$ is uniformly sampled from [0, 1]. If $\mathsf{\varsigma }\ge psurvive$ (where $p_{survive}$ is a user-prescribed survival probability), the photon is kept for further tracking, and its weight is scaled as $w_{n+1}=w_{n+1}/p_{survive}$.

This weighting adjustment preserves statistical representativeness. If $\mathsf{\varsigma }<p_{survive}$, the photon is terminated and replaced with a newly initialized photon. This mechanism balances computational efficiency and accuracy by preferentially retaining photons with higher contribution potential while probabilistically discarding negligible contributors.

3.3. Verification

To validate the reliability of the proposed algorithm for simulating atmospheric radiative transfer of SCLS, we performed numerical simulations of a planar stratified medium system comprising the atmosphere and seawater. The benchmark case refers to the radiative transfer results of solar radiation in [27]. The specific parameters are set as follows: solar radiation incident at a 45° angle, an atmospheric layer thickness of 100 km partitioned into 20 strata, and seawater with a depth of 61 m divided into 12 layers. The detailed layering schemes and optical parameters for the atmosphere and seawater are consistent with those in [27].

The calculated radiance intensities at the sea surface and at a depth of 61 m underwater are shown in Figure 4. The results demonstrate excellent agreement between our model outputs and those reported in [27], thereby validating the accuracy and effectiveness of the proposed algorithm.

To further demonstrate the convergence of the algorithm proposed in this study, we take the radiative transfer of a SCLS under stratiform heavy rain conditions as an example. The root mean square error (RMSE) of irradiance at different reception distances was calculated for photon numbers ranging from ${10}^5$ to ${10}^8$ (specific algorithmic parameters are listed in

Table 2. Parameters for for MC algorithm running.

Item	Parameters
SCLS	Spherical center coordinates (0, 0, 1000); radius 30 m; initial energy 1 w/cm2; Spectrum of homozygous blackbody, wavelength range 0.3~4.0 μm;
Atmospheric environment	Rainfall intensity: light rain (2.5 mm/h), moderate rain (5 mm/h), heavy rain (10 mm/h) and torrential rain (25 mm/h); rainfall distribution is uniform, horizontal range is infinite, vertical range is 0~4000 m; Aerosols are desert type; The atmosphere is a mid-latitude summer atmosphere model; Take no account of the effects of the clouds;
Boundary	The lower boundary is a non-reflective medium;
Receiver	Rectangular receiver and height at 0 m, grid boundary horizontal distance is from 200 m to 3000 m, grid spacing is 200 m × 10 m; half field angle is π/2;
Parameters for MC algorithm	The total number of photons is ${10}^7$; the maximum splitting multiple is 10; the maximum splitting number is 6; the maximum scattering number is ${10}^3$.

). The RMSE values across various distances were averaged, and the results are shown in Figure 5. As visible from the figure, the irradiance RMSE decreases rapidly with increasing photon numbers. When the photon count exceeds ${10}^7$, the result converges to $1.01\times {10}^{-14} \mathrm{w}/\mathrm{c}{\mathrm{m}}^2$. Therefore, a photon number of ${10}^7$ is adopted for subsequent calculations.

4. Results and Discussion

In order to analyze the radiative transmission characteristics of SCLS under different rainfall conditions, the radiative transmission characteristics of SCLS are calculated by selecting four intensities of rainfall, namely light rain (2.5 mm/h), moderate rain (5 mm/h), heavy rain (10 mm/h), and torrential rain (25 mm/h), and three types, namely convective rain, mixed rain, and stratiform rain. The radiative transmission characteristics of SCLS are calculated, and the specific parameters are set as shown in Table 2.

4.1. Impact of Rainfall Type

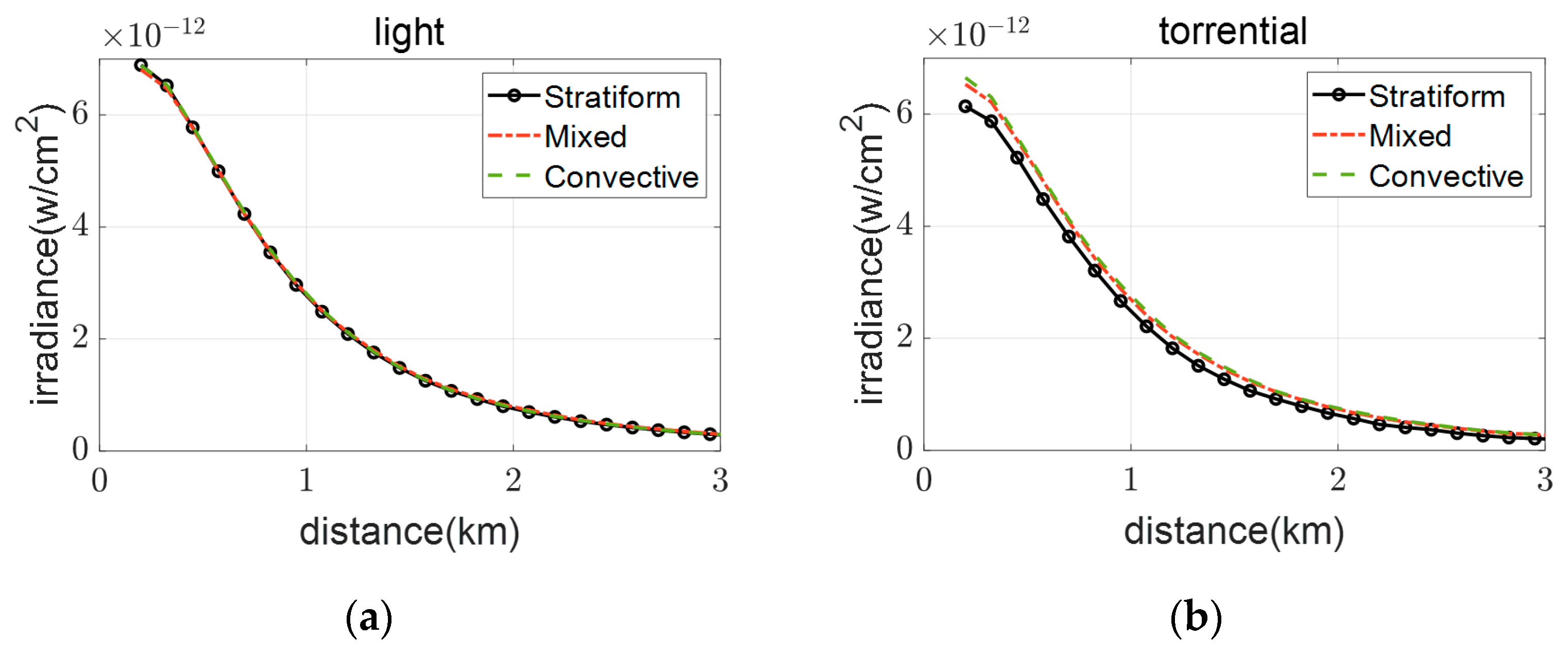
To investigate the influence of different rainfall types on the radiative transfer of SCLS, we calculated the variation in irradiance with distance under varying rainfall intensities and rainfall types (as shown in Figure 6). The results reveal that, for the same rainfall intensity, irradiance declines rapidly with increasing distance across all rainfall types, consistent with the geometric attenuation characteristics of spherical light source propagation. The irradiance differences among the three rainfall types are relatively negligible in light rain. During storm conditions, however, disparities become pronounced: convective and mixed rain exhibit nearly identical irradiance profiles, while stratiform rain demonstrates significantly greater attenuation, deviating more prominently from the other two types.

In order to quantitatively investigate the difference in radiation transmission between different types of rainfall, the relative difference in irradiance under different types of rainfall is calculated (as shown in Figure 7), and the specific calculation method is as follows:

$$\alpha ={\displaystyle \frac{I_{ti,r}-I_{tj,r}}{I_{t0,r}}}\times 100$$

(7)

Among them, r is the rainfall intensity, $ti$ is the rainfall type, I is the irradiance, and $t0$ is the reference irradiance from stratiform rain under the same rainfall intensity.

As can be seen from the graph, the relative difference in irradiance between the three types of rainfall increases with the increase in distance. Under the conditions of light rain and moderate rain, the relative difference in irradiance between the three types of rainfall is less than 6%, while under the condition of heavy rain and torrential rain, the difference between the different types of rainfall begins to increase, and the greater the distance, the greater the difference, especially for stratiform cloud rainfall and the other two types of rainfall, for which the relative difference in irradiance increased greatly, with the relative difference above 2 km being more than 20%. Therefore, in practical applications, when the rainfall intensity is light or moderate, the difference between rainfall types can be ignored. When rainfall intensity is above heavy rain, stratiform rain must be distinguished from non-stratiform systems, while convective and mixed rain may be treated as a unified category.

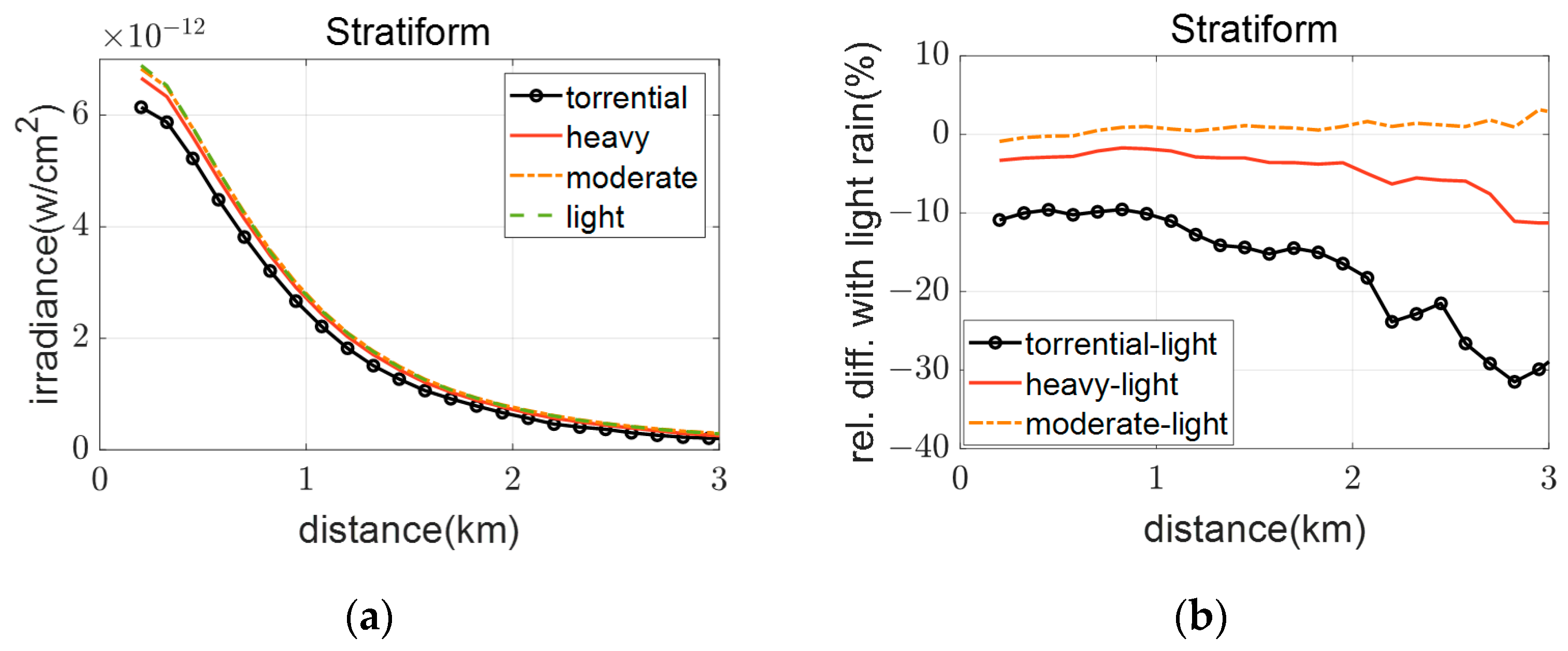
4.2. Impact of Rainfall Intensity

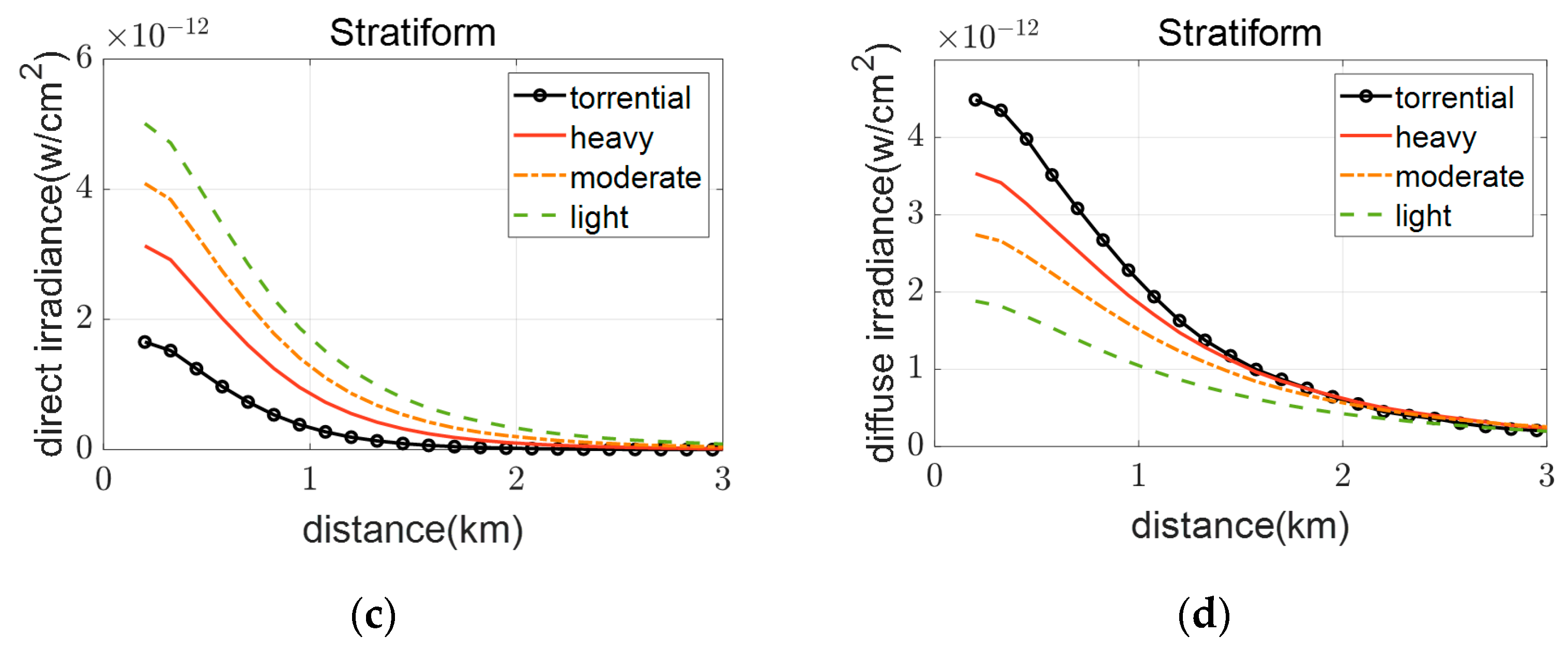
According to the previous analysis, the effect of stratiform rainfall on the radiation transmission of SCLS is the most significant among the three types of rainfall. Figure 8 presents the irradiance, direct irradiance, scattered irradiance, and relative irradiance differences across intensities (light to torrential rain).

As observed in the figure, irradiance decays rapidly with increasing distance, a behavior consistent with the geometric attenuation characteristics of radiative propagation from SCLS. At a fixed distance, irradiance initially increases slightly with enhanced rainfall intensity before subsequently decreasing. Specifically, moderate rainfall shows the highest irradiance values, followed by light and heavy rain scenarios, while the lowest irradiance is observed under storm conditions. This largely aligns with the findings of Zhu Yaolin et al. [9], who also reported irradiance increments with increasing rainfall intensity. However, their conclusions indicated that both moderate and heavy rain cases consistently yielded higher irradiance than light rain, differing from the nuanced trend observed here.

Based on the mechanisms proposed in [9], the scattering phase function of 0.55 µm radiation under varying rainfall intensities was calculated (Figure 2d). Analyses reveal that moderate and heavy rain exhibit stronger forward scattering efficiency compared to light and torrential rain conditions. However, enhanced irradiance was only observed during moderate rainfall relative to light rain scenarios. This indicates that forward scattering efficiency alone does not solely dictate irradiance behavior—the interplay between raindrop absorption-induced attenuation and enhanced multiple scattering effects plays a critical governing role. It is worth noting that first, the RSDs used in this study differ from those in the referenced literature. Second, the rainfall intensity for light rain is defined as 1.0 mm/h in the literature versus 2.5 mm/h in this work. As shown in Figure 1, under three types of rainfall conditions, despite both being classified as light rain, the central diameter of the raindrop size distribution varies between rainfall intensities of 2.5 mm/h and 1.0 mm/h. This discrepancy is a possible cause for the observed differences when directly comparing results.

Based on these analyses, an irradiance attenuation transition phase emerges: attenuation first decreases with rainfall intensity before eventually increasing. The critical transition point occurs after moderate rainfall intensity, with potential extension to heavy rain regimes under extreme meteorological conditions. This non-monotonic relationship reflects the competing dominance of scattering enhancement versus absorption losses as rainfall severity escalates.

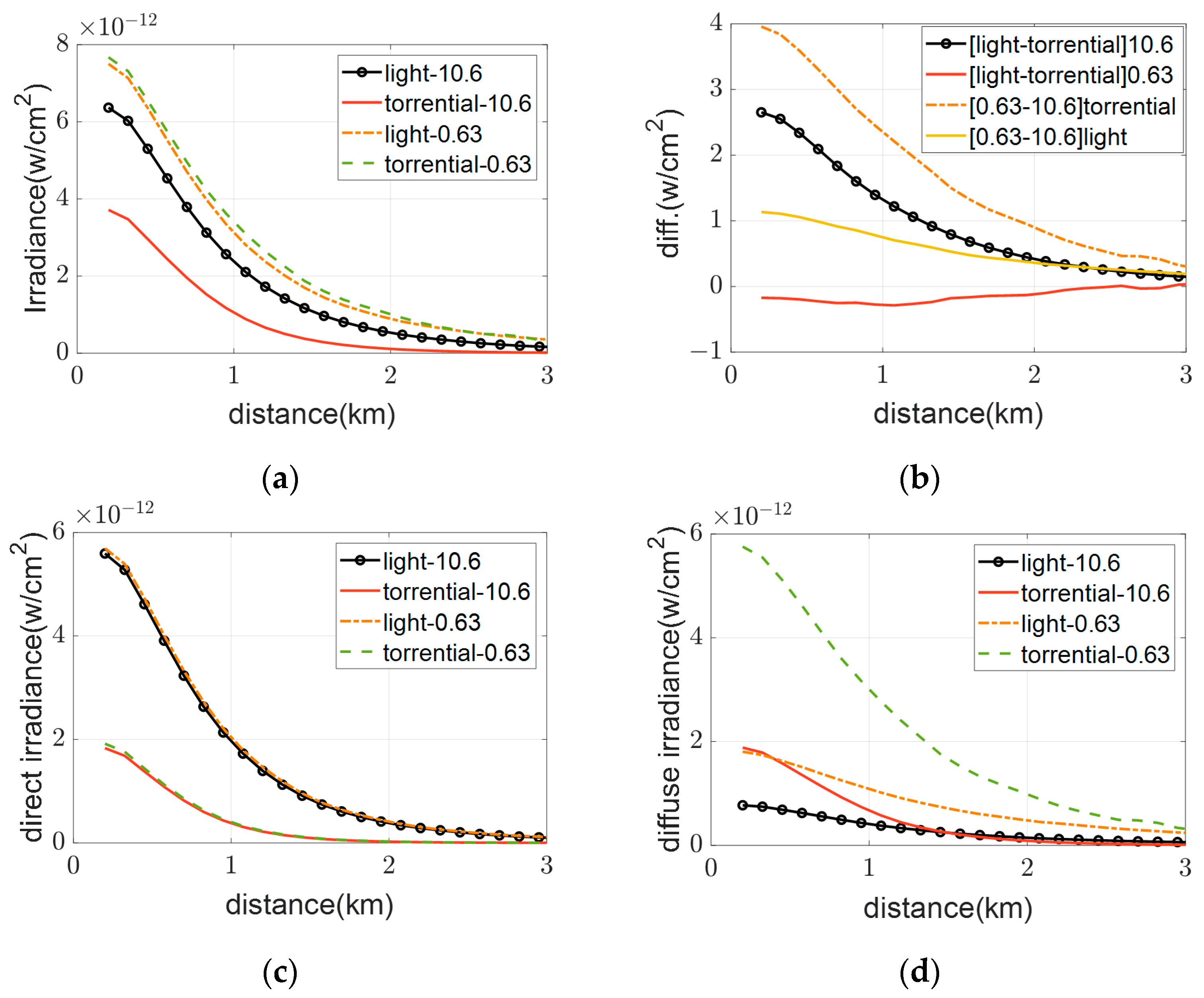
4.3. Impact of Spectral Section of SCLS

The spectral range of radiation emitted by a SCLS varies with its temperature, while differing wavelengths exhibit distinct absorption and scattering characteristics during rainfall propagation. To investigate spectral dependency in radiative transfer under rainfall conditions, this study simulated the performance of two idealized monochromatic spherical sources (0.63 µm and 10.6 µm) under torrential rain (25 mm/h) and light rain (2.5 mm/h) scenarios (Figure 9). All other parameters remained consistent with configurations described in prior sections.

As depicted in Figure 9, irradiance from both spherical sources of differing wavelengths (0.63 µm and 10.6 µm) consistently declines with increasing distance. Under identical rainfall conditions, however, the direct irradiance components across wavelengths show minimal variation, while significant disparities arise in their scattered components, leading to substantial irradiance differences across rainfall intensities.

For the 0.63 µm visible radiation, irradiance exhibits a slight enhancement with increasing rainfall intensity. This phenomenon arises from a combination of two factors: the inherently low absorption coefficient of 0.63 µm radiation ensures slower energy attenuation despite repeated scattering events. In storm conditions characterized by higher droplet concentration and scattering efficiency, a larger portion of photons are redirected through dense scattering fields, thereby increasing the probability of reaching detectors through non-line-of-sight paths. Conversely, the 10.6 µm mid-infrared radiation undergoes pronounced attenuation under enhanced rainfall due to its significantly higher absorption coefficient. Photons at this wavelength experience rapid energy degradation during multiple scattering interactions, resulting in a substantial fraction failing to reach detectors entirely. Even among the photons that successfully propagate through precipitation, their energy levels upon detection remain lower than their 0.63 µm counterparts under equivalent conditions. This pronounced disparity in energy retention directly contributes to the greater attenuation magnitude observed for the 10.6 µm wavelength.

These findings collectively highlight a critical dependency: the optical properties of the wavelength band encompassing the primary energy-emitting spectral region of a SCLS play a decisive role in determining the measurable radiant energy characteristics at a receiver under rainy conditions.

5. Conclusions

Based on Lorenz–Mie scattering theory, this study computed the optical parameters of Gamma-distributed RSD across three rainfall types (stratiform rain, convective rain, and mixed rain) and four rainfall intensities. A numerical radiative transfer model was then established to simulate SCLS propagation under rainfall conditions. Subsequent analysis of the effects of rainfall type, intensity, and wavelength on radiative transfer yielded the following key conclusions:

• Rainfall type is irrelevant below moderate intensity: Distinctions between rainfall types (e.g., stratiform vs. non-stratiform rain) can be disregarded under rainfall intensities below or equal to moderate levels. However, explicit classification becomes critical for heavy to torrential rain conditions where stratiform rainfall demonstrates distinct attenuation characteristics.
• The attenuation dynamics are nonlinear: Contrary to a linear relationship, moderate rainfall induces less attenuation compared to light rain, while heavy and torrential rain produce significantly greater attenuation than both lighter categories. This inverted attenuation hierarchy arises from coupled scattering–absorption processes.
• The spectral dependency is dominant: Radiative attenuation critically depends on the wavelength regime of the source’s primary energy emission. Attenuation optimization should focus on safeguarding dominant energy-emitting spectral regions during precipitation.

This analysis highlights the role of precipitation dynamics in modulating radiative propagation. However, real-world atmospheric systems exhibit far greater complexity, as synergistic meteorological phenomena like cloud–fog–precipitation interactions often occur concomitantly. These coupled processes alter the attenuation dynamics observed in precipitation alone—for example, fog-induced scattering or cloud-layer refraction further modulate photon pathways. Consequently, future investigations must incorporate comprehensive interplay of multiple atmospheric factors (including fog dynamics and cloud structures) to capture the full spectrum of radiative transfer characteristics under combined meteorological conditions.