Abstract
High-power laser diodes (LDs) inherently generate considerable heat during current loading, which presents substantial challenges to the stable operation of laser systems. This study reports a machine learning-based approach that is to be applied to LD temperature control systems, in which a fuzzy neural network (FNN) algorithm is integrated with a proportional-integral-derivative (PID) controller to create an FNN-PID control architecture. The proposed algorithms synergistically integrate fuzzy rule-based systems with neural network learning frameworks, and, furthermore, facilitate adaptive parameter optimization while preserving the interpretability of the decision-making process. Applying the optimized algorithm temperature controller to the LD with output optical power of 110 W @ 888 nm, compared with the conventional PID, the FNN-PID algorithm has shortened the temperature settling time by 77% during 100 W heat generation in LD, the long-term temperature fluctuation is decreased from ±0.126% to ±0.06%, the corresponding optical power steady-state precision is decreased from ±0.09% to ±0.04%, and the step response time of temperature and corresponding power are reduced by 73.4% and 70% from 25 °C to 27 °C, respectively. The FNN-PID outperforms conventional methods (the PID algorithm and the Fuzzy-PID algorithm) in managing thermal fluctuations, and it offers potential for precise laser control applications to enhance beam quality and stability.
1. Introduction
It is well known that the laser diode (LD) generates a large amount of heat during power scaling. This phenomenon leads to the temperature fluctuations and the drift of the central wavelength in the laser, which significantly degrades the output power and the stability. This issue is particularly prominent in high-power LDs, where thermal power can reach 100 W or more, and it causes severe challenges to the reliability and performance of laser systems in applications such as industrial processing, medical equipment, and scientific research [1]. To address this issue, the proportional-integral-derivative (PID) control has been widely adopted [2,3] to control the temperature. However, LD temperature regulation is generally limited to conventional PID control [4] due to the poor adaptability of nonlinear systems [5]. In recent years, some advanced algorithms [6,7] have been increasingly used to overcome the limitations of fixed parameters in the conventional PID. In this case, the fuzzy PID controller emerged [8], this controller leveraged linguistic rules to enable adaptive gain adjustments. In 2001, Tang et al. [9] optimized fuzzy PID gains via multi-objective genetic algorithms, and in 2002, Petrov et al. [10] also advanced fuzzy-neural techniques for nonlinear plant control. These studies demonstrated that the use of fuzzy control to regulate the PID controller could enhance the system’s adaptability to complex environments. However, Chang et al. [11] in 2004 implemented fuzzy control for LD temperature regulation to achieve adaptive tuning; the system encountered oscillations due to Fuzzy-PID with static membership functions. Subsequently, Zang et al. [12] also encountered this problem during the experiment, and the experimental results highlighted the system’s sensitivity to thermal disturbances. In order to solve these problems, the fuzzy neural network-based PID (FNN-PID) algorithm has garnered significant attention due to its more robust self-adjustment capabilities for the fixed membership function parameters and higher adaptability for dynamic temperature regulation. The integration of FNN-PID controllers represents a transformative advancement because the FNN-PID algorithm synergistically combines the interpretability of fuzzy logic with the self-learning capability of neural networks. Shen et al. [13] took the lead in introducing FNN into PID parameter tuning for complex dynamic systems. Meanwhile, Li et al. [14] proposed a fusion strategy that integrates FNN with particle swarm optimization (PSO), which was applied to high-precision servo control scenarios. Their experimental results showed that under nonlinear disturbance conditions analogous to the thermal transient characteristics of LD, the steady-state error was reduced by a factor of five. These results validated the effectiveness of the proposed method in improving control precision under complex disturbances. A key advantage of FNN-PID is online optimization of membership parameters and weight matrices via error back-propagation [15], which overcomes the rigidity of conventional PID (fixed gains) and fuzzy-PID (static membership functions). It enables real-time compensation for dynamic thermal accumulation in high-power LDs and fills a critical gap in prior approaches. However, these intelligent algorithms have not been specifically extended to temperature control of high-power laser diodes with extremely high thermal loads in all-solid-state laser systems, where precise thermal management is essential for maintaining stable operation and optimal performance.
Some research teams have been making continuous efforts in the control system of high-power all-solid-state lasers. With the increase in the output power, a more precise temperature control system should be employed to handle the increasingly large amount of heat. In 2022, Qiao et al. [16] first introduced a machine learning algorithm into the temperature control of the laser to achieve the precise temperature control of the gain crystal (Nd:YVO4) by adopting the back-propagation neural network (BPNN) algorithm. In this case, the output characteristics, environmental adaptability, and stability of the single-frequency continuous-wave laser have also been significantly improved. However, this BPNN with the disadvantage of easily falling into minimum values has not carried out specialized optimization on the pump source LD with the more accumulating waste heat. Then, on this basis, He et al. [17] innovatively integrated the BPNN with an adaptive dynamic adjustment strategy (ADAS) for the LD with a thermal power of 100 W. This method achieved a 73.1% reduction in settling time and a 44.59% improvement in the temperature stability compared to the conventional PID controller, respectively. However, incorporating a constant-current-source circuit has paradoxically rendered the hardware system more complex.
In this paper, an optimized FNN algorithm based on a conventional PID circuit for the high-power LD with a 100 W thermal power is developed. This algorithm synergistically integrates the adaptive reasoning ability of fuzzy logic with the self-learning characteristics of neural networks, which enables dynamic adjustment of PID parameters without relying on complex hardware modifications [18,19]. The FNN-PID algorithm introduces a learning mechanism for membership function parameters and weight matrices during error back-propagation and allows real-time optimization of controller gains [20]. In addition, it avoids local minima issues and enhances transient response through a dynamic coupling mechanism [21] and gain scheduling strategies [22], and it improves long-term stability [23] based on a low-pass filtering method. Lastly, when the conventional PID temperature controller was replaced by the FNN-PID, the temperature settling time was shortened from 1038 s to 235 s, the long-term temperature fluctuation was decreased from ±0.126% to ±0.06%, and the step response time of temperature decreased from 879 s to 234 s. Overall, the optimized algorithm greatly improves power stability and step response speed, and it can offer potential for enhancing beam quality and stability.
2. Experiment Design
In the experiment, a digital signal processor (DSP) chip as the core device (TMS320F28069) [24] is employed to achieve the temperature control of the LD, as shown in Figure 1. When the system starts operating, the temperature collector (TCS610, NTC, 10 kΩ) based on a 100 μA constant current source acquisition circuit [25] immediately begins to continuously acquire the actual temperature of the LD at an approximate rate of once every 0.0875 s. Subsequently, the acquired data are systematically transferred to the microcontroller unit (MCU) through the 24-bit analog-to-digital converter (ADC, ADS1248) and shown on the JS-ARM-LCD as the actual value. To optimize and perform a comparative analysis of the system’s performance, three algorithms are deployed to address the system errors (E = R − Y) of the target value (R) by the JS-ARM-LCD and the actual value (Y) during the computational process of the MCU. These algorithms are the conventional PID control algorithm, the fuzzy-PID control algorithm, and the FNN-PID control algorithm, respectively. Finally, the MCU calculates the system errors to generate a real-time control variable of signal+. This variable of signal+ is outputted as a high-resolution pulse-width modulation (HRPWM) signal through the digital-to-analog converter (DAC, AD5541) to the driver (DRV8432). The driver then acts on four thermoelectric coolers (TECs) to control the temperature (cooling or heating) of the LD. The performance of TEC directly affects the overall thermal control quality of the system through the response speed, thermal load compensation capability, and temperature regulation accuracy, which are interrelated and jointly determine the system stability. During this process, the temperature of the cooling water circulation machine is set at 18 °C. By implementing these methods, the system enables the completion of closed-loop control and rapidly stabilizes the temperature at the target state.
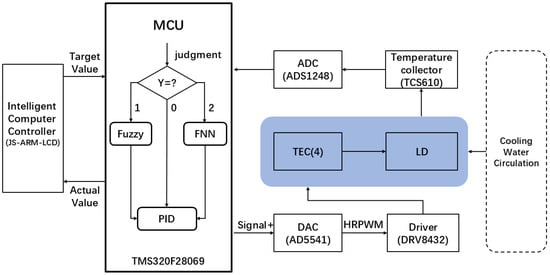
Figure 1.
Framework of the control system.
In Figure 2, an FNN algorithm with a five-layer neural network architecture is designed. Its structure contains two input-layer neurons, six fuzzy-layer neurons, nine rule-layer neurons, one normalization-layer neuron, and three output-layer neurons. On this basis, the temperature error and its rate of change are inputted into the neural network. The network then performs calculations involving fuzzification, rule inference, normalization, and defuzzification, and ultimately outputs three PID parameters (, , and ). To enable the PID parameter values to adapt to temperature variations and thereby eliminate errors as rapidly as possible, the computational process of the neural network encompasses both forward propagation and backward learning.
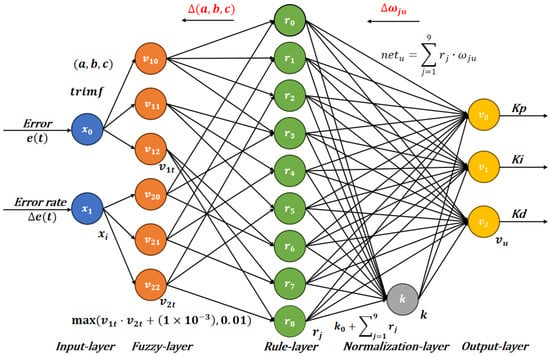
Figure 2.
Schematic diagram of the FNN algorithm.
In the forward propagation process, and are transmitted to the input layer. After that, the fuzzy layer utilizes the triangular membership function () to map the input space to the fuzzy domain, and the semantic fuzzy partitions are defined by parameterizing the triangle vertices (). The function is expressed as
where the input layer neurons are denoted by .
Therefore, the affiliation value of the neurons in the fuzzy-layer is set as
Subsequently, the rule layer generates rule activation strengths based on multiplicative reasoning, constructs a fuzzy rule matrix (), and introduces a bias term () to avoid the zero-activation problem. Therefore, the neurons in the rule layer are expressed as
The normalization layer and output layer employ a protective summation () combined with a weighted average mechanism to ensure the probabilistic distribution characteristics of the rule strengths. The neuron of the normalization layer is expressed as
The connection networks between the rule layer and the output layer are expressed as
where is the weight between the hidden and output layers, j is the number of neurons in the rule layer, and u is the number of neurons in the output layer.
Finally, the output layer achieves nonlinear fitting of the three PID parameter values through a learnable weight matrix and center value parameters. An amplitude limit of ±30 and a low-pass filtering method ( = 0.2) are added to ensure stable performances and parameter smoothness. The output can be obtained by referring to the prior output value
where is the output center value by manual adjustment.
After the forward propagation is completed, the outputs of the three neurons in the output layer are assigned to the PID parameters , , and , respectively. The PID control value () is then transmitted. Meanwhile, the performance metric function of the learning algorithm is defined as
In the backward learning process, the weight update adopts the normalized rule strength as the gradient weights and combines the output center value to scale the error signal. Then the algorithm prevents overfitting through weight constraints (). The formula for calculating the weights are
where is the error array for PID parameter values, is the weights update, is the learning efficiency, and , and are variations in the PID parameters.
The learning of membership function parameters is based on piecewise gradient calculation, where the partial derivatives of the error concerning the triangle vertices () are computed, respectively. The expression formulas are as follows:
where the is the error-centered product quantity.
In the process of backward learning, to exhibit better dynamic performance and robustness in high-inertia systems for temperature control, the algorithm achieves real-time optimization of controller gains through the nonlinear parameter mapping relationship of dynamic coupling mechanism design () and the gain scheduling strategies ( and ) in Equation (11) and Figure 3. Therefore, the objective function for the PID parameter values () is designed as
where the actual PID parameter values are , and . And the gain factors are , and .
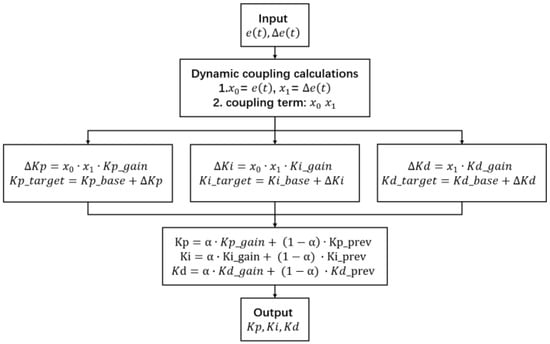
Figure 3.
The flowchart of the real-time optimization of controller gain strategies.
In summary, the FNN-PID algorithm represents a significant advancement in control strategies, integrating the interpretability of fuzzy control with the rapid adaptive parameter adjustment capabilities of neural networks. The algorithm innovatively achieves smooth adjustment and real-time optimization of controller gains through dynamic coupling mechanisms, gain scheduling strategies, and low-pass filter functions. Meanwhile, it introduces a learning mechanism for membership function parameters and weight matrices during error backpropagation, which significantly enhances the system’s adaptability to dynamic processes.
The algorithm flow of FNN-PID is shown in Figure 4. Once the system starts, it begins to collect the temperature and calculate the system error. Subsequently, the system continuously updates the membership parameter values and the weight matrix based on the error and the dynamic change trend of the error. The FNN algorithm dynamically calibrates PID parameters through real-time online learning and achieves rapid thermal equilibrium of the LD at the predefined setpoint. Therefore, this closed-loop optimization strategy minimizes settling time and enhances transient response characteristics.
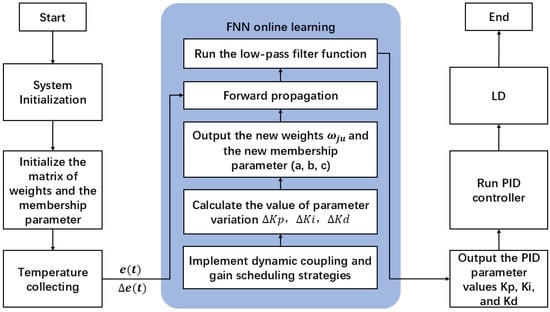
Figure 4.
Flowchart of the FNN-PID algorithm.
3. Experimental Results
To systematically assess and compare the performance of three temperature controllers (PID, Fuzzy-PID, and FNN-PID), we constructed the experimental setup as shown in Figure 5 and comprehensively monitored the LD’s temperature and output power variations, including their step response characteristics.
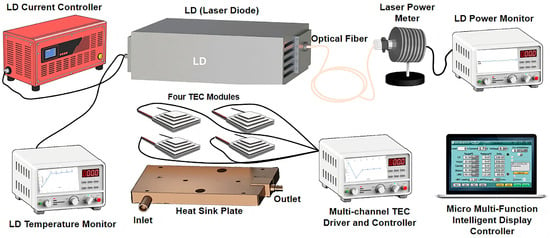
Figure 5.
Experimental measurement setup for the LD temperature and output power. The heat sink plate, TECs, and LD are in close contact.
When the water temperature of the cooling water circulation machine connected to the heat sink plate was set at 18 °C and the target temperature value of the LD was set at 25 °C, we started the system and carried out experimental data collection. At 400 s, the LD (COHERENT. model: M1F4S22-888.3-120C-IS9.15M4O3T3W4) was driven at 53.2 A (3.95 V operating voltage) by the LD current controller, corresponding to an output optical power of 110 W at 888 nm and heat generation of 100 W. As depicted in Figure 6a, the FNN-PID, Fuzzy-PID, and PID algorithms achieved steady-state conditions in 235 s, 373 s, and 1038 s, respectively, with peak temperatures of 26.74 °C, 26.95 °C, and 27.18 °C. Meanwhile, we recorded the voltages of the four TECs used for temperature control. Figure 6b clearly showed that the TECs using the FNN-PID algorithm reached a stable voltage in merely 216 s, whereas for the conventional PID and Fuzzy-PID algorithms, the corresponding times were 485 s and 351 s, respectively. When the system stabilized, the voltage of the TECs was recorded as −2.76 V. During the experiment, the central PID parameters of FNN-PID were configured as follows: = 13.0, = 0.8, and = 1.0. These values were optimized by the real-time response characteristics of the system. For the Fuzzy-PID controller, fixed membership parameters and weight matrices were configured via the uniform division method [26]. For conventional PID, its parameters were set as = 13.5, = 0.6, and = 0.8.
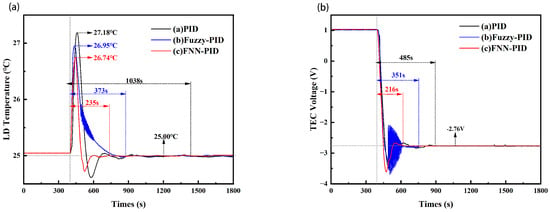
Figure 6.
(a) The temperature variation trend during 100 W heat generation in LD. (b) The variation trend of corresponding TEC voltage. The black curve is PID, the blue curve is Fuzzy-PID, and the red curve is FNN-PID.
Subsequently, we carefully recorded the temperature fluctuation and the corresponding power fluctuation of the LD for 6000 s, respectively. As was clearly shown in Figure 7a,b, the PID algorithm, the Fuzzy-PID algorithm, and the FNN-PID algorithm exhibited different control performances on the temperature control and the corresponding power of the LD. The temperature fluctuation and the power fluctuation were only ±0.06% at 25 °C and ±0.04% at 110.1 W with the FNN-PID algorithm, ±0.114% and ±0.063% with the Fuzzy-PID algorithm, and ±0.126% and ±0.09% with the PID algorithm. The results demonstrated that the FNN-PID algorithm was the most effective in suppressing temperature and power fluctuations, could keep the temperature and output optical power within a much narrower range, and had significantly higher stability compared to the other two algorithms.
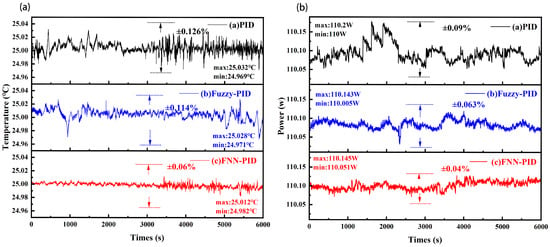
Figure 7.
(a) Temperature fluctuation of LD with 100 W heat. (b) Power fluctuation of LD with 100 W heat. The black curve is PID, the blue curve is Fuzzy-PID, and the red curve is FNN-PID.
Finally, we adjusted the temperature of the LD from 25 °C to 27 °C at a rate of 1 °C/s to test the step-response performance of the system. As shown in Figure 8a, the FNN-PID controller (Curve (c)) achieved a stabilization time of 234 s and an overshoot temperature of 27.41 °C, significantly outperforming the conventional PID algorithm (Curve (a), 879 s, 27.52 °C) and the Fuzzy-PID controller (Curve (b), 604 s, 27.83 °C). The fluctuations in LD output optical power were systematically recorded in Figure 8b. The stabilization time using the FNN-PID controller (curve (c)) was 192 s, significantly outperforming the fuzzy PID controller (curve (b), 474 s) and the conventional PID algorithm (curve (a), 641 s). As could be seen from the experiments, the output power of the LD was closely related to the temperature. These findings collectively indicated that the FNN-PID control algorithm effectively enabled high-power LDs to stabilize around the set-point temperature, thereby ensuring the stabilization of laser output optical power. The results highlighted the superior dynamic response and rapid convergence characteristics of the FNN-PID control strategy in managing thermal and optical power fluctuations in LD systems.
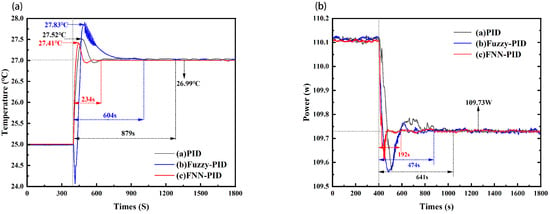
Figure 8.
(a) The temperature step-response performance of the LD with output optical power of 110 W from 25 °C to 27 °C. (b) The corresponding optical power step response performance of LD. The black curve is PID, the blue curve is Fuzzy-PID, and the red curve is FNN-PID.
4. Discussion
In the experimental results, a temperature control method for a 100 W thermal power LD was presented. As shown in Table 1, the experiments demonstrated that the FNN-PID controller decreased settling time by 77% (235 s versus 1038 s), reduced long-term temperature fluctuation from ±0.126% to ±0.06%, and cut the temperature step-response duration from 879 s to 234 s compared with the conventional PID. The extensive testing results demonstrated that the developed approach exhibited superior robustness and adaptability for the higher-power LD. When current was injected into the LD, thermal transients would occur. It was difficult for LD to deal with the thermal accumulation merely by using the conventional PID algorithm. Compared with the PID algorithm, the Fuzzy-PID algorithm shortened the steady-state time by 64.1% and improved the stability by 9.52%. However, the Fuzzy-PID algorithm showed obvious oscillations and hysteresis in terms of step response, and this oscillatory phenomenon was also presented in the variation trend of the steady-state time and the TEC’s control voltage in Figure 6. This was because the parameters of the membership function and the weight matrix were fixed based on the empirical method [27]. No matter how evenly the variation range of the parameters was adjusted, the Fuzzy-PID algorithm would always have computational deviations near its boundary values and thus failed to respond to sudden changes promptly.

Table 1.
Comparison of the experimental results from PID, Fuzzy-PID, and FNN-PID.
In comparative analysis with the reference algorithms, the FNN-PID strategy demonstrated significant performance enhancements, with the temperature settling time reduced by 77.4% and 37%, steady-state temperature accuracy improved by 52.4% and 47.4%, optical power steady-state precision enhanced by 55.6% and 36.5%, temperature step response time shortened by 73.4% and 61.3%, and power step response time decreased by 70% and 59.5%, respectively. This phenomenon could be attributed to the design and characteristics of the FNN-PID algorithm. Firstly, the FNN-PID algorithm established a nonlinear parameter mapping relationship and implemented a gain-scheduling strategy by leveraging a dynamic coupling mechanism, which enabled real-time optimization of controller gains. This fundamental feature effectively overcame the limitation of fixed membership function parameters and weight matrices in the Fuzzy-PID algorithm [28,29], and enhanced the flexibility and adaptability of the control process. Secondly, the FNN-PID algorithm integrated fuzzy control theory. This method effectively mitigated the risk of the system converging to local minimum errors in contrast to the BPNN-PID algorithm [30,31], thereby significantly enhancing control accuracy and system stability. In addition, a low-pass filtering method was added to ensure stable performances and parameter smoothness. As a result, the FNN-PID algorithm demonstrated superior control performance in practical applications [14,32,33,34].
However, the FNN-PID algorithm designed in this paper was constrained by the output central value setting, which required manual adjustment according to actual circumstances. As a result, the overall efficiency and universality of the control system might be compromised. However, it could effectively compensate for this defect depending on the dynamic adjustment of membership function parameters and the weight matrix. In addition, there were some transient lag phenomena during the system initialization process. This was because the FNN-PID algorithm needed to adjust the most appropriate parameters through online learning to match the performance of the system in order to achieve a better control effect. In the future, the more advanced algorithms would be added to automatically generate fuzzy rule centers and map the output center value.
5. Conclusions
In conclusion, this paper presents a high-power LD temperature control system by combining the FNN algorithm with the PID temperature controller. The FNN-PID algorithm achieves a deep integration of fuzzy rules and neural networks. While maintaining the interpretability of fuzzy control, this algorithm has the capability of adaptive parameter adjustment. Especially, it innovatively introduces the learning mechanism of membership function parameters and weight matrix during error backpropagation, and it achieves smooth adjustment and real-time optimization of controller gains through dynamic coupling mechanisms, gain scheduling strategies, and low-pass filter functions. Thus, it significantly enhances the system’s adaptability to dynamic processes. In this case, three experimental results are verified by implementing the FNN-PID algorithm in the LD temperature control system: (1) in the comparative experiment on LD temperature control capabilities, the maximum overshoot temperature of the LD is 26.74 °C with the settling time of 235 s, and the TEC voltage regulation time is 216 s; (2) in the system stability experiment, the long-term stability of LD temperature is maintained at ±0.06%, and the steady-state accuracy of the output optical power is ±0.04%; and (3) in the step response experiment, the step response time is shortened to 234 s with reducing 1.56% of the overshoot, and the power step response time is shortened to 192 s. These experimental results collectively validate that the FNN-PID algorithm achieves superior dynamic response characteristics, such as minimizing overshoot, accelerating convergence, and improving control precision. Therefore, it can highlight its efficacy in mitigating thermal power fluctuations in high-power LD (with 100 W thermal power) systems, and it showcases substantial advantages in both transient regulation speed and long-term stability. Based on this research, the proposed approach is expected to offer innovative solutions for core application scenarios in laser technology, such as precise temperature control, wavelength locking, and power stabilization. These solutions are designed to enhance the intelligence and adaptability of the laser control system, which can improve the overall performance of the laser by increasing control accuracy and operational stability.
Author Contributions
Conceptualization, Y.H., N.L. and X.J.; software, N.L. and Y.H.; investigation, N.L., K.W., Y.H., H.L. and X.J.; data curation, N.L. and K.W.; writing—original draft preparation, N.L. and Y.H.; writing—review and editing, X.J., Y.H. and H.L.; supervision, X.J.; project administration, H.L.; funding acquisition, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Key Research and Development Program of China (2022YFC2204003).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, P.; Wang, M.; Nie, Z.; Yang, W. Performance of high-power diode lasers operated at cryogenic temperature. In Proceedings of the SPIE/COS Photonics Asia, Hangzhou, China, 20–23 October 2019; p. 11182. [Google Scholar]
- Holgate, W.A.; Richardson, M. PID Temperature Control of a Single Mode Fiber Coupled Laser Diode System. In Proceedings of the SoutheastCon, Mobile, AL, USA, 26 March–3 April 2022; pp. 195–202. [Google Scholar]
- Ye, M.; Du, E.; Wang, Q.; Zhao, Y. High-precision temperature control system design for laser diode. Infrared Laser Eng. 2024, 53, 20230713. [Google Scholar]
- Palaniyappan, T.K.; Yadav, V.; Ruchira; Tayal, V.K.; Choudekar, P. PID Control Design for a Temperature Control System. In Proceedings of the 2018 International Conference on Power Energy, Environment and Intelligent Control (PEEIC), Greater Noida, India, 13–14 April 2018; pp. 632–637. [Google Scholar]
- Daryoush, A.; Iyer, S.; Herczfeld, P. Laser Diode Nonlinearity and Its Applications in the Optical Injection Locking of Solid State Oscillators. In Proceedings of the Optoelectronic Signal Processing for Phased-Array Antennas, Bellingham, WA, USA, 12–13 January 1988; Volume 886, pp. 18–31. [Google Scholar]
- Ali, A.; Alaoui, C. FPGA-based control of thermoelectric coolers for laser diode temperature regulation. Int. J. Eng. Sci. Technol. 2012, 4, 1628–1633. [Google Scholar]
- Cong, M.; Xu, W.; Wang, Y. Design of Temperature Controller for Laser Diode Based on DSP and Fuzzy-PID Control. In Proceedings of the 2010 International Conference on Electrical and Control Engineering, Wuhan, China, 25–27 June 2010; pp. 786–789. [Google Scholar]
- Mamdani, E.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Tang, K.; Man, K.F.; Chen, G.; Kwong, S. An optimal fuzzy PID controller. IEEE Trans. Ind. Electron. 2001, 48, 757–765. [Google Scholar] [CrossRef]
- Petrov, M.; Ganchev, I.; Taneva, A. Fuzzy PID control of nonlinear plants. In Proceedings of the First International IEEE Symposium Intelligent Systems, Varna, Bulgaria, 10–12 September 2002; Volume 1, pp. 30–35. [Google Scholar]
- Chang, Y.; Chen, Y.; Lee, C.; Wang, Y.; Chen, Y.; Wang, C. Improving temperature control of laser module using fuzzy logic theory. In Proceedings of the Twentieth Annual IEEE Semiconductor Thermal Measurement and Management Symposium (IEEE Cat. No. 04CH37545), San Jose, CA, USA, 11 March 2004; pp. 198–204. [Google Scholar]
- Zang, H.-Q.; Li, Q. The automatic temperature system with fuzzy self-adaptive PID control in semiconductor laser. In Proceedings of the 2009 IEEE International Conference on Automation and Logistics, Shenyang, China, 5–7 August 2009; pp. 1691–1694. [Google Scholar]
- Shen, J.C. Fuzzy neural networks for tuning PID controller for plants with underdamped responses. IEEE Trans. Fuzzy Syst. 2001, 9, 333–342. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Zhang, Y. Application of Fuzzy Neural PID Controller Based on PSO for High Precision Servo System. In Proceedings of the 2011 Fourth International Symposium on Computational Intelligence and Design, Hangzhou, China, 28–30 October 2011; Volume 2, pp. 291–294. [Google Scholar]
- García-Ródenas, R.; Linares, L.; López-Gómez, J. Memetic algorithms for training feedforward neural networks: An approach based on gravitational search algorithm. Neural Comput. Appl. 2021, 33, 2561–2588. [Google Scholar] [CrossRef]
- Qiao, H.; Peng, W.; Jin, P.; Su, J.; Lu, H. Performance improvement of single-frequency CW laser using a temperature controller based on machine learning. Micromachines 2022, 13, 1047. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Jin, X.; Jin, P.; Su, J.; Li, F.; Lu, H. Temperature Control Performance Improvement of High-Power Laser Diode with Assistance of Machine Learning. Photonics 2025, 12, 241. [Google Scholar] [CrossRef]
- Wang, L.X.; Mendel, J. Fuzzy basis functions, universal approximation, and orthogonal least-squares learning. IEEE Trans. Neural Netw. 1992, 3, 807–814. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Ketenci, A.; Gol, E.A. Learning Parameters of ptSTL Formulas with Backpropagation. In Proceedings of the 2020 28th Signal Processing and Communications Applications Conference (SIU), Gaziantep, Turkey, 5–7 October 2020; pp. 1–4. [Google Scholar]
- Abdoulaye, A.M.; Meli, V.N.; Kongni, S.J.; Njougouo, T.; Louodop, P. Chimera state in neural network with the Proportional-Integral-Derivative coupling. Chaos Solitons Fractals 2025, 191, 115847. [Google Scholar] [CrossRef]
- Garduno-Ramirez, R.; Lee, K. Fuzzy scheduling control of a power plant. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting, Conference Proceedings (Cat. No.00CH37077), Singapore, 23–27 January 2000; Volume 1, pp. 441–445. [Google Scholar]
- Noel, M.M. A new gradient based particle swarm optimization algorithm for accurate computation of global minimum. Appl. Soft Comput. 2012, 12, 353–359. [Google Scholar] [CrossRef]
- Wang, W. Electronic Control System of All-Solid-State Laser Based on Single-Chip Microcomputer. Acta Quantum Opt. Sin. 2013, 19, 182–188. [Google Scholar]
- Jin, X.; Su, J.; Jin, P.; Wang, W.; Peng, K. Study on A High-Precision Digital Temperature-Control System for All-Solid-State Single-Frequency Green Laser. Chin. J. Lasers 2015, 42, 902010. [Google Scholar]
- Zhao, Z.Y.; Tomizuka, M.; Isaka, S. Fuzzy gain scheduling of PID controllers. IEEE Trans. Syst. Man Cybern. 1993, 23, 1392–1398. [Google Scholar] [CrossRef]
- Huang, Y.; Yasunobu, S. A general practical design method for fuzzy PID control from conventional PID control. In Proceedings of the Ninth IEEE International Conference on Fuzzy Systems, FUZZ-IEEE 2000 (Cat. No. 00CH37063), San Antonio, TX, USA, 7–10 May 2000; Volume 2, pp. 969–972. [Google Scholar]
- Yao, Y.; Ma, N.; Wang, C.; Wu, Z.; Xu, C.; Zhang, J. Research and implementation of variable-domain fuzzy PID intelligent control method based on Q-Learning for self-driving in complex scenarios. Math. Biosci. Eng. 2023, 20, 6016–6029. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Lee, S.J.; Yim, S.C. Reinforcement learning-based adaptive PID controller for DPS. Ocean Eng. 2020, 216, 108053. [Google Scholar] [CrossRef]
- Teng, Y.; Huang, X.; Ye, S.; Li, Y. Prediction of particulate matter concentration in Chengdu based on improved differential evolution algorithm and BP neural network model. In Proceedings of the 2018 IEEE 3rd International Conference on Cloud Computing and Big Data Analysis (ICCCBDA), Chengdu, China, 20–22 April 2018; pp. 100–106. [Google Scholar]
- Liu, J.; Li, P.; Tang, X.; Li, J.; Chen, J. Research on improved convolutional wavelet neural network. Sci. Rep. 2021, 11, 17941. [Google Scholar] [CrossRef]
- Ni, Z.; Wang, M. Research on the fuzzy neural network PID control of load simulator based on friction torque compensation. In Proceedings of the 2014 Sixth International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2014; Volume 1, pp. 292–295. [Google Scholar]
- Wang, R.; Zhou, Z.; Qu, G. Fuzzy neural network PID control based on RBF neural network for variable configuration spacecraft. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 October 2018; pp. 1203–1207. [Google Scholar]
- Zhou, X.; Gao, H.; Jia, Y.; Li, L.; Zhao, L.; Yu, R. Parameter Optimization on FNN/PID Compound Controller for a Three-Axis Inertially Stabilized Platform for Aerial Remote Sensing Applications. J. Sens. 2019, 2019, 5067081. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).