A CNN-GS Hybrid Algorithm for Generating Pump Light Fields in Atomic Magnetometers
Abstract
1. Introduction
2. Flat-Top Beam Generation System
2.1. Phase Algorithms and Simulation
2.1.1. Gerchberg–Saxton (GS) Algorithm
2.1.2. Improved Algorithm Based on GS and CNN
- Data preparation
- Model Training
- Phase Prediction
- GS-Based Refinement
3. Training and Experiments
3.1. Dataset Preparation
3.2. Network Architecture and Model Training
- Set parameters: path for datasets saving, input image size 64 × 64, batch−size 8, learning rate 1 × 10−3, training epochs 200, and loss function as RMSE.
- Initialize model weights.
- For each epoch, input training data to perform forward propagation, compute output, and calculate loss against the ground-truth phase. To enhance the credibility of the trained model, in the absence of a separate validation set, we employed 5-fold cross-validation on the 500 generated samples during training. Specifically, the dataset was randomly partitioned into 5 subsets of equal size (100 samples each). In each fold, 4 subsets (400 samples) served as the training data, and the remaining 1 subset (100 samples) was used to monitor performance metrics such as phase correlation coefficients for hyperparameter tuning. This process was repeated 5 times, with each subset acting as the validation data exactly once. The average performance across all folds was taken to guide hyperparameter selection, ensuring that the model optimization was based solely on the training data distribution. Meanwhile, a separate test set, consisting of 100 additional samples generated using the same method but not involved in any training or cross-validation steps, was reserved to provide an unbiased final evaluation of the model’s generalization ability.
- Perform backpropagation to compute gradients.
- Update weights using the Adam optimizer in view of its advantage lies in its balance between convergence speed, stability, and parameter adaptability, with low dependence on hyperparameters, enabling it to quickly achieve favorable results in most deep learning tasks. Although in certain scenarios (such as image classification requiring extreme generalization performance), Stochastic Gradient Descent (SGD) combined with fine hyperparameter tuning may perform slightly better, Adam has become the default choice in both industry and academia due to its comprehensive performance.
- Repeat until convergence or max epochs reached.
- Save model weights upon training completion.
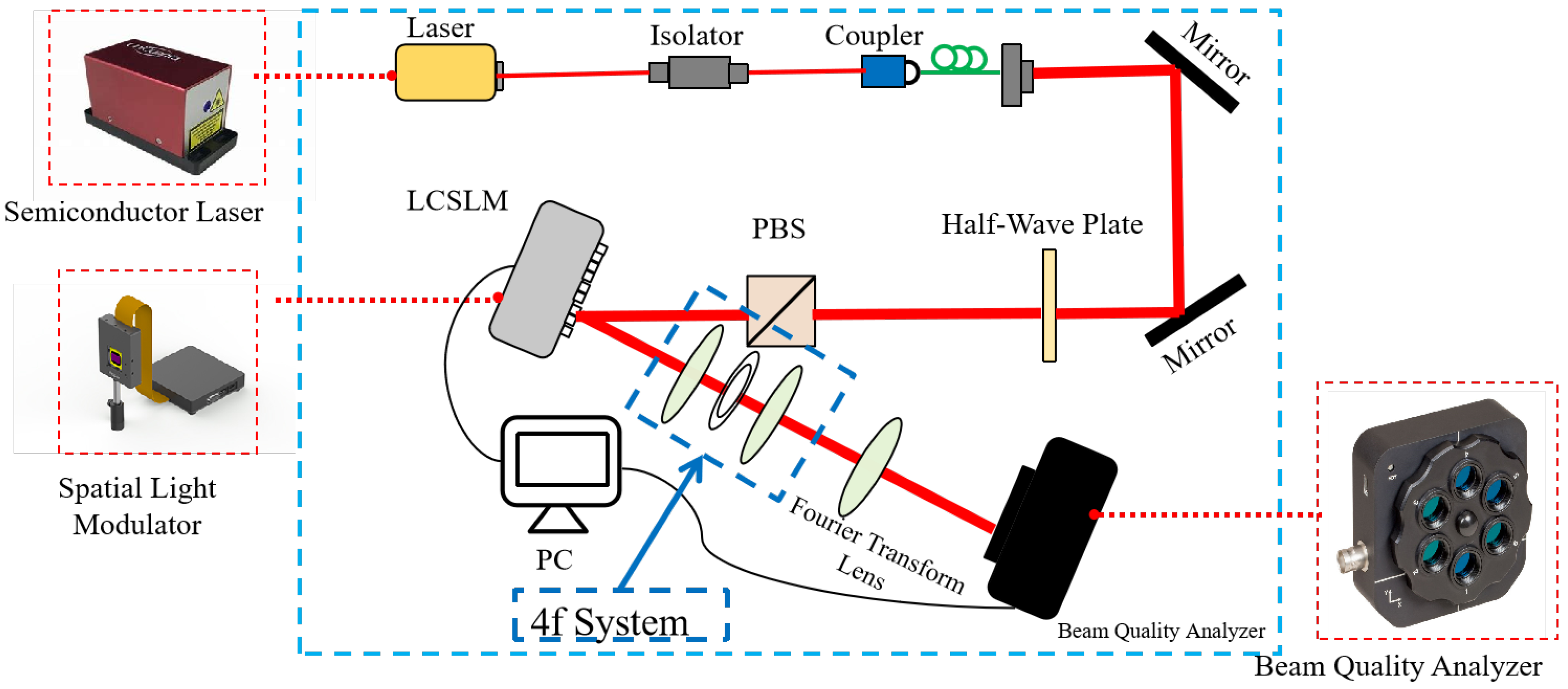
3.3. Optical Setup
3.4. Experimental Procedure
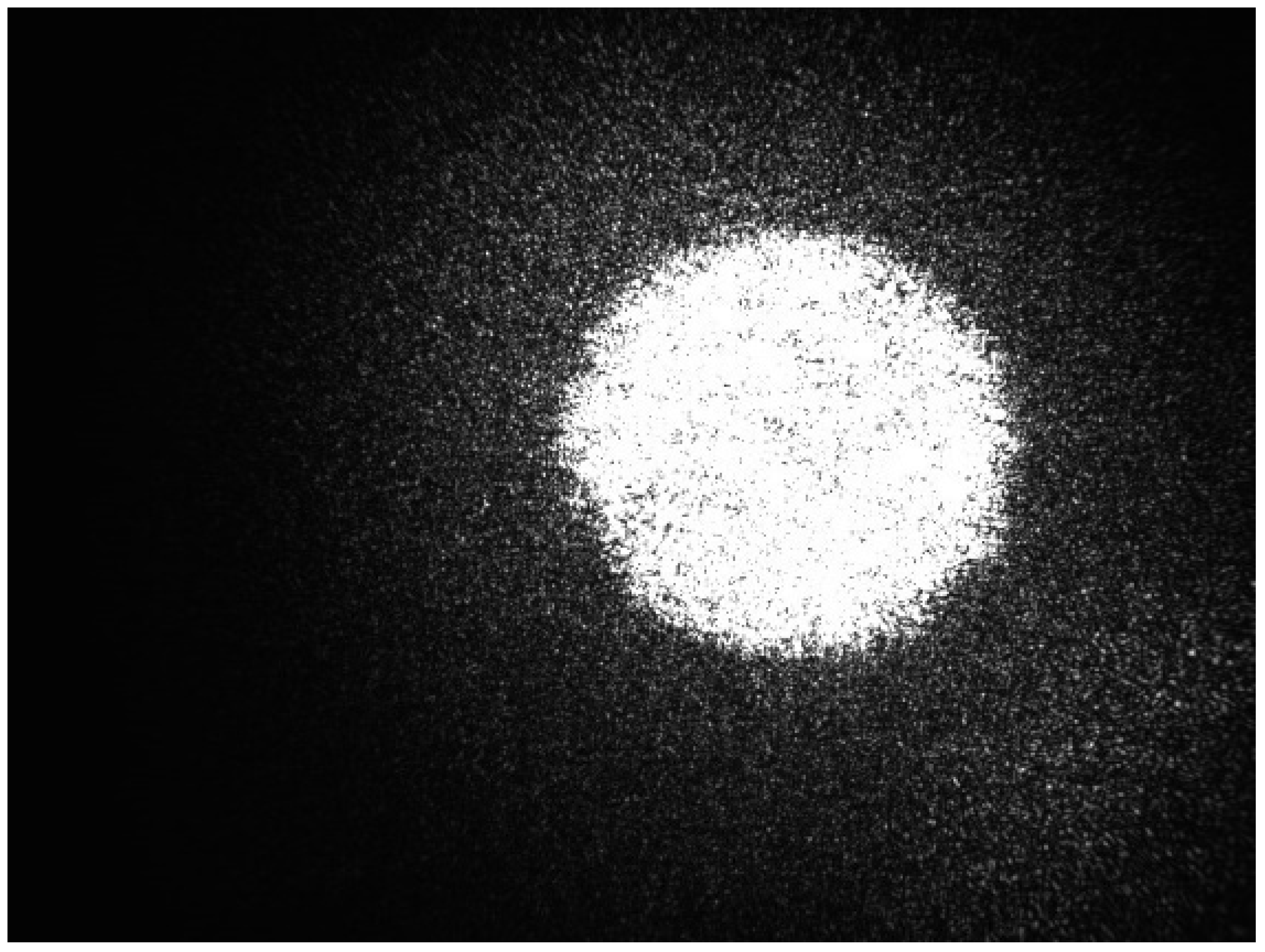
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wei, K.; Xu, Z.; He, Y.; Ma, X.; Heng, X.; Huang, X.; Quan, W.; Ji, W.; Liu, J.; Wang, X.-P. Dmitry Budker and Jiancheng Fang Dark matter search with a resonantly-coupled hybrid spin system. Rep. Prog. Phys. 2025, 88, 057801. [Google Scholar] [CrossRef]
- Dang, H.B.; Maloof, A.C.; Romalis, M.V. Ultra-high sensitivity magnetic field and magnetization measurements with an atomic magnetometer. Appl. Phys. Lett. 2010, 97, 151110. [Google Scholar] [CrossRef]
- Kominis, I.K.; Kornack, T.W.; Allred, J.C.; Romalis, M.V. Dark matter search with a resonantly-coupled hybrid spin system. Nature 2003, 422, 596–599. [Google Scholar] [CrossRef]
- Tian, X.; Bao, B.; Wang, R.; Li, D. An FSM-assisted high-accuracy autonomous magnetic compensation optimization method for dual-channel SERF magnetometers used in weak biomagnetic signal measurement. Sensors 2025, 25, 3690. [Google Scholar] [CrossRef] [PubMed]
- Zhai, Y.; Yue, Z.; Li, L.; Liu, Y. Progress and applications of quantum precision measurement based on SERF effect. Front. Phys. 2022, 10, 969129. [Google Scholar] [CrossRef]
- Shah, V.; Romalis, M.V. Spin-exchange relaxation-free magnetometry using elliptically polarized light. Phys. Rev. A 2009, 80, 013416. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, S.; Liu, Z.; Zhan, D.; Liu, Z.; Li, X.; Zhou, Y.; Lu, J. Optical parameter decoupling and optimization for an elliptically polarized atomic magnetometer. IEEE Trans. Instrum. Meas. 2024, 73, 1500210. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, B.; Li, J.; Li, R.; Zhai, Y. Flow rate estimation based on magnetic particle detection using a miniaturised high-sensitivity OPM. IEEE Trans. Instrum. Meas. 2025, 74, 9518010. [Google Scholar] [CrossRef]
- Zou, S.; Jin, G.; Shi, T.; Zhang, H. Determination of mole fractions in alkali-metal mixtures via collisional broadening from Van der Waals interactions. Measurement 2025, 244, 116544. [Google Scholar] [CrossRef]
- Allred, J.C.; Lyman, R.N.; Kornack, T.W.; Romalis, M.V. High-sensitivity atomic magnetometer unaffected by spin-exchange relaxation. Phys. Rev. Lett. 2002, 89, 130801. [Google Scholar] [CrossRef]
- Wakai, R.T. The atomic magnetometer: A new era in biomagnetism. In Proceedings of the AIP Conference, Baltimore, ML, USA, 15–18 April 2014; pp. 133–136. [Google Scholar]
- Xia, H.; Ben-Amar Baranga, A.; Hoffman, D.; Romalis, M.V. Magnetoencephalography with an atomic magnetometer. Appl. Phys. Lett. 2006, 89, 211104. [Google Scholar] [CrossRef]
- Wyllie, R.; Kauer, M.; Smetana, G.S.; Wakai, R.T.; Walker, T.G. Magnetocardiography with a modular spin-exchange relaxation-free atomic magnetometer array. Phys. Med. Biol. 2012, 57, 2619. [Google Scholar] [CrossRef]
- DeLand, Z.J. Advances in Fetal Magnetocardiography Using SERF Atomic Magnetometers. Ph.D. Thesis, The University of Wisconsin-Madison, Madison, WI, USA, 2017. [Google Scholar]
- Sulai, I.A.; DeLand, Z.J.; Bulatowicz, M.D.; Wahl, C.P.; Wakai, R.T.; Walker, T.G. Characterizing atomic magnetic gradiometers for fetal magnetocardiography. Rev. Sci. Instrum. 2019, 90, 085003. [Google Scholar] [CrossRef]
- Li, X.; Han, B.; Zhang, K.; Liu, Z.; Wang, S.; Yan, Y.; Lu, J. All-optical dual-axis zero-field atomic magnetometer using light-shift modulation. Phys. Rev. Appl. 2024, 21, 014023. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, J.; Xu, X.; Wang, Z.; Zhai, Y. Design and analysis of a high-sensitivity atomic magnetic gradiometer with adjustable baseline. IEEE Trans. Instrum. Meas. 2025, 74, 1501109. [Google Scholar] [CrossRef]
- Tang, J.; Liu, Y.; Wang, Y.; Zhou, B.; Han, B.; Zhai, Y.; Liu, G. Enhancement of bandwidth in spin-exchange relaxation-free (SERF) magnetometers with amplitude-modulated light. Appl. Phys. Lett. 2022, 120, 084001. [Google Scholar] [CrossRef]
- Bell, W.E.; Bloom, A.L. Optical detection of magnetic resonance in alkali metal vapor. Phys. Rev. 1957, 107, 1559–1565. [Google Scholar] [CrossRef]
- Li, R.; Liu, Y.; Cao, L.; Li, S.; Li, J.; Zhai, Y. Parameter optimisation of miniaturised SERF magnetometer below relaxation rate saturation region. Measurement 2023, 214, 112733. [Google Scholar] [CrossRef]
- Li, Z.M.; Wakai, R.T.; Walker, T.G. Research on Optical Frequency Shift Suppression and Beam Uniformity. Chin. J. Lasers 2024, 51, 0312001. [Google Scholar]
- Asphericon. Aspheric Beam Shapers [EB/OL]. Available online: https://www.asphericon.com/en/products/beamtuning/beamshaping (accessed on 25 June 2025).
- Mao, J.Y.; Wang, M.; Wang, Q.T.; Liu, L.R. Laser beam shaping system with a radial birefringent filter. J. Mod. Opt. 2006, 54, 129–136. [Google Scholar]
- Kornack, T.W.; Allred, J.C.; Romalis, M.V. Subfemtotesla atomic magnetometer. Appl. Phys. Lett. 2003, 82, 3498–3500. [Google Scholar]
- Li, Z.M.; Wakai, R.T.; Walker, T.G. Parametric modulation of an atomic magnetometer. Appl. Phys. Lett. 2006, 89, 134105. [Google Scholar] [CrossRef] [PubMed]
- Hamamatsu Photonics. Liquid Crystal on Silicon Spatial Light Modulators (LCoS-SLM) [EB/OL]. Available online: https://lcos-slm.hamamatsu.com/jp/en/learn/about_lcos-slm/comparison.html (accessed on 25 June 2025).
- Gerchberg, R.W.; Saxton, W.O. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Zhang, Y.; Sun, M. Simulated annealing applied to HIO method for phase retrieval. Photonics 2021, 8, 541. [Google Scholar] [CrossRef]
- Taylor, J.R. Phase Retrieval Using a Genetic Algorithm on the Systematic Image-Based Optical Alignment Test Bed; NASA/CR-2003-212397; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2003. [Google Scholar]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef]
- Eglese, R.W. Simulated annealing: A tool for operational research. Eur. J. Oper. Res. 1990, 46, 271–281. [Google Scholar] [CrossRef]
- Ma, W.; Liu, Z.C.; Kudyshev, Z.A.; Boltasseva, A.; Cai, W.S.; Liu, Y.M. Deep learning for the design of photonic structures. Nat. Photonics 2021, 15, 77–90. [Google Scholar] [CrossRef]
- Dawson, R.; O’Dwyer, C.; Irwin, E.; Mrozowski, M.S.; Hunter, D.; Ingleby, S.; Riis, E. Automated Machine Learning Strategies for Multi-Parameter Optimisation of a Caesium-Based Portable Zero-Field Magnetometer. Sensors 2023, 23, 4007. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, Y.; Pei, H.; Lei, X.; Xia, H.; Wang, W. LSA-PINN: A New Method Based on Physics-Informed Neural Network with Lightweight Self-Attention for Solving Modified Bloch Equation. Results Phys. 2024, 61, 107716. [Google Scholar] [CrossRef]
- Babaei, B.; Smith, B.D.; Tretiakov, A.; Narayanan, A.; LeBlanc, L.J. Microwave-Optical Double-Resonance Vector Magnetometry with Warm Rb Atoms. arXiv 2025, arXiv:2507.08791. [Google Scholar]
- Lam, H.S.; Tsang, P.W.M. Invariant classification of holograms of deformable objects based on deep learning. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; IEEE: New York, NY, USA, 2019; pp. 2392–2396. [Google Scholar]
- Eybposh, H.; Caira, N.W.; Atisa, M.; Chakravarthula, P. DeepCGH: 3D computer-generated holography using deep learning. PLoS Comput. Biol. 2020, 16, e1008293. [Google Scholar]
- Tsang, P.W.M.; Lam, H. Holographic vision system based on non-diffractive optical scanning holography and deep learning. In Proceedings of the Holography, Diffractive Optics, and Applications IX, Hangzhou, China, 21–23 October 2019; SPIE: Bellingham, WA, USA, 2019; Volume 11188, pp. 61–66. [Google Scholar]
- Goi, H.; Komuro, K.; Nomura, T. Deep-learning-based binary hologram. Appl. Opt. 2020, 59, 7103–7108. [Google Scholar] [CrossRef]
- Eybposh, M.H.; Caira, N.W.; Chakravarthula, P.; Atisa, M.; Pégard, N.C. High-speed computer-generated holography using convolutional neural networks. In Proceedings of the Optics and the Brain, Virtual, 20–23 April 2020; Optica Publishing Group: Washington, DC, USA, 2020. [Google Scholar]
- Lee, S.J.; Yoon, G.Y.; Go, T. Deep learning-based accurate and rapid tracking of 3D positional information of microparticles using digital holographic microscopy. Exp. Fluids 2019, 60, 170. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Shen, W.; Wu, X.; Zhang, D. Deep learning for optical metrology: A review. Opt. Lasers Eng. 2017, 98, 27–40. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems 25 (NIPS 2012), Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition [EB/OL]. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, L. Speckle noise reduction in optical coherence tomography images using convolutional neural networks. Opt. Lett. 2018, 43, 2651–2654. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
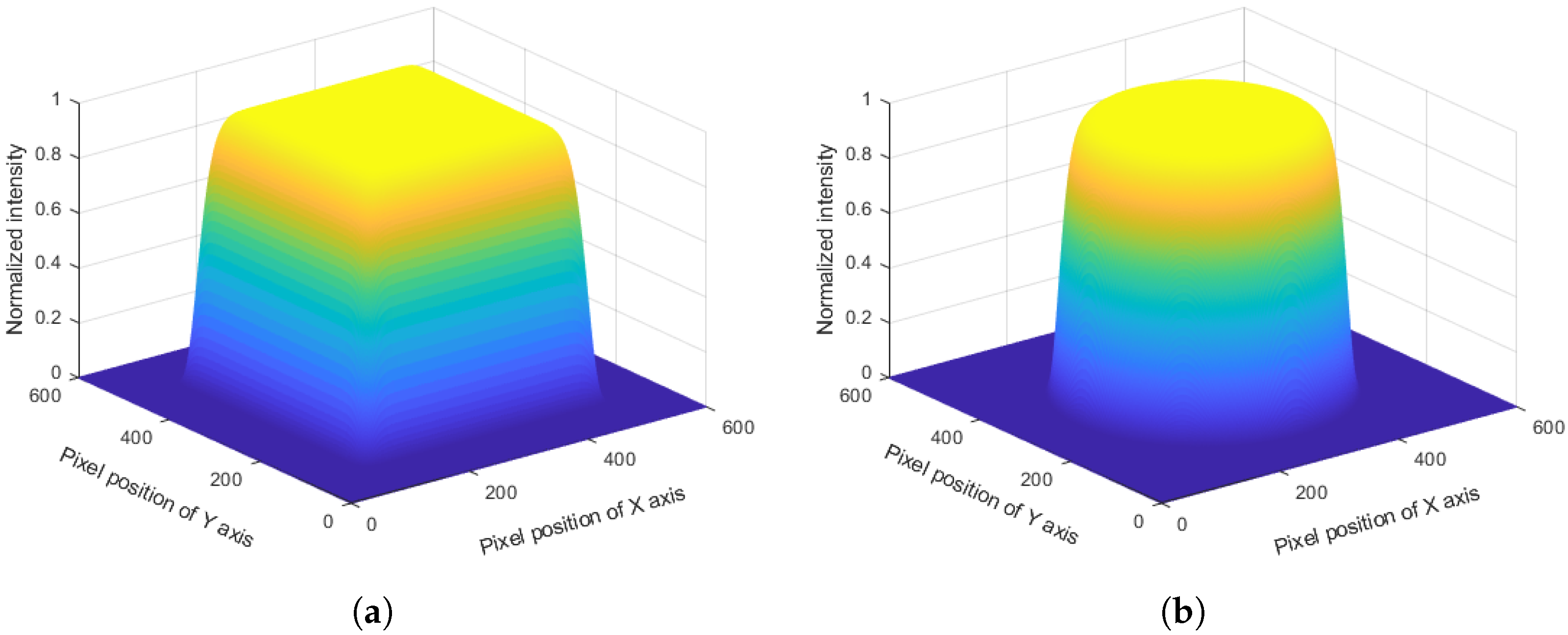


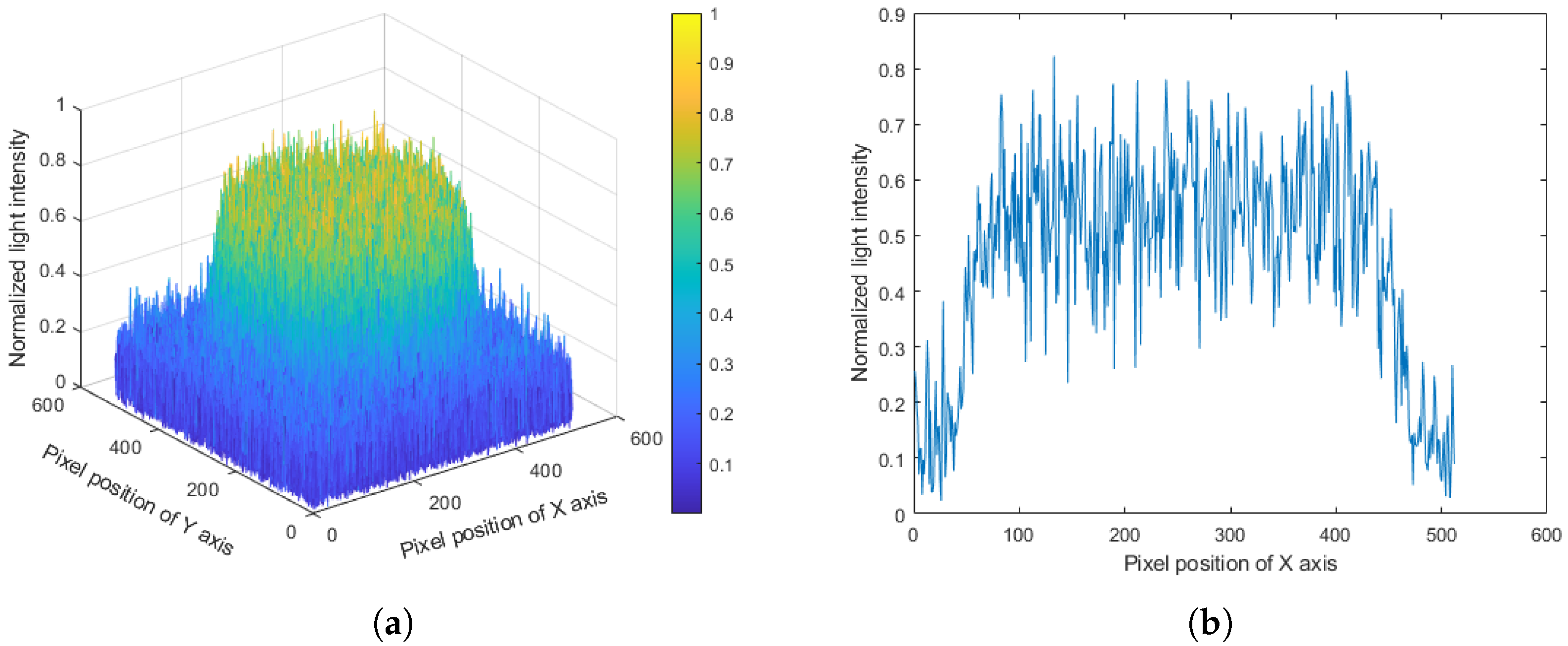




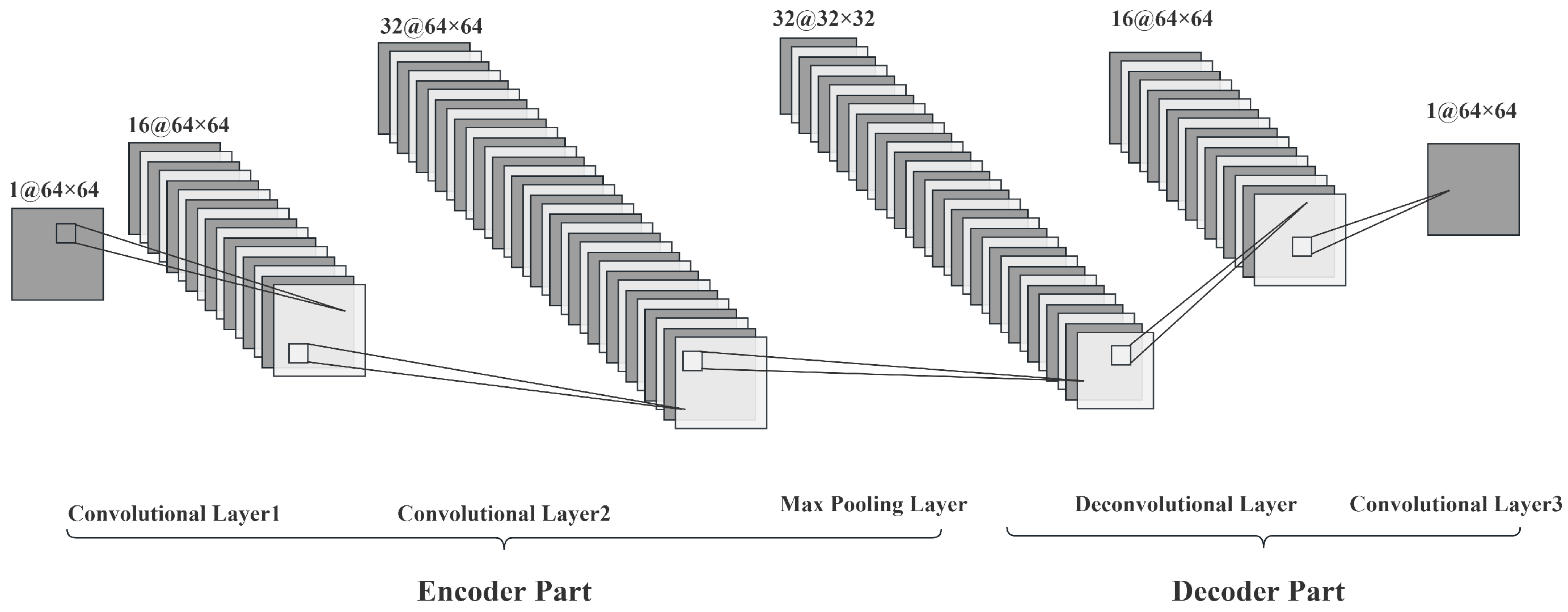
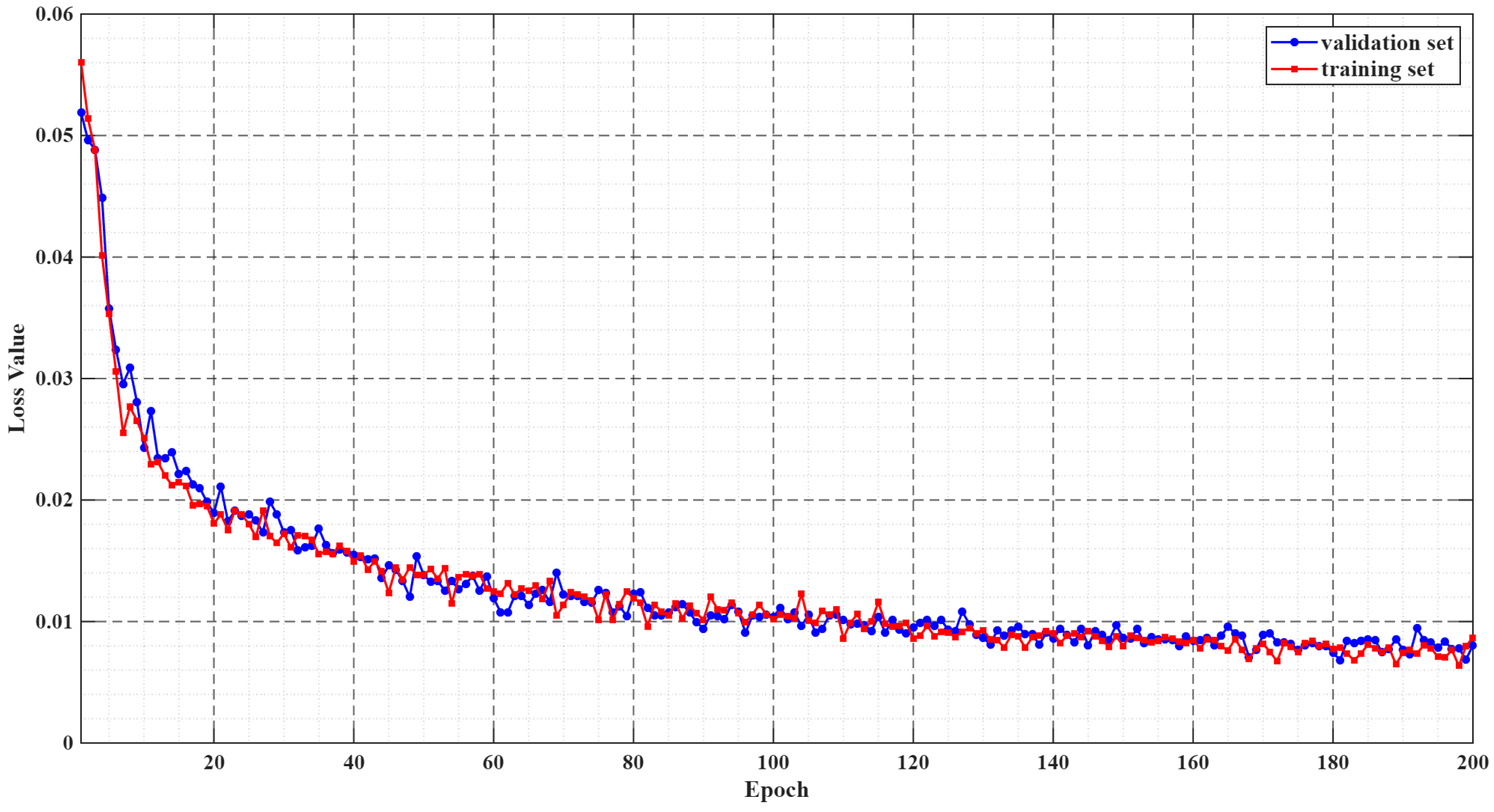




| Algorithm | Mean Squared Error (%) | Peak Non-Uniformity (%) |
|---|---|---|
| GS Algorithm | 35.27 | 20.82 |
| Proposed CNN-GS Hybrid | 18.95 | 7.56 |
| Parameters | Setting |
|---|---|
| convolutional Layer | 3 × 3 |
| max pooling layer | 2 × 2 |
| training epoch | 200 |
| batch−size | 8 |
| learning rate | 0.001 |
| optimization algorithm | Adam |
| loss function | MSE |
| activation function | ReLU |
| regularization | Dropout (0.5) + L2 |
| Before | After | |
|---|---|---|
| Circular Flat-top beam |  |  |
| Square Flat-top beam |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, M.; Liu, Y.; Lu, F.; Cao, Q.; Zhai, Y. A CNN-GS Hybrid Algorithm for Generating Pump Light Fields in Atomic Magnetometers. Photonics 2025, 12, 796. https://doi.org/10.3390/photonics12080796
Song M, Liu Y, Lu F, Cao Q, Zhai Y. A CNN-GS Hybrid Algorithm for Generating Pump Light Fields in Atomic Magnetometers. Photonics. 2025; 12(8):796. https://doi.org/10.3390/photonics12080796
Chicago/Turabian StyleSong, Miaohui, Ying Liu, Feijie Lu, Qian Cao, and Yueyang Zhai. 2025. "A CNN-GS Hybrid Algorithm for Generating Pump Light Fields in Atomic Magnetometers" Photonics 12, no. 8: 796. https://doi.org/10.3390/photonics12080796
APA StyleSong, M., Liu, Y., Lu, F., Cao, Q., & Zhai, Y. (2025). A CNN-GS Hybrid Algorithm for Generating Pump Light Fields in Atomic Magnetometers. Photonics, 12(8), 796. https://doi.org/10.3390/photonics12080796






