Hybrid-Integrated Multi-Lines Optical-Phased-Array Chip
Abstract
1. Introduction
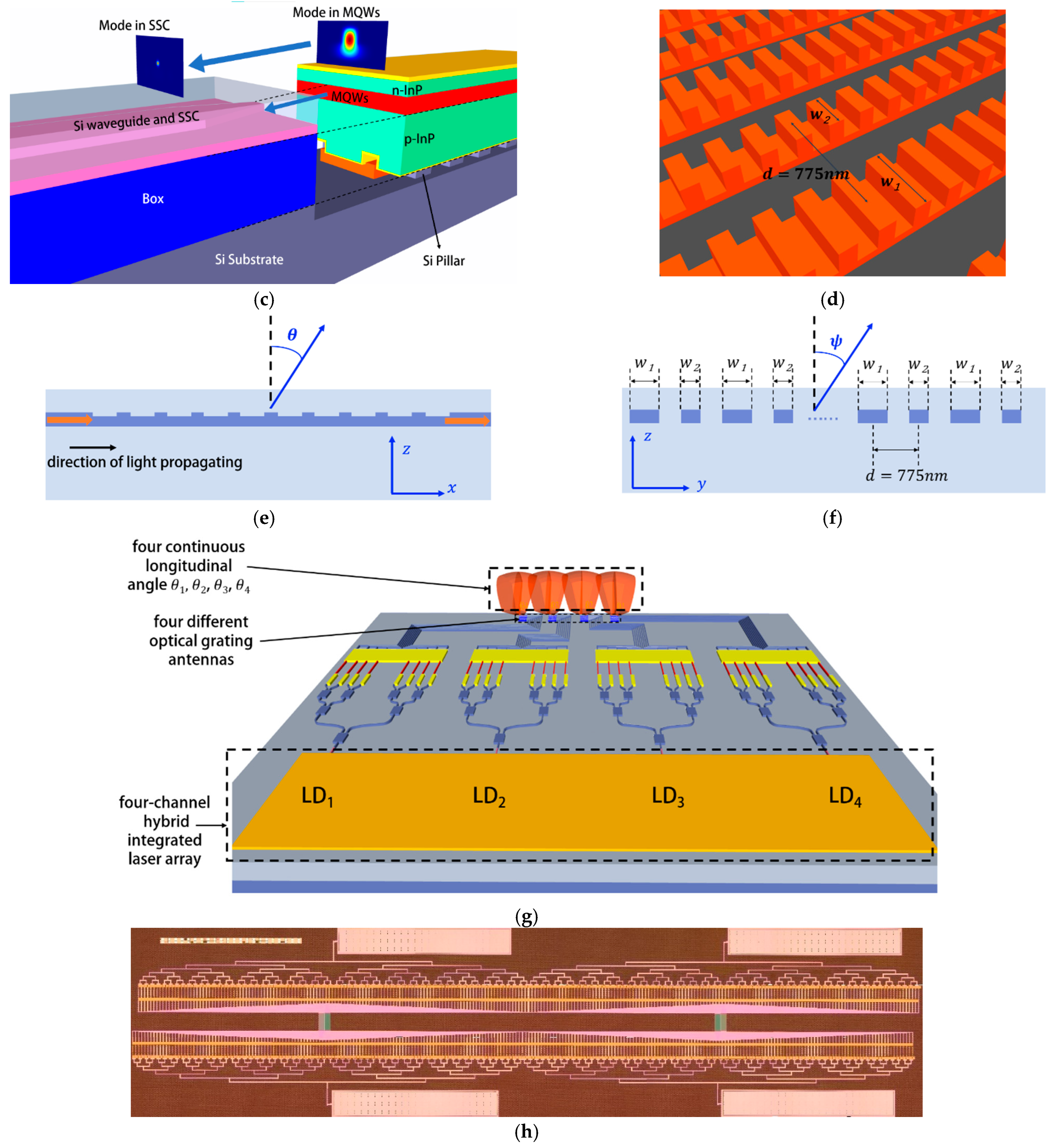
2. Principle and Design
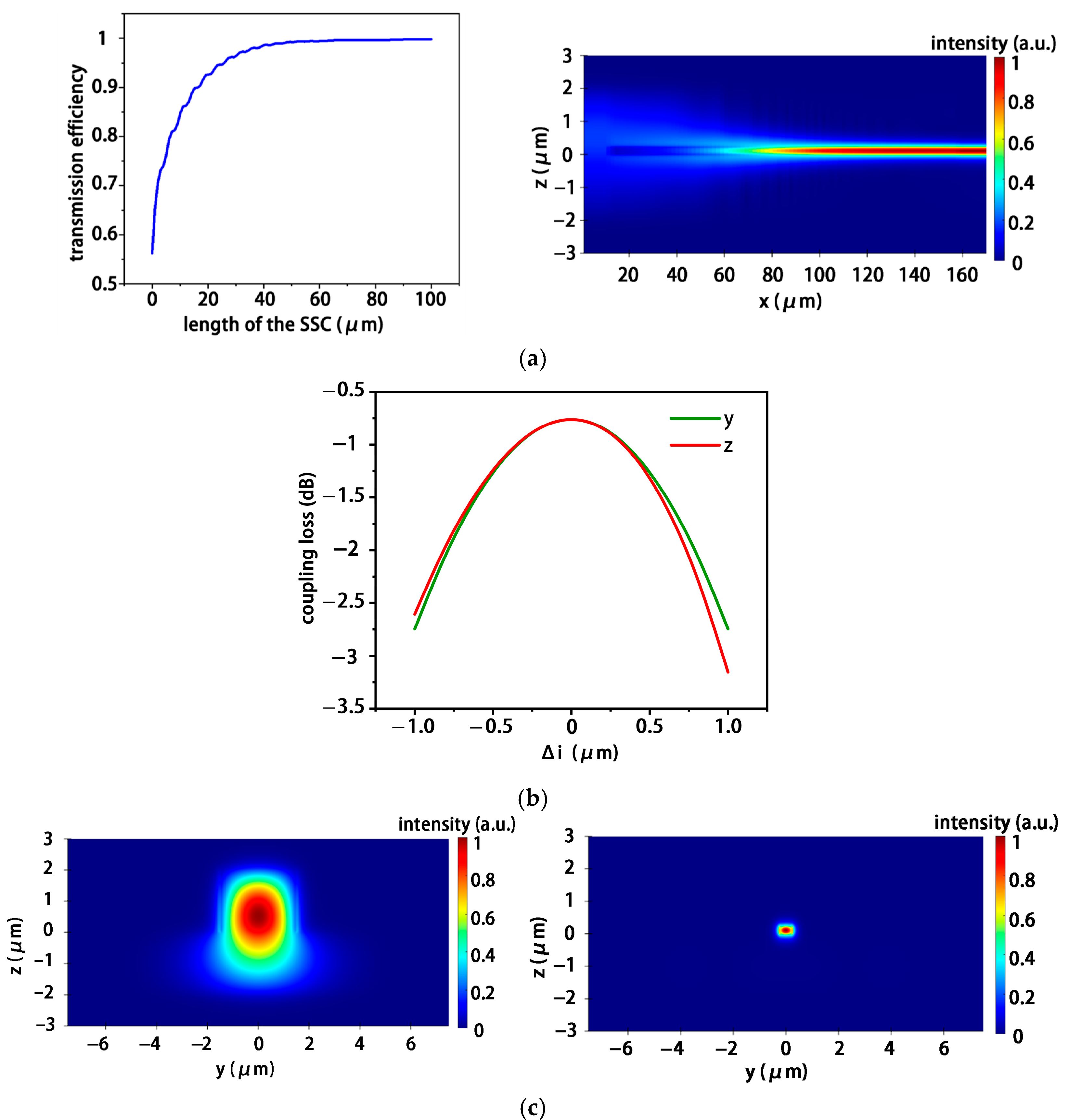
2.1. Semiconductor Laser and SSC
2.2. Vertical Beam-Steering Angle
2.3. Horizontal Beam-Steering Angle
2.4. Far-Field Beamwidth of the Main Lobe
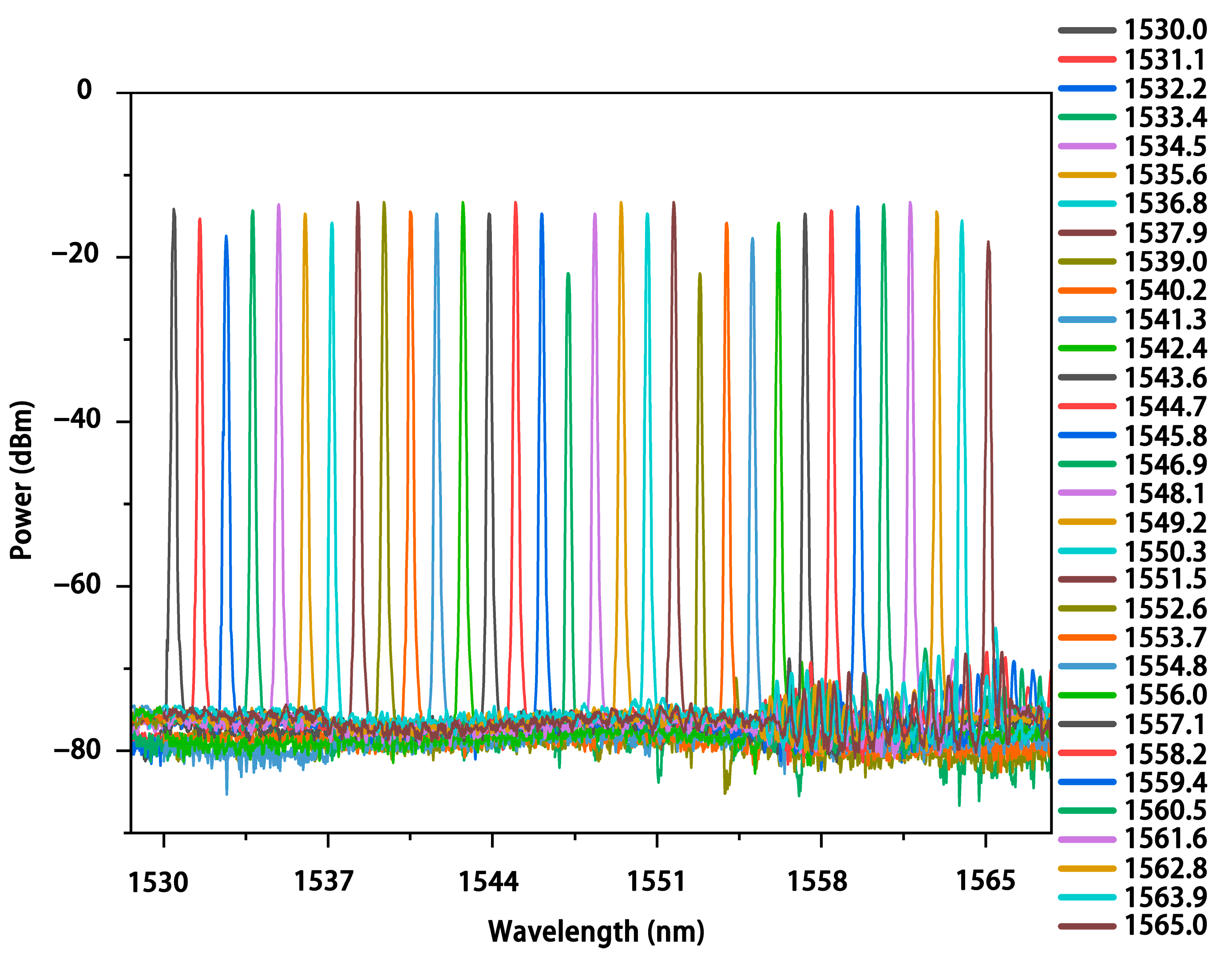
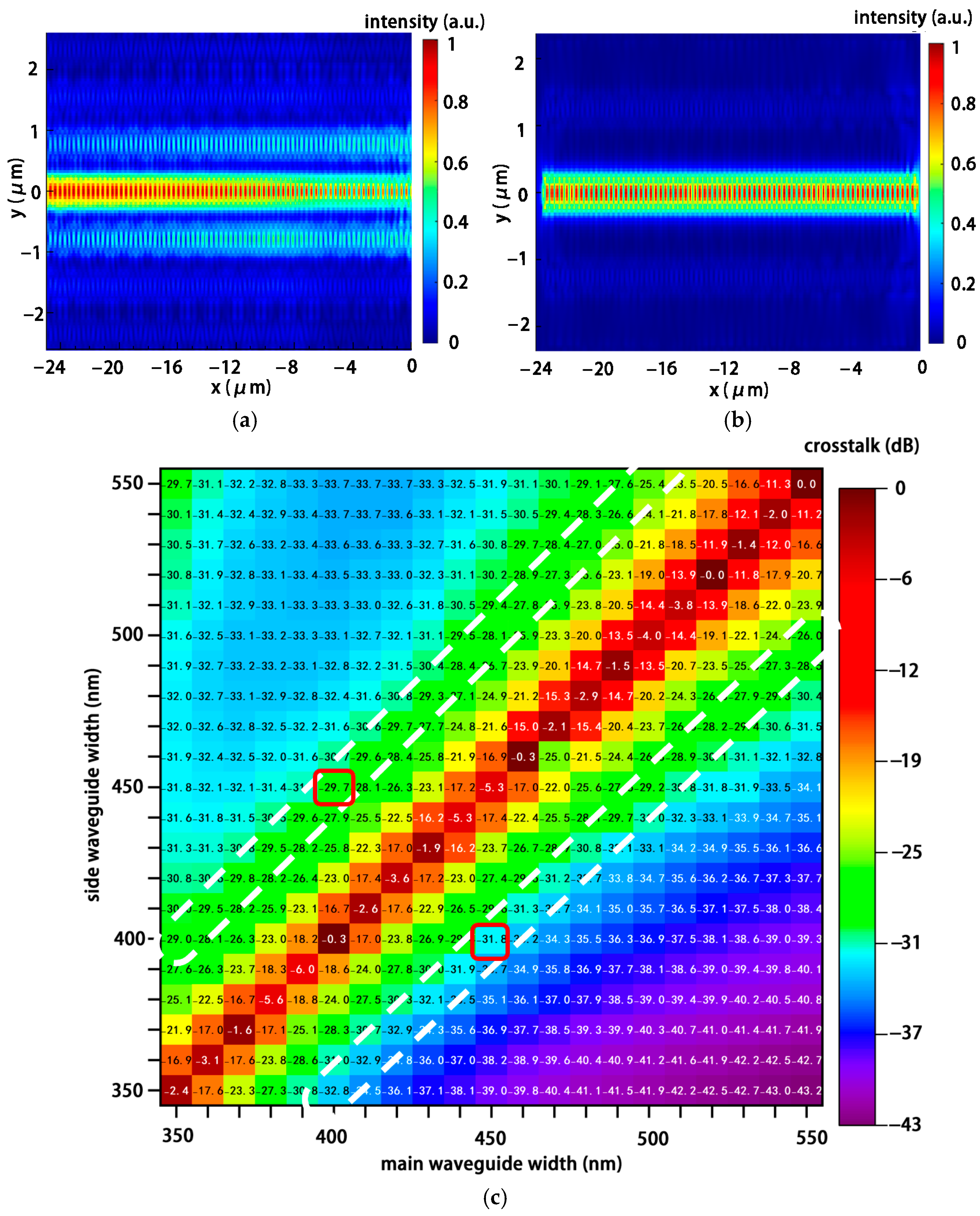
3. Simulation and Results
4. Perspectives and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Ling, Y.-C.; Zhang, K.; Gentry, C.; Sadighi, D.; Whaley, G.; Colosimo, J.; Suni, P.; Yoo, S.J.B. Sub-wavelength-pitch Silicon-Photonic Optical Phased Array for Large Field-of-Regard Coherent Optical Beam Steering. In Proceedings of the 44th Annual European Conference on Optical Communications (ECOC), Rome, Italy, 23–27 September 2018. [Google Scholar]
- Im, C.S.; Bhandari, B.; Lee, K.P.; Kim, S.M.; Oh, M.C.; Lee, S.S. Silicon nitride optical phased array based on a grating antenna enabling wavelength-tuned beam steering. Opt. Express 2020, 28, 3270–3279. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.C.; Zhang, L.X.; Zhang, Q.H.; Zhang, W.F. Si Photonics for Practical LiDAR Solutions. Appl. Sci. 2019, 9, 4225. [Google Scholar] [CrossRef]
- Shuai, Y.Q.; Zhou, Z.P.; Su, H. Toward Practical Optical Phased Arrays through Grating Antenna Engineering. Photonics 2023, 10, 520. [Google Scholar] [CrossRef]
- Vuthea, V.; Toshiyoshi, H. A Design of Risley Scanner for LiDAR Applications. In Proceedings of the International Conference on Optical MEMS and Nanophotonics (OMN), Lausanne, Switzerland, 29 July–2 August 2018; pp. 135–136. [Google Scholar]
- Kamerman, G.W.; Turner, M.D.; Wang, D.; Bai, Y.; Stainsby, A.; Koppal, S.; Strassle, S.; Xie, H. A compact 3D lidar based on an electrothermal two-axis MEMS scanner for small UAV. In Proceedings of the Laser Radar Technology and Applications XXIII, Orlando, FL, USA, 17–18 April 2018. [Google Scholar]
- Kasturi, A.; Milanovic, V.; Atwood, B.H.; Yang, J. UAV-Borne LiDAR with MEMS Mirror-Based Scanning Capability. In Proceedings of the Conference on Laser Radar Technology and Applications XXI, Baltimore, MD, USA, 19–20 April 2016. [Google Scholar]
- Lemmetti, J.; Sorri, N.; Kallioniemi, I.; Melanen, P.; Uusimaa, P. Long-range all-solid-state flash LiDAR sensor for autonomous driving. In Proceedings of the Conference on High-Power Diode Laser Technology XIX, Electronic Network, 6–11 March 2021. [Google Scholar]
- Zhang, C.; Lindner, S.; Antolovic, I.M.; Pavia, J.M.; Wolf, M.; Charbon, E. A 30-frames/s, 252 × 144 SPAD Flash LiDAR with 1728 Dual-Clock 48.8-ps TDCs, and Pixel-Wise Integrated Histogramming. IEEE J. Solid-State Circuit 2019, 54, 1137–1151. [Google Scholar] [CrossRef]
- Jo, S.; Kong, H.J.; Bang, H.; Kim, J.W.; Kim, J.; Choi, S. High resolution three-dimensional flash LIDAR system using a polarization modulating Pockels cell and a micro-polarizer CCD camera. Opt. Express 2016, 24, A1580–A1585. [Google Scholar] [CrossRef]
- Poulton, C.V.; Yaacobi, A.; Cole, D.B.; Byrd, M.J.; Raval, M.; Vermeulen, D.; Watts, M.R. Coherent solid-state LIDAR with silicon photonic optical phased arrays. Opt. Lett. 2017, 42, 4091–4094. [Google Scholar] [CrossRef]
- Nakamura, K.; Narumi, K.; Kikuchi, K.; Inada, Y.; He, S.; Vivien, L. Liquid-crystal tunable optical phased array for LiDAR applications. In Proceedings of the Smart Photonic and Optoelectronic Integrated Circuits XXIII, Online, 6–11 March 2021. [Google Scholar]
- Yoon, J.; Yoon, H.; Kim, J.Y.; Kim, J.; Kang, G.M.; Kwon, N.H.; Kurt, H.; Park, H.H. Demonstration of high-accuracy 3D imaging using a Si optical phased array with a tunable radiator. Opt. Express 2023, 31, 9935–9944. [Google Scholar] [CrossRef]
- Zhao, S.; Lian, D.X.; Chen, J.Y.; Dai, D.X.; Shi, Y.C. Polarization multiplexing silicon photonic optical phased array with a wide scanning range. Opt. Lett. 2023, 48, 6092–6095. [Google Scholar] [CrossRef]
- Desantis, D.M.; Mazur, B.M.; Notaros, M.; Notaros, J. Multi-beam solid-state LiDAR using star-coupler-based optical phased arrays. Opt. Express 2024, 32, 36656–36673. [Google Scholar] [CrossRef]
- Chen, R.X.; Shu, H.W.; Shen, B.T.; Chang, L.; Xie, W.Q.; Liao, W.C.; Tao, Z.H.; Bowers, J.E.; Wang, X.J. Breaking the temporal and frequency congestion of LiDAR by parallel chaos. Nat. Photonics 2023, 17, 306–314. [Google Scholar] [CrossRef]
- Doylend, J.K.; Heck, M.J.R.; Bovington, J.T.; Peters, J.D.; Coldren, L.A.; Bowers, J.E. Two-dimensional free-space beam steering with an optical phased array on silicon-on-insulator. Opt. Express 2011, 19, 21595–21604. [Google Scholar] [CrossRef] [PubMed]
- Van Acoleyen, K.; Bogaerts, W.; Jágerská, J.; Le Thomas, N.; Houdré, R.; Baets, R. Off-chip beam steering with a one-dimensional optical phased array on silicon-on-insulator. Opt. Lett. 2009, 34, 1477–1479. [Google Scholar] [CrossRef]
- Hulme, J.C.; Doylend, J.K.; Heck, M.J.R.; Peters, J.D.; Davenport, M.L.; Bovington, J.T.; Coldren, L.A.; Bowers, J.E. Fully integrated hybrid silicon two dimensional beam scanner. Opt. Express 2015, 23, 5861–5874. [Google Scholar] [CrossRef] [PubMed]
- Misugi, Y.; Okayama, H.; Kita, T. Compact and Low Power-Consumption Solid-State Two-Dimensional Beam Scanner Integrating a Passive Optical Phased Array and Hybrid Wavelength-Tunable Laser Diode. J. Light. Technol. 2023, 41, 3505–3512. [Google Scholar] [CrossRef]
- Liang, D.; Li, W.L.; Wang, X.B.; Zhao, X.; Guo, Z.C.; Han, X.E.; Chen, J.Y.; Dai, D.X.; Shi, Y.C. Grating lobe-free silicon optical phased array with periodically bending modulation of dense antennas. Opt. Express 2023, 31, 11423–11430. [Google Scholar] [CrossRef]
- Chen, J.Y.; Li, W.L.; Lian, D.X.; Zhao, S.; Dai, D.X.; Shi, Y.C. Coaxial transceiving LiDAR based on a silicon photonic optical phased array. Opt. Lett. 2024, 49, 3424–3427. [Google Scholar] [CrossRef]
- Chung, S.; Abediasl, H.; Hashemi, H. A Monolithically Integrated Large-Scale Optical Phased Array in Silicon-on-Insulator CMOS. IEEE J. Solid-State Circuit 2018, 53, 275–296. [Google Scholar] [CrossRef]
- Kwong, D.; Hosseini, A.; Zhang, Y.; Chen, R.T. 1 × 12 Unequally spaced waveguide array for actively tuned optical phased array on a silicon nanomembrane. Appl. Phys. Lett. 2011, 99, 051104. [Google Scholar] [CrossRef]
- Hutchison, D.N.; Sun, J.; Doylend, J.K.; Kumar, R.; Heck, J.; Kim, W.; Phare, C.T.; Feshali, A.; Rong, H.S. High-resolution aliasing-free optical beam steering. Optica 2016, 3, 887–890. [Google Scholar] [CrossRef]
- Phare, C.T.; Shin, M.C.; Sharma, J.; Ahasan, S.; Krishnaswamy, H.; Lipson, M. Silicon Optical Phased Array with Grating Lobe-Free Beam Formation over 180 Degree Field of View. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 13–18 May 2018. [Google Scholar]
- Wang, M.; Dong, F.; Meng, R.; Ma, P.; Liu, J.; Wang, H.; Wang, X.; Zheng, W. Eight-channel hybrid-integrated laser array with 100 GHz channel spacing. Electron. Lett. 2020, 56, 1032–1093. [Google Scholar] [CrossRef]
- Du, F.; Xu, Y.; Li, J.; Wang, H.; Zheng, W. Quasi-continuous tunable semiconductor laser based on the gain-lever effect with full C-band coverage fabricated by standard lithography. Appl. Opt. 2022, 61, 7343–7348. [Google Scholar] [CrossRef]
- Wang, M.J.; Liu, W.Z.; Xu, Y.B.; Fu, T.; Chen, J.X.; Zheng, W.H. Single-chip hybrid integrated silicon photonics transmitter based on passive alignment. Opt. Lett. 2022, 47, 1709–1712. [Google Scholar] [CrossRef] [PubMed]
- Song, W.W.; Gatdula, R.; Abbaslou, S.; Lu, M.; Stein, A.; Lai, W.Y.C.; Provine, J.; Pease, R.F.W.; Christodoulides, D.N.; Jiang, W. High-density waveguide superlattices with low crosstalk. Nat. Commun. 2015, 6, 7027. [Google Scholar] [CrossRef]



| Time | Whether Laser Is Integrated | Tuning Efficiency | Wavelengths | Approach | Literature | ||
|---|---|---|---|---|---|---|---|
| 2023 | No | 60° | 24.8° | 0.31°/nm | 1520 nm~1600 nm | Polarization switch | [14] |
| 2024 | No | 40° | 8° | 0.133°/nm | 1540 nm~1600 nm | Coaxial transceiver | [22] |
| 2023 | Yes | 44.2° | 13.7° | 0.137°/nm | 1500 nm~1600 nm | External cavity | [20] |
| 2023 | No | 120° | - | - | 1550 nm | Bent waveguide arrays | [21] |
| 2025 | Yes | 180° | 39.6° | 1.13°/nm | 1530 nm~1565 nm | Multi-lines lasers and antennas | This work |
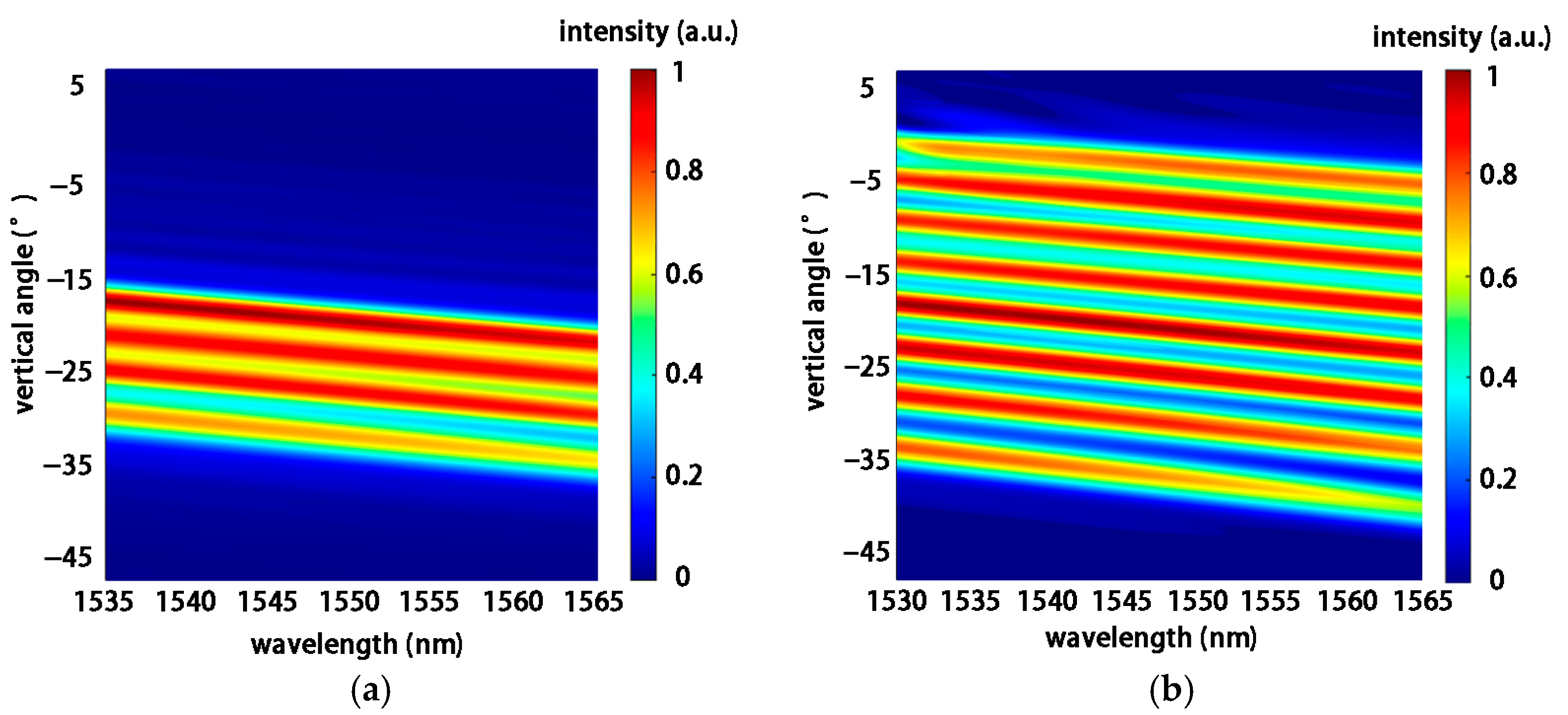
| Period Duty Cycle | 475 nm/ 60% | 500 nm/ 30% | 510 nm/ 30% | 500 nm/ 70% | ||||
| −29.6° | −24.8° | −21.1° | −17.4° | |||||
| −34.6° | −29.7° | −25.7° | −21.9° | |||||
| Single range | 5.0° | 4.9° | 4.6° | 4.5° | ||||
| Intensity | 0.75 | 0.86 | 0.85 | 0.97 | ||||
| Total range | 17.2° | |||||||
| Total overlap Angle | 1.88° | |||||||
| Tuning efficiency | 0.57°/nm | |||||||
| (a) | ||||||||
| Period/ Duty cycle | 476 nm/ 30% | 471 nm/ 70% | 483 nm/ 70% | 495 nm/ 70% | 529 nm/ 30% | 527 nm/ 60% | 541 nm/ 60% | 562 nm/ 50% |
| −33.7° | −28.0° | −22.9° | −18.1° | −13.6° | −9.1° | −4.6° | −0.7° | |
| −40.3° | −34.0° | −28.5° | −23.4° | −18.6° | −13.9° | −9.4° | −5.2° | |
| Single range | 6.6° | 6.0° | 5.6° | 5.3° | 5.0° | 4.8° | 4.8° | 4.5° |
| intensity | 0.75 | 0.80 | 0.85 | 0.89 | 0.80 | 0.76 | 0.79 | 0.71 |
| Total range | 39.6° | |||||||
| Total overlap Angle | 3.0° | |||||||
| Tuning efficiency | 1.13°/nm | |||||||
| (b) | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Wang, M.; Chen, J.; Yi, Z.; Si, J.; Zheng, W. Hybrid-Integrated Multi-Lines Optical-Phased-Array Chip. Photonics 2025, 12, 699. https://doi.org/10.3390/photonics12070699
Zhou S, Wang M, Chen J, Yi Z, Si J, Zheng W. Hybrid-Integrated Multi-Lines Optical-Phased-Array Chip. Photonics. 2025; 12(7):699. https://doi.org/10.3390/photonics12070699
Chicago/Turabian StyleZhou, Shengmin, Mingjin Wang, Jingxuan Chen, Zhaozheng Yi, Jiahao Si, and Wanhua Zheng. 2025. "Hybrid-Integrated Multi-Lines Optical-Phased-Array Chip" Photonics 12, no. 7: 699. https://doi.org/10.3390/photonics12070699
APA StyleZhou, S., Wang, M., Chen, J., Yi, Z., Si, J., & Zheng, W. (2025). Hybrid-Integrated Multi-Lines Optical-Phased-Array Chip. Photonics, 12(7), 699. https://doi.org/10.3390/photonics12070699




