Design of Eye Models for Quantitative Analysis of Interactions Between Ocular Aberrations and Intraocular Scattering

Abstract

Based on the widely used Gullstrand–Le Grand eye model, a scattering individual eye model was constructed with Zemax, which has individual ocular wavefront aberration and the scattering particles distributed in the eye. There are three main steps to build the model. Firstly, the Gullstand-Le Grand eye model was constructed, and converted into a non-sequential model. The axial lengths of all ocular components, and the corneal curvatures were input into the optical model. Secondly, a high-order aspheric surface-Zernike Fringe Sag surface was chosen to fit the wavefront aberrations measured with the ocular wavefront aberrometer. Thirdly, an embedded scattering lens within the crystalline lens was developed, of which parameters of scattering particles can be selected flexibly. The scattering individual eye model can be used to quantitatively investigate interaction between ocular aberrations and scattering light on retina image quality. The results demonstrated that when scattering particles were uniformly distributed across the optical pupil, MTFs at all spatial frequencies decreased proportionally with increasing particle density, independent of aberrations. When scattering particles were located in regions with smaller wavefront aberrations, the combined effect of scattering and aberrations synergistically degraded retinal image quality. In contrast, when particles were concentrated in zones of larger aberrations, the scattered light could partially compensate for the aberrational effects, leading to improved optical performance

1. Introduction

Wavefront aberrations and intraocular scattering are two critical factors governing the optical performance of the human eye. Since the introduction of the Hartmann–Shack wavefront sensor in 1994 [1], ocular aberrations have been extensively studied [2], with hundreds of annual publications elucidating their mechanisms and clinical significance. Low-order aberrations (LOAs) have a significant impact on visual acuity but can be effectively corrected through spectacles or refractive surgery. High-order aberrations (HOAs) are difficult to correct due to their diverse types and complex nature. After LOA correction, HOAs and intraocular scattering emerge as dominant factors compromising visual quality [3], making their investigation both theoretically meaningful and clinically valuable.

Intraocular scattering arises from light interactions with microscopic intraocular structures, such as free-floating cellular debris or imperfections in the eye [3]. In general eyes, this phenomenon is dominated by Mie scattering, attributable to particles with dimensions on the order of micrometers [4]. Scattering can be classified into two modalities: forward scattering creates a veil-like glare that degrades retinal image contrast, while backward scattering reduces retinal illuminance by attenuating incident light intensity [5].

Notably, both wavefront aberrations and intraocular scattering affect retinal imaging. While aberrations predominantly distort foveal imaging, scattering effects extend across broader retinal regions, potentially compromising the entire visual field [6]. Numerous studies have explored the effects of these factors on vision. Kamiya et al. [7] found a significant correlation between contrast sensitivity and intraocular scattering in 201 myopic eyes. Arias et al. also identified a strong correlation between peripheral vision and forward scattering [8]. Nagra et al. observed that intraocular scattering in young individuals increases with refractive error [5]. In addition, Bueno et al. demonstrated that contrast sensitivity across all spatial frequencies decreased as intraocular scattering increased [9]. However, Hiraoka et al. found that visual acuity was unrelated to light scattering based on clinical data [10]. Zhao et al., using an adaptive double-path system to measure the effects of intraocular scattering and wavefront aberrations on contrast sensitivity, discovered a compensatory mechanism between these two factors in visual quality [6]. The notable discrepancies in findings across studies can largely be attributed to differences in methodology, sample size, and measurement accuracy [4]. Therefore, designing a consistent, reproducible, and examiner-independent methodology is essential for accurately studying the joint effects of intraocular scattering and wavefront aberrations [4].

Eye models have become indispensable tools for probing ocular optics for their high consistency, accuracy, and repeatability. Over ten models have been developed to date, enabling breakthroughs in aberration characterization, visual simulation, and corrective lens design. The Gullstrand–Le Grand eye model accurately describes paraxial optical properties, while the Navarro model‌ characterizes spherical and coma aberrations. The ‌Liou-Brennan model‌ incorporates statistical data from real human eyes and accounts for chromatic aberrations. The Arizona eye model‌ demonstrates the accommodation of the human eye. Many studies have introduced wavefront aberrations into classic eye models to analyze the effects of different aberrations on visual quality [11,12], ‌yielding results consistent with clinical tests.‌ DeHoog et al. adapted the Arizona eye model to create a pseudophakic eye with surface scattering [13]. Similarly, William D. presented an advanced human eye model integrating corneal topography, gradient refractive indices, and surface scattering [14]. In prior work, we incorporated surface scattering and higher-order aberrations together into the ‌Gullstrand–Le Grand eye model‌ ‌to investigate the relationship between surface scattering and higher-order aberrations [15].‌ Here, we advance this framework by introducing intraocular scattering particles and HOAs, enabling systematic evaluation of their combined impact on visual quality.

2. Method

2.1. Construction of the Scattering Individual Eye Model

Since this study focuses on paraxial optical properties, a complex initial model was unnecessary. The Gullstrand–Le Grand eye model was selected as the baseline, with the addition of Abbe numbers to account for assessing polychromatic optical quality. The parameters are summarized in

Table 1. Gullstrand–Le Grand eye model.

Surface	Material	Radius (mm)	Thickness (mm)	Refractive Index	Abbe Number
Anterior Cornea	cornea	7.8	0.5	1.376	52
Posterior cornea	aqueous	6.5	3.16	1.336	55
Anterior lens	Lens	12	4.2	1.42	46
Posterior lens	vitreous	−6	16.7	1.336	58
Retina	-	−12.5	-	-

.

Figure 1 illustrates the procedural workflow for constructing the individual scattering eye model, and the detailed steps are described below:

(1)

The Gullstrand–Le Grand eye model was constructed as an initial model, and then the anterior and posterior corneal radii of curvature, corneal thickness, anterior chamber depth, lens, and vitreous thicknesses were replaced with clinically measured values. Click “file” button, and then click “convert to NSC Group” button to convert the eye model into a non-sequential mode.

(2)

The non-sequential mode lacked a pupil. Therefore, a stop plane was introduced anterior to the non-sequential components, with a thickness of −3.6 mm to align it with the original pupil plane, as illustrated in Figure 2.

(3)

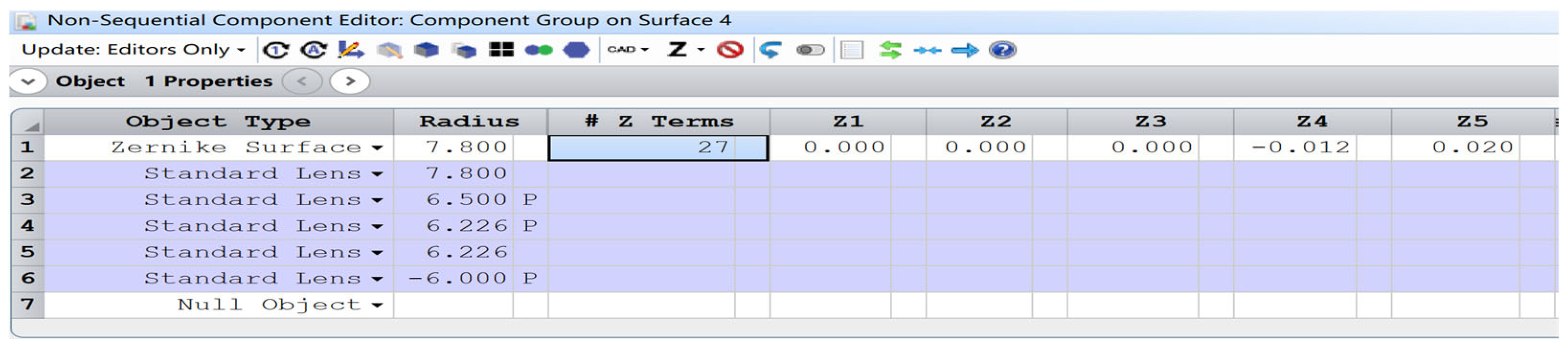
The anterior corneal surface was modeled as a Zernike surface, with the Zernike coefficients designated as optimization variables. Clinically measured wavefront aberrations of the objects were employed as the optimization target, and the surface coefficients were subsequently derived after optimization, shown in Figure 3.

(4)

An embedded scattering lens within the crystalline lens (standard lens No. 5 in Figure 3) is developed, maintaining identical radii of curvature and thickness to those of the crystalline lens. Adjustable parameters include the density of scattering particles, the size, and the central position of the scattering lens to simulate light scattering in the eye.

Through these procedures, a scattering individual eye model is obtained. If necessary, repeat step 4, and multiple embedded scattering lenses can be added to simulate more complex scattering distributions. It serves as an effective tool to analyze the individual and combined effects of scattering particles and wavefront aberrations on the optical quality of the human eye.

2.2. Wavefront Aberrations and Scattering Particles

Wavefront aberrations were measured using an iTrace wavefront aberrometer (Tracey Technology, Houston, TX, USA). Before the measurement, volunteers’ eyes were dilated in a dark room for 5 min to ensure the pupil was large enough.

The thickness of intraocular components was measured using A-scan ultrasonography and the Corneal curvatures were acquired from a Pentacam system (Oculus, Wetzlar, Germany).

The density of scattering particles in the human eye, as reported in previous studies, ranges from several dozen to several million per cubic centimeter [16,17]. In this study, the density was capped at less than 3 million/cm³. Other parameters, such as a refractive index of 1.40 and an average particle diameter of 2.13 µm, were based on literature averages [16,17].

2.3. MTF Calculation

In optics, MTF is a standard metric for evaluating the optical quality of the human eye for it is directly correlated with the perceived image quality [17]. This study utilized Zemax software (model:2022R2.02) for MTF calculations, employing a photopic light source provided by the software. The MTF was computed by navigating to Analyze and then Geometric MTF in the menu bar, which displayed the MTF output window. By enabling the Scatter Rays option in the Settings, the MTF curve incorporating light scattering and wavefront aberrations was generated.

3. Results

3.1. Eye Model

Table 2. Optical parameters of the samples.

Eye			Zernike Coefficients (µm)
Number	Visual Acuity	HOA/µm	Z7	Z8	Z9	Z10	Z11	Z12
1	5.2	0.41	−0.045	0.046	−0.177	−0.104	0.019	0.01
2	5.8	0.53	−0.013	−0.073	0.001	−0.072	−0.047	−0.094
3	4.8	0.61	−0.025	−0.037	−0.203	−0.027	0.074	−0.059

summarizes the clinically measured optical parameters of three objects. These eyes had visual acuities of 1.5, 1.0, and 0.6, respectively, all being emmetropic, with axial lengths of 24.33 mm, 24.39 mm, and 24.40 mm. All participants signed an informed consent form. The study was conducted in accordance with the Declaration of Helsinki and was authorized by the Ethics Review Committee of Tianjin Eye Hospital (No: 2023091066). The wavefront aberrations of three subjects were measured and are presented in

Table 3. Partial Zernike coefficients of the ocular wavefront aberrations.

Eye	Cornea			Lens			Anterior Chamber Depth	Vitreous Chamber Depth
	Anterior Radius	Posterior Radius	Thickness	Anterior Radius	Posterior Radius	Thickness
1	7.80	6.40	0.54	10.20	−6.0	4.10	3.25	16.50
2	7.75	6.30	0.52	9.80	−6.2	3.91	3.10	16.80
3	7.65	6.50	0.56	9.60	−6.2	4.14	3.40	16.30

.

The anterior corneal surface was optimized to match the total ocular aberrations, yielding the Zernike coefficients of the corneal surface as listed in

Table 4. Partial Zernike coefficients of the corneal surface.

Eye	Zernike Coefficients (µm)
	Z7	Z8	Z9	Z10	Z11	Z12
1	0.223	−0.109	0.012	−0.122	0.025	0.005
2	−0.187	0.048	0.02	−0.056	0.025	0.108
3	0.021	0.18	−0.026	−0.02	0.027	0.241

.

The distributions of scattering particles in the real eye are complex [11]. Therefore, three typical distributions were investigated: uniform distribution across the entire wavefront, within regions of small aberrations, and within regions of large aberrations. When scattering occurred in regions of large or small aberrations, the scattering area occupies 1/9 of the pupil. Figure 4 shows the wavefront aberrations corresponding to three eyes.

The novel eye model was established to calculate the MTFs with different scattering particles and wavefront aberrations. Figure 5a shows the cross-sectional schematic of the eye model, while Figure 5b,c present the corresponding MTF curves under scattering and non-scattering conditions, respectively.

3.2. MTF with Uniform Scattering Particles

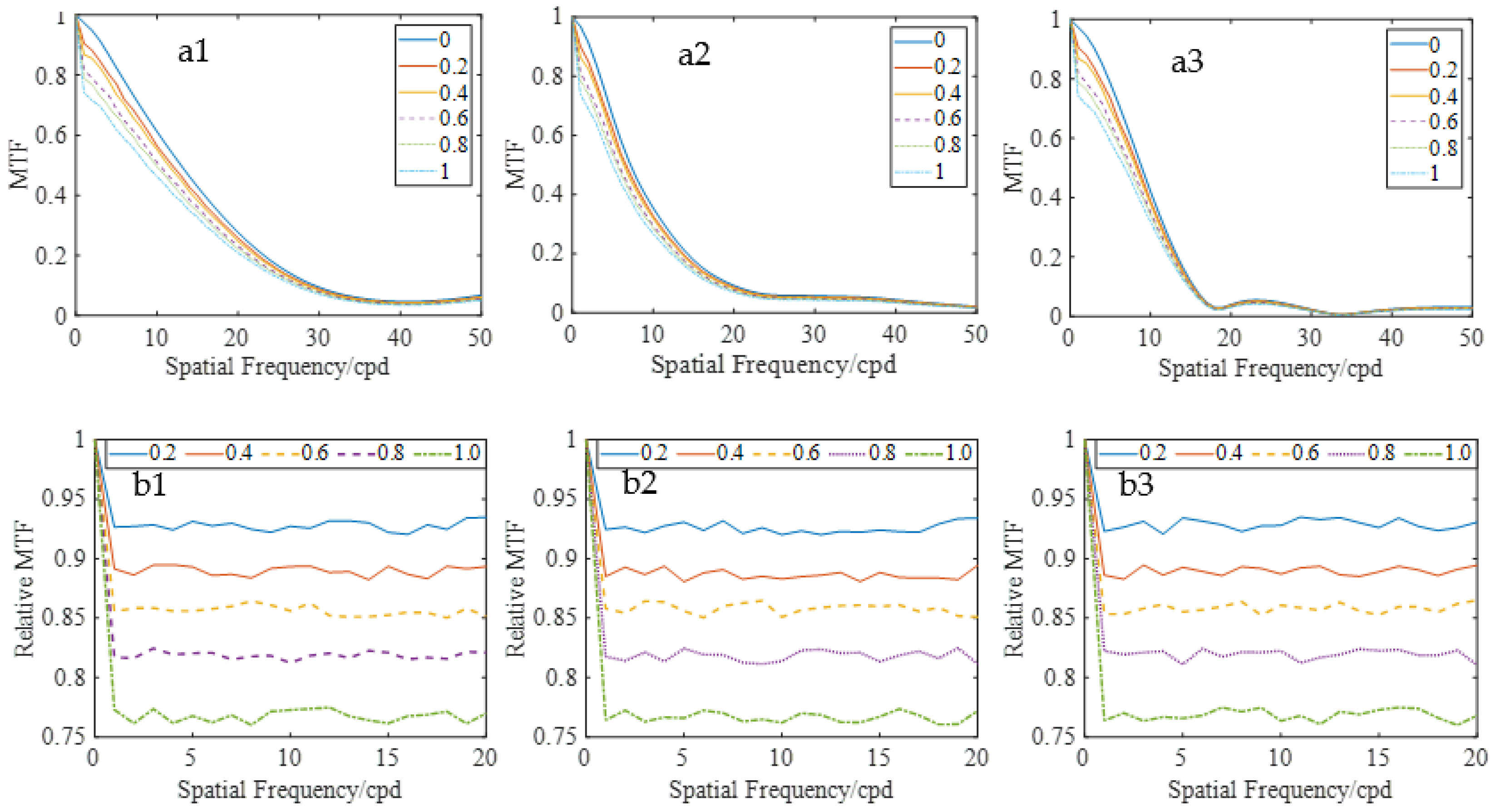
Figure 6(a1–a3) displays the MTF curves for three eyes with different densities of scattering particles, which were uniformly distributed across the pupil. The MTF decreased as the density of scattering particles and spatial frequencies increased. For a clearer characterization of scattering effects, the analysis focused on spatial frequencies lower than 20 cpd, where the MTFs were larger. The relative MTF is defined as the ratio of MTF with scattering to that without scattering. Figure 6(b1–b3) shows the results, which decreased proportionally with increasing particle density across all spatial frequencies, except very low frequencies. Moreover, for the same particle density, the relative MTF remained relatively stable, indicating that uniformly distributed scattering particles had a consistent impact on retinal imaging, regardless of frequency.

Figure 7a displays an original image at the object plan, while Figure 7b,c shows retinal images with the density of 2 million/cm³ and 3 million/cm³, respectively, which were obtained by convolving the original image with the point spread function of the eye 3 [17]. It can be observed that more scattering particles led to a more blurred retinal image.

Although scattering particles can alter the contrast of the retinal image, they do not affect the phase of imaging. Therefore, light scattering is distinct from ocular aberrations.

3.3. MTF with Scattering Particles in Regions of Smaller Aberrations

Figure 8(a1–a3) presents the MTFs with different scattering particles. It was observed that the MTF decreased with increasing particle density. Although the MTF values appeared comparable in the high-frequency region, they actually exhibit a gradual decline with increasing scatterer concentration.

Figure 8(b1–b3) illustrated the relative MTFs of the sample eyes. The relative MTF exhibited a characteristic frequency-dependent decline, decreasing monotonically with increasing spatial frequency. This spatial frequency selectivity suggested that light scattering in low-aberration regions disproportionately affected the transfer of high-frequency optical performance.

3.4. MTF with the Particle Distributed in Larger Aberration Zones

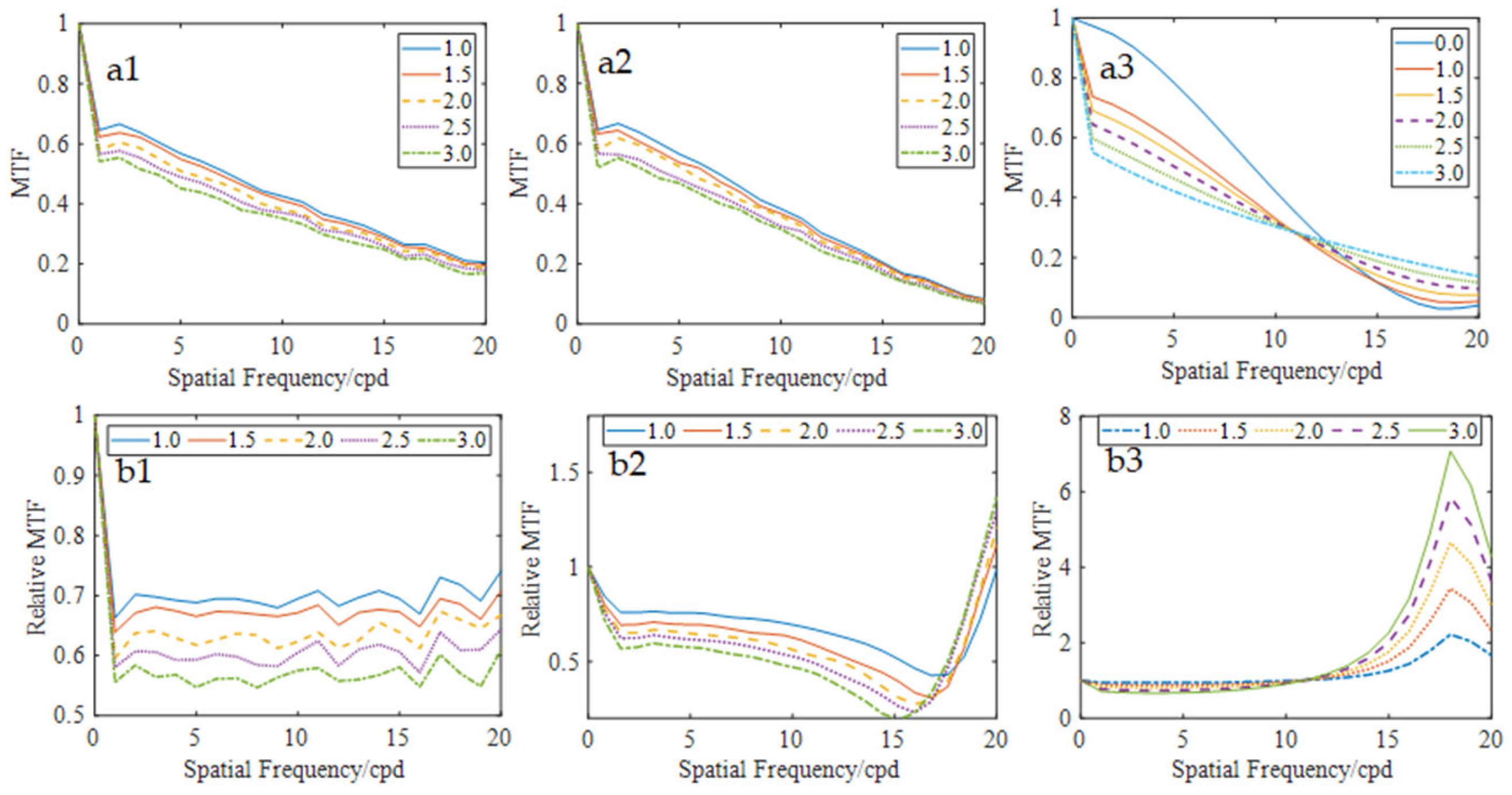
Figure 9(a1–a3) shows the MTFs when the particles are distributed in the larger aberration zones, and Figure 8(b1–b3) are the corresponding relative MTFs. Quantitative analysis of the MTF curves revealed that the relative MTFs of small aberration eye (N0.1) maintained stability across spatial frequencies for certain particle densities, similar to the results in Section 3.2. Notably, for eyes 2 and 3, the relative MTF initially decreased but rapidly increased at high spatial frequencies, and the MTF with scattering particles exceeded that without scattering particles, suggesting that the scattering effects and higher-order aberrations are mutually compensated at these frequencies. Conversely, at lower spatial frequencies, a progressive reduction in MTF values was observed with increasing particle density, demonstrating that scattering light affected MTF performance more. Figure 10c presents the retinal imaging of eye 3, clearly showing that the letter “E” was noticeably clearer in the high-frequency region with a high scattering particle density.

4. Discussion

In optics, Modulation Transfer Function (MTF) was mathematically defined as the normalized auto-correlation of the pupil function $f(x,y)$, which can be expressed as following formulation [17]:

$$f(x,y)=A(x,y)\exp [jkW(x,y)]$$

(1)

where A(x,y) is the energy distribution within the wavefront map, K is the wave vector defined as K = 2πλ/K, with λ of the wavelength of incident light, and W(x,y) represents the wavefront aberration at coordinate (x,y) in the wavefront map. It was generally assumed that A(x,y) = 1 in many past studies [4,6,11,14,15], indicating a uniform light distribution within the pupil and no scattering, reflection and absorption. Even when light scattering was considered, the light distribution was not uniform. Consequently, some elements of A(x,y) were less than 1.

The impact of sparse particles on retinal imaging was challenging to quantify. However, once particle density became larger, scattered light followed statistical patterns and became uniformly distributed across the retina, generating an approximately homogeneous background illumination. Consequently, the MTF decreased proportionally with increasing scattered light intensity.

When scattering particles were uniformly distributed across the pupil, although all elements of A(x,y) were less than 1, they remained identical. According to Equation (1), the MTF under this condition matched the scenario where A(x,y) = 1. When scattering was considered, the MTF in the retina was consistently lower than that without scattering. This indicates a linear superposition of aberration and scattering effects under uniform scattering conditions.

When scattering particles were distributed in small aberration zone, some elements of A(x,y) in these regions were less than 1 for the light scattered, leading to a decrease in the light energy for accurate imaging and a reduction in the MTF compared to the case where A(x,y) = 1. Furthermore, when the background scattering light was considered, the MTF decreased as the scattering light increased, suggesting the existence of synergistic enhancement effects.

When scattering particles were distributed in the large aberration region, the impact of the larger aberrations was mitigated for the reduction of corresponding light. Although MTF decreased when scattering light was considered, for some higher spatial frequencies, it may also exceed the MTF value without scattering, which suggests a compensatory effect between aberrations and light scattering.

5. Conclusions

This study presented a novel optical eye model incorporating clinically measured ocular parameters and configurable intraocular scattering, enabling a mechanistic exploration of wavefront aberration–scattering interactions. The results demonstrated that uniform scattering universally degraded MTF across spatial frequencies, whereas localized scattering exhibited context-dependent effects; scattering in low-aberration regions exacerbated retinal image degradation, while scattering in high-aberration zones partially mitigated aberrational distortions, particularly enhancing MTF at higher spatial frequencies. These multifaceted roles of scattering highlighted its complex interplay with ocular aberrations. Clinically, this model provided a framework for optimizing intraocular lens designs and personalized correction strategies. Future investigations should address dynamic scattering patterns, pupil effects, and validation in pathological eyes.