Exploring the Impact of Inlet Velocity Distribution on the Thermal Performance of a Laser Rod in a Diode Side-Pumped Amplifier
Abstract
1. Introduction
2. Theory
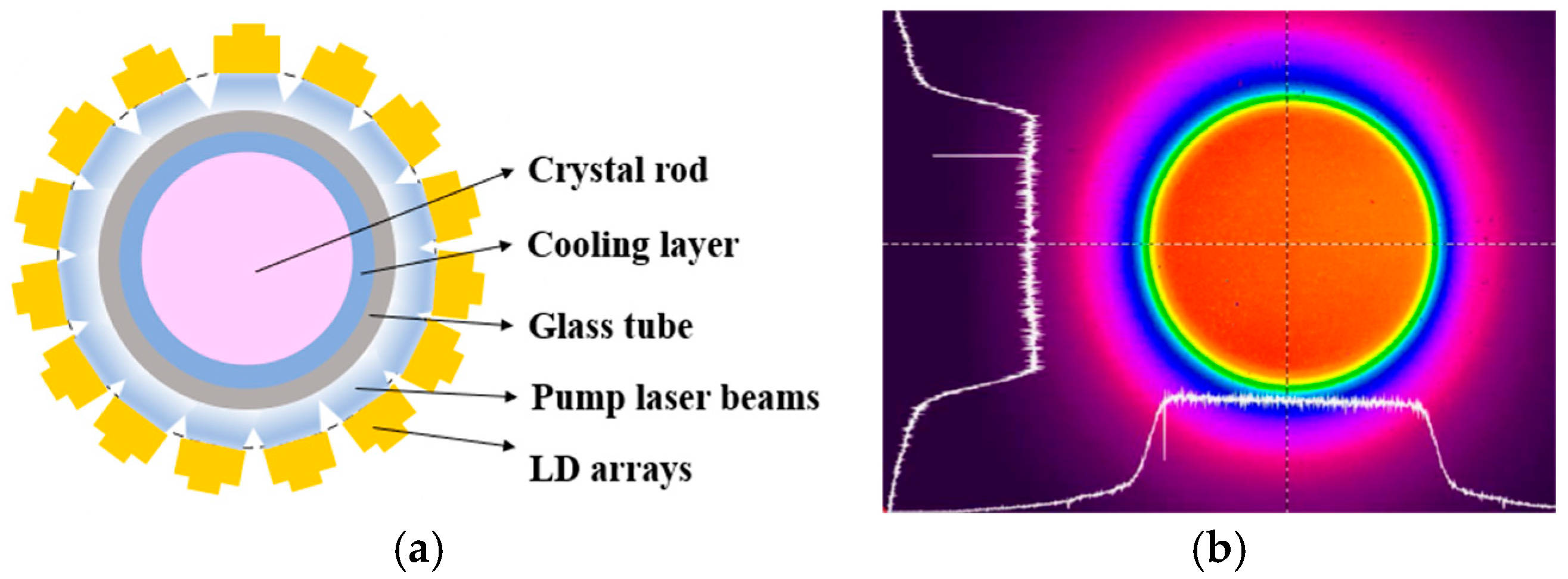
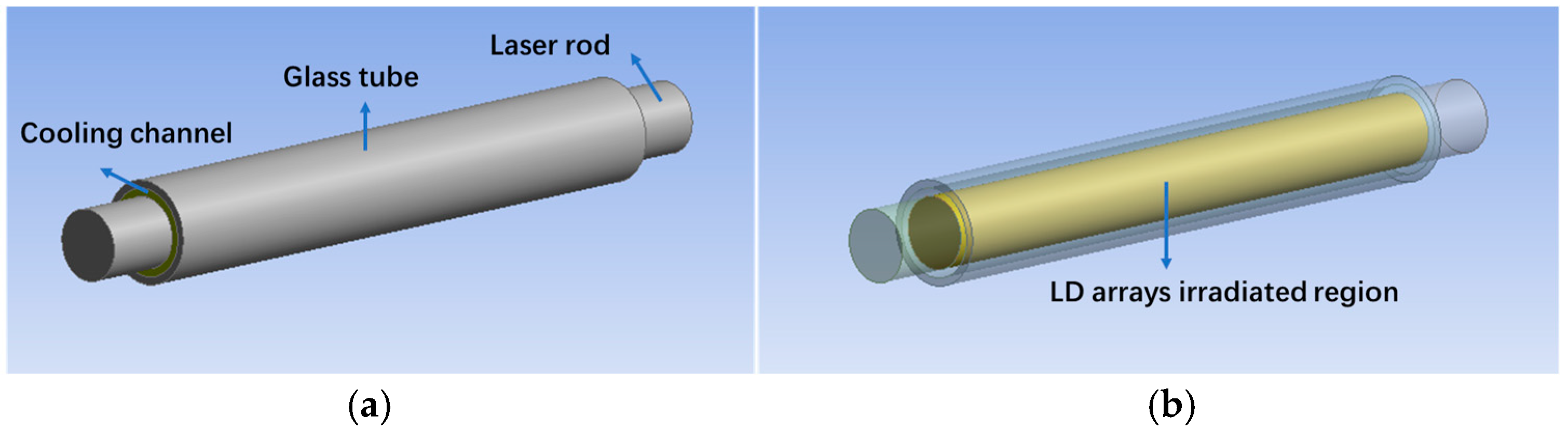
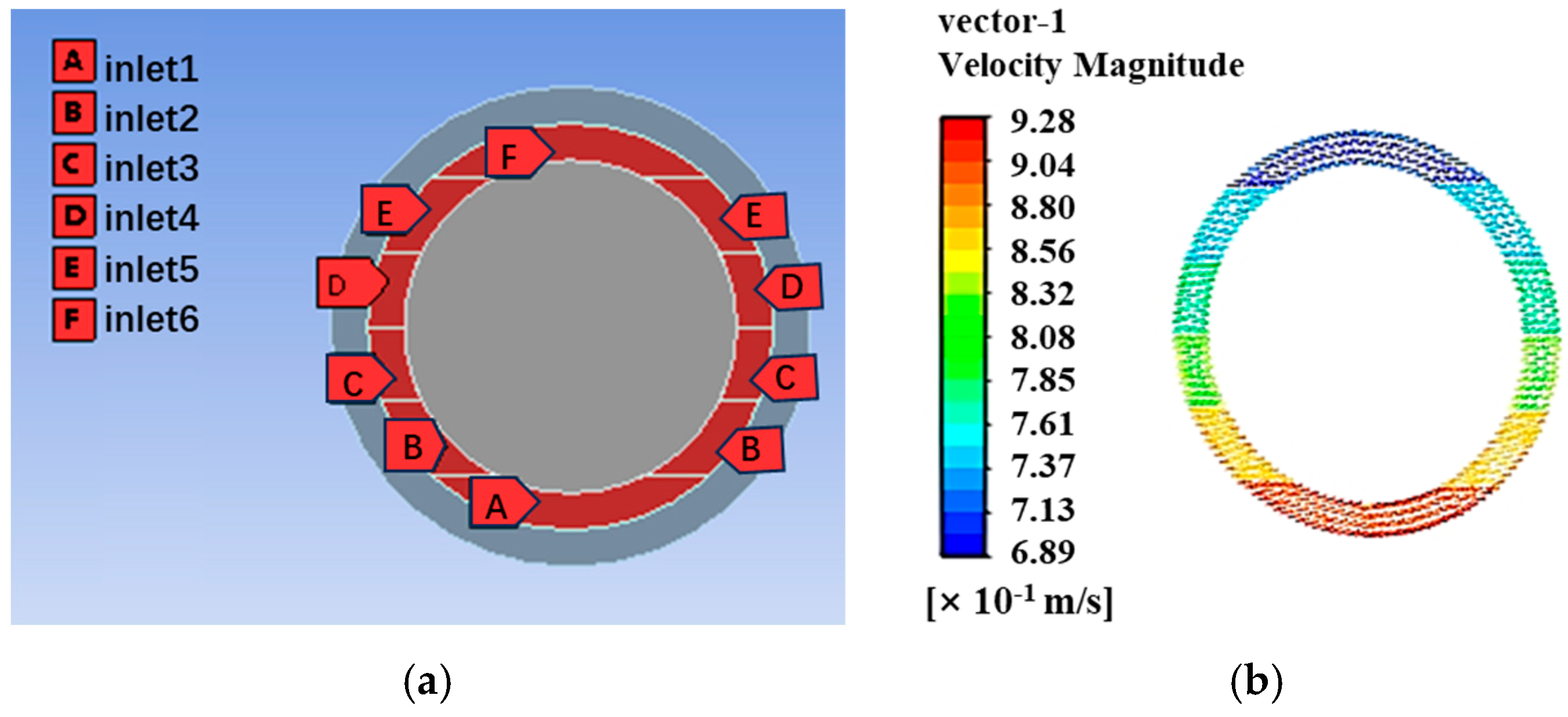
3. Configuration and Modeling
4. Simulation Results
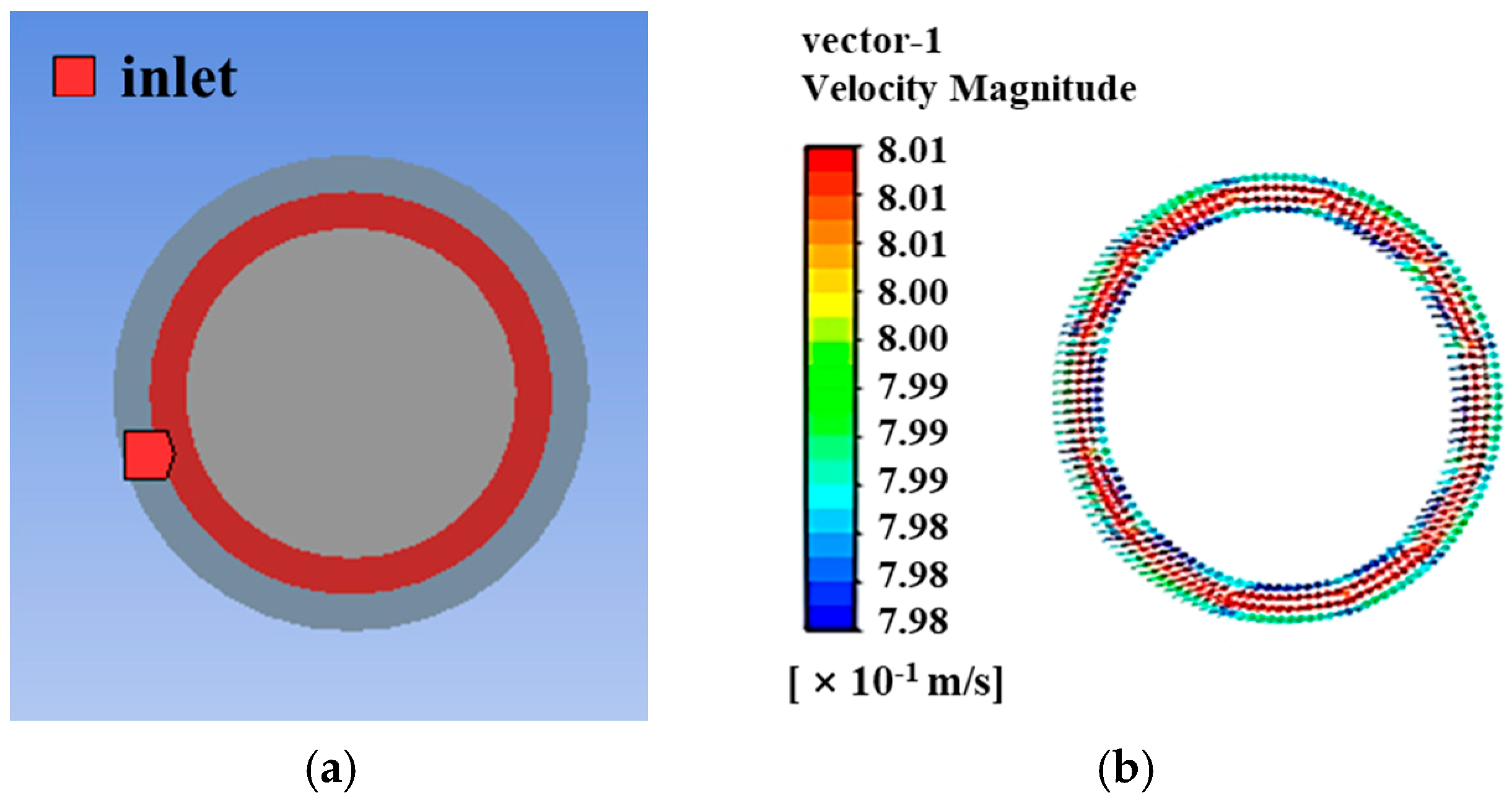
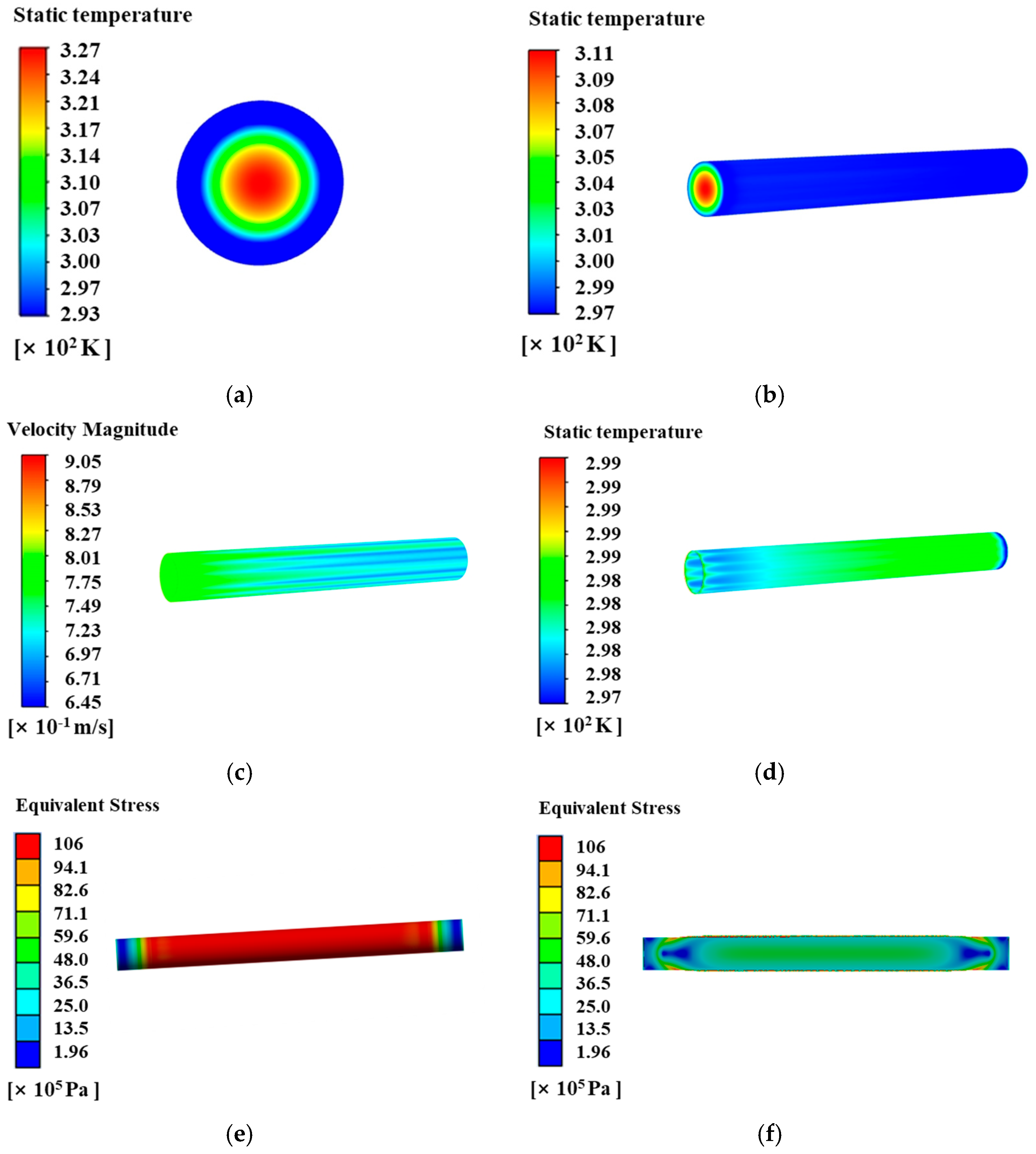
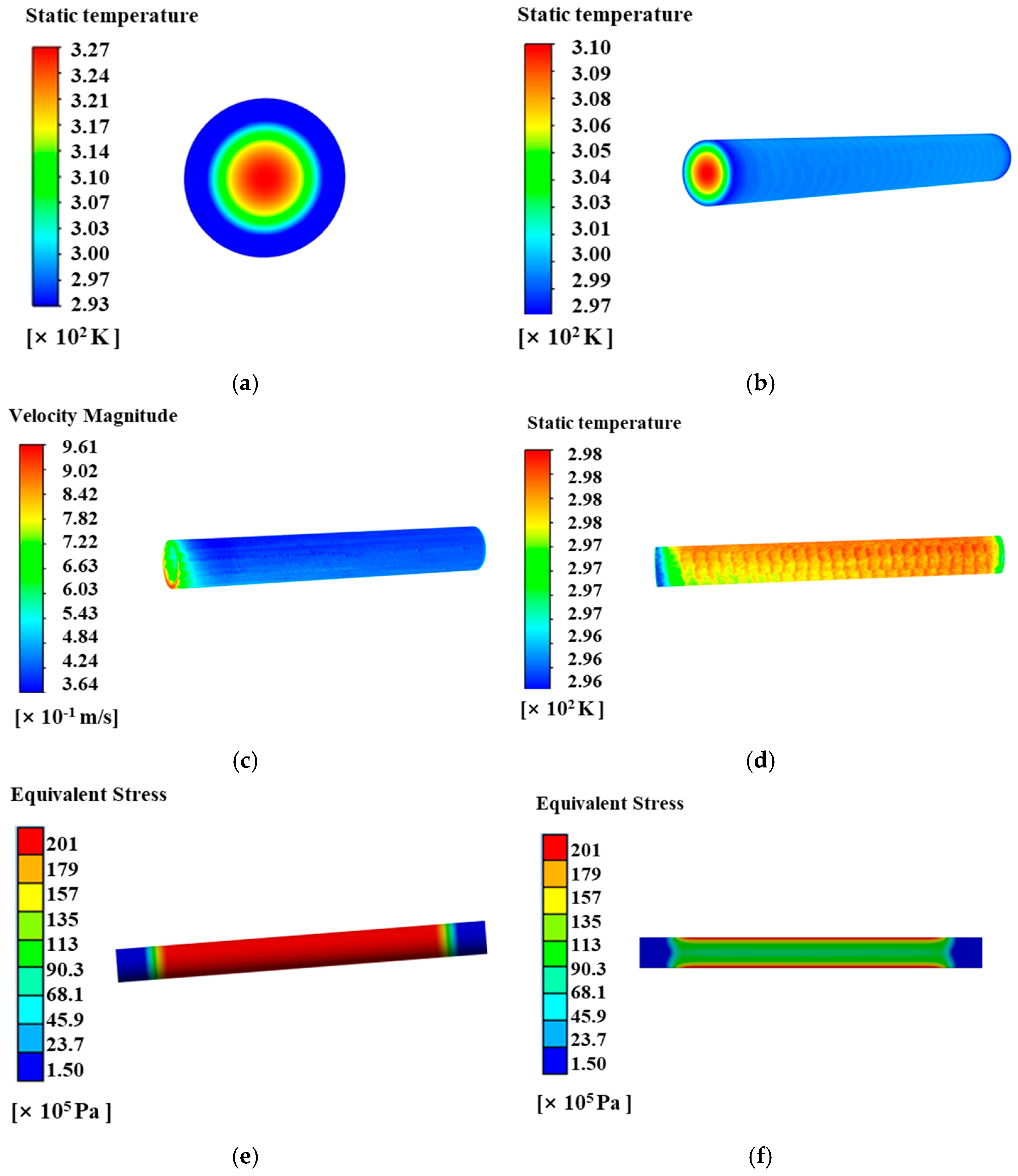
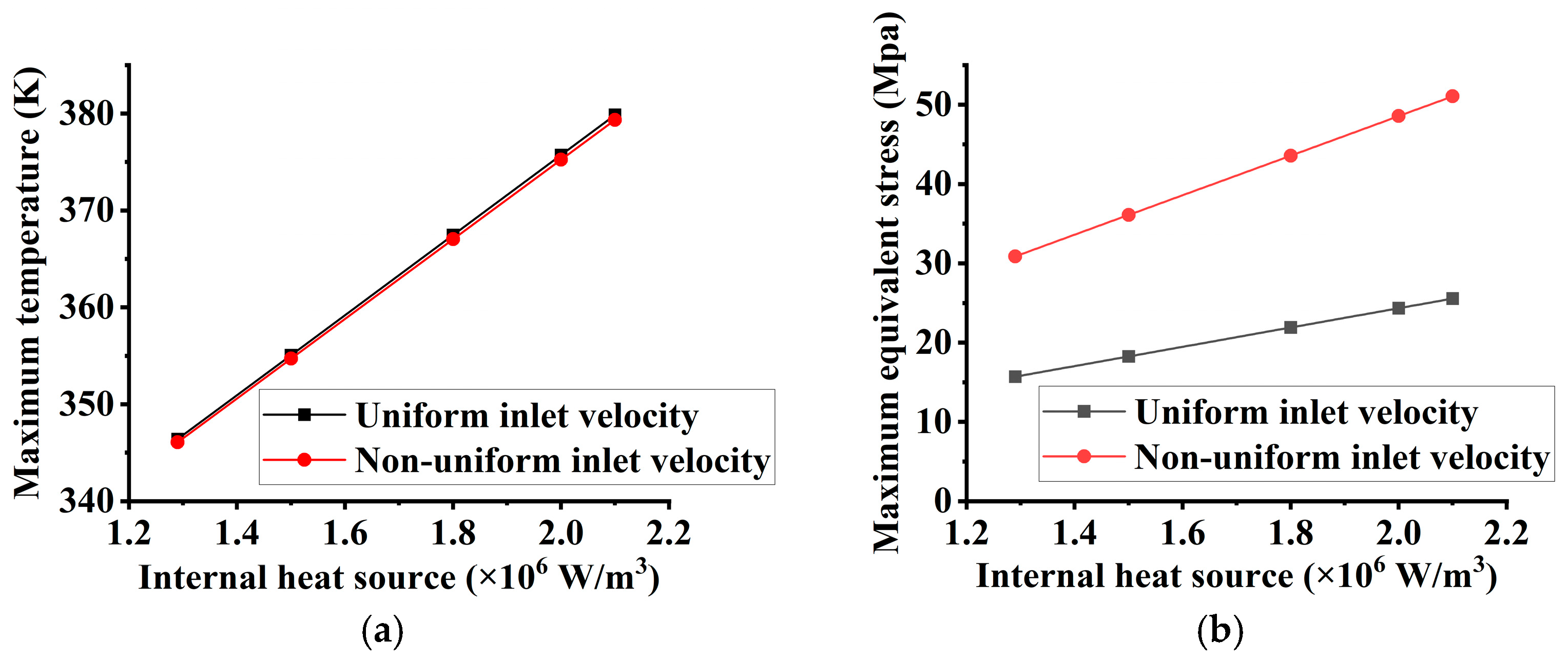
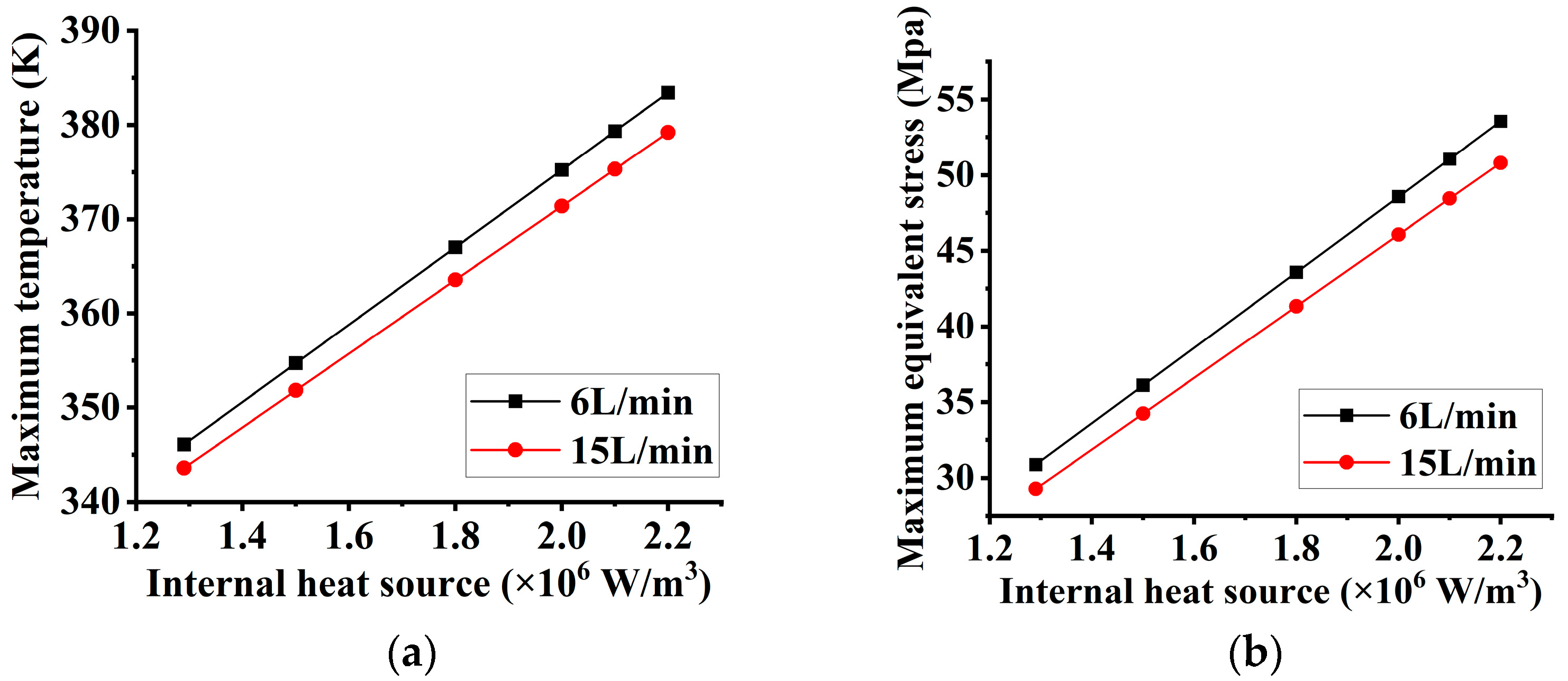
4.1. Unform Inlet Velocity Distribution
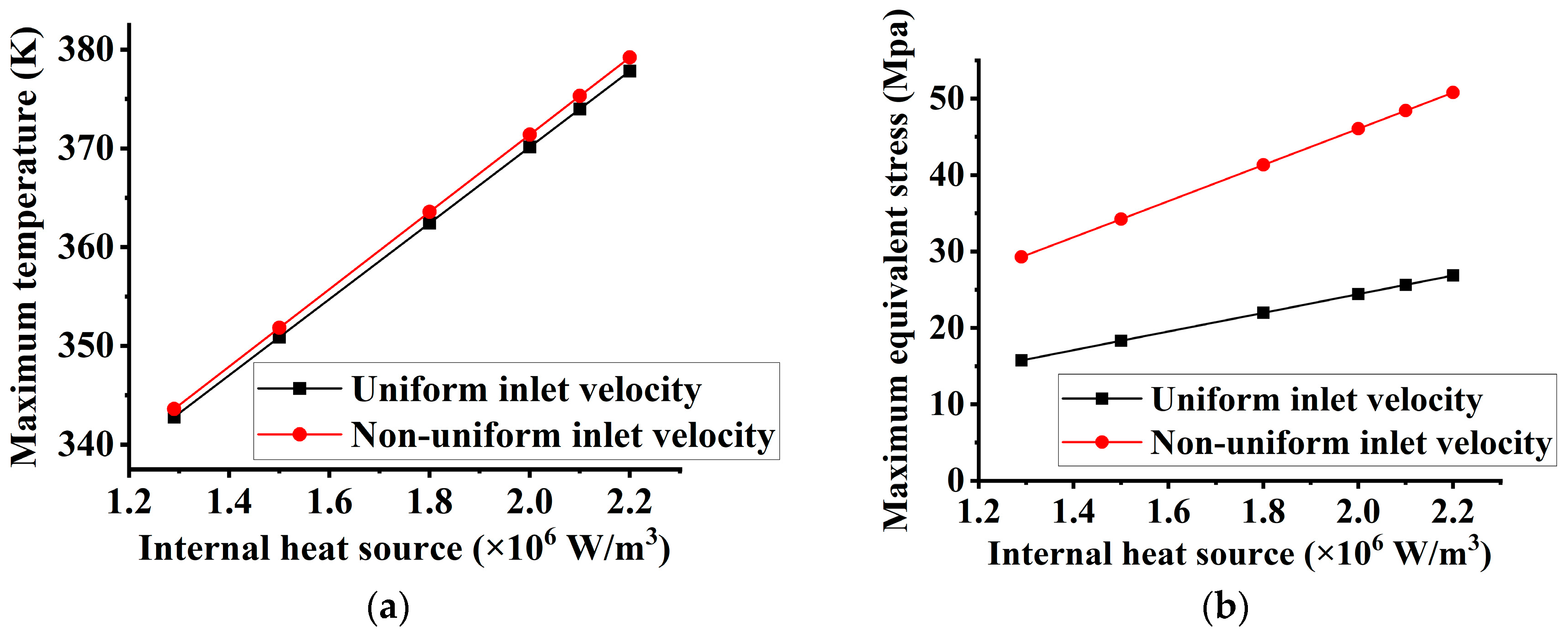
4.2. Non-Uniform Inlet Velocity Distribution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Divoký, M.; Pilař, J.; Hanuš, M.; Navrátil, P.; Denk, O.; Severová, P.; Mason, P.; Butcher, T.; Banerjee, S.; De Vido, M.; et al. 150 J DPSSL operating at 1.5 kW level. Opt. Lett. 2021, 46, 5771–5773. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Kong, M.; Lin, A.; Song, Y.; Han, J.; Xu, Z.; Wu, B.; Gao, S.; Deng, N. Directly modulated green-light diode-pumped solid-state laser for underwater wireless optical communication. Opt. Lett. 2017, 42, 1664–1667. [Google Scholar] [CrossRef] [PubMed]
- Koechner, W. Solid-State Laser Engineering; Springer: New York, NY, USA, 2006. [Google Scholar]
- Nomura, J.; Hirosawa, K.; Yanagisawa, T.; Ohata, N.; Imamura, S.; Sakaizawa, D.; Tomii, N. Single-frequency 45-mJ pulses from a MOPA system using an Er,Yb:glass planar waveguide amplifier and a large mode area Er-doped fiber amplifier. Opt. Lett. 2023, 48, 1758–1761. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, I.; Mukhin, I.; Palashov, O.; Ueda, K.-I. Thin-rod Yb:YAG amplifiers for high average and peak power lasers. Opt. Lett. 2018, 43, 3941–3944. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Fan, Z.; Xiao, H.; Huang, K.; Bai, Z.; Ge, W.; Zhang, H. Realizing Gaussian to flat-top beam shaping in traveling-wave amplification. Opt. Express 2017, 25, 33226–33235. [Google Scholar] [CrossRef]
- Nie, S.; Zhao, T.; Fan, Z.; Hong, X. Thermal effect of large-diameter laser rod in multi-direction side-pump high power pulsed Nd:YAG laser amplifier. In Proceedings of the International Symposium on Optoelectronic Technology and Application 2016, Beijing, China, 9–11 May 2016; p. 101520H. [Google Scholar]
- Ebadian, H.; Maleki, A. Efficient thermal induced birefringence compensation in a QCW diode pumped Nd:YAG laser. Optik 2018, 165, 362–369. [Google Scholar] [CrossRef]
- Huang, W.; Guo, J.; Lu, X.; Wang, J.; Fan, W.; Li, X.; Zhu, J. Diode-end-pumped all-liquid-cooled square rod Nd: Glass amplifier with sub-joule energy extraction and ultralow thermal induced wavefront. Opt. Laser Technol. 2022, 152, 108084. [Google Scholar] [CrossRef]
- Guoying, F.; Qunfei, O.; Jianguo, C.; Mingzhong, L. Simulation of the thermal effects in diode-pumped rod laser. In Proceedings of the Optical Science and Technology, SPIE’s 48th Annual Meeting, San Diego, CA, USA, 3–8 August 2003; pp. 43–48. [Google Scholar]
- Ye, X.; Xu, X.; Ren, H.; Zhang, B.; Lu, Y.; Chen, X.; Zhang, L.; Wei, X.; Wan, M.; He, T. Enhanced high-slope-efficiency and high-power LD side-pumped Er:YSGG laser. Appl. Opt. 2019, 58, 9949–9954. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Gu, H.; Cui, L.; Jiang, J.; Hao, H. Research on the LD side pumping field of solid-state lasers. In Proceedings of the SPIE Security + Defence, Strasbourg, France, 9–12 September 2019; Volume 11162. [Google Scholar]
- Wang, W.; Zhao, Q.; Gao, W.; Hu, Z.; Zhao, Q.; Yang, S. Thermo-Optic Numerical Research on Segmented Circular LD Arrays Side-Pumping a Nd:YAG Laser Rod. Appl. Sci. 2020, 10, 7316. [Google Scholar] [CrossRef]
- Weber, R.; Neuenschwander, B.; Weber, H.P. Thermal effects in solid-state laser materials. Opt. Mater. 1999, 11, 245–254. [Google Scholar] [CrossRef]
- Nie, S.; Zhao, T.; Xiao, H.; Zhao, S. Influence of model characteristic parameters on thermal effect analysis of solid-state laser. In Proceedings of the 24th National Laser Conference & Fifteenth National Conference on Laser Technology and Optoelectronics, Shanghai, China, 17–20 October 2020. [Google Scholar]
- Nie, S.; Zhao, T.; Liu, X.; Qu, P.; Yang, Y.; Wang, Y. The Effect of Cooling Layer Thickness and Coolant Velocity on Crystal Thermodynamic Properties in a Laser Amplifier. Micromachines 2023, 14, 299. [Google Scholar] [CrossRef] [PubMed]
- Hsu, S.T. Engineering Heat Transfer; D. Van Nostrand Company: Princeton, NJ, USA, 1963. [Google Scholar]
- Tao, W. Numerical Heat Transfer; Xi’an Jiaotong University Press: Xi’an, China, 2001. [Google Scholar]
- Yang, S.T.W. Heat Transfer; Higher Education Press: Beijing, China, 2006. [Google Scholar]
- Ding, J.; Li, Y.; Chen, H.; Cai, Y.; Bai, Z.; Qi, Y.; Yan, B.; Wang, Y.; Lu, Z. Thermal modeling of an external cavity diamond Raman laser. Opt. Laser Technol. 2022, 156, 108578. [Google Scholar] [CrossRef]
- Xiao, H.; Zhao, T.; Fan, Z.; Huang, K.; Yu, J. Pump Design of Large-Diameter Axial Non-Uniform Nd:YAG Crystal. Chin. J. Lasers 2015, 42, 0602002. [Google Scholar] [CrossRef]
- Wang, X.; Hu, L.; Chen, S.; Tang, J.; Meng, T.; Chen, W.; Weng, Z.; Chen, H.; Hu, J.; Chen, Y.; et al. Review of Development of Nd⁃Doped Laser Glass in China. Chin. J. Lasers 2024, 51, 1101008. [Google Scholar]
- Li, J. Study on thermal design and thermal analysis of liquid cooling plate with FC-770. Comput. Meas. Control 2023, 31, 160–165. [Google Scholar]
- Wu, G.; Zhao, X.; Shi, D.; Wu, X. Analysis of Fluid–Structure Coupling Vibration Mechanism for Subsea Tree Pipeline Combined with Fluent and Ansys Workbench. Water 2021, 13, 955. [Google Scholar] [CrossRef]

| Parameter (Materials) | Value (Units) |
|---|---|
| Density (laser rod) | 2870 kg/m3 |
| Thermal conductivity (laser rod) | 0.63 W/m/K |
| Specific heat (laser rod) | 680 J/kg/K |
| Coefficient of thermal expansion (laser rod) | 1.27 × 10−5 /K |
| Young’s modulus (laser rod) | 5.85 × 1010 Pa |
| Poisson’s ratio (laser rod) | 0.232 |
| Density (coolant) | 1793 kg/m3 |
| Thermal conductivity (coolant) | 0.063 W/m/K |
| Specific heat (coolant) | 1038 J/kg/K |
| Viscosity (coolant) | 1.359 × 10−3 kg/m/s |
| Density (glass tube) | 2200 kg/m3 |
| Thermal conductivity (glass tube) | 1.4 W/m/K |
| Specific heat (glass tube) | 670 J/kg/K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, S.; Lin, J.; Zhao, T.; Liu, X. Exploring the Impact of Inlet Velocity Distribution on the Thermal Performance of a Laser Rod in a Diode Side-Pumped Amplifier. Photonics 2025, 12, 603. https://doi.org/10.3390/photonics12060603
Nie S, Lin J, Zhao T, Liu X. Exploring the Impact of Inlet Velocity Distribution on the Thermal Performance of a Laser Rod in a Diode Side-Pumped Amplifier. Photonics. 2025; 12(6):603. https://doi.org/10.3390/photonics12060603
Chicago/Turabian StyleNie, Shuzhen, Jinglan Lin, Tianzhuo Zhao, and Xiaolong Liu. 2025. "Exploring the Impact of Inlet Velocity Distribution on the Thermal Performance of a Laser Rod in a Diode Side-Pumped Amplifier" Photonics 12, no. 6: 603. https://doi.org/10.3390/photonics12060603
APA StyleNie, S., Lin, J., Zhao, T., & Liu, X. (2025). Exploring the Impact of Inlet Velocity Distribution on the Thermal Performance of a Laser Rod in a Diode Side-Pumped Amplifier. Photonics, 12(6), 603. https://doi.org/10.3390/photonics12060603




