Large Vessel Segmentation and Microvasculature Quantification Based on Dual-Stream Learning in Optic Disc OCTA Images
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Literature Review
2. Related Works
2.1. U-Net-Based Segmentation Model
2.2. Receptive Fields in Segmentation Models
2.3. Attention Mechanism in CNNs
2.4. Dual-Stream Learning
3. Methods
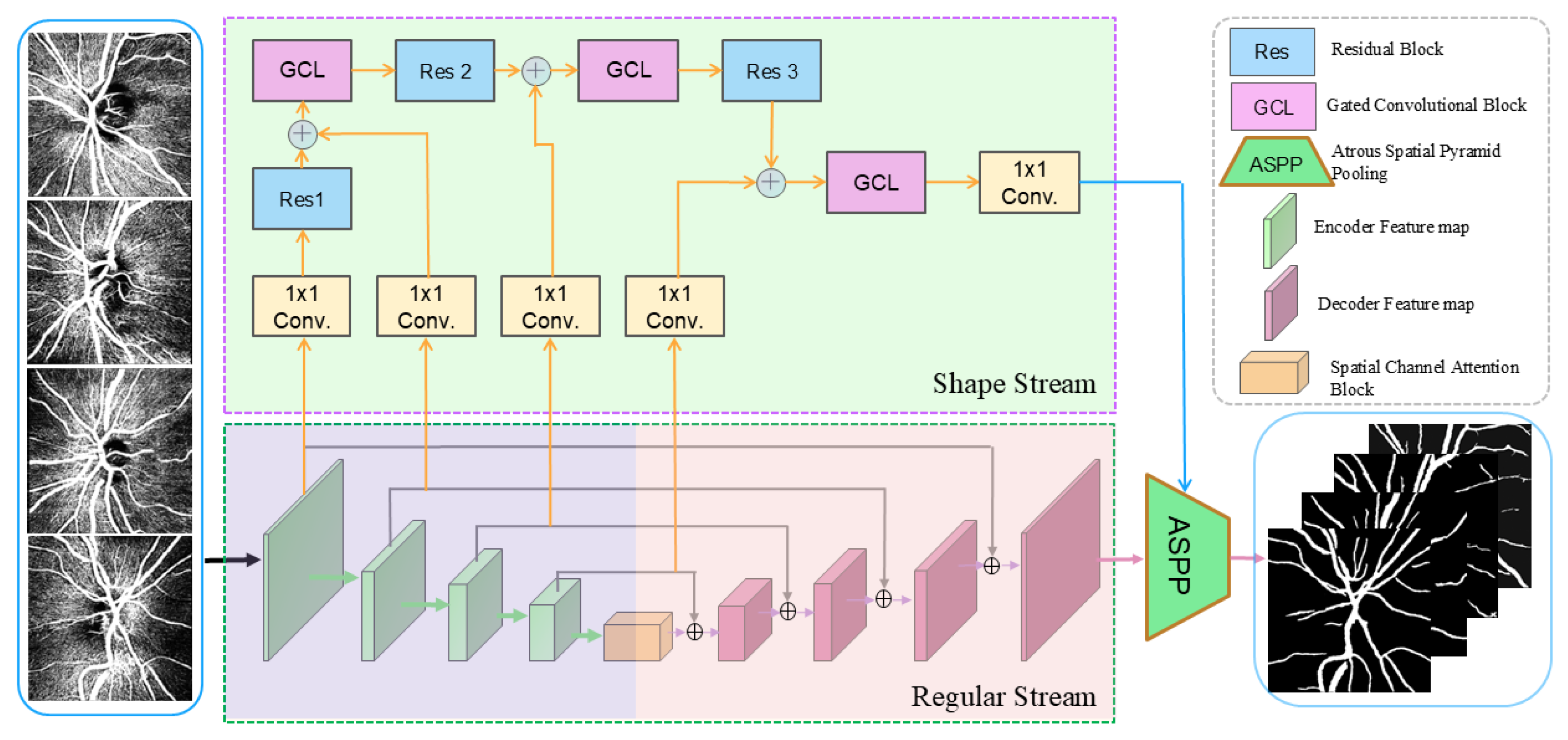
3.1. Network Architecture
3.2. Channel-Spatial Attention Mechanism
3.3. Structural Re-Parameterization
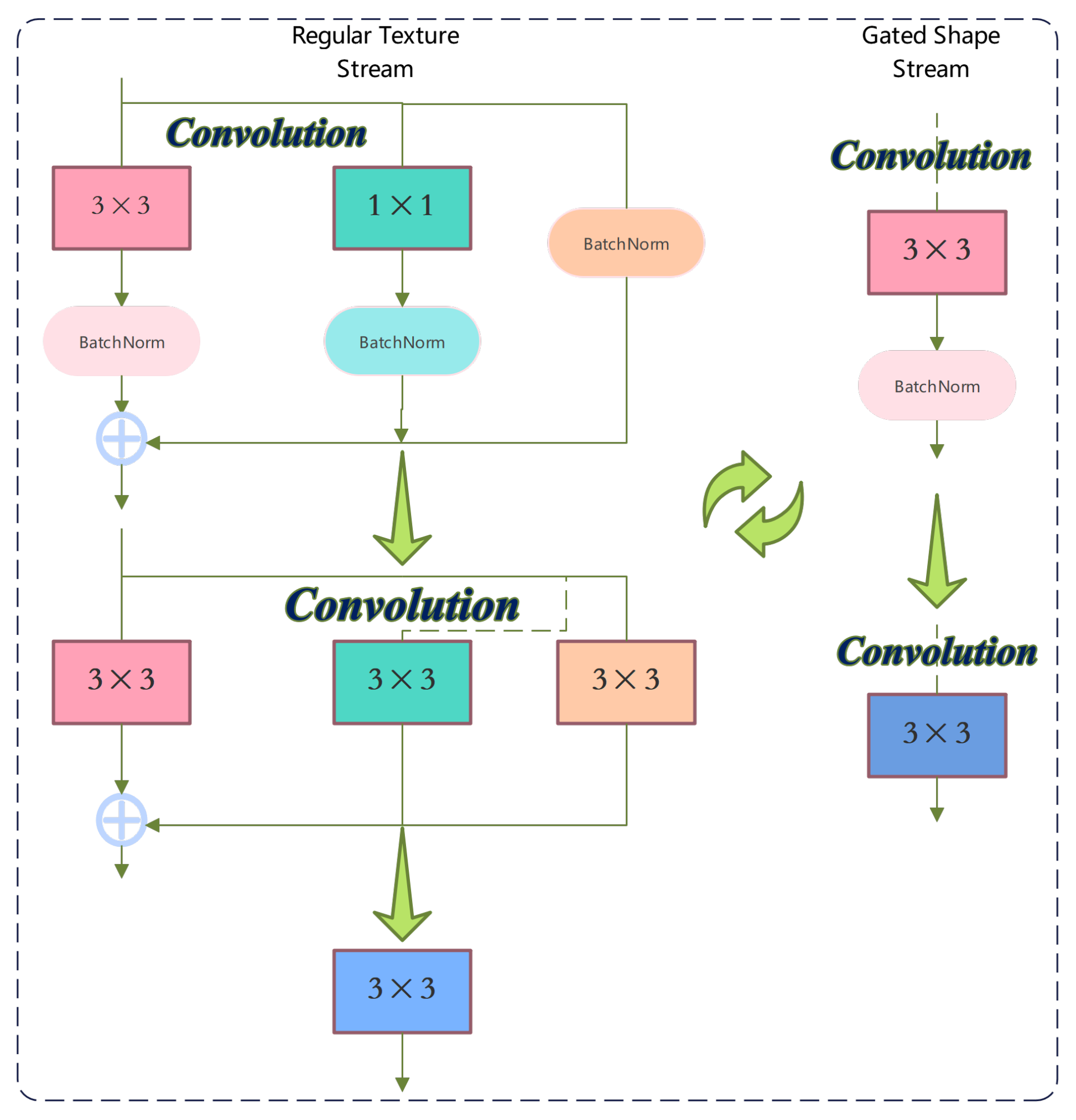
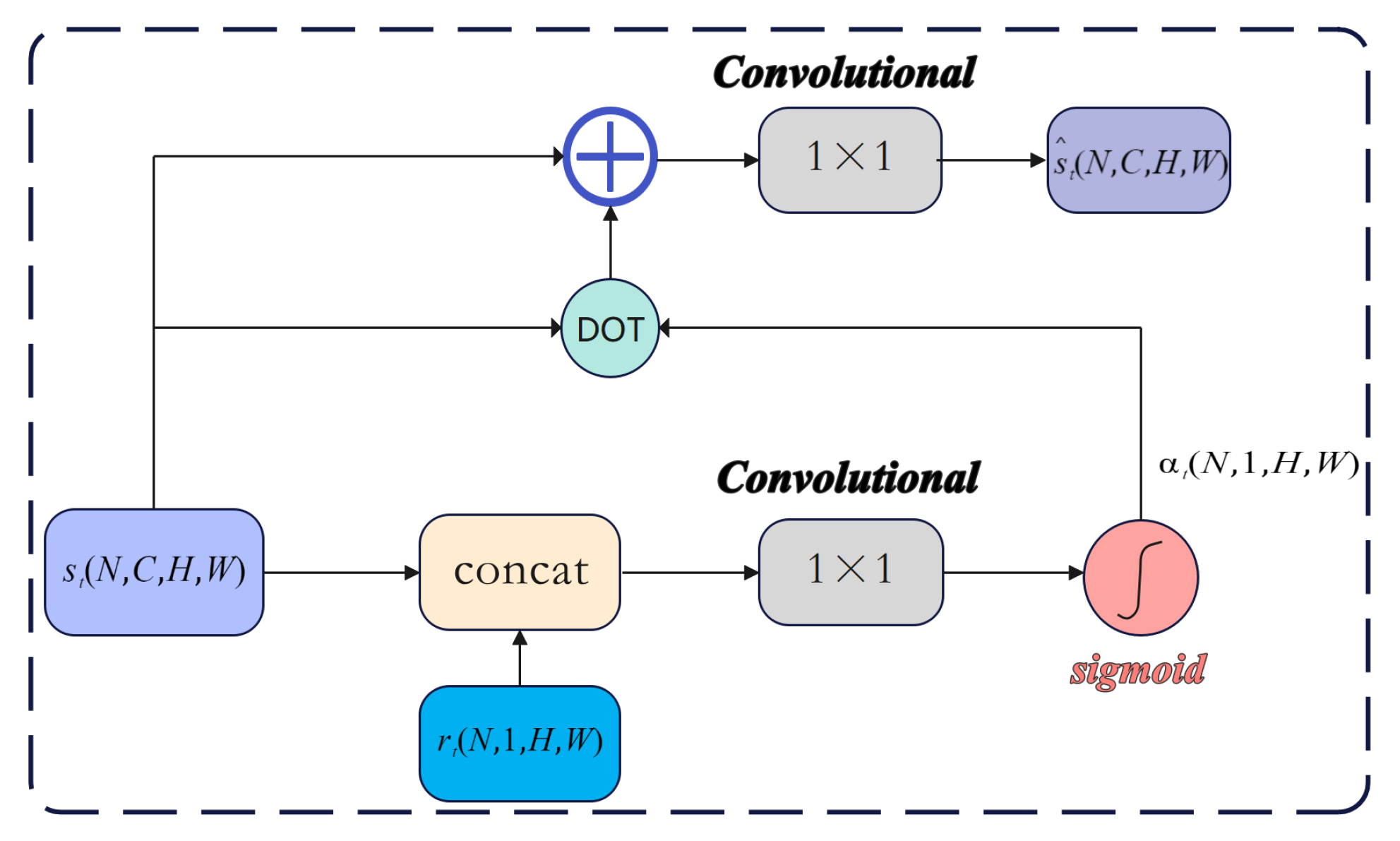
3.4. Gated Convolutional Layer
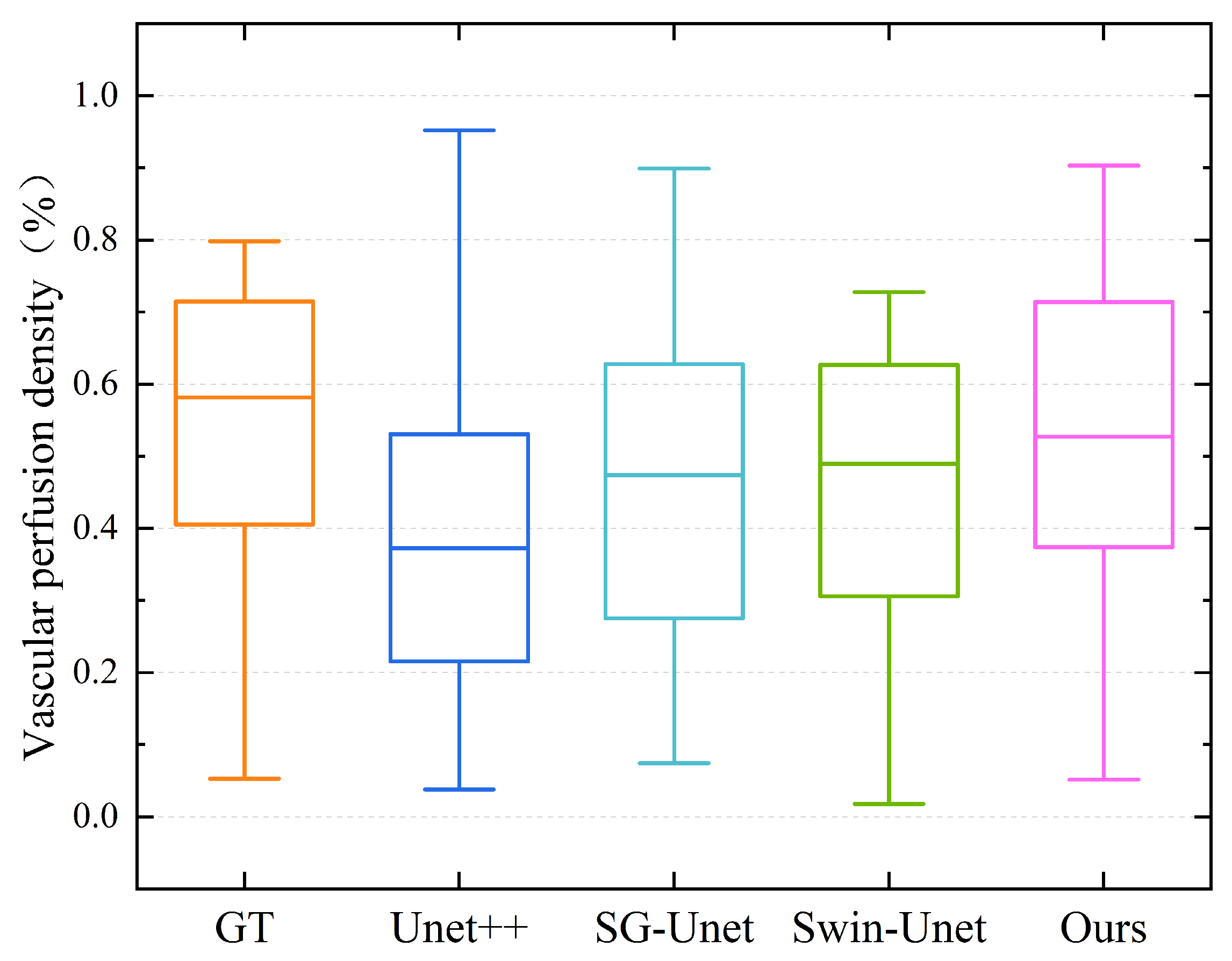
3.5. Quantification of Microvasculature
4. Experiments
4.1. Datasets
4.2. Data Augmentation and Cross-Validation
4.3. Evaluation Metrics
4.4. Implementation Details
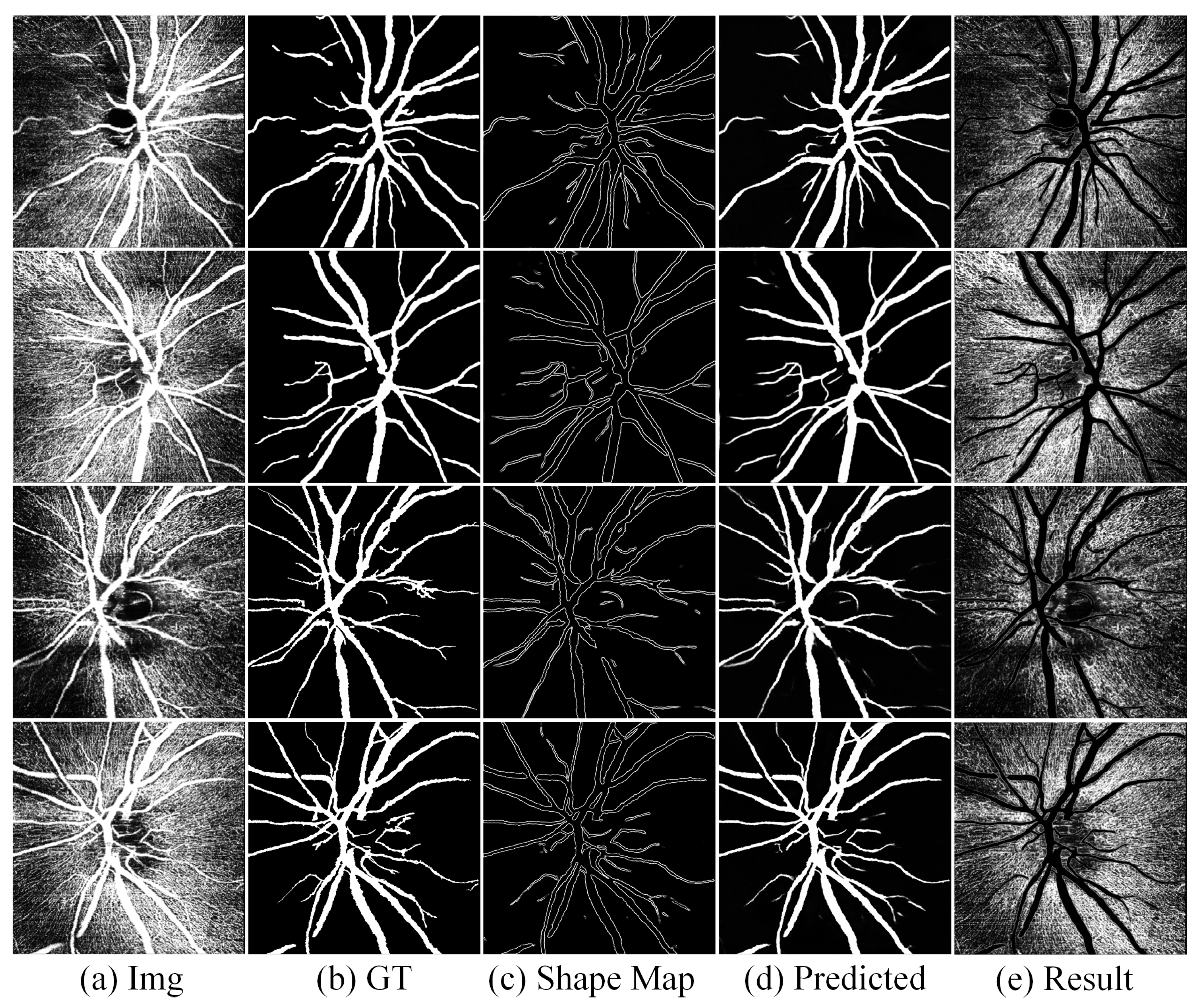
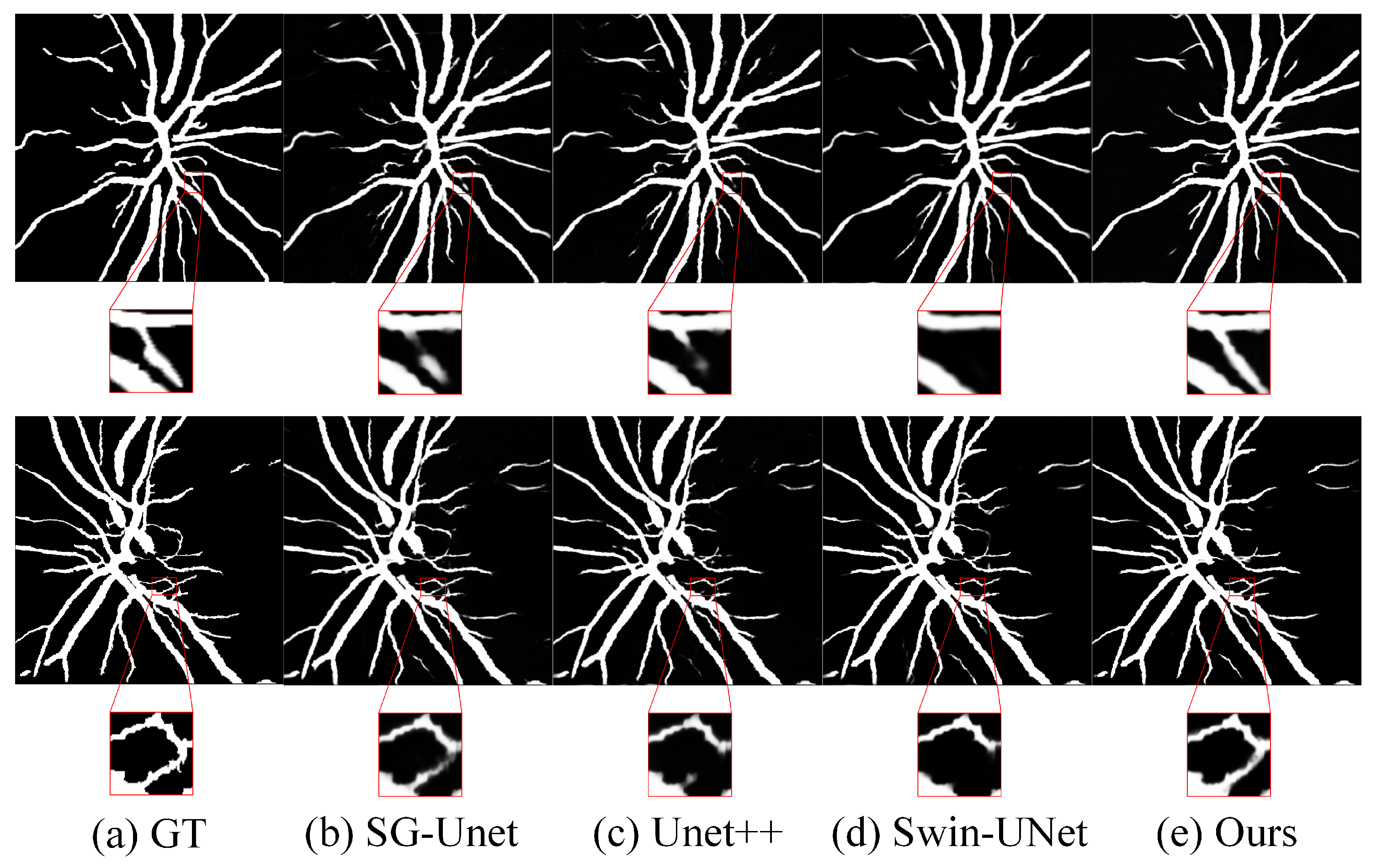
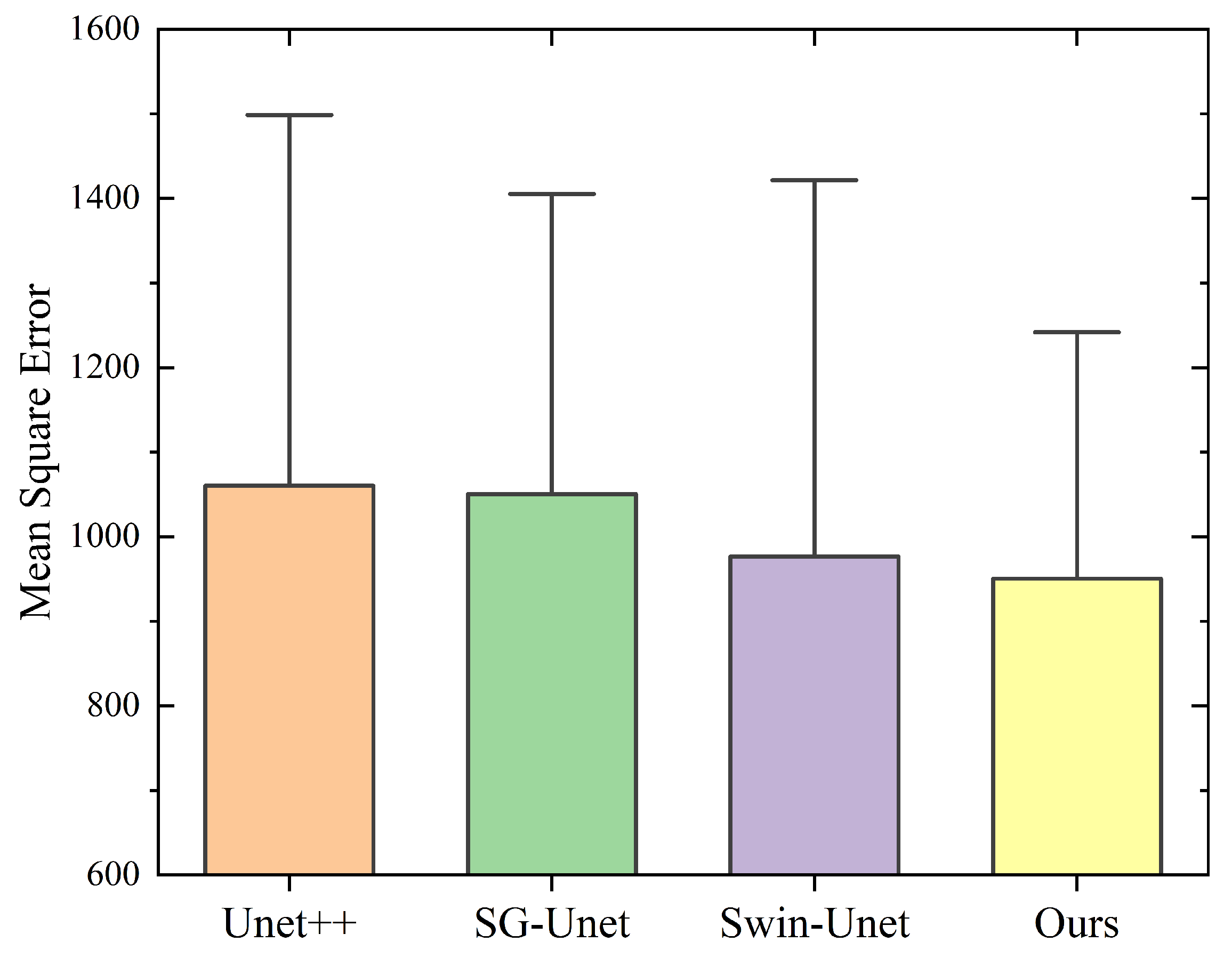
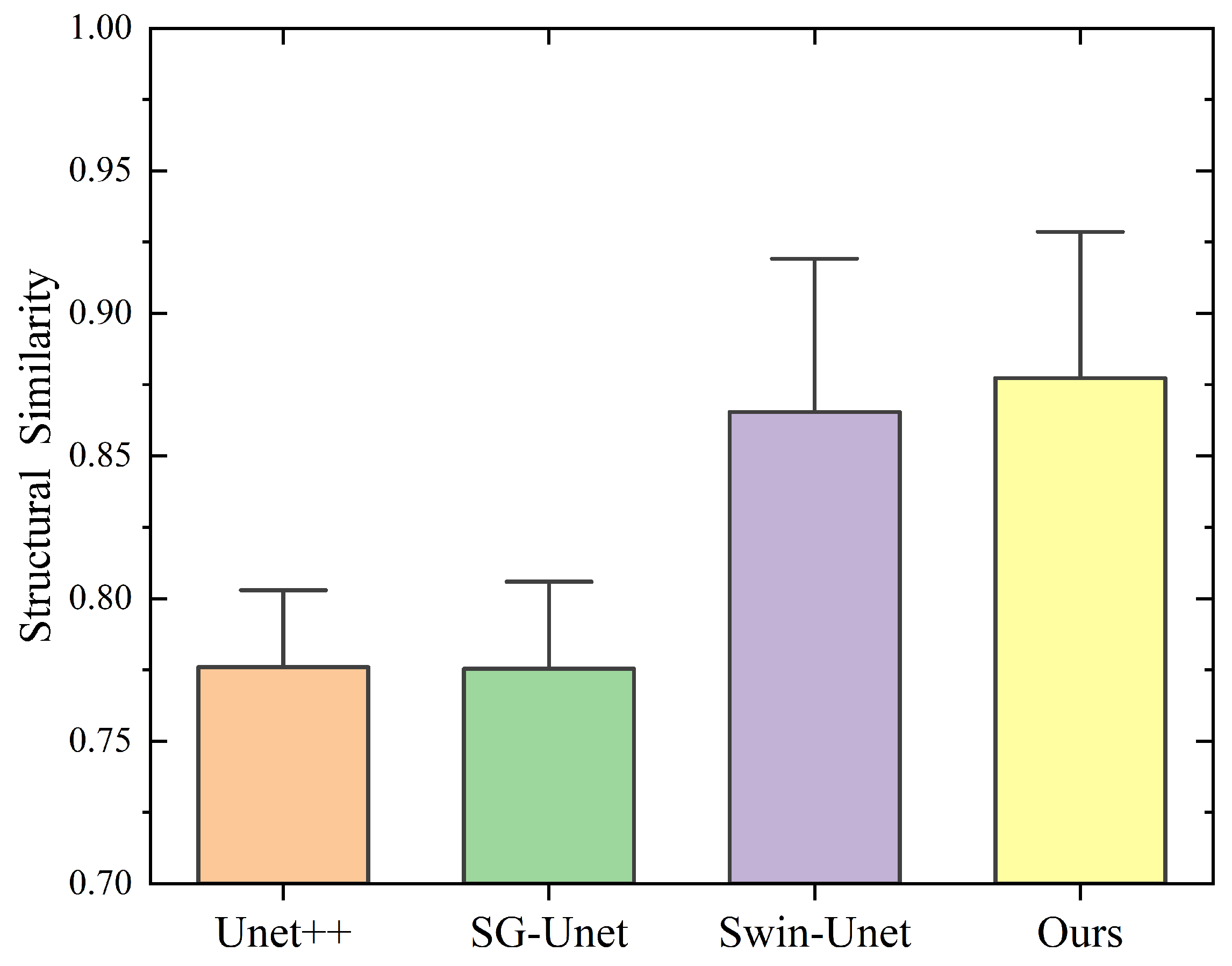
4.5. Results
4.6. Ablation Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oshitari, T.; Hanawa, K.; Adachi-Usami, E. Changes of macular and RNFL thicknesses measured by Stratus OCT in patients with early stage diabetes. Eye 2009, 23, 884–889. [Google Scholar] [CrossRef] [PubMed]
- Leung, C.K.; Choi, N.; Weinreb, R.N.; Liu, S.; Ye, C.; Liu, L.; Lai, G.W.; Lau, J.; Lam, D.S. Retinal Nerve Fiber Layer Imaging with Spectral-Domain Optical Coherence Tomography: Pattern of RNFL Defects in Glaucoma. Ophthalmology 2010, 117, 2337–2344. [Google Scholar] [CrossRef] [PubMed]
- Robbins, C.B.; Grewal, D.S.; Thompson, A.C.; Soundararajan, S.; Yoon, S.P.; Polascik, B.W.; Scott, B.L.; Fekrat, S. Identifying Peripapillary Radial Capillary Plexus Alterations in Parkinson’s Disease Using OCT Angiography. Ophthalmol. Retin. 2022, 6, 29–36. [Google Scholar] [CrossRef]
- Yu, P.K.; Cringle, S.J.; Yu, D.Y. Correlation between the radial peripapillary capillaries and the retinal nerve fibre layer in the normal human retina. Exp. Eye Res. 2014, 129, 83–92. [Google Scholar] [CrossRef]
- Henkind, P. Radial peripapillary capillaries of the retina. I. Anatomy: Human and comparative. Br. J. Ophthalmol. 1967, 51, 115–123. [Google Scholar] [CrossRef]
- Yu, P.; Balaratnasingam, C.; Xu, J.; Morgan, W.; Mammo, Z.; Han, S.; Mackenzie, P.; Merkur, A.; Kirker, A.; Albiani, D.; et al. Label-free density measurements of radial peripapillary capillaries in the human retina. PLoS ONE 2015, 10, e0135151. [Google Scholar] [CrossRef] [PubMed]
- Yarmohammadi, A.; Zangwill, L.M.; Diniz-Filho, A.; Suh, M.H.; Yousefi, S.; Saunders, L.J.; Belghith, A.; Manalastas, P.I.C.; Medeiros, F.A.; Weinreb, R.N. Relationship between optical coherence tomography angiography vessel density and severity of visual field loss in glaucoma. Ophthalmology 2016, 123, 2498–2508. [Google Scholar] [CrossRef]
- Wong, T.Y.; Scott, I.U. Retinal-Vein Occlusion. N. Engl. J. Med. 2010, 363, 2135–2144. [Google Scholar] [CrossRef]
- Waheed, N.K.; Rosen, R.B.; Jia, Y.; Munk, M.R.; Huang, D.; Fawzi, A.; Chong, V.; Nguyen, Q.D.; Sepah, Y.; Pearce, E. Optical coherence tomography angiography in diabetic retinopathy. Prog. Retin. Eye Res. 2023, 97, 101206. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, C.; Kong, X.; Yu, X.; Sun, X. Peripapillary retinal vessel density in eyes with acute primary angle closure: An optical coherence tomography angiography study. Graefe’s Arch. Clin. Exp. Ophthalmol. Albrecht Von Graefes Arch. Fur Klin. Und Exp. Ophthalmol. 2017, 255, 1013–1018. [Google Scholar] [CrossRef]
- Scripsema, N.K.; Garcia, P.M.; Bavier, R.D.; Chui, T.Y.P.; Krawitz, B.D.; Mo, S.; Agemy, S.A.; Xu, L.; Lin, Y.B.; Panarelli, J.F.; et al. Optical Coherence Tomography Angiography Analysis of Perfused Peripapillary Capillaries in Primary Open-Angle Glaucoma and Normal-Tension Glaucoma. Investig. Ophthalmol. Vis. Sci. 2016, 57, OCT611–OCT620. [Google Scholar] [CrossRef]
- Rao, H.L.; Pradhan, Z.S.; Weinreb, R.N.; Reddy, H.B.; Riyazuddin, M.; Dasari, S.; Palakurthy, M.; Puttaiah, N.K.; Rao, D.A.S.; Webers, C.A.B. Regional Comparisons of Optical Coherence Tomography Angiography Vessel Density in Primary Open-Angle Glaucoma. Am. J. Ophthalmol. 2016, 171, 75–83. [Google Scholar] [CrossRef]
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A. Optical coherence tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef]
- Naseripour, M.; Falavarjani, K.G.; Mirshahi, R.; Sedaghat, A. Optical coherence tomography angiography (OCTA) applications in ocular oncology. Eye 2020, 34, 1535–1545. [Google Scholar] [CrossRef]
- Çalışkan, N.E.; Doğan, M.; Çalışkan, A.; Gobeka, H.H.; Ay, İ.E. Optical coherence tomography angiography evaluation of retinal and optic disc microvascular morphological characteristics in retinal vein occlusion. Photodiagnosis Photodyn. Ther. 2023, 41, 103244. [Google Scholar] [CrossRef] [PubMed]
- Ishibazawa, A.; Nagaoka, T.; Takahashi, A.; Omae, T.; Tani, T.; Sogawa, K.; Yokota, H.; Yoshida, A. Optical Coherence Tomography Angiography in Diabetic Retinopathy: A Prospective Pilot Study. Am. J. Ophthalmol. 2015, 160, 35–44.e1. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W.W.; Huang, S.H.; Zheng, Y.; Zuo, J.J.; Qian, S.S.; Zhou, T.Y.; Lin, B. Observational Study of Retinal Branch Vein Occlusion in the Macular Region using DART-OCTA. Int. Eye Sci. 2022, 22, 1391–1395. (In Chinese) [Google Scholar]
- Goliaš, M.; Šikudová, E. Retinal blood vessel segmentation and inpainting networks with multi-level self-attention. Biomed. Signal Process. Control 2025, 102, 107343. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Suen, C.Y. A fast parallel algorithm for thinning digital patterns. Commun. ACM 1984, 27, 236–239. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man, Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Adams, R.; Bischof, L. Seeded region growing. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 641–647. [Google Scholar] [CrossRef]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. IJCV 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Khandouzi, A.; Ariafar, A.; Mashayekhpour, Z.; Pazira, M.; Baleghi, Y. Retinal Vessel Segmentation, a Review of Classic and Deep Methods. Ann. Biomed. Eng. 2022, 50, 1292–1314. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Shankaranarayana, S.M.; Ram, K.; Mitra, K.; Sivaprakasam, M. Joint Optic Disc and Cup Segmentation Using Fully Convolutional and Adversarial Networks. In Proceedings of the International Workshop on Fetal and Infant Image Analysis International Workshop on Ophthalmic Medical Image Analysis, Québec, QC, Canada, 14 September 2017; pp. 168–176. [Google Scholar]
- Guo, C.; Szemenyei, M.; Yi, Y.; Wang, W.; Chen, B.; Fan, C. SA-UNet: Spatial Attention U-Net for Retinal Vessel Segmentation. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 1236–1242. [Google Scholar] [CrossRef]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P.; Wu, C. ResUNet-a: A deep learning framework for semantic segmentation of remotely sensed data. ISPRS J. Photogramm. Remote Sens. 2020, 162, 94–114. [Google Scholar] [CrossRef]
- Zhou, Z.; Rahman Siddiquee, M.M. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Qin, X.; Zhang, Z.; Huang, C.; Dehghan, M. U2-Net: Going deeper with nested U-structure for salient object detection. Pattern Recognit. 2020, 106, 107404. [Google Scholar] [CrossRef]
- Li, X.; Chen, H.; Qi, X.; Dou, Q.; Fu, C.W.; Heng, P.A. H-DenseUNet: Hybrid Densely Connected UNet for Liver and Tumor Segmentation From CT Volumes. IEEE Trans. Med Imaging 2018, 37, 2663–2674. [Google Scholar] [CrossRef]
- Lei, T.; Sun, R.; Du, X.; Fu, H.; Zhang, C.; Nandi, A.K. SGU-Net: Shape-Guided Ultralight Network for Abdominal Image Segmentation. IEEE J. Biomed. Health Inform. 2023, 27, 1431–1442. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Ding, X.; Zhang, X.; Ma, N.; Han, J.; Ding, G.; Sun, J. RepVGG: Making VGG-Style ConvNets Great Again. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 13733–13742. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer: Cham, Switzerland, 2018; pp. 3–19. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 11531–11539. [Google Scholar]
- Li, A.; Zhang, J.; Lv, Y.; Zhang, T.; Zhong, Y.; He, M.; Dai, Y. Joint Salient Object Detection and Camouflaged Object Detection via Uncertainty-aware Learning. arXiv 2023, arXiv:2307.04651. [Google Scholar]
- Takikawa, T.; Acuna, D.; Jampani, V.; Fidler, S. Gated-SCNN: Gated Shape CNNs for Semantic Segmentation. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5228–5237. [Google Scholar] [CrossRef]
- Zhen, M.; Wang, J.; Zhou, L.; Li, S.; Shen, T.; Shang, J.; Fang, T.; Quan, L. Joint Semantic Segmentation and Boundary Detection Using Iterative Pyramid Contexts. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Luo, G.; Zhou, Y.; Sun, X.; Cao, L.; Wu, C.; Deng, C.; Ji, R. Multi-Task Collaborative Network for Joint Referring Expression Comprehension and Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Veit, A.; Wilber, M.J.; Belongie, S. Residual Networks Behave Like Ensembles of Relatively Shallow Networks. In Advances in Neural Information Processing Systems (NIPS); Curran Associates, Inc.: Red Hook, NY, USA, 2016. [Google Scholar]
- Ding, X.; Zhang, X.; Han, J.; Ding, G. Diverse Branch Block: Building a Convolution as an Inception-Like Unit. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 10886–10895. [Google Scholar]
- Ma, Z.; Ding, N.; Yu, Y.; Ma, Y.; Yuan, X.; Wang, Y.; Zhao, Y.; Luan, J.; Liu, J. Quantification of cerebral vascular perfusion density via optical coherence tomography based on locally adaptive regional growth. Appl. Opt. 2018, 57, 10117–10124. [Google Scholar] [CrossRef]
- Perazzi, F.; Pont-Tuset, J.; McWilliams, B.; Gool, L.V.; Gross, M.; Sorkine-Hornung, A. A Benchmark Dataset and Evaluation Methodology for Video Object Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]




| Dataset | OCT-1 |
|---|---|
| Obtained from | OCTA images captured from the patients in local hospital |
| Train/Validation/Test | 460/58/58 (8:1:1) |
| Resolution (pixels) | |
| Resize (pixels) | |
| Augumentation methods | (1) Random crops; (2) horizontal flips; (3) vertical flips; (4) diagonal flips. |
| Fold | Dice | IoU | Accuracy | Recall |
|---|---|---|---|---|
| 1 | 0.8779 | 0.8357 | 0.9558 | 0.9632 |
| 2 | 0.9022 | 0.8604 | 0.9641 | 0.9579 |
| 3 | 0.8741 | 0.8590 | 0.9526 | 0.9759 |
| 4 | 0.8808 | 0.8367 | 0.9548 | 0.9644 |
| 5 | 0.8087 | 0.8223 | 0.9275 | 0.9741 |
| Mean ± SD |
| Method | Acc (Mean ± SD) | IoU (Mean ± SD) | Dice (Mean ± SD) | Recall (Mean ± SD) | vs. Ours (p-Value) | Effect Size (Cohen’s d) |
|---|---|---|---|---|---|---|
| SG-Unet | 0.9645 ± 0.0028 | 0.8393 ± 0.0035 | 0.8063 ± 0.0041 | 0.9402 ± 0.0047 | <0.001 ** | 1.92 |
| UNet++ | 0.9672 ± 0.0023 | 0.8412 ± 0.0031 | 0.8124 ± 0.0046 | 0.9573 ± 0.0042 | 0.002 ** | 1.37 |
| Swin-UNet | 0.9725 ± 0.0026 | 0.8467 ± 0.0033 | 0.8215 ± 0.0048 | 0.9415 ± 0.0045 | 0.006 ** | 1.05 |
| Ours | 0.9785 ± 0.0019 | 0.8625 ± 0.0027 | 0.8461 ± 0.0030 | 0.9447 ± 0.0038 | / | / |
| Model | SG-UNet | UNet++ | Swin-UNet | Ours |
|---|---|---|---|---|
| DCR | 0.6681 | 0.7022 | 0.6775 | 0.7319 |
| MSRR | 0.9461 | 0.9410 | 0.9398 | 0.9723 |
| Model | Acc | F Score | IoU | Recall |
|---|---|---|---|---|
| Ours | 0.9785 | 0.8461 | 0.8625 | 0.9487 |
| w/o Shape Stream | 0.9553 | 0.7861 | 0.8316 | 0.9235 |
| w/o ASPP | 0.9618 | 0.8243 | 0.8294 | 0.9364 |
| w/o CBAM | 0.9684 | 0.8317 | 0.8437 | 0.9353 |
| r CBAM | 0.9736 | 0.8420 | 0.8573 | 0.9496 |
| Model | Total | Trainable | Non-Trainable | Time | FLOPs |
|---|---|---|---|---|---|
| w/o re-parameterization | 8,885,295 | 8,885,295 | 0 | 62 ms/frame | 287 G |
| w re-parameterization | 8,095,087 | 8,095,087 | 0 | 37 ms/frame | 268 G |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, J.; Wei, Z.; Li, Q.; Liu, J.; Yu, Y.; Yang, D.; Sun, J.; Lu, N.; Zhu, X.; Ma, Z. Large Vessel Segmentation and Microvasculature Quantification Based on Dual-Stream Learning in Optic Disc OCTA Images. Photonics 2025, 12, 588. https://doi.org/10.3390/photonics12060588
Luan J, Wei Z, Li Q, Liu J, Yu Y, Yang D, Sun J, Lu N, Zhu X, Ma Z. Large Vessel Segmentation and Microvasculature Quantification Based on Dual-Stream Learning in Optic Disc OCTA Images. Photonics. 2025; 12(6):588. https://doi.org/10.3390/photonics12060588
Chicago/Turabian StyleLuan, Jingmin, Zehao Wei, Qiyang Li, Jian Liu, Yao Yu, Dongni Yang, Jia Sun, Nan Lu, Xin Zhu, and Zhenhe Ma. 2025. "Large Vessel Segmentation and Microvasculature Quantification Based on Dual-Stream Learning in Optic Disc OCTA Images" Photonics 12, no. 6: 588. https://doi.org/10.3390/photonics12060588
APA StyleLuan, J., Wei, Z., Li, Q., Liu, J., Yu, Y., Yang, D., Sun, J., Lu, N., Zhu, X., & Ma, Z. (2025). Large Vessel Segmentation and Microvasculature Quantification Based on Dual-Stream Learning in Optic Disc OCTA Images. Photonics, 12(6), 588. https://doi.org/10.3390/photonics12060588






