Highly Efficient Digitized Quasi-3D Photolithography Based on a Modified Golomb Coding via DMD Laser Direct Writing
Abstract
1. Introduction
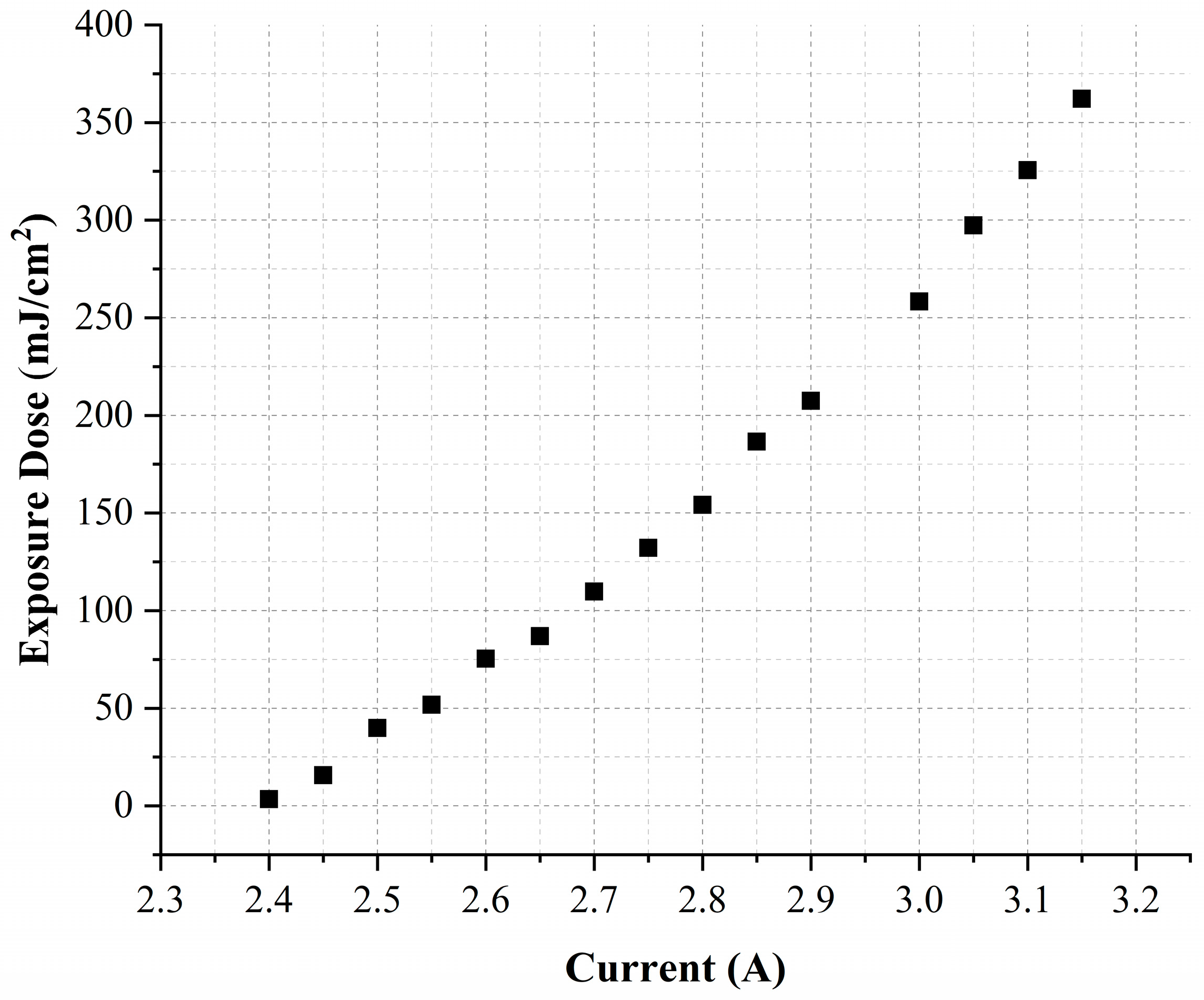
2. The Background of Digitized Quasi-3D Photolithography
3. The Scheme of Quasi-3D Photolithography
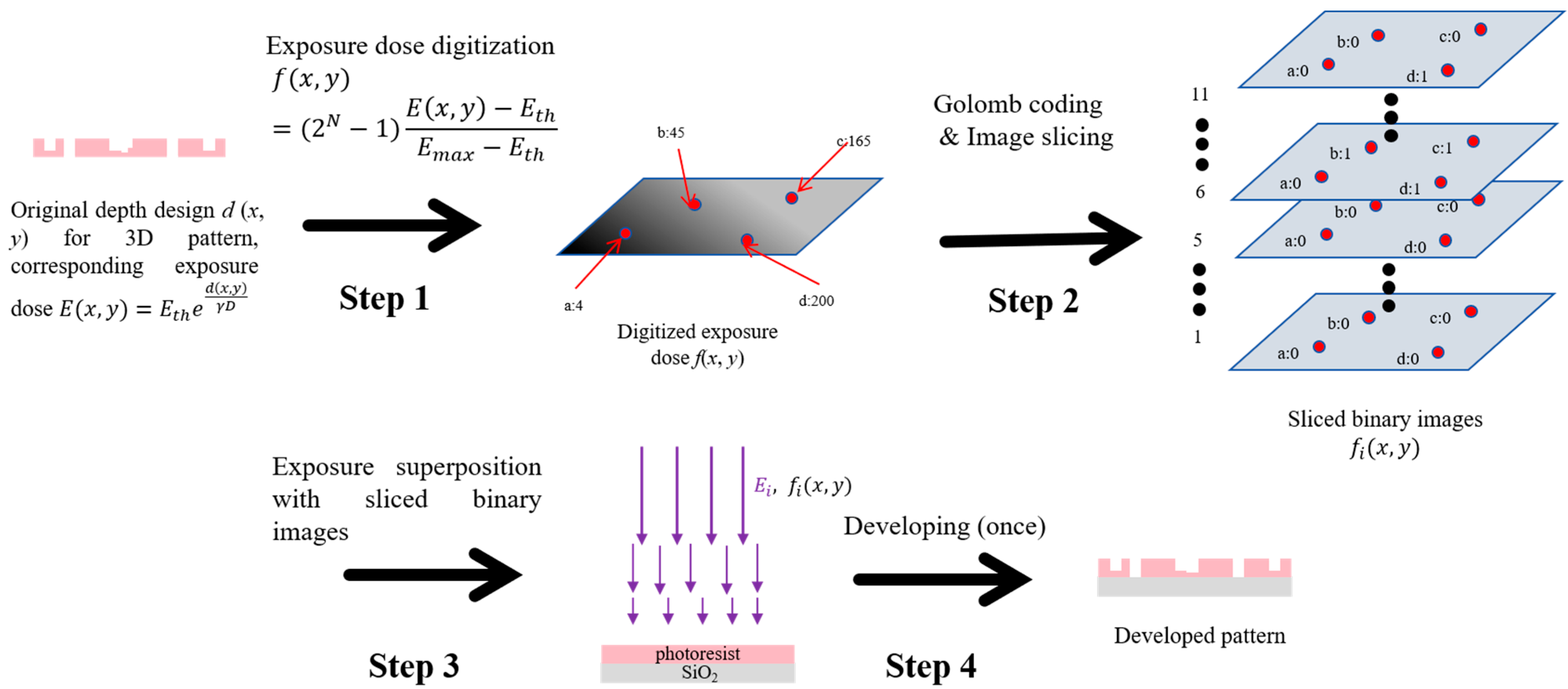
3.1. General Steps of Quasi-3D Photolithography
3.2. Numerical Illustration of Image Slicing with the Golomb Coding
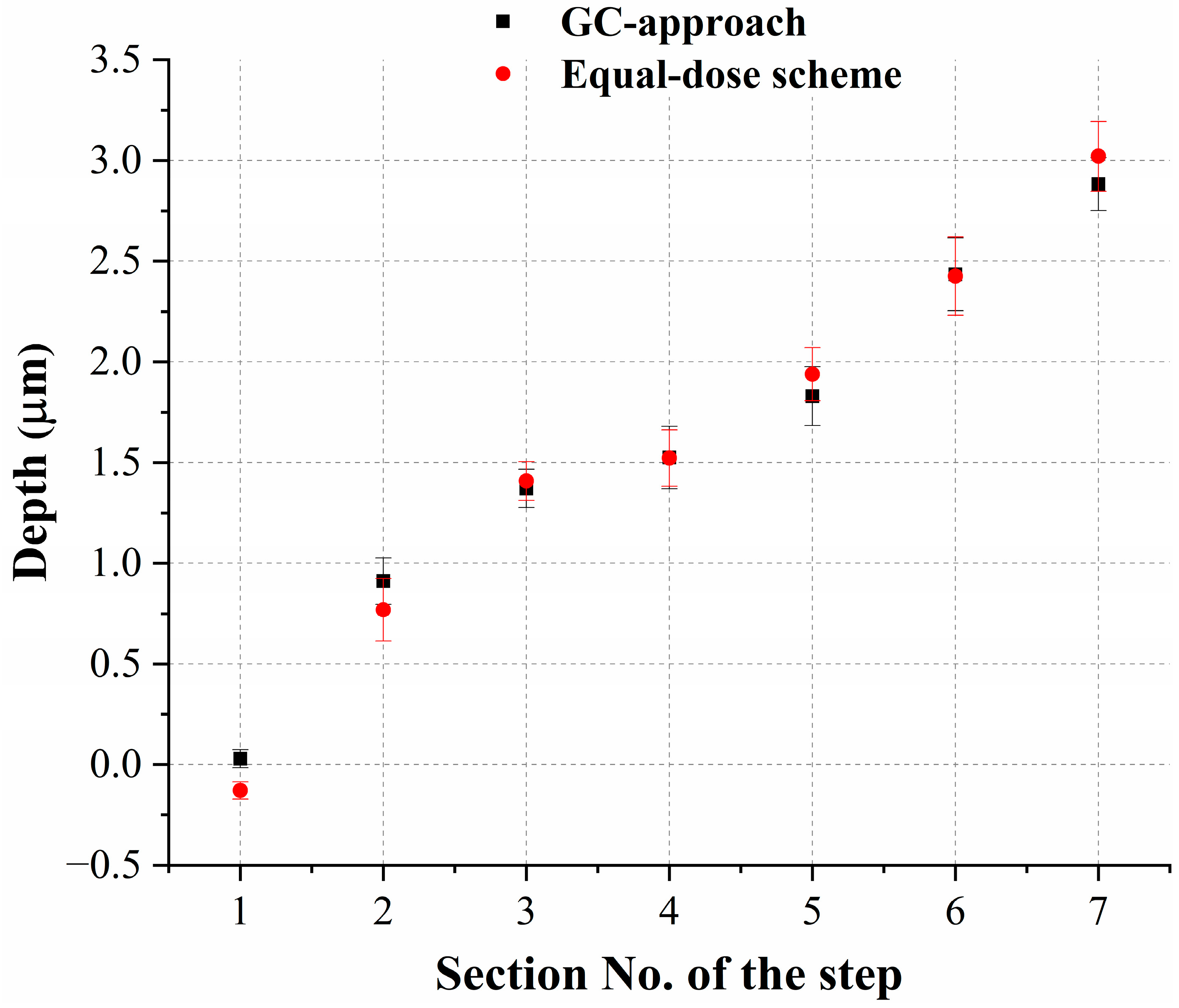
4. The Experimental Results
4.1. One-Dimensional Multi-Step Patterns
4.2. DOEs—2D Multi-Step Patterns
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LDW | Laser direct writing |
| DMD | Digital micromirror device |
| DOE | Diffractive optical device |
| MLA | Microlens array |
| μROE | Micro-refractive optical element |
| GC | Golomb coding |
| LSCM | Laser scanning confocal microscopy |
References
- Lu, J.; Wu, W.; Colombari, F.M.; Jawaid, A.; Seymour, B.; Whisnant, K.; Zhong, X.; Choi, W.; Chalmpes, N.; Lahann, J.; et al. Nano-achiral complex composites for extreme polarization optics. Nature 2024, 630, 860–865. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Hu, G.; Ye, H.; Wei, M.; Guo, Z.; Chen, K.; Liu, C.; Tang, B.; Zhou, G. Mold-free self-assembled scalable microlens arrays with ultrasmooth surface and record-high resolution. Light Sci. Appl. 2023, 12, 143. [Google Scholar] [CrossRef] [PubMed]
- Tong, Z.; Niu, F.; Jian, Z.; Sun, C.; Ma, Y.; Wang, M.; Jia, S.; Chen, X. Micro-refractive optical elements fabricated by multi-exposure lithography for laser speckle reduction. Opt. Express 2020, 28, 34597–34605. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Fan, X.; Liu, Y.; Xu, K.; Zhou, Y.; Zhang, Z.; Chen, F.; Yu, X.; Deng, L.; Gao, H.; et al. 3D nanolithography via holographic multi-focus metalens. Laser Photonics Rev. 2024, 18, 2400181. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.; Zhao, C.; Zhang, L.; Li, J.; Din, S.U.; Wang, Z.; Sun, J.; Torres, S.A.G.; Fan, Z.; et al. Aluminum surface work hardening enables multi-scale 3D lithography. Nat. Mater. 2025, 24, 39–47. [Google Scholar] [CrossRef]
- Skliutas, E.; Merkininkaitė, G.; Maruo, S.; Zhang, W.; Chen, W.; Deng, W.; Greer, J.; von Freymann, G.; Malinauskas, M. Multiphoton 3D lithography. Nat. Rev. Methods Primers 2025, 5, 15. [Google Scholar] [CrossRef]
- Feng, F.; Liu, Y.; Zhang, K.; Yang, H.; Hyun, B.-R.; Xu, K.; Kwok, H.-S.; Liu, Z. High-power AlGaN deep-ultraviolet micro-light-emitting diode displays for maskless photolithography. Nat. Photon. 2025, 19, 101–108. [Google Scholar] [CrossRef]
- Qin, N.; Qian, Z.-G.; Zhou, C.; Xia, X.-X.; Tao, T.H. 3D electron-beam writing at sub-15 nm resolution using spider silk as a resist. Nat. Commun. 2021, 12, 5133. [Google Scholar] [CrossRef]
- Brown, M.A.; Zappitelli, K.M.; Singh, L.; Yuan, R.C.; Bemrose, M.; Brogden, V.; Miller, D.J.; Smear, M.C.; Cogan, S.F.; Gardner, T.J. Direct laser writing of 3D electrodes on flexible substrates. Nat. Commun. 2023, 14, 3610. [Google Scholar] [CrossRef]
- Harinarayana, V.; Shin, Y.C. Two-photon lithography for three-dimensional fabrication in micro/nanoscale regime: A comprehensive review. Opt. Laser Technol. 2021, 142, 107180. [Google Scholar] [CrossRef]
- Singhal, A.; Dalmiya, A.; Lynch, P.T.; Paprotny, I. 2-photon polymerized IP-dip 3D photonic crystals for mid IR spectroscopic applications. IEEE Photonics Technol. Lett. 2023, 35, 410–413. [Google Scholar] [CrossRef]
- Gonzalez-Hernandez, D.; Varapnickas, S.; Merkininkaitė, G.; Čiburys, A.; Gailevičius, D.; Šakirzanovas, S.; Juodkazis, S.; Malinauskas, M. Laser 3D printing of inorganic free-form micro-optics. Photonics 2021, 8, 577. [Google Scholar] [CrossRef]
- Hwang, E.; Hong, J.; Yoon, J.; Hong, S. Direct writing of functional layer by selective laser sintering of nanoparticles for emerging Applications: A Review. Materials 2022, 15, 6006. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-M.; Shin, Y.-K.; Seo, M.-H. Development of shape prediction model of microlens fabricated via diffuser-assisted photolithography. Micromachines 2023, 14, 2171. [Google Scholar] [CrossRef]
- Luan, S.; Peng, F.; Zheng, G.; Gui, C.; Song, Y.; Liu, S. High-speed, large-area and high-precision fabrication of aspheric micro-lens array based on 12-bit direct laser writing lithography. Light Adv. Manuf. 2022, 3, 47. [Google Scholar] [CrossRef]
- Chen, J.T.; Zhao, Y.-Y.; Guo, X.; Duan, X.-M. Deep learning-driven digital inverse lithography technology for DMD-based maskless projection lithography. Opt. Laser Technol. 2025, 180, 111578. [Google Scholar] [CrossRef]
- Choi, J.; Kim, G.; Lee, W.-S.; Chang, W.S.; Yoo, H. Method for improving the speed and pattern quality of a DMD maskless lithography system using a pulse exposure method. Opt. Express. 2022, 30, 22487–22500. [Google Scholar] [CrossRef]
- Zhong, K.; Gao, Y.; Li, F.; Luo, N.; Zhang, W. Fabrication of continuous relief micro-optic elements using real-time maskless lithography technique based on DMD. Opt. Laser Technol. 2014, 56, 367–371. [Google Scholar] [CrossRef]
- Dinh, D.-H.; Chien, H.-L.; Lee, Y.-C. Maskless lithography based on digital micromirror device (DMD) and double sided microlens and spatial filter array. Opt. Laser Technol. 2019, 113, 407–415. [Google Scholar] [CrossRef]
- Gao, Y.; He, S.; Luo, N.; Rao, Y. Research on dynamical-gradual greyscale digital mask lithography. J. Mod. Optic. 2011, 58, 573–579. [Google Scholar] [CrossRef]
- Golomb, S. Run-length encodings (Corresp.). IEEE T. Inform. Theory 1966, 12, 399–401. [Google Scholar] [CrossRef]
- Stern, M.B. Binary optics: A VLSI-based microoptics technology. Microelectron. Eng. 1996, 32, 369–388. [Google Scholar] [CrossRef]
- Levy, U.; Mendlovic, D.; Marom, E. Efficiency analysis of diffractive lenses. J. Opt. Soc. Am. A 2001, 18, 86–93. [Google Scholar] [CrossRef] [PubMed]
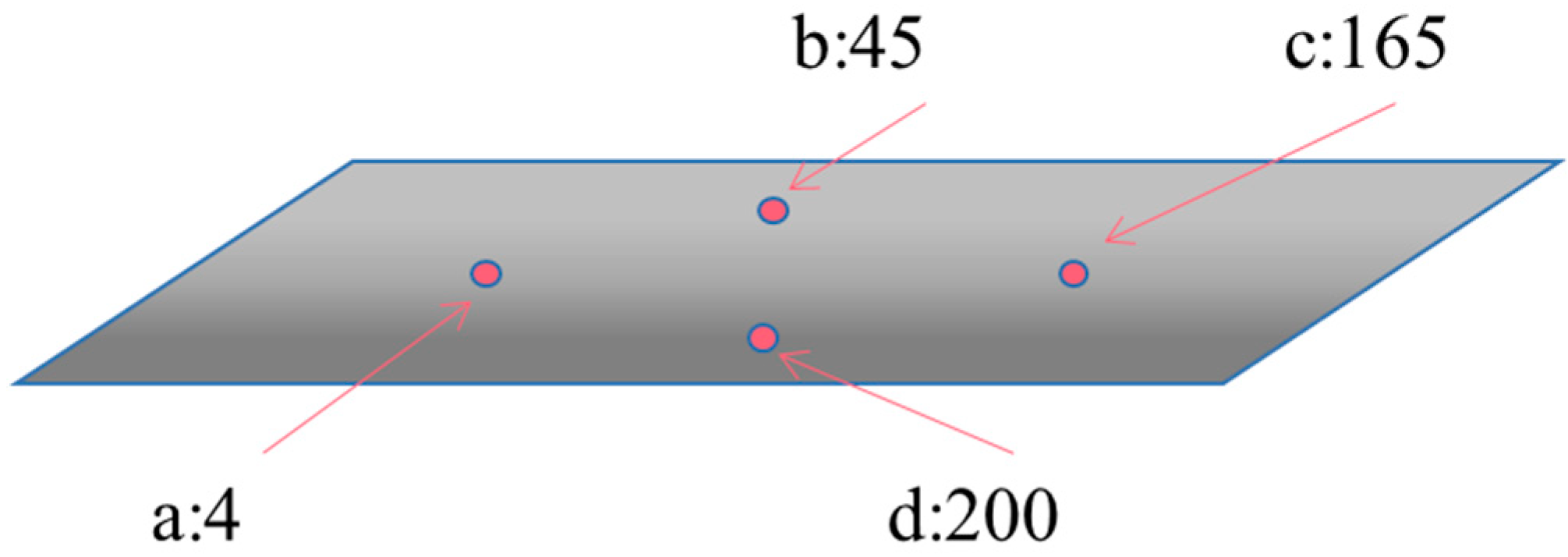
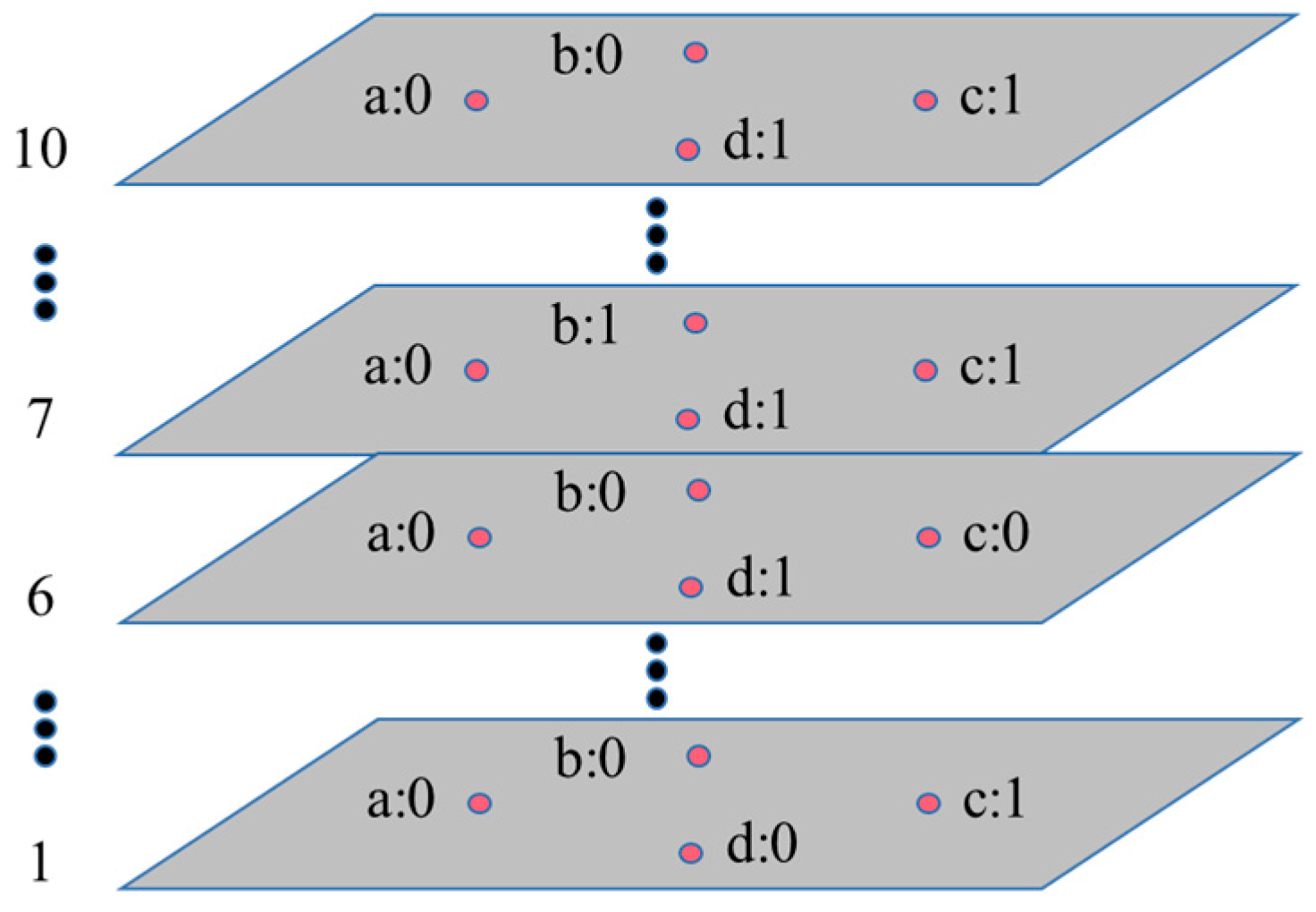



| Point | Seg. 1 of Golomb Coding | Seg. 2 of Golomb Coding |
|---|---|---|
| a | 0000 | 000100 |
| b | 0001 | 000100 |
| c | 1111 | 000001 |
| d | 1111 | 100100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Huang, Z.; Shen, Y.; Zhou, S. Highly Efficient Digitized Quasi-3D Photolithography Based on a Modified Golomb Coding via DMD Laser Direct Writing. Photonics 2025, 12, 587. https://doi.org/10.3390/photonics12060587
Wang H, Huang Z, Shen Y, Zhou S. Highly Efficient Digitized Quasi-3D Photolithography Based on a Modified Golomb Coding via DMD Laser Direct Writing. Photonics. 2025; 12(6):587. https://doi.org/10.3390/photonics12060587
Chicago/Turabian StyleWang, Hui, Zhe Huang, Yanting Shen, and Shangying Zhou. 2025. "Highly Efficient Digitized Quasi-3D Photolithography Based on a Modified Golomb Coding via DMD Laser Direct Writing" Photonics 12, no. 6: 587. https://doi.org/10.3390/photonics12060587
APA StyleWang, H., Huang, Z., Shen, Y., & Zhou, S. (2025). Highly Efficient Digitized Quasi-3D Photolithography Based on a Modified Golomb Coding via DMD Laser Direct Writing. Photonics, 12(6), 587. https://doi.org/10.3390/photonics12060587






