Multi-Partition Mapping Simulation Method for Stellar Spectral Information

Abstract

Stellar radiation simulation is critical in the space industry; however, with the current simulation methods, only a single color temperature and magnitude can be modulated at a time. Furthermore, star sensors rely on star observation tests for accurate calibration; this seriously restricts their development. This paper presents a novel star spectral information multi-partition mapping simulation method to closely simulate real sky star map information, thus replacing non-scenario-specific field stargazing experiments. First, using the stellar spectral simulation principle, a multi-partition mapping principle based on a digital micro-mirror device is proposed, and the theoretical basis of sub-region division is provided. Second, multi-component mapping simulation of stellar spectral information is expounded, and a general architecture for the same based on a double-prism symmetry structure is presented. Next, the influence of peak spectral half-peak width and peak interval on spectral simulation accuracy is analyzed, and a pre-collimated beam expansion system, multi-dimensional slit, and spectral splitting system are designed accordingly. Finally, a test platform is set up, and single-region simulation results and multi-region consistency experiments are conducted to verify the feasibility of the proposed method. Our method can realize high-precision simulation and independently control the output of various color temperatures and magnitudes. It provides a theoretical and technical basis for the development of star sensor ground calibration tests and space target detection light environment simulation.

1. Introduction

Deep space exploration is characterized by large communication delays between the spacecraft and ground, numerous unknown factors in the flight environment, few braking acquisition opportunities, and high operational autonomy requirements of the spacecraft. Terrestrial radio navigation is unable to meet the needs of continuous and real-time measurements. Currently, astronomical angle measurement, pulsar ranging, and spectral velocity measurement navigation using stellar spectral information are the only effective means of autonomous navigation for deep space exploration. With the increasing number and complexity of satellite missions, the development of large-scale cluster networking has become inevitable. The accuracy of satellite instantaneous velocities provided by spectral velocity measurements has become an important prerequisite for determining the safe operation and cooperative control of star clusters in orbit. Simulating stellar spectral radiation characteristics with high consistency multi-channel synchronization and cooperative control on the ground, ensuring authenticity and reliability of the performance verification of automatic navigation and cooperative control in the constellation networking, and supplementing experimental conditions for accurate calibration and performance verification of emerging navigation methods poses a challenge to their development, principles, and technologies in satellite navigation and cluster cooperative control.

Presently, there are two main stellar spectral information simulation methods; one involves a variety of peak wavelength LED mixed simulation methods, and the other is a space light modulation method. Within these, the LED hybrid simulation method mainly uses a variety of peak wavelengths of narrow-band LEDs through the adjustment of different wavelengths of LED radiation energy [1,2,3]; however, the lack of LED types limits the simulation accuracy of this method [4]; therefore, the use of a wide spectrum light source as the base light source, and a variety of peak wavelength LEDs to simulate the target spectral details to compensate for and adjust the spectral simulation method is preferred [5,6,7]. Although the single-point spectral simulation accuracy of this method can reach 10–15%, it is limited by principle and cannot achieve the characteristic spectral resolution required by spectral velocity measurement navigation [8,9].

The spatial light modulation method uses optical methods to accurately subdivide the wide spectral beam; it then projects the subdivided beam on a spatial light modulator and uses the spatial light modulator to achieve pixel-level beam modulation and output. Its beam resolution and monochromaticity are far superior to those of a number of peak wavelength LED hybrid simulation methods; hence, the former is a more ideal stellar spectral information simulation method. Zhai et al. described the design of a tunable digital micro-mirror device (DMD) spectral source using a prism as a distribution mechanism. However, owing to the nonlinear dispersion of the prism, its spectral resolution gradually decreases with decreasing wavelength, which affects the accuracy of spectral modeling [10]. Ma et al. designed a spectral tunable light source based on the Offner configuration of DMD and a convex grating. Although the convex grating has good aberration correction ability, it requires a large slit to acquire sufficient energy, resulting in lower spectral resolution bandwidth of monochromatic light [11]. Xu et al. proposed a design method for a spectrally tunable light source optical system of a star simulator based on DMD; this method has a high simulation accuracy of the wideband spectrum; however, it is limited by the slit size of the system, and its energy utilization is extremely low [12]. Wang et al. used the spatial light modulation characteristics of DMD to develop a tunable double-grating spatial spectrum based on the Ebert–Fastie structure [13]; they improved the spectral correction capabilities and produced narrow-band spectral output. The uncertainties of the system’s spectral radiation were 14.68%, 1.54%, and 1.48% at 450, 550, and 654.6 nm, respectively. However, the spectral modulation and output beam monochromatic capabilities of the system were still inadequate. Xu et al. improved the tunable light source for stellar spectral simulation, and enhanced the system’s energy utilization by increasing the inlet slit width from 0.4 to 8 mm [12].

In summary, although the stellar spectrum simulation method has been developed from the mixed simulation method of the LED with multiple peak wavelengths to the spatial light modulation method, and considerable progress has been made in terms of the principles, device, output spectral resolution, and other performance indicators, stellar spectrum simulation devices can only achieve a single output of the spectral radiation characteristics of a star [14,15]. Hence, multi-channel stellar spectrum ground calibration required for automatic navigation and cooperative control in the current international cluster networking can only be realized by networking multiple sets of stellar spectrum simulation devices [16,17]. At the same time, owing to the inherent differences among these multiple sets, it is difficult to calibrate and quantify them [18,19]. As a result, a gap still exists between the current multi-channel stellar spectrum ground calibration experiments and the natural working environment of star observation in a cluster network; consequently, the requirements of ground performance verification required for automatic navigation and cooperative control in the cluster network cannot be adequately met.

Therefore, a multi-component mapping simulation method for stellar spectral information was proposed in this study. By dividing the region of the spatial light modulator, multi-channel independent output control under the condition of one beam input source was realized. By ensuring the high resolution of the output characteristic spectrum, the inconsistent error sources in the ground performance verification experiment were effectively reduced. The proposed method is of considerable significance to study and verify new methods for aspects such as astronomical spectrum test navigation, and new schemes for autonomous coordination and allocation for cluster tasks, to enrich the observation of deep space probe navigation in different flight stages, and provide effective cluster coordination strategies and control methods.

2. Principle of Multivariate Mapping Simulation of Stellar Spectral Information

2.1. Principle of Stellar Spectral Information Simulation

The spectral information of stellar radiation is related to its surface temperature, and usually, the star is equivalent to an ideal blackbody. Therefore, in the visible and near infrared bands, the stellar radiation can be approximated to blackbody radiation at a certain temperature. When the colors of the radiation of the stars and a blackbody are the same at a certain temperature, the temperature of the blackbody is called the color temperature of the star. At this time, Planck’s formula can be used to characterize the spectral radiation distribution of a blackbody [1,20]; therefore, the spectral information of the star at a certain color temperature can be expressed as

$$M_{\lambda B}\left(\lambda ,T\right)={\displaystyle \frac{2\pi h{c}^2}{{\lambda }^5}}\cdot {\displaystyle \frac{1}{exp\left(\frac{hc}{kT\lambda }\right)-1}}$$

(1)

where $M_{\lambda B}\left(\lambda ,T\right)$ is the blackbody spectral radiation exitance [$\mathrm{W}\cdot {\mathrm{cm}}^{-2}\cdot \mathrm{nm}$]; $\lambda$ is the specified radiation wavelength [$\mathrm{nm}$]; $T$ is the thermodynamic temperature of the blackbody [$\mathrm{K}$]; $h$ is the Planck’s constant [$h=6.6256\times {10}^{-34} \mathrm{W}\cdot {\mathrm{s}}^2$]; $k$ is the Boltzmann constant [$k=1.38054\times {10}^{-23} \mathrm{W}\cdot \mathrm{s}\cdot {\mathrm{K}}^{-1}$]; and $c$ is the speed of light in vacuum [$c=2.99793\times {10}^{10} \mathrm{cm}\cdot {\mathrm{s}}^{-1}$].

Currently, the spectral response range of astronomical navigation equipment is typically between 500 and 800 nm. With 80% of the stars being at temperatures between 3000 and 9000 K [21], the spectral information of stars within this color temperature range at 1000-K intervals can be illustrated as shown in Figure 1.

The spectral information curve of stars is a continuous smooth curve (Figure 1). Therefore, according to the principle of spectral superposition, the spectral information of stars can be simulated and transformed into a scalar summation of spectral superposition units in different band ranges, which can be expressed as

$$L\left(\lambda ,{\rm T}\right)=k_T{M}_{\lambda B}\left(\lambda ,T\right)={\displaystyle \sum K_i{S}_i\left(\lambda \right)}$$

(2)

In Equation (2), $L\left(\lambda ,{\rm T}\right)$ is the spectral information curve of a certain color temperature; $k_T$ is the proportionality coefficient between the spectral radiation energy of the star and ideal blackbody radiation energy; $S_i\left(\lambda \right)$ is the spectral curve distribution function of the spectral superposition unit of different bands, as it is the smallest spectral segment of the spectral superposition (also called the unit spectrum segment); and $K_i$ is the radiation coefficient of the corresponding unit spectral segment.

From Equation (2), stellar spectral simulation is essentially the solution of the radiation coefficient $K_i$ of different unit spectral segments $S_i\left(\lambda \right)$. The greater the number of $S_i\left(\lambda \right)$s, the better the independence; the more accurate the control of the radiation coefficient $K_i$, the higher the simulation accuracy of the target spectrum, and the better the dynamic modulation capability of the spectrum. However, $S_i\left(\lambda \right)$s of an infinite subdivisional unit with peak wavelength cannot be obtained in an actual stellar spectral simulation process; therefore, the solution of $K_i$ in Equation (2) can be converted into a mathematical problem of finding the least quadratic solution of the overdetermined Equation (2) [7].

2.2. Multi-Partition Mapping Principle Based on DMD

The spatial light modulation spectral simulation method uses the dispersion principle to subdivide wide spectral beams, separate spectra of different wavelengths at different angles, and form a continuous set of spectral segments arranged in wavelength order on the DMD entire surface; this continuous set is regarded as a two-dimensional spectral distribution curve [12], as shown in Figure 2. Then, by controlling the switching state of the elemental lens on the DMD array surface, the modulation and control of the spectral segments of different elements are completed, and the simulation of the spectral information of the stars is finally realized.

According to Figure 1, in the normalized spectral curve over the color temperature range 3000–9000 K, the ratio $t$ of maximum to minimum radiation energies at 3000 K can be expressed as

$$t={\displaystyle \frac{I{\left(\lambda \right)}_{\max }}{I{\left(\lambda \right)}_{\min }}}$$

(3)

Here, $I{\left(\lambda \right)}_{\max }$ is the radiation energy at 800 nm after the normalization of 3000 K color temperature, that is, $I{\left(800\right)}_{\max }=1.0$; $I{\left(\lambda \right)}_{\min }$ is the radiation energy at 500 nm after the normalization of 3000 K color temperature, that is, $I{\left(500\right)}_{\min }=0.28$; this is substituted in Equation (3) to obtain $t=3.57$.

Under ideal conditions, the weight modulation ratio of the unit spectral segment is greater than 3.57; assuming that the spectral simulation error is less than 10%, the weight subdivision modulation accuracy of the unit spectral segment is higher than 3.57/10%; that is, under ideal conditions, as long as the radiation coefficient adjustment ratio is higher than 35.7, it can meet the spectral information modulation requirements of the spectral simulation error of 10%. As the resolution of the DMD is considerably higher than 35.7, when the entire DMD array surface is used to complete a single spectrum modulation, a large adjustment margin still exists on the array surface; that is, most pixels are in the off state and do not participate in spectral modulation. Therefore, the DMD array surface can be partitioned to realize the multi-channel stellar spectrum mapping simulation using a single DMD device with a light source.

To ensure that each sub-region of the DMD after zoning has sufficient adjustment ability, the resolution of the DMD sub-intervals was set to m×n (where m and n represent the dispersion and modulation directions, respectively); the difference multiple of the highest and lowest energies of the simulated target color temperature curve is $t$; and the simulation accuracy index is $c$; then, theoretically the modulation capability of the sub-region must satisfy the following relation:

$$n\ge {\displaystyle \frac{t}{c}}$$

(4)

3. Multi-Component Mapping Simulation of Stellar Spectral Information and System Design

3.1. Analysis of Multi-Component Mapping Simulation of Stellar Spectral Information

According to the principle of multi-component mapping simulation of stellar spectral information, the central concept of simulation is divided into two steps: DMD partition modulation and its corresponding output, of which DMD partition modulation is the core step.

(1)

Using the spectral optical system based on the principle of optical dispersion and combining with the spatial light modulation characteristics of DMD [7], the multi-component mapping spectral modulation system of stellar spectral information is composed, so that the subdivided wide spectral beam is partitioned. That is, the DMD modulation region is partitioned, and the simulation of a single spectral curve in the whole region is changed to the independent modulation of each region after the regional division. Therefore, a higher energy utilization rate is needed to compensate for the weak energy of the sub-region. Presently, most of the energy is located in the 0-order diffraction, which cannot be applied, and the energy utilization rate is low. As a prism has no diffraction effect and no energy loss, it is selected as the dispersive element of the multicomponent mapping spectral modulation system of stellar spectral information in this study. The spectral modulation system will be elaborated in Section 3.2 and Section 4.

(2)

After the multi-component mapping spectral modulation system completes the spectral modulation in each sub-region of the DMD, the beams in each sub-region of the DMD are non-uniform and are arranged adjacent according to the sequence of the regions. To evenly mix the beams in different sub-regions of the DMD and output them, a multi-channel integrating sphere coupling system is adopted. The multi-channel output fiber completes the beam output. Each integrating sphere in the multi-channel integrating sphere coupling system is dislocated in turn, and the light beam in the corresponding sub-region is deflected by the reflector to make it merge into the corresponding integrating sphere channel.

3.2. Design of the Overall Structure of the Multicomponent Mapping Spectral Modulation System for Stellar Spectral Information

In the multivariate mapping simulation, we need to utilize the entire DMD receiving surface for partitioning and debugging, between the DMD regions, and the modulated beams are very compatible with each other before the output. At the same time, considering that the deflection angle of the DMD is along the diagonal direction and not in the same plane as the incident beam, the outgoing divergent beams would inevitably interfere with each other, resulting in an overflow of the beam in a single channel.

To solve this problem, the structure of the double prism is symmetrically placed; the beam is divided by the first prism; and the second prism re-collimates the beam after the separation, so that the beam incident on the DMD is a parallel beam, and the output is also a parallel beam after the DMD reflection modulation; this effectively avoids the influence of the divergent beam caused by the structure of the traditional spectral modulation system.

At the same time, because the spectral resolution of the double-prism symmetrical placement structure depends on the dispersion coefficient of the prism and size of the slit, the larger the slit size, the higher the system energy, the lower the spectral resolution, and the lower the spectral simulation accuracy. The smaller the slit size, the lower the system energy, the higher the spectral resolution, and the higher the spectral simulation accuracy. In addition, the quality and collimation of the incident slit beam also have a significant influence on the spectral resolution.

Therefore, to integrate the energy and spectral simulation accuracy of the system, it is necessary to design a pre-collimated beam-expanding system with better beam quality and collimation to replace the collimated objective lens (usually composed of a single mirror) in the traditional spectral modulation system, and add a multi-size slit, that is, a slit group composed of a wide slit and a narrow slit distributed up and down. Each DMD region corresponds to a slit group, and a wide slit can improve the energy of the system; however, the spectral modulation ability is low, and a narrow slit can improve the spectral modulation capability of the system; conversely, its passing energy is small; therefore, the matching of the wide slit can effectively increase the modulation capability of the system and energy utilization rate of the system. The overall structure of the spectral modulation system based on multivariate mapping of stellar spectral information is shown in Figure 3.

3.3. Overall Design of Multivariate Mapping Simulation System for Stellar Spectral Information

Based on the overall structure of the multi-component mapping spectral modulation system, a supercontinuous laser light source, pre-collimated beam expanding system, DMD, spectral splitting system, multi-channel integrating sphere coupling system, and multi-output fiber group are added to form the multi-component mapping simulation system architecture of stellar spectral information, as shown in Figure 4.

The light source emits a wide spectral beam covering a range of 500–800 nm. The beam passes through the pre-collimated beam expansion part of the modulation system and fills the entire DMD array surface in the non-dispersive direction. After the beam is expanded, it enters the beam splitting system with double prisms placed symmetrically through multi-dimensional slits. After the beam splitting and collimating, the beam is incident on the DMD array plane in parallel. As the propagation direction of the beam does not change in the entire system, the beam is incident on the DMD array plane in a collimated state, and after modulation by the DMD micro-mirror, it is discharged as an oblique collimated beam. Light modulated by the overall structure of the multicomponent mapping spectral modulation system for stellar spectral information is incident on the multi-channel integrating sphere coupling system. The modulated target spectrum enters the integrating sphere group through the multi-channel coupling system for light mixing and is outputted through the multi-channel output fiber group to realize the independent modulation of each analog star point color temperature and magnitude.

The basis for the selection and specific parameters of the supercontinuum laser light source, DMD, and multi-channel integrating sphere coupling system components are as follows:

(1)

Supercontinuous laser light source:

SC-PRO (YSL Photonics, Wuhan, China), which is a wide-spectrum laser light source, was employed in this research. SC-PRO has clear advantages in the collimation and energy density of the output beam compared with a traditional xenon lamp or tungsten halide light source. The main parameters and spectral data of the SC-PRO light source are presented in

Table 1. Key parameters of SC-PRO light source.

Parameter	Value
Spectral range	420–2400 nm
Maximum optical power	8 W ± 0.5 W
Output spot size	2 mm
Angle of divergence	0.0859° ± 0.0005°

and Figure 4, respectively.

(2)

DMD

In this study, DLP6500 was selected as the modulator for system design and feasibility verification, with a resolution of 1920 × 1080, single pixel size of 7.4 μm, and pixel deflection angle of ±12° along the diagonal direction; according to the DMD deflection direction and requirements and rationalization of the optical element arrangement, the resolution-1920 direction was chosen as the dispersion direction and resolution-1080 direction as the modulation direction. The DMD parameters are presented in

Table 2. Key parameters of DMD.

Parameter	Value
DMD model	DLP6500
Resolution	1920 × 1080
Single pixel size	7.4 μm
Pixel deflection angle	In a diagonal direction ±12°

.

(3)

Multi-channel integrating sphere coupling system

The multi-channel integrating sphere coupling system is mainly composed of an integrating sphere and a reflector. The function of the integrating sphere is to mix the light processing of the beam in the corresponding modulation area so that the beam is evenly emitted; conversely, the function of the reflector is to act as a mechanical interference between the integrating sphere and the incident beam. It is arranged successively through the reflector group at a clip angle of 45° with the incident beam and reflected by 90°. Through the focusing lens, the beam is coupled to the integrating sphere. The arrangement of the integrating sphere, mirror, and coupled lens is shown in Figure 5.

To facilitate the compact arrangement of the integrating sphere between the regions, the selected integrating sphere size should be as small as possible; therefore, an integrating sphere with a diameter of 15 mm, made of PTFE, and having a reflectivity of higher than 85% in the spectral range of 200–2400 nm was chosen. The integrating sphere has two openings, one of 5 mm size, acting as the entrance for the incident beam, and the other of 2 mm size. The SMA905 optical fiber base is used to connect the output fiber. The integrating sphere parameters are presented in

Table 3. Parameters of multi-channel integrating sphere.

Parameter	Value
Diameter	15 mm
Materials	PTFE
Reflectance	Higher than 85% in the 200–2400 nm range
Diameter of the incident optical port	5 mm
Exit port diameter	2 mm

.

(4)

Multi-output optical fiber group

Each fiber in the multi-output fiber group is connected with the corresponding integrating sphere, and the beam with specific star color temperature information and magnitude information is derived to realize the simulation of the real star map with multi-color temperature and multi-magnitude. The optical fiber in the multi-output fiber is made of a quartz material, namely SMA905 optical fiber head, with a core diameter of 50 μm and NA (optical fiber numerical aperture) of 0.2. Its spectral range spans 200–2400 nm. The optical fiber parameters are presented in

Table 4. Parameters of optical fiber.

Parameter	Value
Fiber type	Step-Index Fiber, SI
Material	Quartz
Optical fiber head	SMA905
Core diameter	50 μm
NA	0.2
Spectral range	200–2400 nm

.

4. Design Optimization of Multivariate Mapping Spectral Modulation System

4.1. Effect of Spectral Simulation Accuracy on Half-Peak Width and Peak Interval of Peak Spectrum of Unit Spectrum Segment

According to the principle of spectral synthesis, the more unit spectrum segments participate in the simulation (the higher the $S_i\left(\lambda \right)$ number) and the higher the adjustment range of the radiation system (the larger the numerical value of $K_i$), the higher the simulation accuracy and modulation capability of the spectrum [22,23]; however, more $S_i\left(\lambda \right)$s means that the system has higher requirements for spectral resolution; thus, the complexity of the system will be higher [10,11,24], which is not conducive to system design. Therefore, starting from the spectral half-peak width and peak interval, combined with the principle of spectral superposition, an analysis of how they would affect the spectral simulation accuracy is necessary.

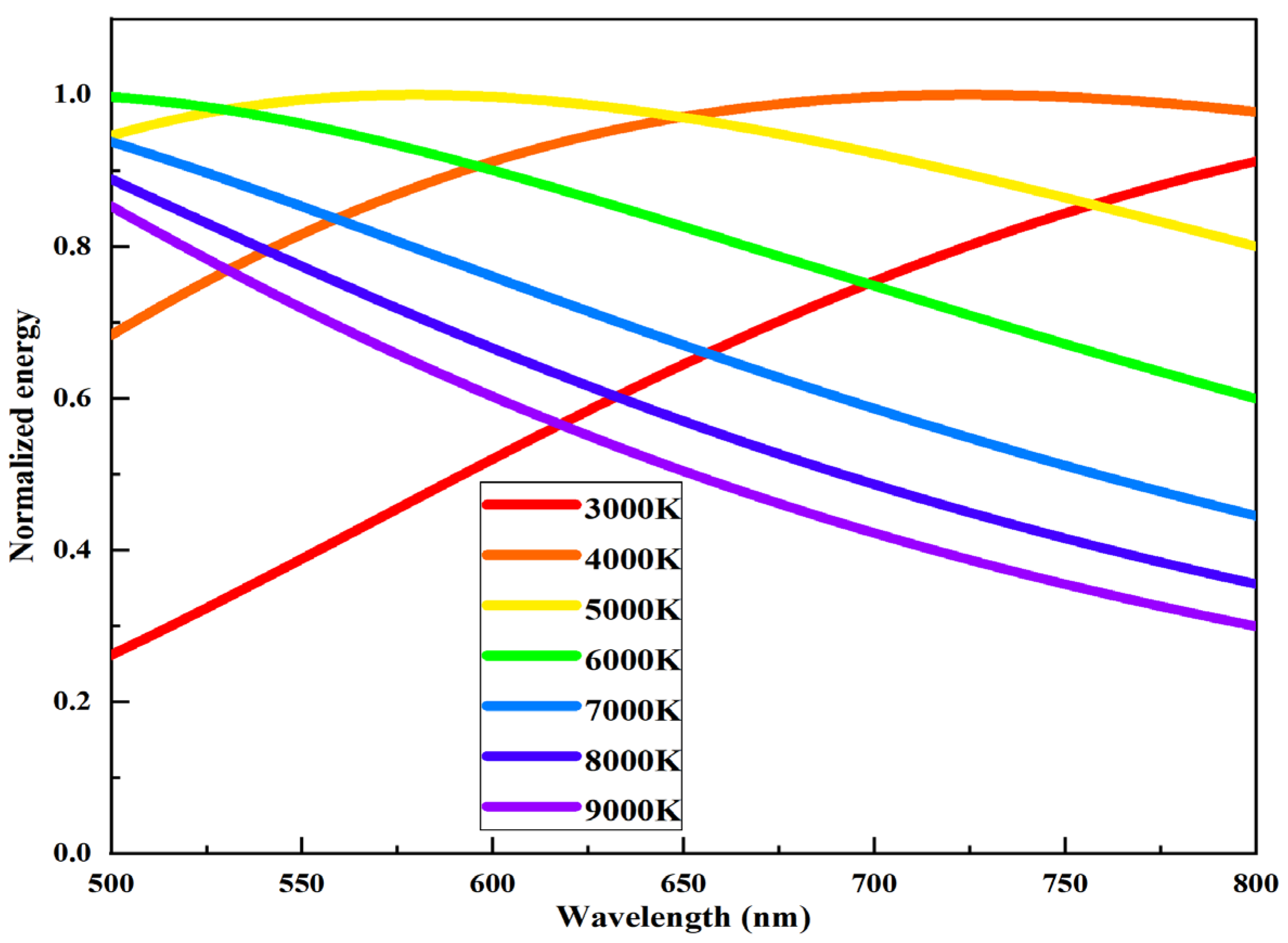
Using the Gaussian distribution model to simulate the element spectrum $S_i\left(\lambda \right)$, the same can be expressed as:

$$S\left({\lambda }_i\right)=\tau ·exp\left[\frac{-(\lambda -{\lambda }_i{)}^2}{2{\omega }^2}\right]$$

(5)

Here ${\lambda }_i$ is the peak wavelength; $\tau$ is the scale coefficient; and $\omega$ is the spectral half-peak width coefficient. By setting different values for ${\lambda }_i$ and $\omega$, different peak intervals and $\omega$ were simulated and analyzed to explore how they would affect the spectral simulation accuracy.

$\omega$ values of 10, 20, and 50 nm, and wavelength peak intervals ($\Delta \lambda$) of 5, 10, and 20 nm were considered to simulate the three color temperatures of 3000, 6000, and 9000 K. Finally, the target and simulation spectra were normalized and analyzed.

(1)

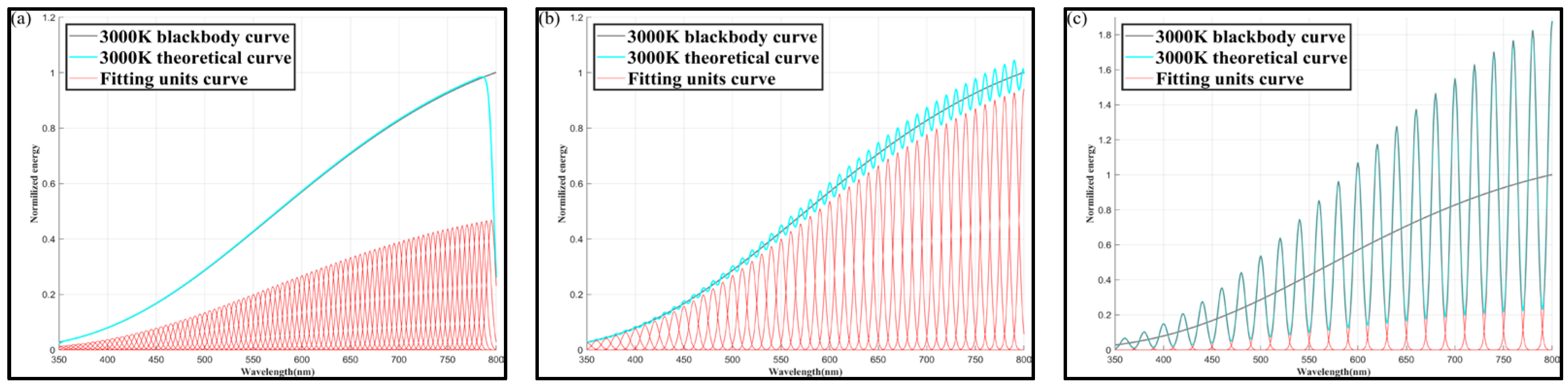
Simulation results for 3000 K color temperature:

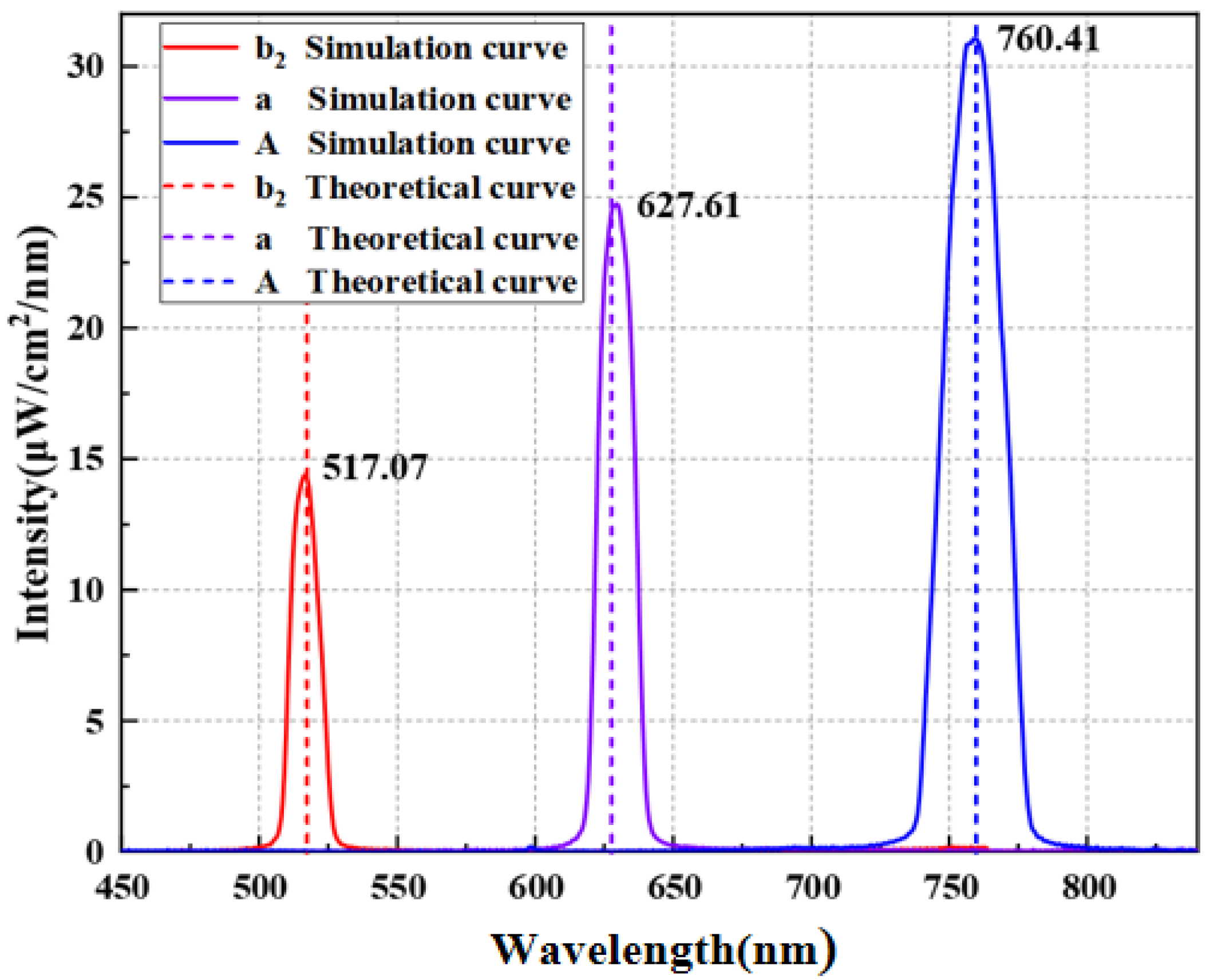
➀ Figure 6 shows the color temperature simulation results at $\omega$ = 10 nm, for $\Delta \lambda$ values of 5, 10, and 20 nm.

➁ Figure 7 shows the color temperature simulation results at $\omega$ = 20 nm, for $\Delta \lambda$ values of 5, 10, and 20 nm.

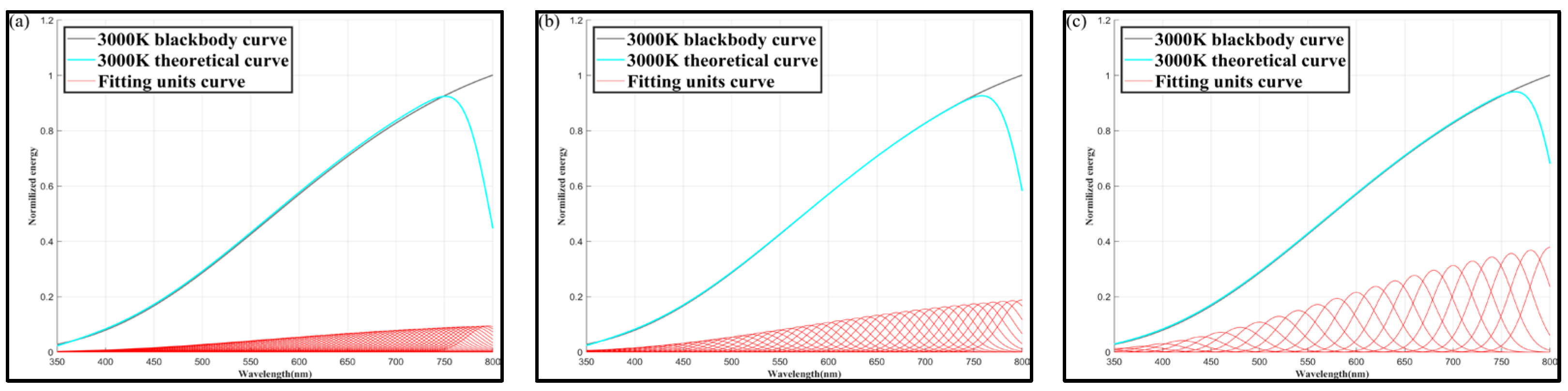
➂ Figure 8 shows color temperature simulation results at $\omega$ = 50 nm, for $\Delta \lambda$ values of 5, 10, and 20 nm.

(2)

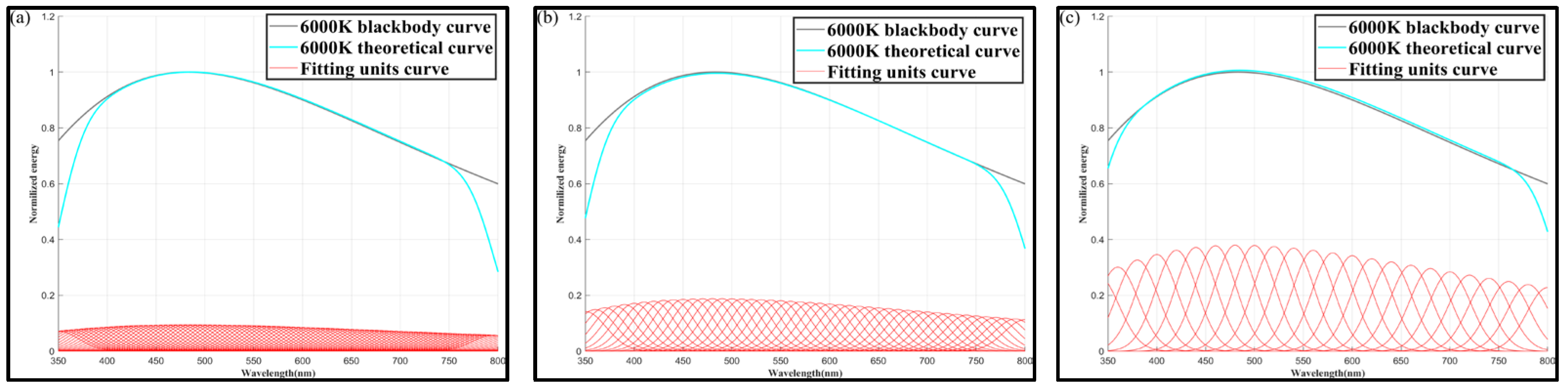
Simulation results for 6000 K color temperature:

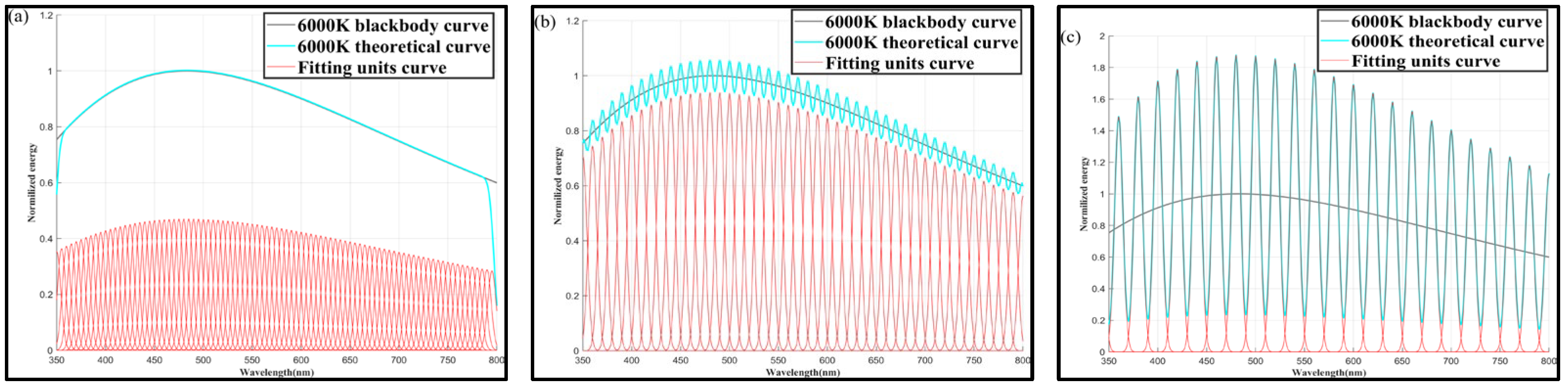
➀ Figure 9 shows the color temperature simulation results at $\omega$ = 10 nm, for $\Delta \lambda$ values of 5, 10, and 20 nm.

➁ Figure 10 shows the color temperature simulation results at $\omega$ = 20 nm, for $\Delta \lambda$ values of 5, 10, and 20 nm.

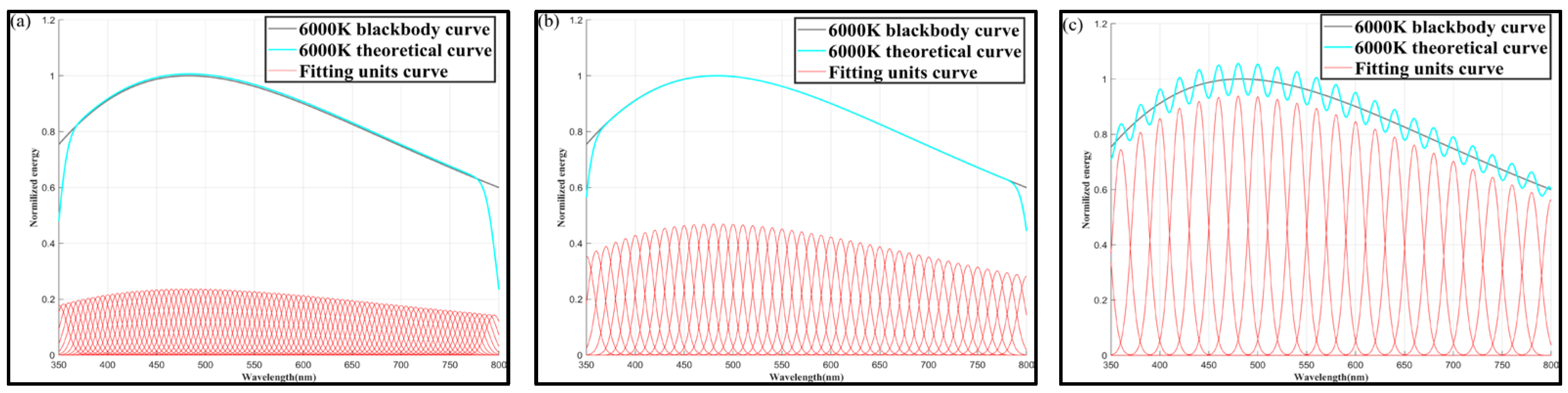
➂ Figure 11 shows the color temperature simulation results at $\omega$ = 50 nm, for $\Delta \lambda$ values of 5, 10, and 20 nm.

(3)

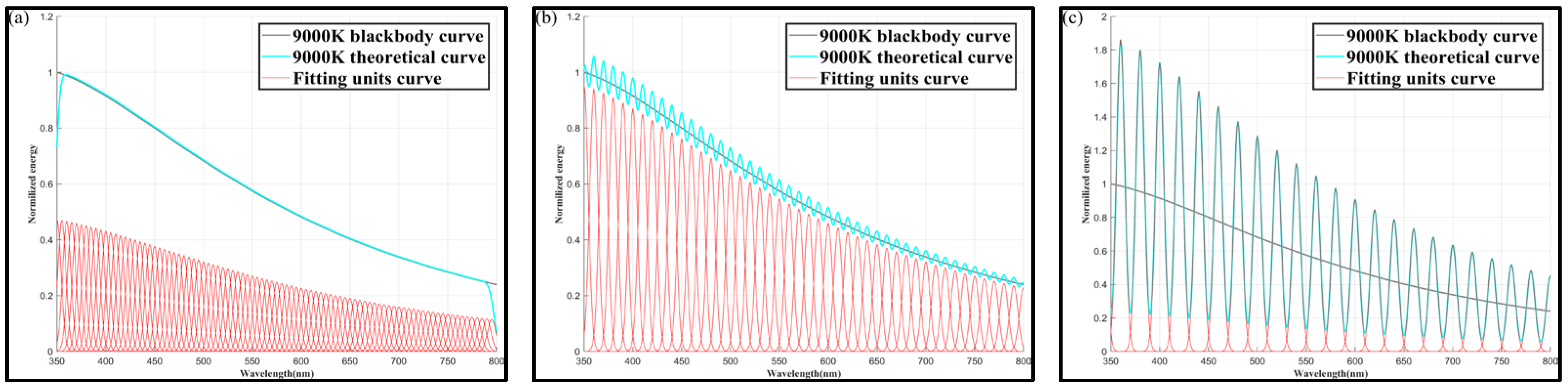
Simulation results for 9000 K color temperature:

➀ Figure 12 shows the color temperature results at $\omega$ = 10 nm, for $\Delta \lambda$ values of 5, 10, and 20 nm.

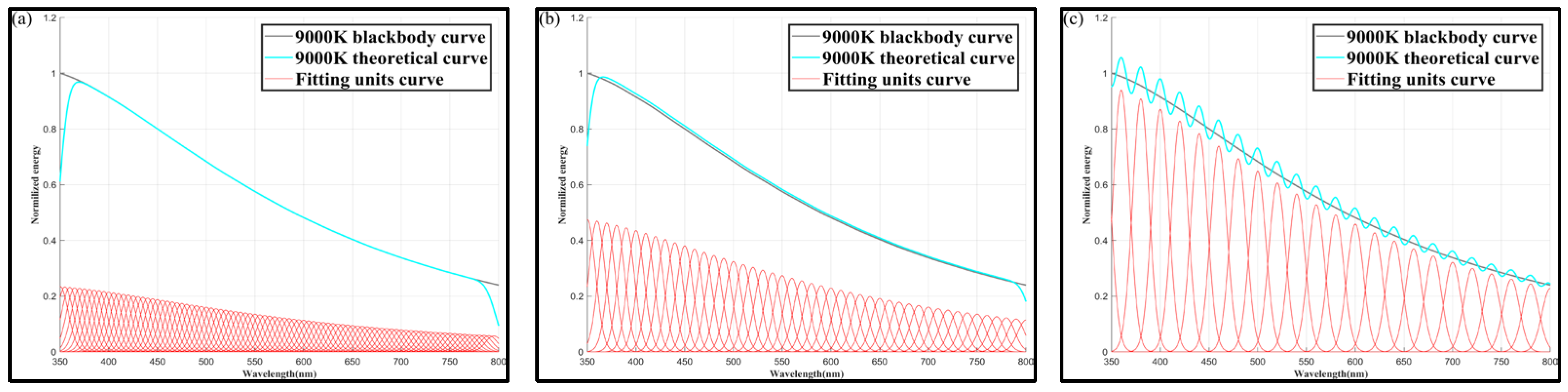
➁ Figure 13 shows the color temperature results at $\omega$ = 20 nm, for $\omega$ values of 5, 10, and 20 nm.

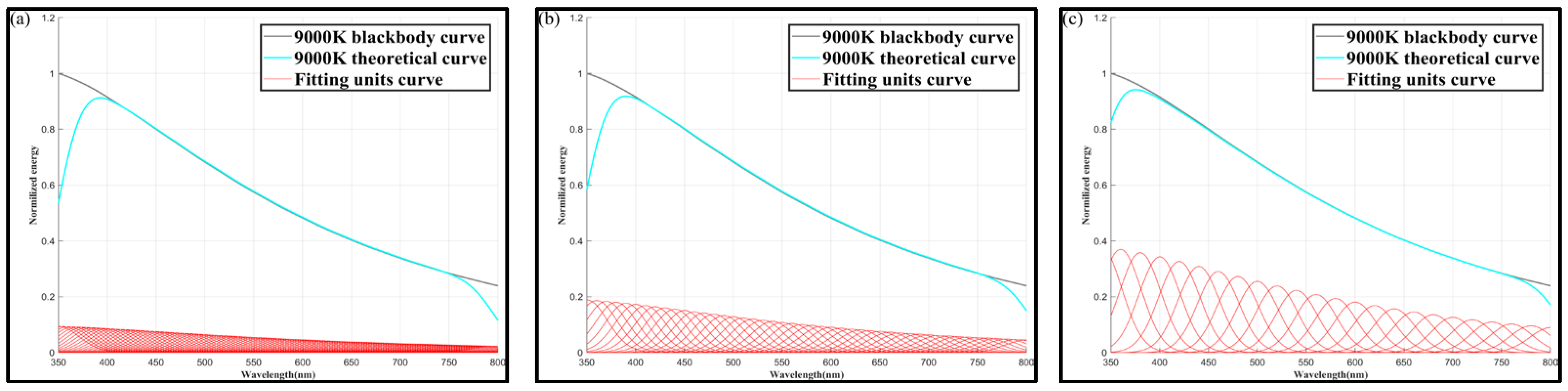
➂ Figure 14 shows the color temperature results at $\omega$ = 50 nm, for $\Delta \lambda$ values of 5, 10, and 20 nm.

The fitting results for the color temperatures, as obtained from the results presented in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 are summarized in

Table 5. Color temperature fitting results for 3000, 6000, and 9000 K.

Unit Spectrum Parameters		Color Temperature Fitting Results for 3000 K (%)	Color Temperature Fitting Results for 6000 K (%)	Color Temperature Fitting Results for 9000 K (%)
ω (nm)	Δλ (nm)
10	5.0	<1.0	<1.0	<1.0
	10.0	<6.6	<6.6	<6.6
	20.0	<5.8	<5.8	<5.8
20	5.0	<1.0	<1.0	<1.0
	10.0	<1.0	<1.0	<1.0
	20.0	<6.8	<6.8	<6.8
50	5.0	<1.0	<1.0	<1.0
	10.0	<1.0	<1.0	<1.0
	20.0	<1.0	<1.0	<1.0

.

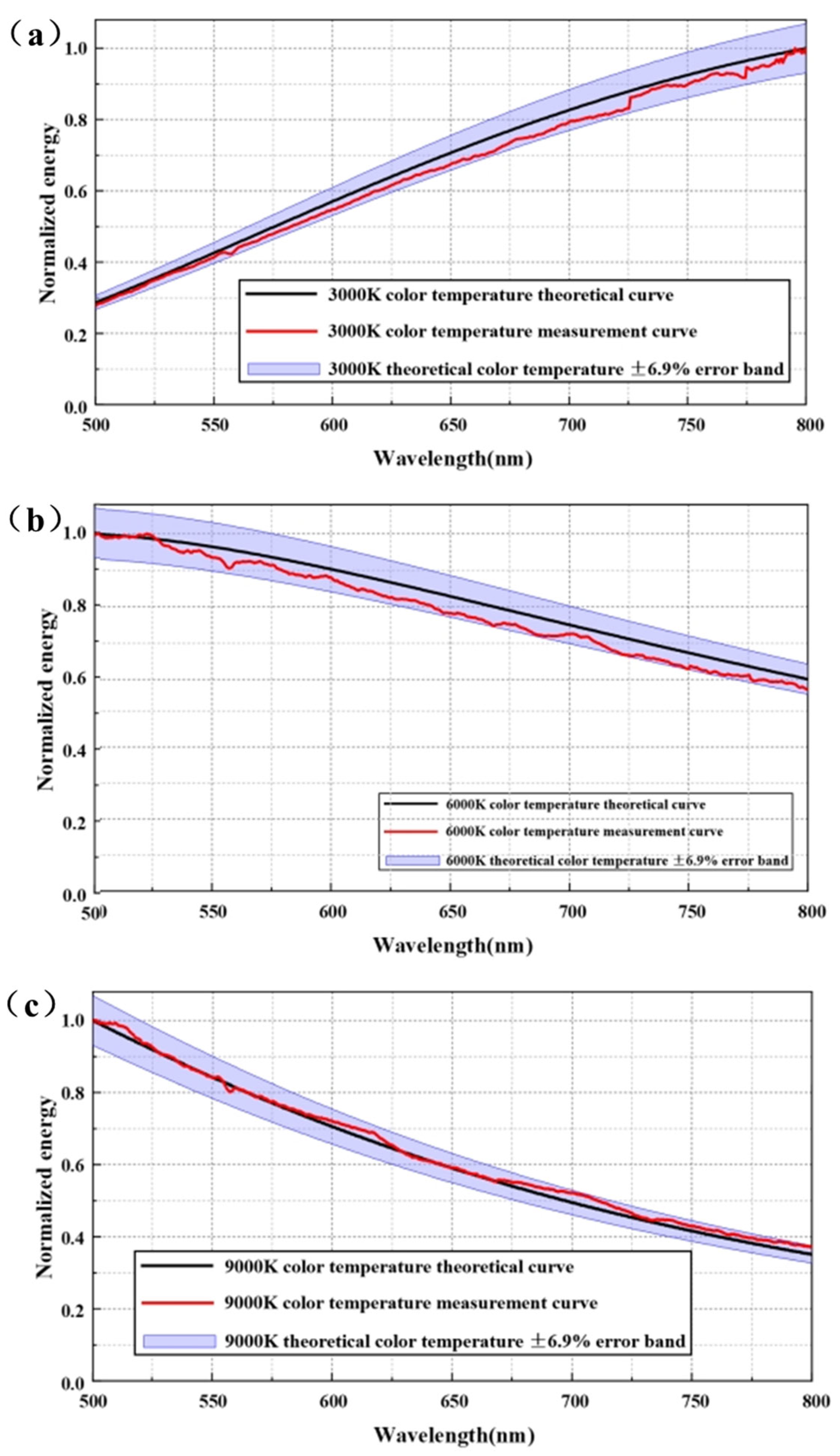
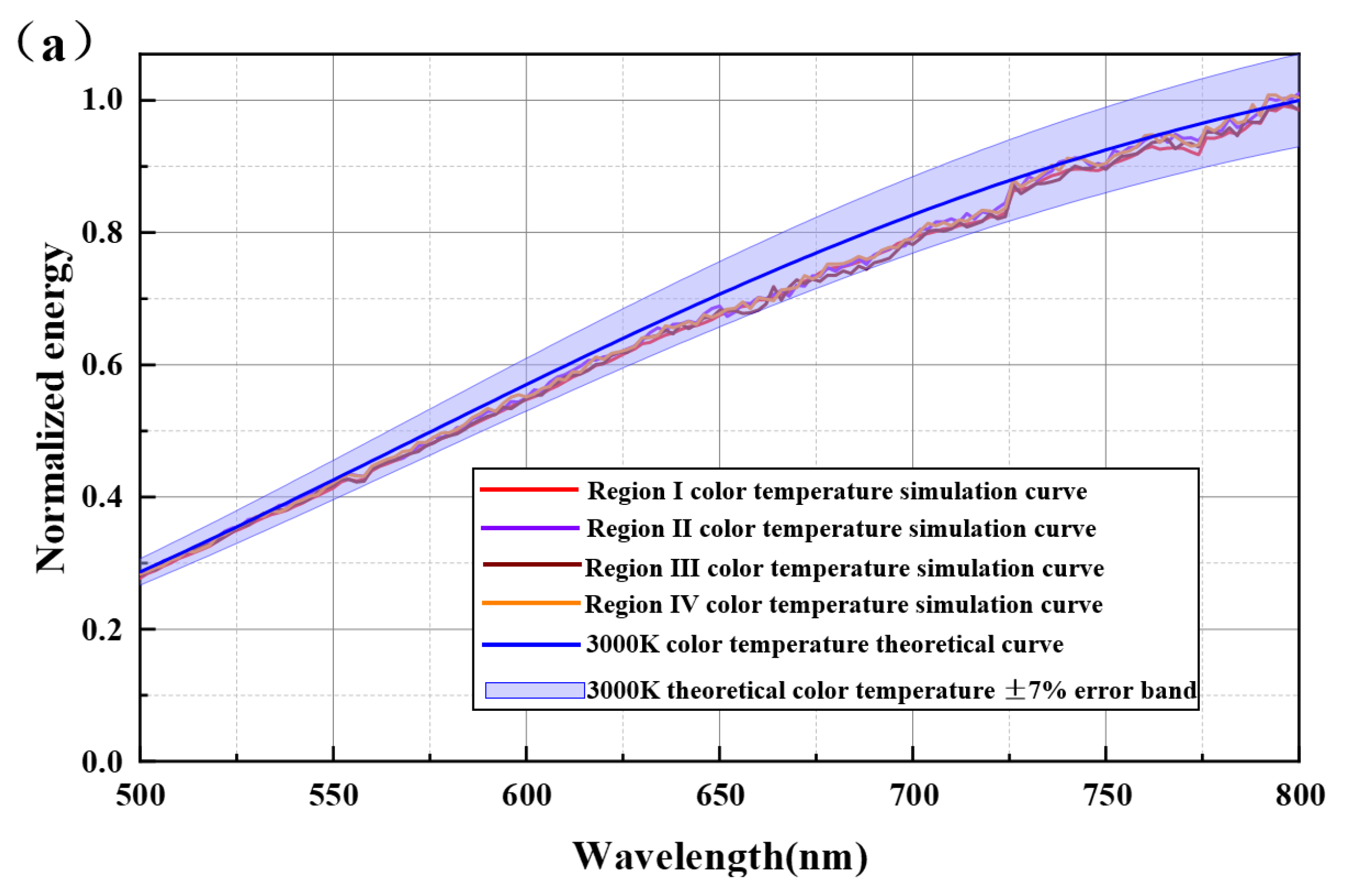
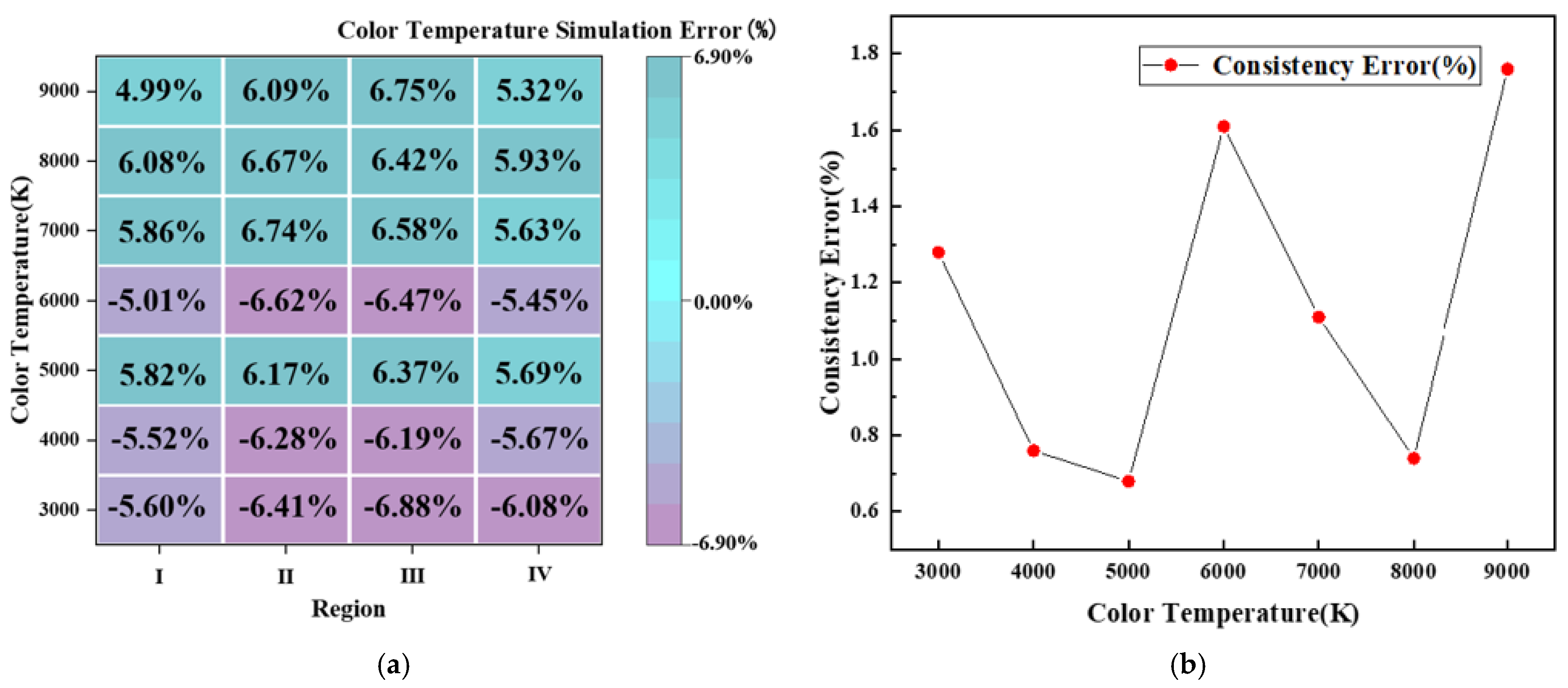
From Table 5, it can be observed that when $\omega$ = 50 nm, for all $\Delta \lambda$ values, the simulation of a color temperature range of 3000–9000 K could be satisfactorily realized. Although the smaller the $\Delta \lambda$, the higher the spectral modulation capability, according to the results, there is almost no difference in the spectral simulation accuracy at different $\Delta \lambda$ values.

However, it is worth noting that the color temperature simulation accuracy is larger in three cases, namely ($\omega$ = 10 nm and $\Delta \lambda$ = 10 nm); ($\omega$ = 10 nm and $\Delta \lambda$ = 20 nm); and ($\omega$ = 20 nm and $\Delta \lambda$ = 20 nm); furthermore, the peak interval is smaller when the $\omega$ width is certain. This results in higher simulation accuracy, as seen in, for example, Figure 6b,c, Figure 9b,c and Figure 12b,c, this is because $\omega$ is fixed, the peak interval is large, and the position in the middle of the unit spectrum cannot be covered during the modulation, resulting in an insufficient modulation capacity of the system.

Thus, based on the above analysis, owing to the smooth nature of the stellar color temperature curve [21], the main factor affecting the spectral simulation accuracy is the relationship between $\Delta \lambda$ and $\omega$. Therefore, for simulating the stellar color temperature spectrum curve, it is necessary to enhance the beam splitting capability of the system as much as possible, that is, enhance $\Delta \lambda$. For $\omega$, the monochromatic requirements of the beam of the unit spectrum segment can be appropriately relaxed. Therefore, in the design of the spectral modulation system, the requirement of spectral half-peak width can be appropriately reduced, and the spectral splitting ability of the system can be improved to the extent possible, to improve the simulation accuracy of the system.

4.2. Design of Pre-Collimated Beam Expansion System

The function of the pre-collimated beam expanding system is to collimate the beam so that the beam can fill the entire DMD array surface; therefore, the design is mainly based on the size of the DMD array surface in the non-dispersing direction.

According to the output beam size of the supercontinuous laser source (beam diameter of 2 mm) and the surface size of the DMD array (non-dispersive direction size of 1080 × 7.56 μm = 8.16 mm), it can be calculated that the magnification of the pre-collimated beam expanding system is at least 4.08, and the system magnification β is 4.2. The system design results and the parallelism of the outgoing beam are shown in Figure 15 and

Table 6. Parallelism of outgoing beam.

Normalized Field of View	Normalized Pupil	Angle to the Optical Axis (°)
0	1.0	0.0042
	0	0.0001
	−1.0	−0.0051
0.7	1.0	0.0043
	0	0.0002
	−1.0	−0.0050
1.0	1.0	0.0048
	0	0.0001
	−1.0	−0.0049

, respectively.

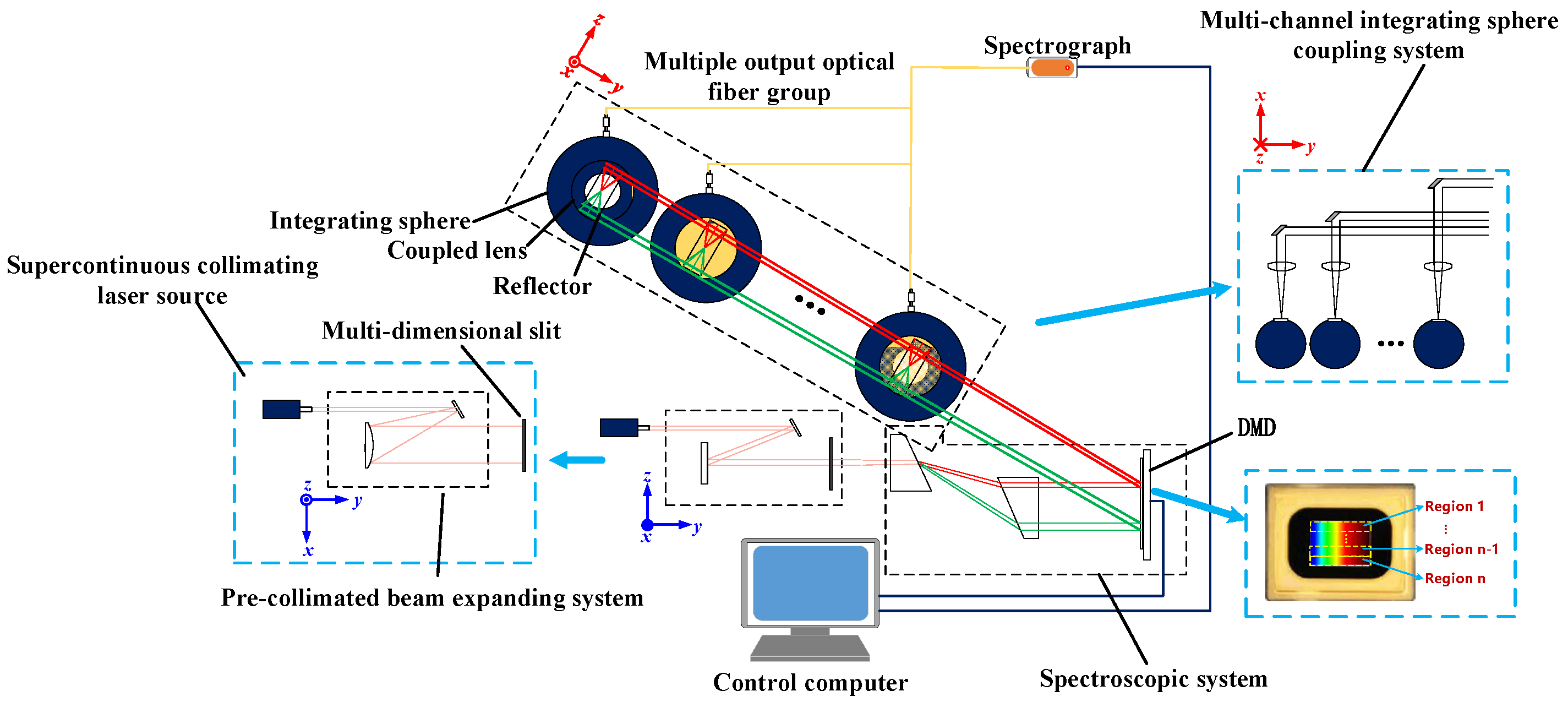
4.3. Multi-Dimensional Slit Design

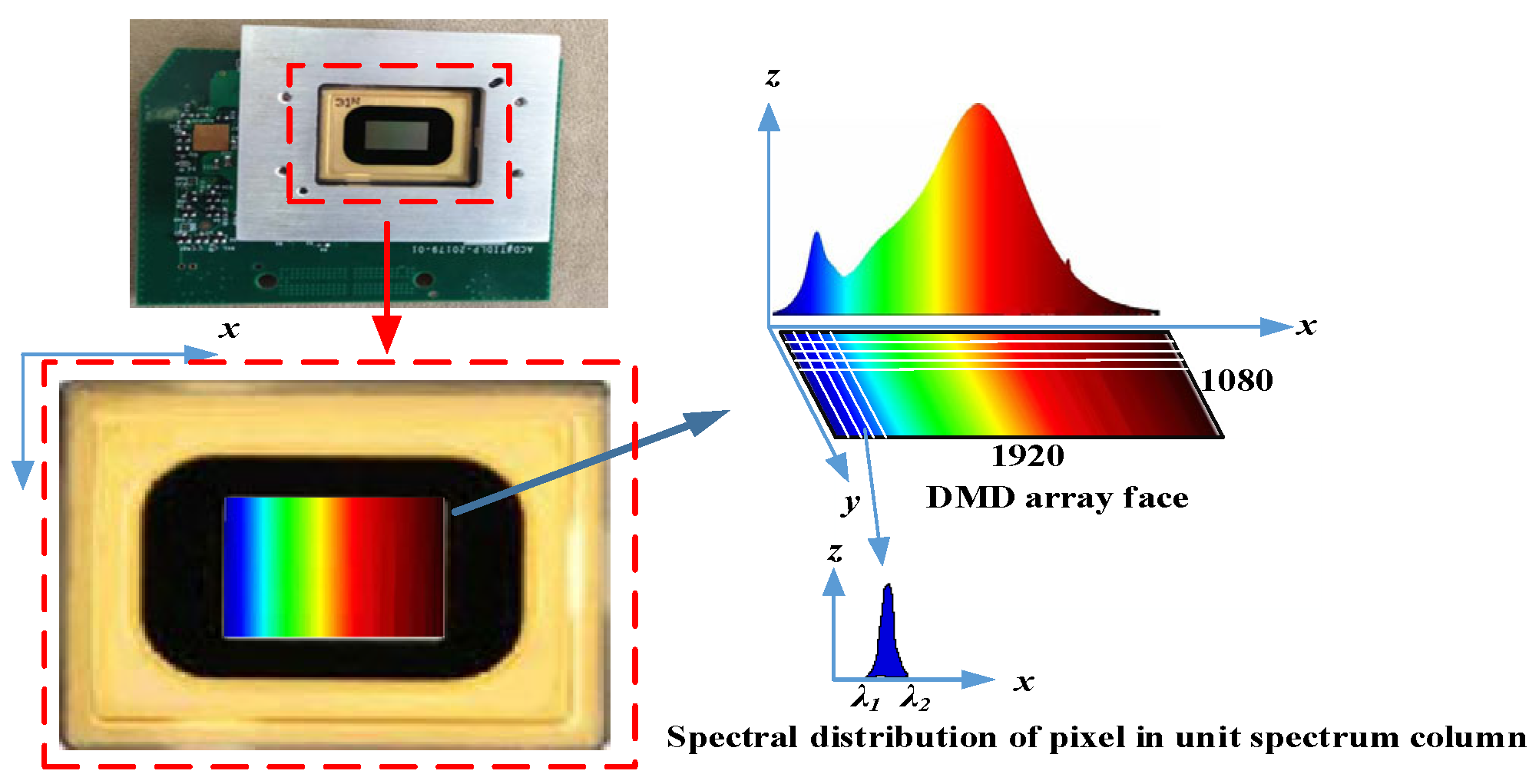
In this study, DLP6500 was selected as the modulator. According to the analysis presented in Section 2.2, the simulation of a 3000–9000 K color temperature spectral curve in the spectral range of 500–800 nm must theoretically meet the modulation capacity n > 3.57/c. Considering the diffraction effect of the DMD itself, the non-smoothness of the spectral radiation distribution of SC-PRO, and the possible beam overflow in adjacent regions, the modulation magnification of a single region should be improved to the extent possible. If the target spectral simulation accuracy c = 7%, the modulation capability of the system must theoretically meet the requirement of n > 51. Therefore, the digital micro-mirror array was divided into four parts along the non-dispersive direction, as shown in Figure 4. The resolution of each region is 1920 × 270; that is, the radiation coefficient adjustment ratio of the element spectral segment is 270, and the theoretical spectral simulation accuracy is approximately 3.57/270 ≈ 1.32%, which meets the requirement of 7% target spectral simulation accuracy.

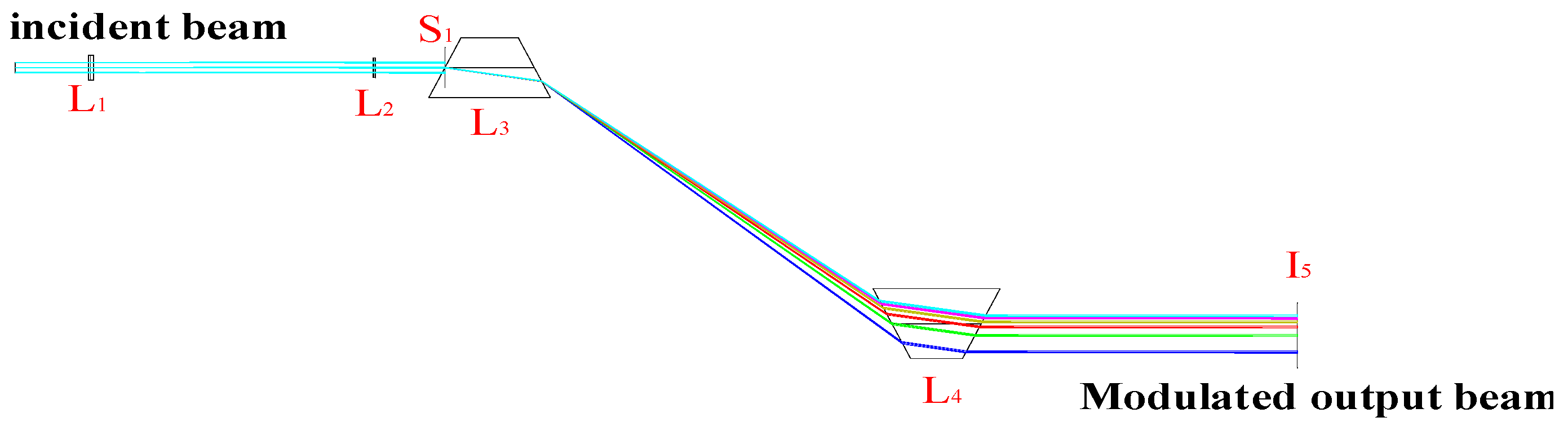
Multi-dimensional slits were designed according to the number of partitions, and the beam was processed twice along the dispersion direction. The slits were set up as shown in Figure 16. The same area has two groups of slits, namely wide and narrow groups, and different areas have the same slit group, among which, the size of the wide channel slit is 0.2 mm and the size of the narrow channel slit is 0.01 mm. As the spectrum between adjacent pixel groups in the DMD array surface is not completely independent, the spectrum between each adjacent group has a certain superposition, and the role of different sizes of slits is to compensate for the modulation interference between adjacent pixel groups on the DMD array surface.

4.4. Design of Spectral Splitting System

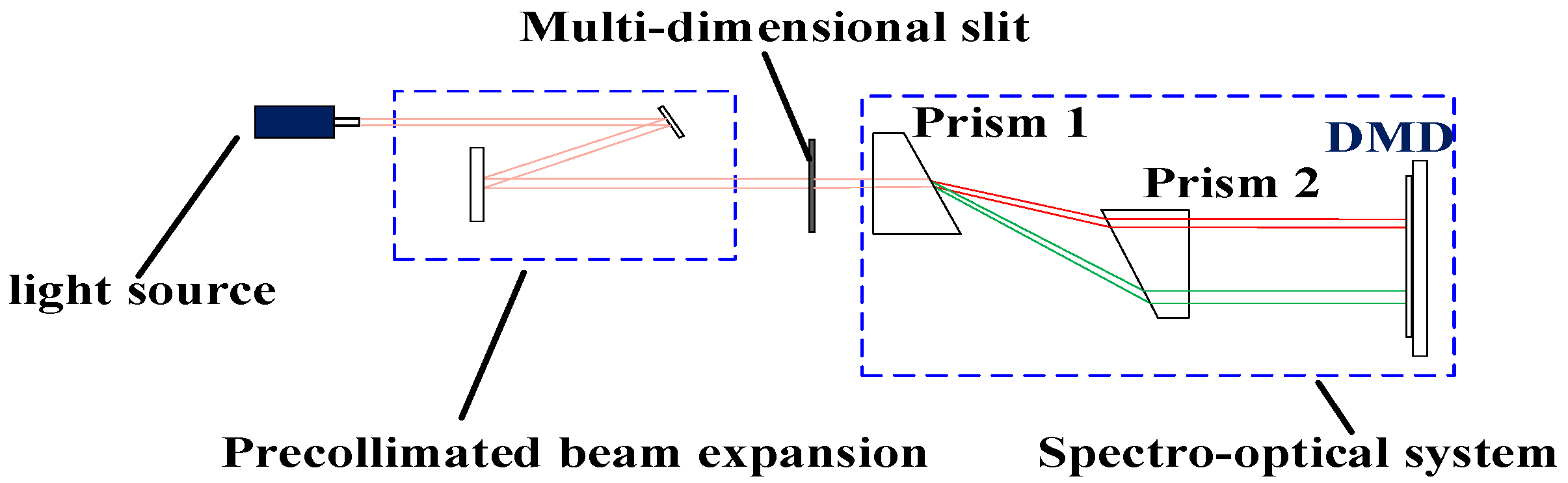
According to the analysis presented in Section 3.1, the system adopts the design method of a beam-splitting system with double prisms symmetrically placed. Prisms I and II are responsible for beam splitting and collimating separate beams, respectively. The spectral resolution of the beam-splitting system with double prisms symmetrically placed is proportional to the length of the system (the distance between the prisms). Materials with high dispersion (such as TIF6, BASF54, F7, and LAF9) are recommended for the prism. In this study, TIF6 was selected as the prism material.

The design process of the splitting system is as follows:

a.

Select the prism material (n, v);

b.

Calculate the refractive index nλ of the prism for each spectrum;

c.

Calculate the exit angle i′λ of each spectrum according to the refraction law (n Sin(i) = n′ Sin(i′));

d.

Using trigonometric relations, calculate the distance between the two prisms L, so that the difference between the incident height of the limiting wavelength λ₁ and λ₂ on Prism II is the length of the DMD short side (dispersive direction);

e.

According to the calculated L, set Prism II so that it is placed symmetrically with Prism I.

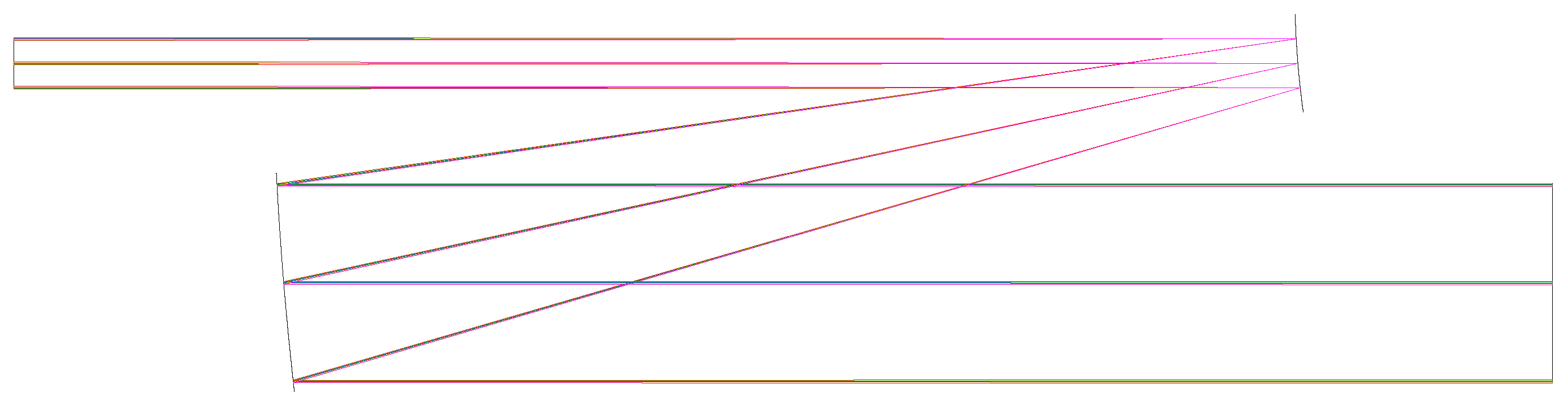
The optical path of the beam splitting system with symmetrical placement of the designed double prisms is shown in Figure 17. Here, L₁ and L₂ are the mirrors of the pre-collimated beam expansion system; S₁ is the slit; L₃ and L₄ are the dispersion prisms I and II; and I₅ is the DMD.

Although the beam splitting system is not an imaging system, the spot size and spectral resolution of the system can still be evaluated by a dot plot. The imaging quality of the system is shown in Figure 18 and Figure 19. According to the design results, under wide channels, the spectral resolution of the spectral collimation system is better than 5 and 30 nm at 500 and 800 nm, respectively. For narrow channels, the spectral resolution of the spectral collimation system is better than 3 and 13 nm at 500 and 800 nm, respectively.

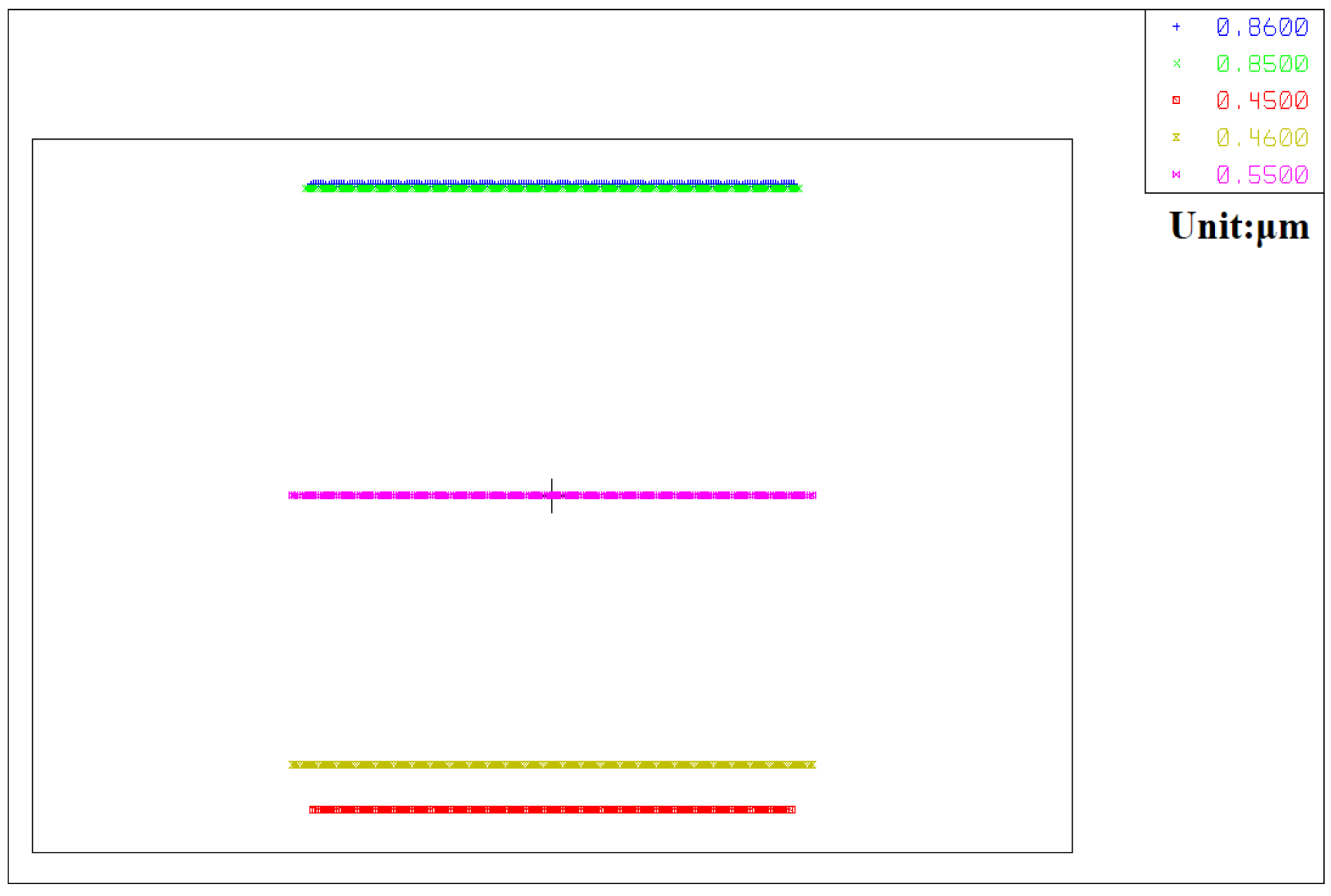
A group of 10 pixels was taken as the unit spectrum segment for modulation. The spectral half-peak widths of the unit spectrum segment under wide and narrow channels are shown in Figure 20. Under the wide channel, the maximum spectral peak width of the unit is approximately 40 nm, while the same under the narrow channel is approximately 29 nm.

According to Figure 20, the maximum spectral resolution error of the system appears at 800 nm, which is due to the dispersive nonlinearity of the prism, which has high spectral resolution at short wavelengths and low spectral resolution at long wavelengths.

5. Experiment and Discussion

5.1. Experimental Platform Construction

As shown in Figure 21, a multivariate mapping modulation system was built for stellar spectral information, and the monochromatic light resolution and half-peak width, spectral simulation accuracy, and regional consistency of the system were evaluated to verify the correctness of the system’s zoning theory.

The system includes a supercontinuous laser source, spectral modulation system (composed of pre-collimated beam expansion system, multi-dimensional slit, and beam precise subdivision system), spatial light modulation DMD, single-channel regionally adjustable integrating sphere coupling system group, and single-output fiber group.

5.2. Test of Single-Region Simulation Results

As the DMD array surface is divided into four independent regions, each region is affected by the modulation of adjacent regions. Theoretically, regions I and IV are similarly affected, and so are regions II and Ⅲ; this is because regions I and Ⅳ are edge regions, and are only affected by the beam overflow of regions II and Ⅲ, while regions II and Ⅲ are the central regions. Region Ⅱ is affected by the beam overflow of regions Ⅰ and Ⅲ, and Region Ⅲ is affected by the beam overflow of regions Ⅱ and Ⅳ. Therefore, regions II and Ⅲ are the most affected; consequently, Region II was selected as the test region of the monochromatic light resolution, half-peak width, and spectral simulation accuracy.

(1)

Peak resolution of unit spectral segment

The spectral resolution of the output beam in Region II was tested, taking every 10 columns of pixels as a unit, and the edge position (pixel columns 1–10 and 1911–1920) and the middle position (pixel columns 951–960) in Region II were tested. The spectral resolution is presented in

Table 7. Peak resolution of unit spectrum.

Channel Number	1	2	3	4	5	6
Pixel position	1–10	11–20	951–960	961–970	1901–1910	1911–1920
Resolution (nm)	0.55		0.81		2.74

.

The astronomical spectrum is critical for deep space navigation; therefore, the Fraunhofer line of the solar spectrum is taken as the simulation target, and spectral lines A, a, and b2 are simulated [25]. The spectrometer is used to test the spectral characteristics of the system’s output Fraunhofer line to verify the simulation capability under specific peak wavelength targets. The output spectral line is as shown in Figure 22. The bandwidth of the output Fraunhofer spectral line and the simulation accuracy of the peak spectral line are presented in

Table 8. Simulation results of Fraunhofer spectral lines.

Designation	Chemical Element	Theoretical Value (nm)	Half-Peak Width (nm)	Peak Value (nm)	Peak Error (nm)
A	O2 (Oxygen)	759.37	11.39	760.41	1.04
a	O2 (Oxygen)	627.66	14.93	627.61	–0.05
b2	Mg (Magnesium)	517.27	24.97	517.07	–0.20

.

By analyzing the uncertainty of the system device [26,27,28] (taking the inclusion factor k = 2), the extended uncertainty is 5.38. As can be seen from Table 8, the maximum peak simulation error of spectral lines A, a, and b2 is −1.04 nm.

(2)

Spectral simulation accuracy

The wide channel coarse modulation is used in Region II; then, the narrow channel is accurately compensated for, and the spectral simulation experiment is carried out for the three typical color temperatures, namely 3000, 6000, and 9000 K. Their spectral simulation curves are shown in Figure 23.

From Figure 23, it can be seen that the simulation errors corresponding to 3000, 6000, and 9000 K are −6.41%, −6.47%, and 6.75%, respectively. In the range 500 to 800 nm, the spectral simulation error distribution is relatively smooth.

5.3. Multi-Region Consistency Test

To achieve consistency in the collaborative simulation of regions I to IV, the design experiment is supplied with the modulated beams in different regions by adjusting and replacing the position and size of the regional diaphragm in the single-channel region-adjustable integrating sphere coupling system, and the spectral simulation accuracies of the output beams in the four regions are obtained to analyze the influence among the regions.

(1)

Optical resolution of unit spectral segment

The output monochromatic light of regions I to IV was tested sequentially, and the peak wavelength was tested by considering groups of 10 columns. The monochromatic light consistency among the regions was characterized by the peak wavelength range, and the results of the edge position of the regions I–IV (pixel columns 1–10 and 1910–1920) and the middle position (pixel columns 951–960) are presented in

Table 9. Monochromatic light consistency test results.

	Peak Wavelength Error
Channel location	Columns 1–10	Columns 951–960	Columns 1910–1920
Peak wavelength error (nm)	0.20	0.15	0.21

.

The peak wavelength error is the maximum difference in the peak wavelength of the regions I–IV in the measurement channel. As can be seen from Table 9, the monochromatic light consistency of the system is better than 0.21 nm. Theoretically, the imaging conditions of regions I–IV are the same, and the monochromatic light should also be the same. The main reason for the monochromatic light deviation is the installation position of the slit, and the perpendicularity between the slit and DMD affected the spectrum.

The peak value consistency of Fraunhofer spectral line output in regions I–IV is presented in

Table 10. Results of Fraunhofer line simulation consistency test.

Designation	Peak Maximum Error (nm)
A	0.19
a	0.145
b2	0.2

.

Among them, the maximum peak error is the maximum peak range of the simulated Fraunhofer spectral line in the measurement channel regions I–IV. It can be seen from Table 10 that the peak consistency of Fraunhofer spectral lines simulated by the system is better than 0.19 nm.

(2)

Spectral simulation accuracy

The spectral simulation accuracy of regions I–IV was tested next, and the spectral simulation curves of the four regions of color temperatures 3000, 6000, and 9000 K are presented in Figure 24.

According to Figure 24, the spectral simulation errors in the four regions with the same color temperature are different, with no clearly evident linear rule. The maximum error is −6.88% at 3000 K in Region III. The range of spectral simulation errors in regions I–IV under different color temperatures indicates the consistency of the spectral simulation accuracy in these regions. The maximum consistency for 9000 K is 1.76%, indicating that the spectral simulation consistency in Regions I–Ⅳ is good, with no clearly evident correlation between the regional consistency and spectral simulation accuracy, as shown in Figure 25.

6. Conclusions

In this study, a method for simulating star radiation of multi-color temperature and magnitude independently based on the spatial light modulation technique was proposed. The system could provide a close to real simulation of multi-color temperature and multi-magnitude star maps in the calibration test of the star sensor. Based on the theoretical analysis of the factors affecting the radiation characteristics of the unit spectrum and spectral simulation accuracy, the DMD was divided into regions. According to the zoning modulation idea, a spectral modulation system with opposed double prisms was designed, which reduced the regional beam overflow and improved the independence of the light information output between adjacent regions. As a ground calibration equipment of a star sensor, it could provide a four-star map simulation with different color temperatures and different magnitudes; furthermore, it could achieve a spectral resolution of higher than 2.74 nm for a single region unit spectrum. The simulation error of the star spectrum simulation in the color temperature range 3000–9000 K was close to 7%, and the consistency error of the optical resolution of the multi-region unit spectrum was less than 0.21 nm. The consistency of the spectral simulation accuracy over the temperature range 3000–9000 K was better than 1.76%, which meets the requirements of the ground calibration of a star sensor; thus, the proposed system can replace the star viewing test to some extent. Additionally, the stellar radiation simulation system is essentially a spectrally tunable light source, and can be extended to other applications, including remote sensing radiation calibration, hyperspectral image projection molecular imaging, and spectroscopy. In summary, in the future, with the improvement of simulation accuracy and in-depth study of the number of channels, stellar simulation will further promote the development of remote sensing technology to higher precision, intelligence, and multi-scene fusion.