The Design of a Circulator Based on Topological Photonic Crystals
Abstract
1. Introduction
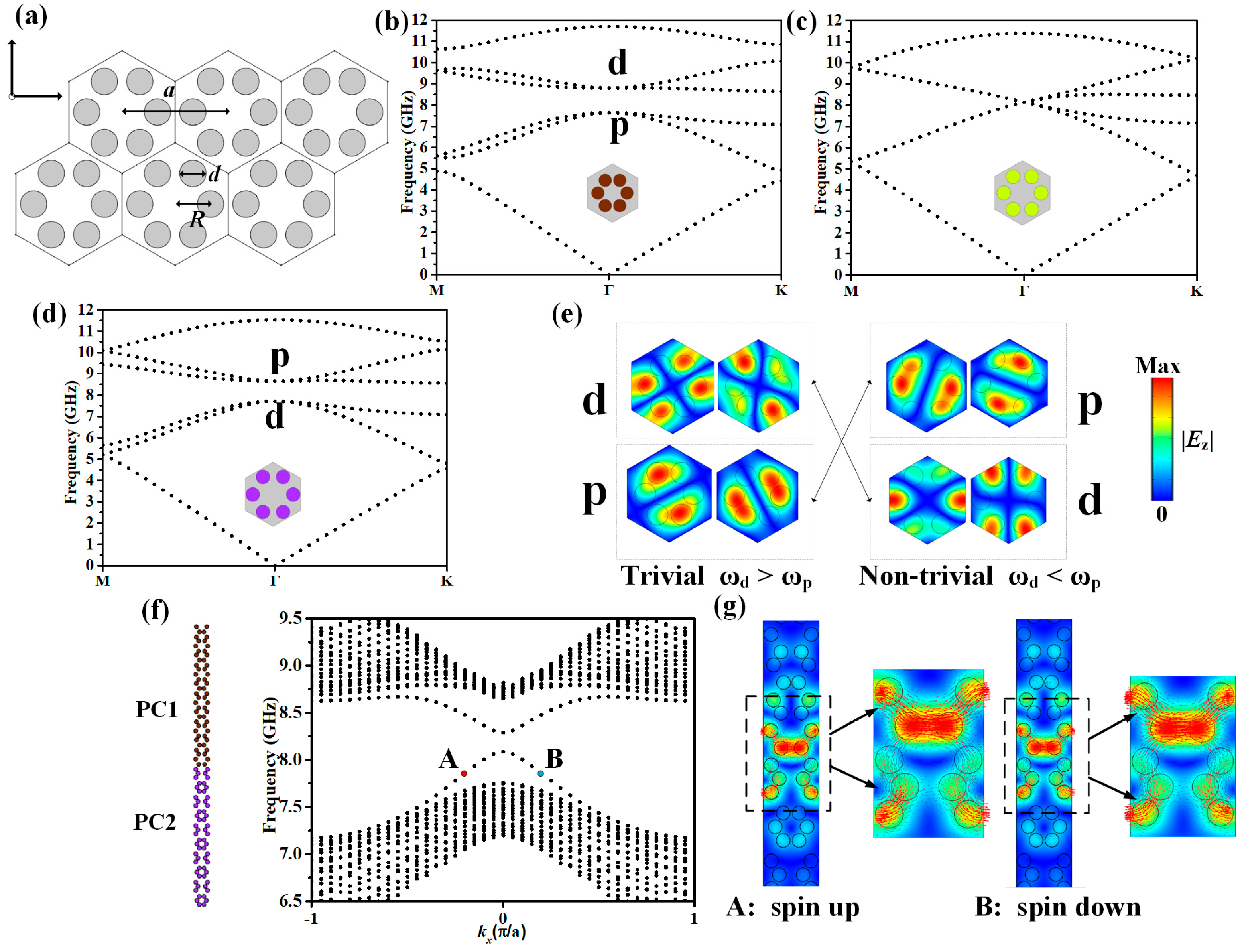
2. Pseudo-Spin Photonic Crystals and Their Topological States
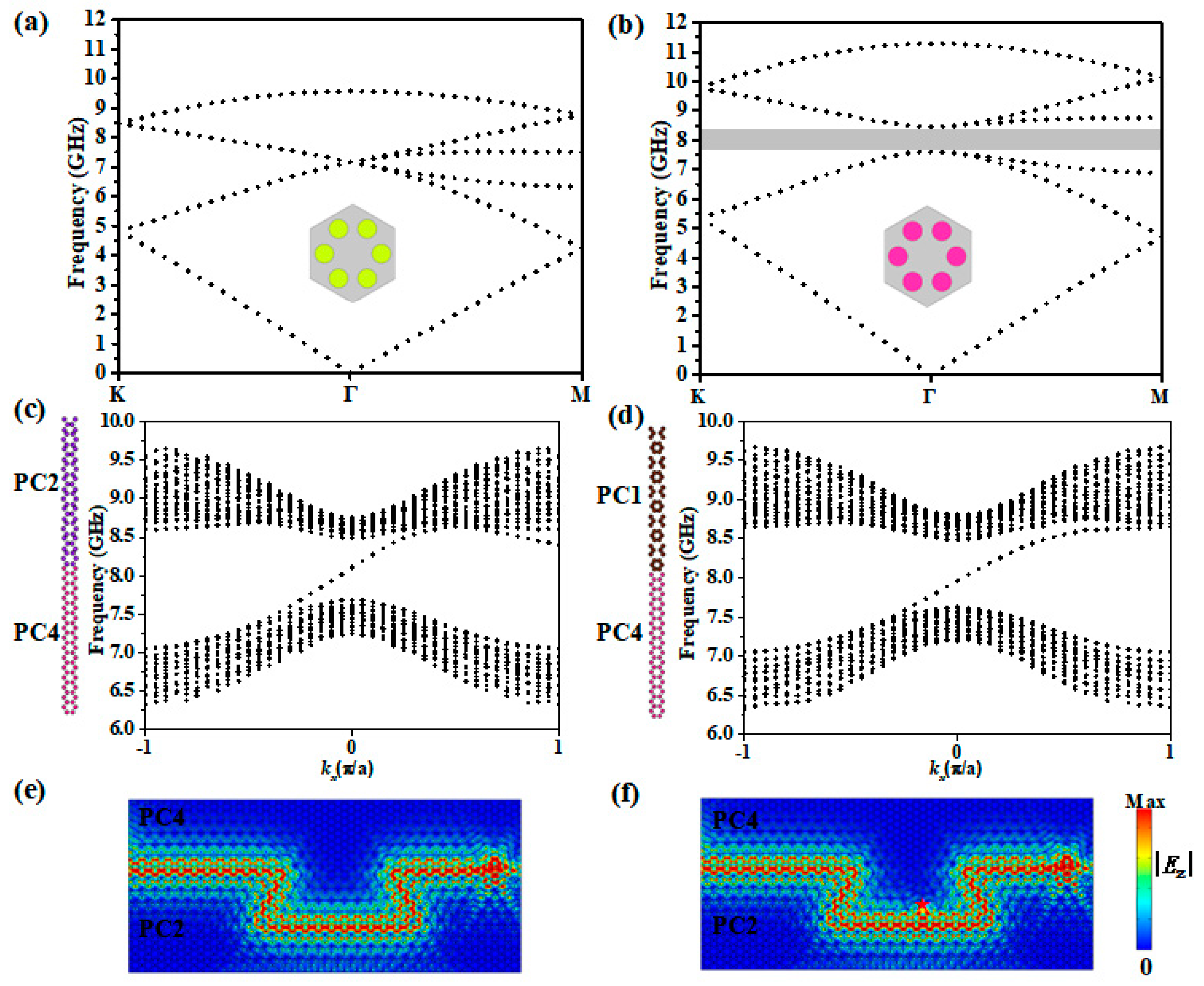
3. Gyromagnetic Photonic Crystals and Their Topological States
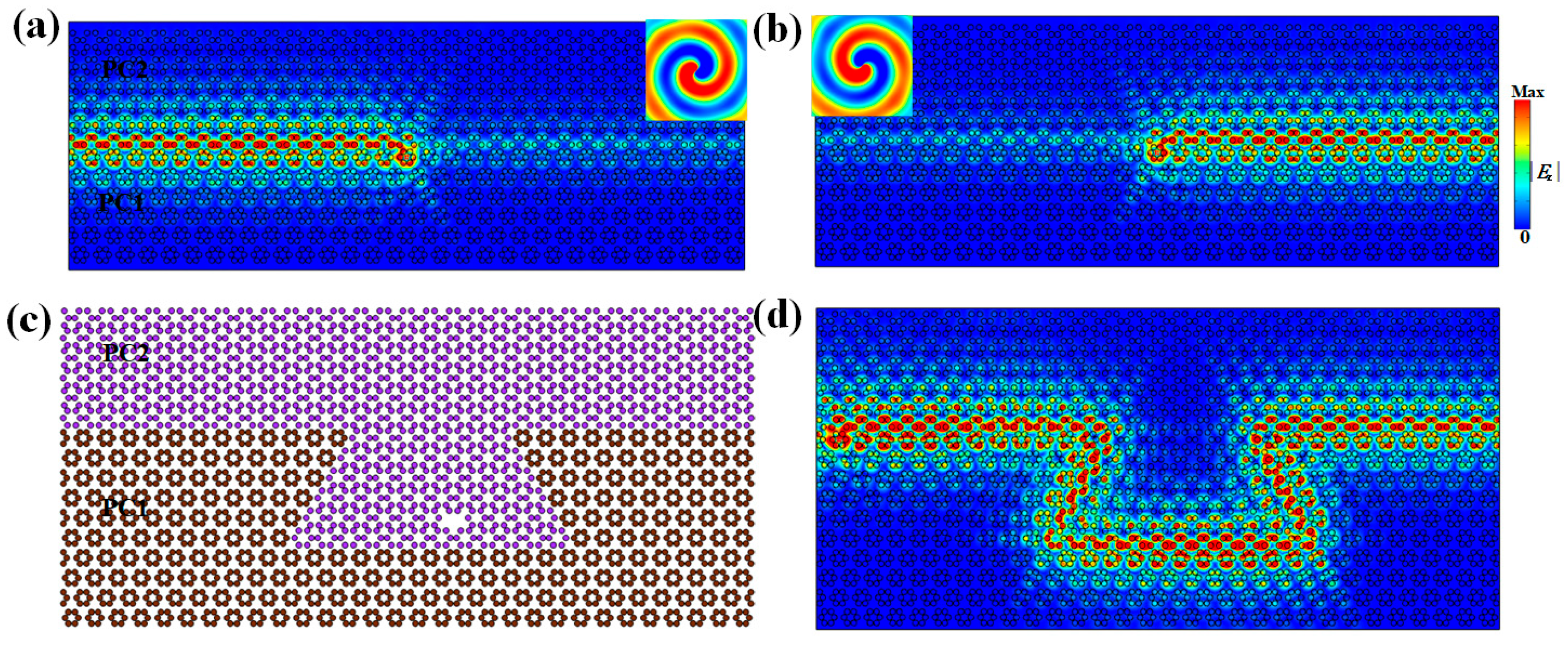
4. Topological Circulator Based on Chiral States and Helical States
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maleki, M.J.; Soroosh, M.; Parandin, F.; Haddadan, F. Photonic Crystal-Based Decoders: Ideas and Structures. In Recent Advances and Trends in Photonic Crystal Technology, 2nd ed.; Goyal, A.K., Kumar, A., Eds.; IntechOpen: London, UK, 2024. [Google Scholar]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O.; et al. Topological photonics. Rev. Mod. Phys. 2019, 91, 15006. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Xie, B.Y.; Wang, H.F.; Zhu, X.Y.; Lu, M.H.; Wang, Z.D.; Chen, Y.F. Photonics meets topology. Opt. Express 2018, 26, 24531–24550. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Anlage, S.M. Microwave applications of photonic topological insulators. Appl. Phys. Lett. 2020, 116, 250502. [Google Scholar] [CrossRef]
- Xue, H.; Yang, Y.; Zhang, B. Topological Valley Photonics: Physics and Device Applications. Adv. Photonics Res. 2021, 2, 2100013. [Google Scholar] [CrossRef]
- Tang, G.J.; He, X.T.; Shi, F.L.; Liu, J.W.; Chen, X.D.; Dong, J.W. Topological Photonic Crystals: Physics, Designs, and Applications. Laser Photonics Rev. 2022, 16, 2100300. [Google Scholar] [CrossRef]
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljačić, M. Reflection-Free One-Way Edge Modes in a Gyromagnetic Photonic Crystal. Phys. Rev. Lett. 2008, 100, 013905. [Google Scholar] [CrossRef]
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljacic, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 2009, 461, 772–775. [Google Scholar] [CrossRef]
- Wu, L.H.; Hu, X. Scheme for Achieving a Topological Photonic Crystal by Using Dielectric Material. Phys. Rev. Lett. 2015, 114, 223901. [Google Scholar] [CrossRef]
- Barik, S.; Miyake, H.; DeGottardi, W.; Waks, E.; Hafezi, M. Two-dimensionally confined topological edge states in photonic crystals. New J. Phys. 2016, 18, 113013. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Y.F.; Xu, T.; Wang, H.X.; Jiang, J.H.; Hu, X.; Hang, Z.H. Visualization of a Unidirectional Electromagnetic Waveguide Using Topological Photonic Crystals Made of Dielectric Materials. Phys. Rev. Lett. 2018, 120, 217401. [Google Scholar] [CrossRef]
- Ma, T.; Shvets, G. All-Si valley-Hall photonic topological insulator. New J. Phys. 2016, 18, 025012. [Google Scholar] [CrossRef]
- Dong, J.W.; Chen, X.D.; Zhu, H.; Wang, Y.; Zhang, X. Valley photonic crystals for control of spin and topology. Nat. Mater. 2017, 16, 298–302. [Google Scholar] [CrossRef]
- Chen, X.D.; He, X.T.; Dong, J.W. All-Dielectric Layered Photonic Topological Insulators. Laser Photonics Rev. 2019, 13, 1900091. [Google Scholar] [CrossRef]
- He, X.T.; Liang, E.T.; Yuan, J.J.; Qiu, H.Y.; Chen, X.D.; Zhao, F.L.; Dong, J.W. A silicon-on-insulator slab for topological valley transport. Nat. Commun. 2019, 10, 872. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, X.; Xu, Y. Topological Phononics: From Fundamental Models to Real Materials. Adv. Funct. Mater. 2019, 30, 1904784. [Google Scholar] [CrossRef]
- Wang, H.; Gupta, S.K.; Xie, B.; Lu, M. Topological photonic crystals: A review. Front. Optoelectron. 2020, 13, 50–72. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, L.; Xu, S.; Wang, Z.; Li, E.; Yang, Y.; Chen, H. Robust waveguiding in substrate-integrated topological photonic crystals. Appl. Phys. Lett. 2020, 116, 231106. [Google Scholar] [CrossRef]
- Yoshimi, H.; Yamaguchi, T.; Ota, Y.; Arakawa, Y.; Iwamoto, S. Slow light waveguides in topological valley photonic crystals. Opt. Lett. 2020, 45, 2648–2651. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, L.; Chen, F.; Yan, Q.; Xi, R.; Chen, H.; Yang, Y. Photonic Topological Valley-Locked Waveguides. ACS Photonics 2021, 8, 1400–1406. [Google Scholar] [CrossRef]
- Yu, X.; Chen, J.; Li, Z.Y.; Liang, W. Topological large-area one-way transmission in pseudospin-field-dependent waveguides using magneto-optical photonic crystals. Photonics Res. 2023, 11, 1105–1112. [Google Scholar] [CrossRef]
- Han, J.F.; Liang, F.; Zhao, Y.L.; Liu, J.; Wang, S.; Wang, X.R.; Zhao, D.S.; Wang, B.Z. Valley kink states and valley-polarized chiral edge states in substrate-integrated topological photonic crystals. Phys. Rev. Appl. 2024, 21, 014046. [Google Scholar] [CrossRef]
- Shalaev, M.I.; Desnavi, S.; Walasik, W.; Litchinitser, N.M. Reconfigurable topological photonic crystal. New J. Phys. 2018, 20, 023040. [Google Scholar] [CrossRef]
- Song, Z.; Liu, H.; Huang, N.; Wang, Z. Electrically tunable robust edge states in graphene-based topological photonic crystal slabs. J. Phys. D Appl. Phys. 2018, 51, 304003. [Google Scholar] [CrossRef]
- Cao, T.; Fang, L.; Cao, Y.; Li, N.; Fan, Z.; Tao, Z. Dynamically reconfigurable topological edge state in phase change photonic crystals. Sci. Bull. 2019, 64, 814–822. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Huang, J.; Chen, H.; Qian, Z.; Ma, J.; Sun, X.; Fan, S.; Sun, Y. Terahertz topological photonic waveguide switch for on-chip communication. Photonics Res. 2022, 10, 1090–1096. [Google Scholar] [CrossRef]
- Liu, J.W.; Shi, F.L.; He, X.T.; Tang, G.J.; Chen, W.J.; Chen, X.D.; Dong, J.W. Valley photonic crystals. Adv. Phys. X 2021, 6, 1905546. [Google Scholar] [CrossRef]
- Lan, Z.; Chen, M.L.N.; Gao, F.; Zhang, S.; Sha, W.E.I. A brief review of topological photonics in one, two, and three dimensions. Rev. Phys. 2022, 9, 100076. [Google Scholar] [CrossRef]
- You, J.W.; Lan, Z.; Ma, Q.; Gao, Z.; Yang, Y.; Gao, F.; Xiao, M.; Cui, T.J. Topological metasurface: From passive toward active and beyond. Photonics Res. 2023, 11, 1090–1096. [Google Scholar] [CrossRef]
- Zeng, Y.; Chattopadhyay, U.; Zhu, B.; Qiang, B.; Li, J.; Jin, Y.; Li, L.; Davies, A.G.; Linfield, E.H.; Zhang, B.; et al. Electrically pumped topological laser with valley edge modes. Nature 2020, 578, 246–250. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, L.; Zhang, D.; Gao, S. Topological cavity laser with valley edge states. Opt. Express 2022, 30, 4965–4977. [Google Scholar] [CrossRef] [PubMed]
- Gu, L.; Yuan, Q.; Zhao, Q.; Ji, Y.; Liu, Z.; Fang, L.; Gan, X.; Zhao, J. A Topological Photonic Ring-Resonator for On-Chip Channel Filters. J. Light. Technol. 2021, 39, 5069–5073. [Google Scholar] [CrossRef]
- Navaratna, N.; Tan, Y.J.; Kumar, A.; Gupta, M.; Singh, R. On-chip topological THz biosensors. Appl. Phys. Lett. 2023, 123, 033705. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.-C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef]
- Xi, X.; Ye, K.P.; Wu, R.X. Influence of bias magnetic field direction on band structure of magnetic photonic crystal and its role in constructing topological edge states. Acta Phys. Sin. 2020, 69, 154102. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, D.; Zeng, X.; Wang, Y.; Dong, Z. Wideband Y-Type Circulator Based on Magneto Photonic Crystals and Triangular Ferrites. IEEE Photonics Technol. Lett. 2019, 31, 743–746. [Google Scholar] [CrossRef]
- Anandan, S.; Vani, D.; Gupta, P.; Krishnan, P. A Low Loss Hexagonal Six-Port Optical Circulator Using Silicon Photonic Crystal. Opt. Quantum Electron. 2023, 55, 1092. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, D.; Wang, Y.; Hong, B.; Shu, G.; He, W. A Terahertz Circulator Based on Magneto-Photonic Crystal Slab. Photonics 2023, 10, 360. [Google Scholar] [CrossRef]
- Chen, J.; Liang, W.; Li, Z.-Y. Antichiral One-Way Edge States in a Gyromagnetic Photonic Crystal. Phys. Rev. B 2020, 101, 214102. [Google Scholar] [CrossRef]
- Han, J.; Liang, F.; Zhao, Y. Highly Efficient Conversion from Classical Guided Waves to Topological Chiral Edge States. Chin. Opt. Lett. 2024, 22, 023902. [Google Scholar] [CrossRef]

| Reference | Array Structure | Working Frequency | Wave Transport Modes | Topological Characteristic |
|---|---|---|---|---|
| [37] | Triangular lattice | GHz | Wave transport modes based on line defect | No |
| [38] | Triangular lattice | THz | Wave transport modes based on line defect | No |
| [39] | Triangular lattice | THz | Wave transport modes based on line defect | No |
| This work | Hexagonal lattice | GHz | Topological edge modes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Liang, F.; Han, J.; Li, J.; Hu, H.; Zhang, W.; Tan, X. The Design of a Circulator Based on Topological Photonic Crystals. Photonics 2025, 12, 581. https://doi.org/10.3390/photonics12060581
Zhao Y, Liang F, Han J, Li J, Hu H, Zhang W, Tan X. The Design of a Circulator Based on Topological Photonic Crystals. Photonics. 2025; 12(6):581. https://doi.org/10.3390/photonics12060581
Chicago/Turabian StyleZhao, Yulin, Feng Liang, Jianfei Han, Jingsen Li, Haihua Hu, Weihao Zhang, and Xiangjun Tan. 2025. "The Design of a Circulator Based on Topological Photonic Crystals" Photonics 12, no. 6: 581. https://doi.org/10.3390/photonics12060581
APA StyleZhao, Y., Liang, F., Han, J., Li, J., Hu, H., Zhang, W., & Tan, X. (2025). The Design of a Circulator Based on Topological Photonic Crystals. Photonics, 12(6), 581. https://doi.org/10.3390/photonics12060581





