Transportable and Ultra-Stable Laser System for ¹³³Cs Rydberg Excitation

Abstract

Recent progress in Rydberg atoms has enabled a wide range of applications in quantum sensing and quantum computation. In these applications, ultra-stable optical reference systems are essential to meet the requirements of a narrow linewidth and low technical noise. However, most existing systems are confined to laboratory settings and are not suitable for measurement-site-independent applications, such as external electric field sensors. This paper presents a transportable ultra-stable optical reference system for Rydberg excitation. The system is based on a 10 cm long ultra-low-expansion glass optical cavity, and it achieves finesse values of 410 k (at 1018 nm) and 200 k (at 852 nm). After being assembled in the experimental environment, it can still operate with only minor adjustments even after being transported over 400 km. Thanks to its vibration-insensitive design, two-stage temperature control, and hybrid locking unit, the system can maintain its locking status for up to 2 h.

1. Introduction

Exciting atoms to a state with a very high principal quantum number n, the so-called Rydberg state [1,2], leads to large dipole moments, which scale as $n^2$ and have a long lifetime compared with low-lying transitions, which scale as $n^3$. These appealing features render the Rydberg atom an ubiquitous tool for use in high-sensitivity detection of microwave electric fields [3,4,5,6,7] and in quantum information applications, such as single-photon sources [8,9] and quantum computation, [10,11,12,13,14] through the incorporation of optical tweezers.

To perform Rydberg excitation, two laser beams are conventionally employed in a ladder-type configuration, resonantly driving the transition between the ground state and the Rydberg states via an intermediate state. In practice, the use of tunable single-frequency diode lasers in combination with a high-power fiber laser amplifier allows for controllable Rydberg excitation in terms of Rydberg state selection and the associated Rabi frequency. Although atomic absorption-based frequency stabilization techniques are generally used in the atomic, molecular, and optical (AMO) physics community, they cannot fulfill the requirements of a narrow linewidth and low technical noise in the Rydberg atom-based applications of precision measurement [3,4,5,6,7] and high-fidelity quantum logic gates [10,11,12,13,14]. Ultra-stable cavity-stabilized optical reference systems have instead demonstrated the ability to address these challenges [15]. In these systems, high-reflectivity mirrors are attached to monolithic spacers, which are typically made of ultra-low-expansion (ULE) glass to prevent changes in the cavity length due to external temperature drifts; temperature stabilization and a high-vacuum environment further enhance performance. A single-crystalline silicon cavity [16] operated at 124 K reached thermal-noise-limited instability at a level of $4\times {10}^{17}$. Most operations of Rydberg excitation stabilized by ultra-stable cavity reference systems have been so far constrained to laboratories [17,18,19,20,21,22]. However, applications like environmental electric field sensors require a transportable system to enable flexibility in the choice of measurement sites [23,24,25,26,27,28].

Here, we report a portable ultra-stable laser for the Rydberg excitation of ${}^{133}Cs$. The entire system is installed in a standard 19-inch 22U rack cabinet, which includes two lasers, a beam delivery system, an ultra-stable cavity, and a complete control system consisting of temperature control, cavity locking, signal generators, and a control PC. To achieve transportability, we have created optimized designs for aspects such as cavity installation, optical path coupling, and the heat sink systems. Through testing, it was determined that the system can adapt to external-field temperature changes ranging from 20 °C to 40 °C, and the temperature tolerance is expected to range from 0°C to 50°C. The system was tested in a noisy environment for two hours, and the test results were satisfactory. Practical use shows that after long-distance transportation (over 400 km), the system only requires slight optimization to resume operation.

2. System Assembly

The purpose of this optical reference system is to stabilize two lasers’ resonance with the ${}^{133}Cs$ atomic transitions $6S_{1/2}\to 6P_{3/2}$ (852 nm) and $6P_{3/2}\to nS$ (or $nD$) (509 nm), respectively. Taking into account the characteristics of the field test, we installed all the systems in a 22U cabinet. This included two lasers, an ultra-stable cavity, and all the control components. 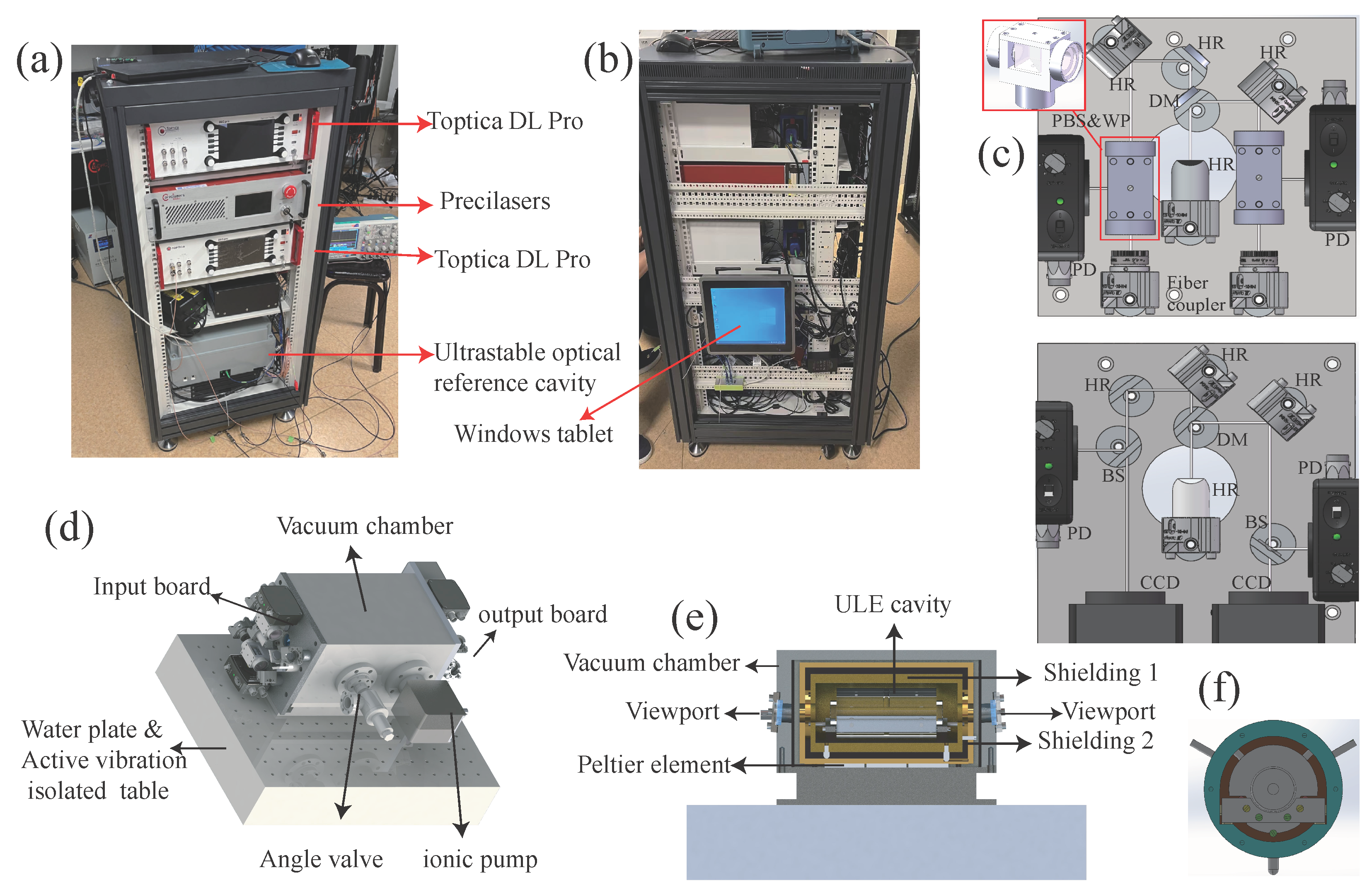As shown in Figure 1a, the laser controllers consist of two controllers for Toptica lasers and a controller for Precilasers fiber amplification and frequency doubling, which occupy around half of the cabinet space. The lasers and the Beamsplitter Kits system (PFS-FFT-1X2, Thorlabs, Newton, NJ, USA) are installed at the back zone of the cabinet, and are not shown in the picture. The 852 nm laser is produced by a tunable single-frequency diode laser (DL Pro, Toptica, Gräfelfing, Germany), while the 509 nm laser is generated via frequency doubling of the 1018 nm laser, and the 1018 nm laser is produced by a tunable single-frequency diode laser (Toptica DL Pro) and amplified by a high-power fiber amplifier (Precilaser, Berrioplano, Spain). A small amount of 852 nm and 1018 nm light (by Beamsplitter Kits, Thorlabs, Newton, NJ, USA) is picked up and then directed into the reference cavity for laser locking.

There are also many control components in the system, such as the ion pump controller for maintaining the vacuum, the temperature controller for maintaining the cavity temperature, the controller of the vibration isolation system, the signal source of the locking system, the locking controller, the detector power supply, etc. We placed these systems below the laser controller and above the ultra-stable cavity, which occupy approximately 10% of the cabinet space. In the system, the radio frequency signals, locking modules, cavity mode monitoring, 1018 frequency doubling, etc., are all controlled by a Windows tablet (SK-12ZLGKSH, Kechu, Shanghai, China), as shown in Figure 1b.

In order to avoid light and dust pollution, the ultra-stable cavity is encapsulated within an aluminum casting shell. The overall size of the encapsulated system is 400 mm × 300 mm × 185 mm. The system is set upon an active vibration isolation platform (Accurion Nano30) with a size of 400 mm × 300 mm × 75 mm, which features an active bandwidth of 1 Hz–200 Hz and passive isolation beyond 200 Hz. The encapsulated ultra-stable cavity is placed at the bottom of the system, occupying the remaining 8U of space. When testing the system, we found that due to the effect of large fluctuations in the temperature of the environment, the temperature-control system could collapse. In order to obtain a wider temperature-tolerance range, a water-cooled heat dissipation plate was added. The water cooling system is used to control the temperature of the entire system’s housing. A rough test showed that the system can work well within a temperature range of 20 °C to 40 °C. We expect that high-precision temperature-control effects can be achieved in an external environment with a temperature range of 0 °C to 50 °C.

2.1. Cavity, Optical Light Path, and Vacuum Design

Two cavity mirrors were double-coated at 852 nm and 1018 nm: one was a concave mirror with a radius of curvature of 500 mm, and the other was a plane mirror. Both mirrors were high-reflectivity-coated ($T=0.00045356\%@852\mathrm{nm}$, $T=0.00075818\%@1020\mathrm{nm}$ for concave mirror, and $T=0.0011771\%@852\mathrm{nm}$, $T=0.00095997\%@1020\mathrm{nm}$ for plane mirror; purchased from FiveNine optics company, Boulder, CO, USA) for high-finesse purposes. The cavity finesse was calculated as $385.3\mathrm{k}@852\mathrm{nm}$ and $365.7 \mathrm{k}@1020\mathrm{nm}$. The two cavity mirrors were connected by a 10 cm spacer. Both ends of the spacer were polished, and a parallelism of less than 10 arcminutes was achieved. The cavity mirrors and the spacer were connected by optical cementing. The free spectral range of the cavity corresponding to this cavity length is 1.5 GHz.

Before building the optical path, we obtained optimal mode-matching for the waist of the cavity of 509 µm @ 1018 nm and 466 µm @852 nm by numerical simulation. Through Gaussian beam transformation formula calculations, we selected a 4.6 mm adjustable fiber-coupler for mode matching. The total length of the optical path is within 300 mm. This minimizes the number of optical components and ensures cavity mode matching with the shortest possible optical path, thus guaranteeing the stability of the system. In addition, to minimize the instability factors of the system, we built the input- and output-coupling optical paths on two aluminum plates with dimensions of 120 mm × 120 mm × 10 mm, as shown in Figure 1c, and fixed these two aluminum plates at the two ends of the vacuum.

To maximize the stability of the system, we took several aspects into consideration. Firstly, we used adjustable mounts as little as possible in the system. There are only two adjustable mirror mounts (MHX-12.7A, Sigmakoki, Japan) in each mode-matching optical path. The height of the optical path in the system is approximately 25 mm, and the distance between the fiber output-coupling head and the vacuum chamber is about 170 mm. In addition, during the system installation, we applied screw-locking adhesive (Loctite 290) to all screws to ensure that the system could remain in place even after long-term exposure to vibrations. In front of the input couplers are fiber-coupled electro-optic modulators (EOM) (KY-PM-08-10G-PP-FAKY-PM-08-10G-PP-FA, Keyang Photonics, China) for modulation. Therefore, after the system is properly adjusted, we can encapsulate the fiber EOM and the ultra-stable cavity together, leaving the input end of the fiber EOM as the packaging interface.

The 10 cm long ULE glass cavity is housed in a vacuum system with a 5 L/s ion pump (B2020-5L5LA, Limit Vacuum Techology, Beijing, China) to maintain the pressure at the ${10}^{-6}$ Pa level. The cutting position provides support and rotational limitation for the cavity. At the same time, a set of three limiting screws are arranged at equal angular positions in the axial direction of the cavity, and two sets of such limiting screws are set in the axial direction. In addition, three pairs of limiting screws are added on the two parallel surfaces of the cavity, which ensures that the displacement and rotation of the system are as small as possible during transportation and collisions. The vacuum system consists of three-layer shielded structure. The innermost layer is a structure with copper plated with gold, which provides thermal shielding for the inner layer. The middle layer is an Invar structure, which provides stable support and temperature control. The outermost layer is an aluminum alloy vacuum chamber, which provides a vacuum environment. Three Peltier elements are placed between the second-layer shield and the vacuum chamber, and a thermistor is placed in the second-layer structure for temperature control. Figure 1e illustrates the vacuum assembly designed by us. The cavity is placed inside a two-stage heat shield, which is actively temperature-stabilized at the zero-crossing point (26 °C) by a commercial digital PID controller (TED200c, Thorlabs, Newton, NJ, USA).

2.2. ULE Cavity’s Support Structure

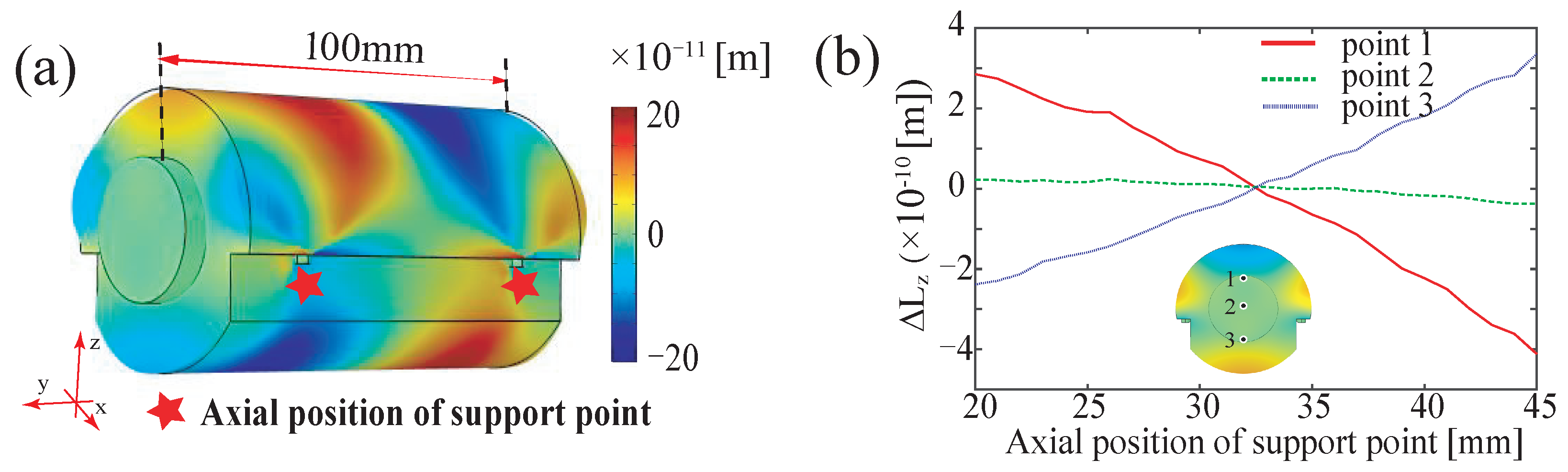
We designed and fabricated a notched ULE glass cavity with square “cutouts” on the underside of a cylindrical spacer, as shown in Figure 2a. The notched cavity [29,30] is improved by the cylindrical cavity. The notched structure can provide stable support and restrict rotation, with the force direction not along the radial direction. Furthermore, its low processing cost makes it the most commonly used structure at present. To achieve vibration insensitivity in the horizontal plane, a four-point symmetrical mounting is employed and implemented with two pairs of 3.2 mm diameter Teflon spheres. We further searched for the optical support points through finite-element analysis of cavity deformation with 14,950 mesh elements. Considering the axial symmetry, we numerically simulated the axial displacements for the three points at the end of the cavity marked in the insert of Figure 2b by varying the axial position of the support points with a step length of 1 mm.

Figure 2a shows a representation of the solution at y = 32.5 mm, where values of $67.6\times {10}^9\mathrm{Pa}$ and 0.17 for the Young’s modulus and Poisson’s ratio are used for both the mirror and spacer, which are made of ULE glass. Figure 2b gives the axial displacement as a function of the support point location. It is found that the minimum displacement at the three points is achieved at y = 32.5 mm, and the axial displacement at the mirror surface is also minimized. We therefore chose this location as the support point to minimize the cavity deformation when loaded.

3. System Tests and Results

The lasers of the two wavelengths were locked onto a set of ultra-stable cavities simultaneously. Therefore, a pair of dichroic mirrors (DMLP950T, Thorlabs, Newton, NJ, USA) was used to couple the lasers, and the modulation frequencies were set to 10 MHz and 12 MHz, respectively, so as to avoid disturbance between the two locking systems.

We used this high-finesse cavity as the optical reference to perform sideband Pound–Drever–Hall (PDH) locking [15,31] and thus stabilize the laser frequency. As shown in Figure 3, the output of a tunable single-frequency diode laser (DL Pro, Toptica, Germany) passes through a fiber-coupled EOM (bandwidth 10 GHz) following the optical-power-splitting elements. The phase-modulated light transmits through a polarizing beam splitter (PBS) and passes through a quarter-wave plate (QWP), then is directed into the cavity. The reflected light passes through the QWP and PBS and is collected by the photodiode. The cavity transmission is split into two parts for monitoring the coupling mode and the locking status. The photodiode outputs of both reflection and transmission are induced to the PreciLock for producing the error signal. The produced signal is fed into the piezoceramic (PZT) and diode currents of the laser. The control signal of the EOM consists of two parts: the carrier signal provided by the synthHD (V2) and the modulation signal provided by the Precilock. After the two signals are combined by a power splitter (ZFRSC-42-S+, mini-circuit), they respectively provide the sideband frequency and the modulation frequency. This sideband locking is implemented to provide wide-range tunability of the laser frequency.

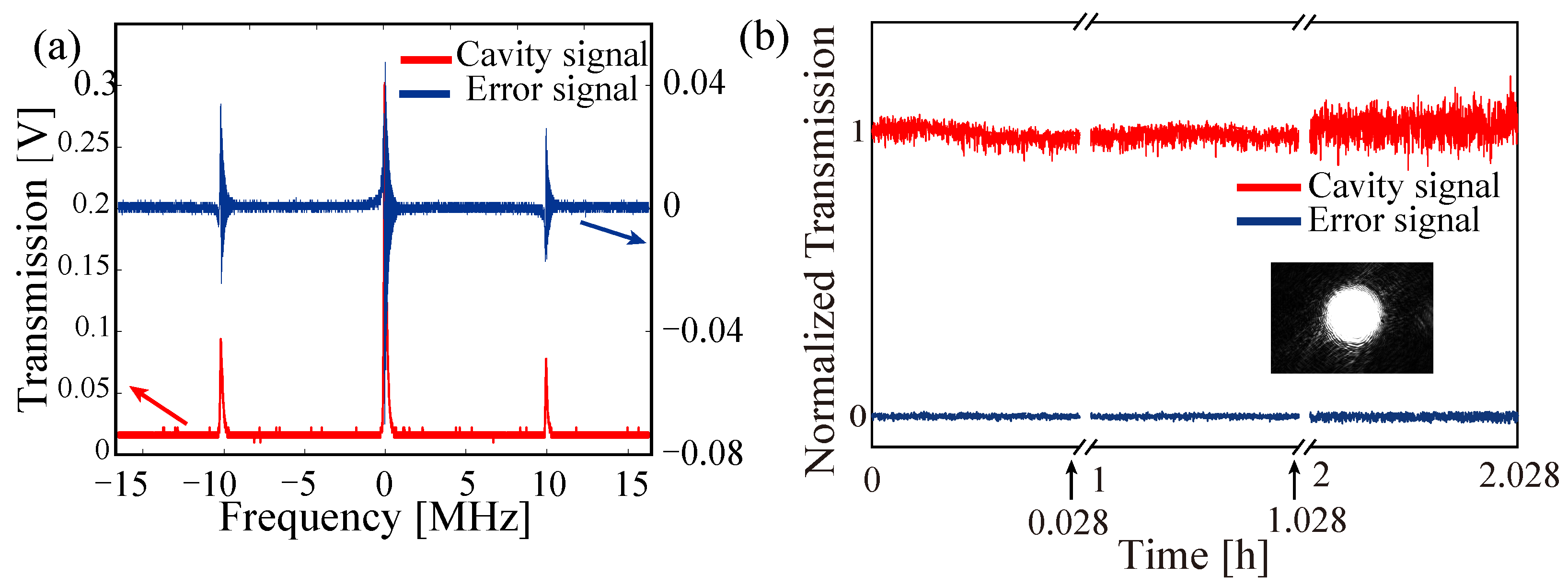
Figure 4a,b illustrate the transmission and error signals at the scanning and locking modes. After this system was set up in the laboratory environment, it was transported over 400 km away. During the transportation, it experienced situations like being carried by car and train, being dragged, and getting bumped. After the system was delivered, it only required minor adjustments to resume operation. However, the system test was not conducted while the system was in motion. Instead, it was tested in a very noisy environment. The system was placed on the eighth floor, and during the test, there were noises such as people talking, walking, and the sound of a fan. During the 2 h monitoring period, the system maintained its locking status, as shown in Figure 4b.

We proceed to characterize the optical cavity in terms of cavity FSR and finesses. To obtain the FSR, we linearly scanned the laser frequency over two adjacent cavity fundamental modes (TEM00 mode). By tuning the modulation frequency, the +1st order sideband resonance of the high-frequency fundamental mode could overlap with the −1st order sideband signal of the lower-frequency one. We thus found that the FSR was twice the modulation frequency. Experimentally, the FSR was determined as 1.495849 GHz, corresponding to a cavity length of 10.02775 cm.

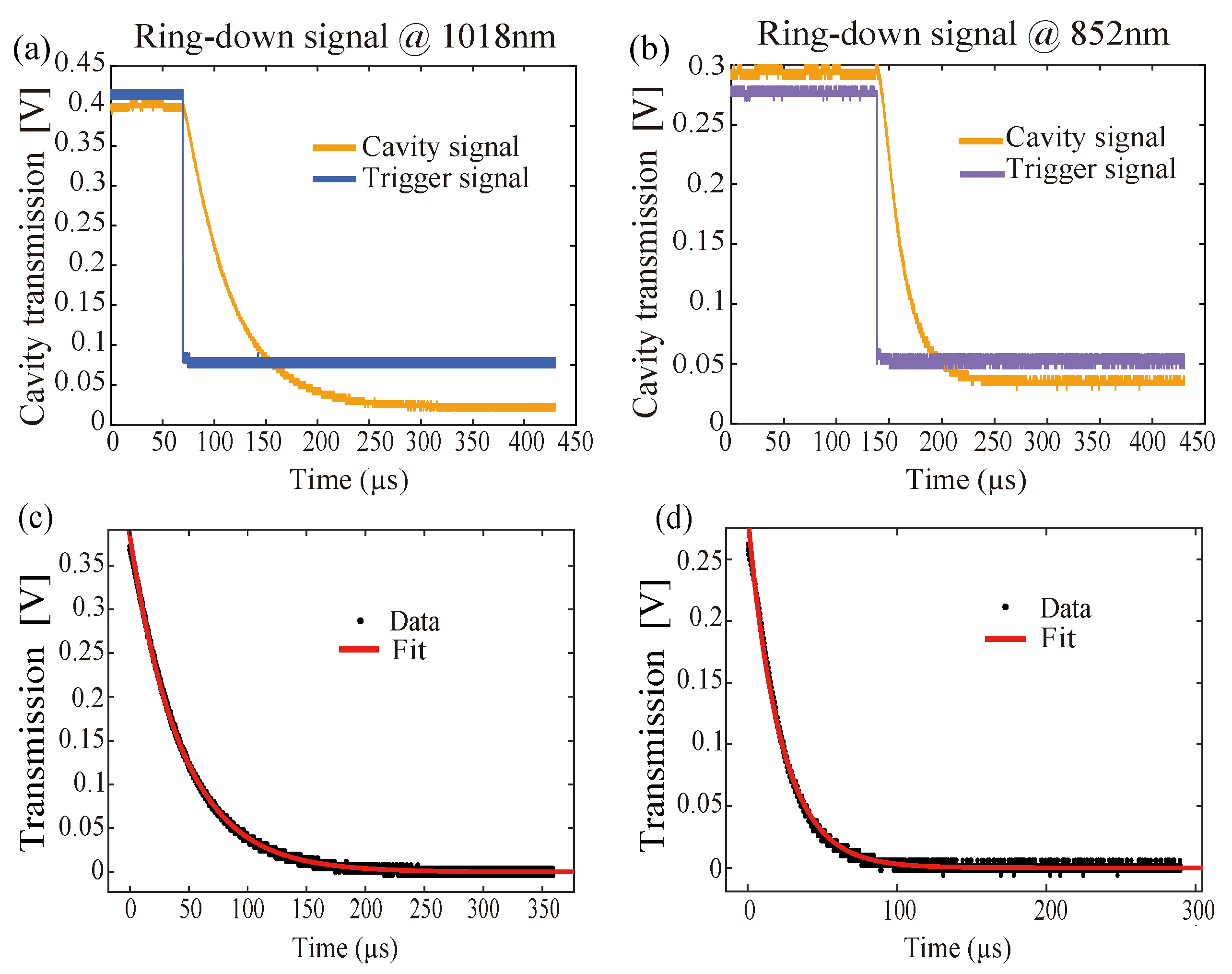
A cavity ring-down measurement was performed to determine the cavity finesses. The laser was initially locked to the optical reference cavity. The fiber-coupled EOM driving frequency was instantaneously turned off, and the cavity transmission at 1018 nm and 852 nm thus underwent exponential decay, as shown in Figure 5a,b, respectively. The exponential fit gave a $1/e$ decay time $\tau$ of 43.8447 ± 0.1997 μs at 1018 nm and 21.8088 ± 0.3107 μs at 852 nm. Finally, the fitting formula $F=2\pi \tau {\nu }_{FSR}$ determined the finesses of 412,081 ± 1877 at 1018 nm and 20,4971 ± 2918 at 852 nm.

For external field measurements, the primary concern is narrowing the laser linewidth, which can be effectively achieved by a high-Q cavity design. However, two additional critical challenges arise: First, ULE cavity drift must be managed during transit or shortly after relocation. Key drift-inducing factors include heat conduction and gradual cavity creep. Second, while transportability necessitates securing the cavity with multiple limit screws to minimize displacement between the optical light path and cavity, this mechanical rigidity creates a tradeoff: deformations in the vacuum structure, due to external environmental changes, inevitably impose stress on the cavity, inducing ULE cavity distortion. In addition, in noisy environments, over-rigid fixation exacerbates noise transmission, as mechanical perturbations couple more directly with the cavity. Balancing these constraints during system assembly requires careful engineering.

Notably, Doppler broadening of thermal atomic systems offers partial tolerance for residual drift in microwave electric field measurements, but full optimization remains essential. A promising solution involves integrating the optical path system with the ULE cavity. Such integration would eliminate the need for mechanical constraints to restrict relative displacement. However, this remains a technical challenge at present. In this case, we only need to focus on the phase noise caused by temperature and vibration, as well as the servo noise caused by the locking loop, etc., which will greatly reduce the difficulty of system design.

4. Conclusions and Perspectives

Through elaborate mechanical design and wide-range tunable sideband Pound–Drever–Hall (PDH) locking, we have developed a transportable ultra-stable laser system for two-photon Rydberg excitation applications, like microwave electric field sensors. We characterized the optical reference cavity, and the cavity ring-down measurement results showed dual-wavelength finesses of 412,081 ± 1877 (at 1018 nm) and 204,971 ± 2918 (at 852 nm). By incorporating an auto-relock unit and an active vibration isolation unit, the system can operate continuously for over 2 h, which makes long-term operation at various measurement sites possible. Future research will focus on upgrading cavity structure, characterizing the long-term instability or drift of the system, further reducing the intensity of noise, servo noise, etc., and exploring the system’s practical applications.