High-Q Resonances Enabled by Bound States in the Continuum for a Dual-Parameter Optical Sensing
Abstract
1. Introduction
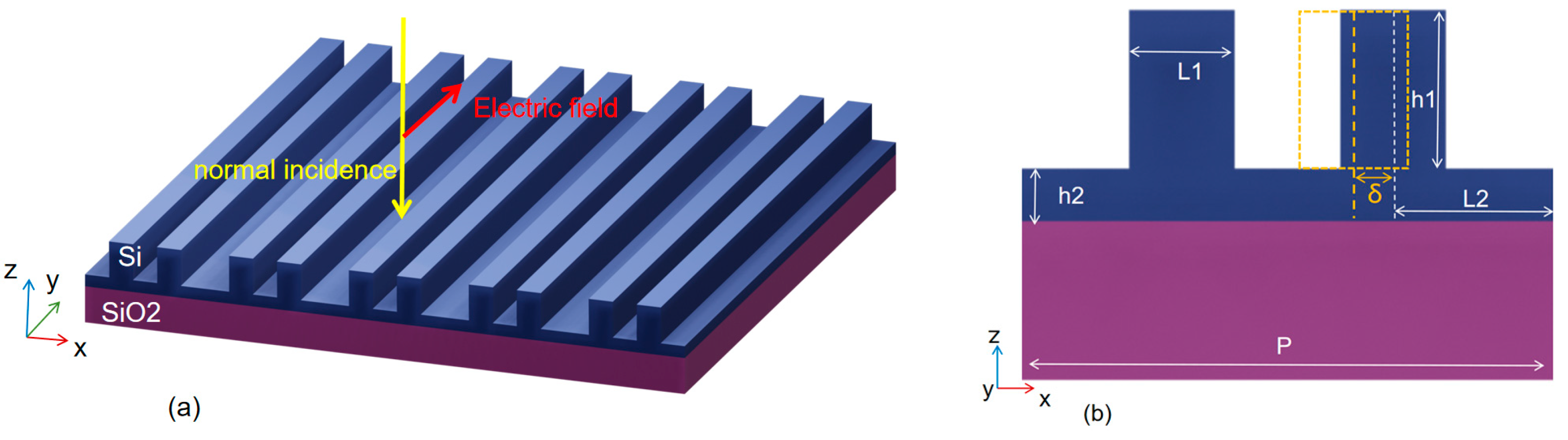
2. Design of Dual-Mode Grating-Based Temperature−Refractive Index Sensor
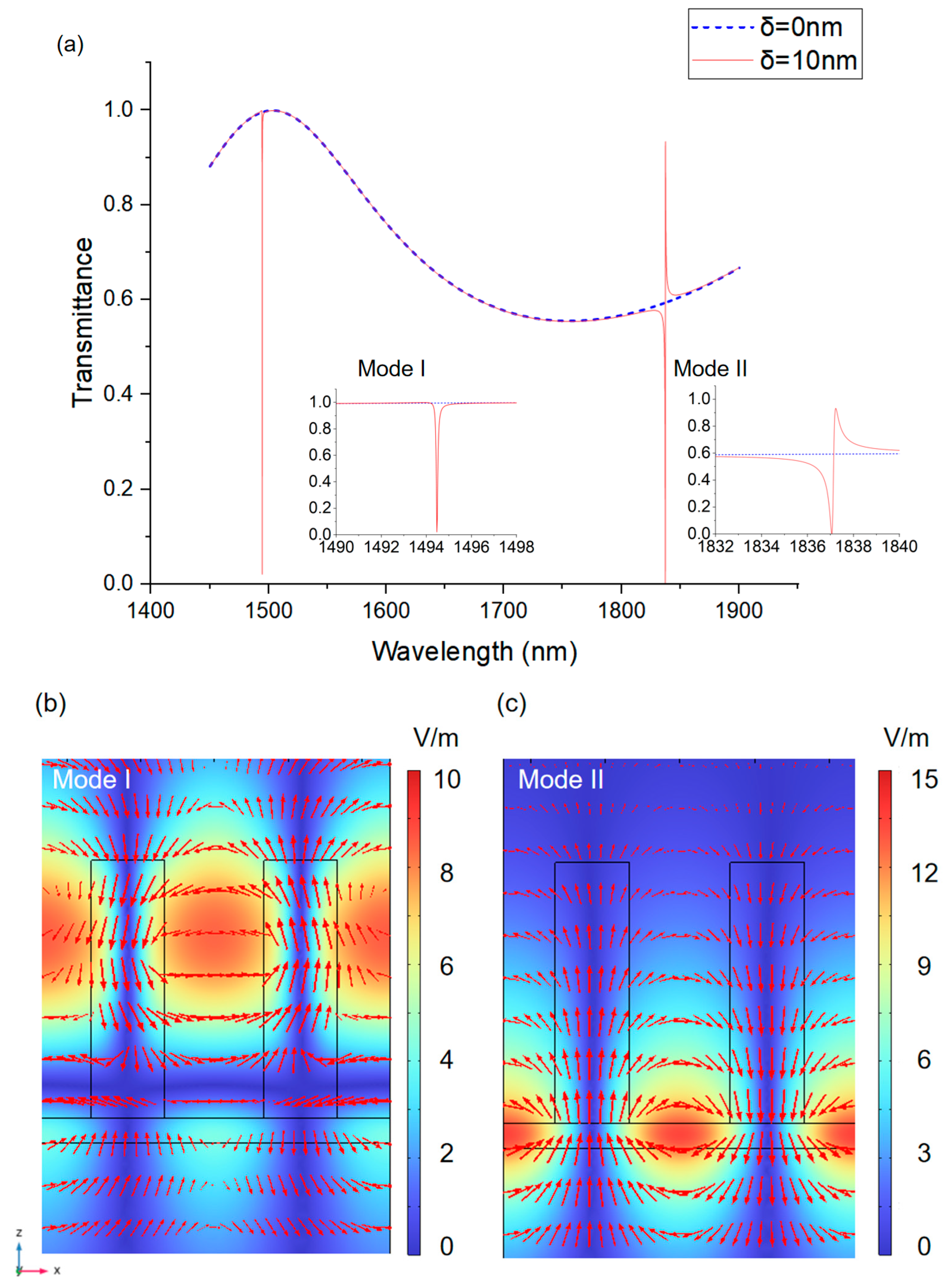
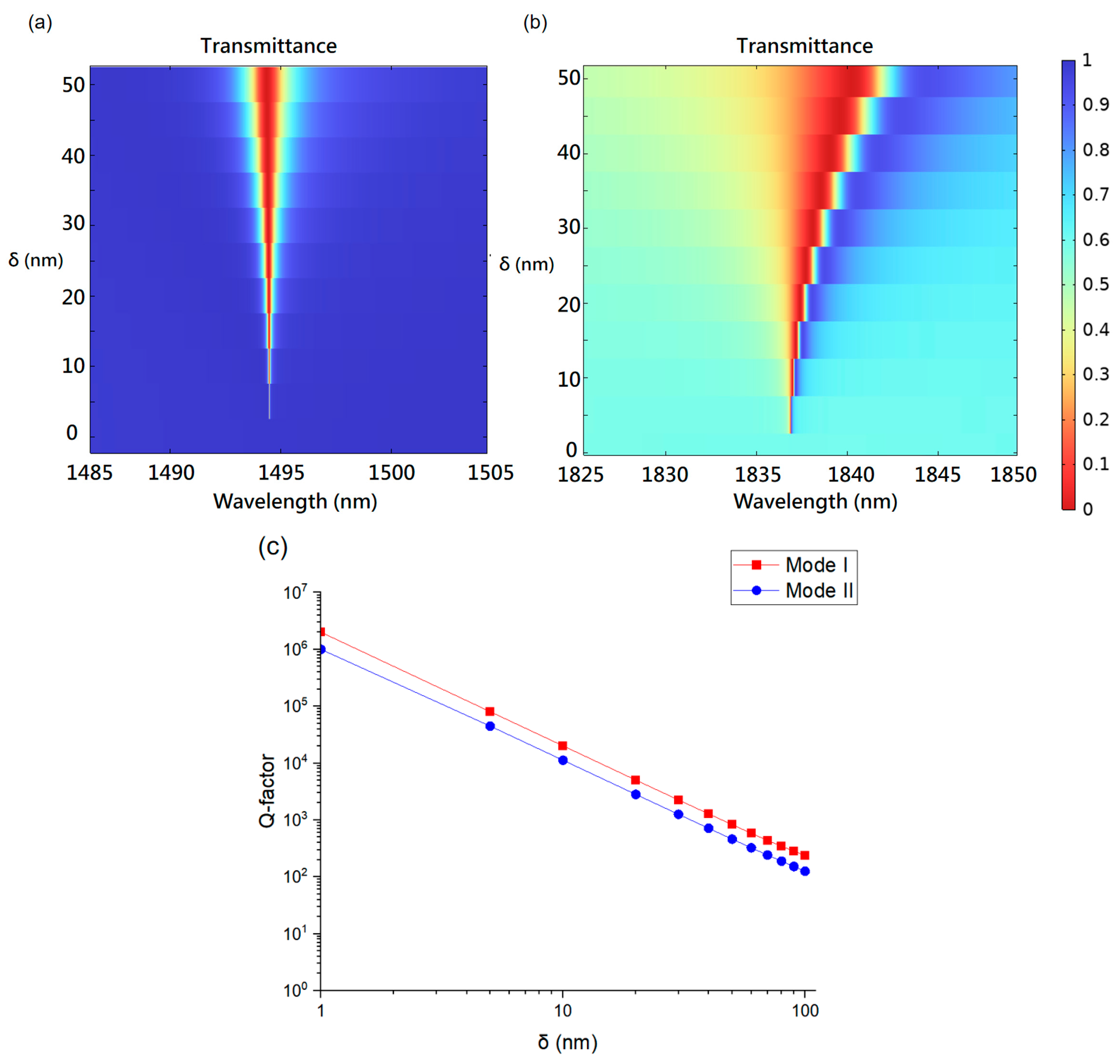
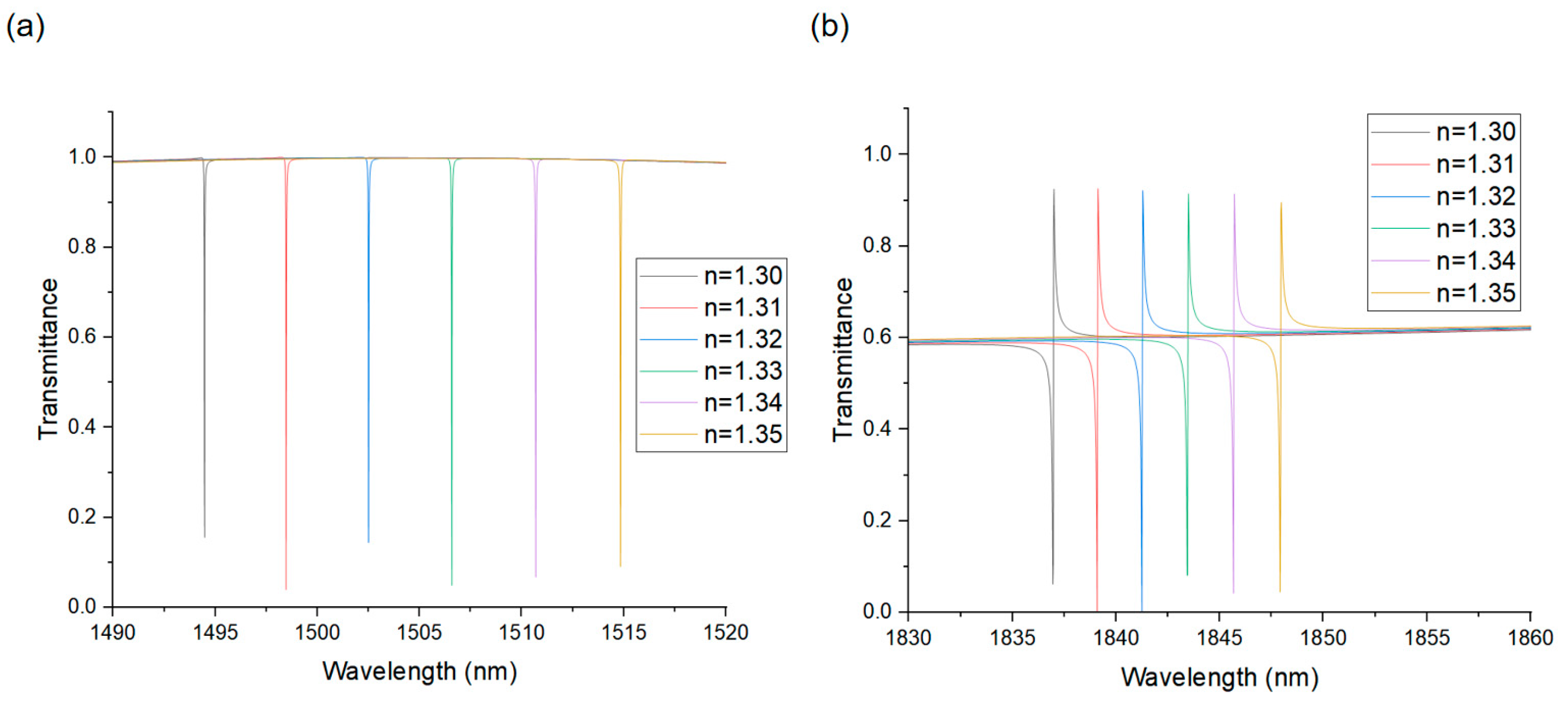
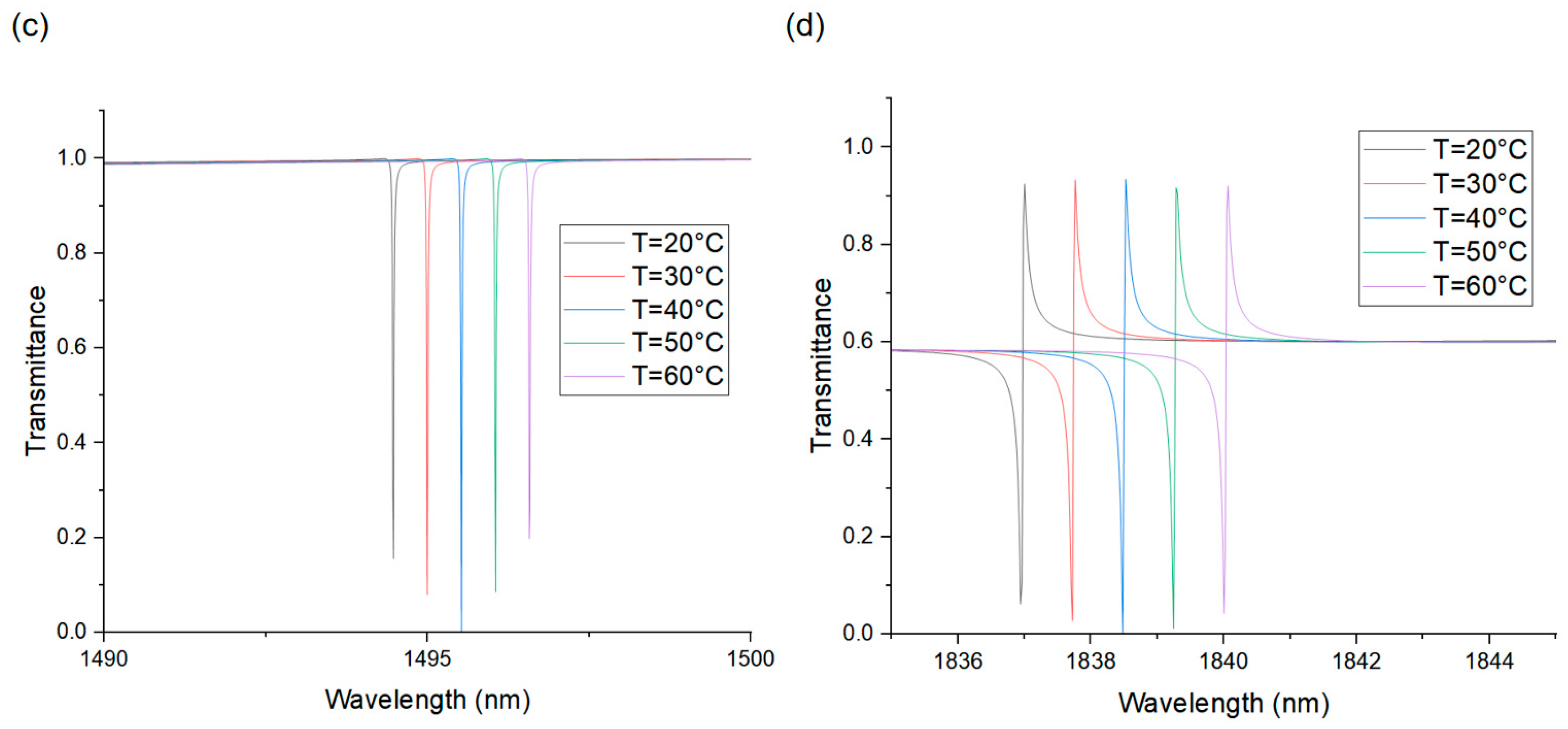
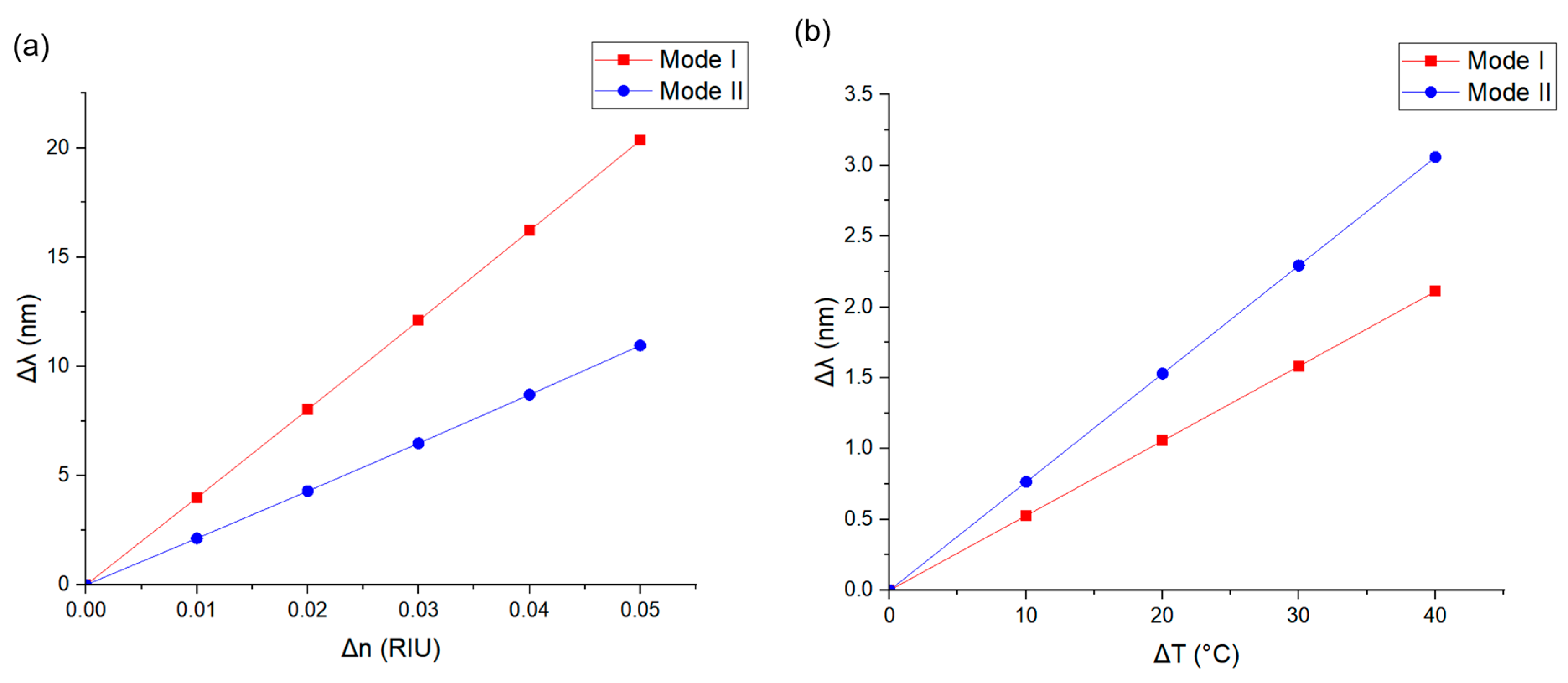
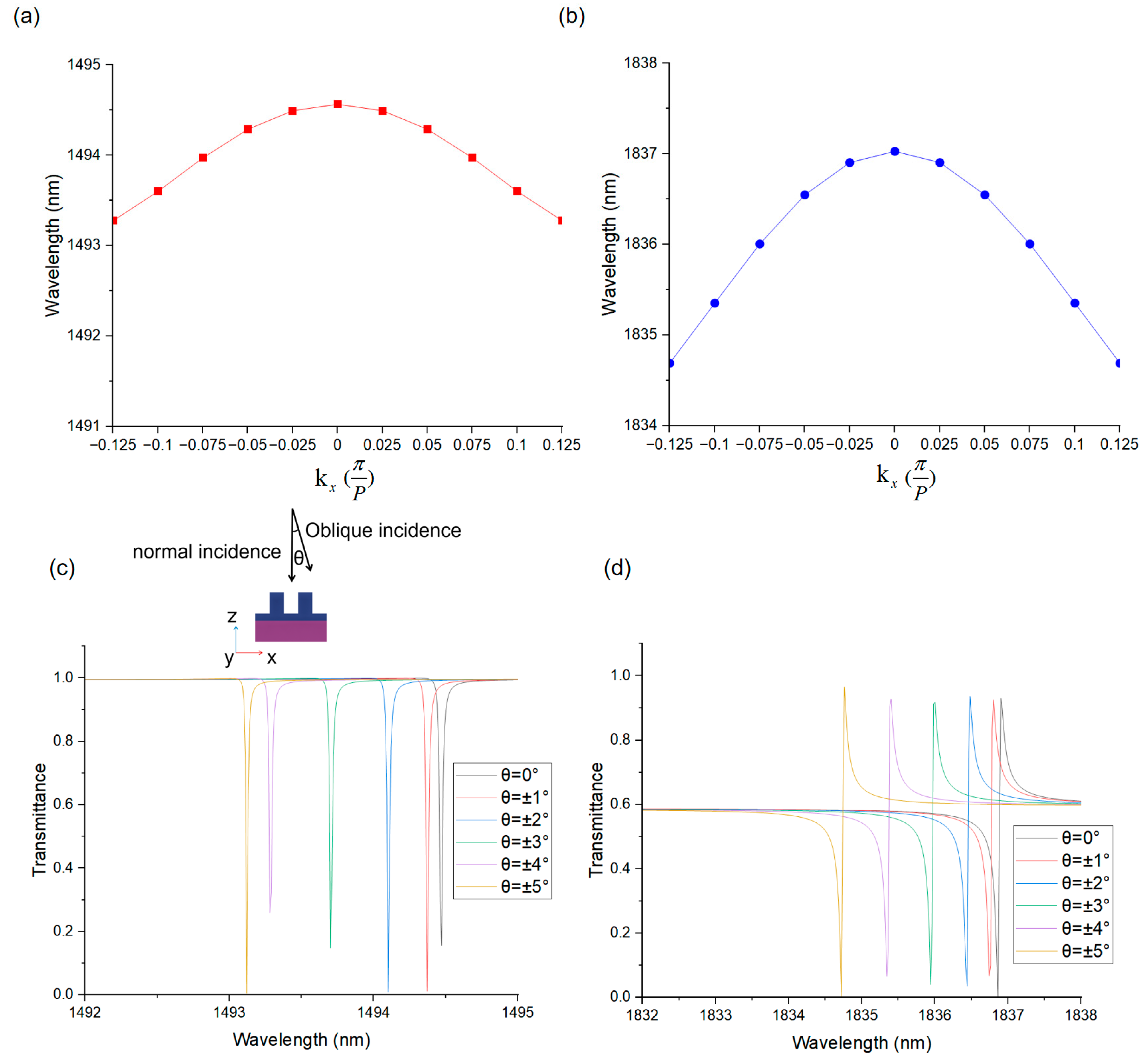
3. Principle of Sensing and Discussion of Result
4. Uncertainty Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rao, Y.-J. In-fibre Bragg grating sensors. Meas. Sci. Technol. 1997, 8, 355. [Google Scholar] [CrossRef]
- Homola, J. Surface plasmon resonance sensors for detection of chemical and biological species. Chem. Rev. 2008, 108, 462–493. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Roh, S.; Park, J. Current status of micro-and nano-structured optical fiber sensors. Opt. Fiber Technol. 2009, 15, 209–221. [Google Scholar] [CrossRef]
- Kersey, A.D.; Davis, M.A.; Patrick, H.J.; LeBlanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J. Fiber grating sensors. J. Light. Technol. 1997, 15, 1442–1463. [Google Scholar] [CrossRef]
- Erdogan, T. Fiber grating spectra. J. Light. Technol. 2002, 15, 1277–1294. [Google Scholar] [CrossRef]
- Leng, J.; Asundi, A. Structural health monitoring of smart composite materials by using EFPI and FBG sensors. Sens. Actuators A Phys. 2003, 103, 330–340. [Google Scholar] [CrossRef]
- Homola, J.; Dostalek, J.; Chen, S.; Rasooly, A.; Jiang, S.; Yee, S.S. Spectral surface plasmon resonance biosensor for detection of staphylococcal enterotoxin B in milk. Int. J. Food Microbiol. 2002, 75, 61–69. [Google Scholar] [CrossRef]
- Kretschmann, E.; Raether, H. Radiative decay of non radiative surface plasmons excited by light. Z. Für Naturforschung A 1968, 23, 2135–2136. [Google Scholar] [CrossRef]
- Otto, A. Excitation of nonradiative surface plasma waves in silver by the method of frustrated total reflection. Z. Für Phys. A Hadron. Nucl. 1968, 216, 398–410. [Google Scholar] [CrossRef]
- Brambilla, G. Optical fibre nanowires and microwires: A review. J. Opt. 2010, 12, 043001. [Google Scholar] [CrossRef]
- Fan, X.; White, I.M.; Shopova, S.I.; Zhu, H.; Suter, J.D.; Sun, Y. Sensitive optical biosensors for unlabeled targets: A review. Anal. Chim. Acta 2008, 620, 8–26. [Google Scholar] [CrossRef]
- Monat, C.; Grillet, C.; Collins, M.; Clark, A.; Schroeder, J.; Xiong, C.; Li, J.; O’Faolain, L.; Krauss, T.F.; Eggleton, B.J. Integrated optical auto-correlator based on third-harmonic generation in a silicon photonic crystal waveguide. Nat. Commun. 2014, 5, 3246. [Google Scholar] [CrossRef]
- Shu, X.; Zhang, L.; Bennion, I. Sensitivity characteristics of long-period fiber gratings. J. Light. Technol. 2002, 20, 255. [Google Scholar]
- Vengsarkar, A.M.; Lemaire, P.J.; Judkins, J.B.; Bhatia, V.; Erdogan, T.; Sipe, J.E. Long-period fiber gratings as band-rejection filters. J. Light. Technol. 1996, 14, 58–65. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef] [PubMed]
- Saad-Bin-Alam, M.; Reshef, O.; Mamchur, Y.; Carlow, G.; Sullivan, B.; Ménard, J.-M.; Huttunen, M.J.; Dolgaleva, K.; Boyd, R.W. Ultra-High-Q Resonance in a Plasmonic Metasurface. In Proceedings of the Conference on Lasers and Electro-Optics, Washington, DC, USA, 10–15 May 2020; p. FF3E.3. [Google Scholar]
- Li, T.; Liu, M.; Hou, J.; Yang, X.; Wang, S.; Wang, S.; Zhu, S.; Tsai, D.P.; Wang, Z. Chip-scale metaphotonic singularities: Topological, dynamical, and practical aspects. Chip 2024, 3, 100109. [Google Scholar] [CrossRef]
- Bulgakov, E.; Sadreev, A. Symmetry breaking in a T-shaped photonic waveguide coupled with two identical nonlinear cavities. Phys. Rev. B—Condens. Matter Mater. Phys. 2011, 84, 155304. [Google Scholar] [CrossRef]
- Friedrich, H.; Wintgen, D. Interfering resonances and bound states in the continuum. Phys. Rev. A 1985, 32, 3231. [Google Scholar] [CrossRef]
- Marinica, D.C.; Borisov, A.G.; Shabanov, S.V. Bound states in the continuum in photonics. Phys. Rev. Lett. 2008, 100, 183902. [Google Scholar] [CrossRef]
- Ning, T.; Li, X.; Zhao, Y.; Yin, L.; Huo, Y.; Zhao, L.; Yue, Q. Giant enhancement of harmonic generation in all-dielectric resonant waveguide gratings of quasi-bound states in the continuum. Opt. Express 2020, 28, 34024–34034. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Qi, X.; Qin, M.; Luo, M.; Long, Y.; Wu, J.; Sun, Y.; Jiang, H.; Liu, T.; Xiao, S.; et al. Momentum mismatch driven bound states in the continuum and ellipsometric phase singularities. Phys. Rev. B 2024, 109, 085436. [Google Scholar] [CrossRef]
- Wu, F.; Wu, J.; Guo, Z.; Jiang, H.; Sun, Y.; Li, Y.; Ren, J.; Chen, H. Giant Enhancement of the Goos-Hänchen Shift Assisted by Quasibound States in the Continuum. Phys. Rev. Appl. 2019, 12, 014028. [Google Scholar] [CrossRef]
- Kodigala, A.; Lepetit, T.; Gu, Q.; Bahari, B.; Fainman, Y.; Kanté, B. Lasing action from photonic bound states in continuum. Nature 2017, 541, 196–199. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Y.; Lin, Y.; Xiang, J.; Feng, T.; Cao, Q.; Li, J.; Lan, S.; Liu, J. High-Q quasibound states in the continuum for nonlinear metasurfaces. Phys. Rev. Lett. 2019, 123, 253901. [Google Scholar] [CrossRef]
- Tan, T.C.; Srivastava, Y.K.; Ako, R.T.; Wang, W.; Bhaskaran, M.; Sriram, S.; Al-Naib, I.; Plum, E.; Singh, R. Active control of nanodielectric-induced THz quasi-BIC in flexible metasurfaces: A platform for modulation and sensing. Adv. Mater. 2021, 33, 2100836. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Li, T.; Bi, Q.; Wang, S.; Zhu, S.; Wang, Z. Quasi-bound states in the continuum-based switchable light-field manipulator. Opt. Mater. Express 2022, 12, 1232–1241. [Google Scholar] [CrossRef]
- Fan, J.; Zhou, Y.; Xue, Z.; Xu, G.; Chen, J.; Xing, H.; Lu, D.; Cong, L. Active Singularity Metadevices Enabled by Bound States in the Continuum. Laser Photon. Rev. 2025, 2401869. [Google Scholar] [CrossRef]
- Li, N.; Chen, H.; Zhao, Y.; Wang, Y.; Su, Z.; Liu, Y.; Huang, L. Ultrasensitive metasurface sensor based on quasi-bound states in the continuum. Nanophotonics 2025, 14, 485–494. [Google Scholar] [CrossRef]
- Maksimov, D.N.; Gerasimov, V.S.; Romano, S.; Polyutov, S.P. Refractive index sensing with optical bound states in the continuum. Opt. Express 2020, 28, 38907–38916. [Google Scholar] [CrossRef]
- Romano, S.; Zito, G.; Lara Yépez, S.N.; Cabrini, S.; Penzo, E.; Coppola, G.; Rendina, I.; Mocellaark, V. Tuning the exponential sensitivity of a bound-state-in-continuum optical sensor. Opt. Express 2019, 27, 18776–18786. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, Y.K.; Ako, R.T.; Gupta, M.; Bhaskaran, M.; Sriram, S.; Singh, R. Terahertz sensing of 7 nm dielectric film with bound states in the continuum metasurfaces. Appl. Phys. Lett. 2019, 115, 151105. [Google Scholar] [CrossRef]
- Chen, W.; Li, M.; Zhang, W.; Chen, Y. Dual-resonance sensing for environmental refractive index based on quasi-BIC states in all-dielectric metasurface. Nanophotonics 2023, 12, 1147–1157. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Sun, F.; Wang, J.; Liu, Y.; Tian, H. Design and Theoretical Analysis of a Low Demodulation Deviation PhC Dual-Parameter Sensor Based on Quasi-BIC and Guided Mode Resonance. IEEE Sens. J. 2024, 24, 29841–29850. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, Z.; Xie, Q.; Li, W.; Xia, F.; Wang, M.; Feng, H.; You, C.; Yun, M. Toroidal dipole bound states in the continuum in all-dielectric metasurface for high-performance refractive index and temperature sensing. Appl. Surf. Sci. 2023, 615, 156408. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, X.; Fang, W.; Xiao, W.; Sun, F.; Li, C.; Wei, X.; Tao, J.; Wang, Y.; Kumar, S. High-Performance Refractive Index and Temperature Sensing Based on Toroidal Dipole in All-Dielectric Metasurface. Sensors 2024, 24, 3943. [Google Scholar] [CrossRef]
- Chen, R.; Bi, Q.; Li, T.; Wang, S.; Zhu, S.; Wang, Z. Dual-wavelength chiral metasurfaces based on quasi-bound states in the continuum. J. Opt. 2023, 25, 045001. [Google Scholar] [CrossRef]
- Li, T.; Liu, M.; Qin, J.; Ren, J.; Hou, J.; Liu, Y.; Yang, X.; Chu, H.; Lai, Y.; Wang, S.; et al. Configurable Topological Photonic Polycrystal Based on a Synthetic Hybrid Dimension. Natl. Sci. Rev. 2025, nwaf107. [Google Scholar] [CrossRef]
- Li, T.; Xu, X.; Fu, B.; Wang, S.; Li, B.; Wang, Z.; Zhu, S. Integrating the optical tweezers and spanner onto an individual single-layer metasurface. Photon. Res. 2021, 9, 1062–1068. [Google Scholar] [CrossRef]
- Li, T.; Kingsley-Smith, J.J.; Hu, Y.; Xu, X.; Yan, S.; Wang, S.; Yao, B.; Wang, Z.; Zhu, S. Reversible lateral optical force on phase-gradient metasurfaces for full control of metavehicles. Opt. Lett. 2023, 48, 255–258. [Google Scholar] [CrossRef]
- Li, T.; Xu, H.; Panmai, M.; Shao, T.; Gao, G.; Xu, F.; Hu, G.; Wang, S.; Wang, Z.; Zhu, S. Ultrafast Metaphotonics. Ultrafast Metaphotonics 2024, 4, 0074. [Google Scholar] [CrossRef]
| Ref. | Sensitivity of RI (nm/RIU) | Sensitivity of Temperature (nm/°C) | Capability for Dual-Parameter Sensing | Q Factor | Structure |
|---|---|---|---|---|---|
| Maksimov et al. [31] | 137.2; 229.7 | / | No | Not given | Silicon grating |
| Romano et al. [32] | 4000 | / | No | Not given | Silicon nitride PhC slab with nanoholes |
| Chen et al. [34] | 122.2 | / | No | 415 | Elliptic poly-Si nanopillars metasurface |
| Han et al. [35] | 833; 1068 | −0.043; −0.083 | Yes | 34,000; 160,000 | Silicon PhC slab with nanoholes |
| Guo et al. [36] | 746 | 0.054 | No | 54,757 | Metasurface with split-disk unit |
| Zhao et al. [37] | 262 | 0.0595 | No | 4225; 10,135 | Metasurface with “H”-shaped disks and tilted gaps unit |
| This work | 406; 220 | 0.052; 0.078 | Yes | 80,300; 44,800 | Silicon grating and slab |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Pan, Y.; Lu, H.; Chen, Z.; Huang, X.; Yu, C. High-Q Resonances Enabled by Bound States in the Continuum for a Dual-Parameter Optical Sensing. Photonics 2025, 12, 554. https://doi.org/10.3390/photonics12060554
Liu H, Pan Y, Lu H, Chen Z, Huang X, Yu C. High-Q Resonances Enabled by Bound States in the Continuum for a Dual-Parameter Optical Sensing. Photonics. 2025; 12(6):554. https://doi.org/10.3390/photonics12060554
Chicago/Turabian StyleLiu, Hongshun, Yuntao Pan, Hongjian Lu, Zongyu Chen, Xuguang Huang, and Changyuan Yu. 2025. "High-Q Resonances Enabled by Bound States in the Continuum for a Dual-Parameter Optical Sensing" Photonics 12, no. 6: 554. https://doi.org/10.3390/photonics12060554
APA StyleLiu, H., Pan, Y., Lu, H., Chen, Z., Huang, X., & Yu, C. (2025). High-Q Resonances Enabled by Bound States in the Continuum for a Dual-Parameter Optical Sensing. Photonics, 12(6), 554. https://doi.org/10.3390/photonics12060554







