MgO-Based Fabry-Perot Vibration Sensor with a Fiber-Optic Collimator for High-Temperature Environments
Abstract
1. Introduction
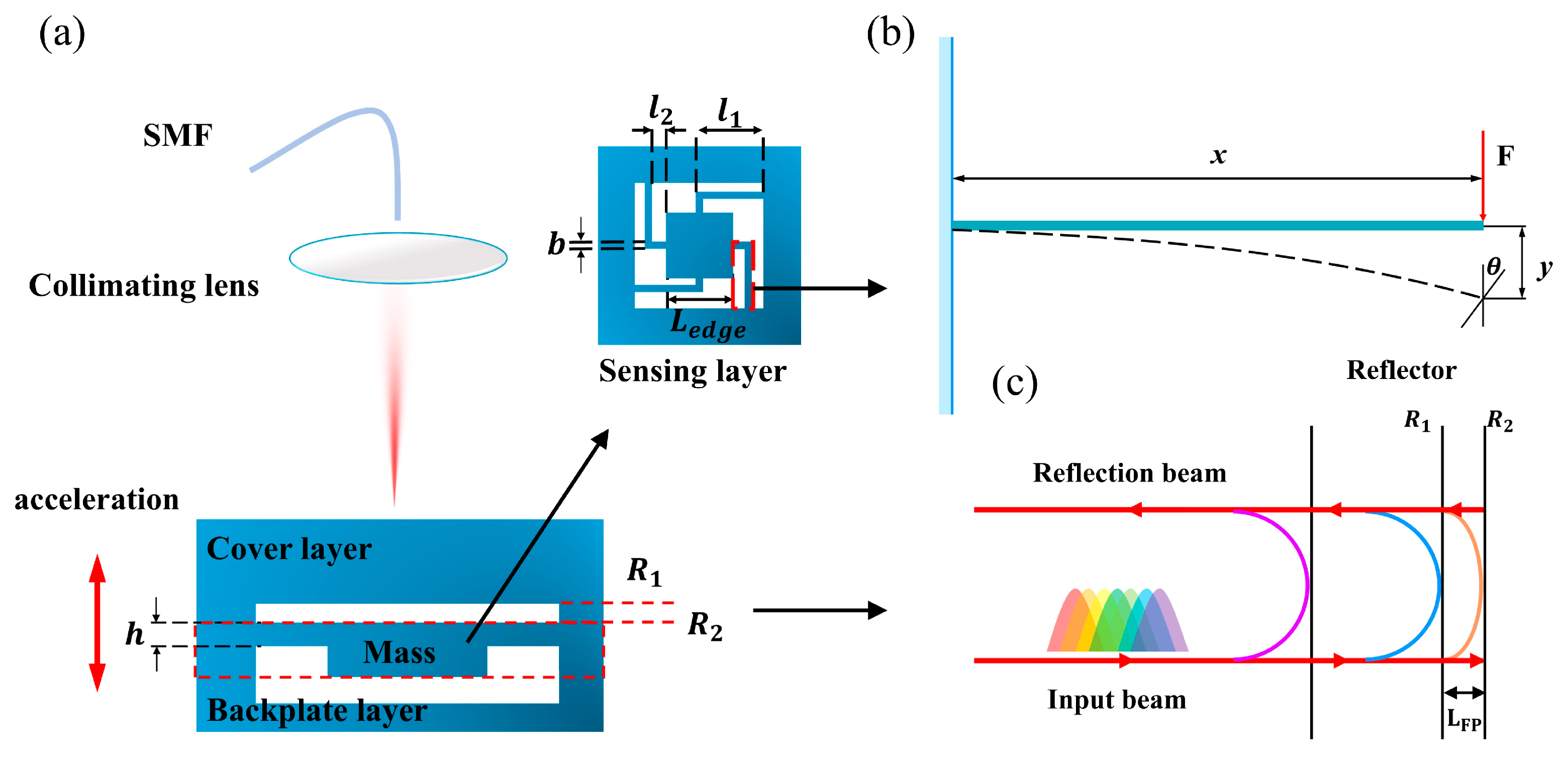
2. Operating Principle
2.1. Mechanical Principle of the Sensor
2.2. Demodulation Principle of the Sensor
2.3. Principle of the Collimating Lens
3. Sensor Preparation
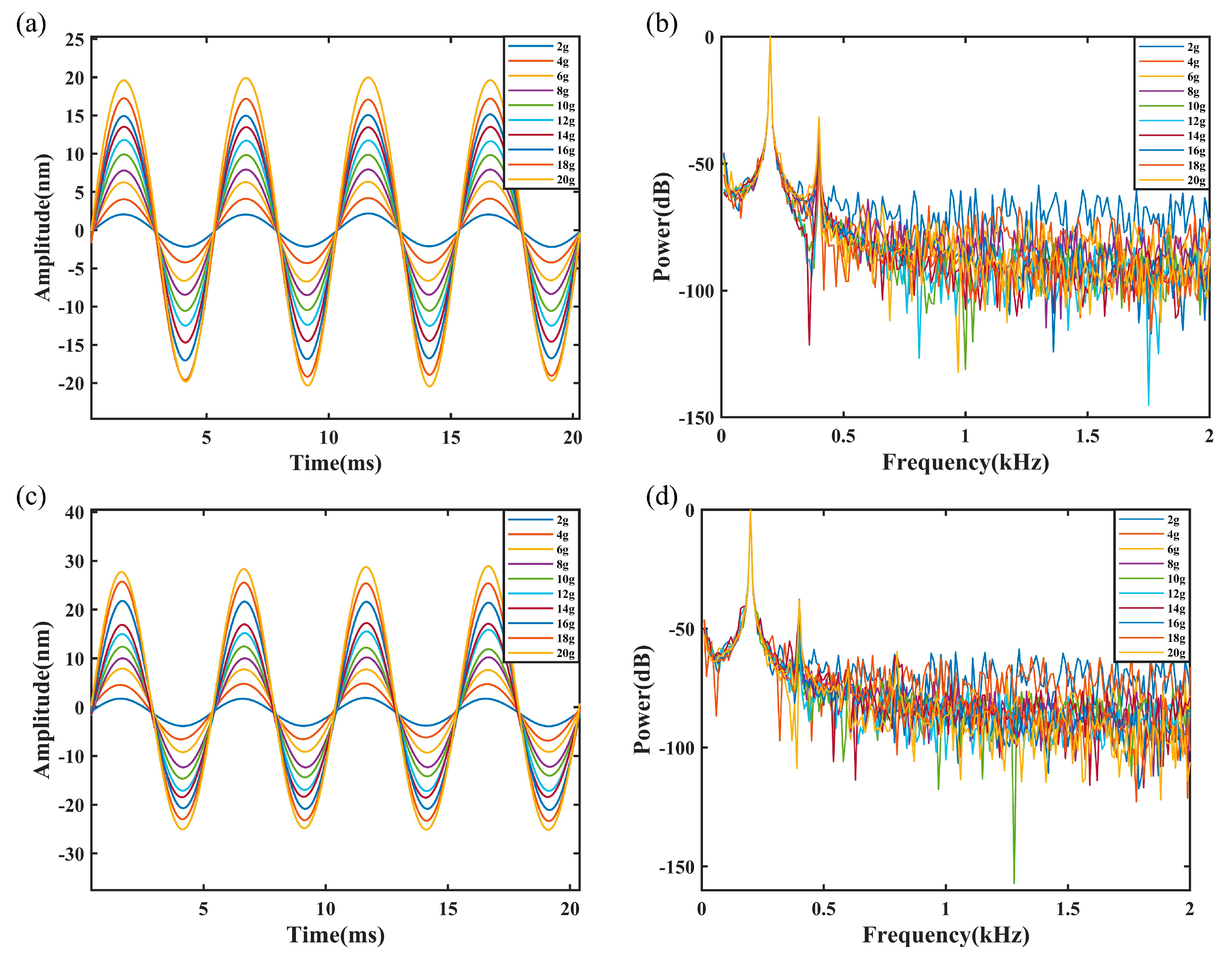
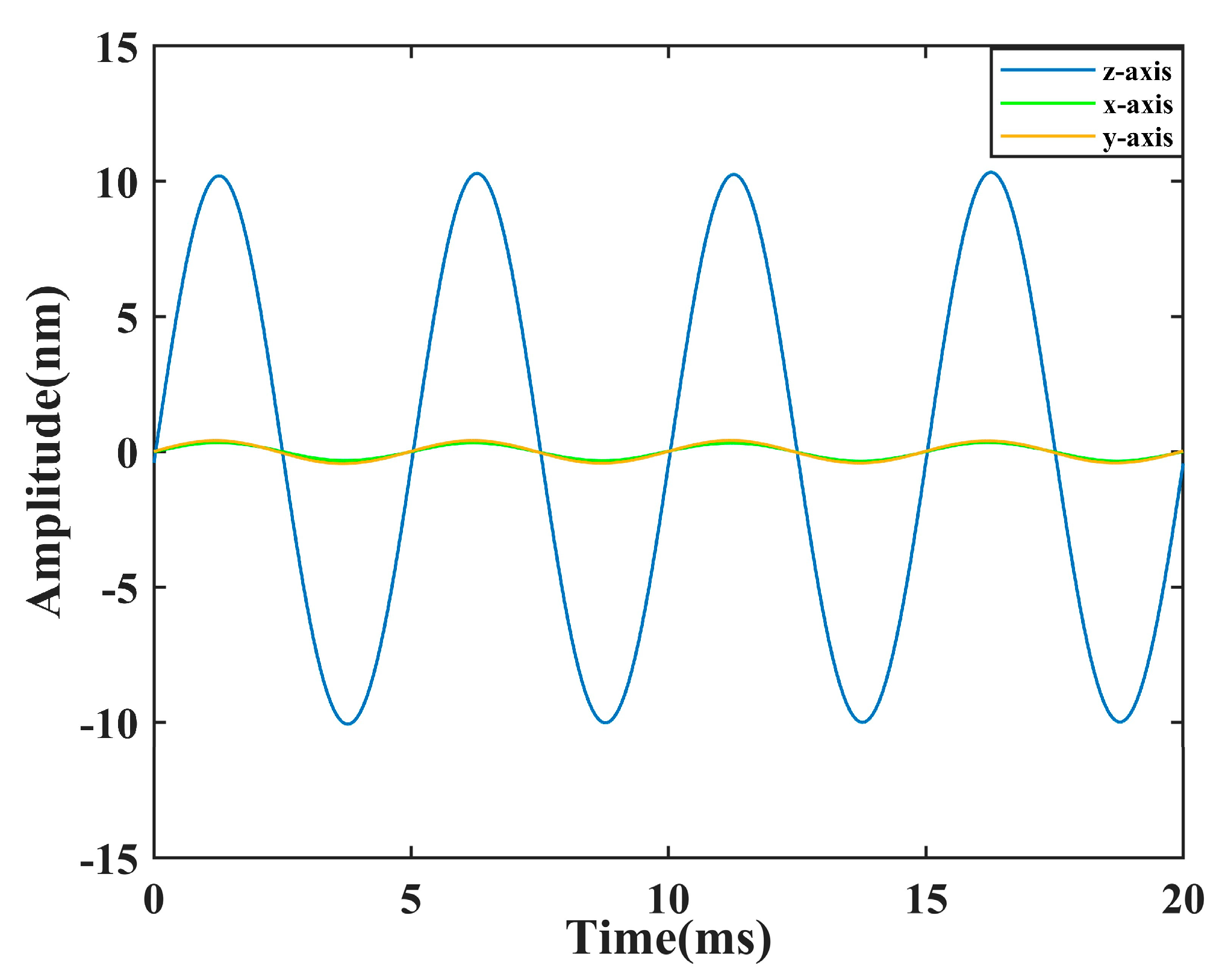
4. Experiments and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mills, A.R.; Kadirkamanathan, V. Sensing for aerospace combustor health monitoring. Aircr. Eng. Aerosp. Technol. 2020, 92, 37–46. [Google Scholar] [CrossRef]
- Wu, D.; Lin, L.; Ren, H. Thermal/Vibration Joint Experimental Investigation on Lightweight Ceramic Insulating Material for Hypersonic Vehicles in Extremely High-Temperature Environment up to 1500 °C. Ceram. Int. 2020, 46, 14439–14447. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, X. Combustor Technology of High Temperature Rise for Aero Engine. Progress. Aerosp. Sci. 2023, 140, 100927. [Google Scholar] [CrossRef]
- Kummitha, O.R.; Suneetha, L.; Pandey, K.M. Numerical Analysis of Scramjet Combustor with Innovative Strut and Fuel Injection Techniques. Int. J. Hydrogen Energy 2017, 42, 10524–10535. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, X.; Yu, F.; Zhang, S.; Fang, H.; Cheng, X.; Zhao, X. High-temperature Vibration Sensor Based on Ba2TiSi2O8 Piezoelectric Crystal with Ultra-Stable Sensing Performance up to 650 °C. IEEE Trans. Ind. Electron. 2021, 68, 12850–12859. [Google Scholar] [CrossRef]
- Kubasov, I.V.; Kislyuk, A.M.; Malinkovich, M.D.; Temirov, A.A.; Ksenich, S.V.; Kiselev, D.A.; Bykov, A.S.; Parkhomenko, Y.N. A Novel Vibration Sensor Based on Bidomain Lithium Niobate Crystal. Acta Phys. Pol. A 2018, 134, 106–108. [Google Scholar] [CrossRef]
- Nagmani, A.K.; Behera, B. A Review on High Temperature Piezoelectric Crystal La3Ga5SiO14 for Sensor Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 918–931. [Google Scholar] [CrossRef]
- Ning, H.; Yan, H.; Reece, M.J. Piezoelectric Strontium Niobate and Calcium Niobate Ceramics with Super-High Curie Points. J. Am. Ceram. Soc. 2010, 93, 1409–1413. [Google Scholar] [CrossRef]
- Cao, S.; Bai, J.; Zheng, Y.; Chai, H.; Gao, X.; Xue, C. High-Temperature Fiber-Optic Vibration Sensor Based on an Atomic Frequency Standard. ACS Photonics 2024, 11, 3713–3721. [Google Scholar] [CrossRef]
- Feng, R.; Chu, Y.; Liu, Z.; Wang, X.; Tang, F. Study on High Temperature Resistant Packaging of Ultra High Temperature Fabry-Perot Optical Fiber Vibration Sensor. IEEE Sens. J. 2021, 21, 27045–27050. [Google Scholar] [CrossRef]
- Lin, C.; Wang, N.; Chen, J.; Yan, X.; Zhang, X.; Cai, Y. Study on Fiber Fabry-Perot Displacement Sensor for Vibration Monitoring of Fuel Pin. Microw. Opt. Technol. Lett. 2024, 66, 34007. [Google Scholar] [CrossRef]
- Sun, S.; Wu, Y.; Pang, K.; Xu, X.; Chen, R.; He, Z. A High-Precision 3-D Vibration Acceleration Sensor Based on FBGs. IEEE Sens. J. 2025, 25, 2321–2330. [Google Scholar] [CrossRef]
- Kishore, P.; Dinakar, D.; Srimannarayana, K.; Vengal Rao, P. Vibration Sensor Using 2 × 2 Fiber Optic Coupler. Opt. Eng. 2013, 52, 107104. [Google Scholar] [CrossRef]
- Kimura, M.; Toshima, K. Vibration Sensor Using Optical-Fiber Cantilever with Bulb-Lens. Sens. Actuators A Phys. 1998, 66, 178–183. [Google Scholar] [CrossRef]
- Zhou, W.; Dong, X.; Ni, K.; Chan, C.C.; Shum, P. Temperature Insensitive Accelerometer Based on a Strain-Chirped FBG. Sens. Actuators A Phys. 2010, 157, 15–18. [Google Scholar] [CrossRef]
- Basumallick, N.; Chatterjee, I.; Biswas, P.; Dasgupta, K.; Bandyopadhyay, S. Fiber Bragg Grating Accelerometer with Enhanced Sensitivity. Sens. Actuators A Phys. 2012, 173, 108–115. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Xiao, L.; Bai, Q.; Liu, X.; Gao, Y.; Zhang, H.; Jin, B. Phase Demodulation Methods for Optical Fiber Vibration Sensing System: A Review. IEEE Sens. J. 2022, 22, 1842–1866. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, K.; Jiang, J.; Xu, T.; Wang, S.; Guo, H.; Zhou, Z.; Xue, K.; Huang, Y.; Liu, T. Dynamic Phase Extraction in an Ameliorated Distributed Vibration Sensor Using a Highly Stable Homodyne Detection. IEEE Sens. J. 2021, 21, 27005–27014. [Google Scholar] [CrossRef]
- Liu, Q.; Peng, W. Fast Interrogation of Dynamic Low-Finesse Fabry-Perot Interferometers: A review. Microw. Opt. Technol. Lett. 2021, 63, 2279–2291. [Google Scholar] [CrossRef]
- Wang, D.; Wu, Y.; Song, Y.; Wang, Y.; Zhu, L. High Sensitivity Fiber Optic Acceleration Sensor Based on Fabry-Perot Interferometer. Opt. Fiber Technol. 2022, 72, 102989. [Google Scholar] [CrossRef]
- Huang, Y.; Tang, F.; Ma, D.; Liu, Z.; Wang, X. Design, Fabrication, Characterization, and Application of an Ultra-High Temperature 6H-SiC Sapphire Fiber Optic Vibration Sensor. IEEE Photonics J. 2019, 11, 6802512. [Google Scholar] [CrossRef]
- Mahissi, M.; Tong, X.L.; Zhang, C.; Deng, C.; Wei, J.; Chen, S. Study on the Vibration Performances for a High Temperature Fiber F-P Accelerometer. Opt. Fiber Technol. 2021, 62, 102471. [Google Scholar] [CrossRef]
- Cui, Y.; Jiang, Y.; Zhang, Y.; Feng, X.; Hu, J.; Jiang, L. Sapphire Optical Fiber High-Temperature Vibration Sensor. Opt. Express 2022, 30, 1056–1065. [Google Scholar] [CrossRef]
- Qian, J.; Jia, P.; Liu, H.; Ren, Q.; Liu, J.; Qin, L.; Xiong, J. A MEMS Fiber-Optic Fabry-Perot Vibration Sensor for High-Temperature Applications. IEEE Access 2022, 10, 42908–42951. [Google Scholar] [CrossRef]
- Liu, H.; Jia, P.; Su, C.; Zhao, A.; Liu, J.; Ren, Q.; Xiong, J. High-Temperature Fiber-Optic Fabry-Perot Vibration Sensor Based on Single-Crystal Sapphire. Sensors 2023, 23, 4952. [Google Scholar] [CrossRef]
- Su, C.; Jia, P.; Zhao, A.; Tu, J.; Liu, J.; Ren, Q.; Xiong, J. Temperature-Decoupled Single-Crystal MgO Fiber-Optic Fabry-Perot Vibration Sensor Based on MEMS Technology for Harsh Environments. Micromachines 2024, 15, 616. [Google Scholar] [CrossRef] [PubMed]
- Ren, Q.; Jia, P.; An, G.; Liu, J.; Fang, G.; Liu, W.; Xiong, J. Dual-Wavelength Demodulation Technique for Interrogating a Shortest Cavity in Multi-Cavity Fiber-Optic Fabry-Perot Sensors. Opt. Express 2021, 29, 32658. [Google Scholar] [CrossRef]
- Ren, Q.; Jia, P.; An, G.; Liu, J.; Liu, W.; Xiong, J. Self-Compensation Three-Wavelength Demodulation Method for the Large Phase Extraction of Extrinsic Fabry-Perot Interferometric Sensors. Opt. Lasers Eng. 2023, 164, 107535. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Gangopadhyay, S.; Sarkar, S. Coupling of a Laser Diode to a Monomode Elliptic-Core Fiber via a Hyperbolic Microlens on the Fiber Tip: Efficiency Computation with the ABCD Matrix. Opt. Eng. 2007, 46, 025008. [Google Scholar]






| Parameters | Symbol | Value (Unit) |
|---|---|---|
| Length of the beam | 3.3 (mm) | |
| Length of the beam | 0.5 (mm) | |
| Width of the beam | 0.3 (mm) | |
| Thickness of the beam | 0.3 (mm) | |
| Side length of inertial mass | 3 (mm) | |
| Density of MgO | 3580 (kg·) | |
| Young’s modulus of MgO | 300 (GPa) | |
| Sensitivity | 0.9917 (nm·) | |
| Frequence | 15.829 (kHz) |
| Signal Transmission Method (in High-Temperature Area) | Packaging Method | The Highest Working Temperature (°C) | Sensitivity | |
|---|---|---|---|---|
| [21] | Sapphire optical fiber | High-temperature glue | 1200 | 44.64 mv/g |
| [23] | Sapphire optical fiber | Inorganic glue | 1500 | 20.91 nm/g |
| [24] | Quartz optical fiber | Welded by CO2 laser | 400 | 2.48 nm/g |
| [25] | Quartz optical fiber | Ceramic glue | 800 | 0.876 nm/g |
| [26] | Quartz optical fiber | High-temperature glue | 1000 | 0.0073 rad/g |
| this work | Fiber-optic collimator | Mechanical coupling | 1000 | 0.9971 nm/g |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, J.; Zhao, Q.; Hu, J.; Huang, Y.; Wang, H.; Liu, J.; Jia, P. MgO-Based Fabry-Perot Vibration Sensor with a Fiber-Optic Collimator for High-Temperature Environments. Photonics 2025, 12, 524. https://doi.org/10.3390/photonics12060524
Tu J, Zhao Q, Hu J, Huang Y, Wang H, Liu J, Jia P. MgO-Based Fabry-Perot Vibration Sensor with a Fiber-Optic Collimator for High-Temperature Environments. Photonics. 2025; 12(6):524. https://doi.org/10.3390/photonics12060524
Chicago/Turabian StyleTu, Jiacheng, Qirui Zhao, Jiantao Hu, Yuhao Huang, Haiyang Wang, Jia Liu, and Pinggang Jia. 2025. "MgO-Based Fabry-Perot Vibration Sensor with a Fiber-Optic Collimator for High-Temperature Environments" Photonics 12, no. 6: 524. https://doi.org/10.3390/photonics12060524
APA StyleTu, J., Zhao, Q., Hu, J., Huang, Y., Wang, H., Liu, J., & Jia, P. (2025). MgO-Based Fabry-Perot Vibration Sensor with a Fiber-Optic Collimator for High-Temperature Environments. Photonics, 12(6), 524. https://doi.org/10.3390/photonics12060524






