Determination of Angle of Refraction in X-Ray Phase-Contrast Imaging Using Geometric Optics Method
Abstract
1. Introduction
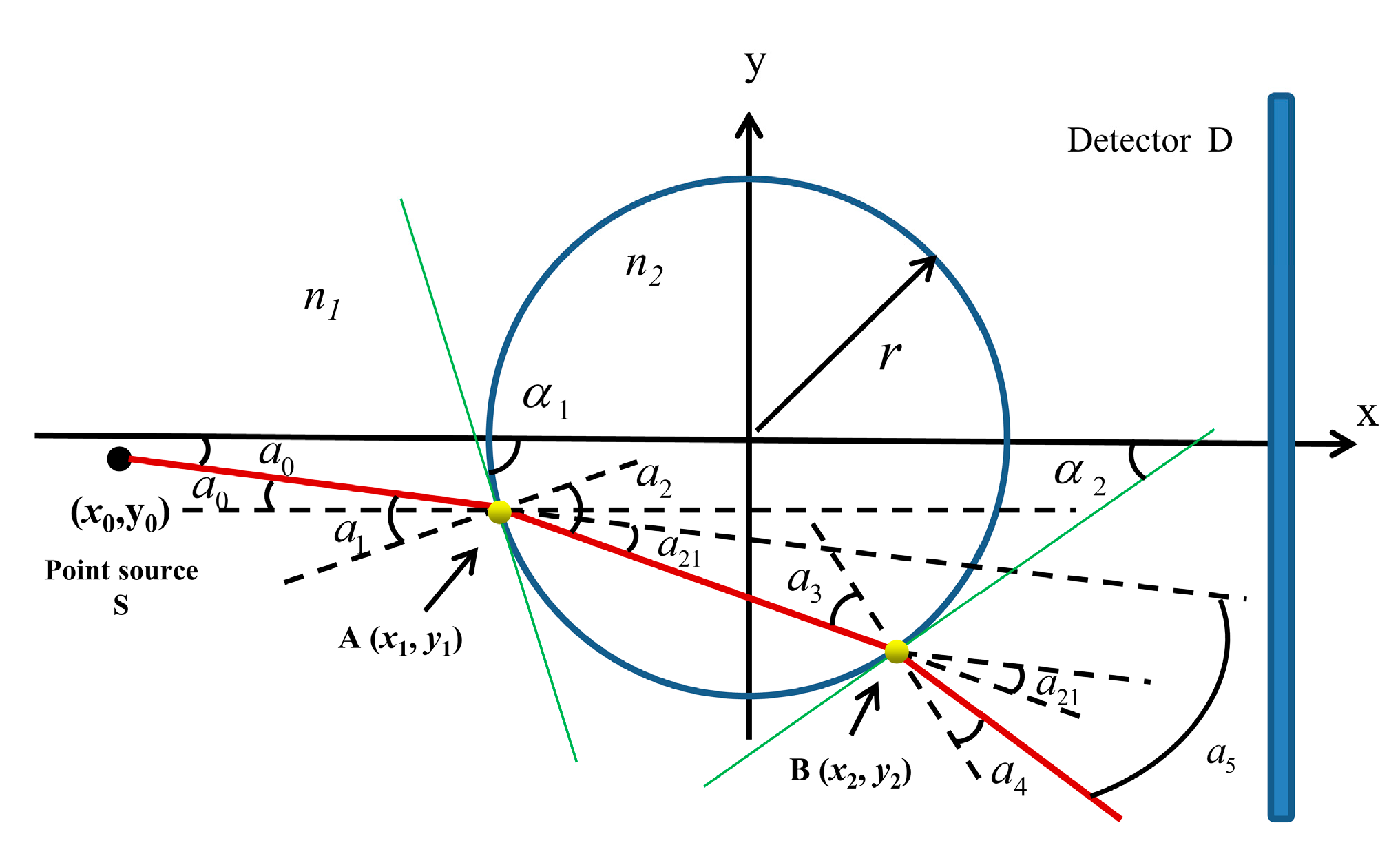
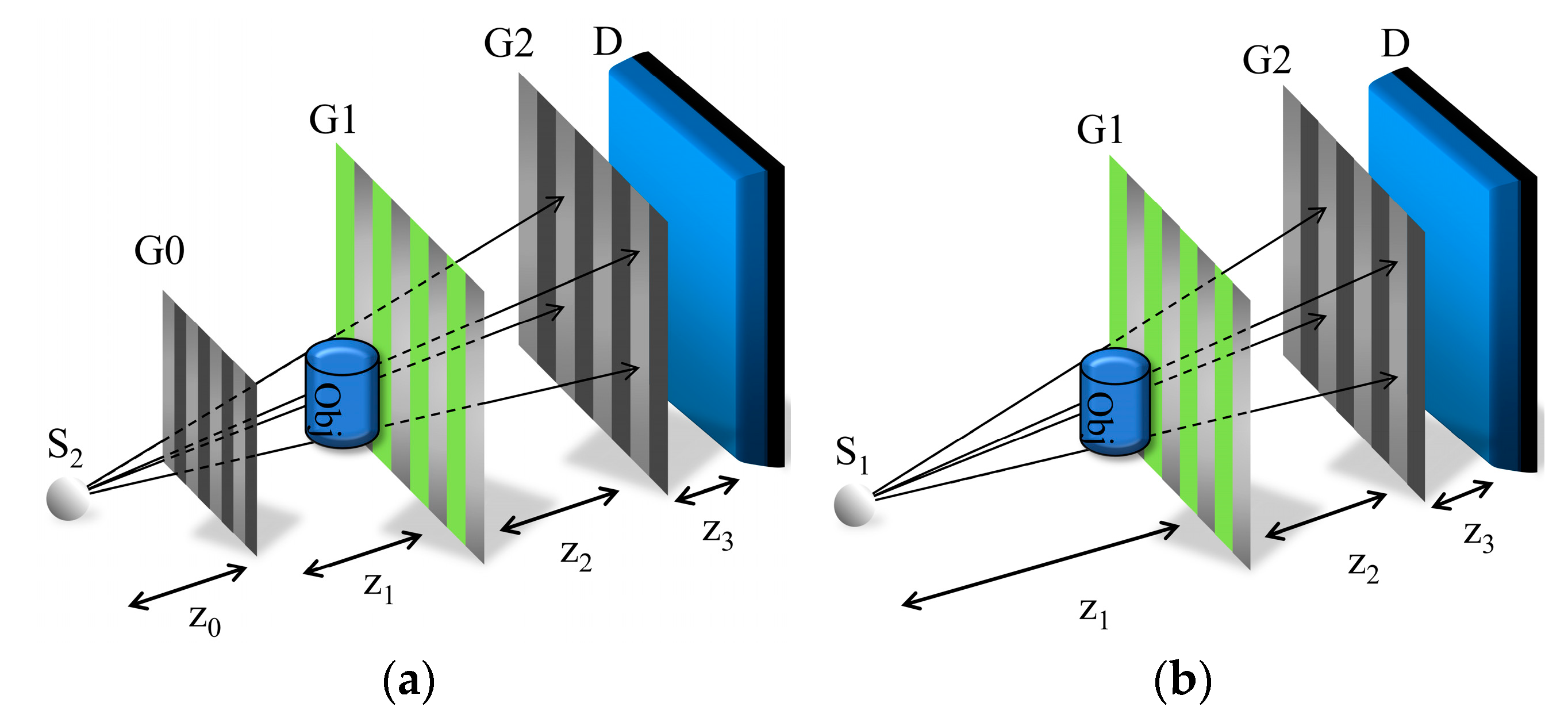
2. Theory
3. Results
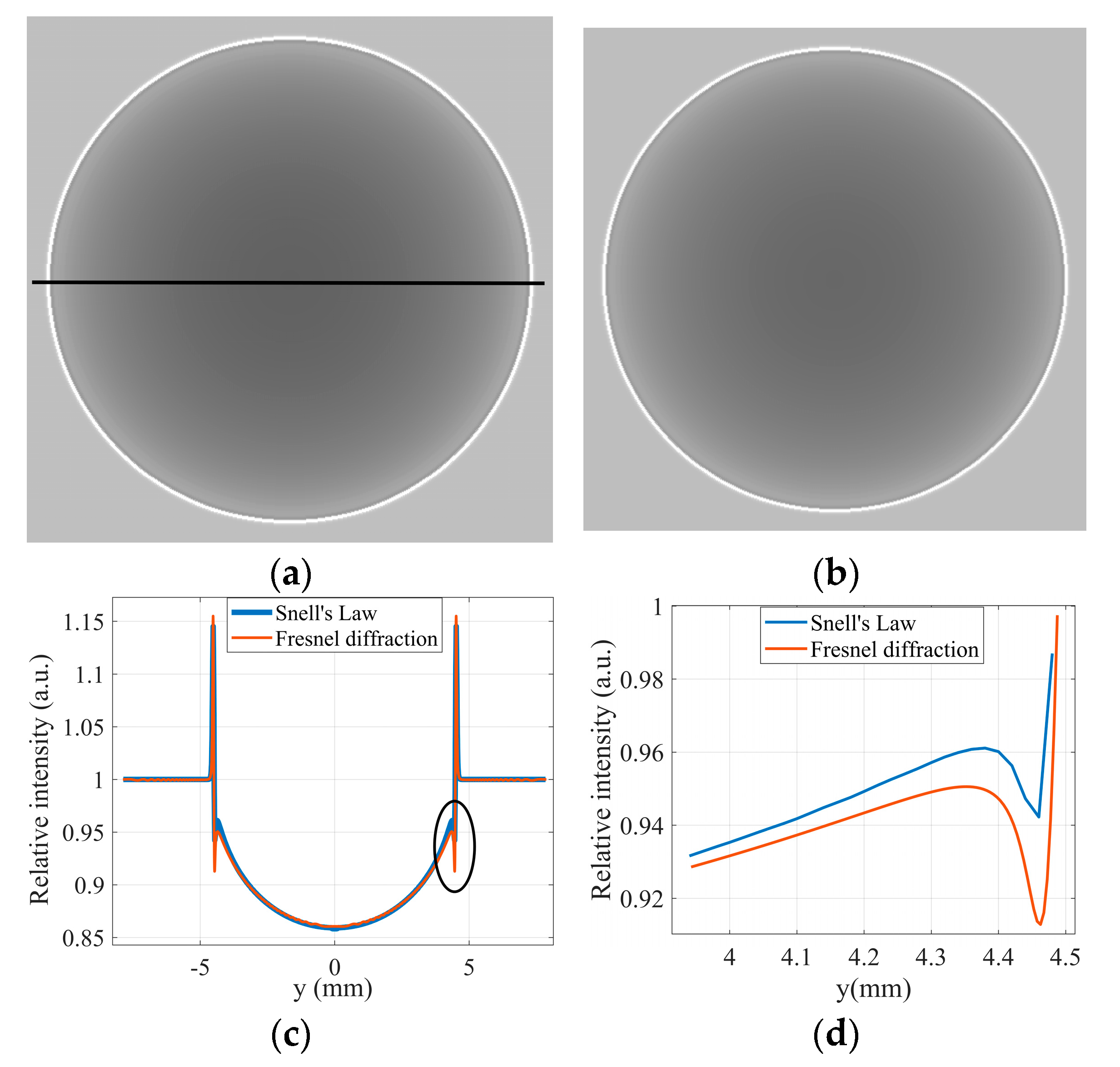
3.1. Comparison of Intensity Distributions
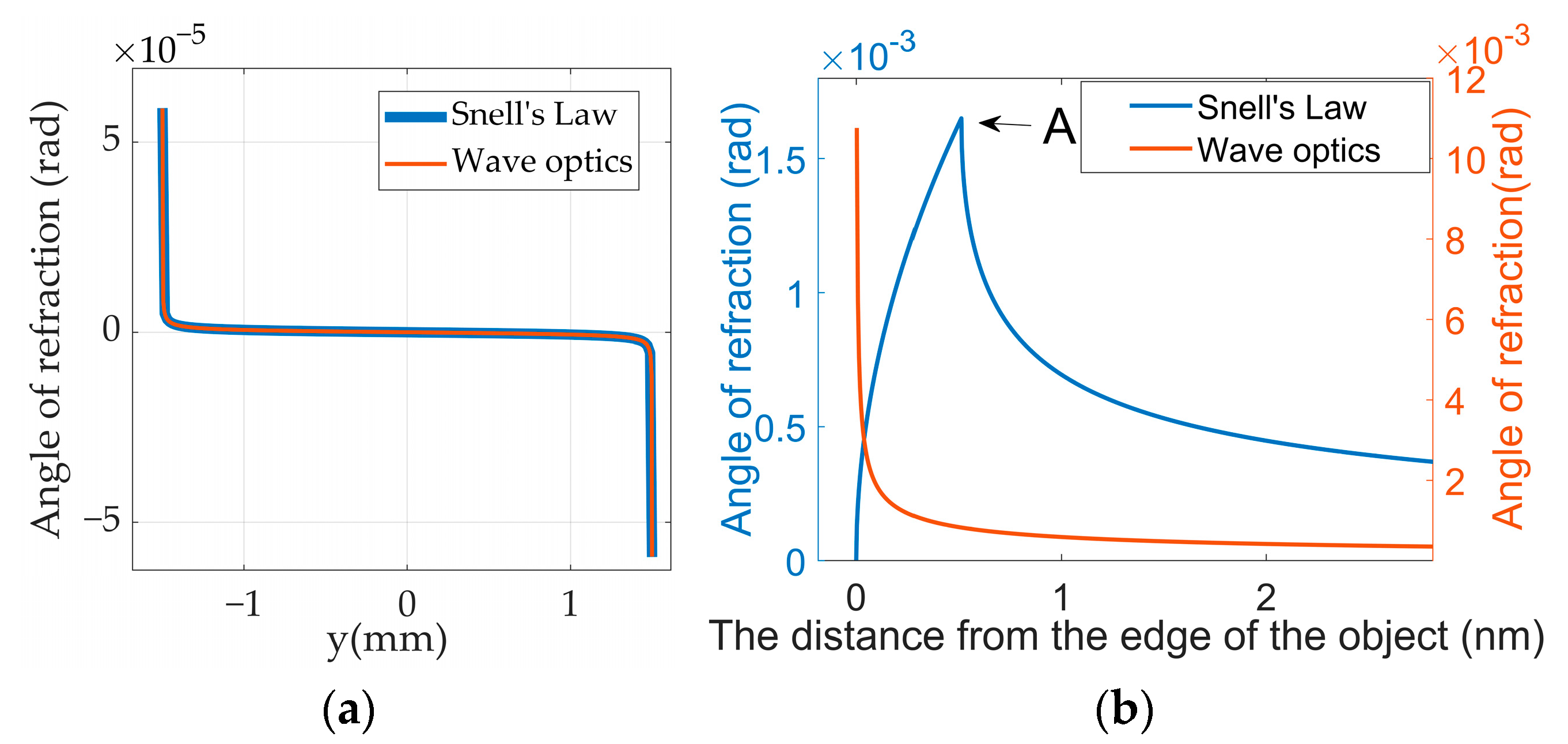
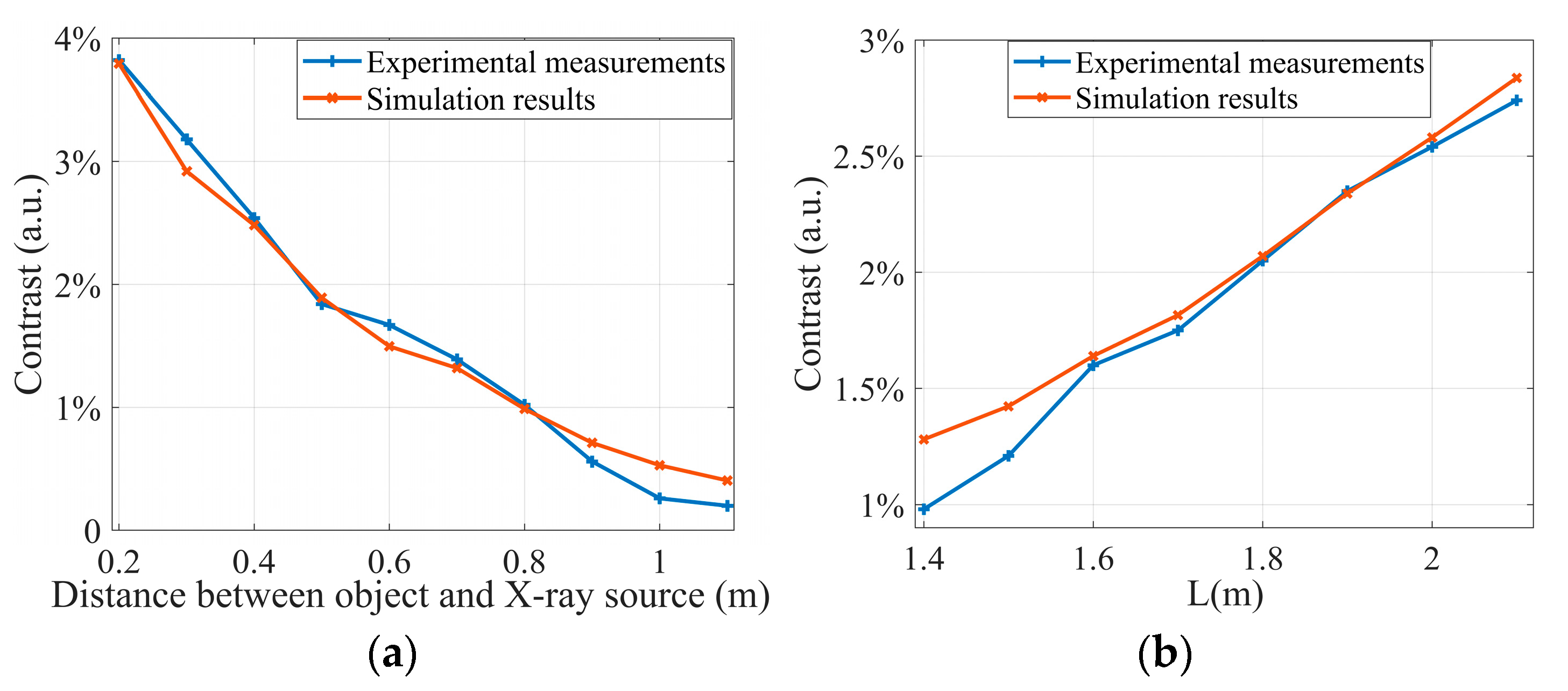
3.2. Calculation of Angles of Refraction and Object Contrast
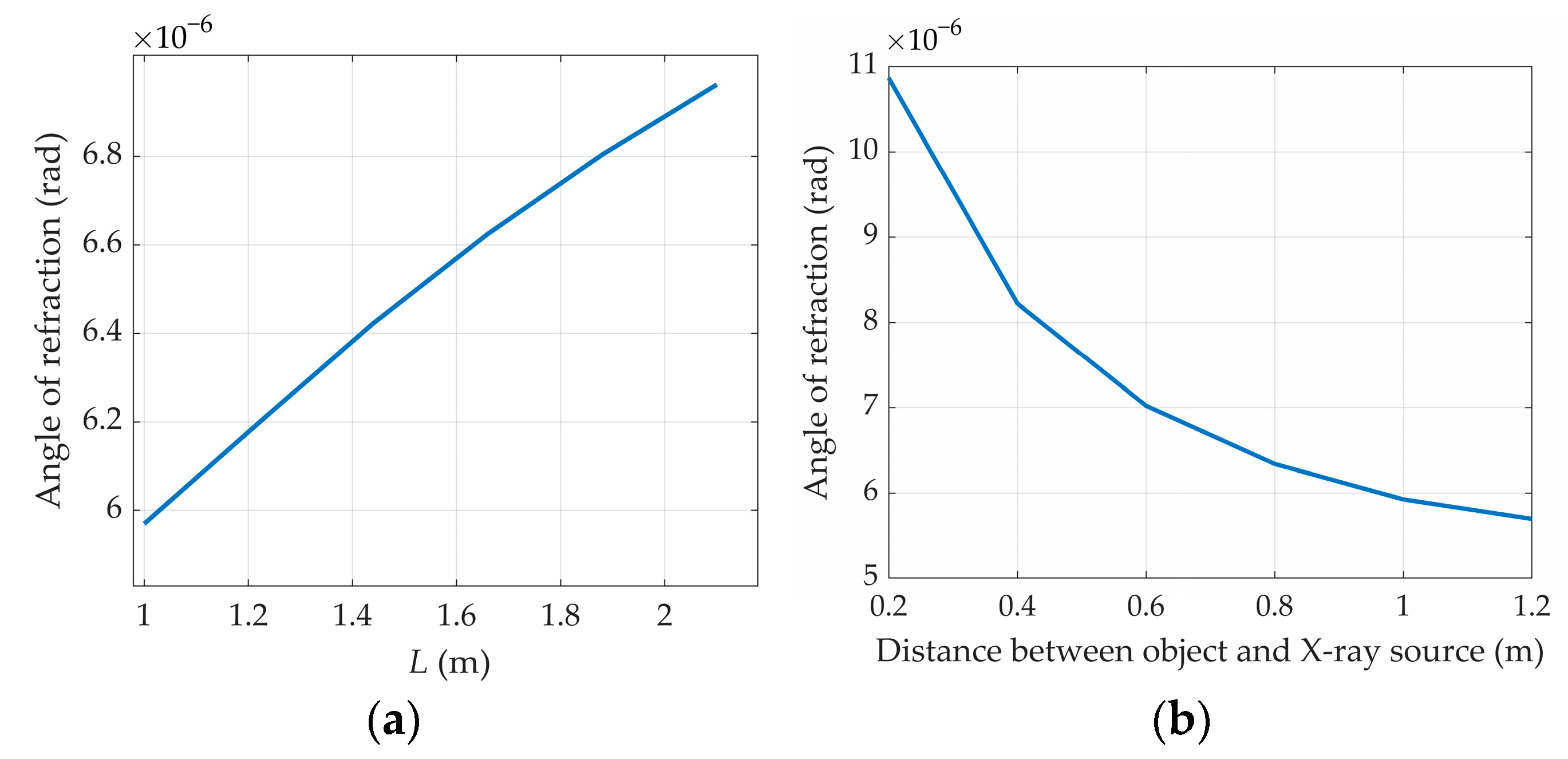
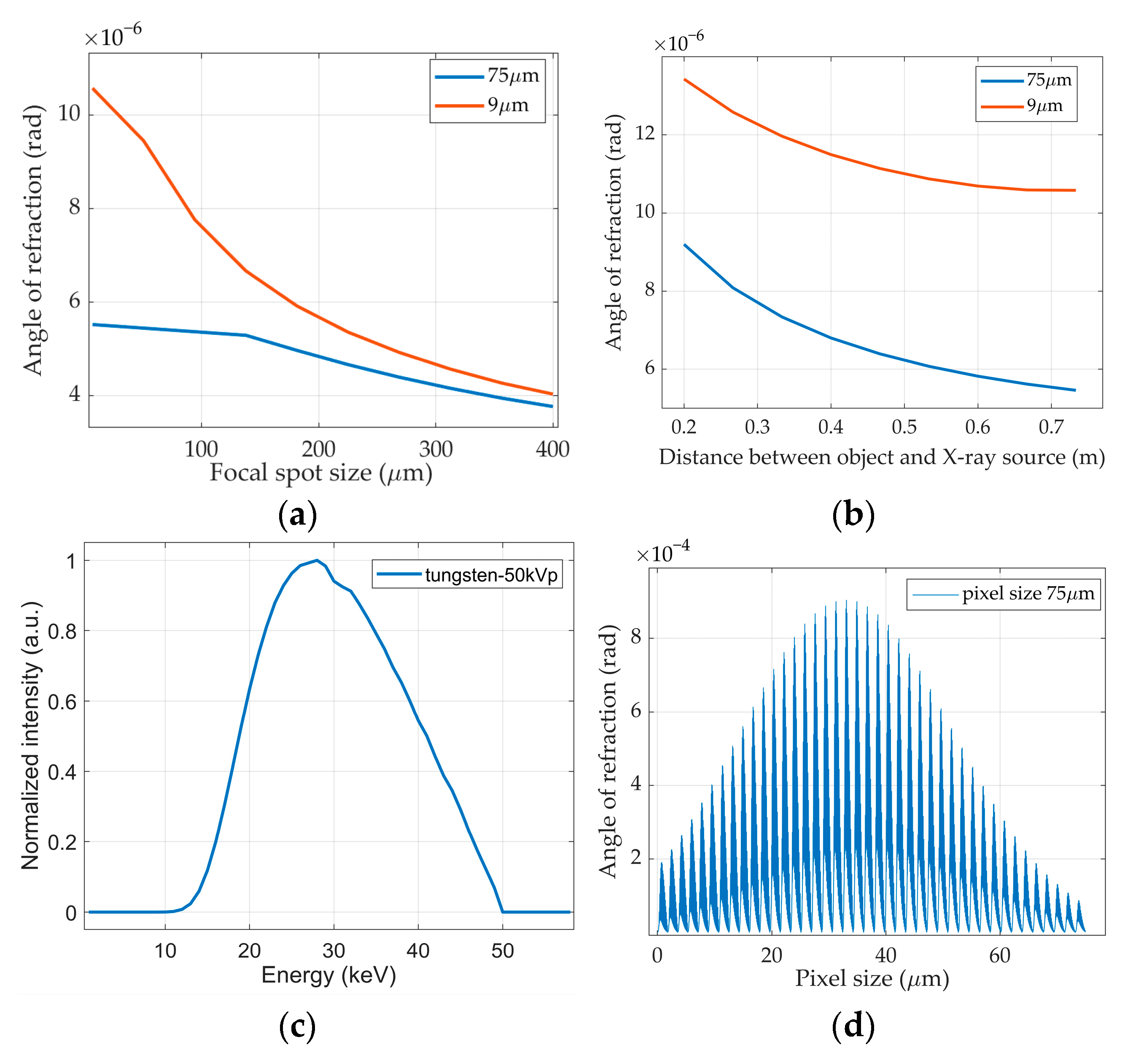
3.3. Factors Affecting the Angles of Refraction
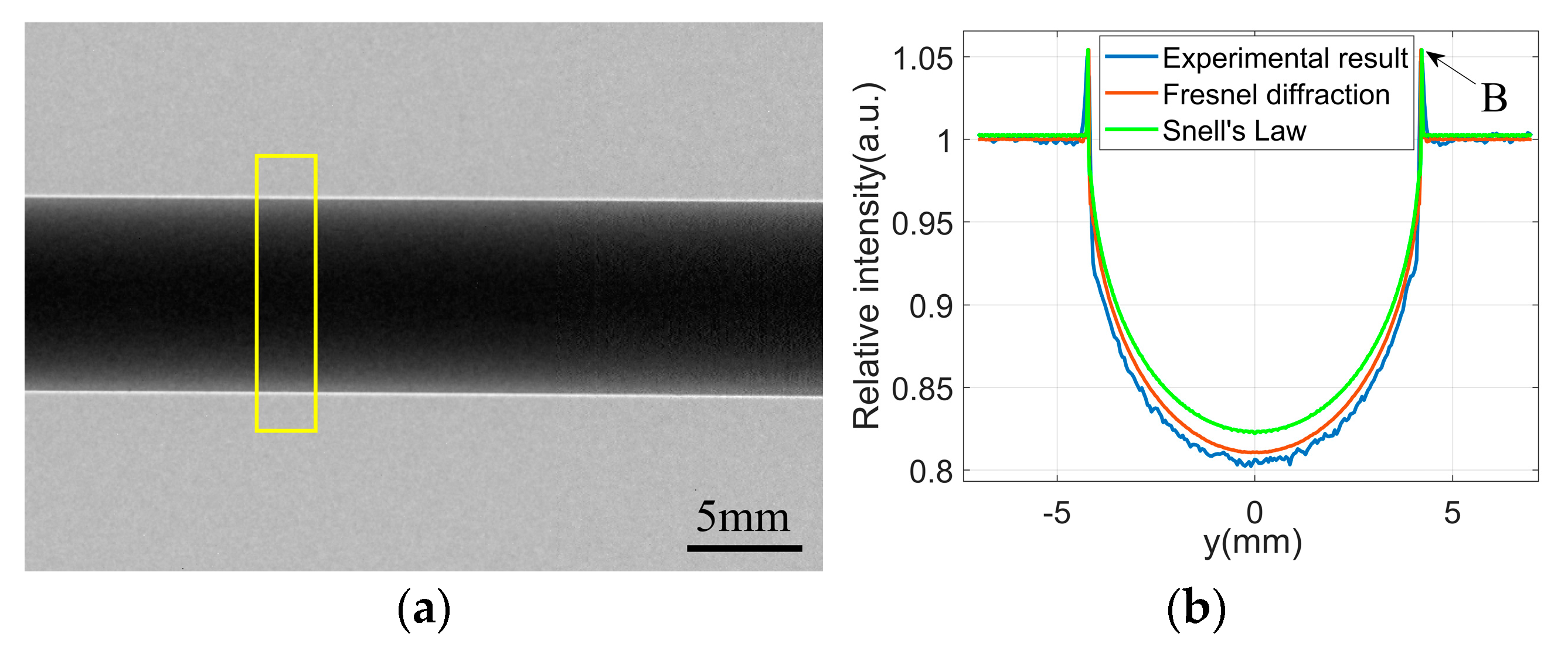
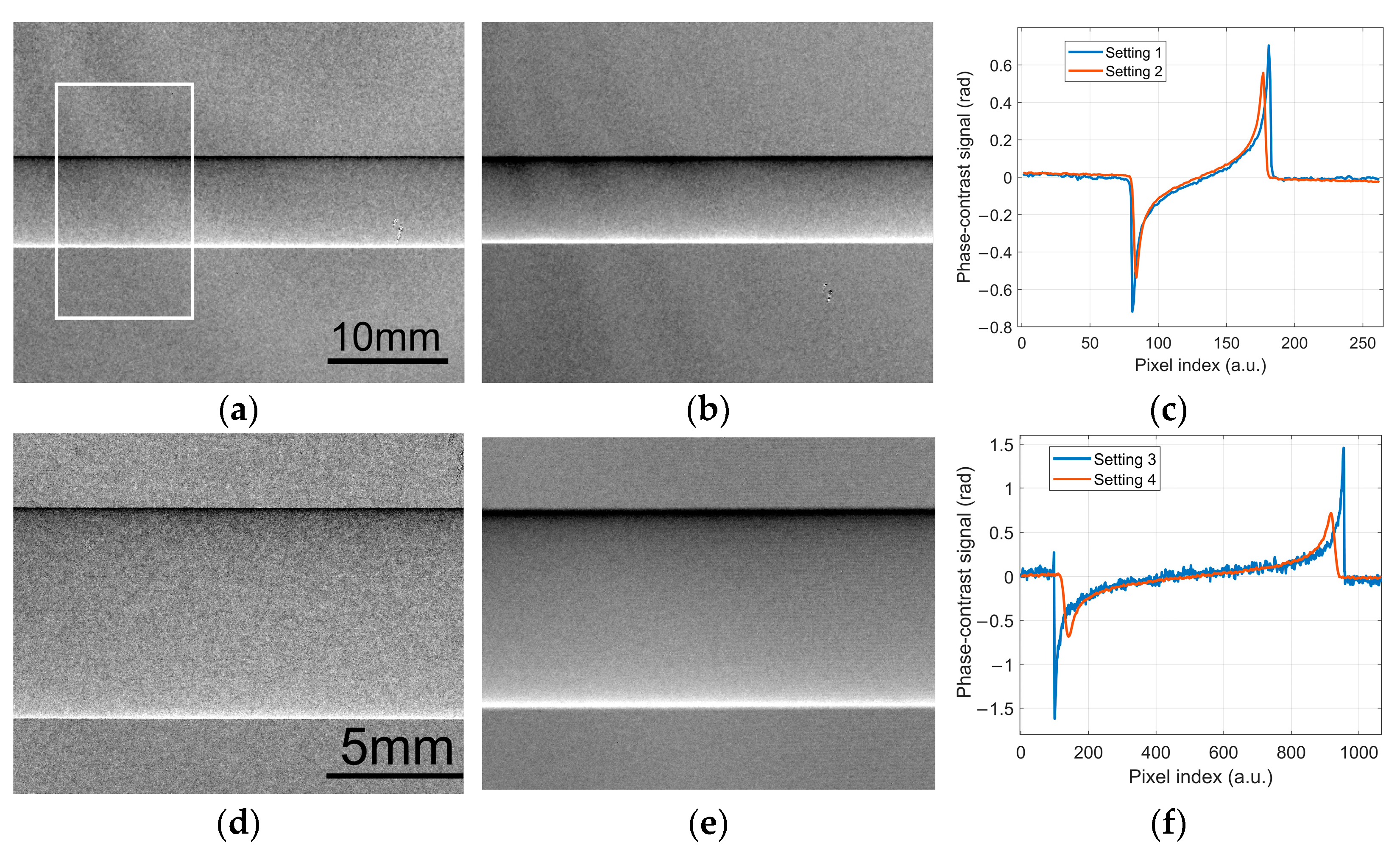
3.4. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Momose, A.; Kawamoto, S.; Koyama, I.; Hamaishi, Y.; Takai, K.; Suzuki, Y. Demonstration of X-ray Talbot Interferometry. Jpn. J. Appl. Phys. 2003, 42, L866–L868. [Google Scholar] [CrossRef]
- David, C.; Nöhammer, B.; Solak, H.; Ziegler, E. Differential X-ray phase contrast imaging using a shearing interferometer. Appl. Phys. Lett. 2002, 81, 3287–3289. [Google Scholar] [CrossRef]
- Zhu, P.; Zhang, K.; Wang, Z.; Liu, Y.; Liu, X.; Wu, Z.; McDonald, S.; Marone, F.; Stampanoni, M. Low-dose, simple, and fast grating-based X-ray phase-contrast imaging. Proc. Natl. Acad. Sci. USA 2010, 107, 13576–13581. [Google Scholar] [CrossRef]
- Momose, A. Recent advances in X-ray Phase Imaging. Jpn. J. Appl. Phys. 2005, 44, 6355–6367. [Google Scholar] [CrossRef]
- Pfeiffer, F.; Weitkamp, T.; Bunk, O.; David, C. Phase retrieval and differential phase-contrast imaging with low-brilliance X-ray sources. Nat. Phys. 2006, 2, 258–261. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, K.; Wang, D.; Wu, Z.; Chen, H.; Wang, S.; Wu, Z. Single-shot X-ray phase imaging with grating interferometry and photon-counting detectors. Opt. Lett. 2014, 39, 877–879. [Google Scholar] [CrossRef]
- Liu, X.; Liu, L.; Huang, J.; Lei, Y.; Li, J. Single-Shot Phase-Contrast Imaging with a Single Grating. Photonics 2023, 10, 968. [Google Scholar] [CrossRef]
- Yoshioka, H.; Kadono, Y.; Kim, Y.; Oda, H.; Maruyama, T.; Akiyama, Y.; Mimura, T.; Tanaka, J.; Niitsu, M.; Hoshino, Y.; et al. Imaging evaluation of the cartilage in rheumatoid arthritis patients with an X-ray phase imaging apparatus based on Talbot-Lau interferometry. Sci. Rep. 2020, 10, 6561. [Google Scholar] [CrossRef] [PubMed]
- Nagashima, M.; Tanaka, J.; Kiyohara, J.; Makifuchi, C.; Kido, K.; Momose, A. Application of X-ray grating interferometry for the imaging of joint structures. Anat. Sci. Int. 2014, 89, 95–100. [Google Scholar] [CrossRef]
- Momose, A.; Yashiro, W.; Kido, K.; Kiyohara, J.; Makifuchi, C.; Ito, T.; Nagatsuka, S.; Honda, C.; Noda, D.; Hattori, T.; et al. X-ray phase imaging: From synchrotron to hospital. Philos. Trans. A Math. Phys. Eng. Sci. 2017, 372, 20130023. [Google Scholar] [CrossRef][Green Version]
- Massimi, L.; Clark, S.; Marussi, S.; Doherty, A.; Shah, S.; Schulz, J.; Marathe, S.; Rau, C.; Endrizzi, M.; Lee, P.; et al. Time resolved in-situ multi-contrast X-ray imaging of melting in metals. Sci. Rep. 2022, 12, 12136. [Google Scholar] [CrossRef] [PubMed]
- Braig, E.; Böhm, J.; Dierolf, M.; Jud, C.; Günther, B.; Mechlem, K.; Allner, S.; Sellerer, T.; Achterhold, K.; Gleich, B.; et al. Direct quantitative material decomposition employing grating-based X-ray phase-contrast CT. Sci. Rep. 2018, 8, 16394. [Google Scholar] [CrossRef]
- Mao, L.; Liu, H.; Zhu, Y.; Zhu, Z.; Guo, R.; Chiang, F. 3D Strain Mapping of Opaque Materials Using an Improved Digital Volumetric Speckle Photography Technique with X-ray Microtomography. Appl. Sci. 2019, 9, 1418. [Google Scholar] [CrossRef]
- Xiao, T.; Bergamaschi, A.; Dreossi, D.; Longo, R.; Olivo, A.; Pani, S.; Rigon, L.; Rokvic, T.; Venanzi, C.; Castelli, E. Effect of spatial coherence on application of in-line phase contrast imaging to synchrotron radiation mammography. Nucl. Instrum. Meth. A. 2005, 548, 55–162. [Google Scholar] [CrossRef]
- Preissner, M.; Murrie, R.; Pinar, I.; Werdiger, F.; Carnibella, R.; Zosky, G.; Fouras, A.; Dubsky, S. High resolution propagation-based imaging system for in vivo dynamic computed tomography of lungs in small animals. Phys. Med. Biol. 2018, 63, 08NT03. [Google Scholar] [CrossRef]
- Grandl, S.; Scherer, K.; Sztrokay, G.; Birnbacher, L.; Willer, K.; Chabior, M.; Herzen, J.; Mayr, D.; Auweter, S.; Pfeiffer, F.; et al. Improved visualization of breast cancer features in multifocal carcinoma using phase-contrast and dark-field mammography: An ex vivo study. Eur. Radiol. 2015, 25, 3659–3668. [Google Scholar] [CrossRef]
- Bonse, U.; Hart, M. An X-ray Interferometer. Appl. Phys. Lett. 1965, 6, 155–156. [Google Scholar] [CrossRef]
- Wilkins, S.; Gureyev, T.; Gao, D.; Pogany, A.; Stevenson, A. Phase-contrast imaging using polychromatic hard X-rays. Nature 1996, 384, 335–338. [Google Scholar] [CrossRef]
- Gureyev, T.; Mayo, S.; Myers, D.; Nesterets, Y.; Paganin, D.; Pogany, A.; Stevenson, A.; Wilkins, S.J. Refracting Röntgen’s rays: Propagation-based x-ray phase contrast for biomedical imaging. Appl. Phys. 2009, 105, 102005. [Google Scholar] [CrossRef]
- Zhao, Y.; Ji, D.; Li, Y.; Zhao, X.; Lv, W.; Xin, X.; Han, S.; Hu, C. Three-dimensional visual ization of microvasculature from few-projection data using a novel CT reconstruction algorithm for propagation-based X-ray phase-contrast imaging. Biomed. Opt. Express 2020, 11, 364–387. [Google Scholar] [CrossRef]
- Caro, L.; Cedola, A.; Ciannini, C.; Bukreeva, I.; Lagomarsino, S. In-line phase-contrast imaging for strong absorbing objects. Phys. Med. Biol. 2008, 53, 6619. [Google Scholar] [CrossRef]
- Chapman, D.; Thomlinson, W.; Johnston, R.; Washburn, D.; Pisano, E.; Gmur, N.; Zhong, Z.; Menk, R.; Arfelli, F.; Sayers, D. Diffraction enhanced X-ray imaging. Phys. Med. Biol. 1997, 42, 2015–2025. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, F.; Bech, M.; Bunk, O.; Kraft, P.; Eikenberry, E.; Bronnimann, C.; Grunzweig, C.; David, C. Hard-X-ray dark-field imaging using a grating interferometer. Nat. Mater. 2008, 7, 134–137. [Google Scholar] [CrossRef]
- Miao, H.; Panna, A.; Gomella, A.; Bennett, E.; Znati, S.; Chen, L.; Han, W. A Universal Moire Effect and Application in X-ray Phase-Contrast Imaging. Nat. Phys. 2016, 12, 830–834. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y.; Liu, X.; Huang, J.; Du, Y.; Guo, J.; Zhao, Z.; Li, J. Cascade Talbot Lau interferometers for X-ray differential phase-contrast imaging. J. Phys. D Appl. Phys. 2018, 51, 385302. [Google Scholar] [CrossRef]
- Zhang, C.; Pan, X.; Shang, H.; Li, G. Alternative edge illumination set-up for single-shot X-ray phase contrast imaging. J. Appl. Phys. 2018, 124, 164906. [Google Scholar] [CrossRef]
- Kallon, G.; Wesolowski, M.; Vittoria, F.; Endrizzi, M.; Basta, D.; Millard, T.; Diemoz, P.; Olivo, A. A laboratory based edge-illumination X-ray phase-contrast imaging setup with two-directional sensitivity. Appl. Phys. Lett. 2015, 107, 204105. [Google Scholar] [CrossRef]
- Comamala, J.; Romano, L.; Guzenko, V.; Kagias, M.; Stampanoni, M.; Jefimovs, K. Towards sub-micrometer high aspect ratio X-ray gratings by atomic layer deposition of iridium. Microelectron. Eng. 2018, 192, 19–24. [Google Scholar] [CrossRef]
- Kageyama, M.; Okajima, K.; Maesawa, M.; Nonoguchi, M.; Koike, T.; Noguchi, M.; Yamada, A.; Morita, E.; Kawase, S.; Kuribayashi, M.; et al. X-ray phase-imaging scanner with tiled bent gratings for large-field of view nondestructive testing. NDT E Int. 2019, 105, 19–24. [Google Scholar] [CrossRef]
- Alloo, S.; Paganin, D.; Morgan, K.; Gureyev, T.; Mayo, S.; Mohammadi, S.; Lockie, D.; Menk, R.; Arfelli, F.; Zanconati, F.; et al. Tomographic phase and attenuation extraction for a sample composed of unknown materials using X-ray propagation-based phase-contrast imaging. Opt. Lett. 2022, 47, 1945–1948. [Google Scholar] [CrossRef]
- Monnin, P.; Bulling, S.; Hoszowska, J.; Valley, J.; Meuli, R.; Verdun, F. Quantitative characterization of edge enhancement in phase contrast X-ray imaging. Am. Assoc. Med. Phys. 2004, 31, 1372–1383. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z. Research on Methods and Technologies for Grating-Based Imaging with Conventional X-Ray Source. Ph.D. Thesis, Tsinghua University, Beijing, China, 2010. [Google Scholar]
- Born, M.; Wolf, E. Principle of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Siewerdsen, J. Spektr: A computational tool for X-ray spectral analysis and imaging system optimization. Am. Assoc. Med. Phys. 2004, 31, 3057–3067. [Google Scholar] [CrossRef] [PubMed]
- Donath, T.; Chabior, M.; Pfeiffer, F.; Bunk, O.; Reznikova, E.; Mohr, J.; Hempel, E.; Popescu, S.; Hoheisel, M.; Schuster, M.; et al. Inverse geometry for grating-based X-ray phase-contrast imaging. J. Appl. Phys. 2009, 106, 054703. [Google Scholar] [CrossRef]
- Ge, Y.; Chen, J.; Yang, J.; Zhu, P.; Zhang, H.; Zheng, H.; Liang, D. Angular sensitivity of an X-ray differential phase contrast imaging system with real and virtual source images. Opt. Lett. 2021, 46, 2791–2794. [Google Scholar] [CrossRef]

| X-Ray Tube Focal Spot Size (μm) | Detector Pixel Size (μm) | Current (μA) | Exposure Time (s) | |
|---|---|---|---|---|
| Setting 1 | 7 | 75 | 160 | 11 |
| Setting 2 | 400 | 75 | 4000 | 1 |
| Setting 3 | 7 | 9 | 160 | 120 |
| Setting 4 | 400 | 9 | 7000 | 15 |
| Measured Angle of Refraction (Rad) | Angle of Refraction Calculated by Geometric Optics (Rad) | Angle of Refraction Calculated by Wave Optics (Rad) | |
|---|---|---|---|
| Setting 1 | 2.796 × 10−6 | 5.668 × 10−6 | 7.648 × 10−6 |
| Setting 2 | 2.150 × 10−6 | 3.766 × 10−6 | 7.648 × 10−6 |
| Setting 3 | 6.043 × 10−6 | 10.838 × 10−6 | 22.065 × 10−6 |
| Setting 4 | 2.754 × 10−6 | 4.033 × 10−6 | 22.065 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Zong, F.; Tang, H.; Du, Y.; Chen, R. Determination of Angle of Refraction in X-Ray Phase-Contrast Imaging Using Geometric Optics Method. Photonics 2025, 12, 442. https://doi.org/10.3390/photonics12050442
Yang J, Zong F, Tang H, Du Y, Chen R. Determination of Angle of Refraction in X-Ray Phase-Contrast Imaging Using Geometric Optics Method. Photonics. 2025; 12(5):442. https://doi.org/10.3390/photonics12050442
Chicago/Turabian StyleYang, Jun, Fangke Zong, Haoqi Tang, Yang Du, and Rongchang Chen. 2025. "Determination of Angle of Refraction in X-Ray Phase-Contrast Imaging Using Geometric Optics Method" Photonics 12, no. 5: 442. https://doi.org/10.3390/photonics12050442
APA StyleYang, J., Zong, F., Tang, H., Du, Y., & Chen, R. (2025). Determination of Angle of Refraction in X-Ray Phase-Contrast Imaging Using Geometric Optics Method. Photonics, 12(5), 442. https://doi.org/10.3390/photonics12050442






