Classical Ghost Imaging with Unknowing Pseudo-Thermal Light

Abstract

Classical ghost imaging (CGI), an extension of quantum ghost imaging (QGI), enables object reconstruction by leveraging the spatial correlation between a pair of beams. Traditionally, CGI requires a camera or point scan to capture the spatial information of the illumination source with intensity fluctuations. In this work, we propose a novel CGI scheme that utilizes an incoherent source to illuminate both the object and the modulations, without introducing any mutual interference between them. Through theoretical analysis and experimental validation, we demonstrate that the reconstruction process relies solely on the modulations and correlation signals of two single-pixel detectors. Concurrently, this scheme is also extended to ghost diffraction, verifying the correlation between two planes that are Fourier transform pairs of the speckle field. Moreover, our study reveals the intricate relationships between the speckle field, modulations, and object, and experimentally verifies the impact of speckle fields on image quality. Notably, this work provides a more comparable framework between CGI and QGI, offering a promising avenue to explore the classical–quantum relationship.

1. Introduction

Ghost imaging (GI) is an immensely intriguing technology that has garnered intensive attention and sparked debates due to its counter-intuitive physical model [1,2]. While initial experiments were considered to arise from the non-local quantum correlation between bi-photons, subsequent discoveries have revealed that classical sources of illumination can also exhibit GI capabilities [3,4,5,6]. Since then, researchers have expanded dual-path ghost imaging to various applications, including diffraction imaging [2], low-light imaging of light-sensitive objects [7,8,9], and the reconstruction of 3D geometry of an object [10]. Notably, a surprising conclusion is that dual-path correlated imaging exhibits greater robustness to turbulences than direct single-path imaging [11,12,13,14]. Furthermore, a spatial light modulator (SLM) is used to generate illumination patterns that are directly projected onto the object performing computational GI [15], i.e., single-pixel imaging (SPI). Because of the ease of controlling illumination, the applications of GI encompass diverse fields such as 3D imaging [16,17,18], phase imaging [19,20,21], and encryption communication [22,23]. Additionally, the concept of GI goes beyond spatial measurement and has been extended to the time domain [24,25] and spectral domain [26]. In conventional CGI setups using pseudo-thermal light, the object is captured by a bucket detector in the test arm, while in the reference arm employs one of two detection methods: a single scanning pinhole, which collects the light field distribution pixel by pixel, but is inefficient in terms of illumination usage, or an array CCD, which conveniently records the light field but only captures intensity information without spatial encoding, requiring multiple detection times. However, most natural images exhibit characteristics such as sparsity in their spatial frequencies [15], enabling compressive techniques to represent images with reduced information. This is particularly relevant in near-infrared and mid-infrared wavelength imaging, where the cost of pixelated sensors is a concern [27]. For these cases, compressive QGI using nonlocal modulation has shed light [28]. The modulation for retrieval is spatially separated from the object, and the application of the compressed sensing algorithm can obtain better imaging results in the case of a small amount of modulation sampling at low light levels.

In this work, we propose a new ghost imaging scheme using pseudo-thermal speckles as the illumination source, which conforms to Gaussian statistics, and extend it to ghost diffraction at a similar experimental framework. We start from the independent modulations, object, and light source, and derive the information contained in the final correlated signal. We also elaborate on the mathematical relationship between dual-path correlated imaging and single-pixel imaging, theoretically proving the possibility of reconstructing a 2D object using only two single-pixel detectors that appear to be independent of the lighting source. We investigate the impact of pseudo-thermal light field sampling on image quality and highlighted the role of speckles in correlated imaging with structured-light encoding. Our imaging approach can be further enhanced by incorporating compressive sensing to improve the imaging efficiency, and can also be expanded to time and spectral domains.

2. Theory and Methods

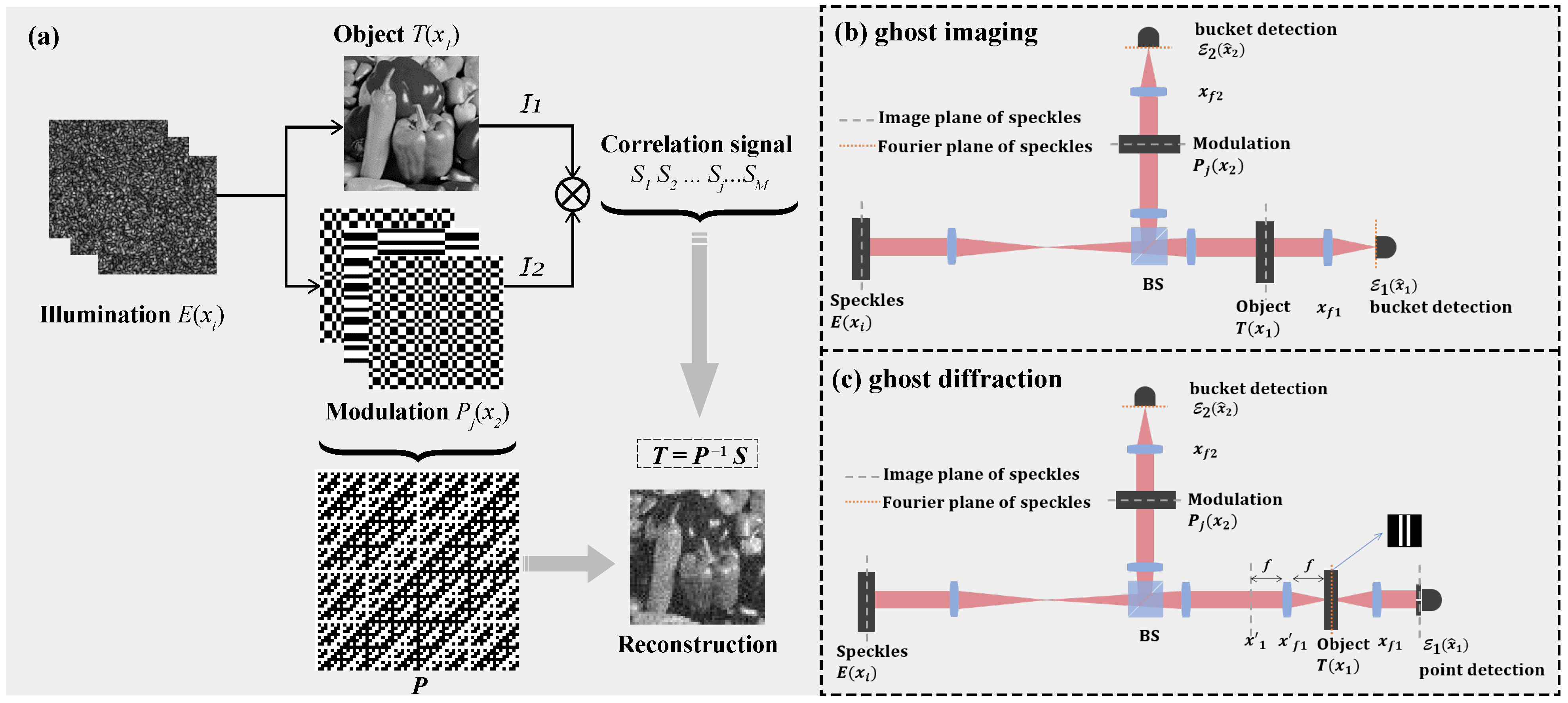
A schematic diagram of the proposed method is shown in Figure 1a.

For ease of discussion, we consider a 1D imaging scenario, with the horizontal coordinate aligned along the x-axis. Two spatial correlated beams are prepared and sent to two transverse planes $\left\{x_i\right\}(i=1, 2)$, where the object and modulation are placed. One beam interacts with the amplitude-only object $T\left(x_1\right)$, while the other is modulated by a series of structured patterns $\left\{P_j\left(x_2\right)\right\}$. $j=1, 2, \dots , 2M$ and M is the resolution of pixelated object. Lenses transform both the object and modulation planes into their far field ${\widehat{x}}_i(i=1,2)$, where the intensities ${\mathcal{I}}_i(i=1,2)$ are detected by two bucket detectors. For correlation imaging, the lens focuses two information-carrying light fields, enabling the efficient collection of light into the bucket detector. In both scenarios, under certain modulations $P_j\left(x_2\right)$, a series of speckle patterns are used to retrieve the correlation between the two light fields carrying the modulation and object information. The correlation coefficient (c.c.) between two intensity signals can be defined as

$${\langle {\mathcal{I}}_1·{\mathcal{I}}_2\rangle }_j=\int d{\widehat{x}}_{1}d{\widehat{x}}_2\langle {\mathit{\varepsilon }}_1^{*}{\mathit{\varepsilon }}_1{\mathit{\varepsilon }}_{2,j}^{*}{\mathit{\varepsilon }}_{2,j}\rangle .$$

(1)

Here, $\langle \cdots \rangle$ is the ensemble average over all of the different speckle patterns. ${\mathit{\varepsilon }}_i$ is the light field over the surface of the i-th detector,

$$\begin{array}{l}\hfill {\mathit{\varepsilon }}_i=\int d{x}_{i}d{x}_{fi}E\left(x_i\right)[{\displaystyle \frac{e^{\mathrm{i}2kf}}{\lambda f}}{e}^{{\displaystyle \frac{-\mathrm{i}k}{2f}}{(x_{fi}-x_i)}^2}{e}^{{\displaystyle \frac{\mathrm{i}k}{2f}}{\left(x_{fi}\right)}^2}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} {\displaystyle \frac{e^{\mathrm{i}2kf}}{\lambda f}}{e}^{{\displaystyle \frac{-\mathrm{i}k}{2f}}{(x_{fi}-{\widehat{x}}_i)}^2}K\left(x_i\right)].\hfill \end{array}$$

(2)

Here, $K\left(x_1\right)=T\left(x_1\right)$, $K\left(x_2\right)=P_j\left(x_2\right)$, where the term within the square brackets is regarded as the impulse response function $h_i\left(x_i\right)$ from plane $\left\{x_i\right\}$ to the back focal plane $\left\{{\widehat{x}}_i\right\}$ of the lens under paraxial approximation. $\left\{x_{fi}\right\}$ represents the plane of the lens. f is the focal length of the lens.

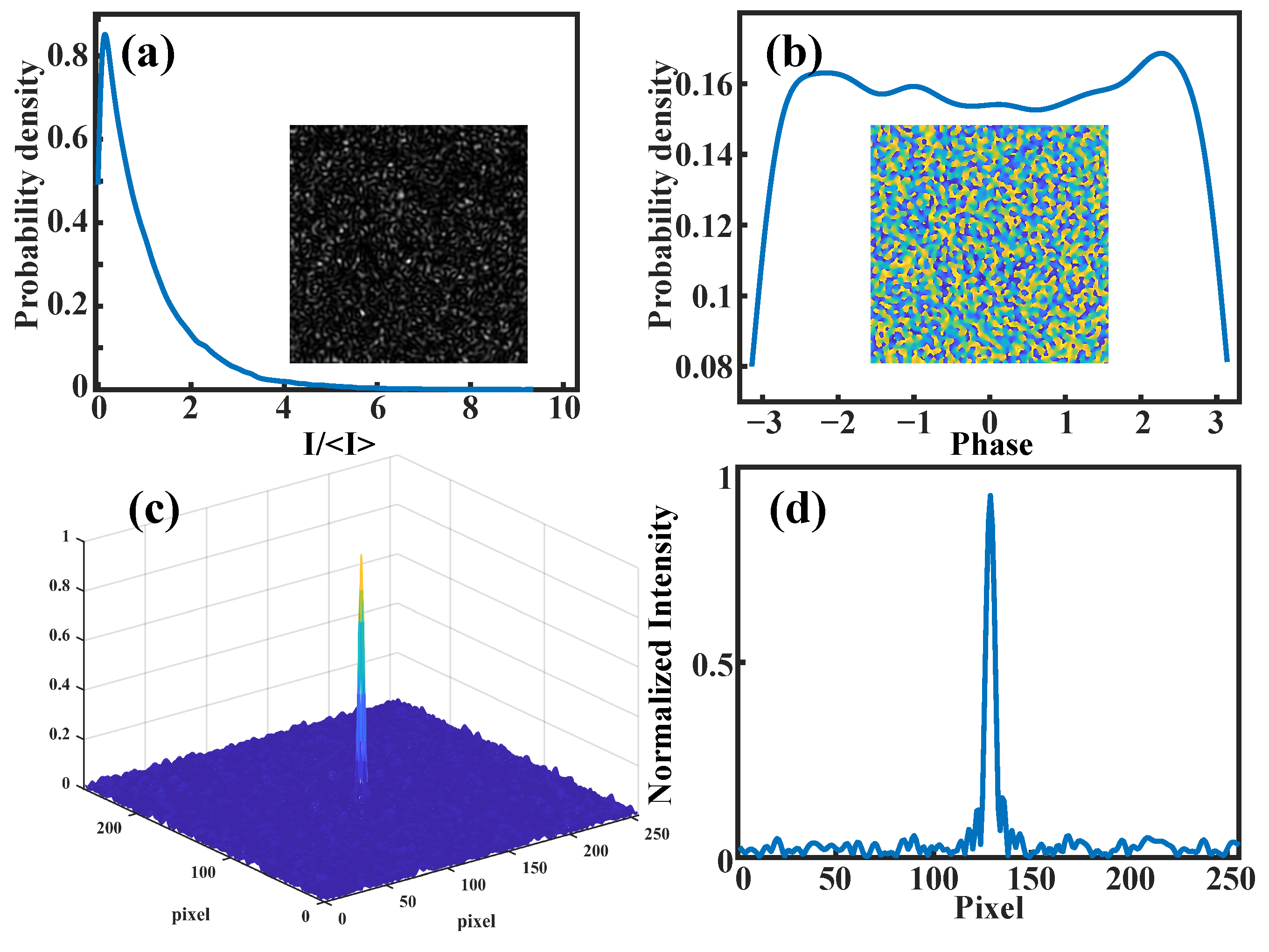
For the pseudo-thermal light field with an exponentially distributed intensity and uniformaly distributed phase, as shown in Figure 2a,b, the statistical properties satisfy the complex Gaussian moment theorem [29]; therefore

$$\begin{array}{cc}\hfill & \langle E^{*}\left(x_1^{\prime }\right)E^{*}\left(x_2^{\prime }\right)E\left(x_1\right)E\left(x_2\right)\rangle =\langle E^{*}\left(x_1^{\prime }\right)E\left(x_2\right)\rangle ·\hfill \\ \hfill & \langle E^{*}\left(x_2^{\prime }\right)E\left(x_1\right)\rangle +\langle E^{*}\left(x_2^{\prime }\right)E\left(x_2\right)\rangle \langle E\left(x_1\right)E^{*}\left(x_1^{\prime }\right)\rangle .\hfill \end{array}$$

(3)

Substituting Equations (2) and (3) into Equation (1), we have

$$\begin{array}{cc}\hfill {\langle {\mathcal{I}}_1·{\mathcal{I}}_2\rangle }_j=\int d{\widehat{x}}_{1}d{\widehat{x}}_2& [\langle \int d{x}_1^{\prime }d{x}_2{E}^{*}\left(x_1^{\prime }\right)E\left(x_2\right)h_1^{*}\left(x_1^{\prime }\right)h_2\left(x_2\right)\rangle \hfill \\ & \langle \int d{x}_2^{\prime }d{x}_1{E}^{*}\left(x_2^{\prime }\right)E\left(x_1\right)h_2^{*}\left(x_2^{\prime }\right)h_1\left(x_1\right)\rangle \hfill \\ \hfill +& \langle \int d{x}_1^{\prime }d{x}_1{E}^{*}\left(x_1^{\prime }\right)E\left(x_1\right)h_1\left(x_1\right)h_1^{*}\left(x_1^{\prime }\right)\rangle \hfill \\ & \langle \int d{x}_2^{\prime }d{x}_2{E}^{*}\left(x_2^{\prime }\right)E\left(x_2\right)(h_2^{*}\left(x_2^{\prime }\right)h_2\left(x_2\right)\rangle ].\hfill \end{array}$$

(4)

On the right-hand side of Equation (4), the first term represents the intensity fluctuation, where the object information is concentrated. The second term is the DC component of the correlation, which can be subtracted directly. By further taking into account the incoherent property of the two beams that $\langle E^{*}\left(x_1\right)E\left(x_2\right)\rangle =\delta (x_1-x_2)$, we can define the correlation factor as follows:

$$\begin{array}{cc}\hfill S_j=& {\langle {\mathcal{I}}_1·{\mathcal{I}}_2\rangle }_j-\langle {\mathcal{I}}_1\rangle \langle {\mathcal{I}}_{2_j}\rangle \hfill \\ \hfill =& \int d{\widehat{x}}_{1}d{\widehat{x}}_2|\langle \int d{x}_{1}d{x}_2{E}^{*}\left(x_1\right))E\left(x_2\right))h_1^{*}\left(x_1\right)h_2\left(x_2\right){\rangle |}^2\hfill \\ \hfill =& \int dx|P_j\left(x\right)T^{*}{\left(x\right)|}^2=\int dx|P_j{\left(x\right)|}^2{\left|T^{*}\left(x\right)\right|}^2.\hfill \end{array}$$

(5)

This correlation factor reveals the degree of spatial correlation between the object and modulation; the final imaging mechanism neglects any dependence on the spatial information of the illumination. This format is consistent with that of the traditional bucket signal in SPI [27,30,31], which means that an ordinary SPI algorithm can apply for this dual-arm scheme. In the process of imaging, the modulation and object are pixelated and have positive real values; the correlation signal of the j-th modulation can be further written in the following discrete form:

$$S_j=\sum _{m=1}^M{P}_j\left(m\right)T\left(m\right).$$

(6)

Here, $P_j\left(m\right)$ and $T\left(m\right)$ are the discrete form of the matrix $|P_j{\left(x\right)|}^2$ and $|T^{*}{\left(x\right)|}^2$, respecitvely; $m=1, 2\dots .M$ is the discrete pixel of the object and modulation; and ${\sum }_{m=1}^M$ is the summation of the 1D matrix with index m. The above equation can be further written as a linear equation

$$\mathit{S}=\mathit{PT}.$$

(7)

Here, $\mathit{S}$ is an $M\times 1$ vector obtained by traversing M modulations. $\mathit{P}$ is an $M\times M$ matrix formed by arranging all $P_j\left(m\right)$, and $\mathit{T}$ is an $M\times 1$ vector representing the object. It is worth noting that for more general two-dimensional imaging, the above process still holds, provided that both the two-dimensional modulation and the object are rearranged into an $M\times 1$ vector. If the measurement matrix forms an orthogonal basis, such as the Fourier bases and Hadamard bases used in our experiment, the object $\mathit{T}$ can be reconstructed through an inverse transformation process:

$$\mathit{T}={\mathit{P}}^{-1}\mathit{S}.$$

(8)

We have examined the feasibility of our scheme based on near field correlation between two classical beams. Referring to previous GI works, it is natural to extend our scheme to the far field correlation for ghost diffraction. The schematic diagram showing the comparison between ghost imaging and ghost diffraction is shown in Figure 1b,c. This can be achieved when the modulation is located in the image plane of the speckles and the object is located in the Fourier plane. The lens after the object acts as a Fourier transform element that works with the point detector to isolate light fields of specific spatial frequencies in the object arm. Compared with Equation (2), the optical field over the surface of the point detector, i.e., ${\mathit{\varepsilon }}_1$, is written as follows

$$\begin{array}{cc}\hfill {\mathit{\varepsilon }}_1=& \int d{x}_1^{\prime }d{x}_{f1}^{\prime }d{x}_{1}d{x}_{f1}E\left(x_1^{\prime }\right)[{\displaystyle \frac{e^{\mathrm{i}2kf}}{\lambda f}}{e}^{{\displaystyle \frac{-\mathrm{i}k}{2f}}{(x_{f1}^{\prime }-x_1^{\prime })}^2}\ast e^{{\displaystyle \frac{\mathrm{i}k}{2f}}{\left(x_{f1}^{\prime }\right)}^2}\hfill \\ & {\displaystyle \frac{e^{\mathrm{i}2kf}}{\lambda f}}{e}^{{\displaystyle \frac{-\mathrm{i}k}{2f}}{(x_{f1}^{\prime }-x_1)}^2}T\left(x_1\right){\displaystyle \frac{e^{\mathrm{i}2kf}}{\lambda f}}{e}^{{\displaystyle \frac{-\mathrm{i}k}{2f}}{(x_{f1}-x_1)}^2}\ast e^{{\displaystyle \frac{\mathrm{i}k}{2f}}{\left(x_{f1}\right)}^2}\hfill \\ & {\displaystyle \frac{e^{\mathrm{i}2kf}}{\lambda f}}{e}^{{\displaystyle \frac{-\mathrm{i}k}{2f}}{({\widehat{x}}_1-x_{f1})}^2}].\hfill \end{array}$$

(9)

For consistency with point detection, we set ${\widehat{x}}_1=0$. The subsequent derivation process is similar to ghost imaging, except that the final result is the Fourier transform image of the object.

3. Simulation and Experimental Results

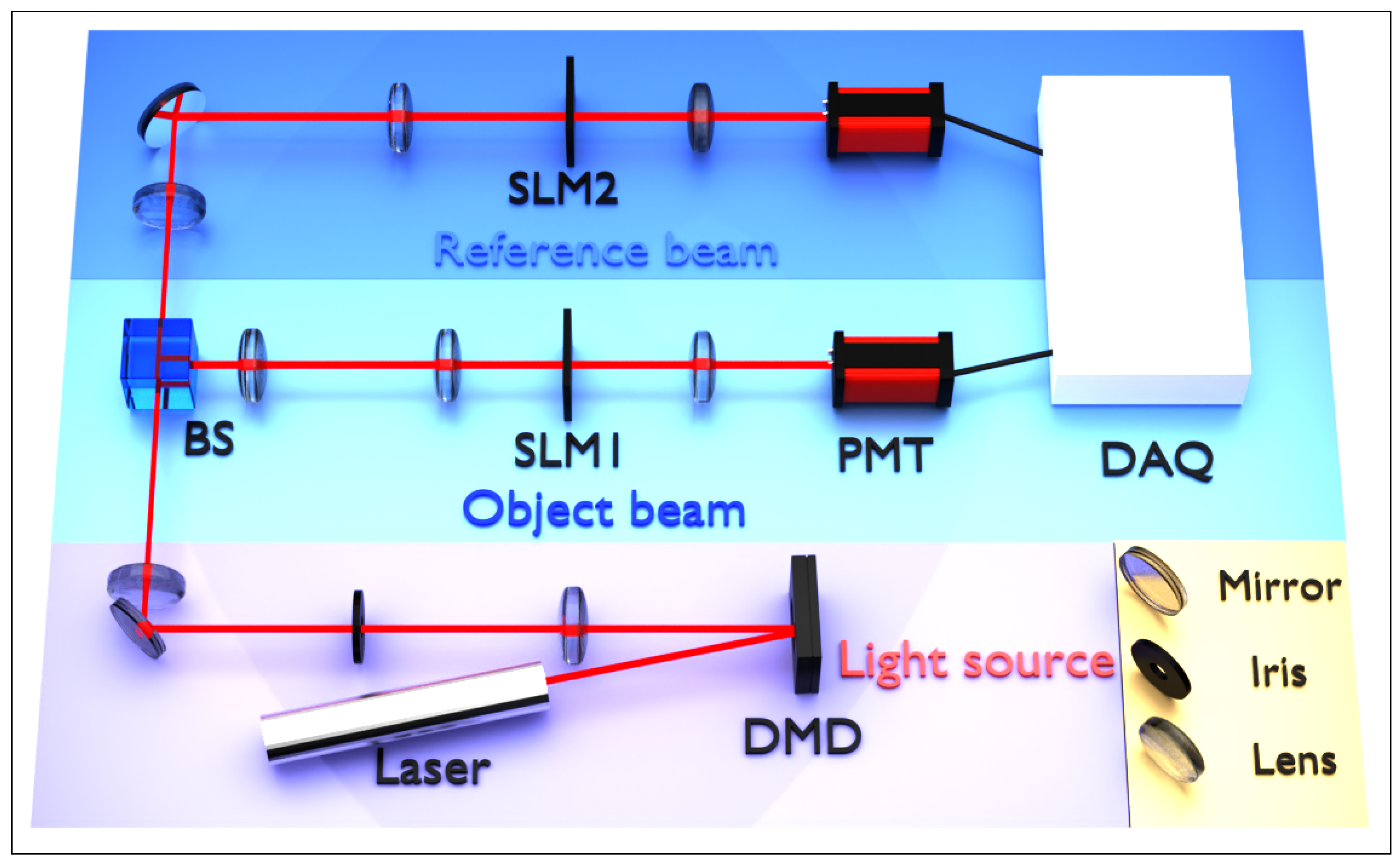
To demonstrate our method, we designed an imaging experiment, as shown in Figure 3.

A collimated and expanded He–Ne laser illuminates the DMD (DLP7001, TI) with a pixel pitch of 13.7 µm. To achieve complex field modulation and a high refresh rate for pattern switching, we use the super-pixel technology to allow for full field control over the amplitude and phase [32]. We group every $4\times 4$ DMD micromirrors into a superpixel. After low-pass filtering, individual DMD mirrors within a superpixel overlap together and become interfered at the back focal plane of the $4f$ system. We show a speckle intensity map of $256\times 256$ pixels generated through simulation in Figure 2, and the autocorrelation of this speckle is shown in Figure 2b,c. In the experiment, the projected speckle pattern is set to $256\times 256$ DMD pixels, with a lateral coherence length of 4 pixels, matching the size of an individual pixel in the modulation pattern. Here, the full width at half maximum (FWHM) of the autocorrelation is the coherence length, i.e., the average particle size of the speckle. The FWHM of the autocorrelation function becomes sharper with the increase in incoherence of the illumination, corresponding to smaller coherence lengths at both the modulation and object planes. A 50:50 beam splitter (BS) divides the speckles into two identical copies that impinge on the target object (SLM₁) and the known modulation (SLM₂). The SLMs (X15213-07, HAMAMATSU), each with $1024\times 1280$ pixels and a pixel pitch of 12.5 µm, are placed in the image plane of DMD in both arms to achieve ghost imaging. Here, we group $4\times 4$ SLM pixels into a modulation superpixel. The outgoing beams pass through the collecting lens and are then measured by two photomultiplier tubes (PMT, Hamamatsu, Japan, H10722-20), which are placed on the Fourier plane of two SLMs. For ghost imaging, the object and modulation are both located in the image plane of the speckle pattern and are collected in the same manner. In contrast, ghost diffraction involves a Fourier transform relationship between the object and modulation, whereby the speckle field of the object arm undergoes a Fourier transform via a single lens. The light field transmitted or reflected by the object is then Fourier transformed again through another single lens, and a single-point detector is positioned at the Fourier plane of the object. A small pinhole with a diameter of 25 µm is placed in front of the PMT to select a single spatial frequency, effectively creating a spatial filter.

We use randomized Hadamard patterns for modulation in the full sampling mode, which are constructed into a set of orthogonal bases and can achieve perfect reconstruction through the processes of Hadamard transformation and inverse transformation. For the reconstruction resolution of M, a total of $2M$ modulation patterns are used in the differential measurement method [33]. Here, the binary coding of Hadamard bases is realized by multiplying the SLM-loaded blazed grating with the bases. For ghost imaging, we selected a 64 × 64 amplitude double-slit as a binary object and a 64 × 64 grayscale amplitude object "GI" displayed on the SLM₁, where the latter is displayed using a method of complex holographic coding [34]. The number of illumination speckles needed for each modulation pattern is 168 k, and the integration time of each one is set to 50 µs. Under a fixed modulation pattern, the DMD projects the N speckle patterns, while two PMTs simultaneously measure the corresponding N intensity values. The data acquisition system collects the dual-channel intensity signals and rtransfers them to the processing program. The expected value of the intensity correlation $S_j$ is then calculated for that modulation pattern. Subsequently, SLM₂ switches to another modulation pattern, and the process is repeated. Finally, the M correlated signals $\mathit{S}$ reconstruct the object with the Hadamard matrix $\mathit{P}$.

The experimental and simulation results are shown in Figure 4. The number of speckle patterns corresponding to each modulation in the simulation is consistent with the experiment. Unlike in single-pixel imaging, the ultimate imaging resolution is determined by the greater of the speckle’s coherence length and the modulation pixel size. To optimize the imaging quality, we maintained consistency between these two parameters in our experimental setup.

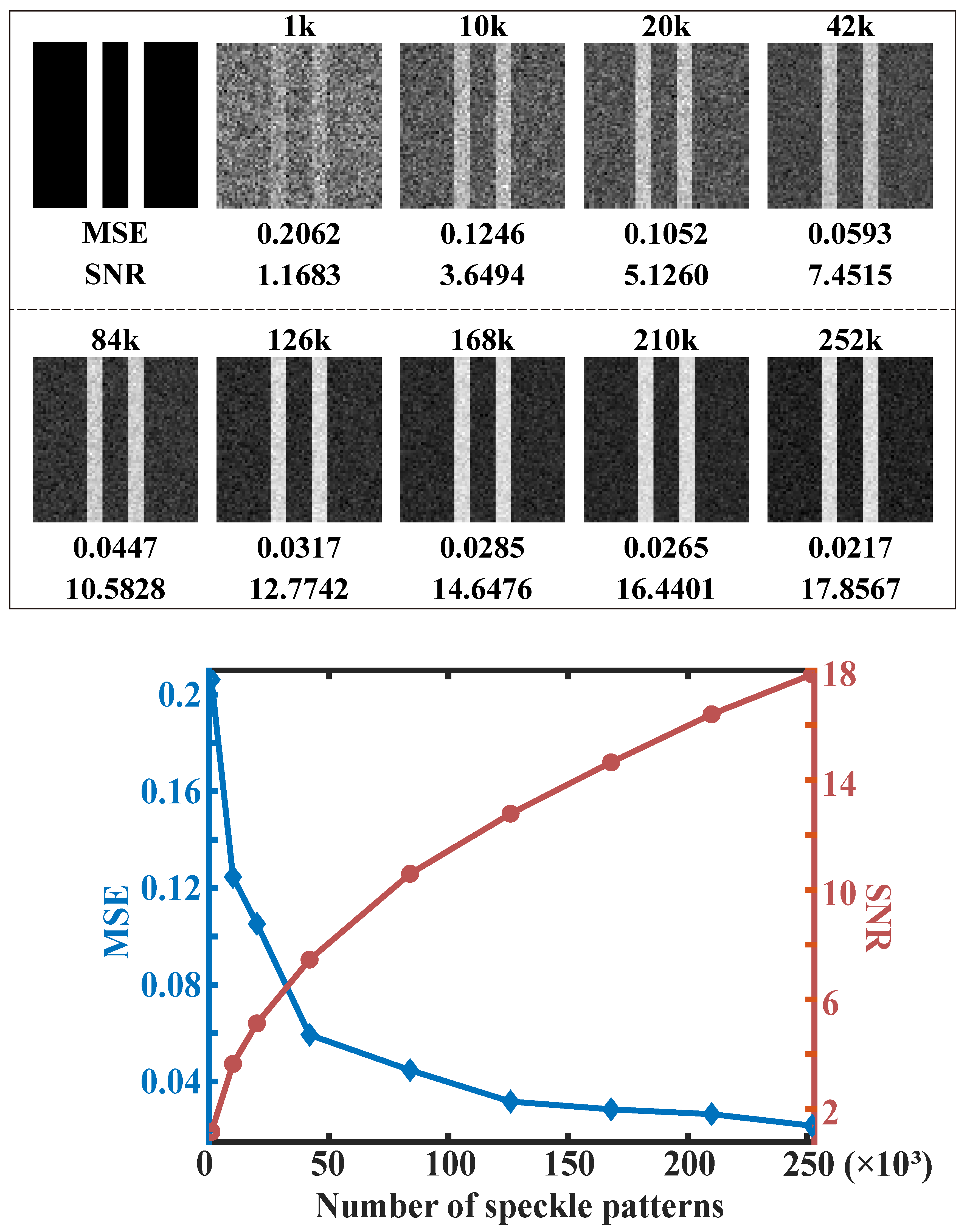
For this dual-path correlation imaging, various factors can affect image quality, including the number of illumination speckles, coherent length of speckles, modulation mode, and noise in the whole system. We investigated the impact of basic illumination source parameters on reconstruction quality through experiments and simulations. Specifically, we maintained a constant speckle coherence length, detection time, and imaging resolution, while varying the number of speckles per modulation from 1 k to 252 k, to image a double-slit amplitude object. We then calculated the signal-to-noise ratio (SNR) and mean squared error (MSE) of the reconstructed images. SNR primarily compares the signal-to-background noise contrast in the reconstructed image, while MSE describes the difference between the reconstructed amplitude and the original target. Figure 5 shows the simulation results, where the reconstructed image quality improves significantly as the number of speckles per modulation increases from 1 k to 252 k. MSE decreased rapidly, while SNR increased, indicating a notable improvement in image quality. We present both the reconstructed images and the parameter variation curves in the figure. Figure 6 illustrates the experimental results, where the number of speckles per modulation is the same as in the simulation. Despite the presence of discrepancies in the experimental results, particularly with regards to the minimum MSE and maximum SNR values, the overall trend remains consistent: an increase in the number of speckles per modulation yields an improvement in image quality. The observed discrepancies can be attributed to various factors of error in the experimental setup, including stray light interference, minor fluctuations in the light source, and spatial positioning errors in the SLMs. Nonetheless, both simulations and experiments converge on a clear conclusion: a higher number of speckles per modulation correlates with an enhanced image quality. This finding prompted us to investigate the role of the speckle field in this imaging modality, with a view to optimizing its performance.

In each speckle pattern, the field distribution is deterministic. As illumination with the dynamic field distribution increases, and after accumulating a large number of iterations, the illumination process trends to being ergodic. When switching between a large number of speckle patterns, the high value of the signal in either arm (${\mathcal{I}}_1$ or ${\mathcal{I}}_2$) indicates a high degree of similarity between the speckle and modulation (or object) due to the speciality of the bucket detection. Furthermore, the correlation value, i.e., the product of the single-arm signal ($\langle {\mathcal{I}}_1·{\mathcal{I}}_2\rangle$), represents the degree of similarity between the modulation and object. In essence, in this dual-arm scenario, the speckle field acts as an information carrier, conveying information about the object with each modulation basis indirectly. Consequently, a larger number of speckle fields can enhance the accuracy of this judgment. Compared with the existing experiments of entangled photon illumination, we can see that the pseudo-thermal light after beam splitting is equivalent to a pair of entangled photons, which are in all possible states at the same time, while pseudo-thermal fields are in a specific state after production. Switching between different speckles is equivalent to an expansion of all spatial modes of entangled photons in time, that is, we can use the pseudo-thermal light after splitting the beam to simulate a pair of entangled photons by trying as many states as possible. Therefore, with the increase in the number of speckles, the quality of the recovered image also increases.

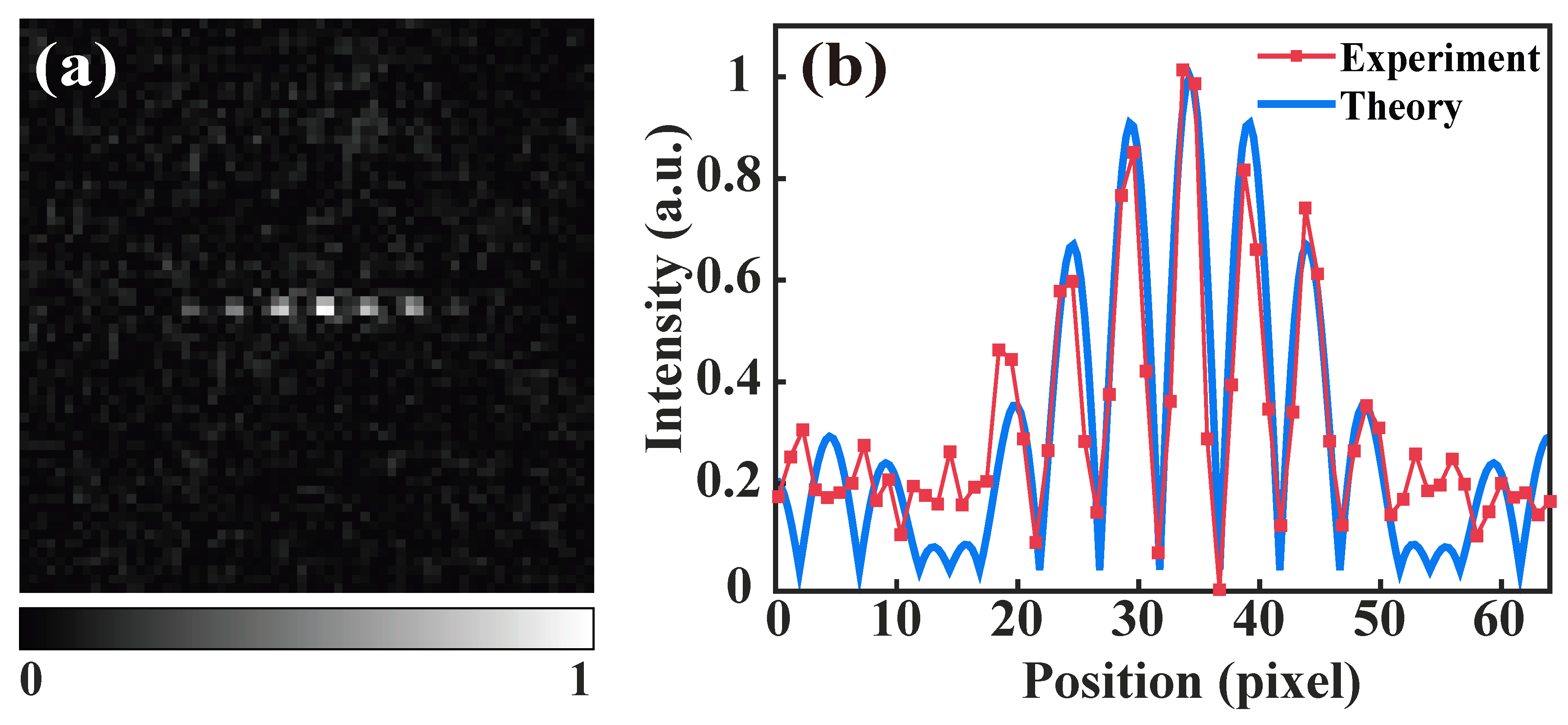
Figure 7b shows the comparison between the reconstructed double-slit diffraction and theoretical values. The classical light source employed in our scheme exhibits spatial correlation between the far and near fields, allowing for a reconstruction of the object diffraction, as the light sources in the traditional scheme do.

For the ghost diffraction experimental scheme, a 25 µm pinhole is incorporated in front of the PMT as a point detector in the object beam. The object is an amplitude-only double-slit (200 µm–600 µm–200 µm). The number of illumination speckles needed for each modulation pattern is N = 84,000, and the integration time of one speckle is 50 µs. The experimental results are shown in Figure 7.

4. Conclusions and Discussion

In summary, we have theoretically and experimentally demonstrated novel ghost imaging and ghost diffraction schemes that separate the object and the modulation in the two arms of the incoherent light field, and reconstructed the imaging of the amplitude object and diffraction based on the correlation of intensities in the near and far field. We also investigated the impact of speckle pattern quantity on the imaging performance of amplitude objects through simulations and experiments. Futhermore, we uncovered the physical significance of both the single-path bucket detection signal and the two-path intensity correlation value.

In contrast with traditional pseudothermal ghost imaging, our method eliminates the need for point-by-point scanning or array cameras, significantly increasing the utilization efficiency of the light field. Additionally, it offers an improved detection sensitivity and can be combined with compressive sensing techniques to reduce the sampling rate. In addition, existing single-pixel imaging technologies have matured and are widely adopted, while our imaging scheme based on high-order optical correlations offers significant advantages in specific scenarios where single-pixel imaging is insufficient. For instance, in long-distance imaging LiDAR, where the object arm or both arms are affected by fluctuating environmental light or atmospheric turbulence, research has shown that this correlation approach can render the reconstructed imaging immune to atmospheric disturbances. Furthermore, in applications such as biological tissue or crystal imaging, which require low-light conditions with special light sources like X-rays or fluorescence, our modulation-based imaging scheme can independently control the photon level in the object arm, avoiding light damage while achieving high-sensitivity imaging. Additionally, the proposed approach, which bears a close analogy to the QGI scheme, is envisioned as an additional tool to complement CGI theory in understanding the statistical characteristics of both classical and quantum states in forthcoming research.

Notwithstanding the advantages of our proposed method, it is not without limitations. The refresh rate of existing SLMs is typically limited to around 60 Hz, which can significantly impede imaging speed under sparse illumination conditions. Additionally, the cost of SLMs is a substantial consideration. In certain experimental scenarios, replacing SLMs with spinning masks can be a viable strategy to enhance imaging speed while reducing system costs. Moreover, our scheme is restricted to imaging amplitude objects due to the constraints of bucket detectors, making quantitative phase imaging under incoherent light illumination a significant challenge. We will investigate the feasibility of overcoming this limitation in future work.