Research on Maximum Likelihood Decoding Algorithm and Channel Characteristics Optimization for 4FSK Ultraviolet Communication System Based on Poisson Distribution

Abstract

This study focuses on a 4FSK-modulated ultraviolet (UV) communication system, introducing an innovative symbol-level maximum likelihood decoding approach based on Poisson statistics. A forward error correction (FEC) coding mechanism is integrated to enhance system robustness. Through Monte Carlo simulations, the proposed decoding scheme and the error correction performances of Reed–Solomon (RS) and Low-Density Parity-Check (LDPC) codes are evaluated in UV channels. Both RS and LDPC codes significantly improve the Bit Error Rate (BER), with LDPC codes achieving superior gains under low SNR conditions. Hardware implementation and field tests validate the decoding algorithm and LDPC-optimized 4FSK system. Under non-line-of-sight (NLOS) conditions (10–45° transmit elevation angle), stable 60 m communication with BER < 10⁻³ is achieved. In line-of-sight (LOS) scenarios, the system demonstrates 900 m range with BER < 10⁻³, highlighting practical applicability in challenging atmospheric environments.

1. Introduction

UV light in the 200–280 nm wavelength range of sunlight is absorbed by ozone in the atmosphere, resulting in extremely low intensity reaching the Earth’s surface. This band of UV light is utilized for communication with minimal background noise [1,2]. Due to the scattering effect of particles in the atmosphere on UV light, UV signals can bypass obstacles, enabling UV wireless communication systems to achieve non-line-of-sight (NLOS) communication. Compared to other wireless optical communications, the transmitter and receiver of a UV wireless optical communication system can communicate without alignment [3]. Therefore, UV communication is an ideal choice in scenarios with strong solar background noise or obstacle-obstructed environments [4,5].

Studies on UV light scattering communication systems can be divided into theoretical modeling and experimental aspects. In terms of theoretical analysis, Refs. [6,7,8] investigated the single scattering model of UV photons. Ref. [9] analyzed the relationship among BER, transmission rate, and communication distance of a communication system under an atmospheric scattering transmission channel. Ref. [10] proposed an empirical model for channel attenuation. Ref. [11] developed Monte Carlo-based scattering channel models to study the impact of obstacles on UV scattering communication. Ref. [12] presented a theoretical framework for analyzing the performance of NLOS UV communication systems under multi-user interference (MUI), and Ref. [13] introduced a sample-based non-Monte Carlo method for UV channel analysis. Refs. [4,6] explored photon-counting reception techniques. Ref. [14] proposed a decode-and-forward relaying-based multi-hop UV communication system to mitigate turbulence effects in short-range scenarios, and Ref. [15] analyzed the performance of cooperative relays for multiple NLOS UV links in turbulent channels. In experimental studies, Ref. [4] successfully demonstrated real-time voice transmission at 2.4 kbps, and Refs. [16,17] carried out theoretical analysis and experimental measurements of long-distance UV light scattering communication channels. Receiving diversity techniques were investigated in Refs. [18,19]. Ref. [20] achieved a 75 Mbps NLOS communication link using on–off keying (OOK) modulation, and Ref. [21] extended the NLOS UV communication range to 500 m using a 200 mW 266 nm solid-state laser. Ref. [22] designed a 2 × 1 MISO optical Pulse Position Modulation (PPM) system with a photon-counting receiver and discussed the problem of incomplete synchronization in the optical PPM MISO system equipped with a photon-counting detector. Ref. [23] studied the adaptive modulation coding and retransmission of Low-Density Parity-Check (LDPC) codes in ultraviolet communication.

With the wide application of UV wireless optical communication in deep space communication and other high-demand fields, the stability and reliability of communication systems have become critical design challenges. Particularly in complex channel environments, communication signals are susceptible to noise and interference, resulting in high BER and communication interruptions. Most of the existing studies on ultraviolet scattering communication adopt OOK modulation and PPM. OOK modulation technology is relatively mature, and there is limited room for performance improvement. The PPM algorithm is rather difficult, which will increase the complexity and cost of system development. Frequency shift keying (FSK) modulation controls the transmitter to output signals of different frequencies by using different symbols, and its implementation is relatively simple. FSK is sensitive to the frequency changes in signals and has good resistance to amplitude fading and noise. As a frequency modulation method, 4FSK, while having the above advantages, can also achieve a relatively high communication rate.

Regarding the 4FSK demodulation schemes in ultraviolet optical communication, current research is rather limited. Commonly used demodulation methods include the waveform detection method and the laser pulse response method. When these two methods are used for signal demodulation, they have relatively high requirements for the detection intensity of light. Especially in ultraviolet optical communication, signals are prone to being affected by atmospheric attenuation and noise. Therefore, a highly sensitive detection system is required to ensure good signal quality. This study proposes a Poisson distribution-based codeword-level maximum likelihood decoding method for four-frequency shift keying (4FSK) modulation in UV communication systems, incorporating channel coding for system optimization. The method integrates key technologies including frame header statistical modeling, photon pulse counting, frequency correlation detection, and clock synchronization/tracking to enhance decoding reliability in low-light environments. To evaluate algorithm performance, computer simulations were conducted, and the algorithm was successfully implemented in hardware. Experimental results demonstrate that the UV communication system achieves a maximum communication range of 900 m. When LDPC coding is added, the system achieves a BER as low as 10⁻⁵ at a communication distance of 500 m.

The second section analyzes the discrete Poisson channel, pulse frequency slicing counting, frequency correlation detection, and clock synchronization/following techniques. In the third section, the link model of UV LOS communication and the single scattering model of NLOS communication are analyzed; the computer simulation results and experimental results are provided. Finally, the fourth section summarizes the entire paper.

2. Signal Processing Principles

This section focuses on the decoding algorithm developed in this paper. Given that the algorithm is formulated based on the Poisson distribution probability density function, we first provided a detailed mathematical formulation of the Poisson statistics in ultraviolet communication systems to establish the theoretical foundation for subsequent algorithm design. Section 2.2, Section 2.3, Section 2.4 and Section 2.5 then present a step-by-step analysis of the decoding process, sequentially detailing the signal processing flow: pulse photon counting, frequency cross-correlation calculation, CDR clock synchronization implementation, and threshold decision-making. Section 2.6 introduces the encoding and decoding of LDPC and RS codes.

2.1. Poisson Statistical Properties in Optical 4FSK Communications

In optical wireless communication systems employing 4FSK, the transmission process is inherently random due to the discrete nature of photon arrivals. When the optical signal is modulated to one of the four specified frequencies $f_a$$\left(a\in \left\{1,2,3,\left.4\right\}\right.\right)$, the receiver measures the received intensity by photomultiplier tube (PMT) and converts the incident photon flux into discrete photoelectron signals. Since the photon arrival process obeys Poisson distribution, its mathematical model can be expressed as follows:

$$P(S_i|{\lambda }_i)={\displaystyle \frac{{\lambda }_i^{S_i}{e}^{-{\lambda }_i}}{S_i!}}$$

(1)

where $S_i$ is the observed photon count at the i-th frequency channel, and ${\lambda }_i$ denotes the expected photon count at a given the transmitted data. When $i=s$, ${\lambda }_s$ corresponds to the expected photon count for transmitting bit value 1. When $i=b$, ${\lambda }_b$ represents the number of environmental noise photons. The λ-value expressions for both are as follows:

$${\lambda }_s={\displaystyle \frac{P_t\cdot F(f_c,t)\cdot \eta }{L\cdot R\cdot h\nu }}$$

(2)

$${\lambda }_b={\displaystyle \frac{J}{R}}$$

(3)

where η represents the detector quantum efficiency. The sequence composed of probability density functions for different frequencies $f_c$ is represented by $F(f_c,t)$, which is a function of time $t$. $h$ represents Planck’s constant, $\nu$ represents the signal frequency, and $R$ denotes the transmission rate of the code elements in the system. $J$ is the number of noisy photons in the environment at 1 s time. In this decoding scheme, the photon probability distribution for the case of different frequency photons can be obtained by determining λ, thus providing theoretical support for channel decoding.

Traditional maximum intensity detection methods are based on single-sample maximum decision, but due to the randomness of photon counting, these methods are prone to noise interference under low SNR conditions, leading to significant BER increases. Therefore, this paper proposes a codeword-level photon accumulation and maximum likelihood estimation method, which enhances decoding reliability by statistically accumulating over the entire symbol duration.

2.2. Pulse Frequency Slicing and Counting

This scheme employs a 4FSK signal as the carrier to transmit symbols with a bit width of 2, thereby sending signals 00, 01, 11, and 10. In UV communication systems, due to the discrete nature of photon signals, it is difficult to use conventional waveform detection or pulse threshold decoding. To improve the recognition and processing of weak signals, a photonic pulse counting strategy is employed in the front-end of the algorithm to ensure efficient signal recovery. A PMT + ADC sampling scheme combined with threshold optimization is used to achieve an efficient photon counting mechanism.

The counting of photon pulses is based on the ADC sampling the voltage signal, which is binarized by setting the voltage threshold V_th

$$N(T)={\displaystyle \sum _{t=0}^T}I(V(t)>V_{th})$$

(4)

$N\left(T\right)$ denotes the number of detected pulses within time interval $T$. The voltage signal sampled by the analog-to-digital converter (ADC) is represented by $V\left(t\right)$. The indicator function $I\left(x\right)$ is defined such that $I(V(t)>V_{th})=1$ if $V(t)>V_{th}$, and 0 otherwise. A slicing approach is employed to partition the single symbol duration, improving synchronization precision from symbol-level to slice time $T$. For signals of different frequencies, eight samples per symbol period are acquired. Given the variable frequency characteristics, the slice time $T$ differs for each frequency component. During decoding, pulse signals are processed through four-channel frequency slicing counting, with distinct slice counts allocated to each of the four frequencies, resulting in four-channel frequency slicing count data output.

2.3. Frequency Correlation Detection

To distinguish the photon pulses corresponding to different carrier frequencies, this study employs the cross-correlation detection method for frequency detection. The specific calculations are as follows:

$$P_i(t)={\displaystyle \sum S_i(t)\cdot {\alpha }_i}$$

(5)

where $S_i(t)$ denotes the sequence of photon pulse counts in the i-th frequency slice at moment t, and ${\alpha }_i$ represents the pre-defined frequency feature set of the system. By analyzing the four frequency window output curves derived from cross-correlation calculations, the transmission frequency carrier at the current moment can be determined. $P_i(t)$ represents the frequency window output sequence for the i-th carrier, which is the result of cross-correlating the frequency slice pulse count at time t with the frequency characteristic value.

2.4. CDR Matrix Synchronization Operations to Obtain Synchronization Moments

To improve the stability of the synchronization signal, reduce the interference of transient noise, and minimize the decoding error, we low-pass-filtered the frequency correlation detection output $P_i(t)$ to obtain a smooth envelope signal.

$$y_i(t)=P_i(t)\times h(t)$$

(6)

where h(t) is the filter response function; this step can effectively suppress high-frequency noise and improve clock synchronization robustness.

The key to frame synchronization lies in the matching between the data received at the receiver and the local link frame header. The locally stored link symbol synchronization frame header matrix $B$ is structured as follows:

$$B=\left[\begin{array}{cccc}{B}_1(1)& B_1(2)& \cdots & B_1(L)\\ B_2(1)& B_2(2)& \cdots & B_2(L)\\ B_3(1)& B_3(2)& \cdots & B_3(L)\\ B_4(1)& B_4(2)& \cdots & B_4(L)\end{array}\right]$$

(7)

$B_c(i)$ represents the preset link synchronization symbol pattern, and L is the length of the frame synchronization stored locally. At time t, we compute the second-order correlation between the current data window $Y(t)$ and the local link frame header $B$ by matrix matching.

$$Z(t)=Y(t)\cdot B^T$$

(8)

$Y(t)$ represents the cross-correlation matching result matrix obtained at time $t$, derived from the combination of the filter output curves. The matrix inner product operation allows fast calculation of symbol synchronization matching at different time points. The synchronization moment is determined by identifying the maximum value of $Z(t)$.

$$t_{CDR}=\arg {\max }_{t}Z(t)$$

(9)

This process employs matrix operations for batch processing to obtain the optimal synchronization position. Meanwhile, data corresponding to successful synchronization of the link frame header is stored in memory.

2.5. Codeword-Level Maximum Likelihood Decoding

To mitigate the effects of channel gain drift and photon statistical noise, a frame header-based statistical estimation method is proposed. In the preamble section of the transmitted frame, a symbol sequence composed of known bits enables the receiver to estimate the expected photon count ${\lambda }_i^{\mathrm{header}}$ for each frequency channel. The estimation formula is given by the following:

$${\lambda }_i^{\mathrm{header}}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{t=1}^N{S}_i^{\mathrm{header}}}(t)$$

(10)

$N$ denotes the number of frame header symbols used for estimation. $S_i^{\mathrm{header}}$ represents photon count received at frequency $f_i$ during frame header period. Due to potential signal gain fluctuations caused by atmospheric turbulence, fiber nonlinear effects, or pointing errors in optical channels, an adaptive normalization factor is further introduced to compensate for these variations.

$${\lambda }_i^{\mathrm{norm}}(b)={\lambda }_i^{\mathrm{header}}\times {\displaystyle \frac{S_i^{\mathrm{sum}}}{{\lambda }_i^{\mathrm{ideal}}}}$$

(11)

where $S_i^{\mathrm{sum}}$ denotes the cumulative photon count over the entire codeword duration. ${\lambda }_i^{\mathrm{ideal}}$ represents the theoretical photon count in the ideal case.

To enhance detection robustness, the received photon counts are accumulated over the entire symbol duration $T_s$ instead of relying on single-point instantaneous sampling. Assuming that each code element contains $T_s$ discrete time sampling points, the accumulated photon count is given by the following:

$$S_i^{\mathrm{sum}}={\displaystyle \sum _{k=t}^{t+T_s}{S}_i}(k)$$

(12)

where $S_i(k)$ denotes the photon count at the sampling moment at time k. $T_s$ denotes the duration of the code element. This method averages out high–frequency noise fluctuations through time integration, thereby enhancing the signal matching degree. The photon counts after code element level accumulation still obey Poisson distribution, and this approach reduces the relative variance and improves signal stability.

After obtaining the cumulative photon counts $S_i^{\mathrm{sum}}$ for all four frequency channels, the receiver needs to determine the most probable transmit bit b. We use maximum likelihood estimation to find the bit value that maximizes the joint likelihood value for all four channels. For a given bit value b, the joint likelihood function can be expressed as follows:

$$L(b)={\displaystyle \prod _{i=1}^{4}P}(S_i^{\mathrm{sum}}|{\lambda }_i^{\mathrm{norm}}(b))$$

(13)

$$\log L(b)={\displaystyle \sum _{i=1}^4\left(S_i^{\mathrm{sum}}\log {\lambda }_i^{\mathrm{norm}}(b)-{\lambda }_i^{\mathrm{norm}}(b)\right)}$$

(14)

$$\widehat{b}=\arg {\max }_b{\displaystyle \sum _{i=1}^4\left(S_i^{\mathrm{sum}}\log {\lambda }_i^{\mathrm{norm}}(b)-{\lambda }_i^{\mathrm{norm}}(b)\right)}$$

(15)

Compared with the traditional maximum intensity detection, the method comprehensively considers the information of four frequency channels to improve the stability of the judgment. It utilizes the statistical characteristics of photons to optimize the likelihood function, enhancing the decoding accuracy and reducing the probability of misjudgment caused by instantaneous photon fluctuations.

2.6. Construction of LDPC and RS Codes

Both Reed–Solomon (RS) codes and Low-Density Parity-Check (LDPC) codes are designed to add redundant information to the original message sequence. Specifically, these redundancies are mathematically correlated with the original data through pre-defined algebraic rules. Upon signal transmission to the receiver, these redundant bits enable systematic error detection and correction operations. The construction of LDPC codes and RS codes is introduced in this subsection.

The encoding of (n,k) LDPC codes (n is the code length and k is the length of the information bits) can be equated to the construction of the checksum matrix $H$. In this paper, a simpler way of construction is the approximate lower triangular method proposed by Richardso [24]. This method obtains the matrix $H^{*}$ by performing a simple row–column substitution on the checksum matrix $H$.

$$H^{\ast }=\left[\begin{array}{l}A B T\\ C D E\end{array}\right]$$

(16)

where A, B, C, D, E are $\left(m-g\right)\times \left(n-m\right)$ dimensional, $\left(m-g\right)\times g$ dimensional, $g\times \left(n-m\right)$ dimensional, $g\times g$ dimensional, $g\times \left(m-g\right)$ dimensional sparse lower triangular matrices, respectively. $T$ is $\left(m-g\right)\times \left(m-g\right)$ dimensional sparse lower triangular matrix. Multiply the matrix $H^{*}$ on the left by the following matrix $L$ to obtain $H_L$.

$$L=\left[\begin{array}{l} I O\\ -E{T}^{-1} I\end{array}\right]$$

(17)

$$H_L=L·H^{*}=\left[\begin{array}{l}\hspace{1em}\hspace{1em}A\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}B\hspace{1em}\hspace{1em}\hspace{1em} T\\ -E{T}^{-1}A+C\hspace{1em}-E{T}^{-1}B+D\hspace{1em}O\end{array}\right]$$

(18)

The LDPC code of length n corresponding to the checksum matrix $H$ is denoted as $c=\left(s,p_1,p_2\right)$, where $s$ is the information bit part with length $\left(n-m\right)$, $p_1$, $p_2$ is the checksum part with lengths $g$ and $m-g$, respectively. According to $H\times c^T=0$, we obtain $H_L\times c^T=0$, which is obtained by expansion.

$$A{s}^T+B{p_1}^T+T{p_2}^T=0$$

(19)

$$\left(-E{T}^{-1}A+C\right)s^T+\left(-E{T}^{-1}B+D\right){p_1}^T=0$$

(20)

Let $\beta =-E{T}^{-1}B+D$, and $\beta$ is an invertible matrix. Thus, the following occurs:

$${p_1}^T=-{\beta }^{-1}\left(-E{T}^{-1}A+C\right)s^T$$

(21)

$${p_2}^T=-T^{-1}\left(A{s}^T+B{p_1}^T\right)$$

(22)

If $\beta$ is not invertible, the column transformation of $H_L$ is performed until it stops when $\beta$ is invertible. In this way, the checksum part of the checksum matrix can be found.

(n,k) RS codes can be determined using either the generator matrix or the parity-check matrix, and the encoding and decoding computations are performed on the $GF\left(2^m\right)$ domain.

Determining an instanton $\alpha$ in the $GF\left(2^m\right)$ domain, the generating polynomial can be expressed as follows:

$$g\left(x\right)=\left(x-{\alpha }^{m_0}\right)\left(x-{\alpha }^{m_0+1}\right)\cdots \left(x-{\alpha }^{m_0+2t}\right)={\displaystyle \prod _{j=m_0}^{m_0+2t}\left(x-{\alpha }^j\right)}$$

(23)

Assuming that the sequence of messages over the $GF\left(2^m\right)$ domain is $s=\left(s_0,s_1,\cdots ,s_{k-1}\right)$, its corresponding message polynomial is as follows:

$$s\left(x\right)=s_0+s_{1}x+s_2{x}^2+\cdots +s_{k-1}{x}^{k-1}={\displaystyle \sum _{i=0}^{k-1}{s}_i}{x}^i$$

(24)

Defining bits 0 through k − 1 in each symbol as information bits and the rest as check bits, the system code polynomial can be written as follows:

$$C\left(x\right)=s_0{x}^{n-k}+s_1{x}^{n-k+1}+\cdots +s_{k-1}{x}^{n-1}+r_{n-k-1}+\cdots +r_0=s\left(x\right)x^{n-k}+r\left(x\right)$$

(25)

The calibration polynomial can be found by the following equation:

$$r\left(x\right)=s\left(x\right)x^{n-k}\mathrm{mod}\left(g\left(x\right)\right)$$

(26)

3. System Design with Simulation and Experimental Results

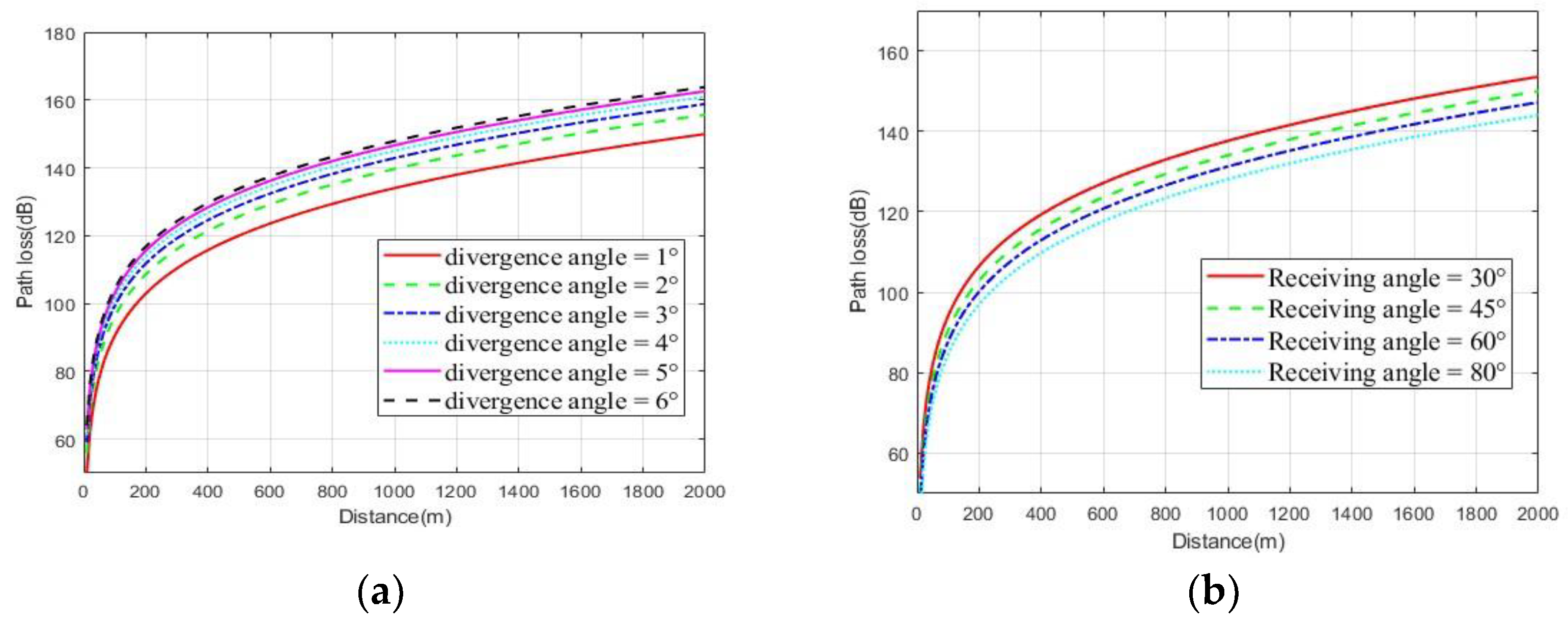
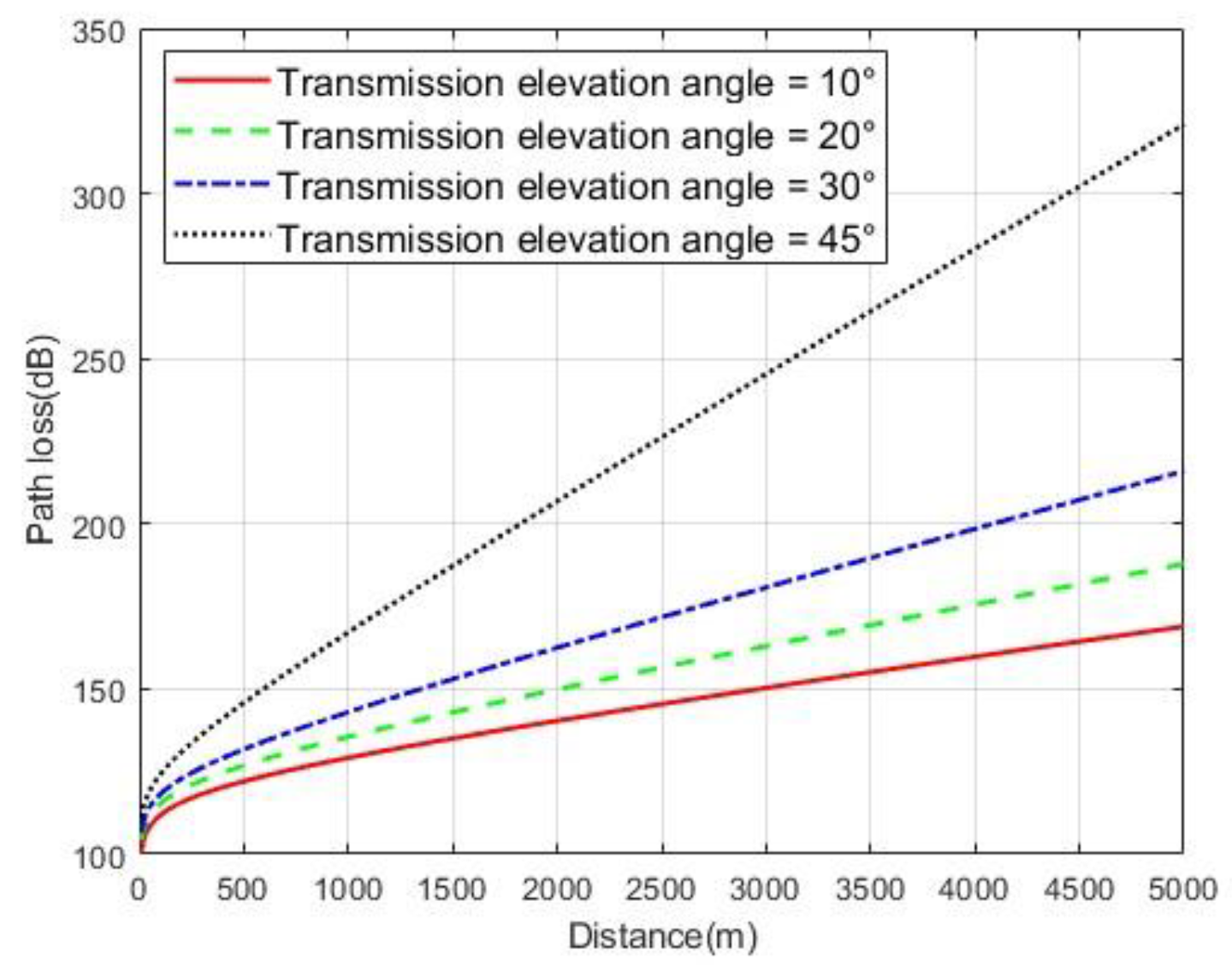
3.1. UV Channel Modeling Analysis and Simulation

3.1.1. LOS Model

Figure 1 represents the UV line-of-sight communication link model. In LOS communication, the vast majority of UV photons go directly from the transmitter to the receiver without scattering. In Figure 1, Tx is the position of the transmitter light source, Rx is the position of the receiver detector, ${\varphi }_1$ is the dispersion angle of the UV light source, and ${\varphi }_2$ is the receiving field of view of the detector.

Assume the transmitted power of the UV light source at the transmitter is $P_t$. After absorption and scattering in the atmosphere over distance $r_1$, the power becomes ${\displaystyle \frac{P_t{e}^{-K_e{r}_1}}{{r_1}^2}}$. Following the distance loss over $r_2$, the remaining power is ${\displaystyle \frac{P_t{e}^{-K_e{r}_1}}{{r_1}^2}}\times {\left({\displaystyle \frac{\lambda }{4\pi r_2}}\right)}^2$. $e^{-K_e{r}_2}$ represents the atmospheric attenuation factor, $K_e$ is the extinction coefficient, $\lambda$ is UV wavelength, $A_r$ is the receiver aperture area, and ${\displaystyle \frac{4\pi A_r}{{\lambda }^2}}$ is the detector reception gain.

The optical power reaching the receiver is as follows:

$$P_{r,LOS}=P_t\left({\displaystyle \frac{e^{-K_e{r}_1}}{{r_1}^2}}\right){\left({\displaystyle \frac{\lambda }{4\pi r_2}}\right)}^2{e}^{-K_e{r}_2}={\displaystyle \frac{P_t{A}_r}{4\pi {r_1}^2{r_2}^2}}{e}^{-K_e\left(r_1+r_2\right)}$$

(27)

According to the geometric relationship in Figure 1, the following equation can be obtained:

$$h_1={\displaystyle \frac{r\sin \left({\varphi }_2/2\right)}{\sin \left({\varphi }_1/2+{\varphi }_2/2\right)}}$$

(28)

$$h_2={\displaystyle \frac{r\sin \left({\varphi }_1/2\right)}{\sin \left({\varphi }_1/2+{\varphi }_2/2\right)}}$$

(29)

$$r_1=h_1\cos \left({\varphi }_1/2\right)={\displaystyle \frac{r\sin \left({\varphi }_2/2\right)\cos \left({\varphi }_1/2\right)}{\sin \left({\varphi }_1/2+{\varphi }_2/2\right)}}$$

(30)

$$r_2=h_2\cos \left({\varphi }_2/2\right)={\displaystyle \frac{r\sin \left({\varphi }_1/2\right)\cos \left({\varphi }_2/2\right)}{\sin \left({\varphi }_1/2+{\varphi }_2/2\right)}}$$

(31)

Therefore, we can obtain the following:

$$P_{r,LOS}={\displaystyle \frac{P_t{A}_r{e}^{-K_e\left(r_1+r_2\right)}}{4\pi {\left(\frac{r\sin \left({\varphi }_2/2\right)\cos \left({\varphi }_1/2\right)}{\sin \left({\varphi }_1/2+{\varphi }_2/2\right)}\right)}^2{\left(\frac{r\sin \left({\varphi }_1/2\right)\cos \left({\varphi }_2/2\right)}{\sin \left({\varphi }_1/2+{\varphi }_2/2\right)}\right)}^2}}$$

(32)

$$L_{LOS}=10{\log }_{10}\left({\displaystyle \frac{P_t}{P_{r,LO{S}_t}}}\right)=10{\log }_{10}\left({\displaystyle \frac{\pi r^4{\sin }^2\left({\varphi }_1\right){\sin }^2\left({\varphi }_2\right)}{4A_r{\sin }^4\left({\varphi }_1/2+{\varphi }_2/2\right)e^{-K_{e}r}}}\right)$$

(33)

As shown in Equations (32) and (33), the factors affecting $P_{r,LOS}$ and $L_{LOS}$ are the transmission distance $r$, the divergence angle of the light source ${\varphi }_1$, the receiving field of view angle of the detector ${\varphi }_2$ and so on.

We simulated the path loss versus distance curve using a computer. In the simulation, the extinction coefficient ${ K}_e=0.9 {\mathrm{k}\mathrm{m}}^{-1}$ and $Ar=5 {\mathrm{c}\mathrm{m}}^2$; the results are shown in Figure 2.

As observed in Figure 2, under identical conditions, path loss exhibits an upward trend with increasing distance. At a fixed distance, as shown in subplot (a), larger transmitter divergence angles result in higher path loss. This phenomenon can be attributed to the reduced energy concentration caused by a more divergent ultraviolet (UV) light source. Conversely, subplot (b) demonstrates that a larger receiver field of view (FOV) corresponds to lower path loss at the same distance, as a broader FOV allows the receiver to capture a broader spatial distribution of UV photons.

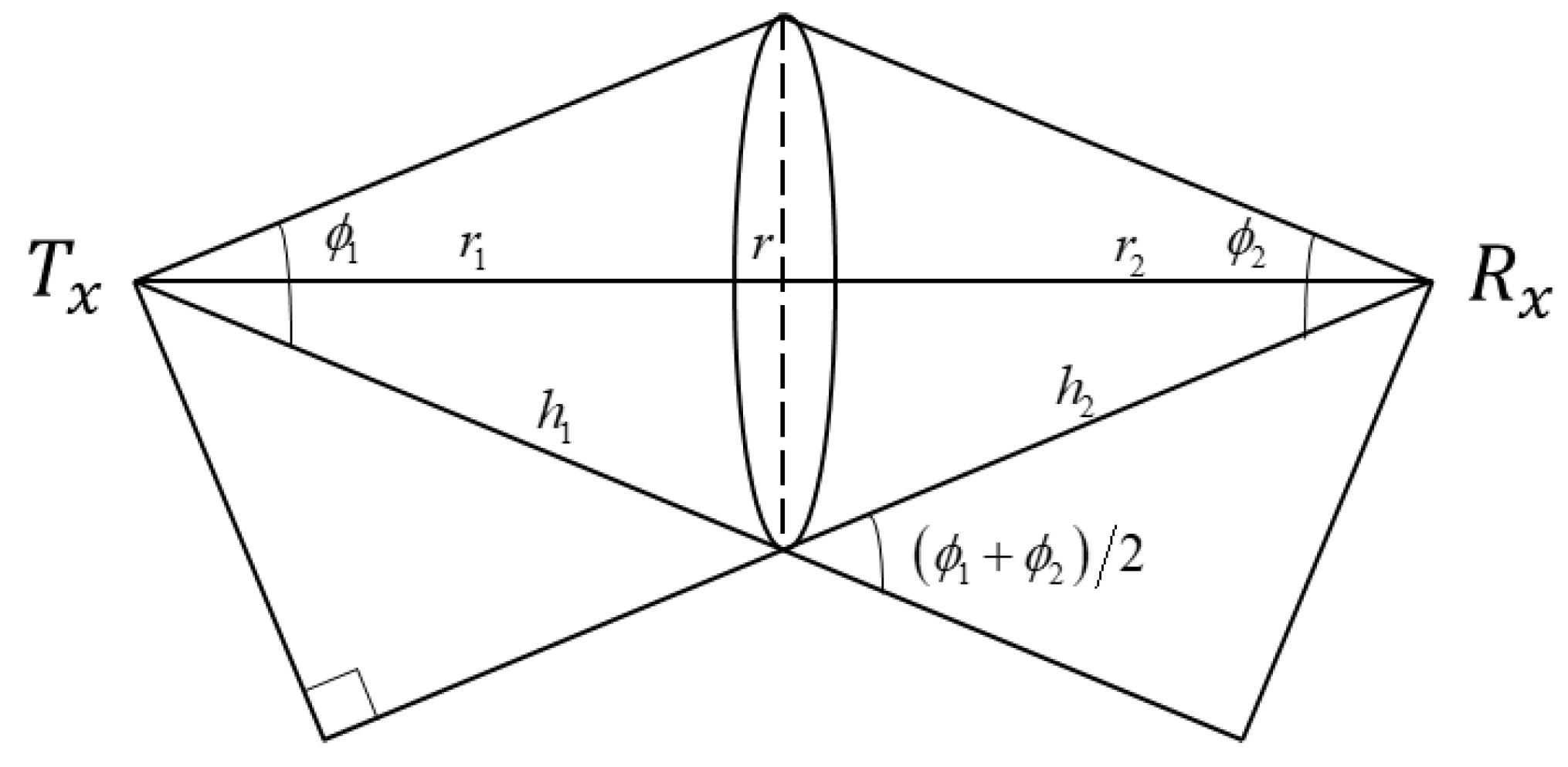
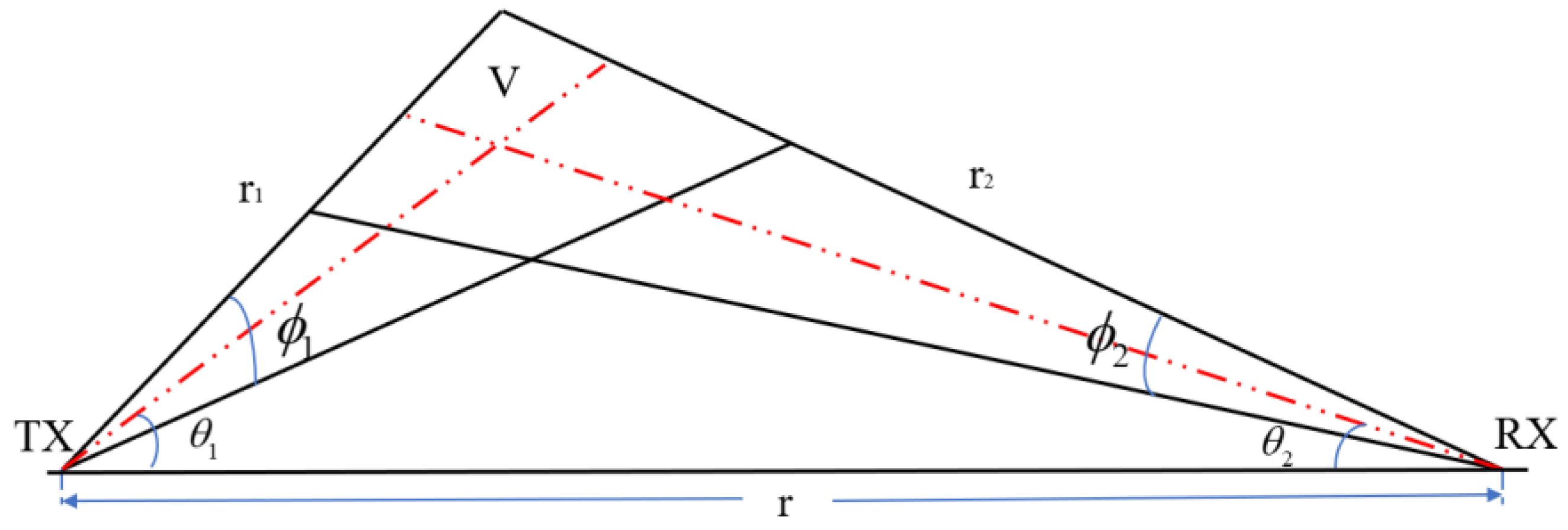
3.1.2. NLOS Single Scattering Model

The single scattering model is a simplified model that considers a photon emitted from a transmitter to arrive at the receiving end after only one scattering. Van de Hulst proposed that when the optical depth τ < 0.1, the single scattering transmission dominates the main aspect [6]. Therefore, for UV NLOS communication over short distances, the energy received at the receiving end is mainly the energy after the single scattering of photons.

Figure 3 shows a single scattering schematic of UV NLOS communication, TX and RX are the transmitting and receiving ends of the system, respectively, ${\varphi }_1$ is the dispersion angle of the UV light source, ${\varphi }_2$ is the receiving field of view angle of the detector, and ${\theta }_1$ and ${\theta }_2$ are the transmitting elevation angle and the receiving elevation angle of the system, respectively. Assuming that the output power at the transmitting end is $P_t$, the power per unit of stereo angle is ${\displaystyle \frac{P_t}{{\Omega }_T}}$; considering the path loss and attenuation, the power becomes ${\displaystyle \frac{P_t}{{\Omega }_T}}\times {\displaystyle \frac{e^{-K_e{r}_1}}{{r_1}^2}}$ after the path $r_1$. There is a secondary light source at the intersection of $r_1$ and $r_2$, and the optical power from the secondary light source is ${\displaystyle \frac{P_t}{{\Omega }_T}}\times {\displaystyle \frac{e^{-K_e{r}_1}}{{r_1}^2}}\times {\displaystyle \frac{K_S{P}_{S}V}{4\pi }}$. $V$ is the volume of the effective scatterer and $P_S$ is the phase function of the scattering angle ${\theta }_S$.

The path from the secondary light source to the receiving end can be equated to the LOS model. Therefore, the optical power detected at the receiving end can be obtained as follows:

$$P_{r,NLOS}={\displaystyle \frac{P_t}{{\Omega }_T}}\times {\displaystyle \frac{e^{-K_e{r}_1}}{{r_1}^2}}\times {\displaystyle \frac{K_S{P}_{S}V}{4\pi }}\times {\left({\displaystyle \frac{\lambda }{4\pi r_2}}\right)}^2{e}^{-K_e{r}_2}{\displaystyle \frac{4\pi A_r}{{\lambda }^2}}$$

(34)

where ${\left({\displaystyle \frac{\lambda }{4\pi r_2}}\right)}^2$ is the free space path loss factor, $e^{-K_e{r}_2}$ is the atmospheric attenuation factor, and ${\displaystyle \frac{4\pi A_r}{{\lambda }^2}}$ is the detector reception gain.

Moreover, according to the geometric relations, it can be obtained as follows:

$${\Omega }_T=2\pi \left[1-\cos \left({\varphi }_1/2\right)\right]$$

(35)

$$r_1=r\sin {\theta }_2/\sin {\theta }_S$$

(36)

$$r_2=r\sin {\theta }_1/\sin {\theta }_S$$

(37)

$${\theta }_S={\theta }_1+{\theta }_2$$

(38)

$$V=r_2{\varphi }_2{\left(r_1{\varphi }_1\right)}^2$$

(39)

$$P_{r,NLOS}={\displaystyle \frac{P_t{A}_r{K}_S{P}_S{\varphi }_2{{\varphi }_1}^2\sin \left({\theta }_1+{\theta }_2\right)}{32{\pi }^{3}r\sin {\theta }_1\left(1-\cos {\varphi }_1/2\right)}}{e}^{-{\displaystyle \frac{K_{e}r\left(\sin {\theta }_1+\sin {\theta }_2\right)}{\sin \left({\theta }_1+{\theta }_2\right)}}}$$

(40)

$$L_{NLOS}=10{\log }_{10}\left({\displaystyle \frac{32{\pi }^{3}r\sin {\theta }_1\left(1-\cos {\varphi }_1/2\right)}{A_r{K}_S{P}_S{\varphi }_2{{\varphi }_1}^2\sin \left({\theta }_1+{\theta }_2\right)}}{e}^{{\displaystyle \frac{K_{e}r\left(\sin {\theta }_1+\sin {\theta }_2\right)}{\sin \left({\theta }_1+{\theta }_2\right)}}}\right)$$

(41)

$r$ represents the direct line-of-sight distance between the transmitter and receiver, $K_e=K_{\alpha }+K_S$, $K_{\alpha }$ is the absorption coefficient, and $K_S$ is the scattering coefficient.

In atmospheric channel propagation, UV photons undergo both Rayleigh scattering and Mie scattering processes. Consequently, the scattering phase function can be mathematically formulated as a weighted sum of these two scattering mechanisms.

$$P_S=P\left({\theta }_S\right)={\displaystyle \frac{K_{SR}}{K_{SR}+K_{SM}}}{P}_R\left({\theta }_S\right)+{\displaystyle \frac{K_{SM}}{K_{SR}+K_{SM}}}{P}_M\left({\theta }_S,g\right)$$

(42)

$K_{SR}$ and $K_{SM}$ are the Rayleigh and Mie scattering coefficients, respectively, $P_R\left({\theta }_S\right)$ is the Rayleigh scattering phase function, and $P_M\left({\theta }_S,g\right)$ is the Mie scattering phase function, which can be expressed as follows [25]:

$$P_R({\theta }_S)={\displaystyle \frac{3}{16\pi \left(1+2\gamma \right)}}\left[\left(1+3\gamma \right)+\left(1-\gamma \right){\cos }^2{\theta }_S\right]$$

(43)

$$P_M({\theta }_S,g)={\displaystyle \frac{1-g^2}{4\pi }}\left[{\displaystyle \frac{1}{{\left(1+g^2-2g\cos {\theta }_S\right)}^{3/2}}}+f{\displaystyle \frac{0.5\left(3{\cos }^2{\theta }_S-1\right)}{{\left(1+g^2\right)}^{3/2}}}\right]$$

(44)

where $\gamma ,g,f$ are the model parameters.

As shown in Equations (40) and (41), $P_{r,NLOS}$ and $L_{NLOS}$ are influenced by $K_e$, ${\theta }_1$, ${\theta }_2$. In computer simulations with parameters configured as $\gamma =1.815\times {10}^{-2}, g=0.72, f=0.5$; the relationships between path loss and distance are presented in Figure 4 and Figure 5.

Figure 4 illustrates the path loss versus launch elevation angle. As the distance increases, the path loss tends to increase for all transmission elevation angles. Additionally, at the same distance, the smaller the transmission elevation angle is, the lower the path loss is. For instance, the path loss at a 10° elevation angle remains lower than those at 20°, 30°, and 45° across all distance segments. This is attributed to the reduced propagation distance of ultraviolet light through the atmosphere at smaller elevation angles. The shorter propagation distance directly results in a corresponding reduction in path loss. Conversely, increasing the elevation angle enhances forward scattering effects according to Mie scattering theory. As the angle deviated from the transmission direction increases, scattered energy decreases significantly, leading to a degradation in SNR.

Figure 5 illustrates the effect of different receiver elevation angles on the path. At shorter distances (0–500 m), the path loss increases significantly with distance, and notable discrepancies exist among curves corresponding to different elevation angles. Specifically, the 10° elevation angle exhibits relatively higher path loss compared to the 90° and 120° configurations. At longer distance (4500–4600 m), while path loss continues to increase with propagation distance, the growth rate decelerates appreciably. Moreover, the path loss curves for different elevation angles converge to parallelism, indicating that the influence of receiver elevation becomes less pronounced under these conditions. Notably, the 45° and 30° elevation angles demonstrate relatively lower path loss values in this regime. These results suggest that in practical communication systems, optimizing receiver elevation angles can effectively mitigate path loss in short-range scenarios. However, for long-distance transmissions, adjusting receiver elevation provides limited improvement, necessitating the consideration of alternative strategies to enhance communication quality.

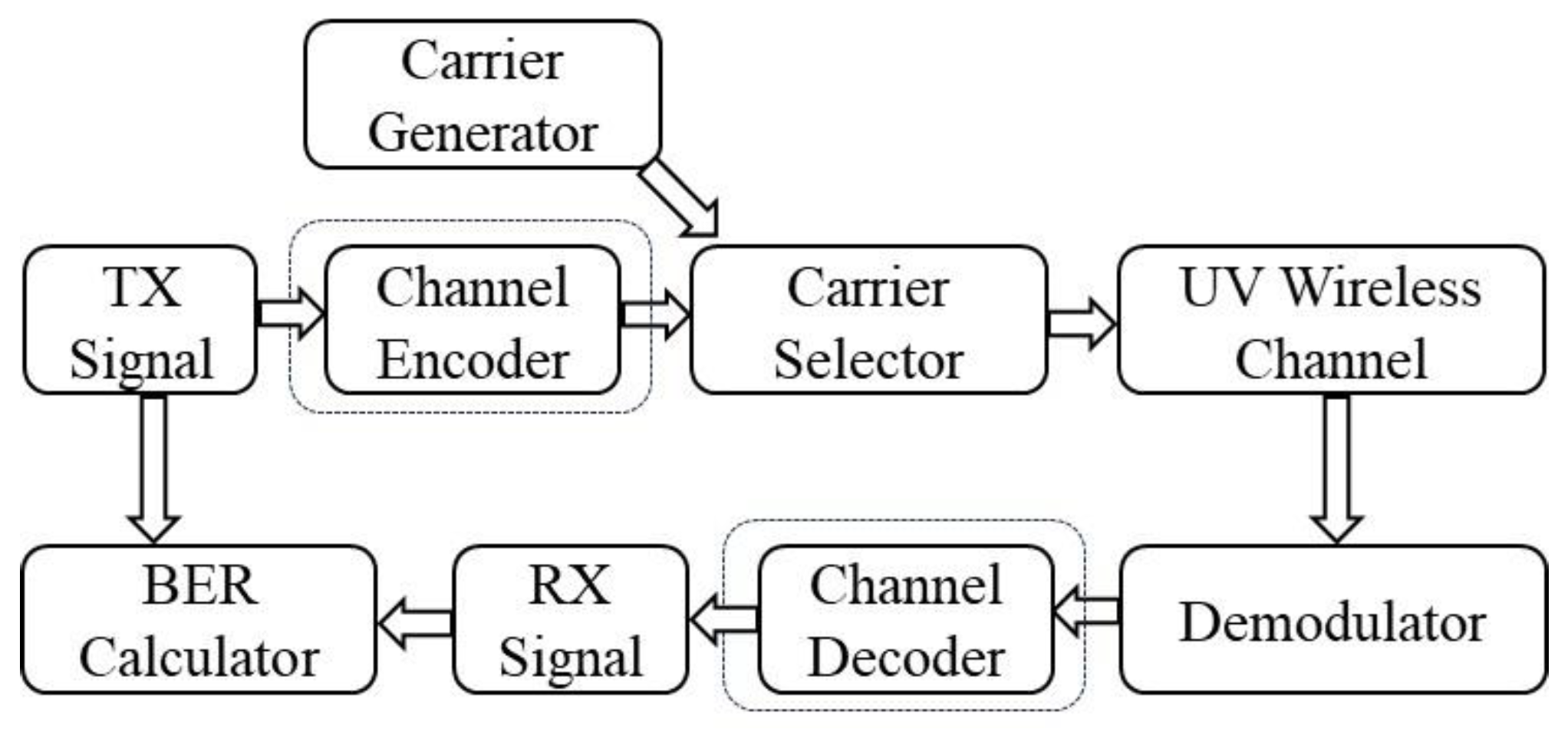
3.2. 4FSK Communication System Simulation Design

To comprehensively analyze the system performance, we have constructed a simulation platform for an ultraviolet (UV) wireless communication system based on 4-FSK modulation. The composition of the simulation platform is shown in Figure 6.

The Carrier Generator is used to generate carriers of four different frequencies. The Carrier Selector selects the carrier with the corresponding frequency for output based on the current symbol. The UV Wireless Channel is designed to simulate the real ultraviolet wireless channel environment. Based on the Poisson distribution probability model and using the Monte Carlo simulation method, it generates signal photons and noise photons to accurately reproduce the photon characteristics in the channel. The Demodulator performs the task of signal demodulation. The Channel Encoder and Channel Decoder are used for encoding and decoding, respectively, and these two modules will play a role in the system with encoding and decoding added. Finally, the BER is calculated by comparing the bit information at the transmitting end (TX) and the receiving end (RX).

3.3. System Simulation and Experimentation

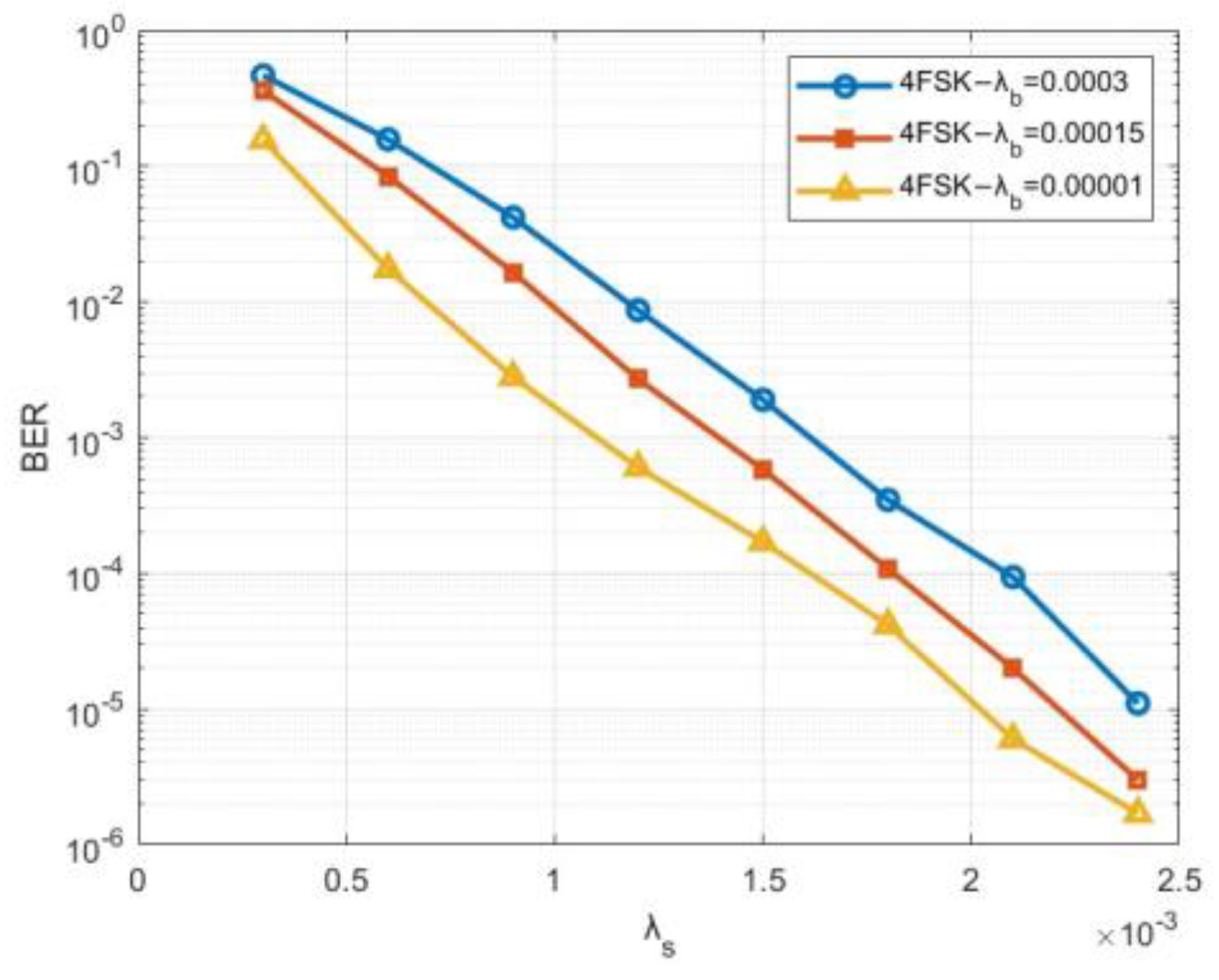
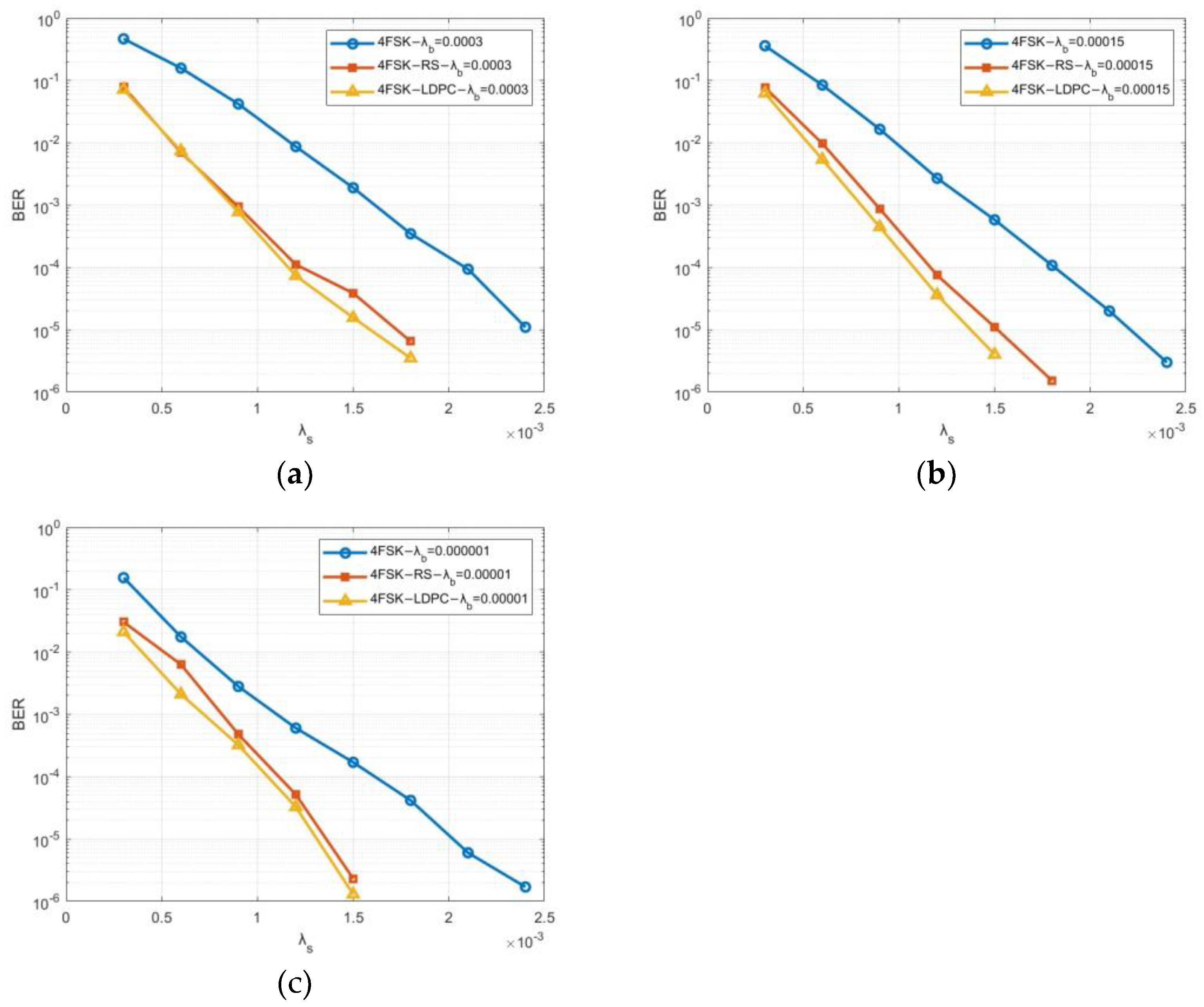
3.3.1. Communication System Simulation

Based on the above simulation framework, computer-based simulations of the communication system were performed. In the simulations, the 4FSK modulation scheme was configured with a bit rate R = 2.5 kbps, where the carrier frequencies corresponding to symbols 00, 01, 11, and 10 were set to f₁ = 40 kHz, f₂ = 45 kHz, f₃ = 50 kHz, f₄ = 55 kHz, respectively. The selection of this frequency band is based on bandwidth requirements and interference control considerations in practical communication environments, with the rationale behind choosing this band and its relationship to communication rates being thoroughly analyzed in our prior research [26].

Figure 7 demonstrates the relationship between ${\lambda }_s$ and the BER of the simulated system at different ambient noise levels when the symbol rate is 2.5 kbps. The results show that BER increases with rising noise levels, indicating a direct correlation between noise intensity and error probability. Under identical noise conditions, BER decreases as the parameter ${\lambda }_s$ increases. At the three noise levels shown in the figure, when ${\lambda }_s$ approaches 2.5 × 10⁻³, the BER can be reduced to below 10⁻⁵ due to the increased number of effective UV photons, which enhances frequency discriminability and enables the receiver to distinguish carrier frequencies more accurately.

To further reduce the BER, considering the error correction mechanism of the channel coding, RS code and LDPC code are introduced into this system. Computer simulations were conducted to evaluate the impact of both codes on system BER performance under varying SNR. The RS and LDPC codes were configured with identical code rates of 1/2. Figure 8 demonstrates the relationship between BER and ${\lambda }_b$ for the three systems under different noise levels. 4FSK denotes the uncoded system, while 4FSK-RS and 4FSK-LDPC represent the original system with RS code and LDPC code incorporated, respectively.

As shown in Figure 8, under identical noise levels, both the 4FSK-RS and 4FSK-LDPC systems exhibit significantly lower BER compared to the 4FSK system. A performance comparison between these two coded schemes reveals that the 4FSK-LDPC system outperforms the 4FSK-RS configuration across all tested noise levels, specifically at higher noise levels (e.g., noise power level ${\lambda }_b$ = 0.0003). This observation highlights the inherent advantages of LDPC codes in mitigating noise impairments under adverse channel conditions, thereby ensuring reliable information transmission in UV scattering communication systems.

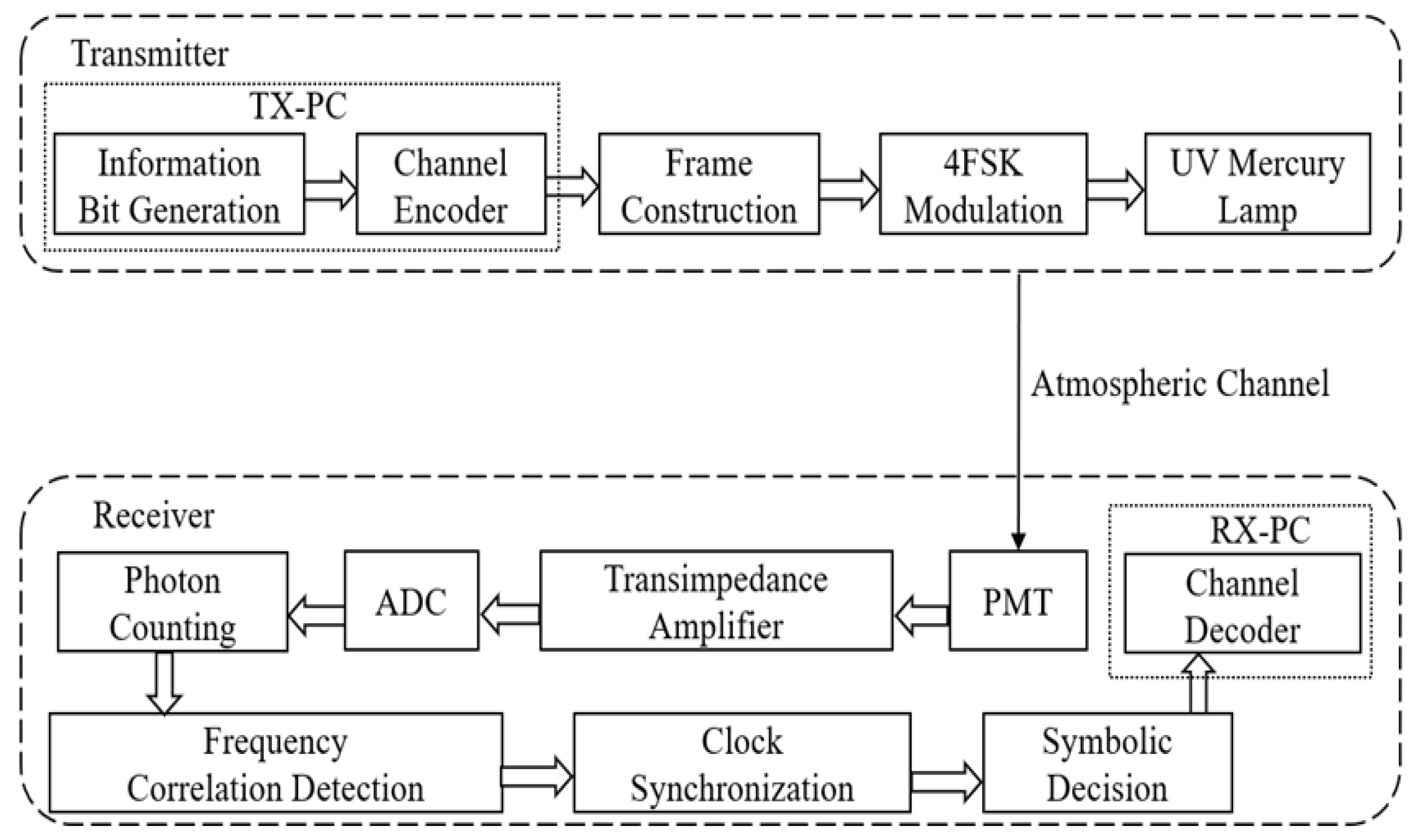
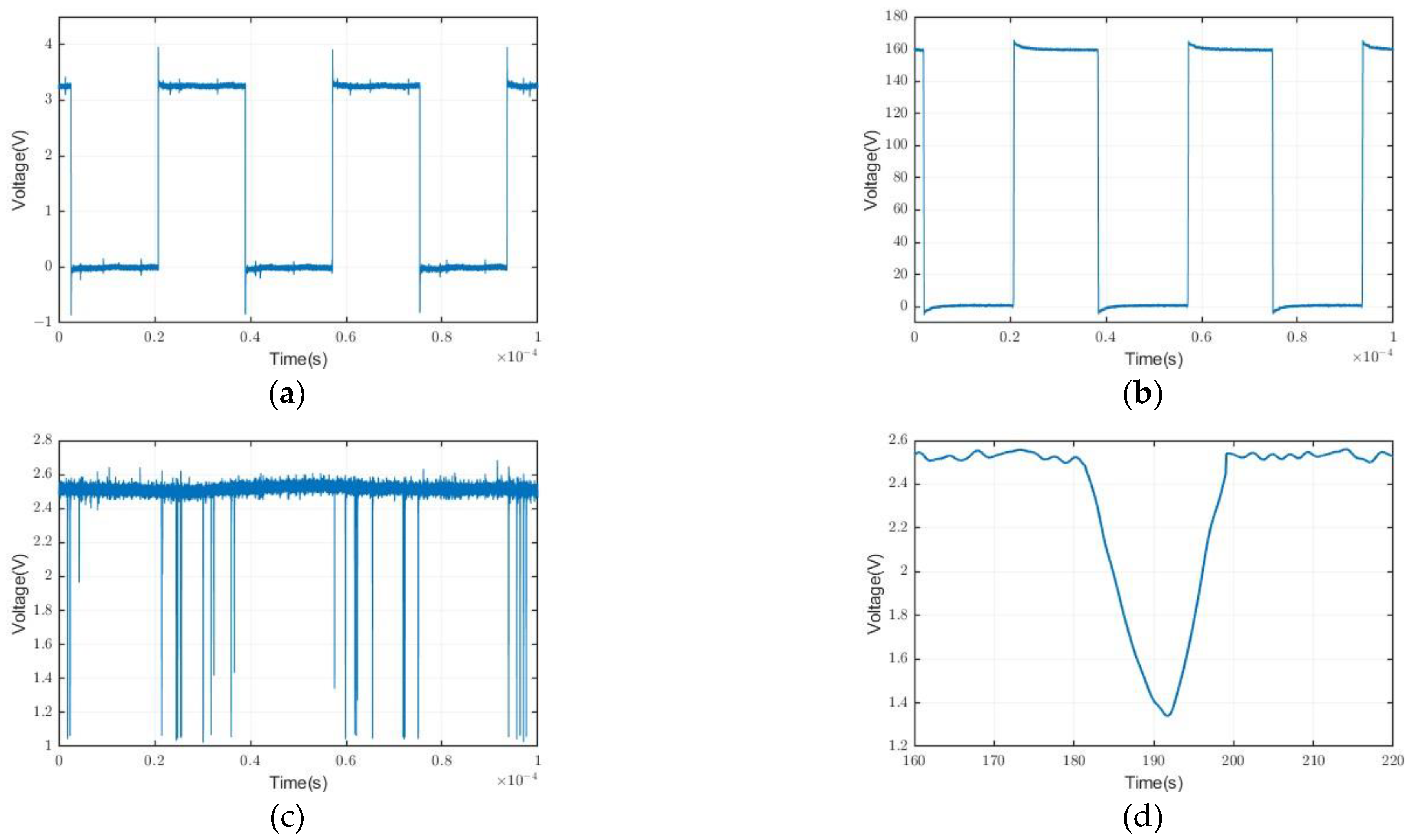
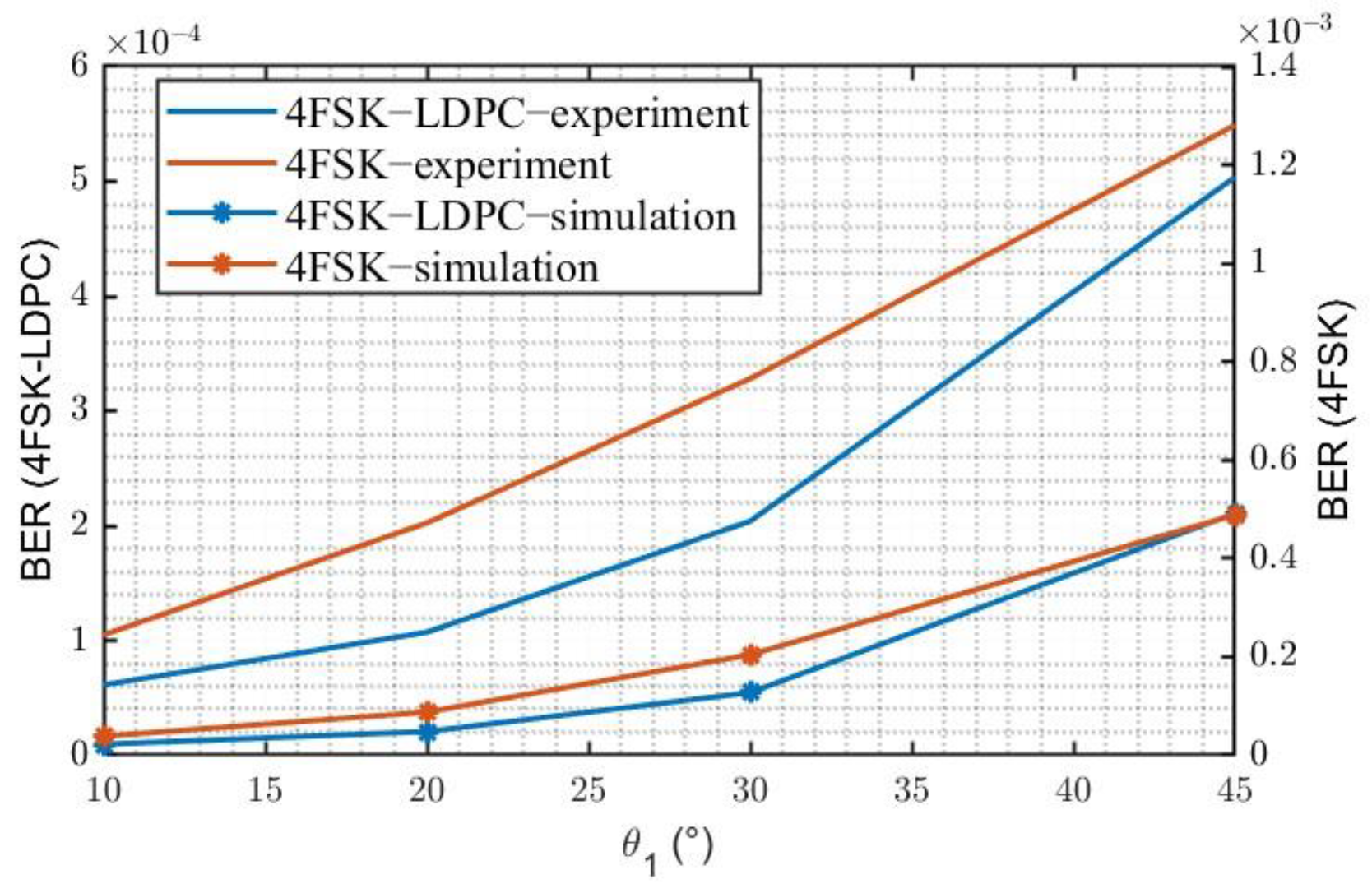
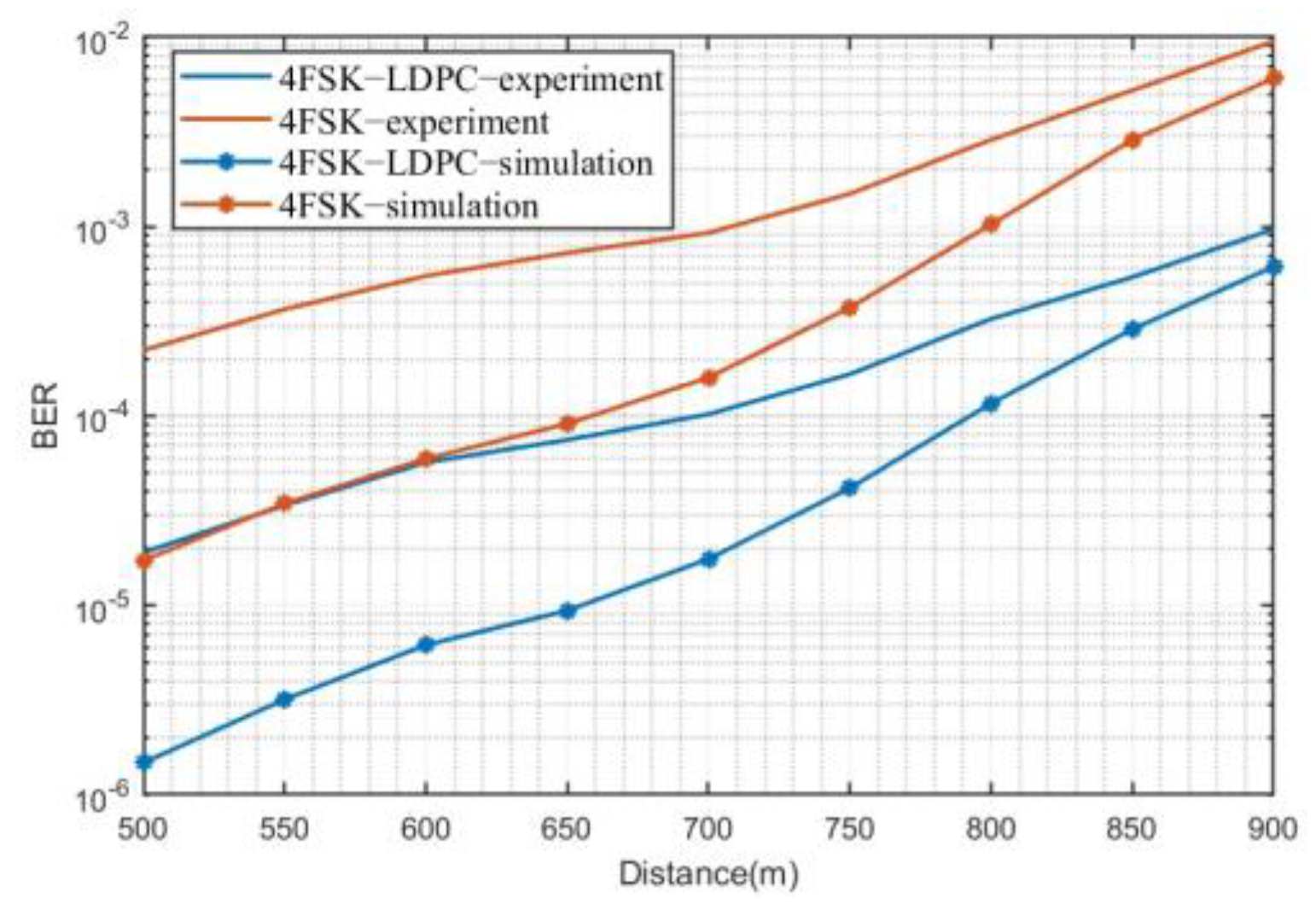
3.3.2. Experimental Test

Based on the above analysis and the BER simulation results in Section 3.3.1, this paper implements a UV communication system incorporating optimized 4FSK modulation algorithm and LDPC error-correcting code. The system block diagram is shown in Figure 9.

At the TX side, a low-pressure mercury lamp is employed as the optical source, and the TX-PC generates information and performs LDPC encoding on the data. At the RX side, the H10720-113 photomultiplier tube (PMT) from Hamamatsu Photonics (Hamamatsu, Japan) acts as a photodetector, converting ultraviolet (UV) light signals into electrical signals. The PMT output is processed through a transimpedance amplifier circuit, which converts the current signal to a voltage signal and amplifies it. The signal is then digitized by an analog-to-digital converter (ADC) module, which transmits the sampled data to an xc7k325tffg-676 FPGA chip (XLINX, San Jose, CA, USA). FPGA implements threshold-based photon pulse detection by comparing sampled data against predefined thresholds, performs pulse counting, and executes channel estimation and cross-correlation calculations for data demodulation. The demodulated data are transmitted via UART to the receiving PC, where LDPC decoding is completed by the RX-PC module.

During the experiment, we first characterize the signals of the transmitter and receiver using an oscilloscope, as shown in Figure 10. In Figure 10, subplot (a) displays the carrier signal output from the FPGA of the transmitter. Subplot (b) presents the carrier signal output from the modulation circuit of the transmitter. Subplot (c) illustrates multiple electrical pulse signals at the receiver circuit output. By analyzing Figure 10a, it is observed that when the FPGA outputs a logic ‘1’, the receiver circuit generates discrete electrical pulses; conversely, when the FPGA outputs a logic ‘0’, the received pulses become negligible. Subplot (d) shows a single electrical pulse from the receiver, revealing a pulse duration of approximately 20 ns.

To evaluate the communication performance of the system, field tests were conducted. These tests were divided into non-line-of-sight (NLOS) and line-of-sight (LOS) scenarios, with

Table 1. Parameters of outdoor NLOS field test.

Parameters	Values
UV light wavelength	254 nm
Center wavelength of the optical filter	261 nm
Power of UV light	3 W
Bit Rate	5 kbps
Receiver elevation angle (NLOS)	≈45°
Transmitter elevation angle (NLOS)	10~45°
Transmission range (NLOS)	60 m
Height of obstacle (NLOS)	4~5 m
Transmission range (LOS)	500–900 m

presenting the experimental parameters.

During NLOS testing, the transmitter and receiver were separated and placed on opposite sides of the obstacles, including vehicles and trees, such that communication could only be established through UV light scattering. The experimental equipment and test scenario are shown in Figure 11.

In Figure 11, UV-TX represents the entire transmitting system, and UV-RX represents the entire receiving system. TX-PC and RX-PC are the computers at the transmitting end and the receiving end, respectively. The DC power supply is a direct-current power supply, which is responsible for generating the voltage and current required by the system. The portable power bank is a mobile power source that supplies power to the DC voltage source.

The distance between the transmitter and the receiver was 60 m in the NLOS communication test. The elevation angle of the receiver was fixed at 45°, while transmitter elevation angles were sequentially adjusted to 10°, 20°, 30°, and 45° to evaluate system performance under different beam orientations. To investigate the optimization effect of LDPC code, the BER comparison test between the 4FSK system and the 4FSK-LDPC system were conducted. The experimental results are presented in Figure 12.

Figure 12 demonstrates that as the transmitter elevation angle increases from near 0° to 45°, BER rises correspondingly. This phenomenon stems from two key factors: increasing path loss reduces the number of received ultraviolet photons at the receiver, and frame header synchronization becomes more challenging, thereby increasing data transmission failure rates. Additionally, the 4FSK-LDPC system consistently outperforms the uncoded 4FSK system in terms of BER across all tested angles. Notably, the BER growth trend of the 4FSK-LDPC system remains more gradual compared to the uncoded counterpart as the elevation angle increases. Furthermore, both experimental and simulation results exhibit consistent trends, with simulation BER generally outperforming experimental BER.

In the LOS experiment, BER tests were performed at line-of-sight distances ranging from 500 to 900 m in 50 m increments, with the results presented in Figure 13. The results demonstrate that as transmission distance increases from 500 m to 900 m, the system BER exhibits a continuous increasing trend. Notably, the rate of BER growth accelerates with longer propagation ranges. At equivalent distances, the LDPC-4FSK system achieves a BER approximately one order of magnitude lower than the uncoded 4FSK system. The experimental BER of both systems is consistently higher than simulated values, primarily due to two factors: (1) high particle density in air causes multiple scattering effects that are not captured by the single scattering model used in simulations, with ultraviolet photons interacting with atmospheric molecules and aerosol particles leading to increased path loss; (2) wavelength mismatches between mercury lamp emissions and optical filters combined with temperature-induced efficiency degradation of the light source reduce reception efficiency, as demonstrated by photon loss at the receiver and power output decline under prolonged operation.

Synthesizing the results of the NLOS and LOS experiments, we can evaluate the communication capability of the UV communication system in this paper. In NLOS communication, increasing transmitter elevation angles lead to significant attenuation of scattered energy, resulting in corresponding BER increases. In LOS communication, prolonged propagation distances exacerbate path loss, degrade receiver signal-to-noise ratio (SNR), and thereby elevate BER. The exponential decay of received optical power with distance causes the BER growth rate to accelerate progressively as the communication range increases.

In communication scenarios where angular changes exist, the 4FSK-LDPC system shows superior anti-angle variation interference performance compared to the uncoded 4FSK system. Specifically, when the transmitter elevation angle ranges from 10° to 45° at a propagation distance of 60 m, the 4FSK-LDPC system maintains a BER below 5.04 × 10⁻⁴. For long-distance LOS communication, LDPC coding effectively enhances the anti-interference capability and transmission reliability of the 4FSK modulation scheme. In this study, both the 4FSK and 4FSK-LDPC systems achieve a maximum LOS communication range of 900 m. Notably, the 4FSK-LDPC system achieves a BER of approximately 10⁻⁵ at 500 m.

4. Conclusions

Focusing on the UV optical communication system with 4FSK modulation, this study proposes a Poisson distribution-based code element level maximum likelihood decoding method and introduces LDPC codes to optimize the system performance. Key innovations include the following:

• Poisson modeling of photon statistical properties to optimize the decoding performance at low signal-to-noise ratio.
• Expected photon number normalization based on frame header to improve channel adaptability.
• Combination of code element level accumulation and maximum likelihood estimation to reduce BER.
• Compensation of 4FSK’s BER defects under low-light channels through the error correction capability of LDPC codes.

Based on theoretical analysis and computer simulation, this paper implements the decoding method in hardware and validates it through experiments. The experimental results demonstrate that the LOS communication distance of the 4FSK system achieves 900 m at a transmission rate of 2.5 kbps. After incorporating LDPC code optimization, the 4FSK-LDPC system maintains a stable BER between 10⁻³ and 10⁻⁴ over the 700–900 m range. Specifically, at 500 m LOS distance, the 4FSK-LDPC system achieves a BER as low as 10⁻⁵. In NLOS communication testing, with a straight-line distance of 60 m, receiver elevation angle of 45°, and transmitter elevation angle of 10°, the 4FSK system exhibits a BER of 2.45 × 10⁻⁴, while the 4FSK-LDPC system reduces this to 6.12 × 10⁻⁵. Across transmitter elevation angles ranging from 20° to 45°, the 4FSK-LDPC system maintains BER values below 10⁻³.