Measurement of Coherence Time in Cold Atom-Generated Tunable Photon Wave Packets Using an Unbalanced Fiber Interferometer
Abstract
1. Introduction
2. Theoretical Basis and Methods
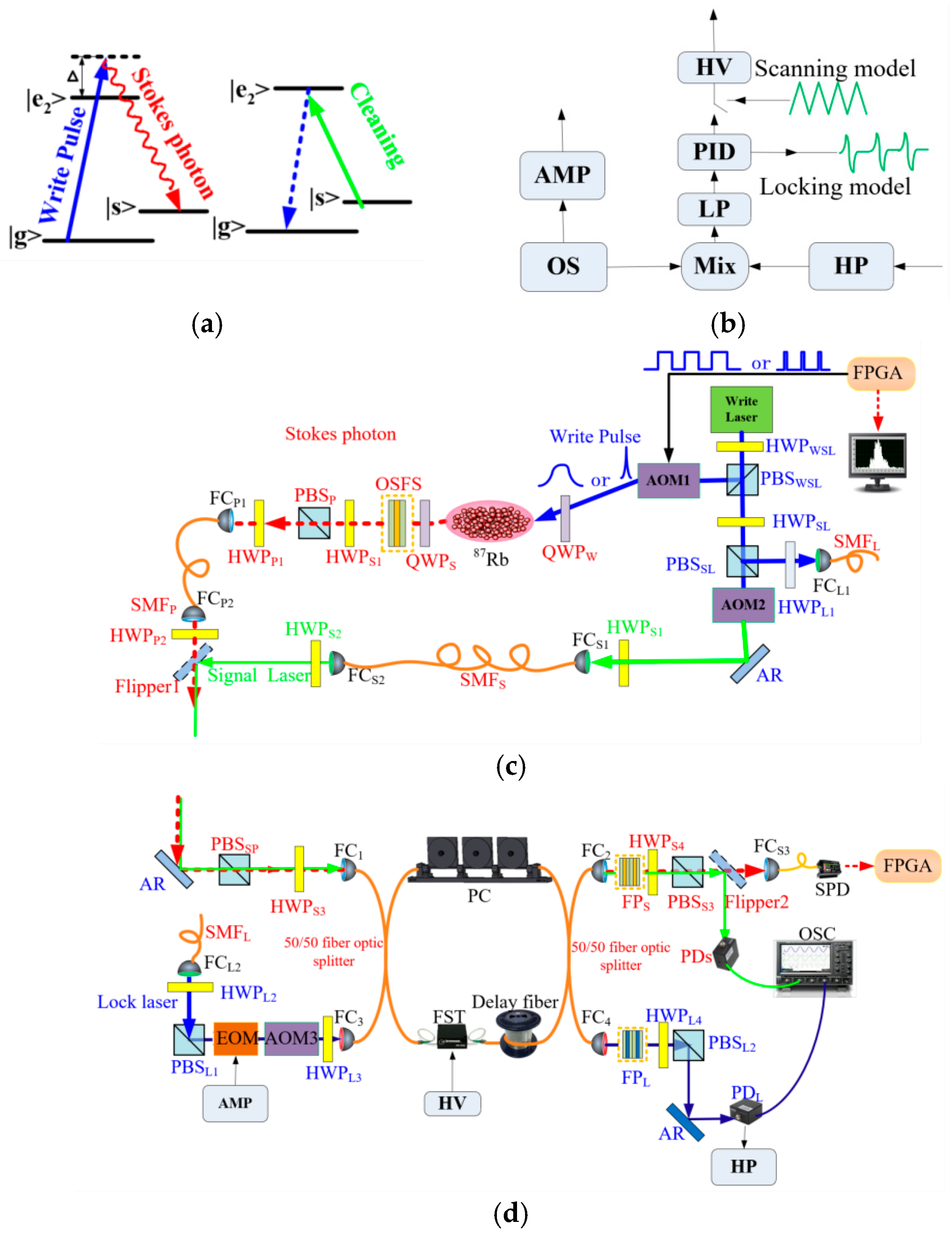
2.1. Cold Atom-Generated Tunable Photon Wave Packets
2.2. Theoretical Basis of the Unbalanced Fiber Interferometer
2.3. Experimental Setup
2.4. Filtering Techniques
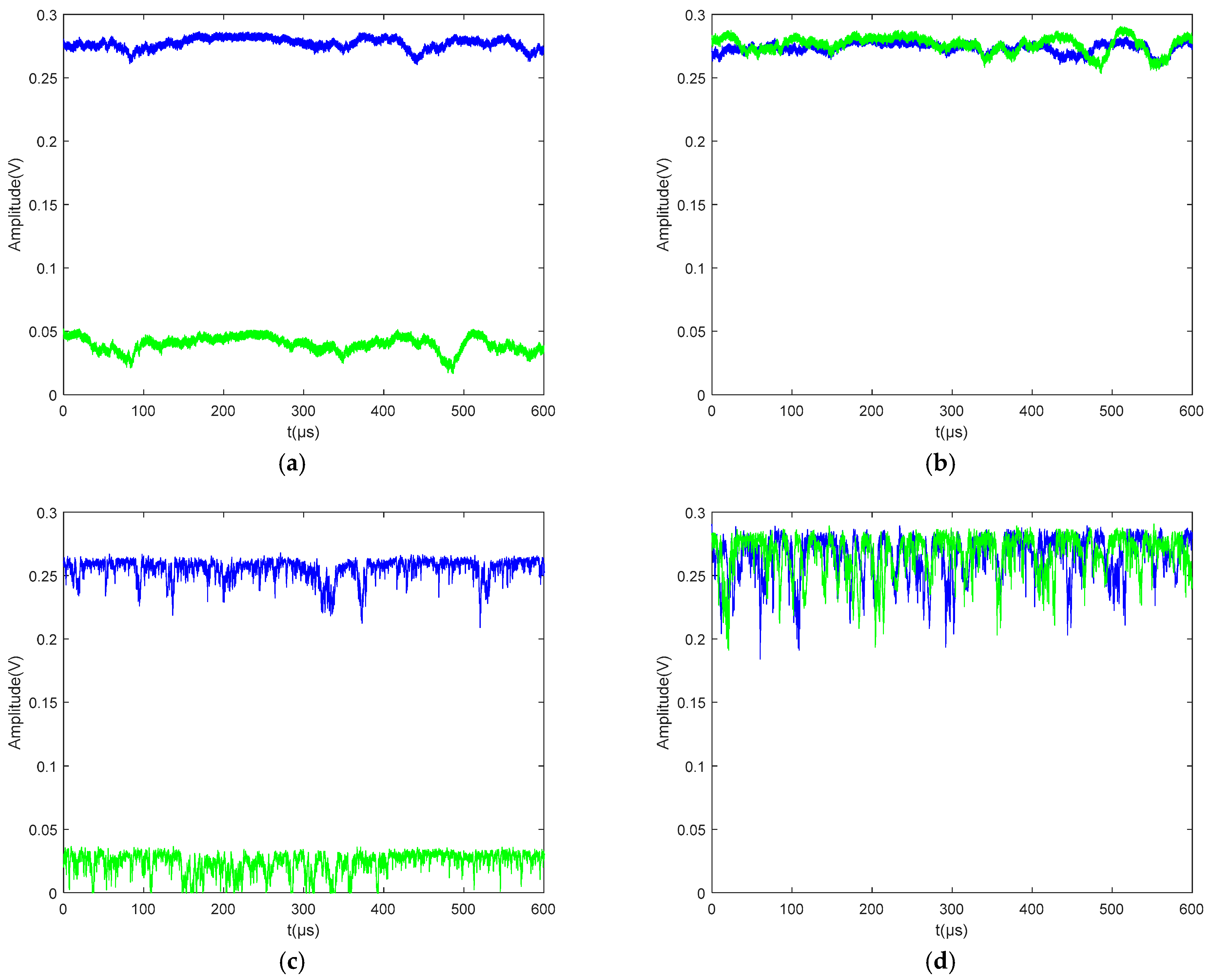
2.5. Phase Control Technology
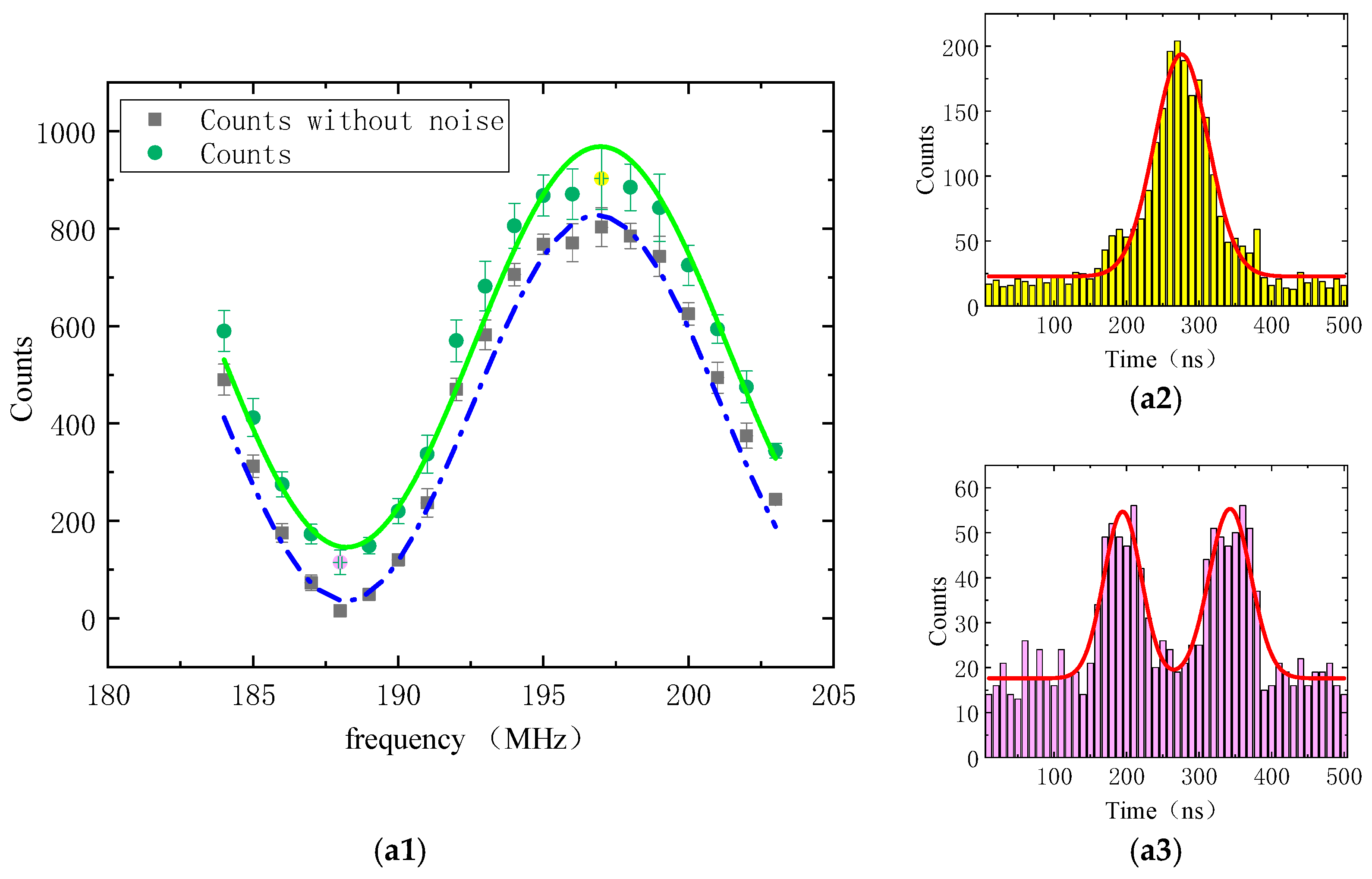
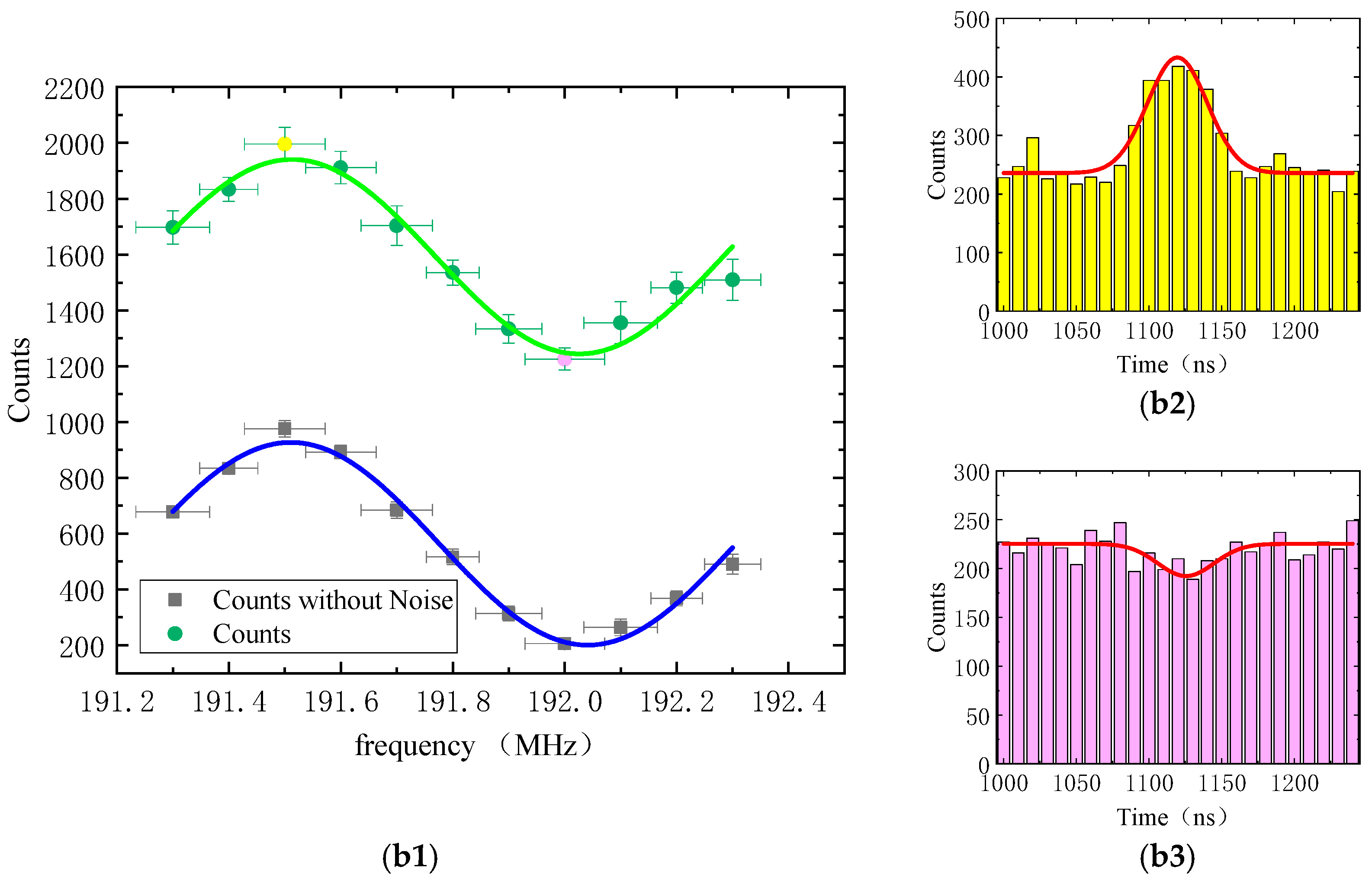
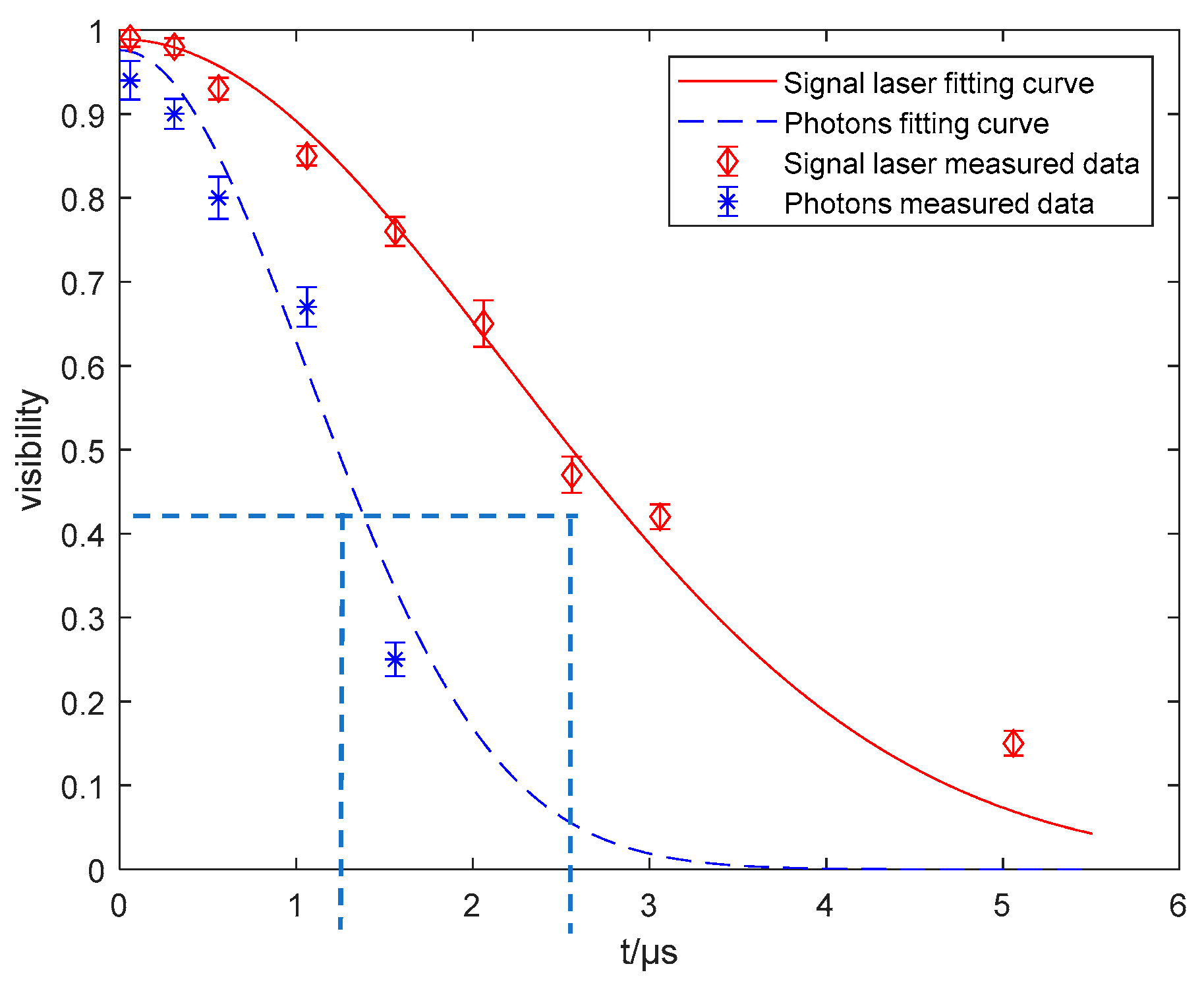
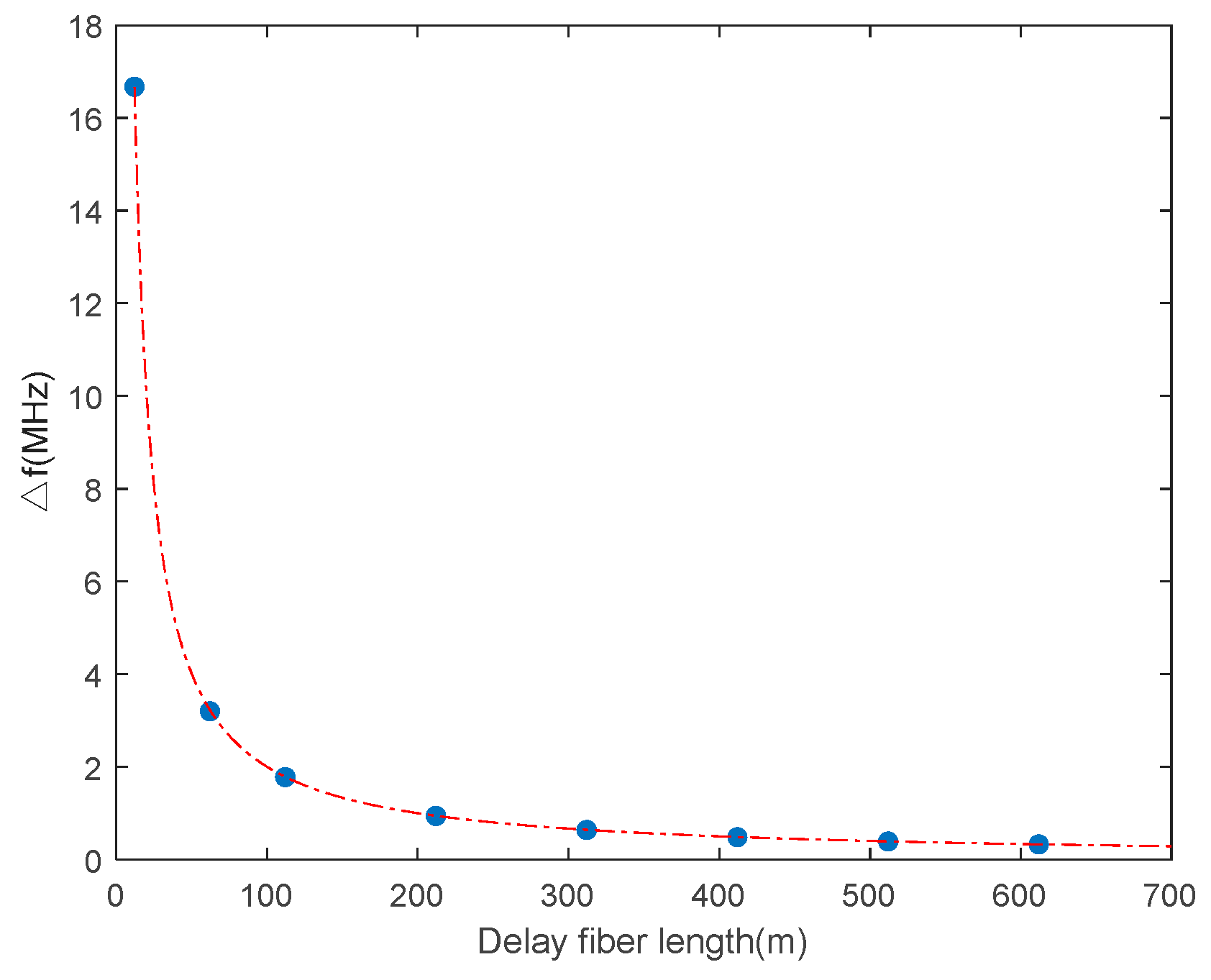
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| OSFS | Optical Spectrum Filter Set |
| FP | Fabry–Perot |
| PBS | Polarizing Beam Splitter |
| FPGA | Field-Programmable Gate Array |
| FC | Fiber Collimator |
| AOM | Acousto-Optic Modulator |
| SMF | Single-Mode Optical Fiber |
| QWP | Quarter-Wave Plate |
| HWP | Half-Wave Plate |
| FST | Fiber Stretcher |
| PC | Polarization Controller |
| AMP | Power Amplifier |
| PID | Proportional-Integral-Derivative Controller |
| SPD | Single-Photon Detector |
| PD | Photodetector |
References
- Jeong, T.; Lee, Y.-S.; Park, J.; Kim, H.; Moon, H.S. Quantum interference between autonomous single-photon sources from Doppler-broadened atomic ensembles. Optica 2017, 4, 1167–1170. [Google Scholar] [CrossRef]
- Park, J.; Kim, H.; Moon, H.S. Two-photon interferences of nondegenerate photon pairs from Doppler-broadened atomic ensemble. Opt. Express 2017, 25, 32064–32073. [Google Scholar] [CrossRef]
- Fulconis, J.; Alibart, O.; O’Brien, J.L.; Wadsworth, W.J.; Rarity, J.G. Nonclassical Interference and Entanglement Generation Using a Photonic Crystal Fiber Pair Photon Source. Phys. Rev. Lett. 2007, 99, 120501. [Google Scholar] [CrossRef] [PubMed]
- Rogers, S.; Mulkey, D.; Lu, X.; Jiang, W.C.; Lin, Q. High Visibility Time-Energy Entangled Photons from a Silicon Nanophotonic Chip. ACS Photonics 2016, 3, 1754–1761. [Google Scholar] [CrossRef]
- Sajeed, S.; Jennewein, T. Observing quantum coherence from photons scattered in free-space. Light Sci. Appl. 2021, 10, 121. [Google Scholar] [CrossRef] [PubMed]
- Srivathsan, B.; Gulati, G.K.; Chng, B.; Maslennikov, G.; Matsukevich, D.; Kurtsiefer, C. Narrow Band Source of Transform-Limited Photon Pairs via Four-Wave Mixing in a Cold Atomic Ensemble. Phys. Rev. Lett. 2013, 111, 123602. [Google Scholar] [CrossRef]
- Shu, C.; Chen, P.; Chow, T.K.; Zhu, L.; Xiao, Y.; Loy, M.M.; Du, S. Subnatural-linewidth biphotons from a Doppler-broadened hot atomic vapour cell. Nat. Commun. 2016, 7, 12783. [Google Scholar] [CrossRef]
- Ding, D.-S.; Zhang, W.; Shi, S.; Zhou, Z.-Y.; Li, Y.; Shi, B.-S.; Guo, G.-C. Hybrid-cascaded generation of tripartite telecom photons using an atomic ensemble and a nonlinear waveguide. Optica 2015, 2, 642–645. [Google Scholar] [CrossRef]
- Qin, X.; Liu, Z.; Shi, H.; Wang, Z.; Guan, X.; Shi, T.; Chen, J. Switchable Faraday laser with frequencies of 85Rb and 87Rb 780 nm transitions using a single isotope 87Rb Faraday atomic filter. Appl. Phys. Lett. 2024, 124, 161104. [Google Scholar] [CrossRef]
- Gu, Z.; Yang, C.; Chen, J.F. Characterization of the photon-number state of a narrow-band single photon generated from a cold atomic cloud. Opt. Commun. 2019, 439, 206–209. [Google Scholar] [CrossRef]
- Jeong, T.; Moon, H.S. Temporal- and spectral-property measurements of narrowband photon pairs from warm double-Λ-type atomic ensemble. Opt. Express 2020, 28, 3985–3994. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Liu, S.; Lee, C.-M.; Michler, P.; Reitzenstein, S.; Srinivasan, K.; Waks, E.; Liu, J. Telecom-band quantum dot technologies for long-distance quantum networks. Nat. Nanotechnol. 2023, 18, 1389–1400. [Google Scholar] [CrossRef]
- Wang, M.; Wang, S.; Xu, Z.; Ma, T.; Li, Y.; Li, S.; Wang, H. Lifetime reductions and read-out oscillations due to imperfect initial level preparations of atoms in a long-lived DLCZ-like quantum memory. Appl. Phys. B 2022, 128, 196. [Google Scholar] [CrossRef]
- Yu, Y.; Ma, F.; Luo, X.Y.; Jing, B.; Sun, P.F.; Fang, R.Z.; Yang, C.W.; Liu, H.; Zheng, M.Y.; Xie, X.P.; et al. Entanglement of two quantum memories via fibres over dozens of kilometres. Nature 2020, 578, 240–245. [Google Scholar] [CrossRef]
- Jin, J.; Grimau Puigibert, M.; Giner, L.; Slater, J.A.; Lamont, M.R.E.; Verma, V.B.; Shaw, M.D.; Marsili, F.; Nam, S.W.; Oblak, D.; et al. Entanglement swapping with quantum-memory-compatible photons. Phys. Rev. A 2015, 92, 12329. [Google Scholar] [CrossRef]
- Jing, B.; Wang, X.-J.; Yu, Y.; Sun, P.-F.; Jiang, Y.; Yang, S.-J.; Jiang, W.-H.; Luo, X.-Y.; Zhang, J.; Jiang, X.; et al. Entanglement of three quantum memories via interference of three single photons. Nat. Photonics 2019, 13, 210–213. [Google Scholar] [CrossRef]
- Zhong, H.-S.; Wang, H.; Deng, Y.-H.; Chen, M.-C.; Peng, L.-C.; Luo, Y.-H.; Qin, J.; Wu, D.; Ding, X.; Hu, P.; et al. Quantum computational advantage using photons. Science 2020, 370, 1460–1463. [Google Scholar] [CrossRef]
- Simon, C.; de Riedmatten, H.; Afzelius, M. Temporally multiplexed quantum repeaters with atomic gases. Phys. Rev. A 2010, 82, 010304. [Google Scholar] [CrossRef]
- Zhao, L.; Guo, X.; Liu, C.; Sun, Y.; Loy, M.M.T.; Du, S. Photon pairs with coherence time exceeding 1 μs. Optica 2014, 1, 84–88. [Google Scholar] [CrossRef]
- Almendros, M.; Huwer, J.; Piro, N.; Rohde, F.; Schuck, C.; Hennrich, M.; Dubin, F.; Eschner, J. Bandwidth-tunable single-photon source in an ion-trap quantum network. Phys. Rev. Lett. 2009, 103, 213601. [Google Scholar] [CrossRef]
- Farrera, P.; Heinze, G.; Albrecht, B.; Ho, M.; Chavez, M.; Teo, C.; Sangouard, N.; de Riedmatten, H. Generation of single photons with highly tunable wave shape from a cold atomic ensemble. Nat. Commun. 2016, 7, 13556. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wen, Y.; Wang, S.; Liu, C.; Liu, H.; Wang, M.; Sun, C.; Gao, Y.; Li, S.; Wang, H. Generation of entanglement between a highly wave-packet-tunable photon and a spin-wave memory in cold atoms. Opt. Express 2022, 30, 2792–2802. [Google Scholar] [CrossRef]
- Maring, N.; Farrera, P.; Kutluer, K.; Mazzera, M.; Heinze, G.; de Riedmatten, H. Photonic quantum state transfer between a cold atomic gas and a crystal. Nature 2017, 551, 485–488. [Google Scholar] [CrossRef] [PubMed]
- Jelezko, F.; Volkmer, A.; Popa, I.; Rebane, K.K.; Wrachtrup, J. Coherence length of photons from a single quantum system. Phys. Rev. A 2003, 67, 041802. [Google Scholar] [CrossRef]
- Qian, P.; Gu, Z.; Cao, R.; Wen, R.; Ou, Z.Y.; Chen, J.F.; Zhang, W. Temporal Purity and Quantum Interference of Single Photons from Two Independent Cold Atomic Ensembles. Phys. Rev. Lett. 2016, 117, 013602. [Google Scholar] [CrossRef] [PubMed]
- Cho, S.-B.; Noh, T.-G. Stabilization of a long-armed fiber-optic singlephoton interferometer. Opt. Express 2009, 17, 19027–19032. [Google Scholar] [CrossRef]
- Li, C.-L.; Bao, X.-H.; Yin, J.-P.; Jin, R.-B.; Jiang, Y.-F.; Zhang, Q.; Peng, K.; Pan, J.-W. Asynchronous quantum repeater using multiple quantum memory. Rep. Prog. Phys. 2024, 87, 127901. [Google Scholar] [CrossRef]
- Jing, X.; Qian, C.; Weng, C.X.; Li, B.H.; Chen, Z.; Wang, C.Q.; Tang, J.; Gu, X.W.; Kong, Y.C.; Chen, T.S.; et al. Experimental quantum Byzantine agreement on a three-user quantum network with integrated photonics. Sci. Adv. 2024, 10, eadp2877. [Google Scholar] [CrossRef]
- Xie, Y.-M.; Lu, Y.-S.; Weng, C.-X.; Cao, X.-Y.; Jia, Z.-Y.; Bao, Y.; Wang, Y.; Fu, Y.; Yin, H.-L.; Chen, Z.-B. Breaking the Rate-Loss Bound of Quantum Key Distribution with Asynchronous Two-Photon Interference. PRX Quantum 2022, 3, 020315. [Google Scholar] [CrossRef]
- Wang, F.-X.; Lu, Q.-H.; Chen, W.; Wang, S.; Fu, H.; Lu, Y.; Hao, P.; Chen, J.-L.; Ding, W.; Ma, J.; et al. Hybrid High-Dimensional Quantum Key Distribution for a Composable Quantum Network. Phys. Rev. Appl. 2023, 19, 054060. [Google Scholar] [CrossRef]
- Minář, J.; de Riedmatten, H.; Simon, C.; Zbinden, H.; Gisin, N. Phase-noise measurements in long-fiber interferometers for quantum-repeater applications. Phys. Rev. A 2008, 77, 052325. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, W.; Wu, Q.; Chen, Y.; Sun, C.; Wang, H.; Qiao, W. Measurement of Coherence Time in Cold Atom-Generated Tunable Photon Wave Packets Using an Unbalanced Fiber Interferometer. Photonics 2025, 12, 415. https://doi.org/10.3390/photonics12050415
Li Y, Wang W, Wu Q, Chen Y, Sun C, Wang H, Qiao W. Measurement of Coherence Time in Cold Atom-Generated Tunable Photon Wave Packets Using an Unbalanced Fiber Interferometer. Photonics. 2025; 12(5):415. https://doi.org/10.3390/photonics12050415
Chicago/Turabian StyleLi, Ya, Wanru Wang, Qizhou Wu, Youxing Chen, Can Sun, Hai Wang, and Weizhe Qiao. 2025. "Measurement of Coherence Time in Cold Atom-Generated Tunable Photon Wave Packets Using an Unbalanced Fiber Interferometer" Photonics 12, no. 5: 415. https://doi.org/10.3390/photonics12050415
APA StyleLi, Y., Wang, W., Wu, Q., Chen, Y., Sun, C., Wang, H., & Qiao, W. (2025). Measurement of Coherence Time in Cold Atom-Generated Tunable Photon Wave Packets Using an Unbalanced Fiber Interferometer. Photonics, 12(5), 415. https://doi.org/10.3390/photonics12050415




