1. Introduction
As the core means of resource exploration and environmental protection [
1,
2], seismic wave exploration technology can accurately identify key geological elements such as lithologic interface, fault structure, and fold shape by analyzing the coupling response characteristics of elastic wave field and geological medium and provide quantitative geophysical parameters such as wave impedance inversion and seismic data quantitative interpretation technology for mineral resource assessment [
3,
4,
5,
6]. Through travel time tomography and a full waveform inversion algorithm [
7], this technology can build a three-dimensional velocity structure model and realize the three-dimensional characterization of oil and gas storage spatial distribution and physical parameters [
8]. However, the traditional seismic exploration has significant exploration blind areas in high altitude no man’s land and complex structural zones. At present, it is urgent to develop the aerial seismic wave laser remote sensing system to achieve large-scale, high-resolution seismic field aerial monitoring.
In recent years, seismic wave laser remote sensing technology has rapidly developed, using high-resolution [
9], non-contact laser measurements to accurately analyze seismic waveforms, identify geological structures [
10,
11], and evaluate the distribution of minerals, oil, and natural gas [
12,
13]. Compared to traditional methods, this technology can detect weak vibrations from a distance [
14,
15], breaking through the limitations of complex terrain and deep exploration. Combining remote sensing [
16], GIS [
17], and satellite data [
18], laser remote sensing has improved exploration efficiency and accuracy, identified resource potential areas at lower costs, and promoted deep geological research and energy development.
Laser remote sensing detection technology has the advantages of non-contact measurement, fewer restrictions, higher efficiency and long-distance detection, and is widely used in object vibration detection. In order to meet the challenges of long-range laser echo signal attenuation and vibration waveform analysis, researchers have explored the use of the He-Ne laser interferometer [
19] and Michelson interferometer [
20] to measure vibration signals. However, these technologies depend on the complex optical system and the setting of the reference arm and the measurement arm, which has certain limitations. Therefore, Silvio Bianchi [
21] proposed a new method without using an interferometer to sense the surface vibration signal by using the speckle pattern formed after laser irradiating the rough surface. This method can effectively detect the vibration signal within a distance of several hundred meters. There are many methods to detect ground vibration signal based on phase, such as wavefront sensor [
22,
23,
24], shear interference [
25,
26], and so on. Jorge ares et al. [
27] used the Shack–Hartmann wavefront sensor as a position sensing device to accurately determine the position of a point or moderately extended plane object.
Compared to traditional seismic wave laser remote sensing technology, wavefront sensors have significant advantages in detecting ground vibrations. Firstly, it eliminates the need for reference arms and measurement arms, making the device more compact and easy to deploy. Secondly, by measuring the phase change of the wavefront, precise mechanical vibration information can be obtained. In addition, wavefront sensors have array detection capabilities, which improve detection accuracy and application range. In 2023, researchers constructed a seismic wave laser remote sensing system based on wavefront sensors [
28] and successfully detected ground vibration signals [
29]. However, existing methods mainly collect single point vibration information, which makes it difficult to process regional vibration signals and has limited detection efficiency. Therefore, based on the research in reference [
28], this article proposes a region vibration detection method based on laser plane scanning, utilizing the array detection characteristics of wavefront sensors, to achieve high-precision and high-resolution vibration measurement.
2. Vibration Signal Laser Plane Scanning Detection System and Its Operational Mechanism
When an earthquake occurs, longitudinal waves cause vertical ground vibrations, which, in turn, change the wavefront of the incident light, causing the backscattered light of the laser to carry the characteristic information of seismic waves. In wavefront measurement systems, laser irradiates the target area in a vertical or oblique manner, and the small fluctuations on the measured surface cause light scattering and reflection. Subsequently, the micro lens array converges and images these reflected or scattered light, and extracts vibration information through wavefront reconstruction to achieve accurate measurement of seismic wave characteristics.
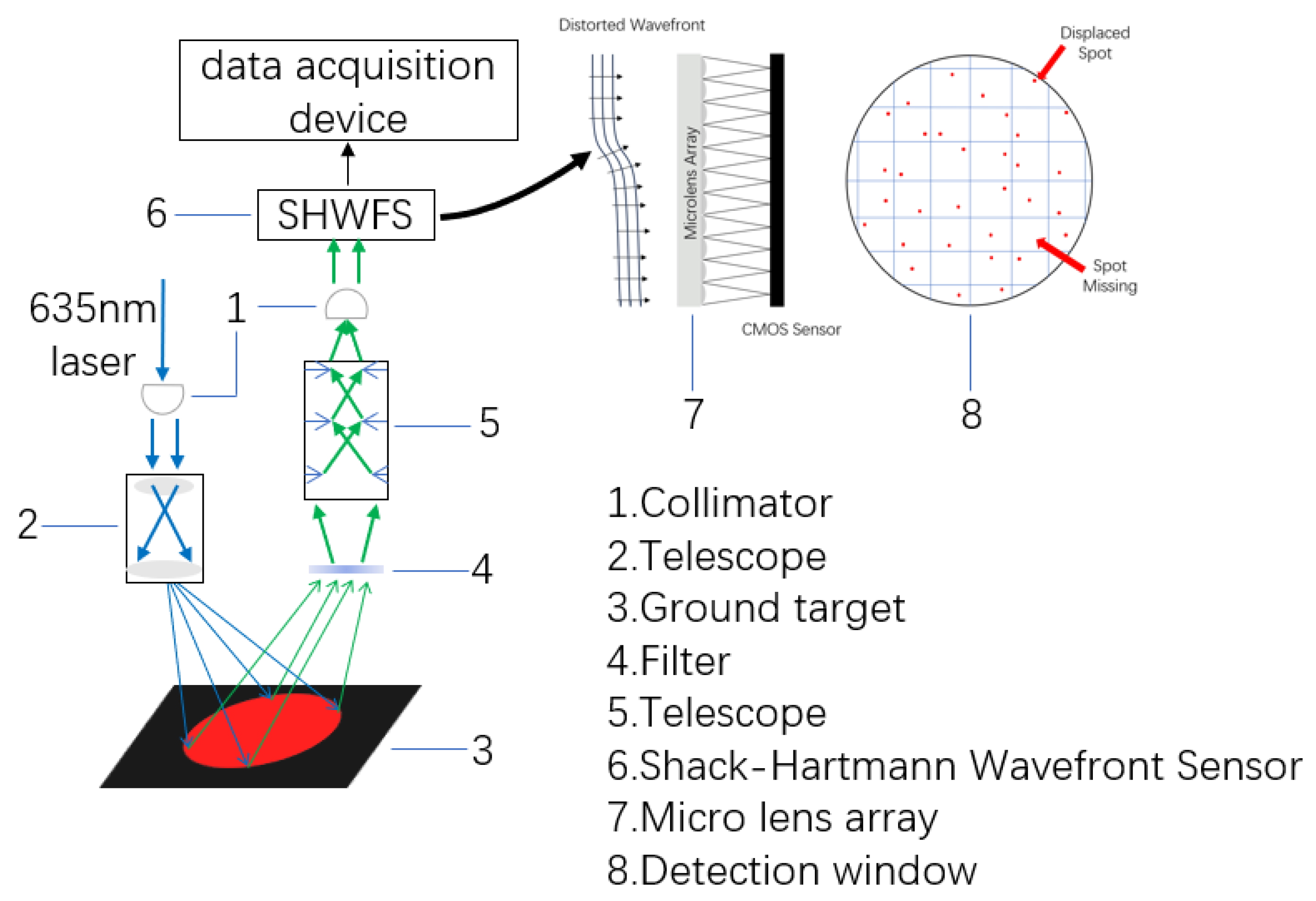
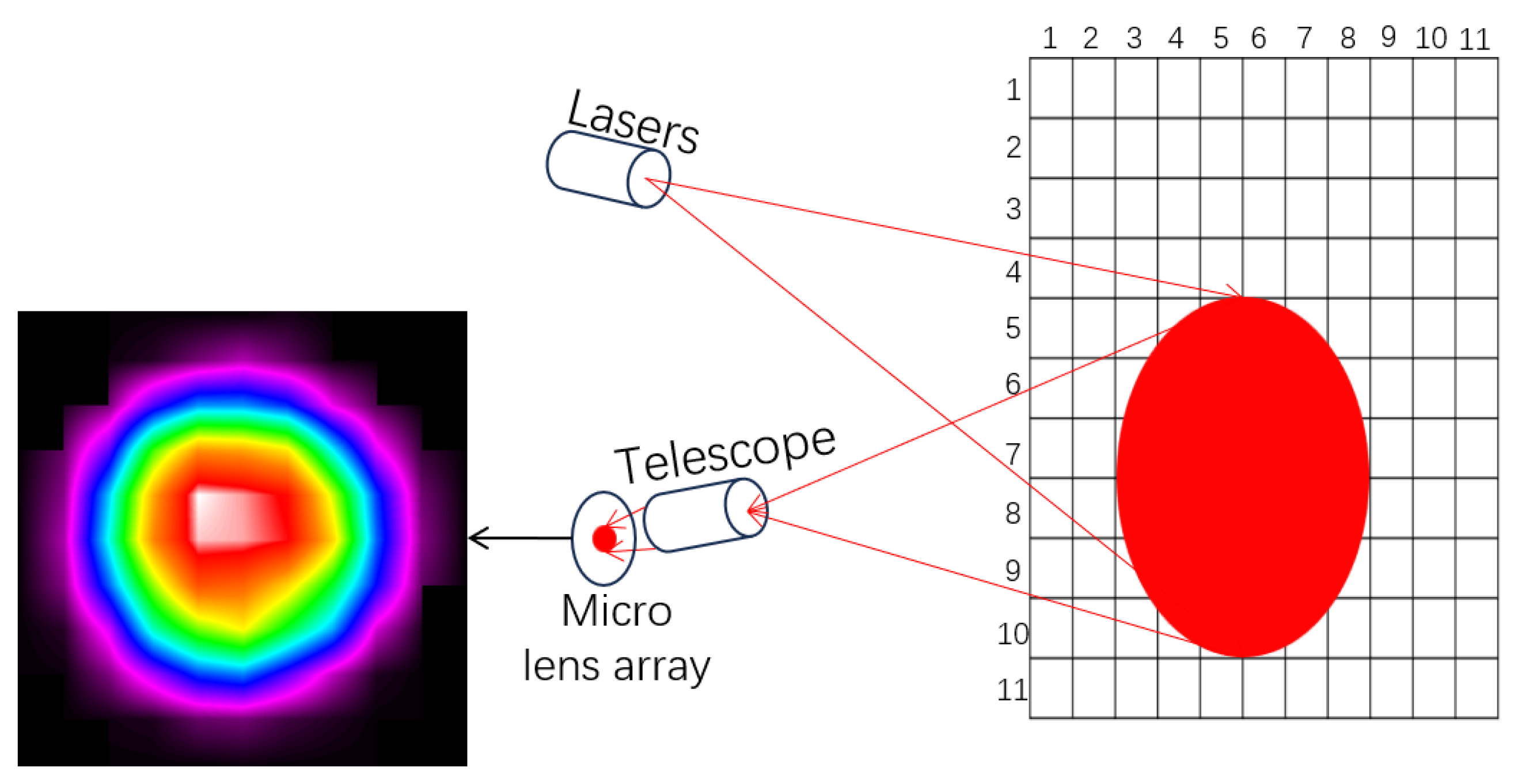
This article proposes a vibration signal remote sensing detection system based on planar scanning that consists of a transmitting end and a receiving end, as shown in
Figure 1. The transmitting end includes a laser, collimator 1, and telescope 2. The system uses a gradient refractive index fiber collimator to emit a laser beam with a divergence angle of 0.25°, and its oxide glass material collimating lens achieves collimated output with a beam quality factor M
2 < 1.1 through a 0.15 numerical aperture. The laser emits a continuous laser with a wavelength of 635 nm and is collimated by a tail fiber type fiber collimator 1 (equipped with a gradient refractive index GRIN lens) to ensure stable illumination of the target area 3. The receiving end consists of telescope 5, filter 4, and wavefront sensor 6. This is a bandpass filter that can filter out 97% of stray light within the wavelength range of 624–750 nm. The telescope is responsible for collecting reflected and scattered light from target area 3, while filter 4 is used to remove stray light from the environment to improve the utilization of echo signals. Subsequently, the light passing through the filter is incident on the wavefront sensor 6, which is composed of a micro lens array 7 and can accurately detect wavefront distortion in the optical system. The micro lens array divides the incident light spot into multiple sub apertures and focuses the imaging onto the light spot detection window 8 in the array. The system extracts vibration information by measuring the offset of the light spot and uses laser remote sensing technology to detect micro vibrations in the target area. We study the relationship between the phase information of the target vibration and the offset of the received light spot on the CMOS sensor. When the target object 3 vibrates, the displacement
of the center of mass of the light spot recorded by the wavefront sensor carries vibration information
. According to reference [
28], the relationship between the two satisfies the equation
, where
is the proportionality coefficient.
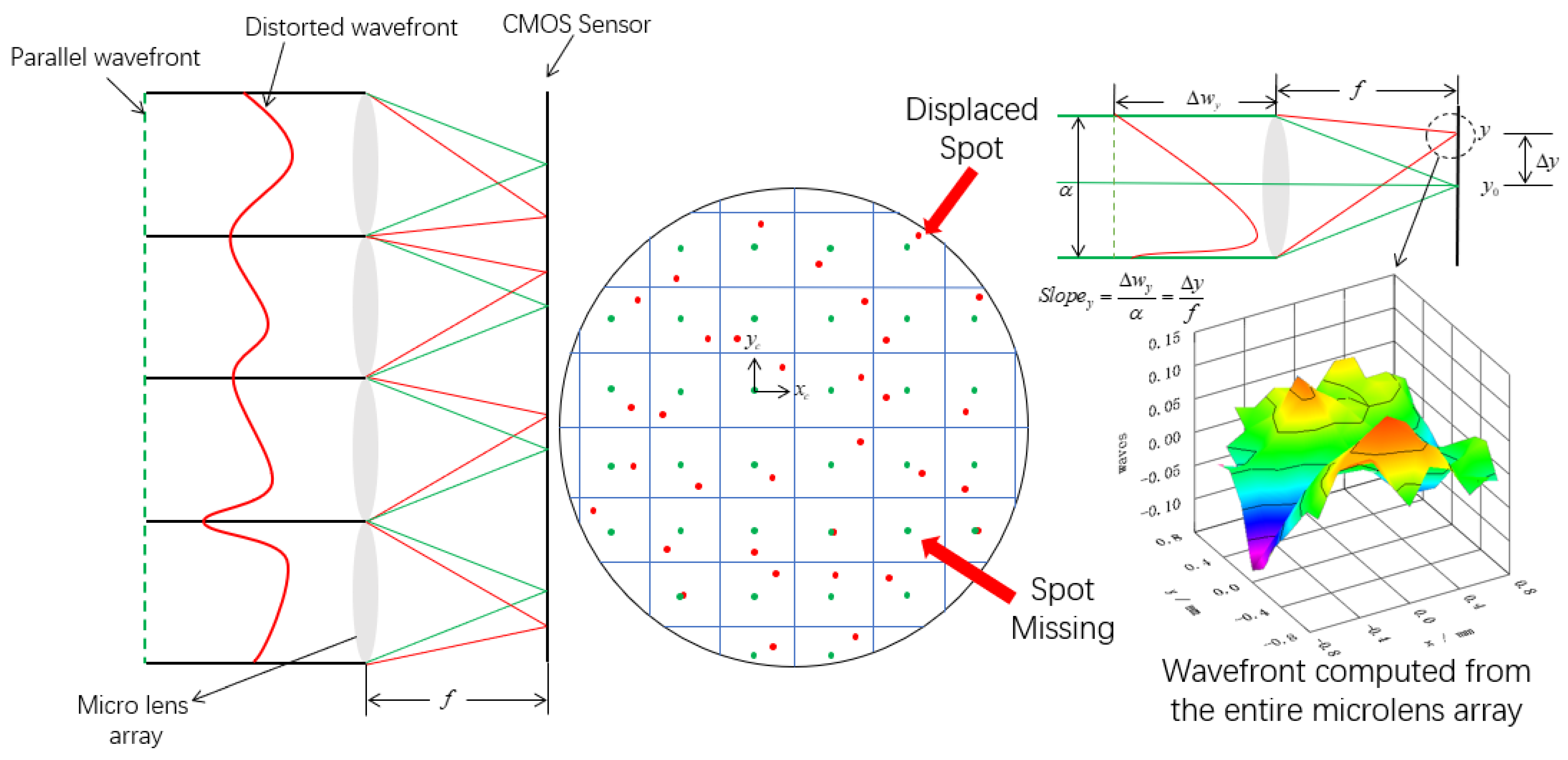
Figure 2 shows the changes in wavefront during the vibration process. In
Figure 2, we simplify the analysis by assuming the ground is flat when not vibrating. This assumption is made to illustrate the basic relationship between the transmitted and reflected wavefronts. In reality, uneven ground may combine with other non-ideal factors to influence the wavefront’s shape.
In an ideal situation, when a parallel wavefront is irradiated onto a micro lens array, each micro lens will focus the incident light, forming a uniformly distributed light spot, and the centroid position of these light spots should be located at the predetermined center position. Therefore, the distribution of light spots formed by the micro lens array is regular and symmetrical, with each light spot representing a local area of the wavefront, reflecting the degree of wavefront tilt in that area. However, when the wavefront undergoes distortion, the incident light no longer maintains a parallel state, and local areas of the wavefront become tilted or deformed. At this point, the micro lens array will convert these wavefront changes into corresponding spot offsets. The difference between the centroid shift of the light spot caused by distorted wavefront and the ideal position can be used to quantify the degree of wavefront distortion, as shown in
Figure 3.
4. Experimental and Result Analysis of the Vibration Signal Laser Plane Scanning Detection System
We use a laser with a wavelength of 635 nm and an output power of 120 mW at a distance of 5 m. In order to reduce the interference of ambient light and increase the reception effect of the laser echo signal of the wavefront sensor, we choose to carry out the experiment at night. The temperature of the laboratory is 14 ℃, the humidity is 23%, and the change in the surrounding environment is very small.
Figure 7 shows the sensor used for research, and
Table 1 shows the detailed parameters of this model of sensor. The sensor has high sampling rate and automatic shutter control function, which can adapt to different optical power inputs, and its sensitivity is significantly affected by wavelength, making it suitable for detecting ground vibration signals. In the single point detection experiment, we used a controllable vibration table to simulate longitudinal wave characteristics by adjusting frequency and amplitude,
Figure 8a shows a diagram of a controllable vibration table; In the surface scanning experiment, a vibration motor is used as the vibration source, and the interference of the vibration source is isolated by a soft white cloth.
Figure 8b shows a diagram of vibration motor. The laser irradiates the surface of the vibration source, and the wavefront sensor receives the reflected echo light and extracts vibration information. To monitor the wavefront changes of the wavefront sensor in real time, we use Wavefront Sensor software to record the wavefront dynamics and use LabView software to calculate and display the changes in individual microlenses in order to deeply analyze the response of the wavefront when excited by the vibration source. The specific program flow is detailed in
Appendix A. The system configuration and data recording method ensure accurate monitoring and analysis of small wavefront changes caused by vibration sources.
Figure 9a shows the deviation in wavefront slope in the horizontal and vertical directions when the vibration source vibrates. When longitudinal waves are detected, the deviation in the y direction is larger, while the deviation in the x direction is smaller. Meanwhile,
Figure 9b shows the vibration signal recorded using a vibrometer.
When testing the light spot received by a single microlens, the laser echo signal is focused onto a certain microlens in the microlens array through a telescope. In the beam view mode of the wavefront sensor, in addition to the target microlens, several adjacent microlenses around it will also display weak spot signals, as illustrated in
Figure 10. This indicates that the relationship between laser echo signals and microlens arrays is not simply “one-to-one” but presents more complex “one to many” characteristics.
We tested the attenuation of laser power, and this effect usually shows a certain pattern. We used a 635 nm continuous laser to irradiate the target area separately and measured the laser power using an optical power meter, as shown in
Table 2. The test results indicate that the laser power shows an exponential decay trend with increasing irradiation distance.
Table 2 is only applicable for small-scale laboratory testing. When the receiving end is a wavefront sensor, the attenuation of laser power will significantly affect the accuracy of surface scanning detection, which is reflected in the reduction in signal amplitude, which leads to the reduction in the contrast and signal-to-noise ratio of the wavefront speckle pattern received by the detector, resulting in the inaccurate estimation of speckle location error and wavefront gradient and further causing the accumulation of wavefront reconstruction error; especially when the sub aperture signal is too weak or missing, local wavefront information will be missing or distorted. In addition, the nonuniformity of energy attenuation in spatial distribution will also destroy the spatial response consistency of the system, which will reduce the geometric reconstruction accuracy of the whole surface scanning, especially in the long distance, edge area or weak reflection surface.
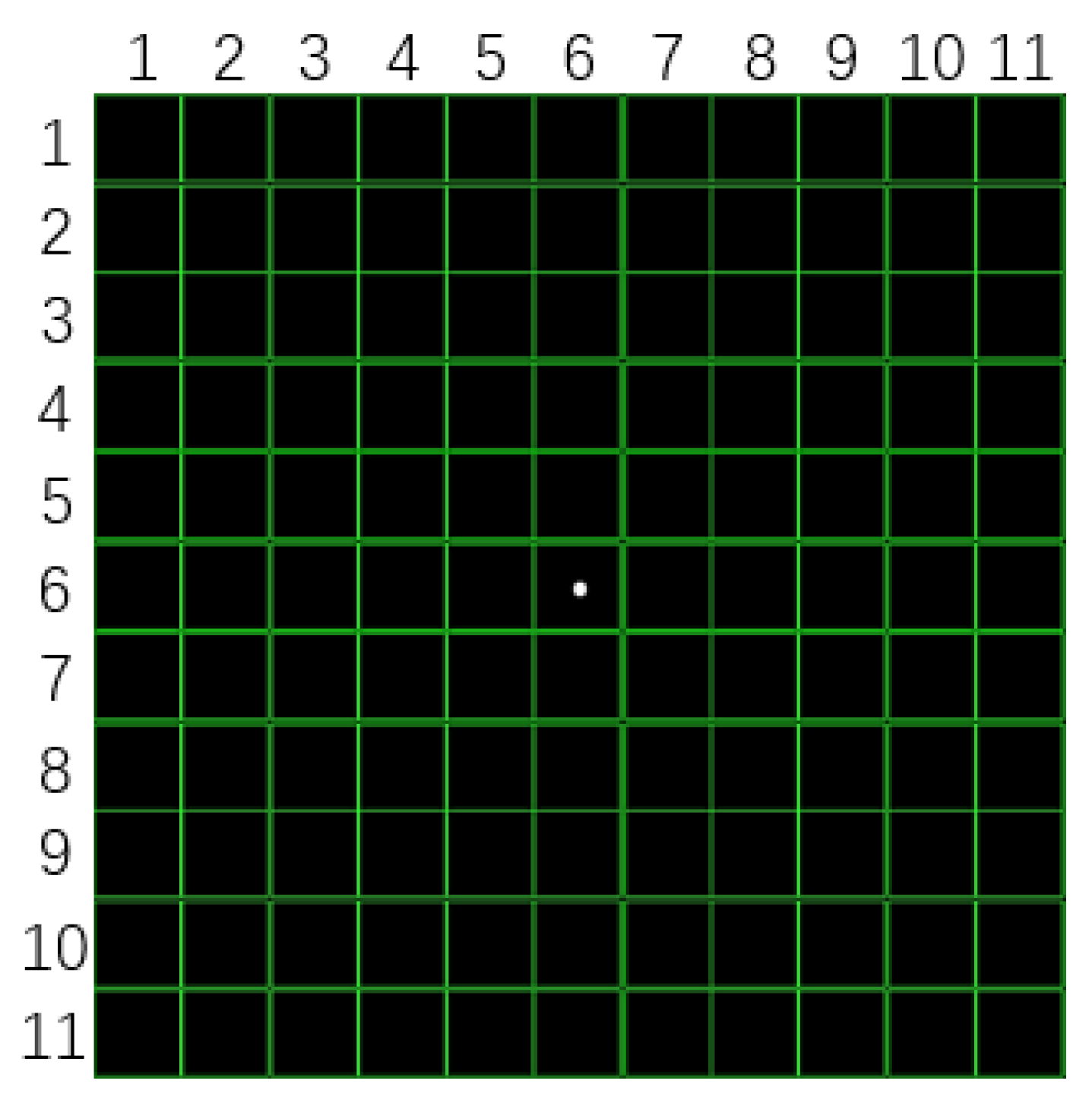
We mark the
microlenses of the wavefront sensor as 1 × 1 coordinates from the upper left corner, as shown in
Figure 11. The laser forms a spot surface on the shaking table, and the echo signal is focused on the microlens with the coordinates of
of the wavefront sensor through the telescope. The wavefront slope and wavefront images of the microlens with coordinates of
and adjacent microlenses were obtained by using LabVIEW software, and the corresponding wavefront images were reconstructed by using the region method. As shown in
Figure 12, with the increase in vibration amplitude, the degree of wavefront distortion increases accordingly, and the microlens around the microlens with coordinates of
is also slightly disturbed. Changes in amplitude and wavefront phase are shown in
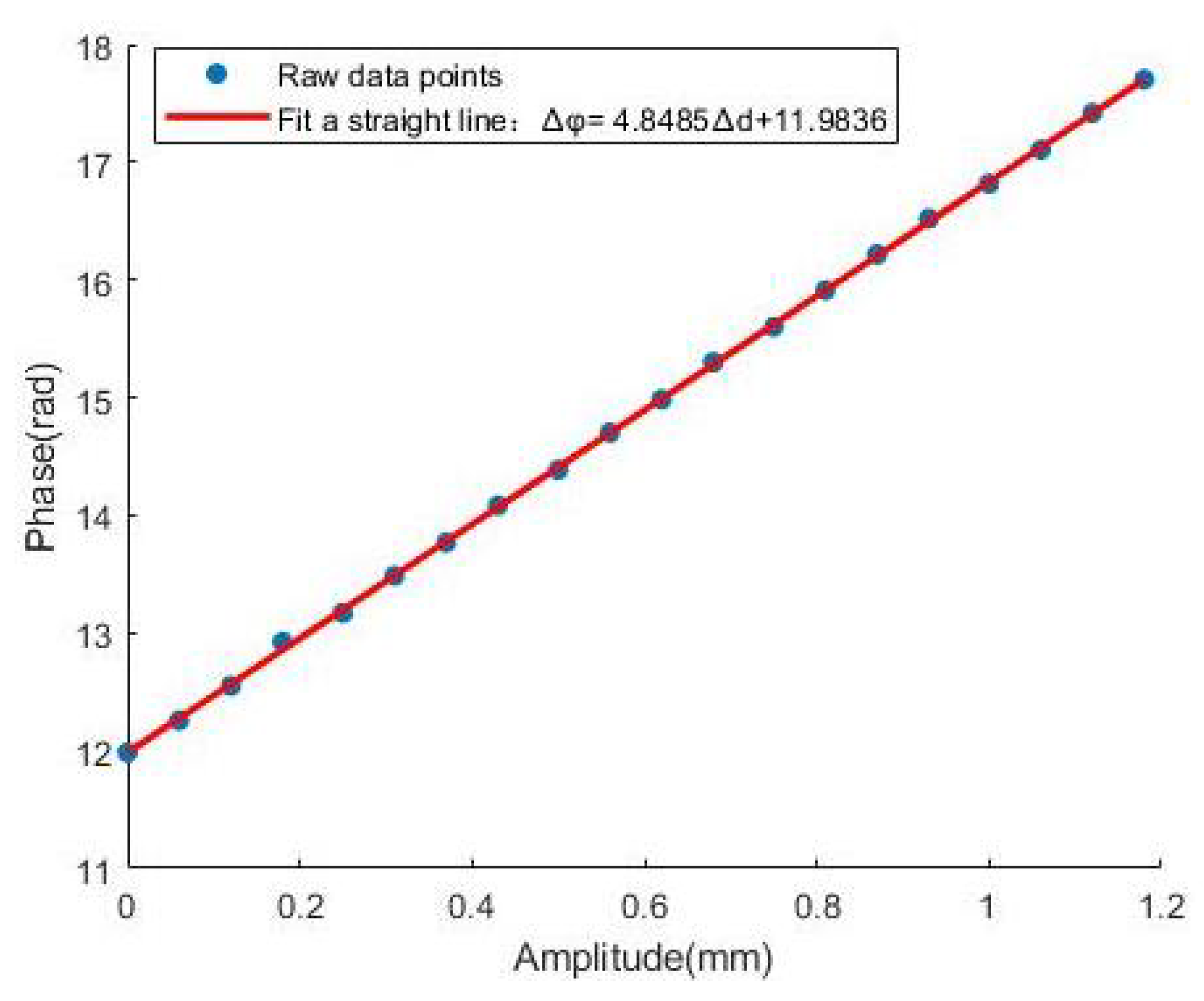
Appendix B. When there are vibration signals with different amplitudes in a certain area, the laser echo signal will carry the vibration information of the area. By receiving these laser echo signals, the wavefront sensor obtains and analyzes the corresponding vibration information. By analyzing the wavefront phase changes under different amplitudes, the relationship between amplitude and phase can be revealed, as shown in
Figure 13. The wavefront phase shifts with the change in amplitude, which makes it possible to deduce the variation law of amplitude by measuring the phase change, as shown in the following formula:
Based on the above experiment, we divided a 1.2 m × 1.2 m target object into
sub regions, starting from the upper left corner, with the first region marked as
coordinate, and established an array in order. We randomly arranged multiple vibration sources within the
sub regions of the target object. We perform planar scanning on each subregion to obtain the corresponding changes in the wavefront slope of the microlens, as seen in
Figure 14. A one meter diameter light spot is formed on the target area, and the laser echo signal is focused onto a microlens array through a telescope. Thirty-two microlenses in the microlens array receive the signal. In the target area, there are 4 sub areas with very small spot signals that cannot cover most of their area. Therefore, there are 4 microlenses in the microlens array that have no signal. We extract the changes in wavefront slope during the vibration of 32 microlenses and reconstruct the corresponding wavefront phase changes for each subregion. We calculate the corresponding vibration amplitude based on the wavefront phase changes in each subregion.Therefore, only one system is needed to obtain vibration information of multiple sub regions within the target area.
Figure 15 shows the physical device of the object and the 1 m light spot formed in the target area. The field of view of the telescope is
–
, and the distance between the telescope and the spot is 5 m. Therefore, the 100 cm spot size is fully within the field of view of the telescope. During the detection process, we first use pan-tilt 1 to project the collimated laser onto the target area. Then, we use a clamp to fix telescope 1 and manually adjust its objective lens and eyepiece to adjust the spot area on the target area. Then, we use pan-tilt 2 to adjust the receiving angle of telescope 2 and further adjust the objective lens and eyepiece of telescope 2 to ensure the best receiving effect. Subsequently, through the high-speed sampling interface of the wavefront sensor, we manually adjust the position of the wavefront sensor so that the laser echo signal can be accurately focused on the corresponding lens in the wavefront sensor microlens array, thereby achieving vibration signal point scanning detection. The spatial resolution of the system in
Figure 15a is 146
μm.
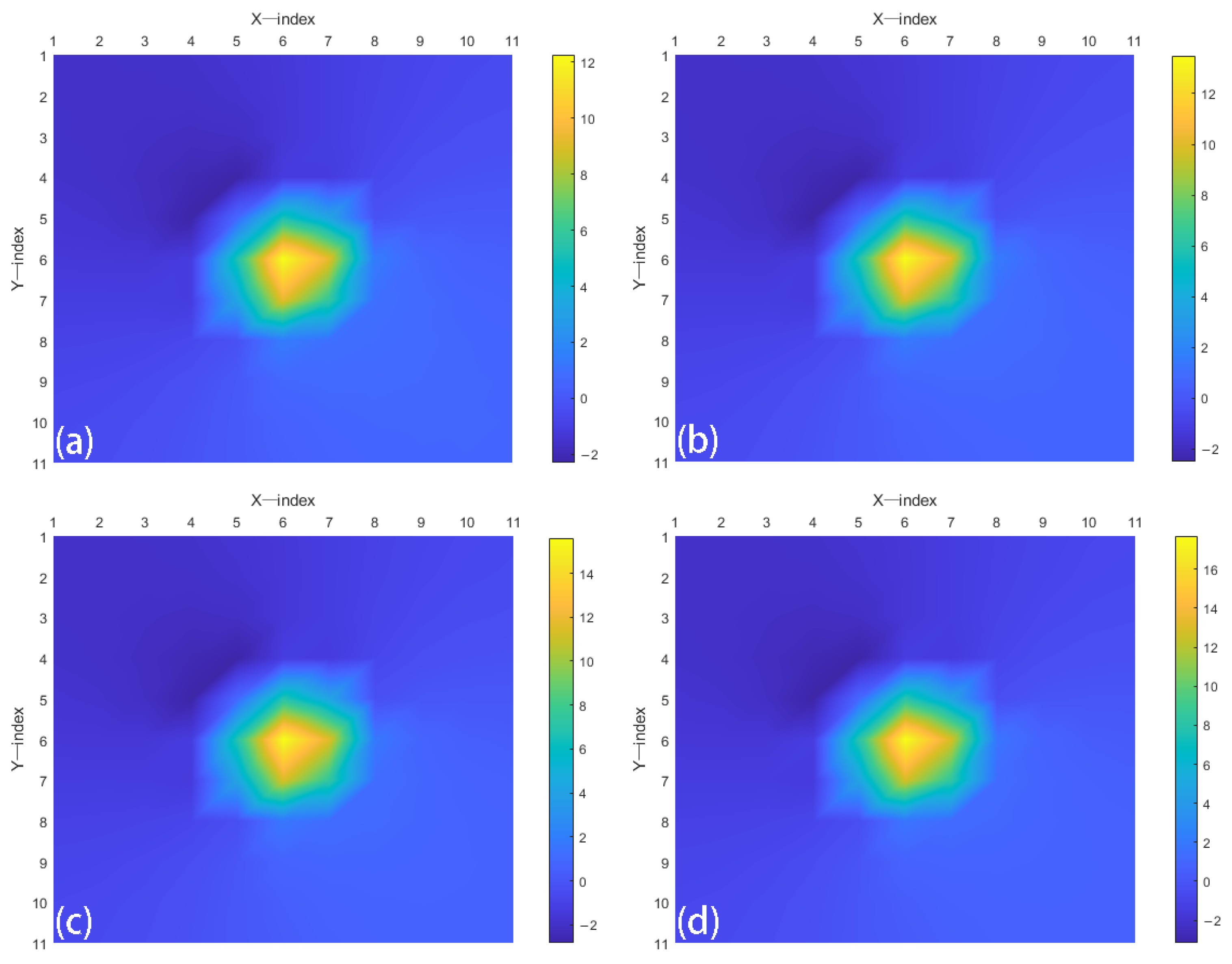
We divide the 1.2 m × 1.2 m target area into 11 × 11 sub areas; divide the target area into four areas, each including 36 sub areas of the target area; and place vibration sources within the 36 sub areas. Using a telescope, a laser beam is directed onto the target object to form a spot with a diameter of 60 cm, while detecting 36 sub regions within the target area. However, due to the shape of the spot, only 32 subregions can actually be detected. The laser echo signal is focused by a telescope and forms a spot surface on the microlens array of the wavefront sensor. In the high-speed sampling mode of the wavefront sensor, the 32 microlenses of the microlens array received laser echo signals within the target area, as shown in
Figure 16. Subsequently, the LabView software was used to accurately locate the microlenses in the array that correspond to the target subregion, thereby obtaining the wavefront slope changes in the corresponding microlenses and calculating the corresponding wavefront phase. As shown in
Figure 16, due to the inconsistent vibration amplitudes in the 32 sub regions of the target area, the wavefront slope of each sub region in the 32 sub regions is different.
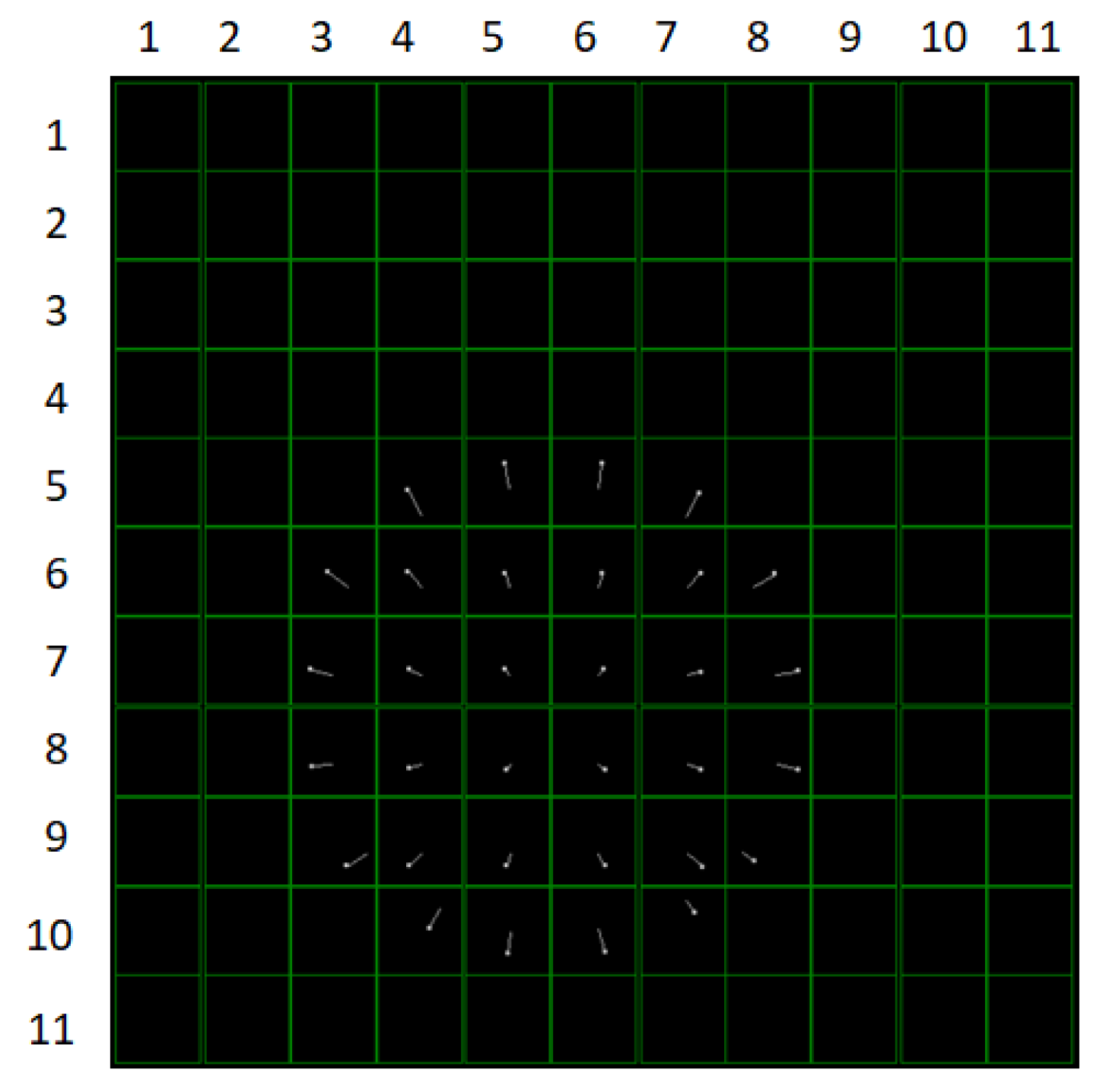
We sample a region multiple times. We selected 8 microlens spot centroid changes from
Figure 16, as shown in
Figure 17.
Figure 17 shows the centroid displacement of the light spot in eight sub regions of the target area. The vibration amplitudes of different subregions in the target area are inconsistent, and the vibration amplitudes displayed on the microlens array of the wavefront sensor are also inconsistent. Due to the use of a vibration motor, the orientation of the echo laser received by the wavefront sensor will undergo a slight change, and the center of mass of the illuminated spot will continue to move. As shown in
Table 3, the offset of the center of mass of each microlens in the microlens array is different due to the inconsistent amplitude of the target subregion.
According to the detection in the vicinity of
Figure 16, the target area of 1.2 m × 1.2 m is partitioned into 11 × 11 sub-regions, placing all sub areas in the target area with vibration sources. The whole target area is divided into a 4 × 4 area, and each area is detected by plane scanning. Utilizing a telescope, the laser beam creates a spot with a diameter of 60 cm on the target area, concurrently identifying the 32 sub-regions within that area. The telescope concentrates the laser echo signal, creating a light spot on the microlens array of the wavefront sensor. Thereafter, the microlens associated with the designated sub-region in the microlens array is accurately identified using LabView software, facilitating the acquisition of the wavefront slope variation of the respective microlens and the computation of the related wavefront phase, as illustrated in
Figure 18.
Figure 18 illustrates that variations in the magnitude of the vibration source correspondingly alter the wavefront phase. This signifies that the vibration signal laser planar scanning detection system can efficiently identify the vibrational states of several small locations inside the designated zone. The calculated vibration amplitude via phase changes exhibits a relative inaccuracy of
to
compared to the amplitude recorded by the vibration meter, as illustrated in
Figure 19.
In order to improve scanning efficiency, we further expanded the spot area. Similarly, a circular spot with a diameter of 1 m can only cover 69 sub areas of the target area. The 1.2 m × 1.2 m target area is divided into 11 × 11 sub areas, and 69 sub areas are selected to place vibration sources. The laser beam uses a telescope to form a spot with a diameter of 1 m on the target area and covers 69 sub areas in the target area. The laser echo signal is focused on the microlens array through the telescope, and 69 microlenses on the microlens array receive the signal, as shown in
Figure 20. We use LabVIEW software to obtain the wavefront slope of 69 microlenses and calculate the wavefront phase change of each microlens so as to obtain the amplitude of the corresponding sub region in the target region. At present, the detection of a 1.2 m × 1.2 m target area is only achieved in a relatively stable laboratory environment. Due to the lack of high-power lasers and telescopes with large viewing angles, it is temporarily impossible to achieve large-scale scanning.
The telescope concentrates the laser echo signal, creating a light spot on the microlens array of the wavefront sensor. LabView software is used to precisely identify the microlens associated with the designated sub-area and acquire the phase variation of the vibrating wavefront through the alterations in wavefront slope induced by vibration. This enables the prediction of amplitude values based on the phase change.
Figure 21 illustrates the outcomes of identifying a region with three vibration sources utilizing a 69 microlens, exhibiting a relative inaccuracy of
to
.
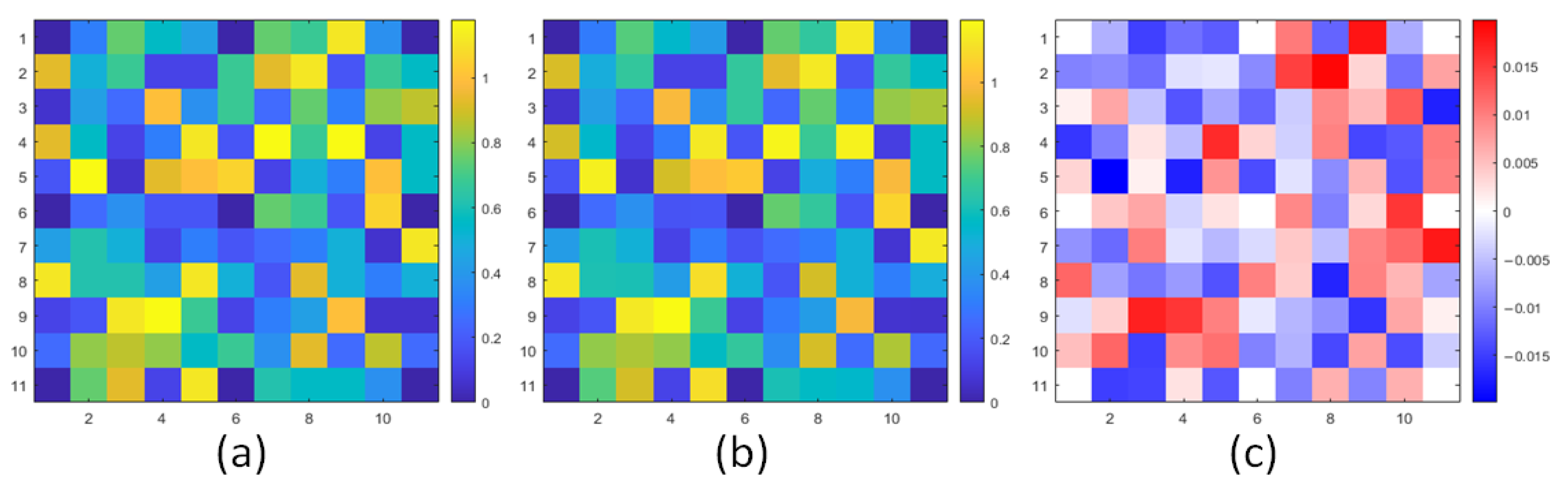
This research employs the zonal approach for wavefront reconstruction of a specified region, deriving the wavefront distortion associated with the microlenses of each sub-region and facilitating an intuitive analysis of the vibrational conditions of each sub-region, as illustrated in
Figure 21. This method enables the effective separation and analysis of the vibration characteristics of each sub-region, elucidating the spatial distribution and variation patterns in the vibrations. In the experiment, we initially process the wavefront data obtained from the wavefront sensor, employing the zonal approach to divide them into several sub-regions. By reconstructing the wavefront of each sub-region, we can achieve higher-resolution vibration images, which are essential for recognizing local vibration sources and comprehending vibration transmission mechanisms.
This article is based on the characteristics of high resolution and sensitivity of wavefront sensors to detect low-frequency vibration signals, as shown in
Figure 22. As shown in
Figure 22, as the frequency of the controllable vibration table gradually increases, the frequency of the detected signal also increases.
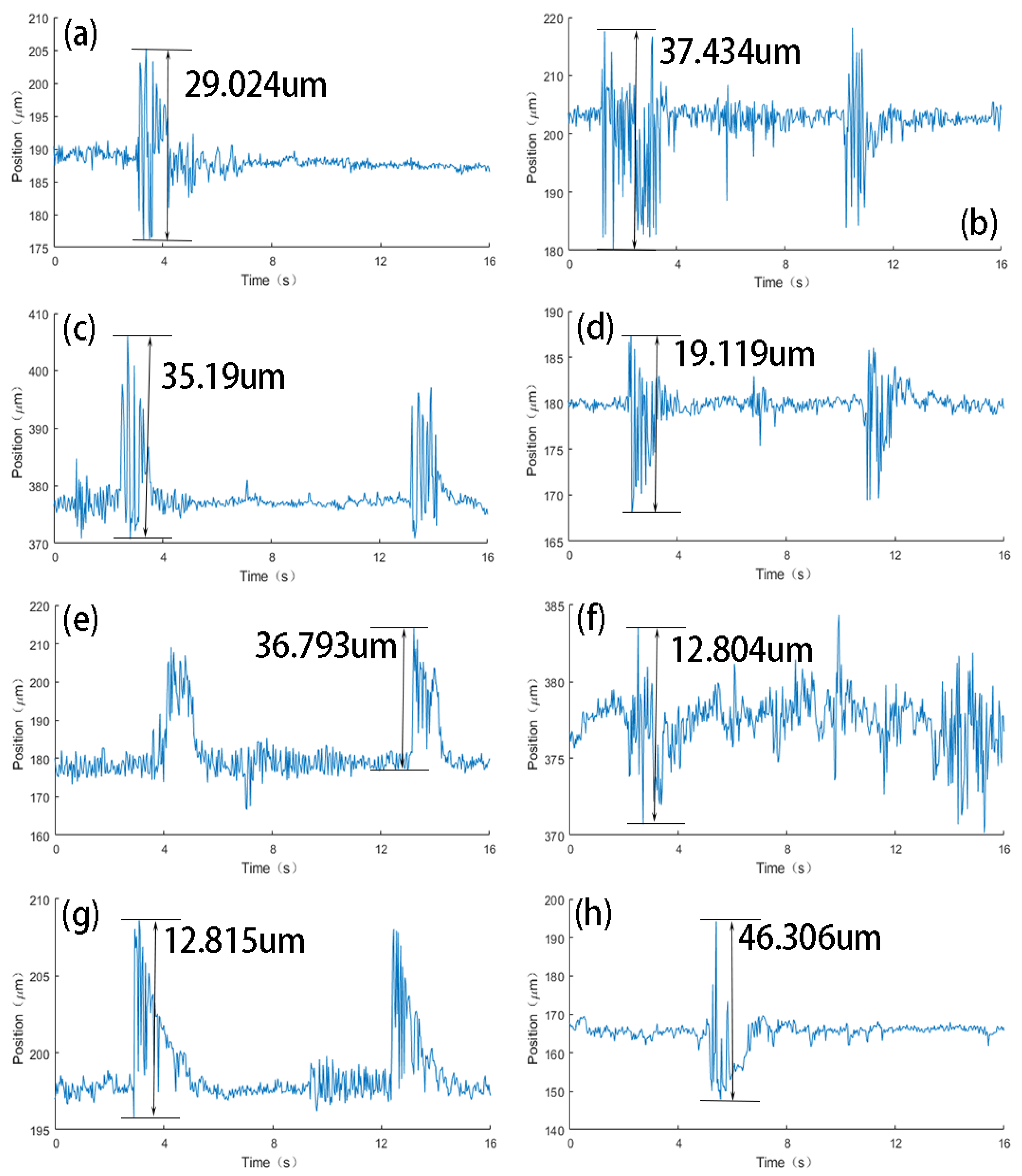
We conducted tests on the maximum and minimum vibration amplitudes using a controllable vibration table. The vibration frequency of the vibration table was set to 0.1 Hz, and the wavefront sensor was set to high-speed sampling mode (sampling rate: 700–880 fps). Therefore, this paper achieved the detection of large amplitude vibration with a vibration amplitude of 5.94 mm and small amplitude vibration with a vibration amplitude of 0.06 mm, as shown in
Figure 23. However, due to the insufficient sampling rate of the wavefront sensor, it is unable to detect high-frequency vibration signals.
The detection accuracy has been markedly enhanced relative to the conventional laser triangulation approach by utilizing minor wavefront alterations to identify a specific area’s vibrational signals. The error in detection by wavefront distortion ranges from
to
, but the error in detection utilizing the laser triangulation method spans from
to
, as illustrated in
Table 4. Wavefront sensors can accurately detect phase alterations in light waves, enabling more sensitive assessments of minute vibrations. In contrast to the laser triangulation method, which depends on variations in the light spot’s position, wavefront sensors can efficiently mitigate environmental noise and external disturbances by examining the comprehensive phase information of the light wave, thereby yielding more stable and dependable vibration monitoring outcomes. Moreover, wavefront sensors possess benefits in spatial resolution, facilitating high-density sampling across extensive areas, hence, rendering vibration analysis more thorough and intricate.
Although the seismic wave laser remote sensing surface scanning method based on the wavefront sensor shows good application prospects in laboratory conditions, it still faces many challenges in the actual environment. Atmospheric turbulence will cause the phase distortion of the laser wavefront, interfere with the measurement accuracy, and its influence fluctuates significantly with the change in altitude, time, and meteorological conditions. In addition, aerosols such as dust and haze will aggravate the scattering and attenuation of laser signals. Uneven distribution of precipitation and humidity will also lead to signal absorption, defocusing or deviation, and even complete signal masking in severe cases, thus affecting the stability and reliability of measurement results. In terms of environmental stability, field deployment faces multiple challenges. Extensive temperature changes lead to laser wavelength drift, optical system thermal expansion mismatch, and detector performance fluctuations. Especially in the presence of a significant thermal gradient, the spatial refractive index change will further distort the wavefront shape. In addition, if the common environmental vibration on site is not effectively isolated, it is easy to introduce artifacts, affecting the measurement accuracy and consistency. Surface complexity is also a major obstacle in practical application. Different from the idealized reflector in the laboratory, the reflectivity of natural surface materials is significantly different. The low reflectivity area easily cause weak echo signals, and the high reflectivity surface may cause detector saturation or artifacts. The surface roughness will also weaken the coherence of the reflected wavefront and reduce the reconstruction accuracy. In addition, surface dynamic changes such as vegetation shaking and water flow disturbance may introduce interference similar to the characteristics of seismic signals, which increases the difficulty of effective identification and classification.