Research Progress on All-Polarization-Maintaining Mode-Locked Fiber Lasers
Abstract
1. Introduction
2. All-Polarization-Maintaining Mode-Locked Fiber Lasers
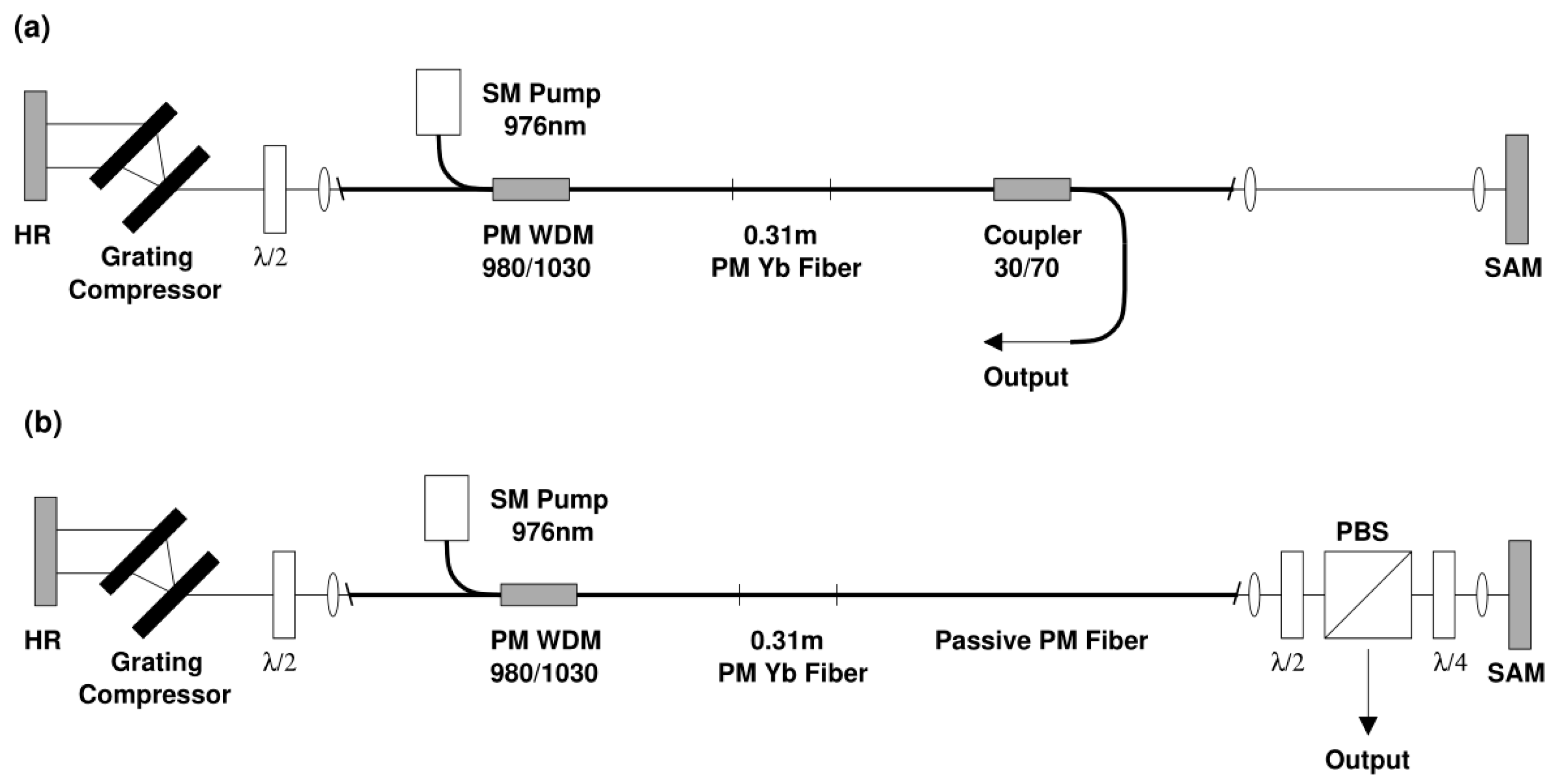
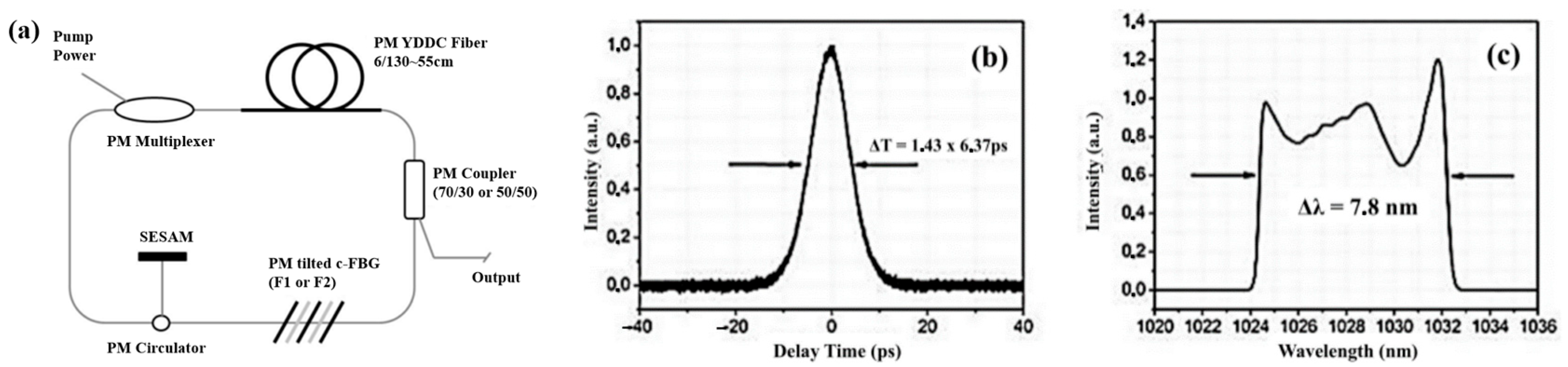
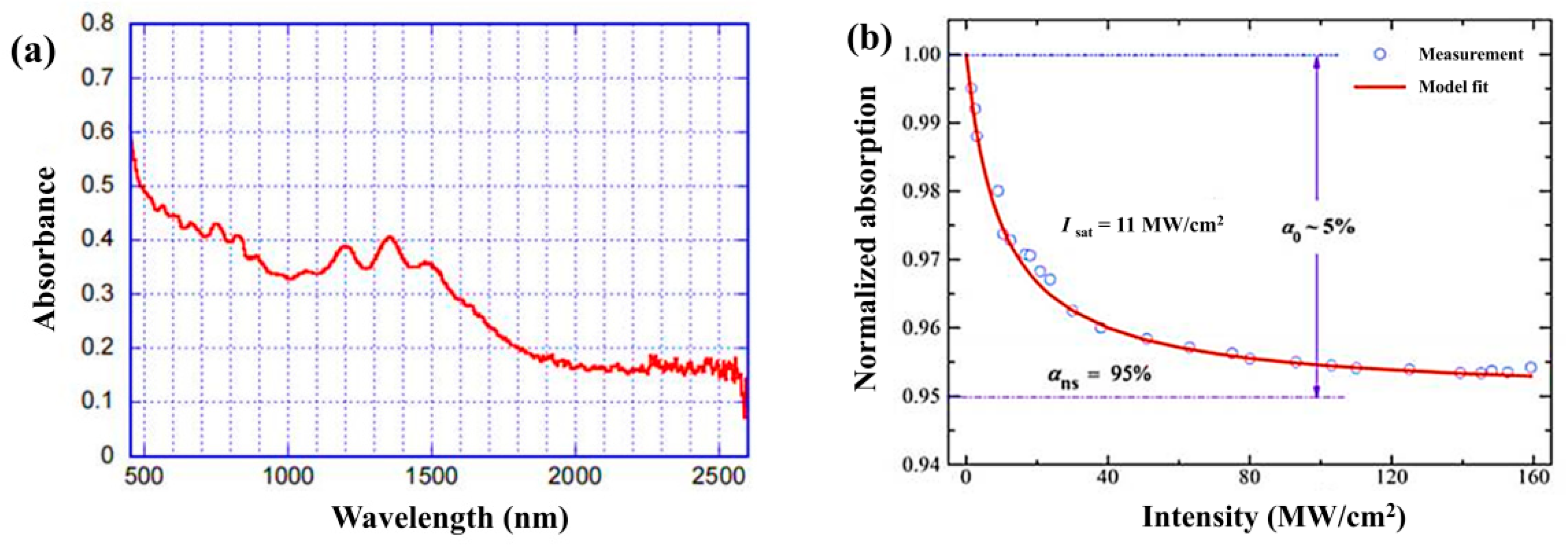
2.1. APM Mode-Locked Fiber Lasers Based on SESAMs
2.2. APM Mode-Locked Fiber Lasers Based on Low-Dimensional-Material Saturable Absorbers
2.3. All-Polarization-Maintaining Mode-Locked Fiber Laser Based on NPR
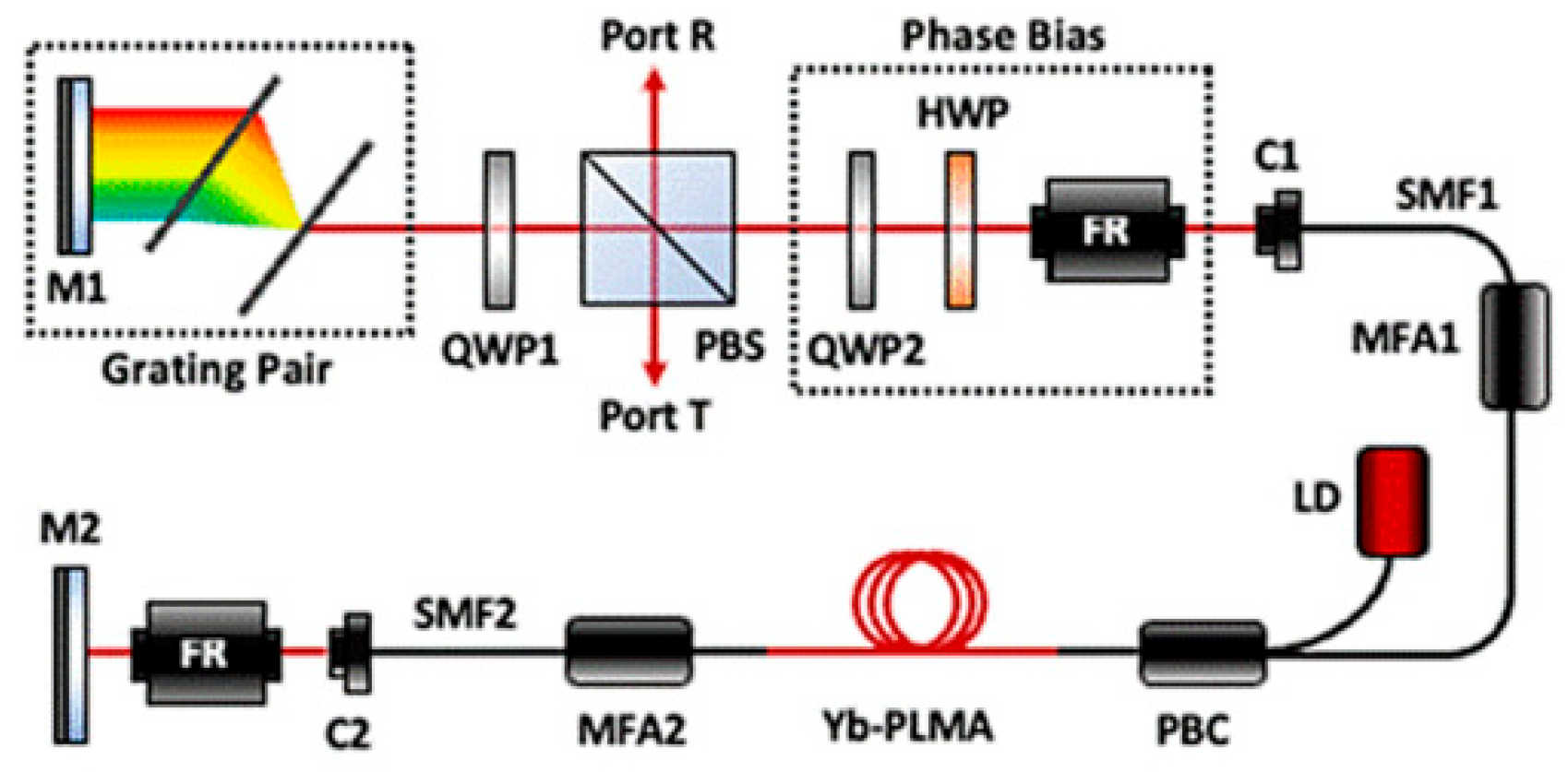
2.3.1. APM Mode-Locked Fiber Laser Based on NPR Without Phase Bias
2.3.2. APM Mode-Locked Fiber Laser Based on NPR with Phase Bias
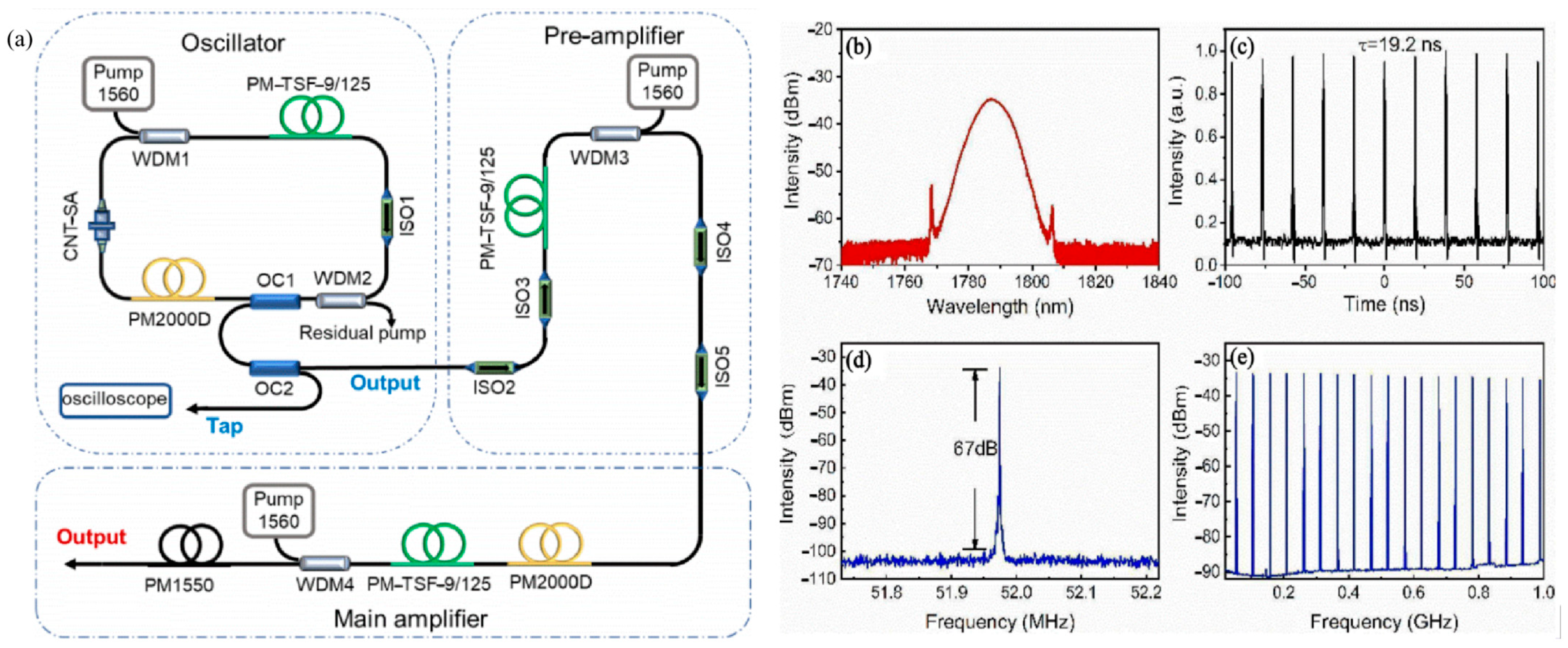
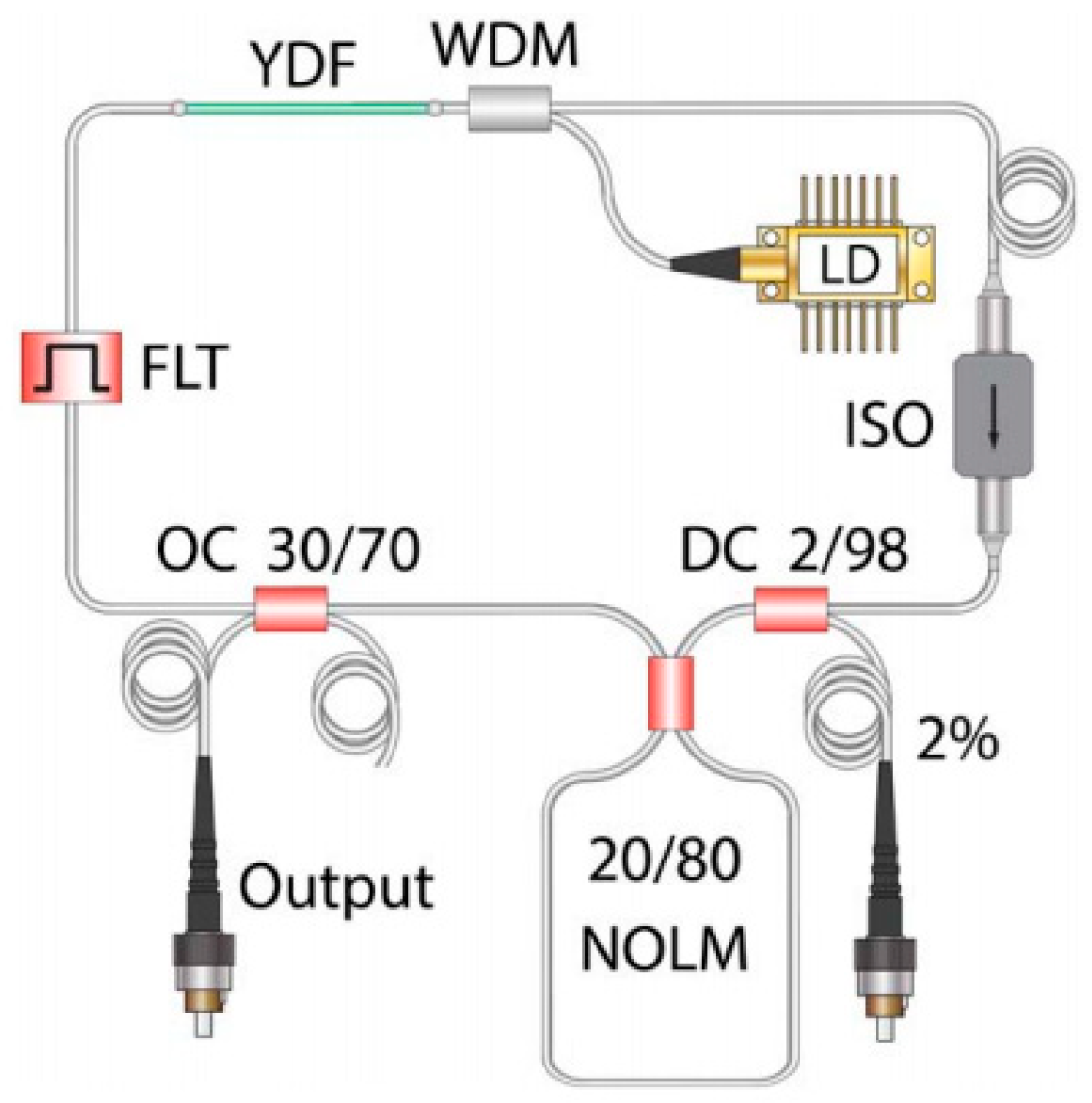
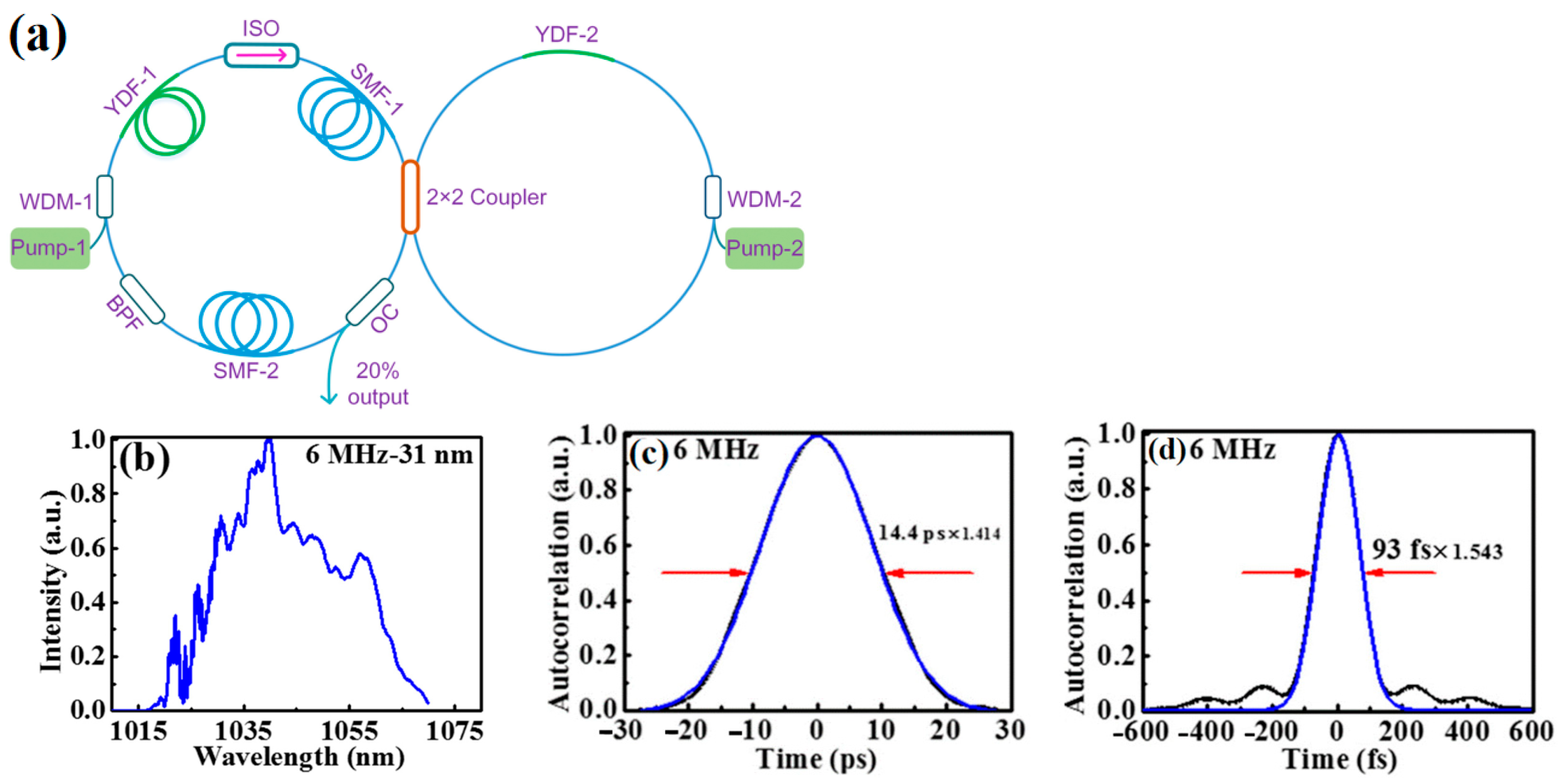
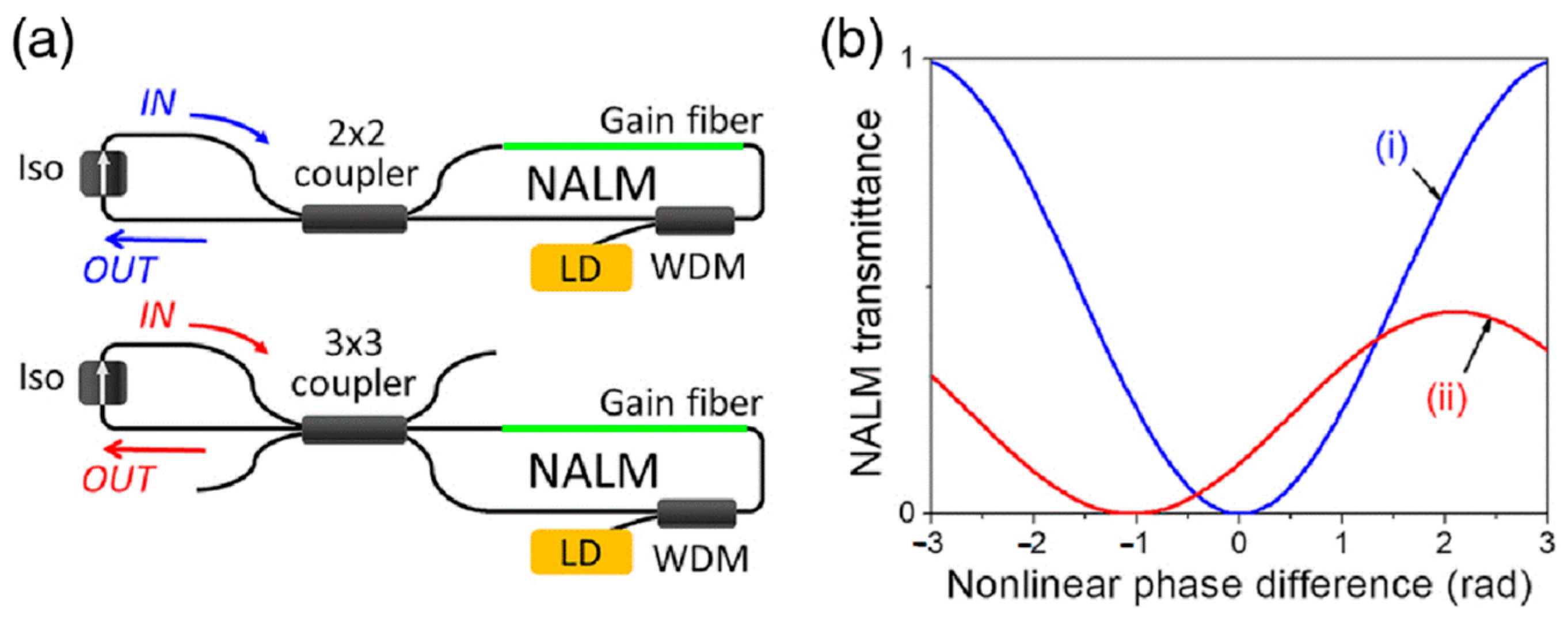
2.4. APM Mode-Locked Fiber Laser Based on the Figure-8 Cavity Using NOLMs/NALMs
2.5. Figure-9 Cavity APM Mode-Locked Fiber Laser
3. Challenges and Future Directions
3.1. Existing Challenges
3.2. Future Trends
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Keller, U. Recent developments in compact ultrafast lasers. Nature 2003, 424, 831–838. [Google Scholar] [CrossRef] [PubMed]
- Chong, A.; Renninger, W.; Wise, F. Environmentally stable all-normal-dispersion femtosecond fiber laser. Opt. Lett. 2008, 33, 1071–1073. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, C.; Schreiber, B.; Hohmuth, J.; Tnnermann, W. Self-starting Self-similar All-polarization Maintaining Yb-doped Fiber Laser. Opt. Express 2005, 12, 9346–9351. [Google Scholar] [CrossRef]
- Verhoef, A.; Zhu, L.; Israelsen, S.; Grüner-Nielsen, L.; Unterhuber, A.; Kautek, W.; Rottwitt, K.; Baltuška, A.; Fernández, A. Sub-100 fs pulses from an all-polarization maintaining Yb-fiber oscillator with an anomalous dispersion higher-order-mode fiber. Opt. Express 2015, 23, 26139–26145. [Google Scholar] [CrossRef]
- Sobon, G.; Sotor, J.; Abramski, K. All-polarization maintaining femtosecond Er-doped fiber laser mode-locked by graphene saturable absorber. Laser Phys. Lett. 2012, 9, 581–586. [Google Scholar] [CrossRef]
- Ali, S.; Raza, A.; Afzal, A.M.; Iqbal, M.W.; Hussain, M.; Imran, M.; Assiri, M.A. Recent advances in 2d-MXene based nanocomposites for optoelectronics. Adv. Mater. Interfaces 2022, 9, 2200556. [Google Scholar] [CrossRef]
- Yang, H.; Qi, M.; Li, X.; Xue, Z.; Cheng, J.; Lu, C.; Han, D.; Li, L.; Zhang, Y.; Zhao, F. Soliton interaction in a MXene-based mode-locked fiber laser. Opt. Express 2023, 31, 38688–38698. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Peng, L.; Zhao, J.; Sun, K.; Chen, S.; Huang, W. Mxene Nb2C/MoS2 heterostructure: Nonlinear optical properties and a new broadband saturable absorber for ultrafast photonics. Mater. Today Phys. 2025, 52, 101678. [Google Scholar] [CrossRef]
- Li, L.; Pang, L.; Wang, R.; Zhang, X.; Hui, Z.; Han, D.; Zhao, F.; Liu, W. Ternary transition metal dichalcogenides for high power vector dissipative soliton ultrafast fiber laser. Laser Photonics Rev. 2022, 16, 2100255. [Google Scholar] [CrossRef]
- Meng, X.; Li, L.; Sun, N.; Xue, Z.; Liu, Q.; Ye, H.; Liu, W. Ultrafast fiber laser based on tungsten sulphoselenide materials. Chin. Phys. Lett. 2023, 40, 124202. [Google Scholar] [CrossRef]
- Liang, S.; Lu, Y.; Liu, H.; Shang, X.; Du, R.; Ji, J.; Yu, Y.; Zhang, S. Saturable absorption of few-layer WS2 and WSe2 at exciton resonance. Opt. Express 2025, 33, 7266–7277. [Google Scholar] [CrossRef]
- Zhang, L.; Zhuo, Z.; Chen, N.-K.; Tian, Z.; Xie, Y. Wave plate-dependent lasing regimes transitions in an all-normal-dispersion fiber laser mode-locked by nonlinear polarization rotation. Opt. Laser Technol. 2020, 126, 106085. [Google Scholar] [CrossRef]
- Borodkin, A.; Honzátko, P. High-energy all-PM Yb-doped fiber laser with a nonlinear optical loop mirror. Opt. Laser Technol. 2021, 143, 107353. [Google Scholar] [CrossRef]
- Tao, J.; Song, Y.; Li, Y.; Jia, X.; Hou, L.; Lu, B.; Bai, J. Pulse type switchable, spectral bandwidth dynamically adjustable all-fiber laser mode-locked by NALM. Opt. Laser Technol. 2023, 157, 108682. [Google Scholar] [CrossRef]
- Lezius, M.; Wilken, T.; Deutsch, C.; Giunta, M.; Mandel, O.; Thaller, A.; Schkolnik, V.; Schiemangk, M.; Dinkelaker, A.; Kohfeldt, A.; et al. Space-borne frequency comb metrology. Optica 2016, 3, 1381–1387. [Google Scholar] [CrossRef]
- Ortaç, B.; Lecaplain, C.; Hideur, A.; Schreiber, T.; Limpert, J.; Tünnermann, A. Passively mode-locked single-polarization microstructure fiber laser. Opt. Express 2008, 16, 2122–2128. [Google Scholar] [CrossRef]
- Lecourt, J.; Duterte, C.; Narbonneau, F.; Kinet, D.; Hernandez, Y.; Giannone, D. All-normal dispersion, all-fibered PM laser mode-locked by SESAM. Opt. Express 2012, 20, 11918–11923. [Google Scholar] [CrossRef]
- Lv, Z.; Yang, Z.; Li, F.; Yang, X.; Tang, S.; Yang, Y.; Li, Q.; Wang, Y.; Zhao, W. SESAM mode-locked all-polarization-maintaining fiber linear cavity ytterbium laser source with spectral filter as pulse shaper. Laser Phys. 2018, 28, 125103. [Google Scholar] [CrossRef]
- Yu, Z.; Ou, S.; Guo, L.; Zhang, Q.; Sui, Q.; Chen, Y.; Zhang, N.; Liu, H.; Shum, P. 109 fs, 553 MHz pulses from a polarization-maintaining Yb-doped ring fiber laser with SESAM mode-locking. Opt. Commun. 2022, 522, 128520. [Google Scholar] [CrossRef]
- Kim, J.W.; Park, S.; Kim, G.H.; Yashin, V.E.; Yang, J. A 1030 nm all-PM SESAM mode-locked dissipative soliton fiber oscillator and its amplification with Yb-doped fiber and a Yb: YAG thin rod. Laser Phys. 2022, 32, 105102. [Google Scholar] [CrossRef]
- Dong, T.; Lin, J.; Gu, C.; Yao, P.; Xu, L. Switchable and tunable dual-wavelength passively mode-locked fiber laser. Opt. Fiber Technol. 2022, 68, 102750. [Google Scholar] [CrossRef]
- Song, D.; Yin, K.; Miao, R.; Zhang, C.; Xu, Z.; Jiang, T. Theoretical and experimental investigations of dispersion-managed, polarization-maintaining 1-GHz mode-locked fiber lasers. Opt. Express 2023, 31, 1916–1930. [Google Scholar] [CrossRef] [PubMed]
- Normani, S.; Idlahcen, S.; Loiko, P.; Hatim, S.; Hanzard, P.H.; Paula, A.R.D.; Guillemot, L.; Godin, T.; Berthelot, T.; Cozic, S.; et al. 2.8-µm polarization-maintaining Er fiber laser mode-locked by a GaSb-based SESAM. Opt. Express 2024, 32, 15106–15114. [Google Scholar] [CrossRef] [PubMed]
- Bai, C.; Feng, Y.; Zhang, W.; Zhang, J.; Zhang, T.; Mei, C.; Liu, P.; Fan, Z.; Qian, J.; Yu, J. Dual-parameter femtosecond mode-locking pulse generation in partially shared all-polarization-maintaining fiber Y-shaped oscillator with a single saturable absorber. Opt. Laser Technol. 2024, 169, 110021. [Google Scholar] [CrossRef]
- Mkrtchyan, A.A.; Mishevsky, M.S.; Gladush, Y.G.; Melkumov, M.A.; Khegai, A.M.; Lagoudakis, P.G.; Nasibulin, A.G. Dispersion managed mode-locking in all-fiber polarization-maintaining Nd-doped laser at 920 nm. J. Light. Technol. 2022, 41, 2494–2500. [Google Scholar] [CrossRef]
- Nishizawa, N.; Seno, Y.; Sumimura, K.; Sakakibara, Y.; Itoga, E.; Kataura, H.; Itoh, K. All-polarization-maintaining Er-doped ultrashort-pulse fiber laser using carbon nanotube saturable absorber. Opt. Express 2008, 16, 9429–9435. [Google Scholar] [CrossRef]
- Senoo, Y.; Nishizawa, N.; Sakakibara, Y.; Sumimura, K.; Itoga, E.; Kataura, H.; Itoh, K. Polarization-maintaining, high-energy, wavelength-tunable, Er-doped ultrashort pulse fiber laser using carbon-nanotube polyimide film. Opt. Express 2009, 17, 20233–20241. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Y.; Zhang, A.P.; Wu, B.; Shen, Y.; Tam, H. Tunable scalar solitons from a polarization-maintaining mode-locked fiber laser using carbon nanotube and chirped fiber Bragg grating. Opt. Express 2016, 24, 22387. [Google Scholar] [CrossRef]
- Zheng, J.; Yang, S.; Nie, X.; Li, L. All-polarization-maintaining passively mode-locked erbium-doped fiber laser based on a WDM-Isolator-Tap hybrid device. J. Russ. Laser Res. 2021, 42, 82–86. [Google Scholar] [CrossRef]
- Zhang, N.; Jiang, W.; Meng, Y.; Wang, F. All-polarization-maintaining mode-locked thulium-doped femtosecond laser at 1.7 µm. Opt. Contin. 2023, 2, 1013–1019. [Google Scholar] [CrossRef]
- Sobon, G.; Sotor, J.; Pasternak, I.; Krajewska, A.; Strupinski, W.; Abramski, K.M. All-polarization maintaining, graphene-based femtosecond Tm-doped all-fiber laser. Opt. Express 2015, 23, 9339–9346. [Google Scholar] [PubMed]
- Tarka, J.; Boguslawski, J.; Sobon, G.; Pasternak, I.; Przewloka, A.; Strupinski, W.; Sotor, J.; Abramski, K.M. Power scaling of an all-PM fiber Er-doped mode-locked laser based on graphene saturable absorber. IEEE J. Sel. Top. Quant. 2017, 23, 60–65. [Google Scholar]
- Meng, K.; Zhu, L.-Q.; Luo, F. Observation of wavelength-switchable solitons in an all-polarization-maintaining erbium-doped fiber cavity based on graphene saturable absorber reflector. Chin. Phys. B 2017, 26, 014205. [Google Scholar]
- Sotor, J.; Bogusławski, J.; Martynkien, T.; Mergo, P.; Krajewska, A.; Przewłoka, A.; StrupiŃski, W.; SoboŃ, G. All-polarization-maintaining, stretched-pulse Tm-doped fiber laser, mode-locked by a graphene saturable absorber. Opt. Lett. 2017, 42, 1592–1595. [Google Scholar]
- Sotor, J.; Sobon, G.; Abramski, K.M. Scalar soliton generation in all-polarization-maintaining, graphene mode-locked fiber laser. Opt. Lett. 2012, 37, 2166–2168. [Google Scholar] [PubMed]
- Guo, C.; Chen, B.; Wang, H.; Zhang, X.; Wang, J.; Wu, K.; Chen, J. Investigation on the stability of WSe2-PVA saturable absorber in an all PM Q-switched fiber laser. IEEE Photonics J. 2016, 8, 1–12. [Google Scholar]
- Hofer, M.; Fermann, M.E.; Haberl, F.; Ober, M.H.; Schmidt, A.J. Mode-locking with cross-phase and self-phase modulation. Opt. Lett. 1991, 16, 502–504. [Google Scholar]
- Wang, J.; Wen, B.; Chen, X.; Zhang, H.; Chen, X.; Yan, P.; Zhang, H. All-polarization-maintaining Ho-doped fiber oscillator mode-locked with nonlinear polarization evolution. Opt. Lett. 2024, 49, 133–136. [Google Scholar]
- Szczepanek, J.; Kardaś, T.M.; Radzewicz, C.; Stepanenko, Y. Nonlinear polarization evolution of ultrashort pulses in polarization maintaining fibers. Opt. Express 2018, 26, 13590–13604. [Google Scholar]
- Wang, Y.; Zhang, L.; Zhuo, Z.; Guo, S. Cross-splicing method for compensating fiber birefringence in polarization-maintaining fiber ring laser mode locked by nonlinear polarization evolution. Appl. Opt. 2016, 55, 5766–5770. [Google Scholar]
- Zhang, W.; Liu, Y.; Wang, C.; Zhu, Z.; Luo, D.; Gu, C.; Li, W. Ultrafast PM fiber ring laser mode-locked by nonlinear polarization evolution with short NPE section segments. Opt. Express 2018, 26, 7934–7941. [Google Scholar] [CrossRef] [PubMed]
- Szczepanek, J.; Kardaś, T.M.; Radzewicz, C.; Stepanenko, Y. Ultrafast laser mode-locked using nonlinear polarization evolution in polarization maintaining fibers. Opt. Lett. 2017, 42, 575–578. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Liu, Y.; Xie, G.; Zhang, W.; Zhu, Z.; Ouyang, C.; Gu, C.; Li, W. Generation of stretched pulses from an all-polarization-maintaining Er-doped mode-locked fiber laser using nonlinear polarization evolution. App. Phys. Express 2019, 12, 052017. [Google Scholar] [CrossRef]
- Wu, Z.; Wei, Q.; Huang, P.; Fu, S.; Liu, D.; Huang, T. Nonlinear polarization evolution mode-locked YDFL based on all-PM fiber cavity. IEEE Photonics J. 2020, 12, 1501807. [Google Scholar] [CrossRef]
- Jiang, Y.; Zheng, S.; Du, G.; Yu, L.; Wang, J.; Chen, H.; Dong, F.; Luo, X.; Wang, J.; Yan, P.; et al. 976 nm all-polarization-maintaining mode-locked fiber laser based on nonlinear polarization evolution. Opt. Express 2023, 31, 15170. [Google Scholar] [CrossRef]
- Tu, L.; Tang, Z.; Li, K.; Wang, J.; Lin, H.; Zhang, W.; Lue, Q.; Guo, C.; Ruan, S. All-polarization-maintaining mode-locked Holmium-doped fiber laser based upon nonlinear polarization evolution. Infrared Phys. Technol. 2024, 136, 105054. [Google Scholar] [CrossRef]
- Nielsen, C.K.; Keiding, S.R. All-fiber mode-locked fber laser. Opt. Lett. 2007, 32, 1474–1476. [Google Scholar] [CrossRef]
- Boivinet, S.; Lecourt, J.-B.; Hernandez, Y.; Fotiadi, A.A.; Wuilpart, M.; Megret, P. All-fiber 1-μm PM mode-lock laser delivering picosecond pulses at sub-MHz repetition rate. IEEE Photonic Technol. 2014, 26, 2256–2259. [Google Scholar] [CrossRef]
- Peng, Z.; Cheng, Z.; Bu, X.; Hong, C.; Li, H.; Shi, Y.; Wang, P. Study of an Er-doped all-PM-fiber laser mode-locked by nonlinear polarization evolution. IEEE Photonic Technol. 2018, 30, 2111–2114. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, W.; Gu, X.; Zhang, L.; Feng, Y. Dissipative-soliton generation with nonlinear-polarization-evolution in a polarization maintaining fiber. Opt. Express 2018, 26, 4166–4171. [Google Scholar] [CrossRef]
- Liang, C.B.; Song, Y.R.; Dong, Z.K.; Wu, Y.F.; Tian, J.R.; Xu, R.Q. Pulse generation in Yb-doped polarization-maintaining fiber laser by nonlinear polarization evolution. Chin. Phys. B 2020, 29, 074206. [Google Scholar] [CrossRef]
- Yu, M.; Cheng, Z.; Hong, C.; Shi, Y.; Peng, Z.; Wang, M.; Wang, P. Numerical modeling and experimental investigation of ultrafast pulses generation from all-polarization-maintaining dispersion-managed nonlinear polarization evolution Yb-doped fiber laser. Opt. Express 2020, 28, 32764–32776. [Google Scholar] [CrossRef] [PubMed]
- Ye, G.; Chow, K.K.; Liu, B.; Dai, M.; Ma, Y.; Shirahata, T.; Yamashita, S.; Set, S.Y. L-band mode-locked fiber laser using all polarization-maintaining nonlinear polarization rotation. Opt. Lett. 2023, 48, 4729–4732. [Google Scholar] [CrossRef]
- Ye, G.; Liu, B.; Dai, M.; Ma, Y.; Shirahata, T.; Yamashita, S.; Set, S.Y. Pump-power-controlled L-band wavelength-tunable mode-locked fiber laser utilizing nonlinear polarization evolution in all-polarization-maintaining fibers. Opt. Lett. 2024, 49, 2433–2436. [Google Scholar] [CrossRef] [PubMed]
- Fermann, M.; Andrejco, M.; Silberberg, Y.; Stock, M. Passive mode locking by using nonlinear polarization evolution in a polarization-maintaining erbium-doped fiber. Opt. Lett. 1993, 18, 894–896. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, R.; Pan, D.; Li, Q.; Fu, H.Y. 115-MHz linear NPE fiber laser using all polarization-maintaining fibers. IEEE Photonic Technol. 2021, 33, 81–84. [Google Scholar] [CrossRef]
- Liu, X.; Li, Q.; Pan, D.; Ye, F.; Malomed, B.; Fu, H. A robust and novel linear fiber laser mode-locked by nonlinear polarization evolution in all-polarization-maintaining fibers. J. Light. Technol. 2021, 39, 7509–7516. [Google Scholar] [CrossRef]
- Liu, G.; Ou, S.; Zhang, Q.; Zhang, M.; Li, X.; Bao, Q. All-polarization-maintaining linear fiber laser mode-locked by nonlinear polarization evolution with phase bias. Opt. Laser Technol. 2021, 142, 107160. [Google Scholar] [CrossRef]
- Peng, S.; Liu, X.; Fu, H.Y.; Li, Q. Intracavity filtering effect in a dual-output linear-cavity all-PM fiber laser mode-locked by NPE. Appl. Opt. 2023, 62, 6323–6332. [Google Scholar] [CrossRef]
- Liu, X.; Ye, F.; Zhao, M.; Malomed, B.A.; Fu, H.Y.; Li, Q. All-polarization-maintaining linear cavity fiber lasers mode-locked by nonlinear polarization evolution in stretched pulse regime. J. Light. Technol. 2023, 41, 5107–5115. [Google Scholar] [CrossRef]
- Peng, S.; Liu, X.; Fu, H.Y.; Li, Q. Generation of harmonic mode-locked pulses and noise-like pulses in an all-PM Tm-doped fiber laser via linear-cavity interferometric NPE. Opt. Laser Technol. 2025, 181, 111848. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, Y.; Hou, Y.; Liu, Y.; Luo, T.; Li, Z.; Wang, T.; Pan, X. Generation and modulation of soliton molecules in an all-polarization-maintaining fiber laser mode-locked by NPE. Opt. Commun. 2025, 574, 131093. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, X.; Fu, H.Y.; Li, Q. Machine-learning iterative optimization for all polarization-maintaining linear cavity Er:fiber laser. Opt. Lett. 2023, 48, 4893–4896. [Google Scholar] [CrossRef] [PubMed]
- Edelmann, M.; Hua, Y.; Kulcsar, G.; Kärtner, F.X. All-polarization-maintaining divided pulse fiber oscillator mode-locked with the optical Kerr effect. Opt. Lett. 2021, 46, 6083–6085. [Google Scholar] [CrossRef] [PubMed]
- Edelmann, M.; Sedigheh, M.M.; Hua, Y.; Vargas, E.C.; Pergament, M.; Kärtner, F.X. Large-mode-area soliton fiber oscillator mode-locked using NPE in an all-PM self-stabilized interferometer. Appl. Opt. 2023, 62, 1672–1676. [Google Scholar] [CrossRef]
- Edelmann, M.; Hua, Y.; Pergament, M.; Kärtner, F.X. Performance enhancement via XPM suppression of a linear all-PM mode-locked fiber oscillator. Opt. Lett. 2024, 49, 1237–1240. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, X.; Ye, F.; Fu, H.Y.; Li, Q. Bidirectional all-PM Er-doped fiber laser based on a self-stabilized interferometer mode-locker. Opt. Laser Technol. 2025, 181, 111914. [Google Scholar] [CrossRef]
- Doran, N.; Wood, D. Nonlinear-optical loop mirror. Opt. Lett. 1988, 13, 56–58. [Google Scholar] [CrossRef]
- Fermann, M.; Haberl, F.; Hofer, M.; Hochreiter, H. Nonlinear amplifying loop mirror. Opt. Lett. 1990, 15, 752–754. [Google Scholar] [CrossRef]
- Szczepanek, J.; Kardaś, T.M.; Michalska, M.; Radzewicz, C.; Stepanenko, Y. Simple all-PM-fiber laser mode-locked with a nonlinear loop mirror. Opt. Lett. 2015, 40, 3500–3503. [Google Scholar] [CrossRef]
- Watanabe, K.; Tsutsui, S.; Asghari, H.; Toda, H.; Suzuki, M. Robust all-polarization maintaining Yb fiber oscillator with a nonlinear optical loop mirror. Opt. Commun. 2023, 538, 129476. [Google Scholar] [CrossRef]
- Pielach, M.; Piechal, B.; Szczepanek, J.; Kabacinski, P.; Stepanenko, Y. Energy Scaling of an Ultrafast All-PM-Fiber Laser Oscillator. IEEE Access. 2020, 8, 145087–145091. [Google Scholar] [CrossRef]
- Shi, J.; Li, Y.; Gao, S.; Pan, Y.; Wang, G.; Ji, R.; Zhou, W. All-polarization-maintaining figure-eight Er-fiber ultrafast laser with a bidirectional output coupler in the loss-imbalanced nonlinear optical loop mirror. Chin. Opt. Lett. 2018, 16, 121404. [Google Scholar]
- Pielach, M.; Szczepanek, J.; Krupa, K.; Stepanenko, Y. Studying the operation of an all-PM Yb-doped fiber laser oscillator at negative and positive net cavity dispersion. IEEE Access 2022, 10, 45689–45694. [Google Scholar] [CrossRef]
- Long, R.; Wen, J.; Li, Y.; Huang, L.; Fan, D.; Jiang, G.; Chen, Y. Spatiotemporal flat-top beam generated from an all-fiber mode-locking laser. Opt. Express 2025, 33, 583–591. [Google Scholar] [CrossRef] [PubMed]
- Qin, L.; Li, M.; Li, X.-W.; Li, S.-G.; Zhang, J.-X.; Zhang, Y.-B.; Li, J.-S. Study on soliton bunch pulse shaping and characteristics in dual sub cavity nonlinear optical loop mirror mode-locked erbium-doped fiber laser. Opt. Laser Technol. 2025, 184, 112480. [Google Scholar] [CrossRef]
- Yu, Y.; Teng, H.; Wang, H.; Wang, L.; Zhu, J.; Fang, S.; Chang, G.; Wang, J.; Wei, Z. Highly-stable mode-locked PM Yb-fiber laser with 10 nJ in 93-fs at 6 MHz using NALM. Opt. Express 2018, 26, 10428–10434. [Google Scholar] [CrossRef]
- Aguergaray, C.; Broderick, N.; Erkintalo, M.; Chen, J.; Kruglov, V. Mode-locked femtosecond all-normal all-PM Yb-doped fiber laser using a nonlinear amplifying loop mirror. Opt. Express 2012, 20, 10545–10551. [Google Scholar] [CrossRef]
- Erkintalo, M.; Aguergaray, C.; Runge, A.; Broderick, N. Environmentally stable all-PM all-fiber giant chirp oscillator. Opt. Express 2012, 20, 22669–22674. [Google Scholar] [CrossRef]
- Aguergaray, C.; Hawker, R.; Runge, A.F.J.; Erkintalo, M.; Broderick, N.G.R. 120 fs, 4.2 nJ pulses from an all-normal-dispersion, polarization-maintaining, fiber laser. Appl. Phys. Lett. 2013, 103, 121111. [Google Scholar] [CrossRef]
- Zhou, J.; Gu, X. 32-nJ 615-fs Stable Dissipative Soliton Ring Cavity Fiber Laser With Raman Scattering. IEEE Photonic Techl. 2016, 28, 453–456. [Google Scholar]
- Bowen, P.; Erkintalo, M.; Provo, R.; Harvey, J.D.; Broderick, N.G.R. Mode-locked Yb-doped fiber laser emitting broadband pulses at ultralow repetition rates. Opt. Lett. 2016, 41, 5270–5273. [Google Scholar]
- Bowen, P.; Singh, H.; Runge, A.; Provo, R.; Broderick, N.G.R. Mode-locked femtosecond all-normal all-PM Yb-doped fiber laser at 1060 nm. Opt. Commun. 2016, 364, 181–184. [Google Scholar]
- Smirnov, S.; Kobtsev, S.; Ivanenko, A.; Kokhanovskiy, A.; Kemmer, A.; Gervaziev, M. Layout of NALM fiber laser with adjustable peak power of generated pulses. Opt. Lett. 2017, 42, 1732–1735. [Google Scholar] [PubMed]
- Ou, S.; Liu, G.; Guo, L.; Zhang, Z.; Zhang, Q. 870 fs, 448 kHz pulses from an all-polarization-maintaining Yb-doped fiber laser with a nonlinear amplifying loop mirror. Appl. Opt. 2018, 57, 5068–5071. [Google Scholar] [PubMed]
- Gao, G.; Zhang, H.; Li, Y.; Deng, D. All-normal-dispersion fiber laser with NALM: Power scalability of the single-pulse regime. Laser Phys. Lett. 2018, 15, 035106. [Google Scholar]
- Deng, D.; Zhang, H.; Gong, Q.; He, L.; Li, D.; Gong, M. Energy scalability of the dissipative soliton in an all-normal-dispersion fiber laser with nonlinear amplifying loop mirror. Opt. Laser Technol. 2020, 125, 106010. [Google Scholar]
- Gong, Q.; Zhang, H.; Deng, D.; Zu, J. Dissipative Soliton Resonance in an All-polarization maintaining fiber laser with a nonlinear amplifying loop mirror. IEEE Photonics J. 2020, 12, 1502708. [Google Scholar]
- Liu, Y.; Liu, G.; Zhao, Q.; Cui, J.; Lin, J.; Zhang, D. 140 kHz, 1.2 ps pulses from an all-PM Yb-doped fiber master oscillator-power amplifier. Laser Phys. 2021, 31, 085102. [Google Scholar]
- Guo, L.; Gan, Z.; Liang, X. 27 nJ, 114 fs pulses from an environmentally stable all-normal all-PM Yb-doped fiber laser mode-locked with a nonlinear amplifying loop mirror. IEEE Photonics J. 2022, 14, 1519406. [Google Scholar]
- Michalska, M.; Swiderski, J. Noise-like pulse generation using polarization maintaining mode-locked thulium-doped fiber laser with nonlinear amplifying loop mirror. IEEE Photonics J. 2019, 11, 1504710. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, J.; Chen, Y.; Liu, M.; Ouyang, D.; Pei, J.; Ruan, S. 10 µJ noise-like pulse generated from all fiberized Tm-doped fiber oscillator and amplifier. Opt. Express 2021, 29, 10172. [Google Scholar] [CrossRef]
- Ren, B.; Li, C.; Wang, T.; Guo, K.; Zhou, P. Stable noise-like pulse generation from a NALM-based all-PM Tm-doped fiber laser. Opt. Express 2022, 30, 26464–26471. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Wang, T.; Chen, B.; Ma, W.; Zhao, Y.; Jiang, H. Square-wave pulse in 2-μm all-polarization-maintaining passively mode-locked fiber laser. Opt. Eng. 2020, 59, 116107. [Google Scholar] [CrossRef]
- Han, L.; Wang, T.; Song, G.; Ma, W.; Fu, Q.; Yang, Q.; Liu, X.; Guo, Y.; Jiang, H. Tunable peak power square-wave pulse based on an all-PM thulium-doped mode-locked fiber laser. Appl. Opt. 2021, 60, 1982–1986. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Liu, M.; Zhao, J.; Chen, Y.; Ouyang, D.; Ruan, S. Stable femtosecond pulse generation relying on a simple NALM-based all PM Tm-doped fiber laser. Results Opt. 2022, 9, 100297. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, Y.; Dai, Y.; Li, J.; Yin, F.; Dai, J.; Xu, K. All-fiber polarization-maintaining erbium-doped dispersion-managed fiber laser based on a nonlinear amplifying loop mirror. Appl. Opt. 2018, 57, 1492–1496. [Google Scholar] [CrossRef]
- Bowen, P.; Erkintalo, M.; Broderick, N.G.R. Large net-normal dispersion Er-doped fibre laser mode-locked with a nonlinear amplifying loop mirror. Opt. Commun. 2018, 410, 447–451. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, Y.; Ge, Z.; Yin, J.; Yin, F.; Dai, J.; Zhang, T.; Xu, K. Low-repetition-rate, high pulse energy all-polarization-maintaining Er-doped fiber laser mode-locked with a nonlinear amplifying loop mirror. Laser Phys. Lett. 2019, 16, 045104. [Google Scholar] [CrossRef]
- Li, Y.; Mu, Y.; Xi, F.; Wang, X.; Li, X. 1.6 µm dissipative soliton resonance fiber laser based on nonlinear amplifying loop mirror. Opt. Laser Technol. 2025, 183, 112304. [Google Scholar] [CrossRef]
- Becheker, R.; Tang, M.; Touil, M.; Robin, T.; Cadier, B.; Laroche, M.; Godin, T.; Hideur, A. Dissipative soliton resonance in a mode-locked Nd-fiber laser operating at 927 nm. Opt. Lett. 2019, 44, 5497–5500. [Google Scholar] [CrossRef] [PubMed]
- Mkrtchyan, A.A.; Gladush, Y.G.; Melkumov, M.A.; Khegai, A.M.; Sitnik, K.A.; Lagoudakis, P.G.; Nasibulin, A.G. Nd-Doped polarization maintaining all-fiber laser with dissipative soliton resonance mode-locking at 905 nm. J. Light. Technol. 2021, 39, 5582–5588. [Google Scholar] [CrossRef]
- Krzempek, K.; Tomaszewska, D.; Abramski, K.M. Dissipative soliton resonance mode-locked all-polarization-maintaining double clad Er:Yb fiber laser. Opt. Express 2017, 25, 24853–24860. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, D.; Hong, Z.; Jiang, Q.; Zhang, B.; Hou, J. 2.1 μJ, 14.9 W dissipative soliton resonance from an all-polarization-maintaining holmium-doped fiber laser system. Opt. Laser Technol. 2025, 183, 112306. [Google Scholar] [CrossRef]
- Kim, D.; Kwon, D.; Lee, B.; Kim, J. Polarization-maintaining nonlinear-amplifying-loop-mirror mode-locked fiber laser based on a 3 × 3 coupler. Opt. Lett. 2019, 44, 1068–1071. [Google Scholar] [CrossRef] [PubMed]
- Boivinet, S.; Vidal, S.; Boullet, J. 178 fs, 1.2 nJ pulses from an all-polarization maintaining fiber Figure 8 laser based on 3 × 3 coupler at 1 μm. Laser Phys. Lett. 2020, 17, 055102. [Google Scholar] [CrossRef]
- Graf, F.; Scelle, R.; Diekamp, H.; Budnicki, A.; Dekorsy, T. Femtosecond fiber oscillator based on a 3 × 3-coupler-NALM: Numerical model and realizations at 1 and 2 µm. Opt. Express 2022, 30, 12555–12564. [Google Scholar] [CrossRef]
- Pielach, M.; Jamrozik, A.; Krupa, K.; Stepanenko, Y. Self-starting mode-locking in an all-PM Yb-doped fiber laser oscillator enabled by a 3x3 nonlinear optical lossy loop mirror. Opt. Express 2023, 31, 42136–42149. [Google Scholar] [CrossRef]
- Ibarra-Escamilla, B.; Pottiez, O.; Kuzin, E.A.; Grajales-Coutiño, R.; Haus, J.W. Experimental investigation of a passively mode-locked fiber laser based on a symmetrical NOLM with a highly twisted low-birefringence fiber. Laser Phys. 2008, 18, 914–919. [Google Scholar] [CrossRef]
- Rodríguez-Morales, L.A.; Ibarra-Escamilla, B.; Armas-Rivera, I.; Pottiez, O.; Andrés, M.V.; Durán-Sánchez, M.; Kuzin, E.A. Sub-200-kHz single soliton generation in a long ring Er-fiber laser with strict polarization control by using twisted fiber. Opt. Laser Technol. 2020, 126, 106068. [Google Scholar] [CrossRef]
- Ibarra-Escamilla, B.; Pottiez, O.; Kuzin, E.A.; Grajales-Coutiño, R.; Haus, J.W.; Rojas-Laguna, R. Experimental investigation of a figure-eight fiber laser with a symmetrical NOLM and highly twisted fiber-in-the-loop. Proc. SPIE 2007, 6453, 645323. [Google Scholar]
- Rodríguez-Morales, L.A.; Armas-Rivera, I.; Durán-Sánchez, M.; Silvestre, E.; Andrés, M.V.; Ibarra-Escamilla, B. Experimental and theoretical study of the nonlinear birefringence in the formation process of vector solitons in a total polarization control ring cavity bias twist fiber. Opt. Laser Technol. 2022, 147, 107675. [Google Scholar] [CrossRef]
- Hänsel, W. Laser with Non-Linear Optical Loop Mirror. EP12001482, 29 August 2018. [Google Scholar]
- Kuse, N.; Jiang, J.; Lee, C.-C.; Schibli, T.R.; Fermann, M.E. All polarization-maintaining Er fiber-based optical frequency combs with nonlinear amplifying loop mirror. Opt. Express 2016, 24, 3095–3102. [Google Scholar] [CrossRef]
- Jiang, T.; Cui, Y.; Lu, P.; Li, C.; Wang, A.; Zhang, Z. All PM fiber laser mode locked with a compact phase biased amplifier loop mirror. IEEE Photonic Technol. 2016, 28, 1786–1789. [Google Scholar] [CrossRef]
- Hänsel, W.; Hoogland, H.; Giunta, M.; Schmid, S.; Steinmetz, T.; Doubek, R.; Mayer, P.; Dobner, S.; Cleff, C.; Fischer, M.; et al. All polarization-maintaining fiber laser architecture for robust femtosecond pulse generation. Appl. Phys. B 2017, 123, 41. [Google Scholar] [CrossRef]
- Chen, F.; Hao, Q.; Zeng, H. Optimization of an NALM mode-locked all-PM Er:fiber laser system. IEEE Photonic Technol. 2017, 29, 2119–2122. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, W.; Fu, X.; Zhang, L.; Feng, Y. Environmentally-stable 50-fs pulse generation directly from an Er:fiber oscillator. Opt. Fiber Technol. 2019, 52, 101963. [Google Scholar] [CrossRef]
- Yin, K.; Li, Y.-M.; Wang, Y.-B.; Zheng, X.; Jiang, T. Self-starting all-fiber PM Er:laser mode locked by a biased nonlinear amplifying loop mirror. Chin. Phys. B 2019, 28, 124203. [Google Scholar] [CrossRef]
- Duan, D.; Wang, J.; Wu, Y.; Ma, J.; Mao, Q. Approach to high pulse energy emission of the self-starting mode-locked figure-9 fiber laser. Opt. Express 2020, 28, 33603–33613. [Google Scholar] [CrossRef]
- Nishizawa, N.; Suga, H.; Yamanaka, M. Investigation of dispersion-managed, polarization-maintaining Er-doped figure-nine ultrashort-pulse fiber laser. Opt. Express 2019, 27, 19218–19232. [Google Scholar] [CrossRef]
- Zhou, Y.; Zeng, Y.; Yin, J.; Dong, T.; Sun, L.; Zhang, Y.; Xu, K. All-polarization-maintaining figure-of-9 soliton and dispersion-managed Er-doped fiber oscillators. Laser Phys. 2020, 30, 045101. [Google Scholar] [CrossRef]
- Łaszczych, Z.; Soboń, G. Dispersion management of a nonlinear amplifying loop mirror-based erbium-doped fiber laser. Opt. Express 2021, 29, 2690–2702. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Zhou, J.; Wang, L.; Huang, Y.; Li, Y.; Feng, Y.; Liu, L.; Li, T. Dissipative solitons in a compact Er-doped all-fiber figure-of-9 laser. Opt. Fiber Technol. 2021, 64, 102550. [Google Scholar] [CrossRef]
- Deng, Q.; Yin, K.; Zhang, J.; Zheng, X.; Jiang, T. A 200 MHz Compact environmentally-stable mode-locked Figure-9 fiber laser. IEEE Photonics J. 2021, 13, 1500605. [Google Scholar] [CrossRef]
- Han, Y.; Tian, H.; Meng, F.; Wang, K.; Cao, S. Environment-stable sub-100 fs Er: Fiber laser with a 3 dB bandwidth of 78 nm. Opt. Express 2022, 30, 48021. [Google Scholar] [CrossRef]
- Xiong, S.; Luo, D.; Liu, Y.; Wang, W.; Deng, Z.; Tang, Z.; Xie, G.; Zhou, L.; Zuo, Z.; Gu, C.; et al. Investigation of stable pulse mode-locking regimes in a NALM figure-9 Er-doped fiber laser. Opt. Express 2023, 31, 514–527. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Xia, H.; Fan, M.; Zheng, J.; Li, J.; Tian, X.; Zhou, D.; Huang, Z.; Zhang, F.; Zhang, R.; et al. Observation of wavelength tuning in a mode-locked Figure-9 fiber laser. Photonics 2023, 10, 184. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, Z.; Pan, R.; Zhang, T.; Feng, Y.; Hu, X.; Wang, Y.; Wu, S. Compact, repetition rate locked all-PM fiber femtosecond laser system based on low noise figure-9 Er:fiber laser. Opt. Laser Technol. 2023, 158, 108818. [Google Scholar] [CrossRef]
- Liu, W.; Shi, H.; Cui, J.; Xie, C.; Song, Y.; Wang, C.; Hu, M. Single-polarization large-mode-area fiber laser mode-locked with a nonlinear amplifying loop mirror. Opt. Lett. 2018, 43, 2848–2851. [Google Scholar] [CrossRef]
- Zhou, J.; Qi, W.; Pan, W.; Feng, Y. Dissipative soliton generation from a large anomalous dispersion ytterbium-doped fiber laser. Opt. Lett. 2020, 45, 5768–5771. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, W.; Feng, Y. Period multiplication in mode-locked figure-of-9 fiber lasers. Opt. Express 2020, 28, 17424–17433. [Google Scholar] [PubMed]
- Ma, Y.; Salman, S.; Li, C.; Mahnke, C.; Hua, Y.; Droste, S.; Fellinger, J.; Mayer, A.; Heckl, O.; Heyl, C.; et al. Compact, all-PM fiber integrated and alignment-free ultrafast Yb:fiber NALM laser with sub-femtosecond timing jitter. J. Light. Technol. 2021, 39, 4431–4438. [Google Scholar]
- Guo, K.; Li, C.; Ren, B.; Wang, T.; Wu, J.; Luo, Z.; Zhou, P.; Jiang, Z. Highly stable Q-switched and mode-locked pulse generation from an all-PM figure-9 fiber laser. Opt. Express 2022, 30, 35636–35646. [Google Scholar] [PubMed]
- Shi, Y.; Peng, Z.; Cheng, Z.; Xia, T.; Zhao, H.; Wan, S.; Wang, P. All-fiber polarization-maintaining dispersion-managed Figure-of-9 mode-locked laser. IEEE Photonic Techl. 2022, 34, 251–254. [Google Scholar]
- Wang, H.; Wang, Z.; Jia, W.; Song, L.; Chen, T.; Zou, J.; Dong, Z.; Luo, Z. 978 nm all-polarization-maintaining mode-locked fiber laser based on phase-biased nonlinear amplifying loop mirror. IEEE J. Sel. Top Quant. 2023, 29, 1100206. [Google Scholar]
- Zhou, J.; Qi, W.; Zeng, X.; Cheng, X.; Jiang, H.; Cui, S.; Feng, Y. All-polarization-maintaining, ultra-compact Tm-doped fiber laser designed for Mid-infrared comb. IEEE Photonics Technol. Lett. 2022, 34, 89–92. [Google Scholar]
- Łaszczych, Z.; Krakowski, M.; Soboń, G. Mode-locking dynamics in an all-PM Figure-nine Tm-doped fiber laser. Appl. Sci. 2022, 12, 10613. [Google Scholar] [CrossRef]
- Ren, B.; Li, C.; Wang, T.; Guo, K.; Zhou, P. All-polarization-maintaining Figure-9 mode-locked Tm-doped fiber laser with amplitude noise and timing jitter suppression. J. Light. Technol. 2023, 41, 733–738. [Google Scholar]
- Yang, K.; Feng, L.; Wei, K.; Liu, C.; Zhu, H.; Guo, C.; Yan, P.; Ruan, S.; Wang, J. All-polarization-maintaining NALM mode-locked Er/Yb-doped large-mode-area fiber oscillator. Opt. Lett. 2022, 47, 4893–4896. [Google Scholar]
- Mahnke, C.; Hua, Y.; Ma, Y.; Salman, S.; Lamb, T.; Schulz, S.; Heyl, C.M.; Cankaya, H.; Hartl, I. Long-term stable, synchronizable, low-noise picosecond Ho:fiber NALM oscillator for Ho:YLF amplifier seeding. Opt. Lett. 2022, 47, 822–825. [Google Scholar]
- Zou, J.; Dong, C.; Wang, H.; Du, T.; Luo, Z. Towards visible-wavelength passively mode-locked lasers in all-fibre format. Light. Sci. Appl. 2020, 9, 61. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.; Mu, X.; An, J.; Qi, Y.; Ding, J.; Bai, Z.; Wang, Y.; Lv, Z. Advances in 2 μm single-longitudinal-mode all-solid-state pulsed lasers. Infrared Laser Eng. 2024, 53, 20230730. [Google Scholar]
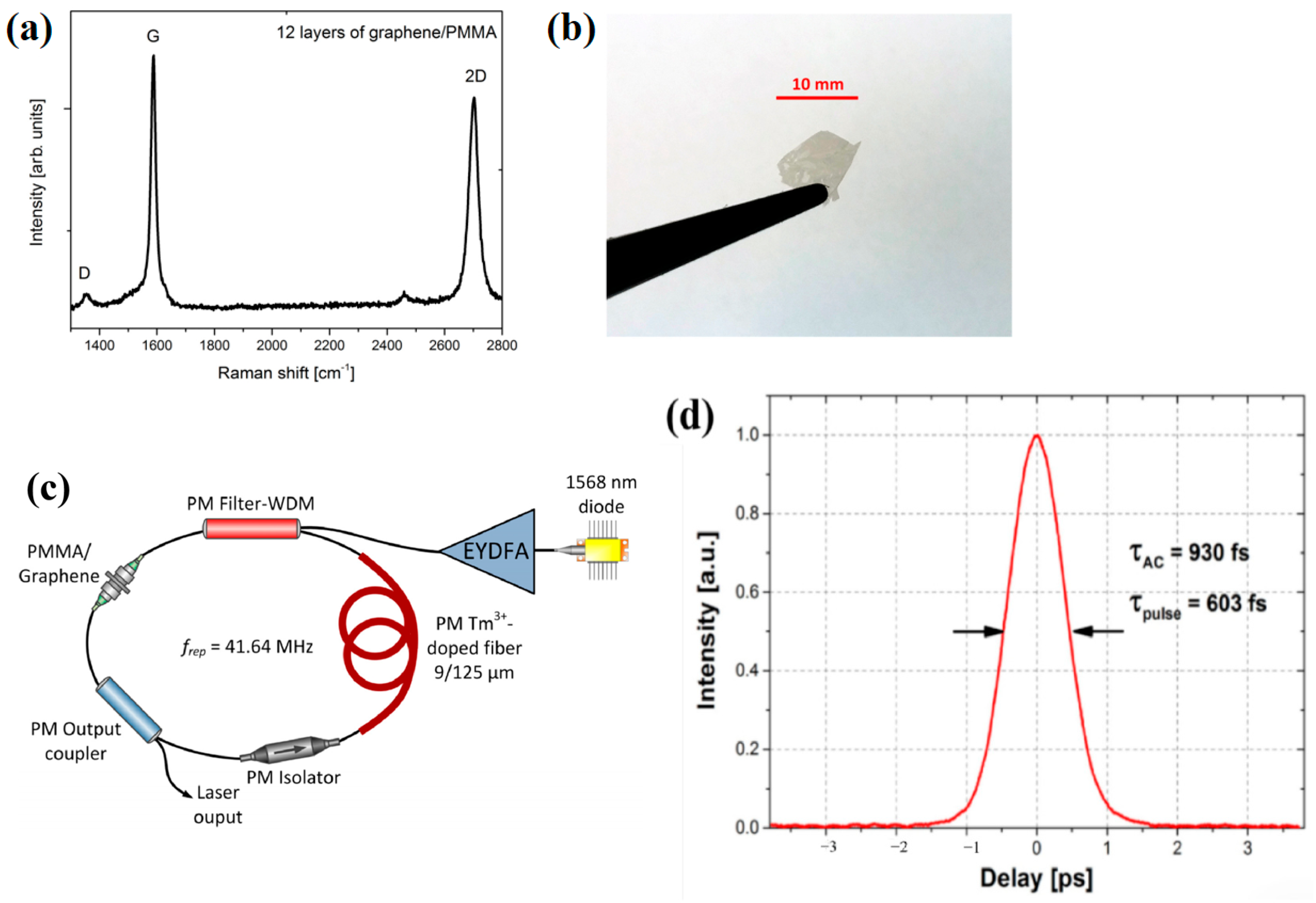
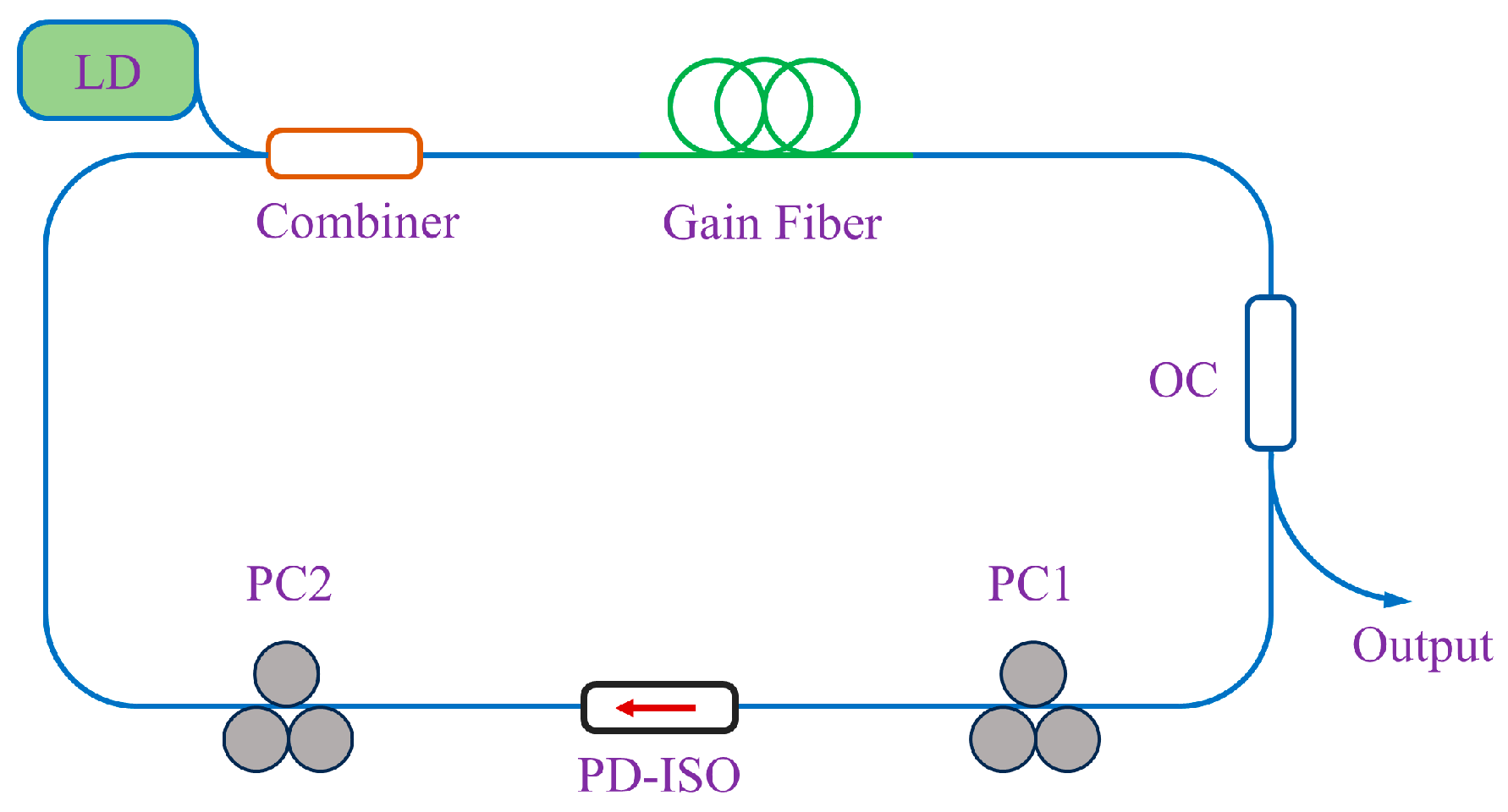

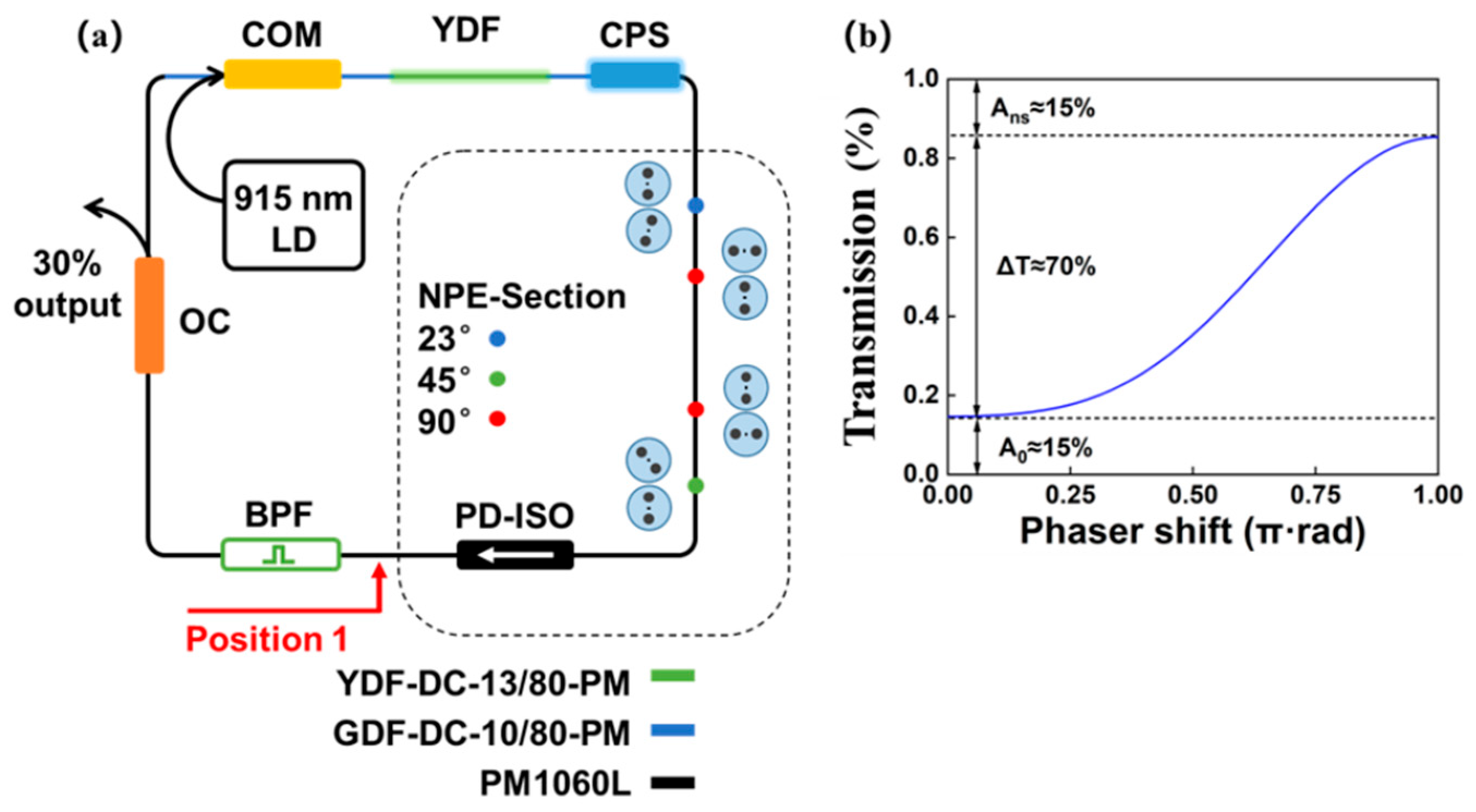
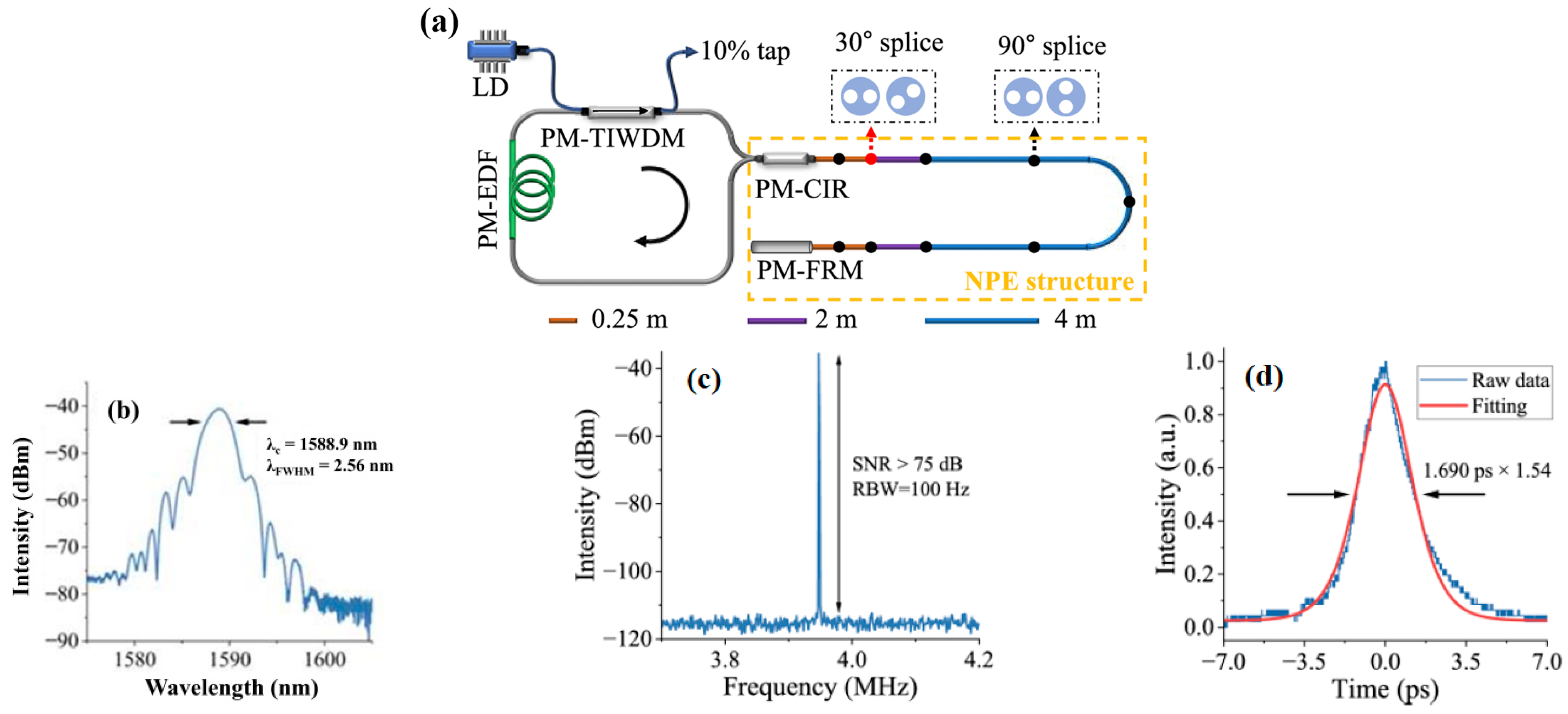

| Year | Gain Fiber | Laser Configuration | Total Dispersion | Duration | Energy | Repetition Rate | Ref. |
|---|---|---|---|---|---|---|---|
| 2005 | Yb | Linear cavity | 0.03 ps2 | 280 fs | 1 nJ | 17 MHz | [3] |
| 2008 | Yb | Sigma cavity | All-normal dispersion | 750 fs | 25 nJ | 63 MHz | [16] |
| 2008 | Yb | Linear cavity | 0.17 ps2 | 310 fs | 2.2 nJ | 33 MHz | [2] |
| 2012 | Yb | Sigma cavity | All-normal dispersion | 475 fs | 1.36 nJ | 38.1 MHz | [17] |
| 2018 | Yb | Linear cavity | All-normal dispersion | 20.6 ps | 1.2 nJ | 29 MHz | [18] |
| 2022 | Yb | Sigma cavity | −1.06 × 104 fs2 | 109 fs | 0.44 nJ | 553 MHz | [19] |
| 2022 | Yb | Sigma cavity | All-normal dispersion | 758 fs | 18.2 μJ | 495 KHz | [20] |
| 2022 | Yb | Linear cavity | NA | 486.5 ps | 0.45 mW | 13.2325 MHz | [21] |
| 2023 | Er | Linear cavity | −1500 fs2 | 303 fs | NA | 1.049 GHz | [22] |
| 2024 | Er | Linear cavity | NA | 30 ps | 6 nJ | 32.07 MHz | [23] |
| 2024 | Er | Linear cavity | NA | 299 fs | 1.71 pJ | 87.3 MHz | [24] |
| 2022 | Nd | Linear cavity | −0.05 ps2 | 1.8 ps | 130 pJ | 51 MHz | [25] |
| Year | Gain Fiber | Material | Total Dispersion | Duration | Energy/Power | Repetition Rate | Ref. |
|---|---|---|---|---|---|---|---|
| 2008 | Er | Carbon nanotubes | −0.104 ps2 | 107 fs | 4.8 mW | 41.3 MHz | [26] |
| 2009 | Er | Carbon nanotubes | −0.149 ps2 | 504 fs | 585 pJ | 21.6 MHz | [27] |
| 2016 | Er | Carbon nanotubes | NA | 6.94 ps | 63 pJ | 28.94 MHz | [28] |
| 2021 | Er | Carbon nanotubes | NA | 1.085 ps | 11.26 pJ | 17.77 MHz | [29] |
| 2023 | Tm | Carbon nanotubes | NA | 206 fs | 8.8 nJ | 52 MHz | [30] |
| 2012 | Er | Graphene | NA | 590 fs | 0.91 mW | 45.88 MHz | [5] |
| 2012 | Er | Graphene | NA | 570 fs | 24.5 pJ | 114.1 MHz | [35] |
| 2016 | Er | Graphene | 0.0172 ps2 | 148 fs | 25 pJ | 101 MHz | [32] |
| 2017 | Er | Graphene | 0.066 ps2 | 402 fs | 96 pJ | 60.64 MHz | [33] |
| 2015 | Tm | Graphene | −0.34 ps2 | 603 fs | 1.5 mW | 41.46 MHz | [31] |
| 2017 | Tm | Graphene | −0.024 ps2 | 205 fs | 220 pJ | 58.87 MHz | [34] |
| Year | Gain Fiber | Compensation Method | Laser Configuration | Total Dispersion | Duration | Energy | Repetition Rate | Ref. |
|---|---|---|---|---|---|---|---|---|
| 2016 | Yb | Cross-splicing | Ring cavity | All-normal dispersion | 11.7 ps | 2.1 nJ | 43.8 MHz | [40] |
| 2018 | Yb | Cross-splicing | Ring cavity | All-normal dispersion | 192 fs | 0.47 nJ | 111 MHz | [41] |
| 2017 | Yb | Cross-splicing | Ring cavity | 0.278 ps2 | 150 fs | 0.85 nJ | 20.54 MHz | [42] |
| 2020 | Yb | Cross-splicing | Ring cavity | All-normal dispersion | 260 fs | 0.2 nJ | 24.5 MHz | [44] |
| 2023 | Yb | Cross-splicing | Ring cavity | 0.316 ps2 | 5.99 ps | 0.54 nJ | 20.47 MHz | [45] |
| 2019 | Er | Cross-splicing | Ring cavity | 0.0099 ps2 | 90 fs | 77 pJ | 90.5 MHz | [43] |
| 2024 | Tm | Cross-splicing | Ring cavity | −1.77 ps2 | 2.02 ns | 21.64 nJ | 10.34 MHz | [46] |
| 2007 | Yb | Faraday mirror | Linear cavity | NA | 5.6 ps | 1.34 nJ | 5.96 MHz | [47] |
| 2014 | Yb | Faraday mirror | Linear cavity | NA | 17.8 ps | 68 pJ | 948 kHz | [48] |
| 2018 | Yb | Faraday mirror | Ring cavity | All-normal dispersion | 5.9 ps | 2.9 nJ | 6.7 MHz | [50] |
| 2020 | Yb | Faraday mirror | Linear cavity | NA | 0.8 ns | 26.9 nJ | 4.54 MHz | [51] |
| 2020 | Yb | Faraday mirror | Linear cavity | 0.039 ps2 | 161.37 fs | 2.265 mW | 6.17 MHz | [52] |
| 2018 | Er | Faraday mirror | Ring cavity | NA | 700 fs | 382 μW | 15.4 MHz | [49] |
| 2023 | Er | Cross-splicing + Faraday mirror | Ring cavity | −1.03 ps2 | 1.25 ps | 102 μW | 3.9 MHz | [53] |
| 2024 | Er | Cross-splicing + Faraday mirror | Ring cavity | −1.03 ps2 | 1.69 ps | 80 μW | 3.9 MHz | [53] |
| Year | Gain Fiber | Laser Configuration | Total Dispersion | Duration | Energy | Repetition Rate | Ref. |
|---|---|---|---|---|---|---|---|
| 2021 | Er | Linear cavity | NA | 1.20 ps | 0.11 nJ | 115 MHz | [56] |
| 2021 | Er | Linear cavity | −0.016 ps2 | 1.35 ps | 0.78 nJ | 133 MHz | [57] |
| 2021 | Yb | Linear cavity | −0.005 ps2 | 91 fs | 263 mW | 105 MHz | [58] |
| 2021 | Yb | Linear cavity | −0.104 ps2 | 0.83 ps | 400 pJ | 36.7 MHz | [64] |
| 2023 | Er | Linear cavity | −0.049 ps2 | 129 fs | 0.17 nJ | 105.8 MHz | [59] |
| 2023 | Er | Linear cavity | −0.0025 ps2 | 90 fs | 67.1 pJ | 116.76 MHz | [60] |
| 2023 | Er | Linear cavity | NA | 1.35 ps | 780 pJ | 133 MHz | [63] |
| 2023 | Yb | Linear cavity | −0.121 ps2 | 1.2 ps | 5.4 nJ | 17.3 MHz | [65] |
| 2024 | Ho | Linear cavity | −0.32 ps2 | 439 fs | 0.12 nJ | 61.67 MHz | [38] |
| 2025 | Er | Linear cavity | −0.62 ps2 | 550 fs | 429 fJ | 7 MHz | [67] |
| 2025 | Tm | Linear cavity | −0.612 ps2 | 409 fs | 259 pJ | 229 MHz | [61] |
| Year | Gain Fiber | NOLM /NALM | Total Dispersion | Duration | Energy/Power | Repetition Rate | Ref. |
|---|---|---|---|---|---|---|---|
| 2015 | Yb | NOLM | All-normal dispersion | 220 fs | 3.46 nJ | 15 MHz | [70] |
| 2020 | Yb | NOLM | Normal dispersion | 250 fs | 12 nJ | 7.56 MHz | [72] |
| 2021 | Yb | NOLM | 0.52 ps2 | 265 fs | 5.9 nJ | 9.45 MHz | [13] |
| 2022 | Yb | NOLM | 0.024 ps2 −0.098 ps2 −0.051 ps2 | 161 fs 98 fs 2.77 ps | 0.7 nJ 2.3 nJ 0.5 nJ | 18.207 MHz 34.083 MHz 25.537 MHz | [74] |
| 2023 | Yb | NOLM | 0.44 ps2 | 220 fs | 0.84 nJ | 10.7 MHz | [71] |
| 2025 | Yb | NOLM | NA | 12.6 ns | 4.1 nJ | 1.085 MHz | [75] |
| 2018 | Er | NOLM | −1.24 ps2 | 530.6 fs | 2.78 nJ | 3.63 MHz | [73] |
| 2025 | Er | NOLM | NA | 3.13 ps | 17.28 μW | 679.56 kHz | [76] |
| 2012 | Yb | NALM | 0.53 ps2 | 344 fs | 0.3 nJ | 10 MHz | [78] |
| 2012 | Yb | NALM | NA | <400 fs | 16 nJ 10 nJ 2.3 nJ | 1.7 MHz 3.7 MHz 10 MHz | [79] |
| 2013 | Yb | NALM | All-normal dispersion | 120 fs | 4.2 nJ | 10 MHz | [80] |
| 2015 | Yb | NALM | NA | 615 fs | 32 nJ | 2.47 MHz | [81] |
| 2016 | Yb | NALM | All-normal dispersion | 500 fs | 6.9 nJ | 506 KHz | [82] |
| 2016 | Yb | NALM | NA | 360 fs | 0.34 nJ | 11.6 MHz | [83] |
| 2017 | Yb | NALM | NA | NA | 11 nJ | 7.26 MHz | [84] |
| 2018 | Yb | NALM | 10.6 ps2 | 870 fs | 134 nJ | 448 kHz | [85] |
| 2018 | Yb | NALM | All-normal dispersion | 200 fs | 60 mW | 8.04 MHz | [86] |
| 2018 | Yb | NALM | 0.759 ps2 | 93 fs | 10 nJ | 6 MHz | [77] |
| 2020 | Yb | NALM | All-normal dispersion | 195 fs | 22 nJ | 8.7 MHz | [87] |
| 2020 | Yb | NALM | NA | 288 ps 1.38 ns | 2.4 nJ 20 nJ | 2.59 MHz | [88] |
| 2021 | Yb | NALM | NA | 1.16 ps | 27 μJ | 140 kHz | [89] |
| 2022 | Yb | NALM | All-normal dispersion | 114 fs | 27 nJ | 7.81 MHz | [90] |
| 2018 | Er | NALM | 0 | 500 fs | 10 nJ | 12 MHz | [97] |
| 2018 | Er | NALM | 0.82 ps2 | 500 fs | 110 pJ | 7.9 MHz | [98] |
| 2019 | Er | NALM | NA | 660 fs | 4 nJ | 1.96 MHz | [99] |
| 2024 | Er | NALM | NA | 20.6 ns | NA | 413.8 kHz | [100] |
| 2019 | Tm | NALM | −3.632 ps2 −0.877 ps2 −0.711 ps2 | >7 ns 388 ps 232 fs | 43.4 nJ 11 nJ 11.6 nJ | 4.06 MHz 16.59 MHz 20.39 MHz | [91] |
| 2020 | Tm | NALM | −4.8 ps2 | 13.5 ns | 29.1 nJ | 1.62 MHz | [94] |
| 2021 | Tm | NALM | −4.88 ps2 | 13.5 ns | 27.5 nJ | 1.59 MHz | [95] |
| 2022 | Tm | NALM | −2.1 ps2 | 357 fs | 20 mW | 7.267 MHz | [96] |
| 2022 | Tm | NALM | −4.8 ps2 | 303 fs | 13.6 mW | 3.25 MHz | [93] |
| 2017 | Er:Yb | NALM | −0.9274 ps2 −4.3084 ps2 | 4.35 ns 92 ns | 199 nJ 1.01 μJ | 4.6 MHz 0.994 MHz | [103] |
| 2019 | Nd | NALM | 2.9 ps2 | 6 ns | 20 nJ | 2.19 MHz | [101] |
| 2024 | Ho | NALM | 1.006 ps2 | 5.8 ns | 2.1 μJ | 7.081 MHz | [104] |
| 2019 | Er | NALM 3 × 3 | −0.133 ps2 | 194 fs | 7 mW | 36.56 MHz | [105] |
| 2020 | Yb | NALM 3 × 3 | All-normal dispersion | 178 fs | 1.2 nJ | 52 MHz | [106] |
| 2022 | Yb Tm | NALM 3 × 3 | 0.01 ps2 −0.58 ps2 | 125 fs 215 fs | 1.2 nJ 580 pJ | NA 30.3 MHz | [107] |
| 2023 | Yb | NALM 3 × 3 | 0.171 ps2 | 162 fs | 1.15 nJ | 11.62 MHz | [108] |
| Year | Gain Fiber | Location of the Phase Shifter | Total Dispersion | Duration | Energy/Power | Repetition Rate | All-Fiber | Ref. |
|---|---|---|---|---|---|---|---|---|
| 2019 | Er | Ring cavity | −0.0027 ps2 | 50 fs | 0.16 nJ | 85 MHz | Yes | [118] |
| 2019 | Er | Ring cavity | −0.015 ps2 | 477 fs | NA | 121 MHz | Yes | [119] |
| 2020 | Er | Linear cavity | +0.0005 ps2 | 70 fs | 1.4 nJ | 112 MHz | No | [120] |
| 2019 | Er | Ring cavity | +0.0036 ps2 | 132 fs | 18 mW | 44.9 MHz | No | [121] |
| 2020 | Er | Ring cavity | NA | 95 fs | 8.2 mW | 41 MHz | Yes | [122] |
| 2021 | Er | Linear cavity | −0.034 ps2 −0.001 ps2 | 250 fs 79 fs | 3.5 mW 6.6 mW | 51.55 MHz 80.12 MHz | No | [123] |
| 2021 | Er | Ring cavity | 0.041 ps2 | 354 fs | 0.29 nJ | 55.6 MHz | Yes | [124] |
| 2021 | Er | Ring cavity | −0.0124 ps2 | 510 fs | 0.66 mW | 201.14 MHz | Yes | [125] |
| 2022 | Er | Linear cavity | −1246 fs2 | 77 fs | 37.72 mW | 199.6 MHz | No | [126] |
| 2023 | Er | Ring cavity | 0.03 ps2 | 96.3 fs | NA | 59.3 MHz | No | [127] |
| 2023 | Er | Linear cavity | −0.09 ps2 | 142 fs | NA | 52 MHz | No | [128] |
| 2023 | Er | Ring cavity | −0.02 ps2 | 48.2 fs | 1.92 nJ | 103.4 MHz | Yes | [129] |
| 2016 | Yb | Reflection type phase shifter | 143,000 fs2 | 538 fs | 4.1 mW | 31.35 MHz | Yes | [115] |
| 2018 | Yb | Linear cavity | −0.04 ps2 −0.004 ps2 0.03 ps2 | 199 fs 68 fs 152 fs | 8 nJ 13 nJ 28 nJ | 26.4 MHz 30 MHz 72 MHz | No | [130] |
| 2020 | Yb | Ring cavity | −39.8 ps2 | 12.9 ps | 3.5 nJ | 26.4 MHz | Yes | [131] |
| 2021 | Yb | Ring cavity | −0.01 ps2 | 88 fs | 51 mW | 54.17 MHz | No | [133] |
| 2022 | Yb | Ring cavity | All-normal dispersion | 378 fs | 4.5 nJ | 12.5 MHz | Yes | [134] |
| 2022 | Yb | Ring cavity | −0.004 ps2 0.019 ps2 | 175 fs 228 fs | 0.26 nJ 0.52 nJ | 47.3 MHz 39.1 MHz | No | [135] |
| 2023 | Yb | Ring cavity | NA | 8.1 ps 5.7 ps | 0.32 nJ 0.37 nJ | 45.438 MHz | Yes | [136] |
| 2022 | Tm | Ring cavity | −0.0008 ps2 | 128 fs | 0.30 nJ | 121.3 MHz | Yes | [137] |
| 2023 | Tm | Linear cavity | −0.091 ps2 | 650 fs | 177 pJ | 52.4 MHz | No | [138] |
| 2023 | Tm | Ring cavity | −0.06 ps2 | 123 fs | 2.61 pJ | 30.6 MHz | Yes | [139] |
| 2022 | Er/Yb | Ring cavity | −0.704 ps2 | 1.7 ps | 13.8 nJ | 49.86 MHz | No | [140] |
| 2022 | Ho | Ring cavity | −0.43 ps2 | 1.3 ps | 140 pJ | 41.6 MHz | No | [141] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, M. Research Progress on All-Polarization-Maintaining Mode-Locked Fiber Lasers. Photonics 2025, 12, 366. https://doi.org/10.3390/photonics12040366
Wang Y, Wang M. Research Progress on All-Polarization-Maintaining Mode-Locked Fiber Lasers. Photonics. 2025; 12(4):366. https://doi.org/10.3390/photonics12040366
Chicago/Turabian StyleWang, Ying, and Minghong Wang. 2025. "Research Progress on All-Polarization-Maintaining Mode-Locked Fiber Lasers" Photonics 12, no. 4: 366. https://doi.org/10.3390/photonics12040366
APA StyleWang, Y., & Wang, M. (2025). Research Progress on All-Polarization-Maintaining Mode-Locked Fiber Lasers. Photonics, 12(4), 366. https://doi.org/10.3390/photonics12040366




