Optical Differentiation and Edge Detection Based on Birefringence of Uniaxial Crystals
Abstract
1. Introduction
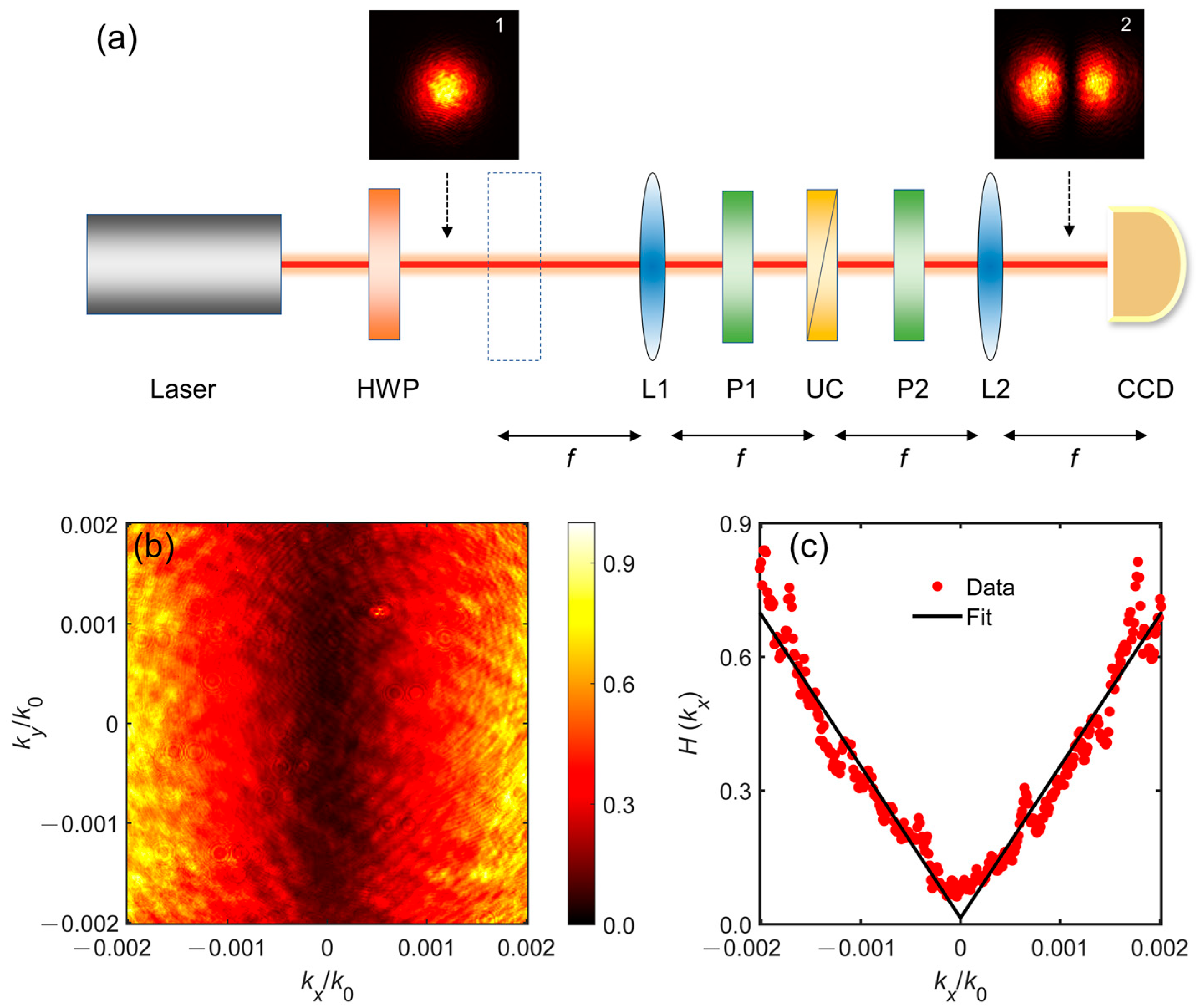
2. Theoretical Model
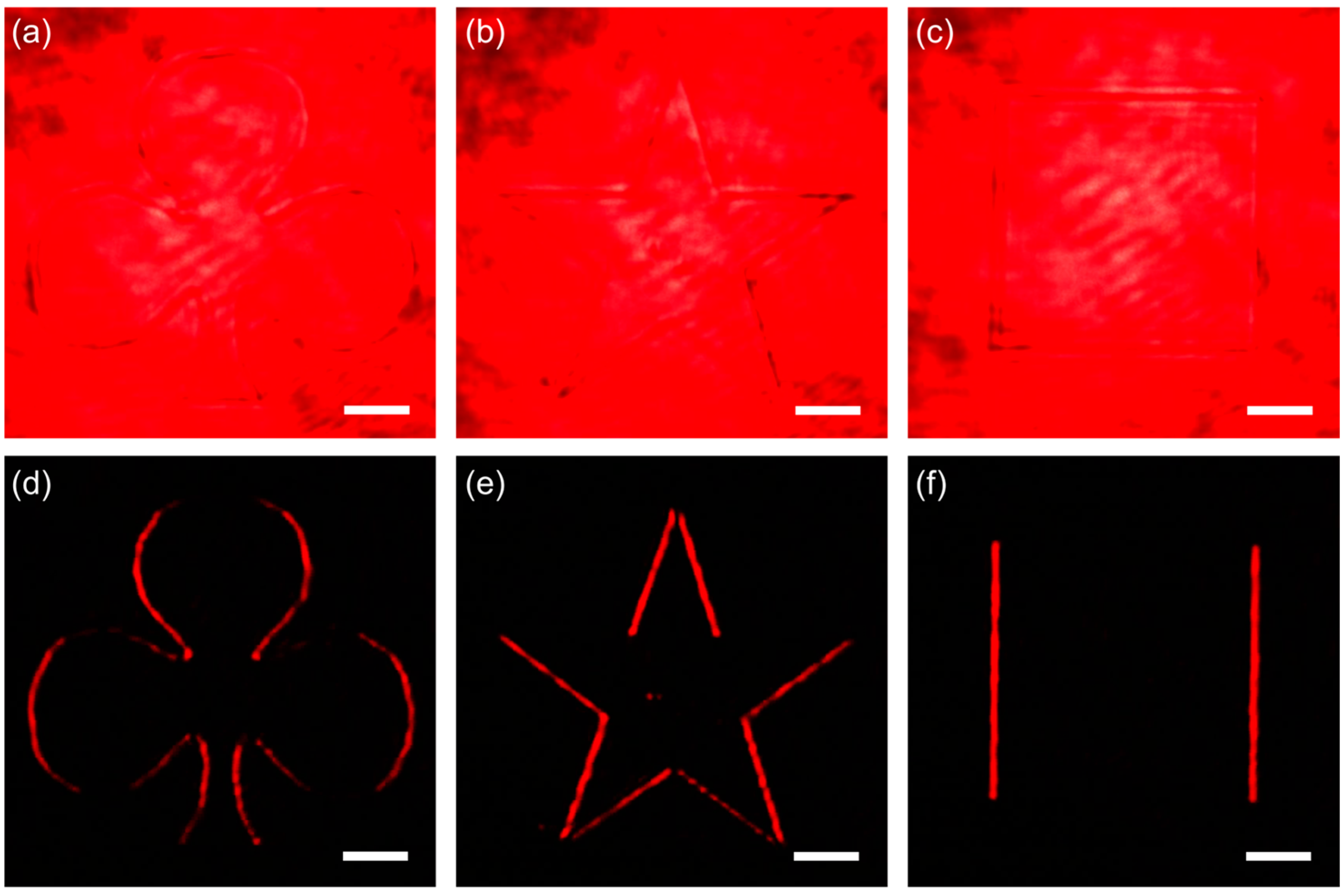
3. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hansson, S.O. Technology and mathematics. Philos. Technol. 2020, 33, 117–139. [Google Scholar]
- Zangeneh-Nejad, F.; Sounas, D.L.; Alù, A.; Fleury, R. Analogue computing with metamaterials. Nat. Rev. Mater. 2021, 6, 207–225. [Google Scholar]
- Huang, Y.D. Twenty years of photonics. ACS Photonics 2021, 8, 384–385. [Google Scholar]
- Vourkas, I.; Stathis, D.; Sirakoulis, G.C. Massively parallel analog computing: Ariadne’s thread was made of memristors. IEEE Trans. Emerg. Top. Comput. 2018, 6, 145–155. [Google Scholar]
- Santagiustina, M.; Chin, S.; Primerov, N.; Ursini, L.; Thévenaz, L. All-optical signal processing using dynamic Brillouin gratings. Sci. Rep. 2013, 3, 1594. [Google Scholar]
- He, S.; Wang, R.; Luo, H. Computing metasurfaces for all-optical image processing: A brief review. Nanophotonics 2022, 11, 1083–1108. [Google Scholar] [PubMed]
- Silva, A.; Monticone, F.; Castaldi, G.; Galdi, V.; Alù, A.; Engheta, N. Performing mathematical operations with metamaterials. Science 2014, 343, 160–163. [Google Scholar]
- Zhou, J.; Qian, H.; Chen, C.F.; Zhao, J.; Li, G.; Wu, Q.; Luo, H.; Wen, S.; Liu, Z. Optical edge detection based on high-efficiency dielectric metasurface. Proc. Natl. Acad. Sci. USA 2019, 116, 11137–11140. [Google Scholar]
- Cordaro, A.; Kwon, H.; Sounas, D.; Koenderink, A.F.; Alù, A.; Polman, A. High-index dielectric metasurfaces performing mathematical operations. Nano Lett. 2019, 19, 8418–8423. [Google Scholar]
- Komar, A.; Aoni, R.A.; Xu, L.; Rahmani, M.; Miroshnichenko, A.E.; Neshev, D.N. Edge detection with Mie-resonant dielectric metasurfaces. ACS Photonics 2021, 8, 864–871. [Google Scholar]
- He, Q.; Zhang, F.; Pu, M.B.; Ma, X.L.; Li, X.; Jin, J.J.; Guo, Y.H.; Luo, X.G. Monolithic metasurface spatial differentiator enabled by asymmetric photonic spin-orbit interactions. Nanophotonics 2020, 10, 741–748. [Google Scholar] [CrossRef]
- Kwon, H.; Cordaro, A.; Sounas, D.; Polman, A.; Alù, A. Dual-polarization analog 2D image processing with nonlocal metasurfaces. ACS Photonics 2020, 7, 1799–1805. [Google Scholar] [CrossRef]
- Wang, R.S.; He, S.S.; Chen, S.Z.; Shu, W.X.; Wen, S.C.; Luo, H.L. Computing metasurfaces enabled chiral edge image sensing. iScience 2022, 25, 104532. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Xu, W.; Yang, Q.; Zhang, W.; Wen, S.; Luo, H. All-optical object identification and three-dimensional reconstruction based on optical computing metasurface. Opto-Electron. Adv. 2023, 6, 230120. [Google Scholar] [CrossRef]
- Zong, M.; Liu, Y.; Lü, J.; Zhang, S.; Xu, Z. Two-dimensional optical differentiator for broadband edge detection based on dielectric metasurface. Opt. Lett. 2023, 48, 1902–1905. [Google Scholar] [CrossRef]
- Golovastikov, N.V.; Bykov, D.A.; Doskolovich, L.L. Resonant diffraction gratings for spatial differentiation of optical beams. Quantum Electron. 2014, 44, 984–988. [Google Scholar] [CrossRef]
- Parthenopoulos, A.; Darki, A.A.; Jeppesen, B.R.; Dantan, A. Optical spatial differentiation with suspended subwavelength gratings. Opt. Express 2021, 29, 6481–6494. [Google Scholar] [CrossRef]
- Fang, Y.S.; Ruan, Z.C. Optical spatial differentiator for a synthetic three-dimensional optical field. Opt. Lett. 2018, 43, 5893–5896. [Google Scholar] [CrossRef]
- Xu, C.Y.; Wang, Y.L.; Zhang, C.; Dagens, B.; Zhang, X. Optical spatiotemporal differentiator using a bilayer plasmonic grating. Opt. Lett. 2021, 46, 4418–4421. [Google Scholar] [CrossRef]
- Bezus, E.A.; Doskolovich, L.L.; Bykov, D.A.; Soifer, V.A. Spatial integration and differentiation of optical beams in a slab waveguide by a dielectric ridge supporting high-Q resonances. Opt. Express 2018, 26, 25156–25165. [Google Scholar] [CrossRef]
- Xu, D.; He, S.; Zhou, J.; Chen, S.; Wen, S.; Luo, H. Optical analog computing of two-dimensional spatial differentiation based on the Brewster effect. Opt. Lett. 2020, 45, 6867–6870. [Google Scholar] [PubMed]
- Youssefi, A.; Zangeneh-Nejad, F.; Abdollahramezani, S.; Khavasi, A. Analog computing by Brewster effect. Opt. Lett. 2016, 41, 3467–3470. [Google Scholar]
- Xu, D.; He, S.; Zhou, J.; Chen, S.; Wen, S.; Luo, H. Goos-Hänchen effect enabled optical differential operation and image edge detection. Appl. Phys. Lett. 2020, 116, 211103. [Google Scholar] [CrossRef]
- Zhu, T.; Lou, Y.; Zhou, Y.; Zhang, J.; Huang, J.; Li, Y.; Luo, H.; Wen, S.; Zhu, S.; Gong, Q.; et al. Generalized spatial differentiation from the spin Hall effect of light and its application in image processing of edge detection. Phys. Rev. Appl. 2019, 11, 034043. [Google Scholar]
- He, S.; Zhou, J.; Chen, S.; Shu, W.; Luo, H.; Wen, S. Spatial differential operation and edge detection based on the geometric spin Hall effect of light. Opt. Lett. 2020, 45, 877–880. [Google Scholar]
- Wang, R.; He, S.; Luo, H. Photonic spin-Hall differential microscopy. Phys. Rev. Appl. 2022, 18, 044016. [Google Scholar] [CrossRef]
- Zhu, T.; Guo, C.; Huang, J.; Wang, H.; Orenstein, M.; Ruan, Z.; Fan, S. Topological optical differentiator. Nat. Commun. 2021, 12, 680. [Google Scholar] [CrossRef] [PubMed]
- Song, B.W.; Wen, S.C.; Shu, W.X. Topological differential microscopy based on the spin-orbit interaction of light in a natural crystal. ACS Photonics 2022, 9, 3987–3994. [Google Scholar] [CrossRef]
- Dai, C.; Li, Z.; Shi, Y.; Wan, S.; Hu, W.; Li, Z. Hydrogel-scalable nanoslide for switchable optical spatial-frequency processing. Laser Photon. Rev. 2023, 17, 2200368. [Google Scholar] [CrossRef]
- Ji, Y.W.; Ma, X.K.; Hu, H.J.; Li, X.Z. Enhanced edge detection based on spin Hall effect in the uniaxial crystal. Front. Phys. 2022, 10, 862156. [Google Scholar]
- Yang, H.; Xie, W.; Chen, H.; Xie, M.; Tang, J.; Zheng, H.; Zhong, Y.; Yu, J.; Chen, Z.; Zhu, W. Spin-orbit optical broadband achromatic spatial differentiation imaging. Optica 2024, 11, 1008. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Shaked, N.T.; Zalevsky, Z.; Satterwhite, L.L. Biomedical Optical Phase Microscopy and Nanoscopy; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Liang, X.; Zhu, D.; Dai, Q.; Xie, Y.; Zhou, Z.; Peng, C.; Li, Z.; Chen, P.; Lu, Y.Q.; Yu, S.; et al. All-Optical Multi-Order Multiplexing Differentiation Based on Dynamic Liquid Crystals. Laser Photon. Rev. 2024, 18, 2400032. [Google Scholar] [CrossRef]
- Yang, Q.; Xu, D.; Chen, S.; Wen, S.; Luo, H. Reconstruction of wave function via spin-orbit interaction of light. Phys. Rev. Appl. 2023, 20, 054011. [Google Scholar]
- Zhu, J.; Wang, A.; Liu, X.; Liu, Y.; Zhang, Z.; Gao, F. Reconstructing the wave function through the momentum weak value. Phys. Rev. A 2021, 104, 032221. [Google Scholar]
- Liu, J.; Yang, Q.; Chen, S.; Xiao, Z.; Wen, S.; Luo, H. Intrinsic Optical Spatial Differentiation Enabled Quantum Dark-Field Microscopy. Phys. Rev. Lett. 2022, 128, 193601. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Huang, P.; Tang, X.; Yi, X. Optical Differentiation and Edge Detection Based on Birefringence of Uniaxial Crystals. Photonics 2025, 12, 336. https://doi.org/10.3390/photonics12040336
Chen X, Huang P, Tang X, Yi X. Optical Differentiation and Edge Detection Based on Birefringence of Uniaxial Crystals. Photonics. 2025; 12(4):336. https://doi.org/10.3390/photonics12040336
Chicago/Turabian StyleChen, Xu, Ping Huang, Xuan Tang, and Xunong Yi. 2025. "Optical Differentiation and Edge Detection Based on Birefringence of Uniaxial Crystals" Photonics 12, no. 4: 336. https://doi.org/10.3390/photonics12040336
APA StyleChen, X., Huang, P., Tang, X., & Yi, X. (2025). Optical Differentiation and Edge Detection Based on Birefringence of Uniaxial Crystals. Photonics, 12(4), 336. https://doi.org/10.3390/photonics12040336



