Reliability Analysis of Multi-Autonomous Underwater Vehicle Cooperative Systems Based on Fuzzy Control
Abstract
1. Introduction
2. Reliability Analysis of Multi-AUV Cooperative Systems
2.1. Reliability Analysis of Multi-AUV Systems
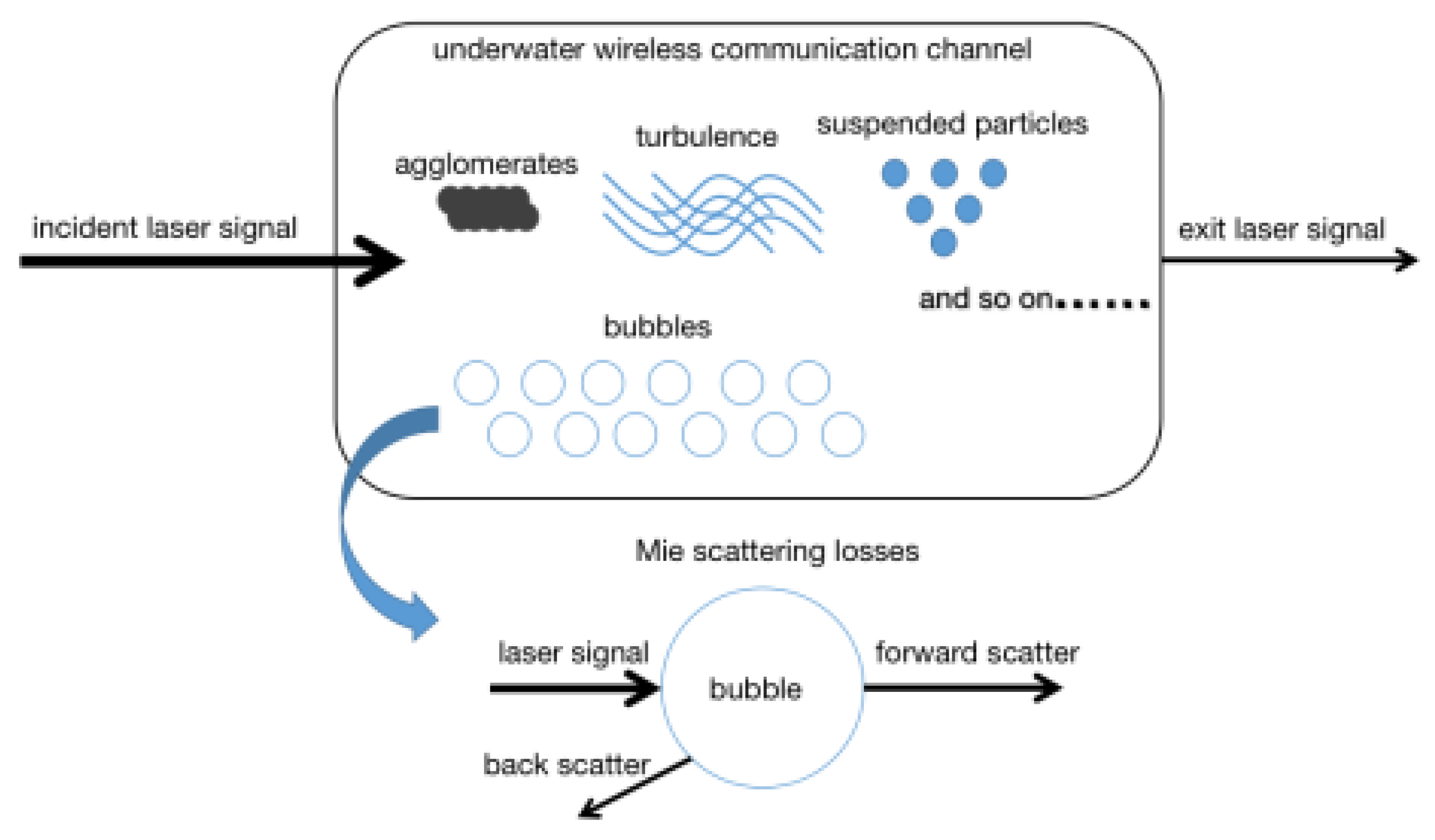
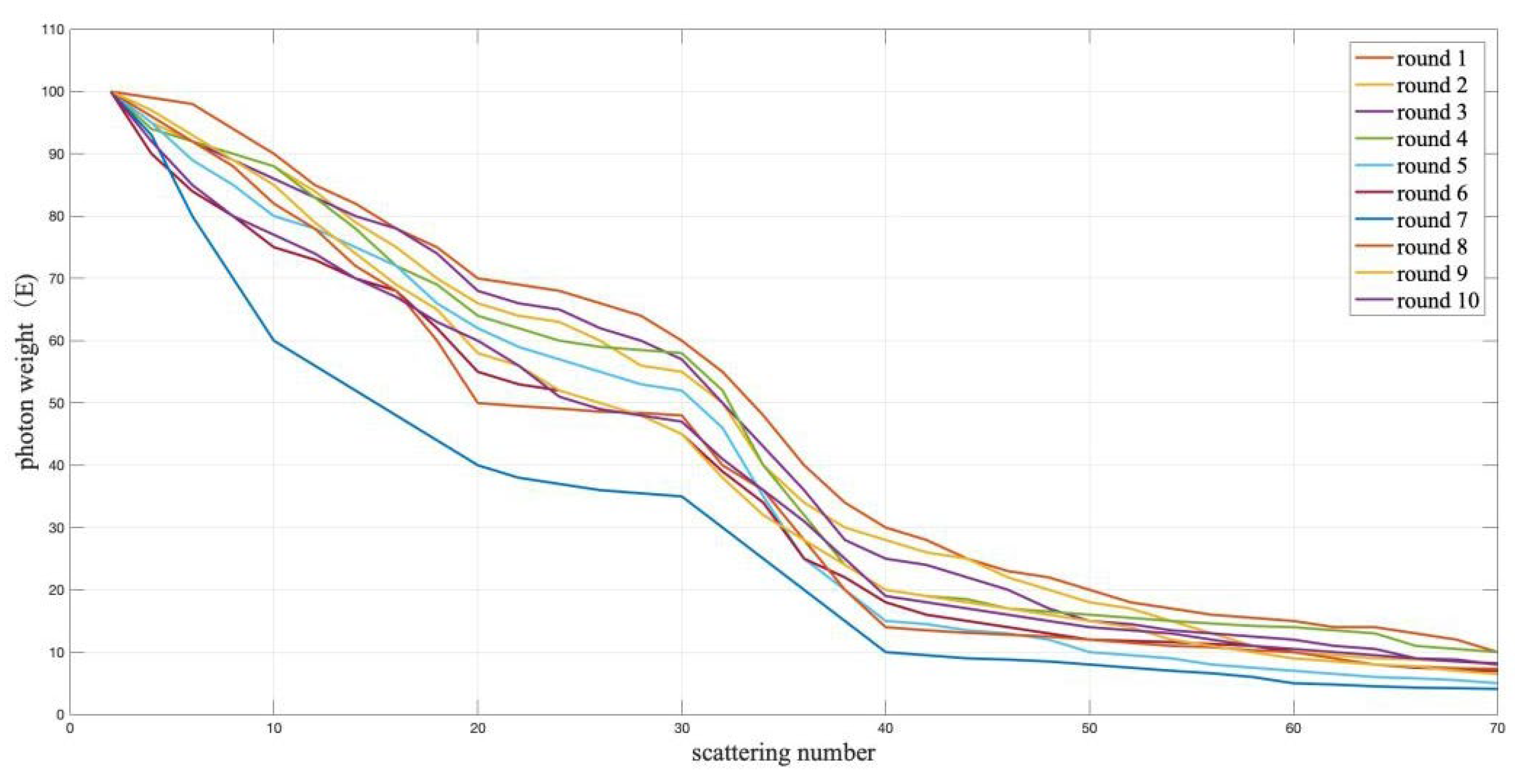
2.2. Influence of Complex Environments on AUVs
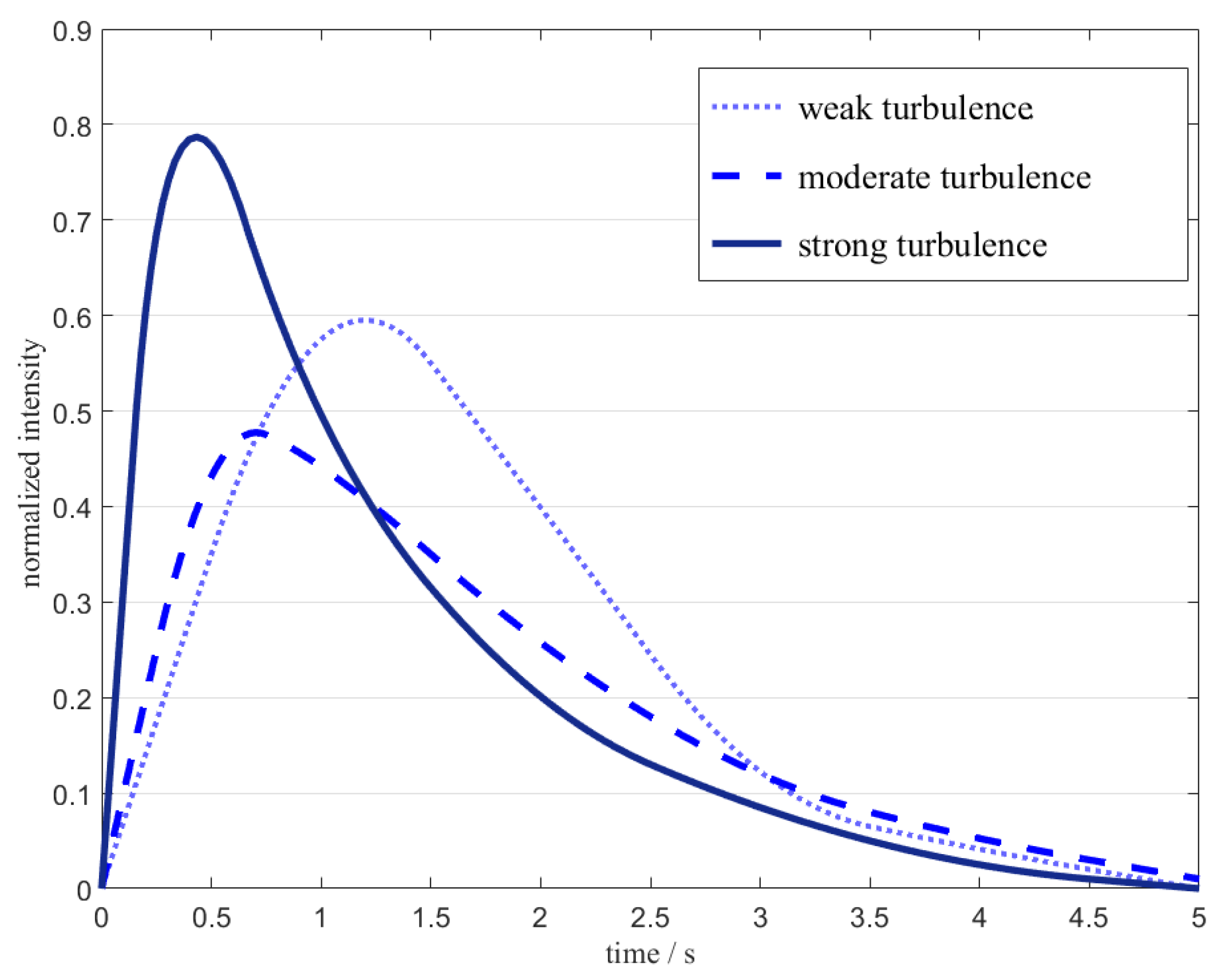
2.3. Influence of Complex Environments on Group Communication
2.4. Reliability Calculation Model Based on Environmental Factors
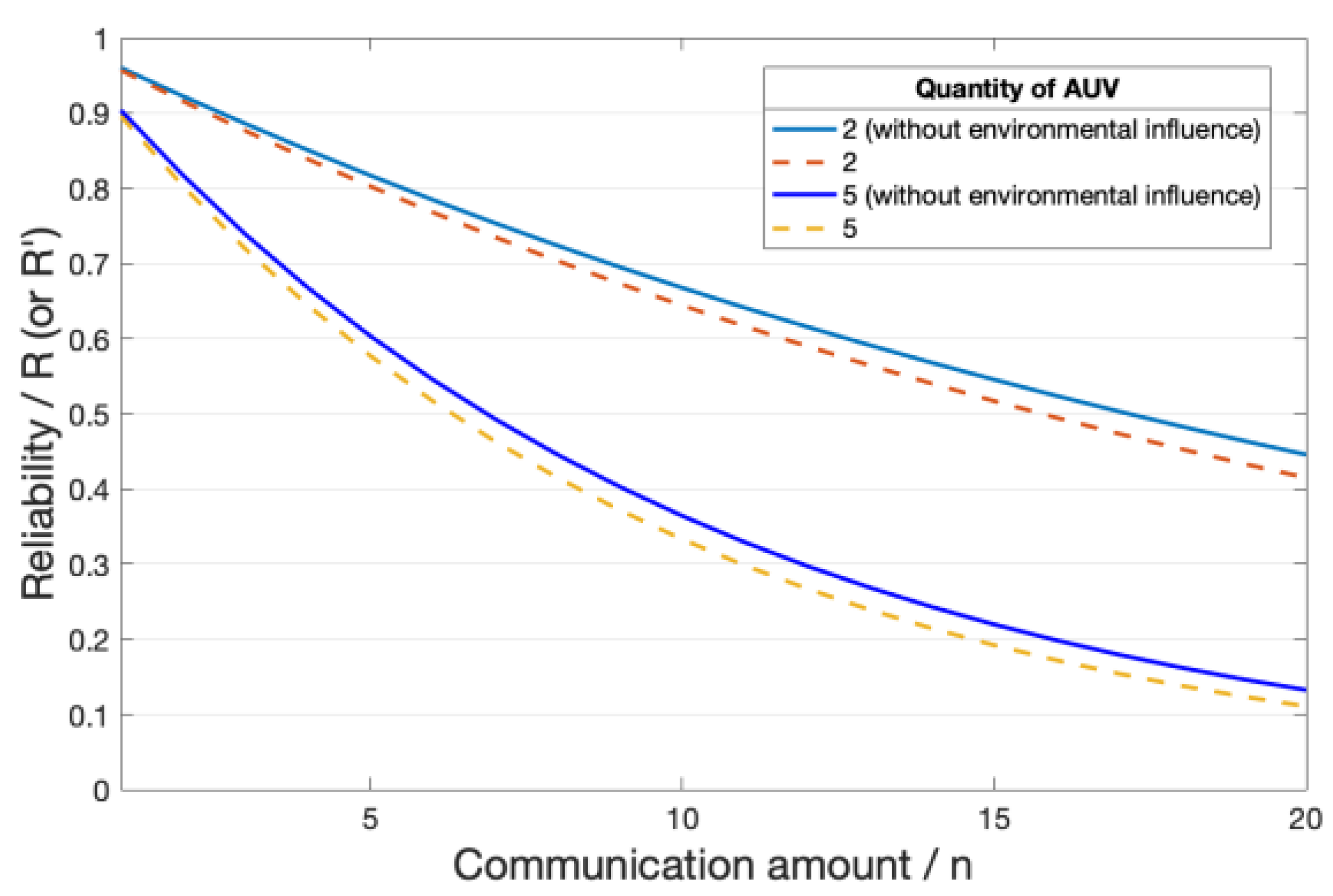
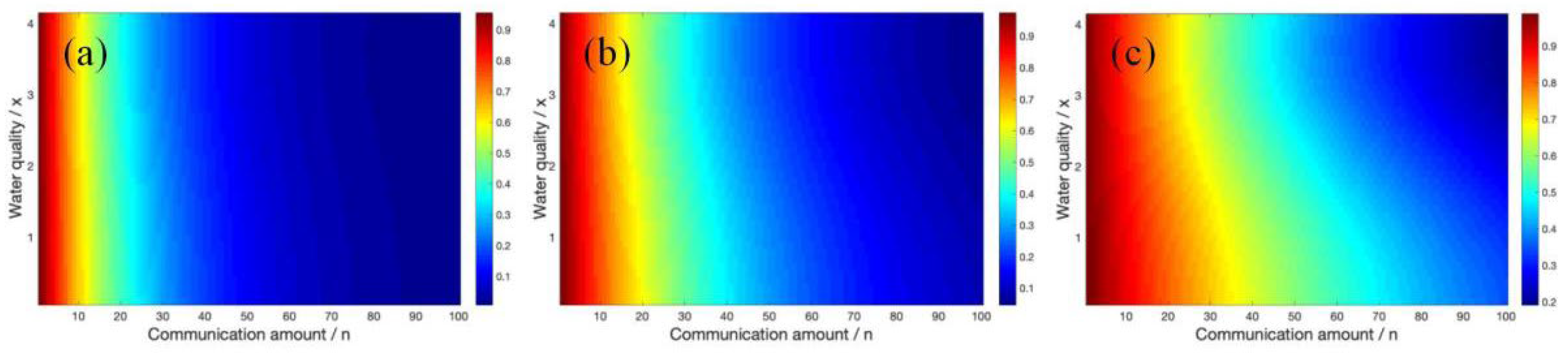
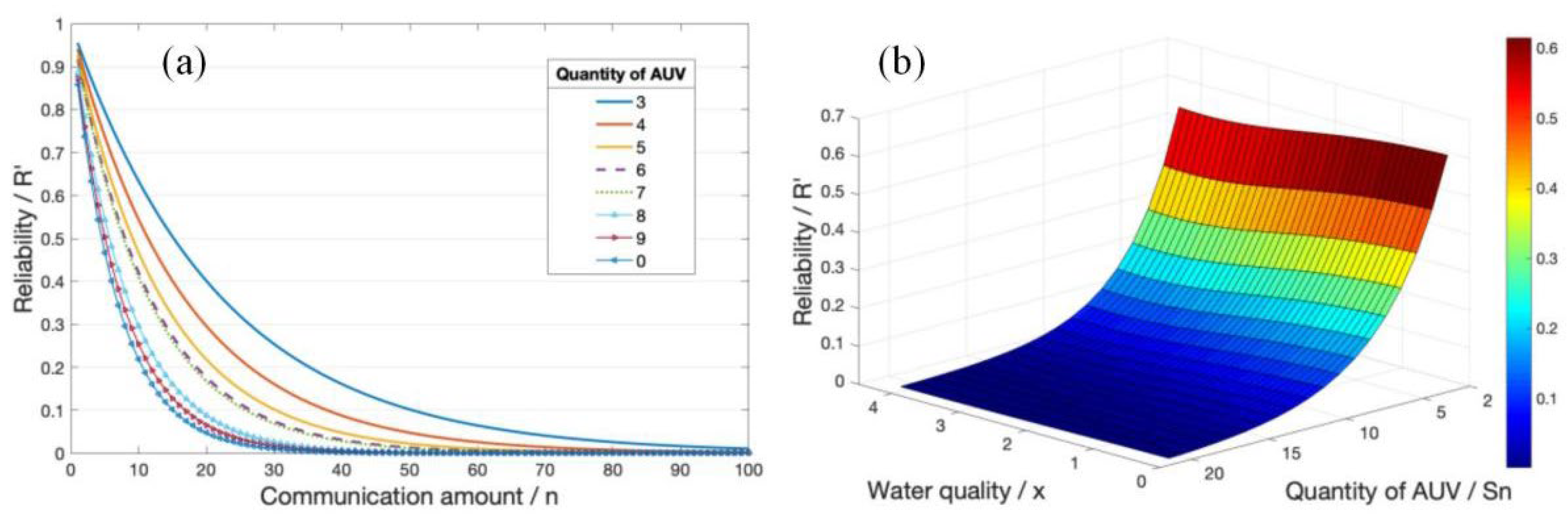
3. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yellepeddi, A.; Preisig, J.C. Representing the structure of underwater acoustic communication data using probabilistic graphical models. J. Acoust. Soc. Am. 2014, 136, 2266. [Google Scholar] [CrossRef]
- Vali, Z.; Gholami, A.; Ghassemlooy, Z.; Michelson, D.G.; Omoomi, M.; Noori, H. Modeling turbulence in underwater wireless optical communications based on Monte Carlo simulation. J. Opt. Soc. Am. A 2017, 34, 1187–1193. [Google Scholar] [CrossRef]
- Saotome, M.; Kozawa, Y.; Umeda, Y.; Habuchi, H. Differential-OOK System for Underwater Visible-Light Communications. J. Signal Process. 2016, 20, 175–178. [Google Scholar] [CrossRef]
- Adnan, S.A.; Alchalaby, A.; Hassan, H.A. Future Optimization Algorithm to Estimate Attenuation in 532 nm Laser Beam of UWOC-Channel: Improved Neural Network Model. Math. Model. Eng. Probl. 2021, 8, 453–460. [Google Scholar] [CrossRef]
- Shen, Y.; Shao, K.; Ren, W.; Liu, Y. Diving control of Autonomous Underwater Vehicle based on improved active disturbance rejection control approach. Neurocomputing 2016, 173 Pt 3, 1377–1385. [Google Scholar] [CrossRef]
- Rigby, P.; Pizarro, O.; Williams, S. Improved AUV navigation through multi-sensor data fusion. Sea Technol. 2007, 48, 15–22. [Google Scholar] [CrossRef]
- Fan, W.; Zhang, D.; Dong, J.; Zhang, Y. Design and implementation of AUV underwater acoustic frequency hopping communication modem. Harbin Gongcheng Daxue Xuebao 2014, 35, 1473–1479. [Google Scholar] [CrossRef]
- Mehrparvar, M.; Majak, J.; Karjust, K. A comparative analysis of Fuzzy AHP and Fuzzy VIKOR methods for prioritization of the risk criteria of an autonomous vehicle system. Proc. Estonian Acad. Sci. 2024, 73, 116–123. [Google Scholar] [CrossRef]
- Sotzing, C.C.; Lane, D.M. Improving the coordination efficiency of limited-communication multi–autonomus underwater vehicle operations using a multiagent architecture. J. Field Robot. 2010, 27, 412–429. [Google Scholar] [CrossRef]
- Chamseddine, A.; Zhang, Y.; Rabbath, C.A.; Theilliol, D. Trajectory Planning and Replanning Strategies Applied to a Quadrotor Unmanned Aerial Vehicle. J. Guid. Control. Dyn. 2012, 35, 1667–1671. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Shen, L.; Zhao, S.; Cong, Y.; Li, J.; Yin, D.; Jia, S.; Xiang, X. Mission Oriented Miniature Fixed-wing UAV Swarms: A Multi-layered and Distributed Architecture. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 52, 1588–1602. [Google Scholar] [CrossRef]
- Singh, M.; Elsayed, E.E.; Alayedi, M.; Aly, M.H.; El-Mottaleb, S.A.A. Performance analysis in spectral-amplitude-coding-optical-code-division-multiple-access using identity column shift matrix code in free space optical transmission systems. Opt. Quantum Electron. 2024, 56, 795. [Google Scholar] [CrossRef]
- Elsayed, E.E. Atmospheric turbulence mitigation of MIMO-RF/FSO DWDM communication systems using advanced diversity multiplexing with hybrid N-SM/OMI M-ary spatial pulse-position modulation schemes. Opt. Commun. 2024, 562, 130558. [Google Scholar] [CrossRef]
- Gerkey, B.P.; Matarić, M.J. A Formal Analysis and Taxonomy of Task Allocation in Multi-Robot Systems. Int. J. Robot. Res. 2004, 23, 939–954. [Google Scholar] [CrossRef]
- Dong, L.; Xu, H.; Feng, X.; Han, X.; Yu, C. An Adaptive Target Tracking Algorithm Based on EKF for AUV with Unknown Non-Gaussian Process Noise. Appl. Sci. 2020, 10, 3413. [Google Scholar] [CrossRef]
- Oubei, H.M.; Zedini, E.; Elafandy, R.T.; Kammoun, A.; Abdallah, M.; Ng, T.K.; Hamdi, M.; Alouini, M.-S.; Ooi, B.S. Simple statistical channel model for weak temperature-induced turbulence in underwater wireless optical communication systems. Opt. Lett. 2017, 42, 2455–2458. [Google Scholar] [CrossRef]
- Song, W.; Chen, Z.; Sun, M.; Sun, Q. Observation reconstruction and disturbance compensation-based position control for autonomous underwater vehicle. Syst. Sci. Control. Eng. 2022, 10, 12. [Google Scholar] [CrossRef]
- He, X.; Li, M.; Rao, L. Underwater Bessel-like beams with enlarged depth of focus based on fiber microaxicon. Chin. Opt. Lett. 2022, 20, 072601. [Google Scholar] [CrossRef]
- Kou, L.; Zhang, J.; Zhang, P.; Yang, Y.; He, F. Composite channel modeling for underwater optical wireless communication and analysis of multiple scattering characteristics. Opt. Express 2023, 31, 11320–11334. [Google Scholar] [CrossRef]
- Jian-Cheng, Y.U.; Chen, K.; Zhang, J. Intelligent Control Method for AUV Formation Under Different Communication and Positioning Methods: A Review. J. Unmanned Undersea Syst. 2023, 31, 30–37. [Google Scholar] [CrossRef]
- Liang, Q.; Sun, T.; Ou, J. System Reliable Probability for Multi-AUV Cooperative Systems under the Influence of Current. J. Navig. 2019, 72, 1649–1659. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, L.; Zhang, C.; Bao, B.; Li, Q.; Wang, L.; Song, Z.; Li, D. Deep-learning enabled smart insole system aiming for multifunctional foot-healthcare applications. Exploration 2023, 4, 20230109. [Google Scholar] [CrossRef] [PubMed]
- Liang, Q.; Ou, J.; Yan, X.; Zhang, X. Effect of Nodes Movement on All-Terminal Reliability of Multi-AUV Cooperative System. In Proceedings of the OCEANS 2018 MTS/IEEE Charleston, Charleston, SC, USA, 22–25 October 2018. [Google Scholar] [CrossRef]
- Chen, X.; Bose, N.; Brito, M.; Khan, F.; Thanyamanta, B.; Zou, T. A Review of Risk Analysis Research for the Operations of Autonomous Underwater Vehicles. Reliab. Eng. Syst. Saf. 2021, 216, 108011. [Google Scholar] [CrossRef]
- Yang, H.; Wang, S.; Liu, K.; Jiang, J.; Li, Y.; Li, Z.; Zhang, P.; Dai, X.; Liub, T. Real-time self-calibrating phase-shifted demodulation method based on polarized low-coherence interference for optical fiber acoustic sensor. IEEE Sens. J. 2022, 22, 8537–8543. [Google Scholar] [CrossRef]
- He, Y.; Gao, H. Risk assessment modelling for power optical backbone communication network based on MLFSR-oriented sampling Markov technique. Int. J. Ind. Syst. Eng. 2018, 30, 468. [Google Scholar] [CrossRef]
- Impicciatore, A.; Lun, Y.Z.; Pepe, P.; D’Innocenzo, A. Optimal Output-Feedback Control Over Markov Wireless Communication Channels. IEEE Trans. Autom. Control. 2024, 3, 69. [Google Scholar] [CrossRef]
- Feng, Q.; Guo, X.; Sun, B.; Dui, H.; Ren, Y.; Hai, X.; Yang, D.; Wang, Z. Reliability Modeling of Dynamic Spatiotemporal IoT Considering Autonomy and Cooperativity Based on Multiagent. IEEE Internet Things J. 2023, 11, 4712–4721. [Google Scholar] [CrossRef]
| H | j | k | σI2 |
|---|---|---|---|
| 1.620 | 0.765 | 1.440 | 0.311 |
| 1.622 | 1.020 | 0.851 | 0.880 |
| 1.408 | 0.630 | 0.840 | 1.025 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Y.; Yao, Y.; Zhang, Y.; Zuo, F. Reliability Analysis of Multi-Autonomous Underwater Vehicle Cooperative Systems Based on Fuzzy Control. Photonics 2025, 12, 333. https://doi.org/10.3390/photonics12040333
Hao Y, Yao Y, Zhang Y, Zuo F. Reliability Analysis of Multi-Autonomous Underwater Vehicle Cooperative Systems Based on Fuzzy Control. Photonics. 2025; 12(4):333. https://doi.org/10.3390/photonics12040333
Chicago/Turabian StyleHao, Yu, Yuan Yao, Yanbo Zhang, and Fang Zuo. 2025. "Reliability Analysis of Multi-Autonomous Underwater Vehicle Cooperative Systems Based on Fuzzy Control" Photonics 12, no. 4: 333. https://doi.org/10.3390/photonics12040333
APA StyleHao, Y., Yao, Y., Zhang, Y., & Zuo, F. (2025). Reliability Analysis of Multi-Autonomous Underwater Vehicle Cooperative Systems Based on Fuzzy Control. Photonics, 12(4), 333. https://doi.org/10.3390/photonics12040333





