Study of Propagation Characteristics of Light Beam with Orbital Angular Momentum (OAM) Through a Chiral Medium

Abstract

The interaction of a Gaussian vortex beam (GVB) with metamaterials during its propagation is of significant interest to the optical community. These GVBs are classified as structured light beams that possess orbital angular momentum (OAM). Understanding the behavior of structured light beams is essential for clarifying fundamental interaction mechanisms with metamaterial structures. So, this work delves into the investigation of the propagation characteristics of a GVB within a chiral material. The analytical expressions for GVB propagating through a chiral medium are obtained by using the extended Huygens–Fresnel diffraction integral formula and the optical ABCD matrix system. In a chiral medium, GVB exhibits a tendency to fragment into a left circularly polarized (LCP) beam and a right circularly polarized (RCP) beam, each following its unique propagation paths. The beam intensity and gradient force are computed and discussed for OAM mode number, beam waist radius, and chirality parameter. This research will be quite helpful for light manipulation, optical sorting, optical radiation force, the radiative transfer process, and optical guiding.

1. Introduction

Since 1992, vortex beams have fascinated the consideration of the scientific community due to their potential applications in research and industry [1]. Vortex beams denote a beam characterized by zero intensity about the propagation axis and a unique phase factor. One of the characteristic vortex beams is the Gaussian vortex beam (GVB). The vortex beams have an axial phase singularity with a spiral wave front. This helical wavefront can be nominated as $exp\left(im\phi \right),$ where $m$ denotes an orbital angular momentum (OAM) mode number $\phi$ specifies an azimuthal angle, respectively [2]. This OAM mode index $m$ symbolizes the number of twists regarding the phase profile. These vortex beams have lots of potential applications in several fields, such as optical communication [3,4], computer-generated holograms, OAM-based radar cross-section (RCS) analysis, imaging, propagation and scattering, optical information transmission, the internet of things, data processing, the shaping of laser beams, and the study of chiral molecules [5,6,7,8,9,10,11].

Due to the ability to transfer OAM of vortex beams to tiny particles, vortex beams are particularly interesting. Thus, vortex beams have potential uses in the processing of quantum information, non-linear optics, optical tweezers, light manipulation, and trapping. Furthermore, studies have demonstrated that GVBs withstand turbulence and electromagnetic scattering phenomena more effectively than other types of beams [5]. GVBs thus provide a potential way to examine and analyze the characteristics of the materials. Recent years have seen an examination of the interaction of vortex beams with diverse materials, mostly due to their distinctive properties and numerous fascinating applications, such as waveguides, remote sensing, light filters, and beam shaping [12,13,14,15,16]. These conventional materials, along with their distinctive properties, have been utilized commercially across various scientific domains, including engineering, the aeronautical industry, materials science, manufacturing, and many others [17].

The optical industry, modernization, and infrastructure are closely associated with the propagation of electromagnetic vortex beams. The micro-particles in any medium can also have an effect on them. The occupation of OAM on the vortex beams has considerable worth in this regard, as it reduces the loss of information while propagating through the medium. As a result, OAM can increase the capacity of wireless communication systems, permitting high bandwidth. Therefore, we analyze the interaction of vortex beams through chiral materials, drawing inspiration from their features.

Chiral materials and electromagnetic field interactions have drawn a lot of attention in recent years [18,19,20]. They have distinct characteristics and uses in the microwave region owing to their remarkable electromagnetic field response, which is absent from natural materials [21,22]. Thanks to their optical activity, chiral media can flip the polarization plane of incoming linearly polarized light. Incorporating the cross-coupling factors between the excitations of electromagnetic fields and the constitutive relations defining the chiral medium causes chiral scatterers to generate the co-polarized and cross-polarized scattered field components, respectively [23,24,25].

To lower the target structure’s radar cross-section, chiral-coated material is often used [26]. Chirality, which signifies structures with broken mirror symmetry, arises universally across various disciplines [27]. Moreover, the chiral medium comprises non-linear, non-centrosymmetric, and thermally stable molecules. As the light wave traverses the chiral media, the beam divides into LCP and RCP components [23]. This polarized beam is referred to as circular birefringence.

The chiral medium possesses extensive capabilities in the realm of non-linear optics owing to its structural and optical characteristics. Both left-handed and right-handed circularly polarized light have quite diverse effects on chiral materials [18]. These unequal responses are recognized as circular dichroism (CD), which has been extensively embraced in various scientific disciplines. Recent research indicates that chiral materials may exhibit varying responses to the handedness of twisted light with OAM [26]. Unlike conventional optical media, chiral media demonstrates a variety of distinct characteristics.

Many studies have been done on the movement of different vortex beams in different types of media, such as random media [28], gradient index [11], biological tissues [2], atmospheric turbulence [29], dispersive media [30], and the atmosphere [31]. Electromagnetic scattering also influences the propagation of a light beam through any material medium [32]. Also, the interaction of light beams with OAM in an astigmatic medium has been considered and yielded an impactful study for optical researchers [33,34,35]. As a result, studying how vortex beams interact with different materials is important for figuring out how well the beams can scatter, propagate, and transmit signals through a wide range of scattering media. To date, GVB propagation characteristics in chiral media have not been documented.

The following is the outline of the paper. We started by utilizing the Huygens–Fresnel diffraction integral formula and the theory of matrix optics in Section 2 “Theoretical Model” to obtain analytical formulas for electric fields regarding the propagation of GVB in a chiral medium. Then, in Section 3 “Results and Discussion”, we examined and discussed the GVB propagation characteristics across chiral media. To figure out the gradient force and intensity of the GVB moving through a chiral medium, we use a range of topological charges, beam waist radii, and chirality parameters. The Section 4 “Conclusions” concludes the work.

2. Theoretical Model

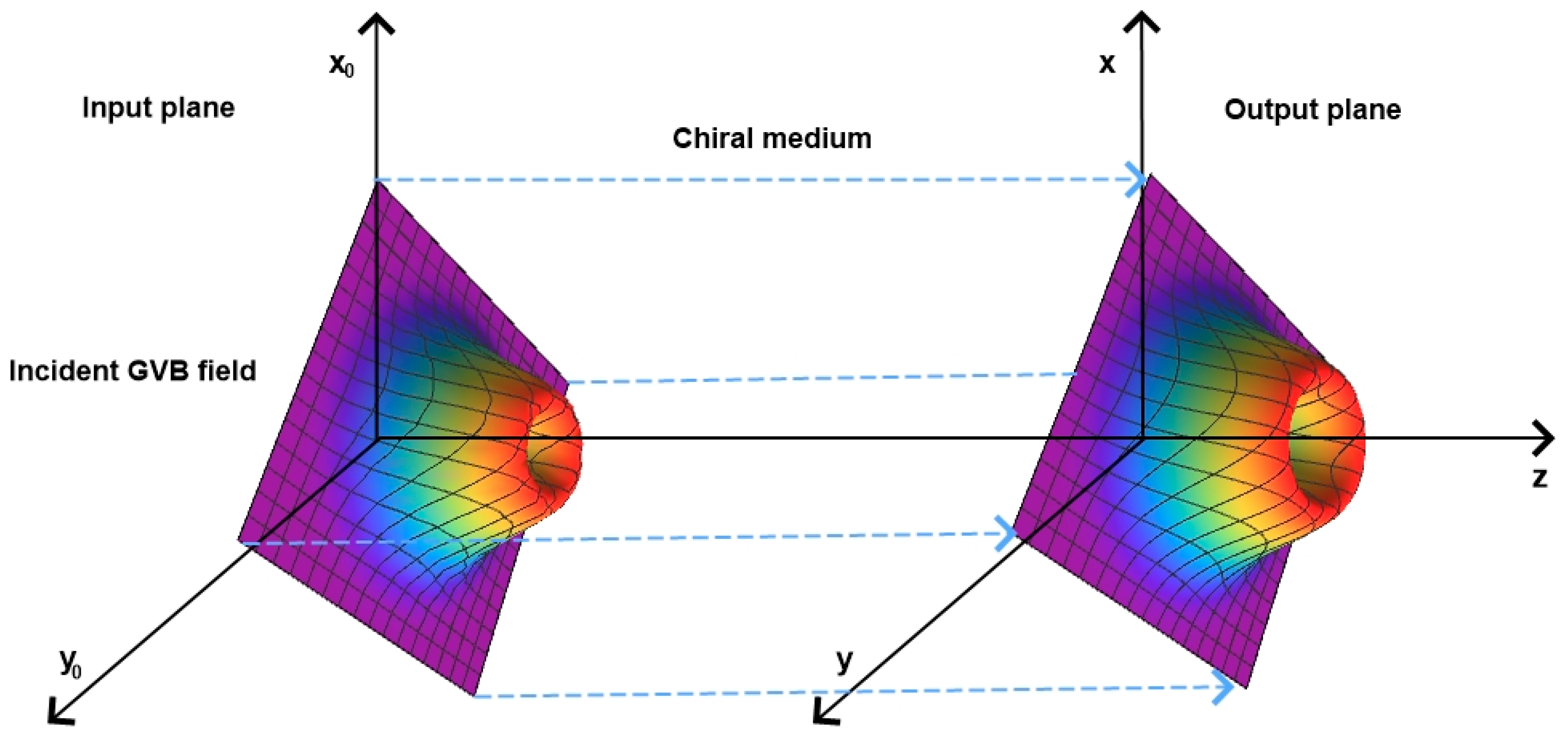
Consider the interaction of GVB with its propagation along the z direction in the presence of chiral media. Here, the total GVB field in chiral media can be written as a sum of the RCP beam and the LCP beam. These two light beam components demonstrate differing propagation paths and phase velocities. The interaction model is sketched in Figure 1.

Consider the expression of the electric field of a laser beam as [36]:

$$\check{E}\left(x,y,z,t\right)=U(x,y,z)e^{i(kz-\omega t+\phi )}$$

(1)

On substituting the given Equation (1) into the wave equation ${\nabla }^2\check{E}-\left(\frac{{\partial }^2\check{E}}{\partial t^2}\right)=0$, which leads to yield the well-known Helmholtz equation:

$${\nabla }^{2}U+k^{2}U=0$$

(2)

To seek the approximate solutions that vary slowly, the following condition holds:

$$\left|{\displaystyle \frac{{\partial }^{2}U}{\partial z^2}}\right|\ll (2k)\left|i{\displaystyle \frac{\partial U}{\partial z}}\right|$$

(3)

Equation (2) is suitable for the description of any electromagnetic wave that propagates paraxially, including vortex beams. So, on solving Equation (2), the electric field considering GVB in cylindrical coordinates can be denoted at the source plane $\left(z=0\right)$ as:

$$E\left({\rho }_0,0\right)={\left[x_0+isgn(m)y_0\right]}^{\left|m\right|}\exp \left[{\displaystyle \frac{-{{\rho }_0}^2}{w_0^2}}\right]$$

(4)

where:

$$\mathrm{s}\mathrm{g}\mathrm{n}\left(\mathrm{m}\right)=\left\{\begin{array}{c}1 if m>0\\ 0 if m=0\\ -1 if m<0\end{array}\right.$$

(5)

whereas, ${\rho }_0=\sqrt{{x_0}^2+{y_0}^2}$. In the source plane, these coordinates, i.e., ($x_0$ and $y_0$) represent transversal Cartesian coordinates. The $m$ parameter defines the OAM mode index or topological charge. This parameter generates twisting in the Gaussian vortex light beam. $w_0$ specifies the beam waist radius and sgn denotes the signum function. For the convenience of analytical calculations, we assume the factor $\mathrm{e}\mathrm{x}\mathrm{p} (-i\omega t)$ and drop it in Equation (2).

By implementing the extended Huygens–Fresnel diffraction integral formula, the propagation of the GVB via the optical ABCD matrix system fulfills the given expression:

$$E\left(x,y,z\right)={\displaystyle \frac{i}{\lambda B}}{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }E\left(x_0,y_0,z_0\right) \mathrm{e}\mathrm{x}\mathrm{p} (-{\displaystyle \frac{ik}{2B}}[A\left(x_0^2+y_0^2\right)-2\left(x_{0}x+y_{0}y\right)+D\left(x^2+y^2\right)]) d{x}_0 d{y}_0$$

(6)

where $A$, $B$, and $D$ characterize different elements regarding transfer matrix. So, the complete ABCD matrix for propagation regarding a chiral medium can be written as [37,38]:

$${\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]}_R=\left[\begin{array}{cc}0& {\displaystyle \frac{\mathrm{z}}{n_R}}\\ 0& 1\end{array}\right]$$

(7)

$${\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]}_L=\left[\begin{array}{cc}0& {\displaystyle \frac{\mathrm{z}}{n_L}}\\ 0& 1\end{array}\right]$$

(8)

where $n_R={\displaystyle \frac{n_0}{1-n_{0}k\gamma }}$ and $n_L={\displaystyle \frac{n_0}{1+n_{0}k\gamma }}$. These specify the refractive indices of the right chiral and left chiral polarized GVBs, where $\gamma$ is the chirality parameter, while $n_0$ represents the original refractive index of the chiral medium.

Using Equation (5) in Equation (4):

$${(x}_0+i sgn{\left(m) y_0 \right)}^{\left|m\right|}={\sum }_{s=0}^{\left|m\right|}{\displaystyle \frac{\left|m\right|!i^s}{s!\left(\left|m\right|-s\right)!}}{\left[sgn\left(m\right)\right]}^s x_0^{\left|m\right|-s}{y}_0^s$$

(9)

So,

$$\begin{gathered} E\left(x,y,z\right)={\displaystyle \frac{i}{\lambda B}}{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\sum }_{s=0}^{\left|m\right|}{\displaystyle \frac{\left|m\right|!i^s}{s!\left(\left|m\right|-s\right)!}}{\left[sgn\left(m\right)\right]}^s x_0^{\left|m\right|-k}{y}_0^s\exp \left(-\frac{\left(x_0^2+y_0^2\right)}{w_0^2}\right) \mathrm{e}\mathrm{x}\mathrm{p} (-\frac{ik}{2B}[A\left(x_0^2+y_0^2\right)- \\ 2\left(x_{0}x+y_{0}y\right)+D\left(x^2+y^2\right)])d{x}_0 d{y}_0 \end{gathered}$$

(10)

By rearranging:

$$\begin{gathered} E\left(x,y,z\right)={\displaystyle \frac{i}{\lambda B}}{\sum }_{s=0}^{\left|m\right|}{\displaystyle \frac{\left|m\right|!i^s}{s!\left(\left|m\right|-s\right)!}}{\left[sgn\left(m\right)\right]}^s {\int }_{-\infty }^{\infty }[{\int }_{-\infty }^{\infty }{x}_0^{\left|m\right|-s} \mathrm{e}\mathrm{x}\mathrm{p} (-\left({\displaystyle \frac{1}{w_0}}+{\displaystyle \frac{iAk}{2B}}\right)x_0^2-2x{x}_0+ \\ D{x}^2) d{x}_0 ] {y^s\mathrm{e}\mathrm{x}\mathrm{p} (-\left({\displaystyle \frac{1}{w_0}}+{\displaystyle \frac{iAk}{2B}}\right)y}_0^2-2y{y}_0+D{y}^2)d{y}_0 \end{gathered}$$

(11)

On plucking and substituting Equation (5) into Equation (4) and using the given integral as well as the property of the Hermite function:

$${\int }_{-\infty }^{\infty }{x}^{n}exp\left(-p{x}^2+2qx\right)dx=n!\exp \left({\displaystyle \frac{q^2}{p}}\right){\left({\displaystyle \frac{q}{p}}\right)}^n\sqrt{{\displaystyle \frac{\pi }{p}}} {\sum }_{k=0}^{[{\displaystyle \frac{n}{2}}]}{\displaystyle \frac{1}{k!\left(n-2k\right)!}}{\left({\displaystyle \frac{p}{4q^2}}\right)}^k$$

(12)

$$H_n\left(l\right)=n!{\sum }_{k=0}^{\left[{\displaystyle \frac{n}{2}}\right]}{\displaystyle \frac{{\left(-1\right)}^k}{k!\left(n-2k\right)!}}{\left(2l\right)}^{n-2k}$$

(13)

Analytical expression regarding GVB by an ABCD optical system for the chiral material medium can be written as:

$$\begin{gathered} E_c\left(x,y,z\right)={\displaystyle \frac{i\pi }{\lambda Bp}} \exp \left(-{\displaystyle \frac{ikD\left(x^2+y^2\right)}{2B}}\right) \exp \left(-{\displaystyle \frac{k^2\left(x^2+y^2\right)}{2{PB}^2}}\right)\times {\sum }_{s=0}^{\left|m\right|}{\displaystyle \frac{\left|m\right|!i^s}{s!\left(\left|m\right|-s\right)!}}{\left[sgn\left(m\right)\right]}^s \times \\ {P}^{-\left|m\right|} H_{\left|m\right|-s}(-{\displaystyle \frac{kx}{2B\sqrt{P}}}) H_s(-{\displaystyle \frac{ky}{2B\sqrt{P}}}) \end{gathered}$$

(14)

where:

$$E_c\left(x,y,z\right)=E_R\left(x,y,z\right)+E_L\left(x,y,z\right)$$

(15)

and:

$$\begin{gathered} E_R\left(x,y,z\right)={\displaystyle \frac{ i\pi n_R}{\lambda zP}} \exp \left(-{\displaystyle \frac{ik{n}_R\left(x^2+y^2\right)}{2z}}\right)\exp \left(-{\displaystyle \frac{k^{2 }{n}_R^2 \left(x^2+y^2\right)}{2{Pz}^2}}\right)\times {\sum }_{s=0}^{\left|m\right|}{\displaystyle \frac{\left|m\right|!i^s}{s!\left(\left|m\right|-s\right)!}}{\left[sgn\left(m\right)\right]}^s \times \\ {P}^{-{\displaystyle \frac{\left|m\right|}{2}}}{2}^{-\left|m\right|}{i}^{-\left|m\right|} H_{\left|m\right|-s}(-{\displaystyle \frac{n_{R}kx}{2z\sqrt{P}}})H_s(-{\displaystyle \frac{n_{R}ky}{2z\sqrt{P}}}) \end{gathered}$$

(16)

and:

$$\begin{gathered} E_L\left(x,y,z\right)={\displaystyle \frac{i\pi n_L}{\lambda zP}} \exp \left(-{\displaystyle \frac{ik{n}_L\left(x^2+y^2\right)}{2z}}\right)\exp \left(-{\displaystyle \frac{k^{2 }{n}_L^2 \left(x^2+y^2\right)}{2{Pz}^2}}\right){\sum }_{s=0}^{\left|m\right|}{\displaystyle \frac{\left|m\right|!i^s}{s!\left(\left|m\right|-s\right)!}}{\left[sgn\left(m\right)\right]}^s \times \\ {P}^{-{\displaystyle \frac{\left|m\right|}{2}}}{2}^{-\left|m\right|}{i}^{-\left|m\right|} H_{\left|m\right|-s}(-{\displaystyle \frac{n_{L}kx}{2z\sqrt{P}}})H_s(-{\displaystyle \frac{n_{L}ky}{2z\sqrt{P}}}) \end{gathered}$$

(17)

where:

$$P=\left({\displaystyle \frac{1}{w_0^2}}+{\displaystyle \frac{ikA}{2B}}\right)$$

(18)

The total field intensity of the GVB field in a chiral medium with its propagation along the z-direction can be expressed as a sum of the RCP beam and the LCP beam with unique propagation characteristics:

$$I_{total}={\left|E_L\left(x,y,z\right)\right|}^2+{\left|E_R\left(x,y,z\right)\right|}^2+I_{interference}$$

(19)

where:

$$I_{interference}=E_L\left(x,y,z\right)E_R^{\ast }\left(x,y,z\right)+E_L^{\ast }\left(x,y,z\right)E_R\left(x,y,z\right)$$

(20)

Here, $I_{interference}$ represents the interference term of right and left optical beam fields in the chiral medium and * terms represents the complex conjugate of beam fields.

To investigate the gradient force of the GVB, we assume that it strikes a microparticle. When the particle maintains its stable condition, the time average gradient force can be expressed as [39]:

$${\overrightarrow{F}}_{grad}=\left({\displaystyle \frac{1}{c}}\right)2\pi r_0^3{n}_2\left({\displaystyle \frac{m_0^2-1}{m_0^2+2}}\right)\nabla \left[\left({\displaystyle \frac{1}{2}}\right)\left(c{\epsilon }_0{n}_2\right){\left|E_{mn}(x,y,z)\right|}^2\right]$$

(21)

where $c$ represents the light velocity while $r_0$ specifies the radius of the microparticle. ${\epsilon }_0$ is the free space permittivity, $m_0={\displaystyle \frac{n_1}{n_2}}$ denotes the relative refractive index of the microparticle, and $n_1$ and $n_2$ represent the refractive index of the particle in addition to the refractive index of the chiral medium, respectively.

3. Results and Discussion

This section presents numerical results regarding the propagation of a Gaussian vortex beam in the presence of chiral media. The characteristics of Equation (19) are solved numerically to compute the intensity distribution of the GVB. The constitutive beam parameters are adopted for the computation as $\lambda =0.632 \mu \mathrm{m}$, $w_0=1.0 \mathrm{m}\mathrm{m}$, and $n_0=1$. For gradient force, we set $n_1=1.592,$ while for the radius of the micro particle, we set $r_0=60 \mathrm{n}\mathrm{m}$.

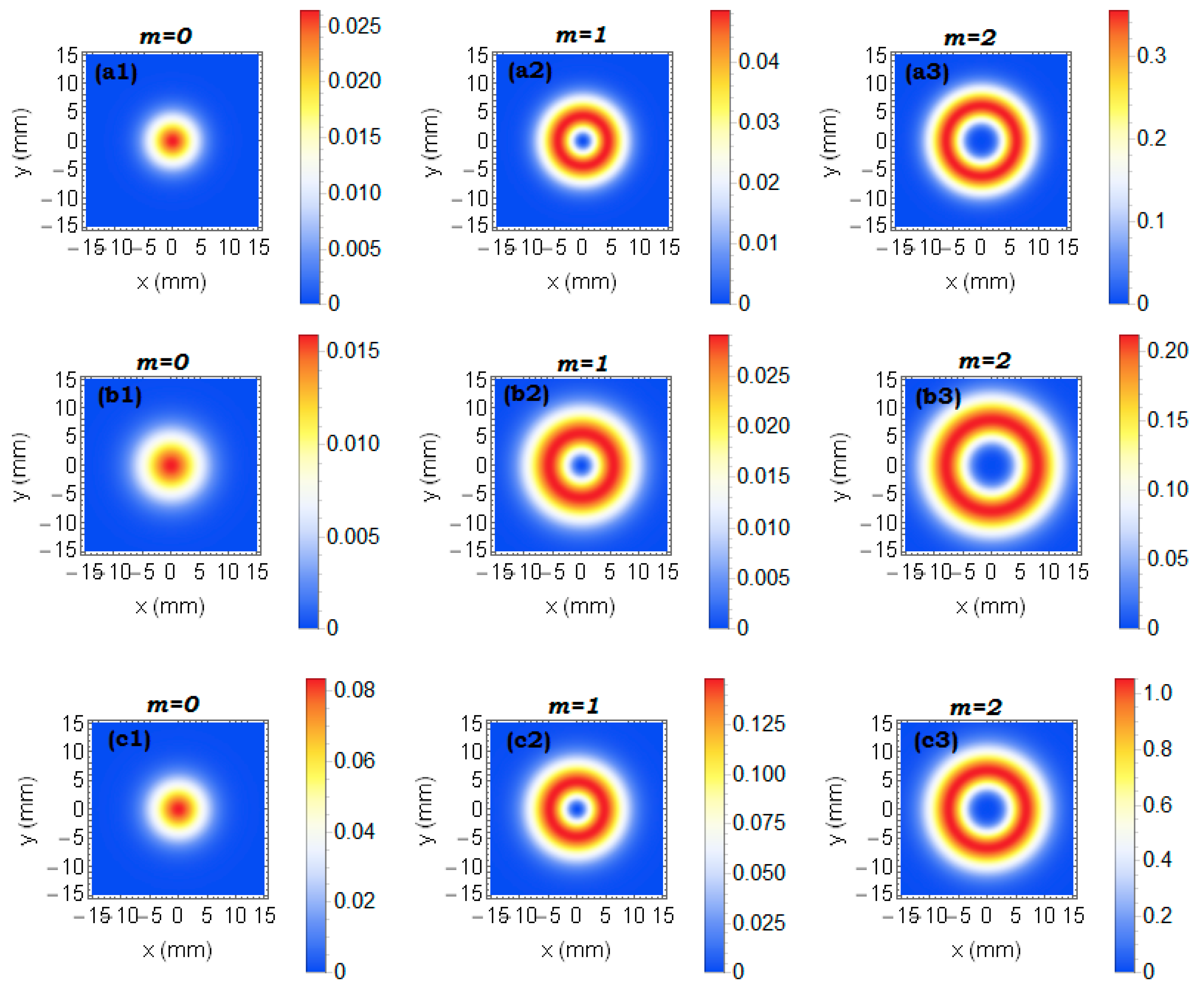
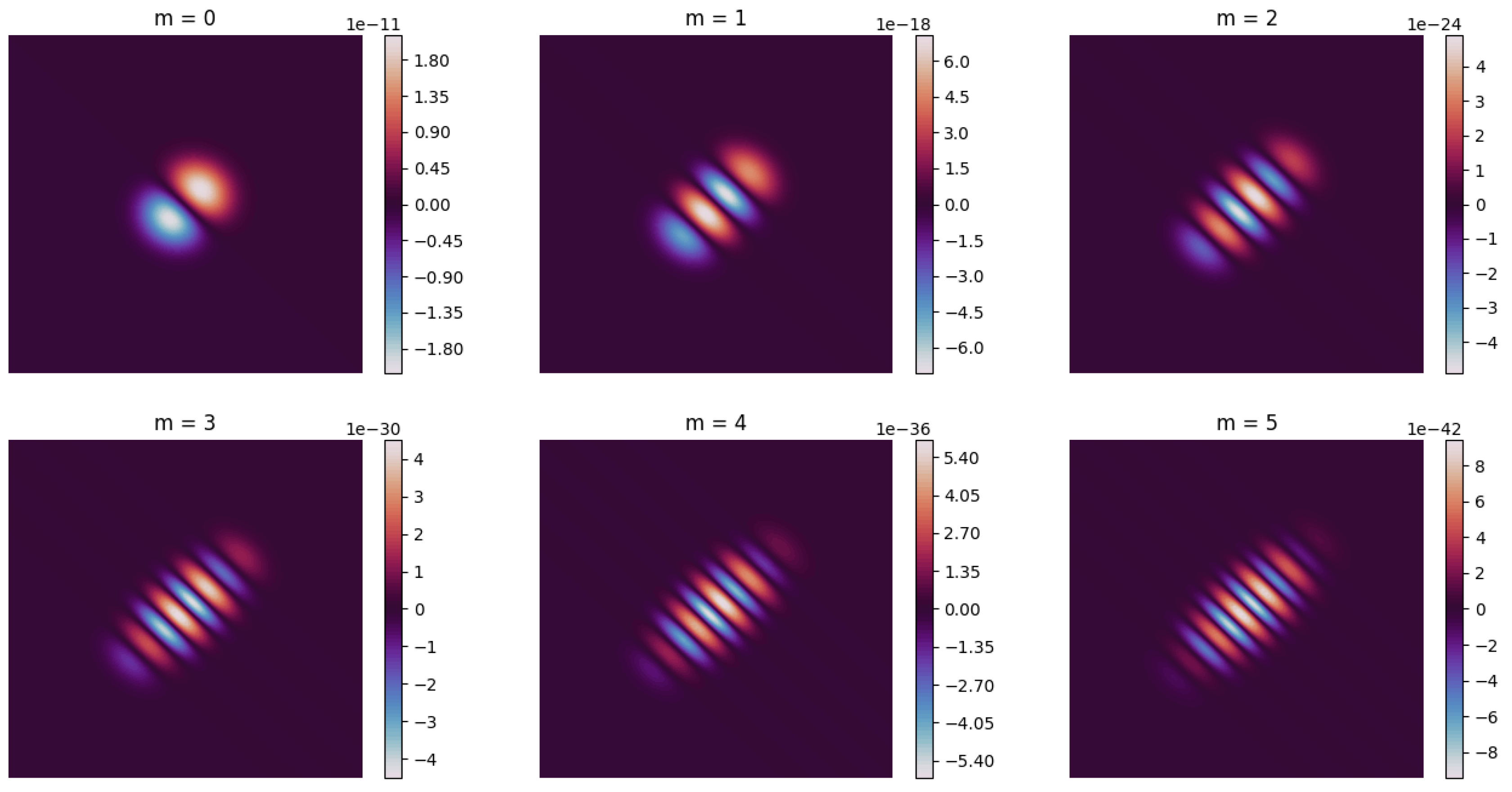
Figure 2 illustrates the impact of the OAM mode number on the intensity distribution of GVB. The interplay of the OAM mode number enhances the beam intensity in relation to GVB. The underlying cause is due to the engagement of inner field modes for different topological charges, specifically. For a topological charge of zero, the scattered electromagnetic field has a small offset along the axis of the optical beam. GVB intensity increases with an increase in the OAM mode index. Overall, an increase in the topological charge enhances the electromagnetic scattering rate of GVB toward a chiral medium. The interaction of GVB with chiral medium causes variations in phase, polarization, and beam intensity. Increasing the OAM mode index yield enhances the beam’s expansion, broadens the beam phase profile, and generates new field intensity lobes. Electromagnetic beam propagation becomes crucial for precise beam control in prospective applications such as communications and light manipulation.

The confinement of the Gaussian envelope, constructive-type interference, effects of beam waist radius, and chiral medium interactions are responsible for the increase in maximum intensity for a GVB when the topological charge rises from $0$ to $2$. Nevertheless, the energy in a GVB is still concentrated in a Gaussian-like envelope, which means that the Gaussian confinement can cause the core intensity to stay high or even rise. The intensity of a GVB also varies based on its waist size. Higher-order modes $(\mathcal{l}>0)$ may have higher peak intensities for small beam waists because of mode structure reinforcement. Interference effects between various beam mode components create the GVB, and when $\mathcal{l}$ rises, some interference effects may intensify the maximum intensity at particular points. This leads to yielding more peak intensity for $\mathcal{l}=1$ or $2$ than $\mathcal{l}=0$ if the beam structure permits constructive type interference in the primary intensity ring. The beam propagation over a chiral medium may also cause spin-orbit coupling, affecting beam intensity distribution. Certain chiral media have the capability to yield self-focusing effects, which can increase local intensity even as $\mathcal{l}$ increases.

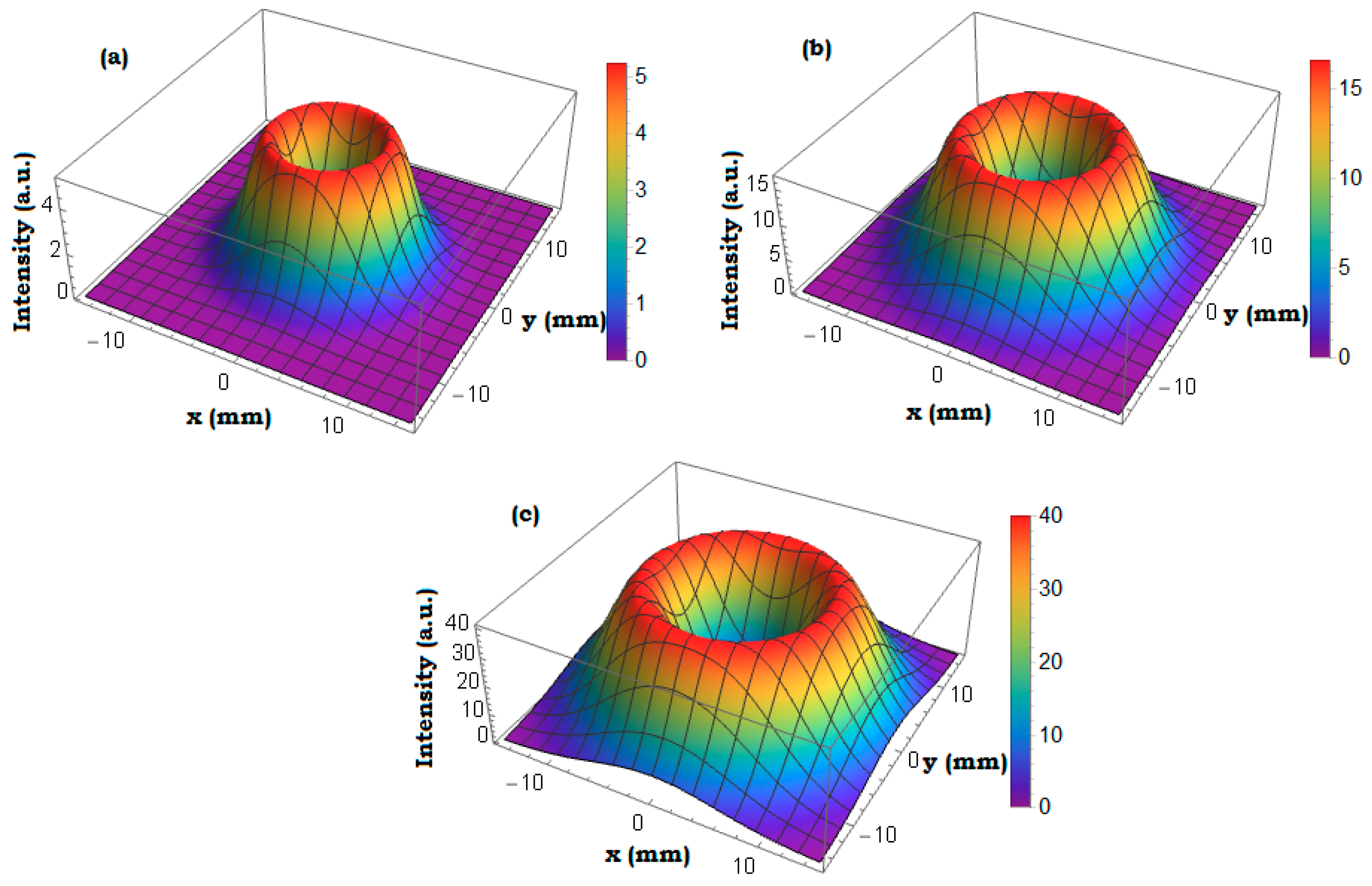
Figure 3 illustrates the intensity distribution for a chiral medium illuminated by a GVB with beam waist radii of $w_0=1.0 \mathrm{m}\mathrm{m}, 1.5 \mathrm{m}\mathrm{m}$, and $2.0 \mathrm{m}\mathrm{m}$, respectively. All intensities increase as the waist radius $(w_0)$ increases. Augmenting the beam waist radius will enlarge the beam width while reducing beam divergence, thereby enhancing the GVB intensity in the chiral medium.

As the waist radius increases, the beam width expands, the ring size considering beam intensity distribution enlarges, and the scattered field distribution increases. As the beam width grows, the chiral medium is lighted by a GVB of distributed energy, resulting in enhanced optical effects such as absorption, scattering, and extinction. Medium-dependent interactions also play their role. An appropriate selection of the chirality of the chiral media, beam waist radius, and topological charge of GVB results in enhanced beam propagation. Indeed, this means that the vortex features remain stable over extended distances. GVBs can be made more stable and resistant to diffraction by carefully choosing the chirality of the chiral media, the size of the beam waist, and the topological charge. Chiral media can modify the optical vortex by lowering distortion, while the beam topological charge and beam waist radius have an impact on the energy distribution and structure of the beam. The vortex properties are maintained over long distances by optimizing these parameters, which also improves the capability of the beam for self-healing and minimizes spreading. The beam waist radius determines the beam intensity and lobe pattern; thus, its meticulous selection leads to improved symmetrical propagation characteristics. Furthermore, when the waist radius of GVB matches the operating wavelength of the input GVB field, it results in optimal beam propagation. A larger beam waist size results in less strongly focused light, which in turn reduces the effects of diffraction and beam divergence during transmission.

Raising the beam waist radius lowers diffraction losses, changes the vortex structure, and improves transmission through a chiral media, all of which contribute to an overall intensification in some parts of the beam profile. This behavior is different from free-space Gaussian beam propagation because of the additional modifications caused by the contact with the chiral medium.

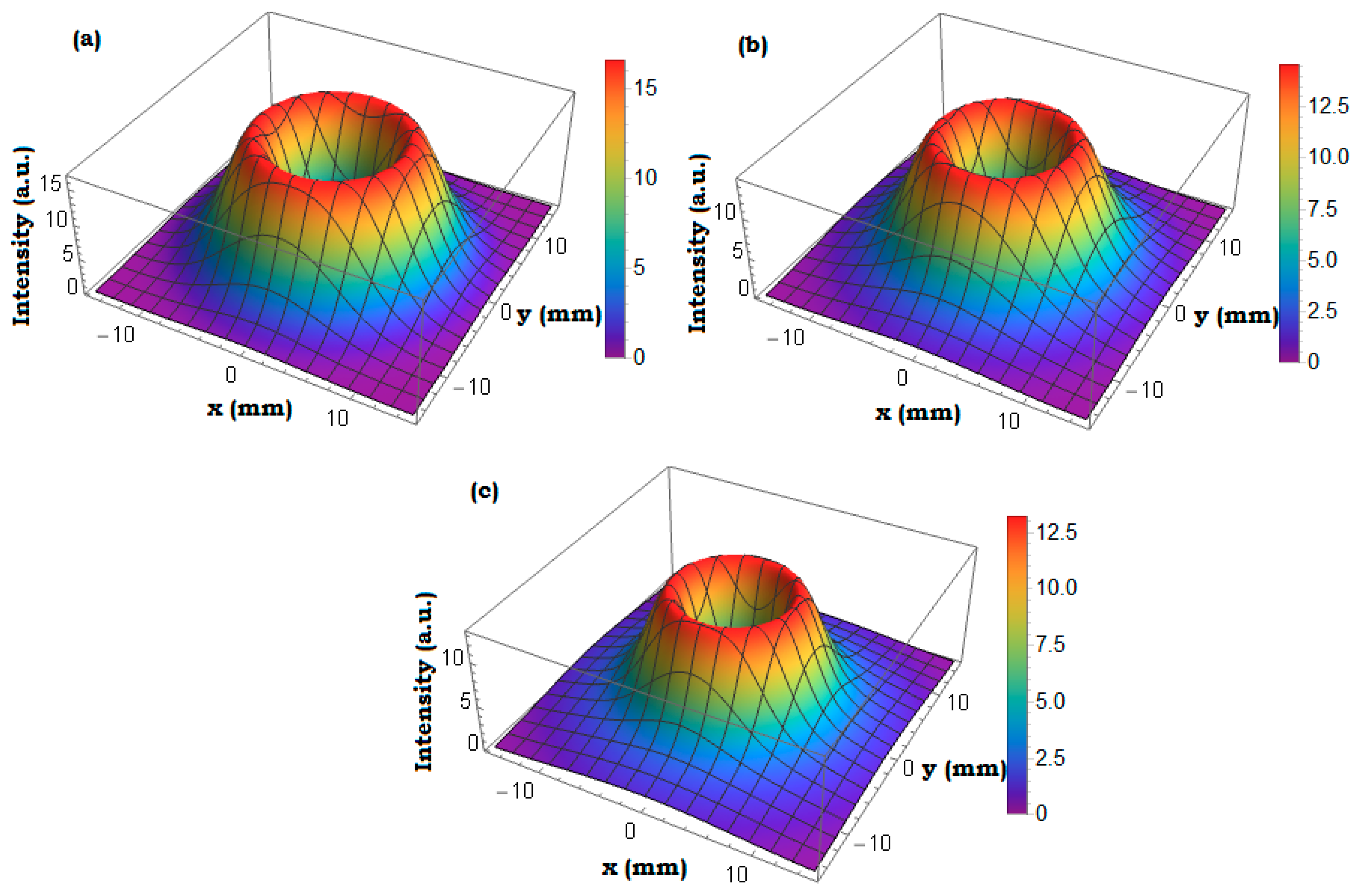
Figure 4 illustrates the computations of intensity for the propagation of GVB regarding chiral media. The chirality parameter is fundamental in determining the optical properties of a vortex light beam. The scattering and absorption characteristics can be substantially affected by the chirality parameter of the chiral media. The chirality parameter $\gamma$ assumes values of $\frac{0.16}{k},\frac{0.32}{k},$ and $\frac{0.48}{k}$, correspondingly. The GVB intensity significantly decreases with an increase in the chirality parameter. It is evident that chirality parameter $(\gamma )$ markedly affects the beam intensity of a chiral media. Also, the field of a Gaussian vortex light beam polarizes the atoms of the chiral media and causes oscillation. These dipoles in turn transmit or scatter the field of the light beam, resulting in the emitted light interfering with the beam field of incident light. This layout manifests as diminished scattering lobes in the intensity pattern. The beam intensity is very sensitive to the chirality parameter. It is important to observe that as the chiral parameter increases, the interference becomes more pronounced, leading to distortions as the GVB travels over shorter distances. In conclusion, the chirality can be utilized to control the extent of diffraction characteristics and the intensity attenuation phenomena of GVB. To summarize, when the chirality parameter grows, the intensity regarding propagating GVB decreases due to increased optical activity, diffraction effects, differential absorption, and decreased efficiency of beam transmission. Strong chirality can further decrease beam intensity by decreasing transmission efficiency through increased scattering losses and optical rotation.

Figure 5 shows the distributions of the gradient force on varying the beam topological charge as m = 0, 1, 2, 3, 4, and 5, respectively. An augmentation in the topological charge $m$ of the light beam significantly affects the gradient force in chiral media. However, the influence is conditional on the OAM mode’s influence on the vortex beam’s spatial distribution and its interaction with the chirality of the medium. With an increase in $m$, the beam’s intensity profile is more “doughnut-shaped”, with a larger core black zone (null intensity) and a less steep radial intensity gradient at the center, but it may get steeper farther from the optical axis of GVB in the presence of chiral media. Based on the handedness of the medium and the spin as well as the orbital properties of the vortex beam, the interaction between OAM beams and chirality in chiral media can reduce the gradient force.

Also, the reason the gradient force drops as the OAM mode number rises is because extending the intensity ring lowers local intensity gradients. Improving the beam’s waist size results in a more gradual fluctuation in intensity and lower intensity gradients weaken the trapping potential. Additionally, the field dispersion was further diffused by chiral medium effects.

The propagation of light beams in chiral metamaterials also depends on dispersion effects. Circular dichroism and optical activity, which define chiral metamaterials, are strongly influenced by dispersion. The dispersion effects of chiral metamaterials are essential for the development of optical devices such as polarization rotators, cloaking devices, and slow-light systems. Understanding the impact of these processes on beam propagation enables accurate control over light manipulation. This leads to advancements in a variety of possible photonics, communication, and sensing applications. Several dispersion phenomena include nonlinear dispersion, circular birefringence and dichroism, negative refraction and superluminal, frequency-based dependency of refractive index, and many more.

In chiral media, the entire field is made up of RCP and LCP beams. Their refractive indices are different for these RCP and LCP beam components. The optical rotation caused by this difference can be very dispersive, meaning that the rotation varies significantly with frequency. Each of the beam components—the RCP and LCP—has an opposing propagation path, phase velocity, and energy flow, which all contribute to the phenomenon known as negative refraction. Superluminal phase velocities may arise in certain frequency ranges due to aberrant dispersion caused by this phenomenon, which is highly frequency-dependent. Pulse broadening and distortion, as well as soliton generation and pulse reshaping, can all result from significant dispersion in chiral metamaterials, endangering the integrity of signals in optical communication systems.

The dispersion of light results in circular birefringence as well, since its multiple circular polarization components travel at different speeds. If absorption varies with frequency and polarization, the material exhibits circular dichroism, where one circular polarization is absorbed more than the other. The dependency of the refractive index on the wavevector is the cause of the spatial dispersion. This causes angular deviation, beam splitting, and potentially self-focusing or self-defocusing phenomena for structured chiral metamaterials.

In Figure 6, the influence of beam waist radius for gradient force can be understood. Increasing the waist radius from $1.0 \mathrm{m}\mathrm{m}, 1.5 \mathrm{m}\mathrm{m}$, and $2.0 \mathrm{m}\mathrm{m}$ has a significant effect on gradient force in the presence of a chiral medium. When the waist radius is small, a strong gradient force, characterized by a high-intensity gradient near the beam center, will be present. The gradient force becomes more effective for the optical trapping of microparticles. However, when the beam waist radius becomes small, the gradient force becomes weak and makes it less operative for the sorting of microparticles or chiral molecule manipulation.

To explore the optical trapping and manipulation of a GVB as it propagates through a chiral material, the gradient force is essential. As the waist radius of the beam rises, the gradient force reduces because as the beam expands, the gradients in intensity are diminished. There is reduced optical trapping efficiency with increasing beam size and energy is further distributed by the actions of the chiral medium. The mathematical relationship with $w_0$ is such that as $w_0$ increases, $𝛻I$ tends to decrease.

The influence of the chirality parameter on the gradient force for the microparticle can be observed in Figure 7. Increasing the chirality parameter results in increasing the gradient force in the chiral medium on the microparticle. The reason behind that chirality parameter adds an extra factor in the form of a helical phase factor in the electromagnetic fields, which impacts the force experienced by the microparticle. Also, owing to this parameter, the force becomes more directionally dependent. This dictates that the force depends not only on the intensity gradient of the electromagnetic fields but also on the chirality parameter of the chiral medium.

Because of various important physical factors, the gradient force diminishes with increasing chirality parameter $(\gamma )$, broadening the intensity distribution using optical rotation. Weakened contacts caused by reduced refractive index contrast. Increased beamwidth and decreased intensity gradients. Intense gradients on chirality are dependent mathematically, where $𝛻I$ becomes weaker as $\gamma$ increases.

In a chiral medium, the gradient force of a GVB is symmetrically distributed along the diagonal due to a combination of the medium characteristics and the beam shape. The electromagnetic gradient force originates from the interaction between the chiral medium and the structured light beam field, as well as from the intensity gradient of the GVB. Owing to its nonreciprocal effects, chirality can lead to symmetry being broken in some circumstances. In the case of gradient force, however, the symmetry of the intensity distribution along the diagonal is guaranteed by the balance between LCP and RCP components.

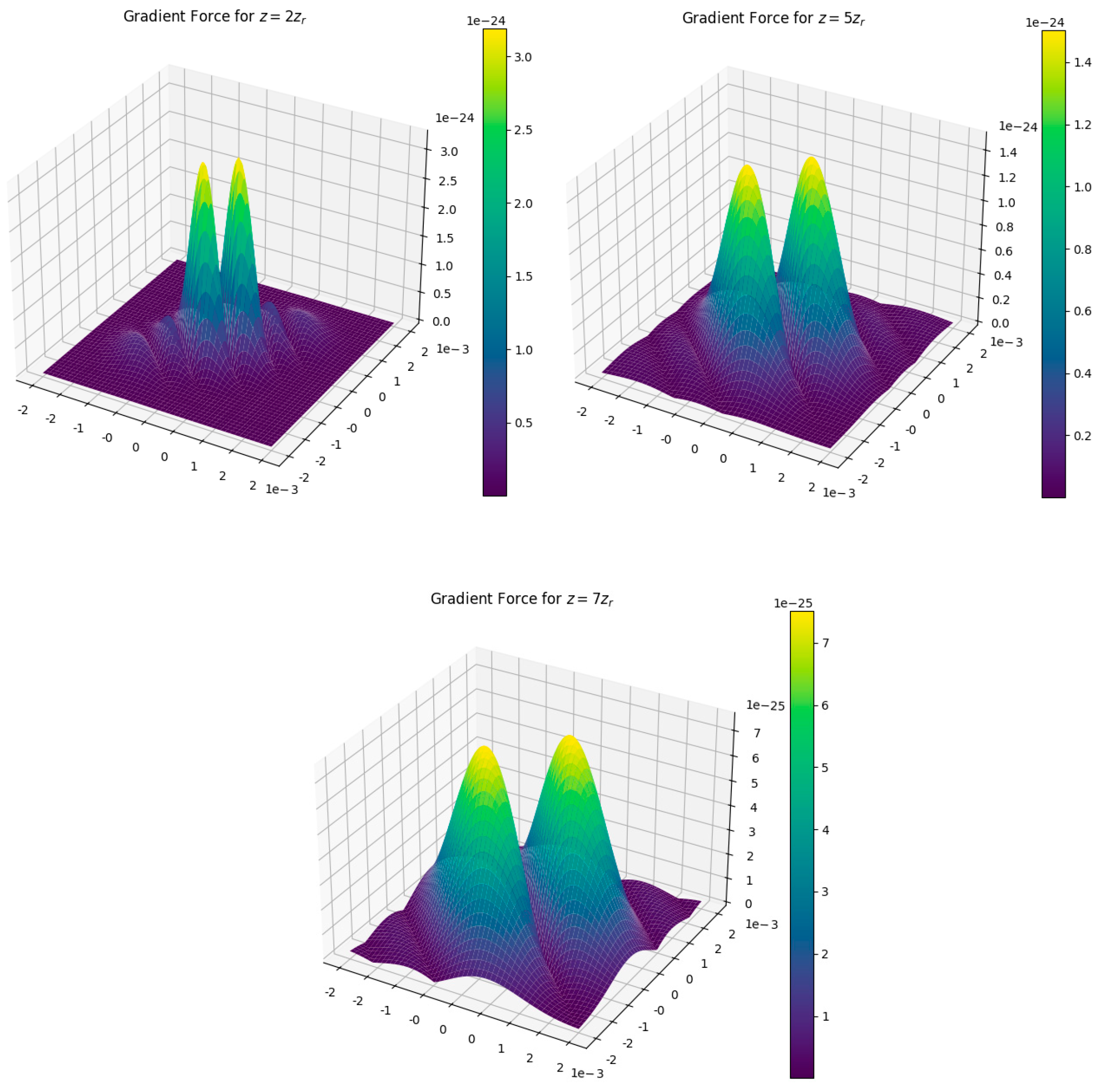
Figure 8 shows the impact of propagation distance on the gradient force. With the increase of propagation distance, the microparticle experiences decaying gradient force because the intensity gradient of the electromagnetic fields that generate the force decreases with the increase of distance. The path of the microparticle is also affected by the increase of the distance and chirality-induced forces also play their role in addition to this. The dynamics and characteristics of microparticle is also influenced by the propagation distance because the force depends on the direction of propagation distance while the non-reciprocal effects can also be observed by the gradient force. This yields to the study of some interesting phenomena, such as chirality-induced light manipulation or optical trapping. The gradient force diminishes as propagation distance $z$ grows due to numerous fundamental physical phenomena: The diffraction phenomena and beam divergence open up the beam and reduce the gradient in intensity. The pulsation of light and the redistribution of energy in a chiral medium serve to mitigate dramatic changes in intensity. As the propagation distance increases, the peak intensity drops, resulting in a reduction in strength. The dispersion and absorption of chiral media further alter the structure of the beam.

In Figure 9, the influence of the chirality parameter on the amplitude and phase distribution can be seen. The impact of the chirality parameter on the beam splitting into right circularly polarized (RCP) and left circularly polarized (LCP) components is also discussed.

The RCP and LCP components can be significantly altered by the chirality parameter $(\gamma )$. The interaction of diffraction, phase shift, and polarization is significantly impacted by the existence of chirality. The strength of $\gamma$ can cause modest phase evolutions, severe beam distortions, asymmetric diffraction patterns, and polarization rotation.

The chirality parameter modifies the optical path length for each polarization state by introducing a phase difference between the LCP and RCP components. Birefringence and polarization-dependent refraction are the outcomes of this phase difference, which indicates that the two circular polarization states accrue phases at varying rates. Furthermore, by causing asymmetric absorption or amplification, it can influence amplitude changes in chiral metamaterials. Chirality can result in asymmetric diffraction, in which the handedness of the medium causes the electromagnetic wave components, i.e., LCP and RCP, to have distinct diffraction angles or intensity distributions.

Spatial variations in polarization states can also result from nontrivial spin-orbit coupling phenomena in the propagation dynamics of structured or inhomogeneous chiral media. Chiral-induced birefringence mostly impacts beam shape and local phase accumulation over short distances. However, over longer distances, the polarization-dependent phase velocity results in beam splitting or rotation of the polarization state, influencing beam divergence and mode structure. The beam divergence and mode structure are affected by beam splitting or rotation of the polarization state caused by the polarization-based phase velocity across longer distances.

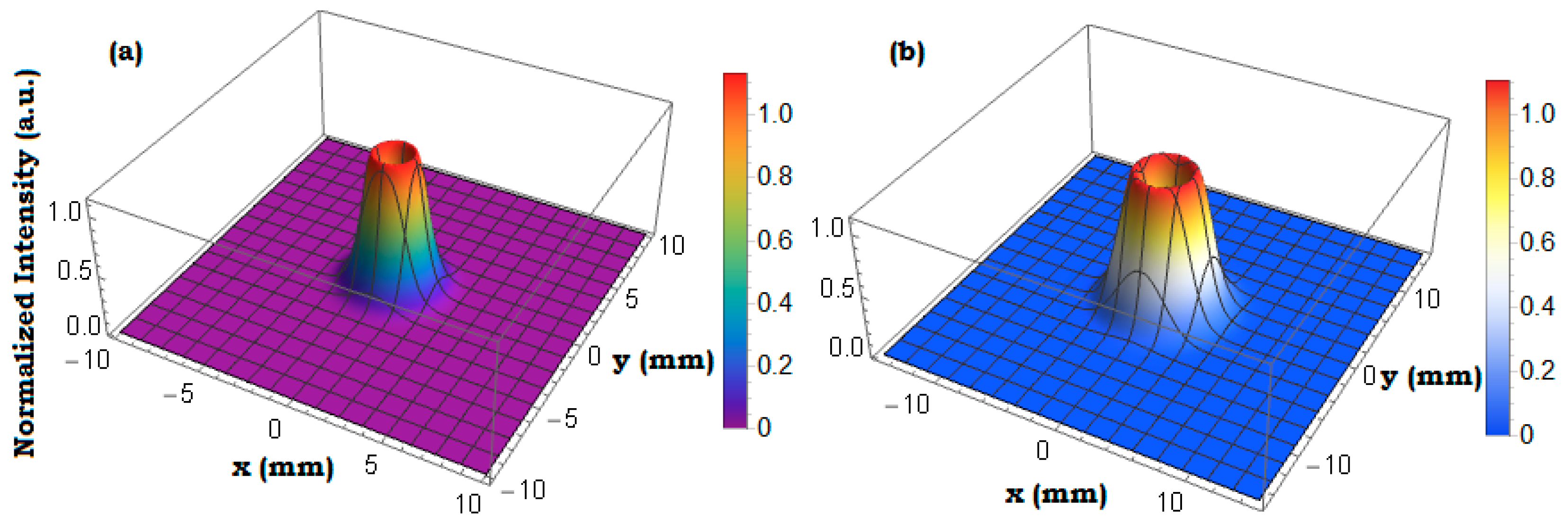
For the justification of the numerical results, the normalized intensity for the propagation of the Bessel Gaussian (BG) vortex beam in a chiral medium has been plotted. The parameters regarding the BG vortex beam are set as the OAM mode number $m=1$, chirality parameter $\gamma =\frac{0.16}{k}$, and half-cone angle regarding the BG vortex beam $\beta ={15}^0$. The comparison shows that enough conformity has been attained according to the published literature in [40]. The numerical results of this comparison have been sketched in Figure 10.

4. Conclusions

In this work, the interaction of the Gaussian vortex beam (GVB) with the chiral media is investigated to analyze the propagation characteristics of the GVB in the framework of the extended Huygens–Fresnel diffraction integral and optical matrix ABCD. This study crucially examines the intensity and optical gradient force of GVB in the presence of chiral metamaterial. Furthermore, numerical simulation is achieved to display the impact of the GVB configuration parameters on the intensity distribution and gradient force within the chiral media. The obtained results reveal that the propagation features of GVB depend on the OAM mode index $l$, beam waist radius $w_0$, and chirality parameter $\gamma$. The inclusion of various internal field modes for GVB in relation to the topological charge parameter $(l)$ contributes a unique characteristic to the study. The beam intensity and gradient force can be tuned using an internally field mode-involved Gaussian laser beam with a topological charge. Results demonstrate that the Gaussian vortex beam reduces to a basic Gaussian beam by substituting the beam’s topological charge $(l=0)$. By manipulating the beam configuration parameters $(l \& w_0)$ and the chirality $(\gamma )$, the beam intensity and gradient force for the chiral material can be controlled. Increasing the waist radius results in increasing the beam intensity profile; however, the opposite is true for the beam chirality parameter. GVB displays a multiring intensity structure and a spiral phase profile, significantly affecting beam intensity and gradient force. This research may provide favorable evidence concerning the investigation of the interaction between various vortex beams and isotropic and anisotropic metamaterial structures. Findings from this work will be very helpful since they may be utilized to better understand how chiral metamaterials boost or dampen propagated GVBs. Lastly, this work can be helpful in applying this kind of non-diffracting beam in a variety of sectors, including light manipulation, optical diagnosis, and small particle trapping employing the technique of optical tweezers, which depends on the electromagnetic forces that this kind of beam applies to the microparticles.