High-Quality-Factor Electromagnetically Induced Transparency in All-Dielectric Metasurfaces Supporting Quasi-Bound States in the Continuum
Abstract
1. Introduction
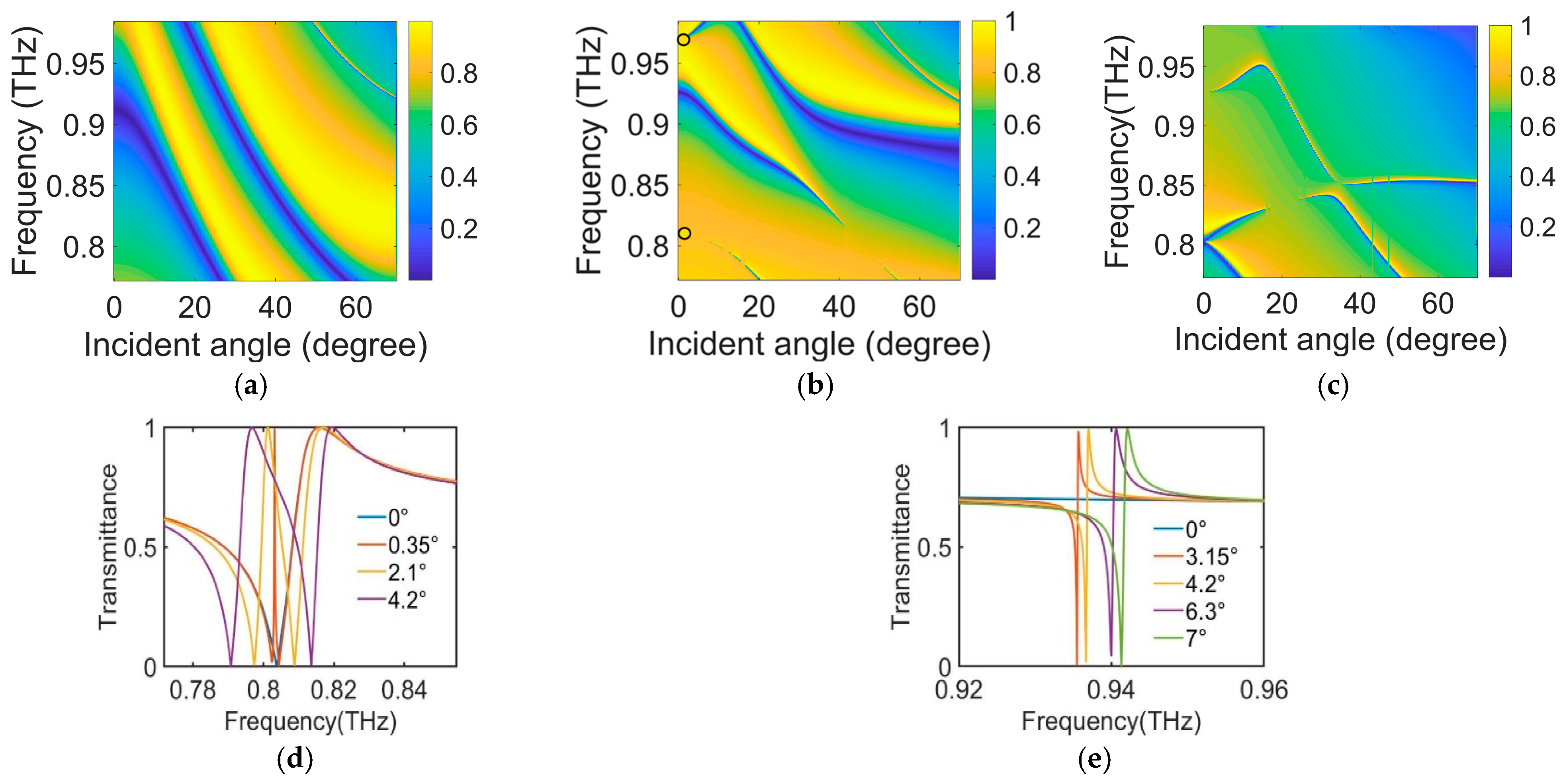
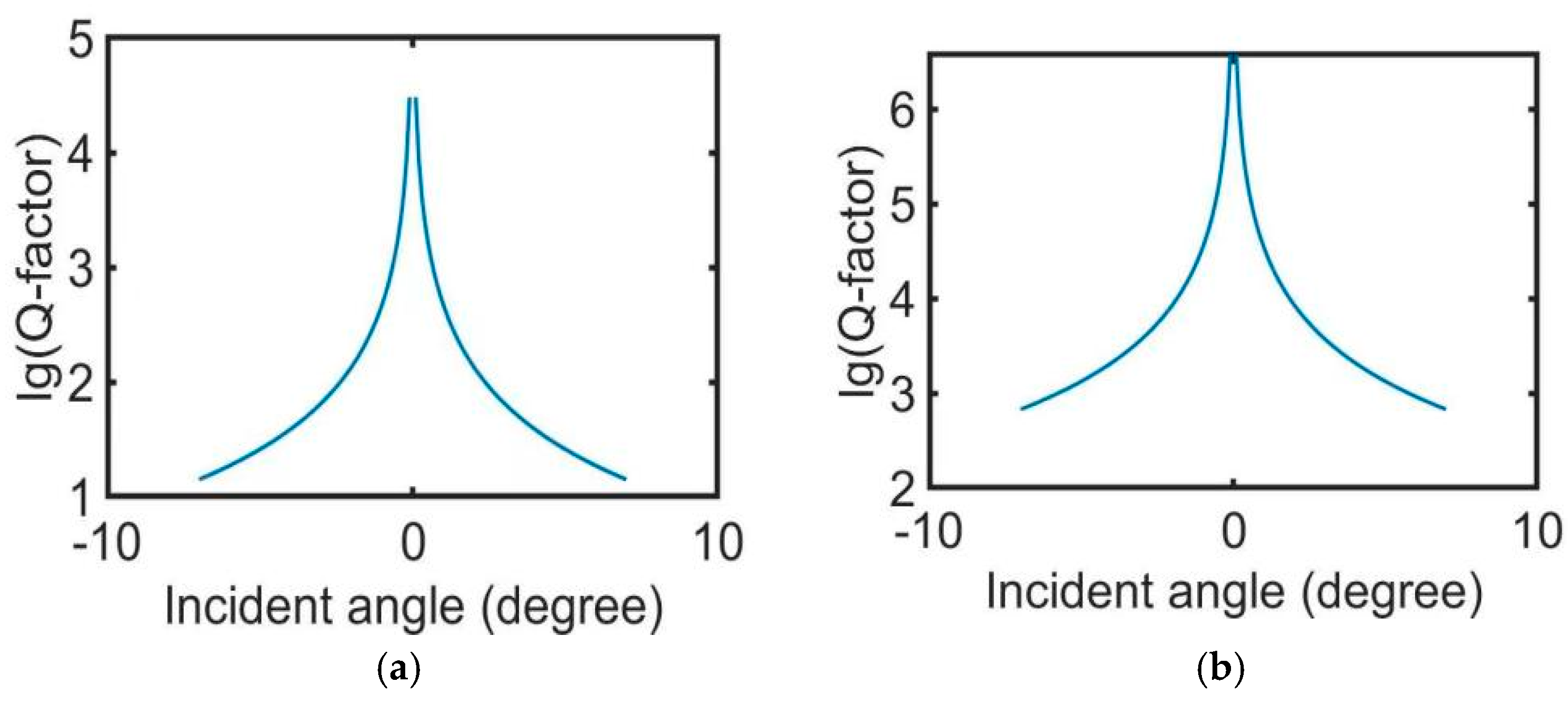
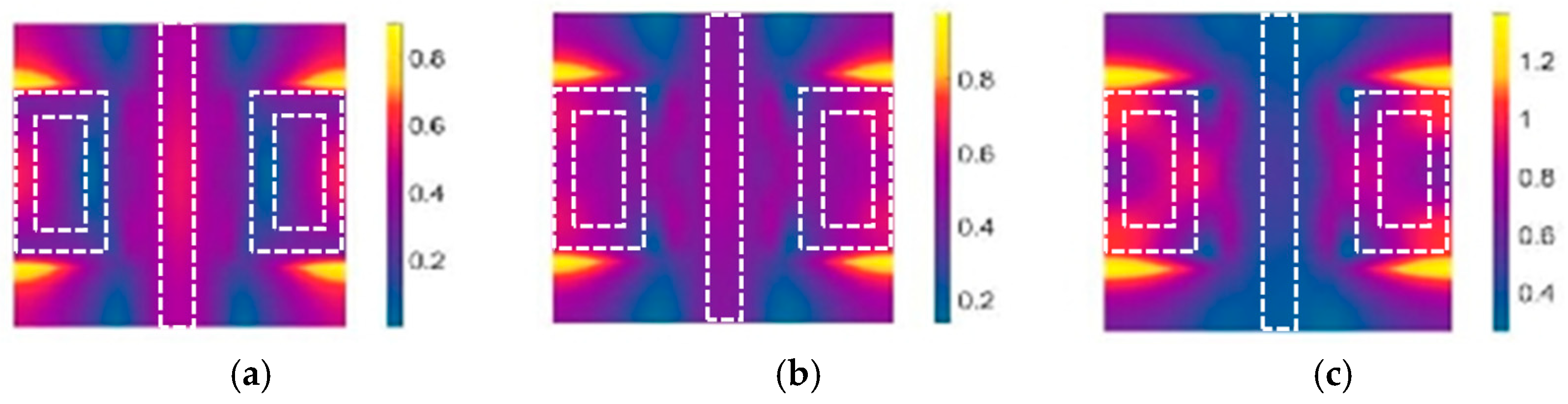
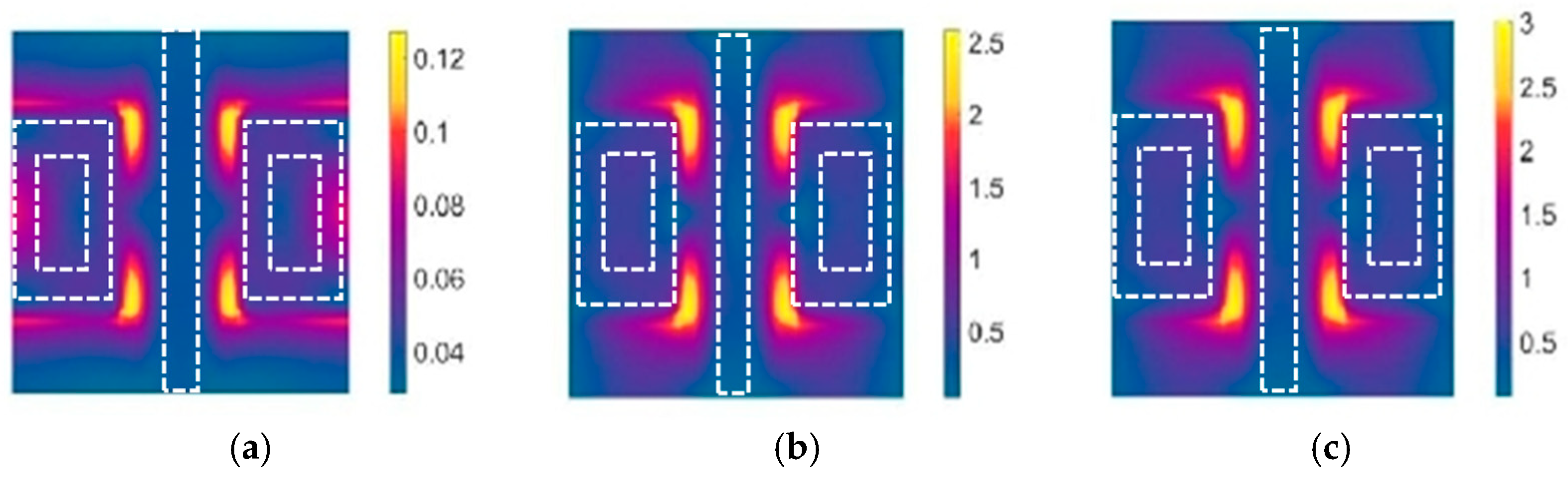
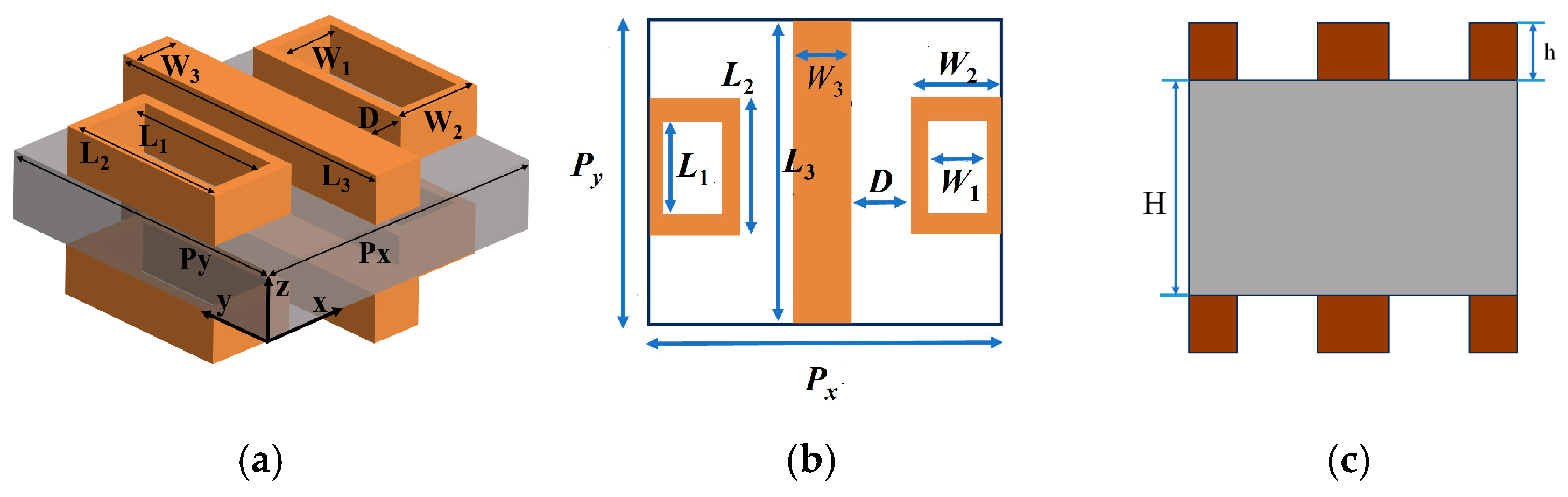
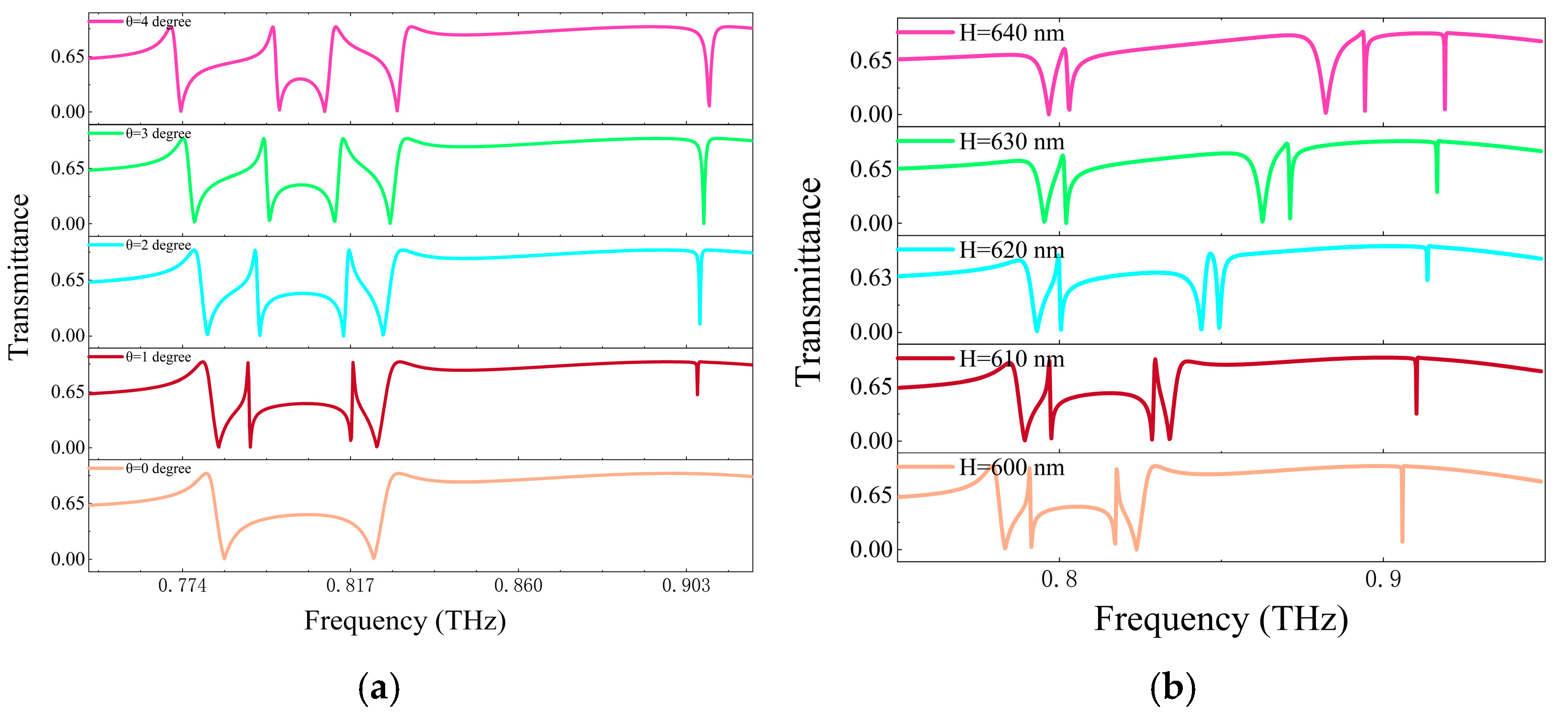
2. Discussion of the Experimental Process and Results
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koshelev, K.; Favraud, G.; Bogdanov, A.; Kivshar, Y.; Fratalocchi, A. Nonradiating photonics with resonant dielectric nanostructures. Nanophotonics 2019, 8, 725. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Callan, M.; Linton, C.M.; Evans, D.V. Trapped modes in two-dimensional waveguides. J. Fluid Mech. 1991, 229, 51–64. [Google Scholar] [CrossRef]
- Cobelli, P.J.; Pagneux, V.; Maurel, A.; Petitjeans, P. Experimental observation of trapped modes in a water wave channel. Europhys. Lett. 2009, 88, 20006. [Google Scholar] [CrossRef]
- Cobelli, P.J.; Pagneux, V.; Maurel, A.; Petitjeans, P. Experimental study on water-wave trapped modes. J. Fluid Mech. 2011, 666, 445–476. [Google Scholar] [CrossRef]
- Linton, C.M.; Mciver, P. Embedded trapped modes in water waves and acoustics. Wave Motion 2007, 45, 16–29. [Google Scholar] [CrossRef]
- Hein, S.; Koch, W.; Nannen, L. Trapped modes and Fano resonances in two-dimensional acoustical duct –cavity systems. J. Fluid Mech. 2012, 692, 257–287. [Google Scholar] [CrossRef]
- Lyapina, A.A.; Maksimov, D.N.; Pilipchuk, A.S.; Sadreev, A.F. Bound states in the continuum in open acoustic resonators. J. Fluid Mech. 2015, 780, 370–387. [Google Scholar] [CrossRef]
- Voo, K.K. Trapped electromagnetic modes in forked transmission lines. Wave Motion 2008, 45, 795–803. [Google Scholar] [CrossRef]
- Longhi, S. Optical analog of population trapping in the continuum: Classical and quantum interference effects. Phys. Rev. A 2009, 79, 023811. [Google Scholar] [CrossRef]
- Plotnik, Y.; Peleg, O.; Dreisow, F.; Heinrich, M.; Nolte, S.; Szameit, A.; Segev, M. Experimental observation of optical bound states in the continuum. Phys. Rev. Lett. 2011, 107, 183901. [Google Scholar] [PubMed]
- Lee, J.; Zhen, B.; Chua, S.L.; Qiu, W.; Joannopoulos, J.D.; Soljačić, M.; Shapira, O. Observation and differentiation of unique high-Q optical resonances near zero wave vector in macroscopic photonic crystal slabs. Phys. Rev. Lett. 2012, 109, 067401. [Google Scholar] [PubMed]
- Weimann, S.; Xu, Y.; Keil, R.; Miroshnichenko, A.E.; Tünnermann, A.; Nolte, S.; Sukhorukov, A.A.; Szameit, A.; Kivshar, Y.S. Compact surface Fano states embedded in the continuum of waveguide arrays. Phys. Rev. Lett. 2013, 111, 240403. [Google Scholar] [PubMed]
- Bulgakov, E.N.; Sadreev, A.F. Robust bound state in the continuum in a nonlinear microcavity embedded in a photonic crystal waveguide. Opt. Lett. 2014, 39, 5212–5215. [Google Scholar]
- Gomis-Bresco, J.; Artigas, D.; Torner, L. Anisotropy-induced photonic bound states in the continuum. Nat. Photonics 2017, 11, 232–236. [Google Scholar] [CrossRef]
- Van Loon, T.; Liang, M.; Delplace, T.; Maes, B.; Murai, S.; Zijlstra, P.; Gómez Rivas, J. Refractive index sensing using quasi-bound states in the continuum in silicon metasurfaces. Opt. Express 2024, 32, 14289–14299. [Google Scholar]
- Wu, F.; Qi, X.; Qin, M.; Luo, M.; Long, Y.; Wu, J.; Sun, Y.; Jiang, H.; Liu, T.; Xiao, S.; et al. Momentum mismatch driven bound states in the continuum and ellipsometric phase singularities. Phys. Rev. B 2024, 109, 085436. [Google Scholar]
- Tittl, A.; Leitis, A.; Liu, M.K.; Yesilkoy, F.; Choi, D.-Y.; Neshev, D.N.; Kivshar, Y.S.; Altug, H. Imaging-based molecular barcoding with pixelated dielectric metasurfaces. Science 2018, 360, 1105–1109. [Google Scholar]
- Li, Z.; Liu, W.; Geng, G.; Li, Z.; Li, J.; Cheng, H.; Chen, S.; Tian, J. Multiplexed nondiffracting nonlinear metasurfaces. Adv. Funct. Mater. 2020, 30, 1910744. [Google Scholar]
- Li, J.; Li, J.T.; Zheng, C.L.; Liu, L.; Yue, Z.; Xu, H.; Hao, X.; Li, F.; Tang, T.; Zhang, Y.; et al. Broadband and tunable terahertz absorption via photogenerated carriers in undoped silicon. Sci. China Phys. Mech. Astron. 2021, 65, 214211. [Google Scholar]
- Li, J.; Zheng, C.L.; Wang, G.C.; Li, J.; Zhao, H.; Yang, Y.; Zhang, Z.; Yang, M.; Wu, L.; Li, J.; et al. Circular dichroism-like response of terahertz wave caused by phase manipulation via all-silicon metasurface. Photonics Res. 2021, 9, 567–573. [Google Scholar] [CrossRef]
- Zheng, C.L.; Li, J.; Yue, Z.; Li, J.; Liu, J.; Wang, G.; Wang, S.; Zhang, Y.; Zhang, Y.; Yao, J. All-dielectric trifunctional metasurface capable of independent amplitude and phase modulation. Laser Photonics Rev. 2022, 16, 2200051. [Google Scholar] [CrossRef]
- Murai, S.; Abujetas, D.R.; Castellanos, G.W.; Sánchez-Gil, J.A.; Zhang, F.; Rivas, J.G. Bound states in the continuum in the visible emerging from out-of-plane magnetic dipoles. ACS Photonics 2020, 7, 2204–2210. [Google Scholar] [CrossRef]
- Overvig, A.C.; Malek, S.C.; Carter, M.J.; Shrestha, S.; Yu, N. Selection rules for quasibound states in the continuum. Phys. Rev. B 2020, 102, 035434. [Google Scholar] [CrossRef]
- Wang, X.; Duan, J.Y.; Chen, W.Y.; Zhou, C.; Liu, T.; Xiao, S. Controlling light absorption of graphene at critical coupling through magnetic dipole quasi-bound states in the continuum resonance. Phys. Rev. B 2020, 102, 155432. [Google Scholar] [CrossRef]
- Xiao, S.H.Y.; Liu, T.T.; Wang, X.; Liu, X.; Zhou, C. Tailoring the absorption bandwidth of graphene at critical coupling. Phys. Rev. B 2020, 102, 085410. [Google Scholar] [CrossRef]
- Van Hoof NJ, J.; Abujetas, D.R.; Ter Huurne, S.E.T.; Verdelli, F.; Timmermans, G.C.; Sánchez-Gil, J.A.; Rivas, J.G. Unveiling the symmetry protection of bound states in the continuum with terahertz near-field imaging. ACS Photonics 2021, 8, 3010–3016. [Google Scholar] [CrossRef]
- Liao, Z.; Ma, Q.; Wang, L.; Yang, Z.; Li, M.; Deng, F.; Hong, W. Guiding-Mode-Assisted Double-Bics in an All-Dielectric Metasurface. Opt. Express 2022, 30, 24676–24688. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Lee, J.; Chua, S.-L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Observation of Trapped Light within the Radiation Continuum. Nature 2013, 499, 188–191. [Google Scholar] [CrossRef]
- Ki, Y.G.; Jeon, B.J.; Song, I.H.; Kim, S.J.; Jeon, S.; Kim, S.J. Realizing Minimally Perturbed, Nonlocal Chiral Metasurfaces for Direct Stokes Parameter Detection. ACS Nano 2024, 18, 7064–7073. [Google Scholar] [CrossRef]
- Baranov, D.G.; Schäfer, C.; Gorkunov, M.V. Toward Molecular Chiral Polaritons. ACS Photonics 2023, 10, 2440–2455. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Chu, Z.; Xie, S. High-Quality-Factor Electromagnetically Induced Transparency in All-Dielectric Metasurfaces Supporting Quasi-Bound States in the Continuum. Photonics 2025, 12, 291. https://doi.org/10.3390/photonics12030291
Zhang L, Chu Z, Xie S. High-Quality-Factor Electromagnetically Induced Transparency in All-Dielectric Metasurfaces Supporting Quasi-Bound States in the Continuum. Photonics. 2025; 12(3):291. https://doi.org/10.3390/photonics12030291
Chicago/Turabian StyleZhang, Lei, Zeyang Chu, and Suxia Xie. 2025. "High-Quality-Factor Electromagnetically Induced Transparency in All-Dielectric Metasurfaces Supporting Quasi-Bound States in the Continuum" Photonics 12, no. 3: 291. https://doi.org/10.3390/photonics12030291
APA StyleZhang, L., Chu, Z., & Xie, S. (2025). High-Quality-Factor Electromagnetically Induced Transparency in All-Dielectric Metasurfaces Supporting Quasi-Bound States in the Continuum. Photonics, 12(3), 291. https://doi.org/10.3390/photonics12030291



