Multi-Beam-Energy Control Unit Based on Triple-Bend Achromats
Abstract
1. Introduction
2. Introduction of SHINE
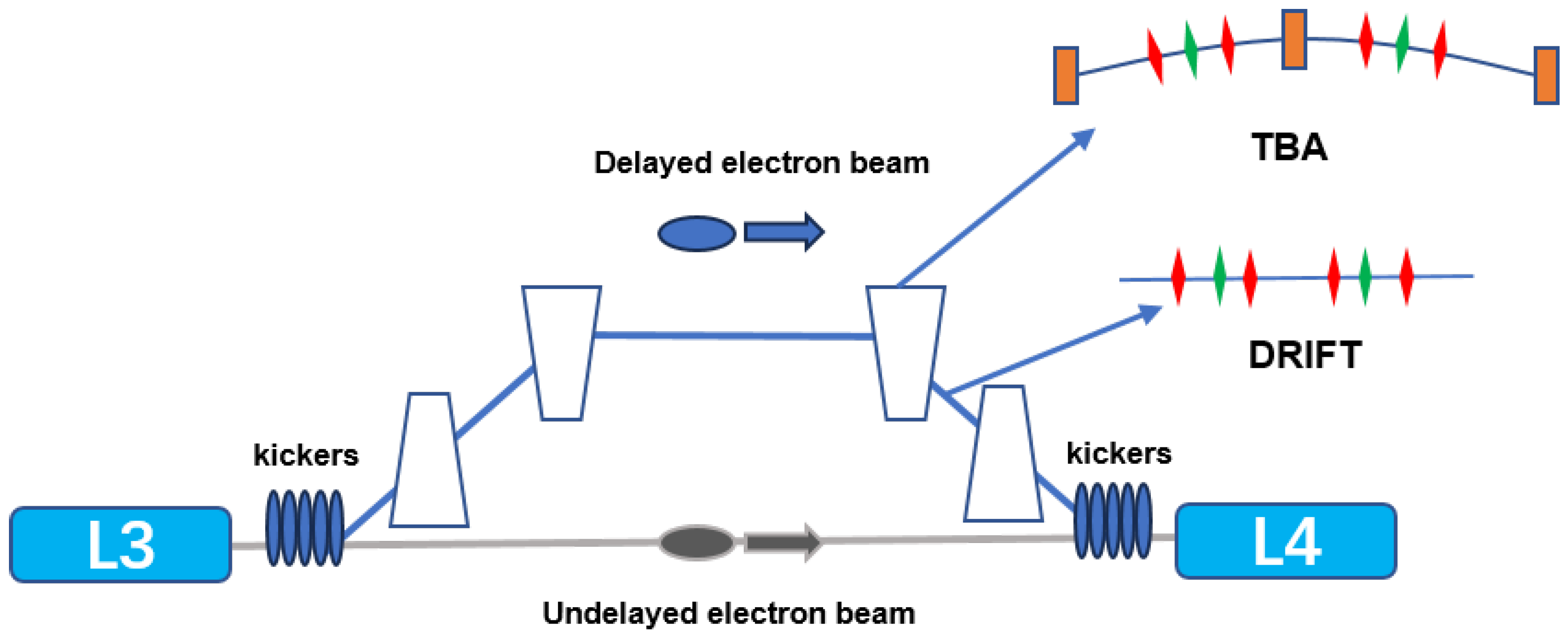
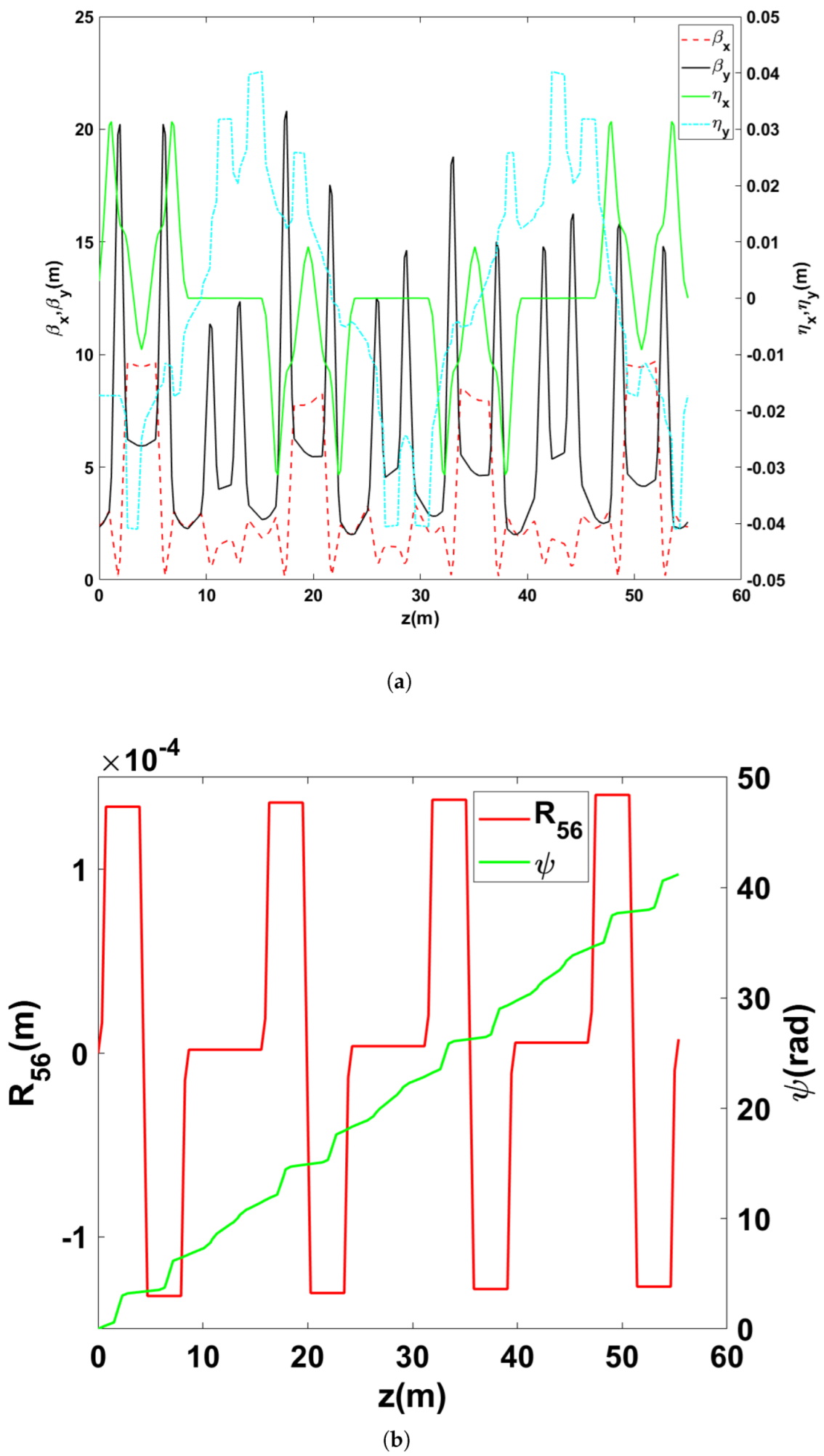
3. Design of TBA-Based Electron Beam Delay System
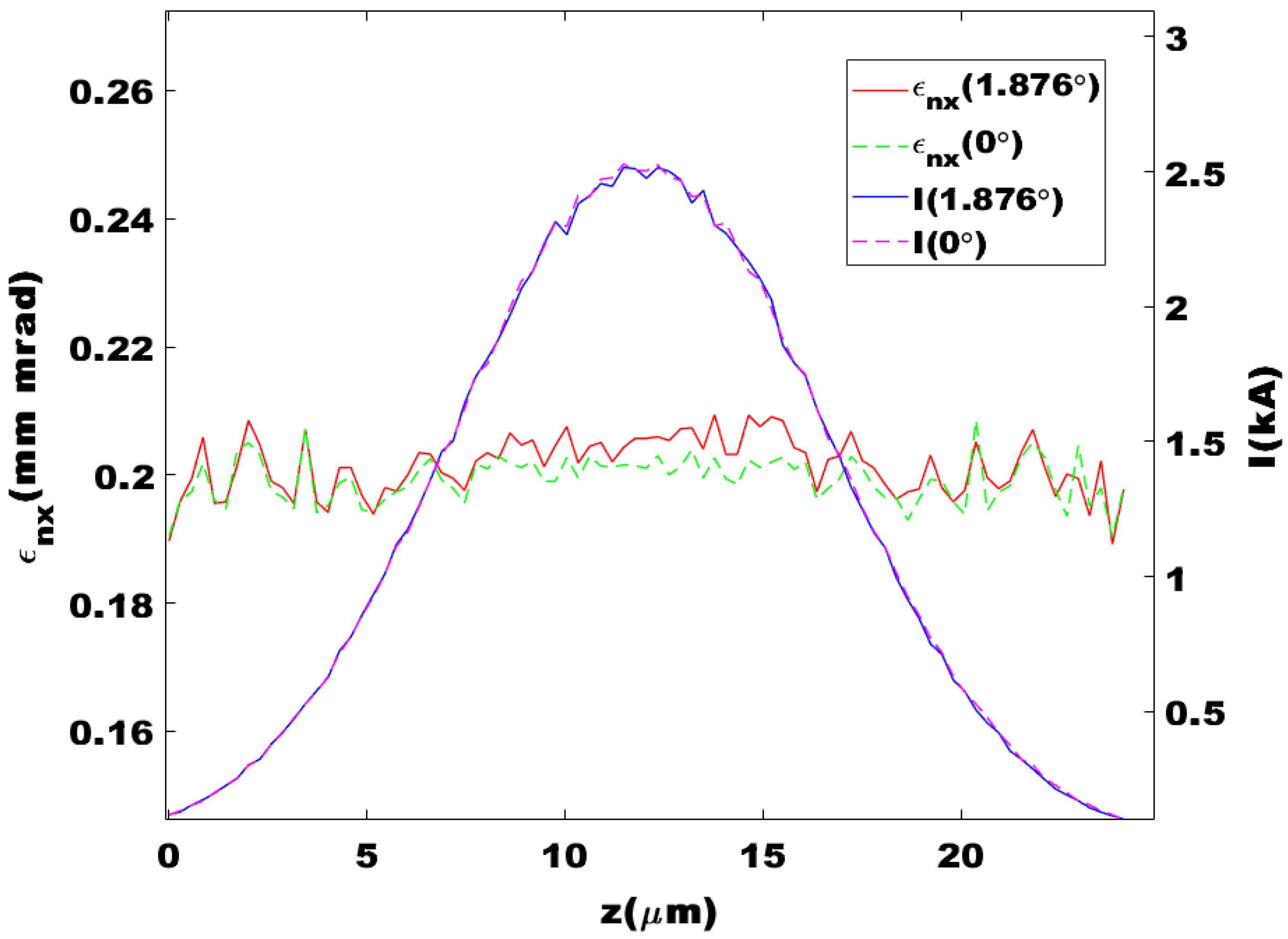
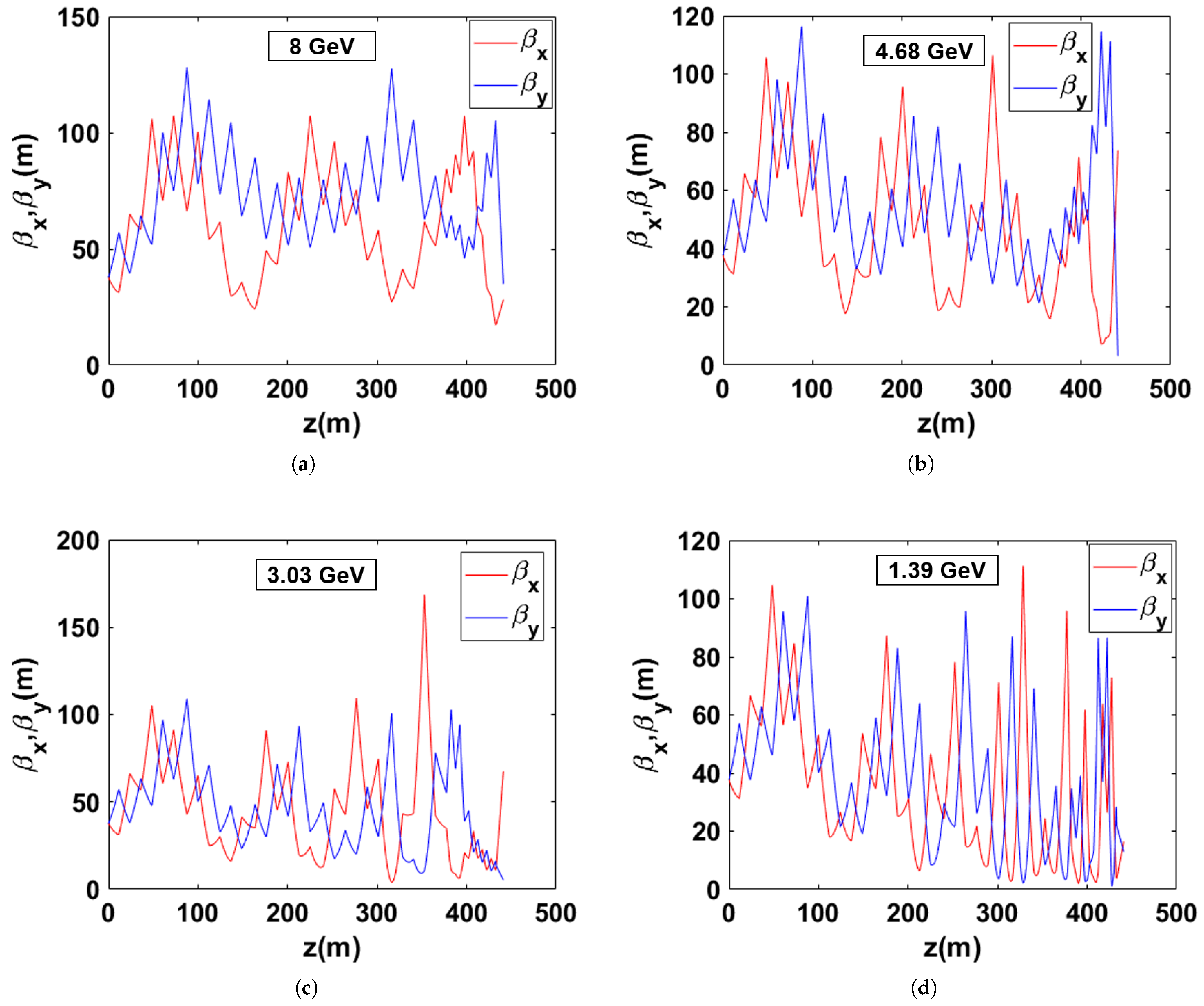
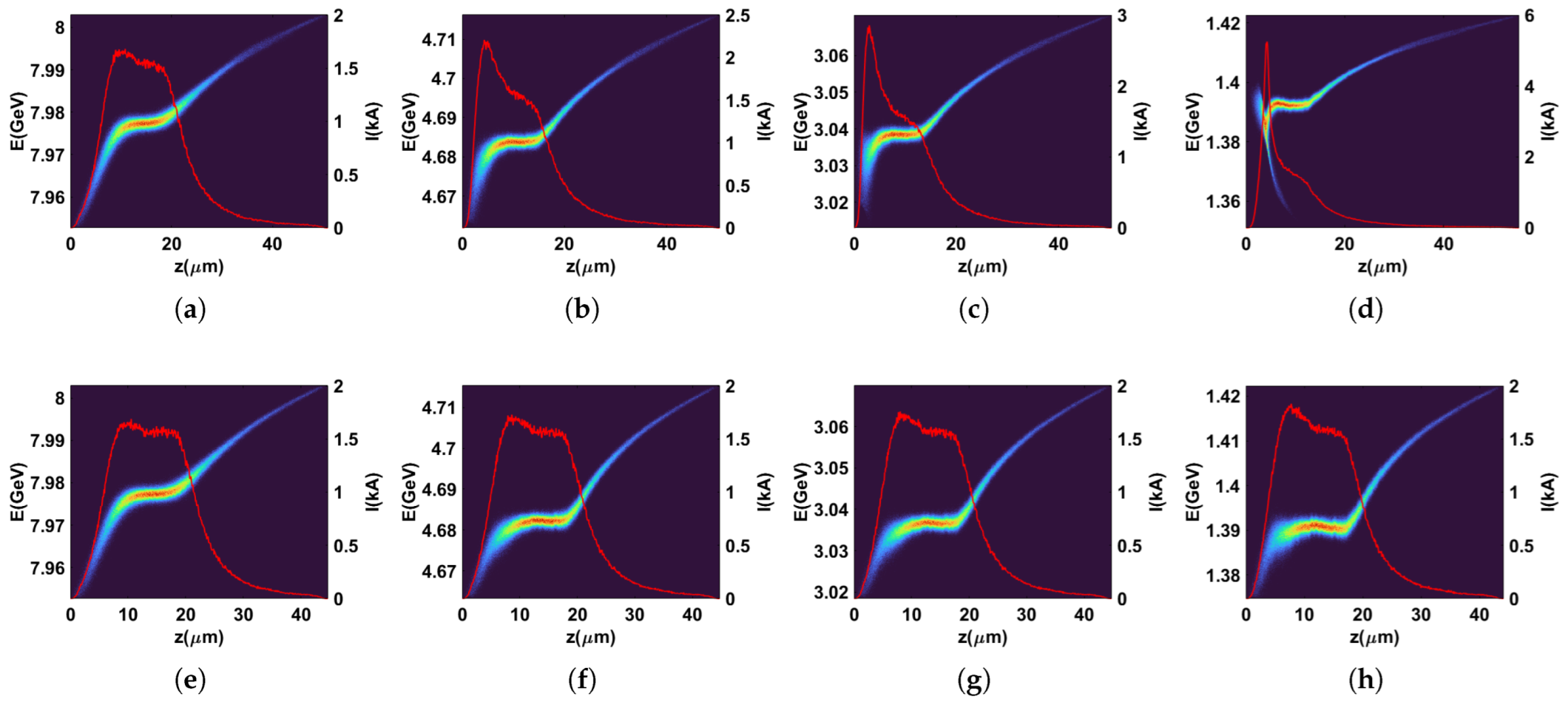
4. Start-to-End Simulations
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bostedt, C.; Boutet, S.; Fritz, D.M.; Huang, Z.; Lee, H.J.; Lemke, H.T.; Robert, A.; Schlotter, W.F.; Turner, J.J.; Williams, G.J. Linac coherent light source: The first five years. Rev. Mod. Phys. 2016, 88, 015007. [Google Scholar] [CrossRef]
- Huang, N.; Deng, H.; Liu, B.; Wang, D.; Zhao, Z. Features and futures of X-ray free-electron lasers. Innovation 2021, 2, 100097. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.; Zhou, X.E.; Gao, X.; He, Y.; Liu, W.; Ishchenko, A.; Barty, A.; White, T.A.; Yefanov, O.; Han, G.W.; et al. Crystal structure of rhodopsin bound to arrestin by femtosecond X-ray laser. Nature 2015, 523, 561–567. [Google Scholar] [CrossRef]
- Faatz, B.; Plönjes, E.; Ackermann, S.; Agababyan, A.; Asgekar, V.; Ayvazyan, V.; Baark, S.; Baboi, N.; Balandin, V.; Von Bargen, N.; et al. Simultaneous operation of two soft x-ray free-electron lasers driven by one linear accelerator. New J. Phys. 2016, 18, 062002. [Google Scholar] [CrossRef]
- Hara, T.; Fukami, K.; Inagaki, T.; Kawaguchi, H.; Kinjo, R.; Kondo, C.; Otake, Y.; Tajiri, Y.; Takebe, H.; Togawa, K.; et al. Pulse-by-pulse multi-beam-line operation for x-ray free-electron lasers. Phys. Rev. Accel. Beams 2016, 19, 020703. [Google Scholar] [CrossRef]
- Bonifacio, R.; Pellegrini, C.; Narducci, L. Collective instabilities and high-gain regime in a free electron laser. Opt. Commun. 1984, 50, 373–378. [Google Scholar] [CrossRef]
- Milne, C.J.; Schietinger, T.; Aiba, M.; Alarcon, A.; Alex, J.; Anghel, A.; Arsov, V.; Beard, C.; Beaud, P.; Bettoni, S.; et al. SwissFEL: The Swiss X-ray free electron laser. Appl. Sci. 2017, 7, 720. [Google Scholar] [CrossRef]
- Hara, T.; Tamasaku, K.; Asaka, T.; Inagaki, T.; Inubushi, Y.; Katayama, T.; Kondo, C.; Maesaka, H.; Matsubara, S.; Ohshima, T.; et al. Time-interleaved multienergy acceleration for an x-ray free-electron laser facility. Phys. Rev. Spec.-Top. Accel. Beams 2013, 16, 080701. [Google Scholar] [CrossRef]
- Decking, W.; Abeghyan, S.; Abramian, P.; Abramsky, A.; Aguirre, A.; Albrecht, C.; Alou, P.; Altarelli, M.; Altmann, P.; Amyan, K.; et al. A MHz-repetition-rate hard X-ray free-electron laser driven by a superconducting linear accelerator. Nat. Photonics 2020, 14, 391–397. [Google Scholar] [CrossRef]
- Bourzac, K. World’s Most Powerful X-Ray Laser Fires up. Nature 2023, 621, 28. [Google Scholar] [CrossRef]
- Liu, T.; Huang, N.; Yang, H.; Qi, Z.; Zhang, K.; Gao, Z.; Chen, S.; Feng, C.; Zhang, W.; Luo, H.; et al. Status and future of the soft X-ray free-electron laser beamline at the SHINE. Front. Phys. 2023, 11, 1172368. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, Y.; Adolphsen, C.; Raubenheimer, T. Multienergy operation analysis in a superconducting linac based on off-frequency detune method. Phys. Rev. Accel. Beams 2019, 22, 110702. [Google Scholar] [CrossRef]
- Pfeiffer, S.; Ayvazyan, V.; Branlard, J.; Buettner, T.; Choroba, S.; Faatz, B.; Honkavaara, K.; Katalev, V.; Schlarb, H.; Schmidt, C.; et al. RF regulation with superconducting cavities and beam operation using a frequency shifted cavity. arXiv 2022, arXiv:2201.06381. [Google Scholar]
- Yan, J.; Deng, H. Multi-beam-energy operation for the continuous-wave x-ray free electron laser. Phys. Rev. Accel. Beams 2019, 22, 090701. [Google Scholar] [CrossRef]
- Deng, H.; Zhang, M.; Feng, C.; Zhang, T.; Wang, X.; Lan, T.; Feng, L.; Zhang, W.; Liu, X.; Yao, H.; et al. Experimental Demonstration of Longitudinal Beam Phase-Space Linearizer in a Free-Electron Laser Facility by Corrugated Structures. Phys. Rev. Lett. 2014, 113, 254802. [Google Scholar] [CrossRef] [PubMed]
- Kondratenko, A.; Saldin, E. Generating of coherent radiation by a relativistic electron beam in an ondulator. Part. Accel. 1980, 10, 207–216. [Google Scholar]
- Bonifacio, R.; Casagrande, F. Instabilities and quantum initiation in the free-electron laser. Opt. Commun. 1984, 50, 251–255. [Google Scholar] [CrossRef]
- Gianluca Geloni, V.K.; Saldin, E. A novel self-seeding scheme for hard X-ray FELs. J. Mod. Opt. 2011, 58, 1391–1403. [Google Scholar] [CrossRef]
- Amann, J.; Berg, W.; Blank, V.; Decker, F.J.; Ding, Y.; Emma, P.; Feng, Y.; Frisch, J.; Fritz, D.; Hastings, J.; et al. Demonstration of self-seeding in a hard-X-ray free-electron laser. Nat. Photonics 2012, 6, 693–698. [Google Scholar] [CrossRef]
- Yu, L.H.; Babzien, M.; Ben-Zvi, I.; DiMauro, L.; Doyuran, A.; Graves, W.; Johnson, E.; Krinsky, S.; Malone, R.; Pogorelsky, I.; et al. High-gain harmonic-generation free-electron laser. Science 2000, 289, 932–934. [Google Scholar] [CrossRef]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.; Bassanese, S.; Biedron, S.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 2012, 6, 699–704. [Google Scholar] [CrossRef]
- Stupakov, G. Using the beam-echo effect for generation of short-wavelength radiation. Phys. Rev. Lett. 2009, 102, 074801. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Wang, D.; Chen, J.; Chen, Z.; Deng, H.; Ding, J.; Feng, C.; Gu, Q.; Huang, M.; Lan, T.; et al. First lasing of an echo-enabled harmonic generation free-electron laser. Nat. Photonics 2012, 6, 360–363. [Google Scholar] [CrossRef]
- Yang, H.; Yan, J.; Zhu, Z.; Deng, H. Optimization and stability analysis of the cascaded EEHG-HGHG free-electron laser. Nucl. Instruments Methods Phys. Res. 2022, 1039, 167065. [Google Scholar] [CrossRef]
- Di Mitri, S.; Cornacchia, M.; Spampinati, S. Cancellation of coherent synchrotron radiation kicks with optics balance. Phys. Rev. Lett. 2013, 110, 014801. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the Parallel Problem Solving from Nature PPSN VI: 6th International Conference, Paris, France, 18–20 September 2000; Proceedings 6. Springer: Berlin/Heidelberg, Germany, 2000; pp. 849–858. [Google Scholar]
- Borland, M. A Flexible SDDS-Compliant Code for Accelerator Simulation, Advanced Photon Source LS-287. In Proceedings of the 6th International Computational Accelerator Physics Conference, Darmstadt, Germany, 11–14 September 2000. [Google Scholar]
- Zhu, Z.; Gu, D.; Yan, J.; Wang, Z.; Yang, H.; Zhang, M.; Deng, H.; Gu, Q. Inhibition of current-spike formation based on longitudinal phase space manipulation for high-repetition-rate X-ray FEL. Nucl. Instruments Methods Phys. Res. 2022, 1026, 166172. [Google Scholar] [CrossRef]
- Zhang, C.; Jiao, Y.; Tsai, C.Y. Quasi-isochronous triple-bend achromat with periodic stable optics and negligible coherent-synchrotron-radiation effects. Phys. Rev. Accel. Beams 2021, 24, 060701. [Google Scholar] [CrossRef]
- England, R.; Rosenzweig, J.; Andonian, G.; Musumeci, P.; Travish, G.; Yoder, R. Sextupole correction of the longitudinal transport of relativistic beams in dispersionless translating sections. Phys. Rev. Spec.-Top.-Accel. Beams 2005, 8, 012801. [Google Scholar] [CrossRef]
- Pellegrini, C.; Marinelli, A.; Reiche, S. The physics of x-ray free-electron lasers. Rev. Mod. Phys. 2016, 88, 015006. [Google Scholar] [CrossRef]
- Rolles, D. Time-resolved experiments on gas-phase atoms and molecules with XUV and X-ray free-electron lasers. Adv. Phys. X 2023, 8, 2132182. [Google Scholar] [CrossRef]
- Ilchen, M.; Allaria, E.; Rebernik Ribič, P.; Nuhn, H.D.; Lutman, A.; Schneidmiller, E.; Tischer, M.; Yurkov, M.; Calvi, M.; Prat, E.; et al. Opportunities for gas-phase science at short-wavelength free-electron lasers with undulator-based polarization control. Phys. Rev. Res. 2025, 7, 011001. [Google Scholar] [CrossRef]
- Dixon, A.; Williams, P.; Thorin, S.; Charles, T.; Wolski, A. Reduction of arrival time jitter or energy spread with arclike variable bunch compressors. Phys. Rev. Accel. Beams 2024, 27, 110702. [Google Scholar] [CrossRef]
- Mansten, E.; Svärd, R.; Thorin, S.; Eriksson, M.; Tavares, P.F. Cancellation of klystron-induced energy and arrival-time variations in linear accelerators with arc-type bunch compressors. Phys. Rev. Accel. Beams 2024, 27, 040401. [Google Scholar] [CrossRef]
- Feng, C.; Liu, T.; Chen, S.; Zhou, K.; Zhang, K.; Qi, Z.; Gu, D.; Wang, Z.; Jiang, Z.; Li, X.; et al. Coherent and ultrashort soft x-ray pulses from echo-enabled harmonic cascade free-electron lasers. Optica 2022, 9, 785–791. [Google Scholar] [CrossRef]
- Yan, J.; Gao, Z.; Qi, Z.; Zhang, K.; Zhou, K.; Liu, T.; Chen, S.; Feng, C.; Li, C.; Feng, L.; et al. Self-Amplification of Coherent Energy Modulation in Seeded Free-Electron Lasers. Phys. Rev. Lett. 2021, 126, 084801. [Google Scholar] [CrossRef]
- Yan, J.; Qin, W.; Chen, Y.; Decking, W.; Dijkstal, P.; Guetg, M.; Inoue, I.; Kujala, N.; Liu, S.; Long, T.; et al. Terawatt-attosecond hard X-ray free-electron laser at high repetition rate. Nat. Photonics 2024, 18, 1293–1298. [Google Scholar] [CrossRef]
- Chen, J.; Zong, Y.; Pu, X.; Xiang, S.; Xing, S.; Li, Z.; Liu, X.; Zhai, Y.; Wu, X.; He, Y.; et al. Ultra-high quality factor and ultra-high accelerating gradient achievements in a 1.3 GHz continuous wave cryomodule. Nucl. Sci. Tech. 2025, 36, 25. [Google Scholar] [CrossRef]
- Wang, G.; Yan, J.; Huang, N.; Gu, D.; Zhang, M.; Deng, H.; Liu, B.; Wang, D.; Yang, X.; Zhao, Z. Energy recovery operation for continuous-wave X-ray free-electron lasers. Nucl. Instruments Methods Phys. Res. 2021, 1005, 165410. [Google Scholar] [CrossRef]

| Delay Distance (mm) | Energy (GeV) | ||
|---|---|---|---|
| 0 | 0 | 8.74 | 0.22/0.22 |
| 1.326 | 57.7 | 5.11 | 0.24/0.23 |
| 1.531 | 76.9 | 3.30 | 0.28/0.23 |
| 1.874 | 115.4 | 1.48 | 0.33/0.25 |
| Delay Distance (mm) | Energy (GeV) | (mm·mrad) DBA/TBA | Peak Current (kA) DBA/TBA | (mm) DBA/TBA |
|---|---|---|---|---|
| 0 | 8.0 | 0.22/0.22 | 1.68/1.68 | 0/0 |
| 57.7 | 4.68 | 0.23/0.26 | 2.21/1.73 | 59.80/10.13 |
| 76.9 | 3.03 | 0.24/0.27 | 2.86/1.76 | 79.75/13.49 |
| 115.4 | 1.39 | 0.35/0.29 | 5.25/1.83 | 119.76/20.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Zhu, Z.; Yan, B.; Yan, J.; Deng, H. Multi-Beam-Energy Control Unit Based on Triple-Bend Achromats. Photonics 2025, 12, 275. https://doi.org/10.3390/photonics12030275
Wu L, Zhu Z, Yan B, Yan J, Deng H. Multi-Beam-Energy Control Unit Based on Triple-Bend Achromats. Photonics. 2025; 12(3):275. https://doi.org/10.3390/photonics12030275
Chicago/Turabian StyleWu, Liuyang, Zihan Zhu, Bingyang Yan, Jiawei Yan, and Haixiao Deng. 2025. "Multi-Beam-Energy Control Unit Based on Triple-Bend Achromats" Photonics 12, no. 3: 275. https://doi.org/10.3390/photonics12030275
APA StyleWu, L., Zhu, Z., Yan, B., Yan, J., & Deng, H. (2025). Multi-Beam-Energy Control Unit Based on Triple-Bend Achromats. Photonics, 12(3), 275. https://doi.org/10.3390/photonics12030275





