Numerical Study of Non-Schell Model Pulses in Nonlinear Dispersive Media with the Monte Carlo-Based Pseudo-Mode Superposition Method
Abstract
1. Introduction
2. Theoretical Model
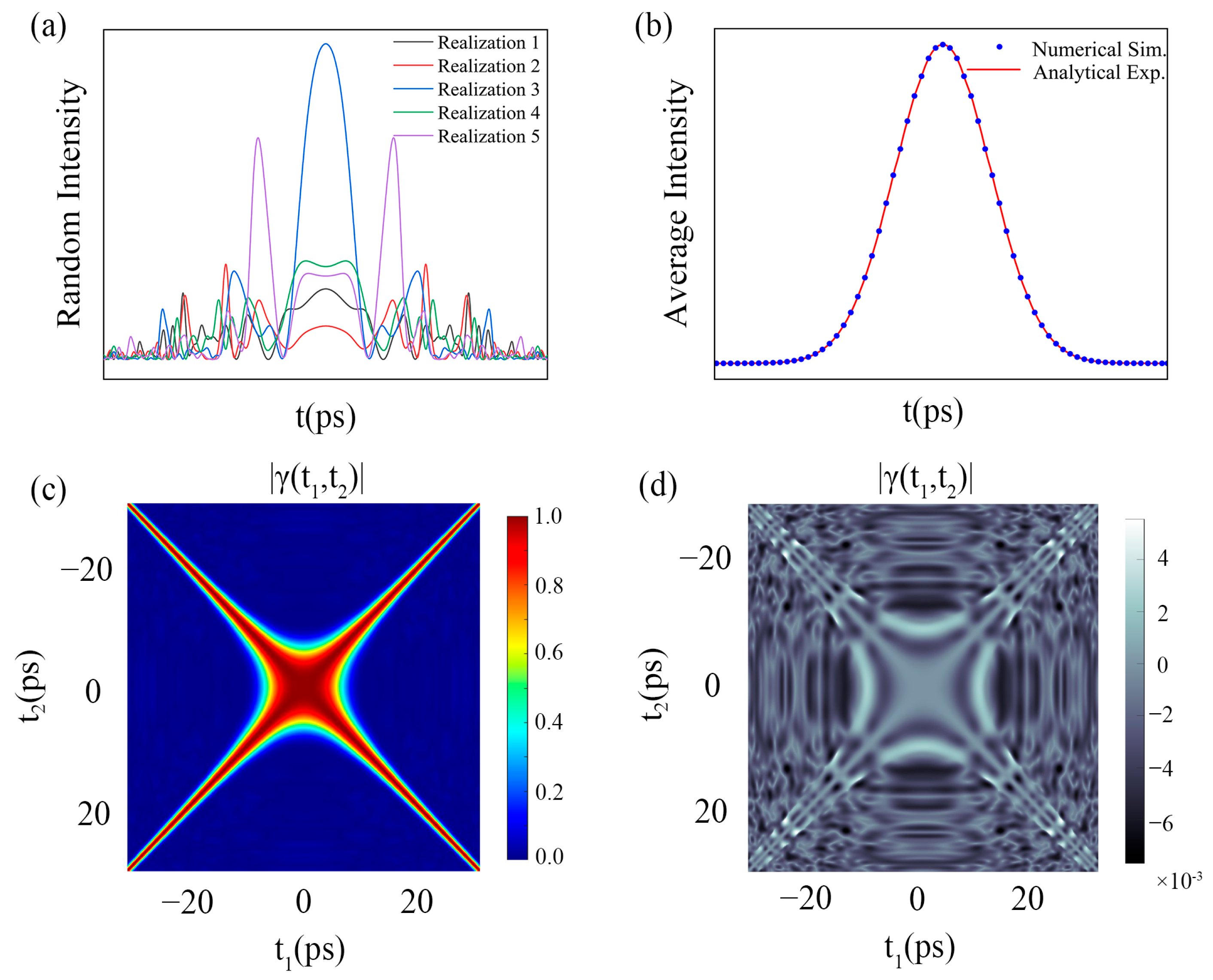
2.1. Introduction to the Monte Carlo-Based Pseudo-Mode Superposition Method
2.2. Description of the Specific nSMPs
2.3. Introduction to the Pulse Propagation Model
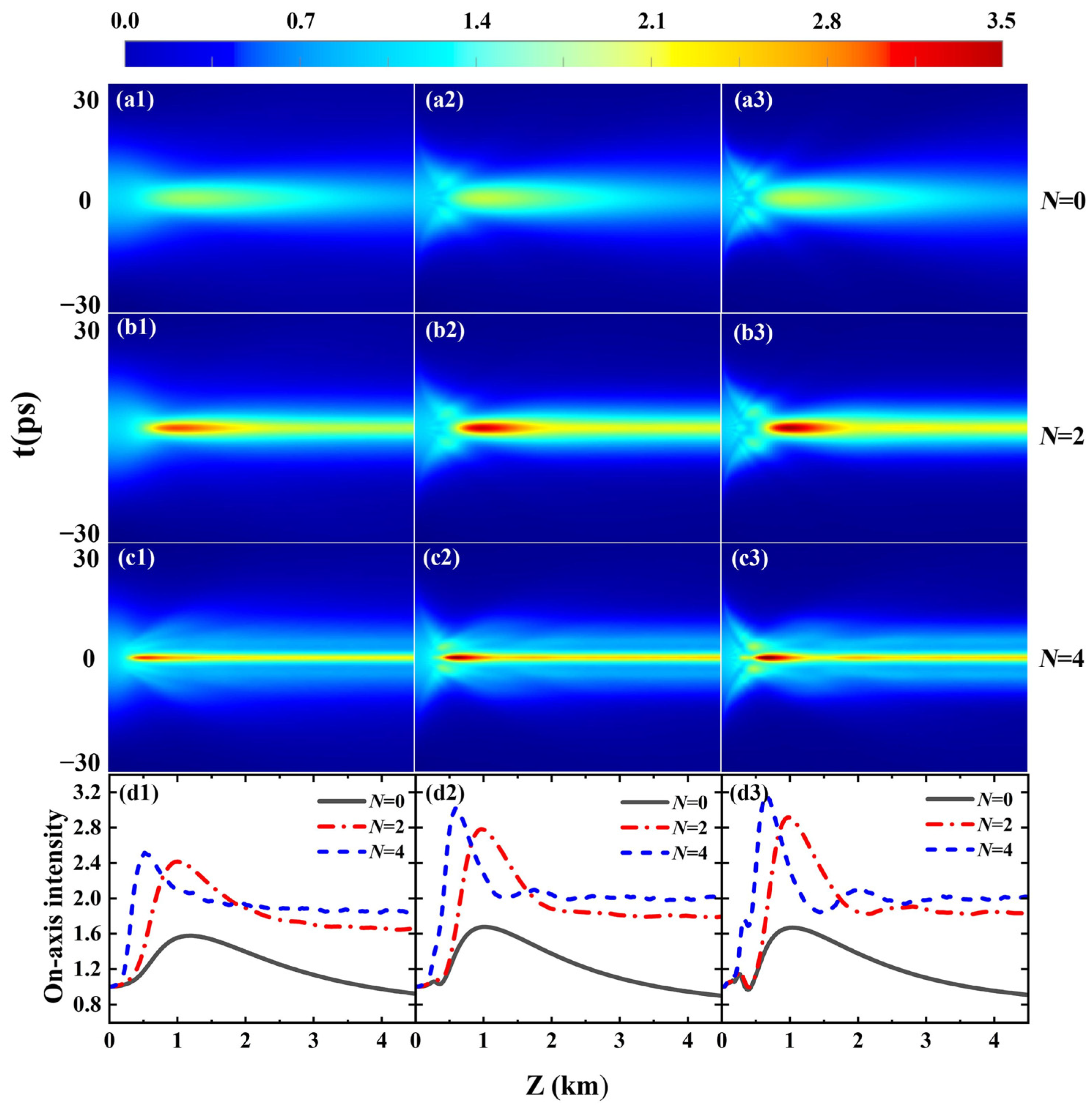
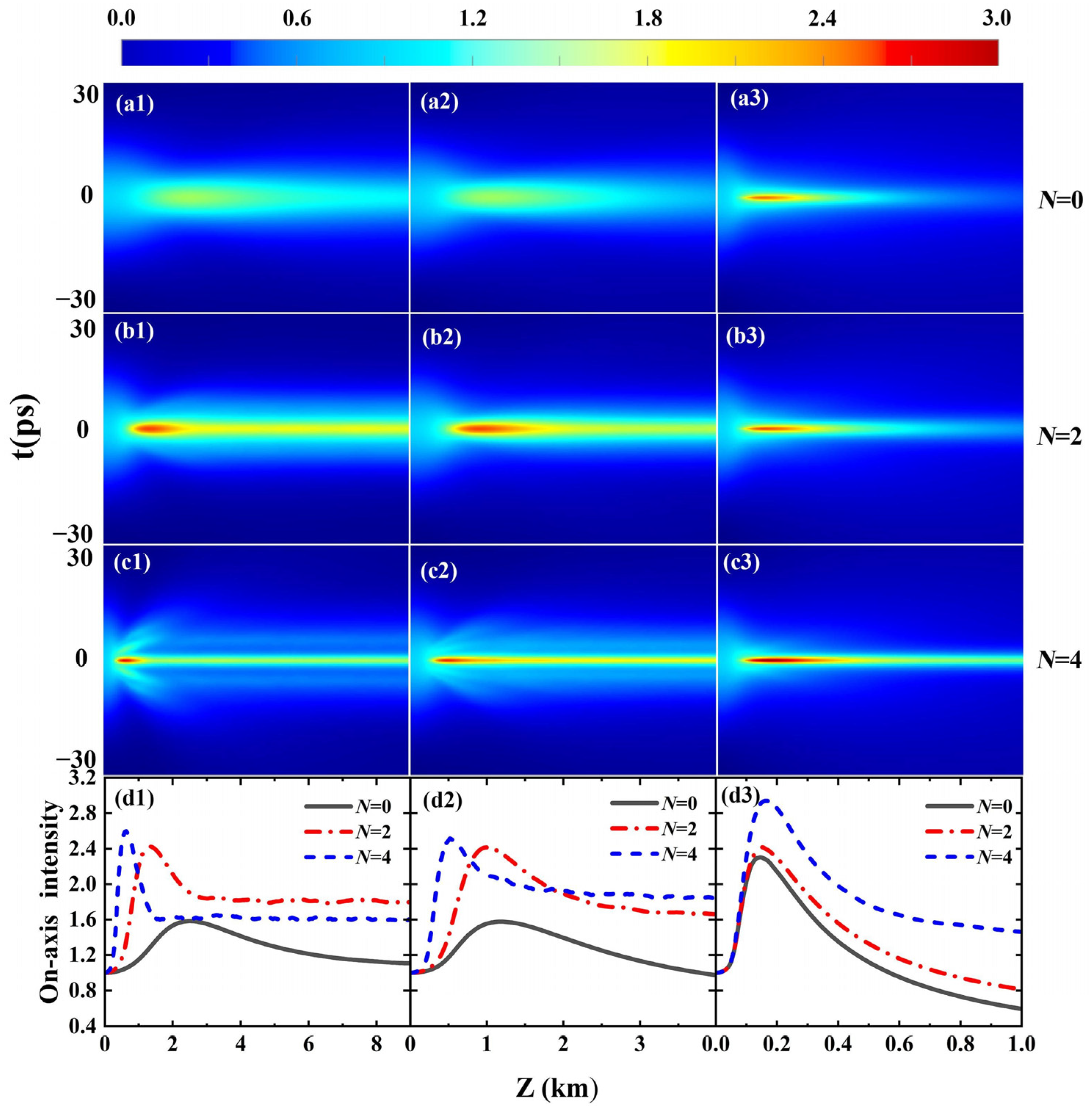
3. Results and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Dong, B.; Plückelmann, F.B.; Meyer, L.; Dijkstra, J.; Bente, I.; Wendland, D.; Varri, A.; Aggarwal, S.; Farmakidis, N.; Wang, M.; et al. Partial coherence enhances parallelized photonic computing. Nature 2024, 632, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Wan, Z.; Zhan, Z.; Liu, K.; Liu, Q.; Fu, X. Super-resolution orbital angular momentum holography. Nat. Commun. 2023, 14, 1869. [Google Scholar] [CrossRef] [PubMed]
- Redding, B.; Choma, M.A.; Cao, H. Speckle-free laser imaging using random laser illumination. Nat. Photon. 2012, 6, 355–359. [Google Scholar] [CrossRef]
- Clark, J.N.; Huang, X.; Harder, R.; Robinson, I.K. High-resolution three-dimensional partially coherent diffraction imaging. Nat. Commun. 2012, 3, 993. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.; Wu, G.; Wang, F.; Li, W.; Cai, Y.; Ponomarenko, S.A. Overcoming the classical Rayleigh diffraction limit by controlling two-point correlations of partially coherent light sources. Opt. Express 2017, 25, 28352–28362. [Google Scholar] [CrossRef]
- Wang, F.; Liang, C.; Yuan, Y.; Cai, Y. Generalized multi-Gaussian correlated Schell model beam: From theory to experiment. Opt. Express 2014, 22, 23456–23464. [Google Scholar] [CrossRef]
- Yu, J.; Zhu, X.; Wang, F.; Chen, Y.; Cai, Y. Research progress on manipulating spatial coherence structure of light beam and its applications. Prog. Quant. Electron. 2023, 91–92, 100486. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, Y.; Wang, F. Generation and propagation of partially coherent beams with nonconventional correlation functions: A review [Invited]. J. Opt. Soc. Am. A 2014, 31, 2083–2093. [Google Scholar] [CrossRef]
- Sahin, S.; Korotkova, O. Light sources generating far fields with tunable flat profiles. Opt. Lett. 2012, 37, 2970–2972. [Google Scholar] [CrossRef]
- Liang, C.; Zhu, X.; Mi, C.; Peng, X.; Wang, F.; Cai, Y.; Ponomarenko, S.A. High-quality partially coherent Bessel beam array generation. Opt. Lett. 2018, 43, 3188–3191. [Google Scholar] [CrossRef]
- Hyde, M.; Bose-Pillai, S.R.; Xiao, X.; Voelz, D.G. A fast and efficient method for producing partially coherent sources. J. Opt. 2017, 19, 025601. [Google Scholar] [CrossRef]
- Mei, Z.; Korotkova, O. Sources for random arrays with structured complex degree of coherence. Opt. Lett. 2018, 43, 2676–2679. [Google Scholar] [CrossRef]
- Peng, D.; Huang, Z.; Liu, Y.; Chen, Y.; Wang, F.; Ponomarenko, S.A.; Cai, Y. Optical coherence encryption with structured random light. PhotoniX 2021, 2, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O. Random Light Beams Theory and Application; CRC: Boca Raton, FL, USA, 2014. [Google Scholar]
- Cao, T.; Liu, X.; Chen, Q.; Ponomarenko, S.A.; Cai, Y.; Liang, C. Prime number factorization and degree of coherence of speckled light beams. Opt. Lett. 2024, 49, 5232–5235. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, Y.; Wang, F.; Cai, Y.; Liang, C.; Korotkova, O. Robust far-field imaging by spatial coherence engineering. Opto-Electron. Adv. 2021, 4, 210027. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Liu, X.; Ma, Y.; Cai, Y.; Ponomarenko, S.A.; Liu, X. Deep learning and random light structuring ensure robust free-space communications. Appl. Phys. Lett. 2024, 124, 214103. [Google Scholar] [CrossRef]
- Korotkova, O.; Gbur, G. Applications of optical coherence theory. Prog. Opt. 2020, 65, 43–104. [Google Scholar]
- Zhou, Y.; Xu, H.; Yuan, Y.; Peng, J.; Qu, J.; Huang, W. Trapping two types of particles using a Laguerre–Gaussian correlated Schell model beam. IEEE Photonics J. 2016, 8, 6600710. [Google Scholar] [CrossRef]
- Lajunen, H.; Saastamoinen, T. Propagation characteristics of partially coherent beams with spatially varying correlations. Opt. Lett. 2011, 36, 4104–4106. [Google Scholar] [CrossRef] [PubMed]
- Tong, Z.; Korotkova, O. Nonuniformly correlated light beams in uniformly correlated media. Opt. Lett. 2012, 37, 3240–3242. [Google Scholar] [CrossRef]
- Yu, J.; Wang, F.; Liu, L.; Cai, Y.; Gbur, G. Propagation properties of Hermite non-uniformly correlated beams in turbulence. Opt. Express 2018, 26, 16333–16343. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Xu, Y.; Lin, S.; Chang, H.; Zhu, X.; Cai, Y.; Yu, J. Enhancing fiber-coupling efficiency of beam-to-fiber links in turbulence by spatial non-uniform coherence engineering. Opt. Express 2023, 31, 25680–25690. [Google Scholar] [CrossRef]
- Song, Z.; Ye, J.; Wang, L.; Liu, Z.; Liu, S.; Liu, B. Radially polarized cosine non-uniformly correlated beams and their propagation properties. J. Opt. Soc. Am. A 2022, 39, 1766–1773. [Google Scholar] [CrossRef]
- Tong, Z.; Korotkova, O. Electromagnetic nonuniformly correlated beams. J. Opt. Soc. Am. A 2012, 29, 2154–2158. [Google Scholar] [CrossRef]
- Wu, D.; Wang, F.; Cai, Y. High-order nonuniformly correlated beams. Opt. Laser Technol. 2018, 99, 230–237. [Google Scholar] [CrossRef]
- Piquero, G.; Santarsiero, M.; Martínez-Herrero, R.; de Sande, J.C.G.; Alonzo, M.; Gori, F. Partially coherent sources with radial coherence. Opt. Lett. 2018, 43, 2376–2379. [Google Scholar] [CrossRef] [PubMed]
- Ponomarenko, S.A.; Huang, W.; Cada, M. Dark and antidark diffraction-free beams. Opt. Lett. 2007, 32, 2508–2510. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Sun, H.; Peng, D.; Chen, Y.; Cai, Q.; Wu, D.; Wang, F.; Cai, Y.; Ponomarenko, S.A. Optical image reconstruction in 4f imaging system Role of spatial coherence structure engineering. Appl. Phys. Lett. 2021, 118, 181102. [Google Scholar] [CrossRef]
- Shiri, A.; Qi, R.; Gbur, G. Circularly coherent vortex beams optimized for propagation through turbulence. J. Opt. Soc. Am. A 2024, 41, B127–B134. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, X.; Cai, Y.; Ponomarenko, S.A.; Liang, C. Structurally stable beams in the turbulent atmosphere: Dark and antidark beams on incoherent background [Invited]. J. Opt. Soc. Am. A 2022, 39, C51–C57. [Google Scholar] [CrossRef]
- Yu, J.; Xu, Y.; Lin, S.; Zhu, X.; Gbur, G.; Cai, Y. Longitudinal optical trapping and manipulating Rayleigh particles by spatial nonuniform coherence engineering. Phys. Rev. A 2022, 106, 033511. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Ponomarenko, S.A.; Wang, F.; Peng, X.; Cai, Y.; Liang, C. Unlocking Secure Optical Multiplexing with Spatially Incoherent Light. Laser Photonics Rev. 2025, in press. [CrossRef]
- Hyde, M.; Bose-Pillai, S.R.; Voelz, D.G.; Xiao, X. Generation of Vector Partially Coherent Optical Sources Using Phase-Only Spatial Light Modulators. Phys. Rev. Appl. 2016, 6, 064030. [Google Scholar] [CrossRef]
- Hyde, M.; Xiao, X.; Voelz, D.G. Generating electromagnetic nonuniformly correlated beams. Opt. Lett. 2019, 44, 5719–5722. [Google Scholar] [CrossRef] [PubMed]
- Hyde, M. Real-time synthesis of a nonuniformly correlated, partially coherent beam using an optical coordinate transformation. APL Photon. 2024, 9, 106107. [Google Scholar] [CrossRef]
- Zhu, X.; Yu, J.; Wang, F.; Chen, Y.; Cai, Y.; Korotkova, O. Synthesis of vector nonuniformly correlated light beams by a single digital mirror device. Opt. Lett. 2021, 46, 2996–2999. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Herrero, R.; Mejías, P.M.; Gori, F. Genuine cross-spectral densities and pseudo-modal expansions. Opt. Lett. 2009, 34, 1399–1401. [Google Scholar] [CrossRef]
- Zhu, S.; Li, P.; Li, Z.; Cai, Y.; He, W. Generating non-uniformly correlated twisted source. Opt. Lett. 2021, 46, 5100–5103. [Google Scholar] [CrossRef]
- Lancis, J.; Torres-Company, V.; Silvestre, E.; Andrés, P. Space–time analogy for partially coherent plane-wave-type pulses. Opt. Lett. 2005, 30, 2973–3975. [Google Scholar] [CrossRef]
- Ding, C.; Koivurova, M.; Turunen, J.; Pan, L. Temporal self-splitting of optical pulses. Phys. Rev. A 2018, 97, 053838. [Google Scholar] [CrossRef]
- Ding, C.; Korotkova, O.; Zhao, D.; Li, D.; Zhao, Z.; Pan, L. Propagation of temporal coherence gratings in dispersive medium with a chirper. Opt. Express 2020, 28, 7463. [Google Scholar] [CrossRef]
- Ding, C.; Korotkova, O.; Zhang, Y.; Pan, L. Cosine-Gaussian correlated Schell model pulsed beams. Opt. Express 2014, 22, 931. [Google Scholar] [CrossRef]
- Koivurova, M.; Laatikainen, J.; Friberg, A.T. Nonstationary optics: Tutorial. J. Opt. Soc. Am. A 2024, 41, 615. [Google Scholar] [CrossRef]
- Liu, H.; Du, Z.; Li, Y.; Chen, H.; Lu, Y. Self-focusing and self-splitting properties of partially coherent temporal pulses propagating in dispersive media. Opt. Express 2023, 31, 7336. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Ponomarenko, S.A. Optical coherence gratings and lattices. Opt. Lett. 2014, 39, 6656. [Google Scholar] [CrossRef] [PubMed]
- Talukder, R.; Halder, A.; Koivurova, M.; Ding, C.; Setälä, T.; Turunen, J.; Friberg, A.T. Generation of pulse trains with nonconventional temporal correlation properties. J. Opt. 2022, 24, 055502. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, L.; Zhu, S. Partially coherent light pulse and its propagation. Opt. Commun. 2003, 219, 65. [Google Scholar] [CrossRef]
- Wang, X.; Tang, J.; Wang, Y.; Liu, X.; Liang, C.; Zhao, L.; Hoenders, B.J.; Cai, Y.; Ma, P. Complex and phase screen methods for studying arbitrary genuine Schell model partially coherent pulses in nonlinear media. Opt. Express 2022, 30, 242222. [Google Scholar] [CrossRef]
- Chen, Q.; Bai, Y.; Wang, X.; Peng, P.; Liu, J.; Cai, Y.; Liang, C. On-demand pulse shaping with partially coherent pulses in nonlinear dispersive media. arXiv 2025, arXiv:2503.02629. [Google Scholar]
- Lajunen, H.; Saastamoinen, T. Non-uniformly correlated partially coherent pulses. Opt. Express 2013, 21, 190–195. [Google Scholar] [CrossRef]
- Ding, C.; Cai, Y.; Zhang, Y.; Wang, H.; Zhao, Z.; Pan, L. Stochastic electromagnetic plane-wave pulses with non-uniform correlation distribution. Phys. Lett. A 2013, 377, 1563–1565. [Google Scholar] [CrossRef]
- Liu, X.; Cai, Z.; Wang, X.; Xu, B. Propagation properties of generalized Schell model pulse sources in dispersive media. Photonics 2023, 10, 1378. [Google Scholar] [CrossRef]
- Ding, C.; Liang, C.; Horoshko, D.; Korotkova, O.; Pan, L.; Liu, Z. Method for generating spatiotemporal coherency vortices and spatiotemporal dislocation curves. Opt. Express 2023, 32, 609–624. [Google Scholar] [CrossRef] [PubMed]
- Rosales-Guzmán, C.; Forbes, A. How to Shape Light with Spatial Light Modulators; SPIE: Washington, DC, USA, 2017. [Google Scholar]
| Exponent Values Soliton Parameter | n = 2 N = 0 N = 2 N = 4 | n = 4 N = 0 N = 2 N = 4 | n = 6 N = 0 N = 2 N = 4 |
|---|---|---|---|
| FWHM (ps) | 6.3 3.1 1.7 | 5.8 2.8 1.5 | 5.3 2.5 1.3 |
| Zf (km) | 1.22 1.01 0.54 | 1.04 0.99 0.63 | 1.06 0.99 0.68 |
| Coherent Time (ps) Soliton Parameter | tc = 25 N = 0 N = 2 N = 4 | tc = 15 N = 0 N = 2 N = 4 | tc = 5 N = 0 N = 2 N = 4 |
|---|---|---|---|
| FWHM (ps) | 7.1 3.3 4.1 | 6.3 3.1 1.6 | 2.6 2.1 1.3 |
| Zf (km) | 2.57 1.35 0.68 | 1.22 1.01 0.54 | 0.14 0.16 0.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, P.; Zhang, Y.; Bai, Y.; Cai, Y.; Liu, J. Numerical Study of Non-Schell Model Pulses in Nonlinear Dispersive Media with the Monte Carlo-Based Pseudo-Mode Superposition Method. Photonics 2025, 12, 236. https://doi.org/10.3390/photonics12030236
Ma P, Zhang Y, Bai Y, Cai Y, Liu J. Numerical Study of Non-Schell Model Pulses in Nonlinear Dispersive Media with the Monte Carlo-Based Pseudo-Mode Superposition Method. Photonics. 2025; 12(3):236. https://doi.org/10.3390/photonics12030236
Chicago/Turabian StyleMa, Pujuan, Yi Zhang, Yanlin Bai, Yangjian Cai, and Jingsong Liu. 2025. "Numerical Study of Non-Schell Model Pulses in Nonlinear Dispersive Media with the Monte Carlo-Based Pseudo-Mode Superposition Method" Photonics 12, no. 3: 236. https://doi.org/10.3390/photonics12030236
APA StyleMa, P., Zhang, Y., Bai, Y., Cai, Y., & Liu, J. (2025). Numerical Study of Non-Schell Model Pulses in Nonlinear Dispersive Media with the Monte Carlo-Based Pseudo-Mode Superposition Method. Photonics, 12(3), 236. https://doi.org/10.3390/photonics12030236





