Spatial Goos–Hänchen Shifts of Airy Vortex Beams Impinging on Graphene/hBN Heterostructure
Abstract
1. Introduction
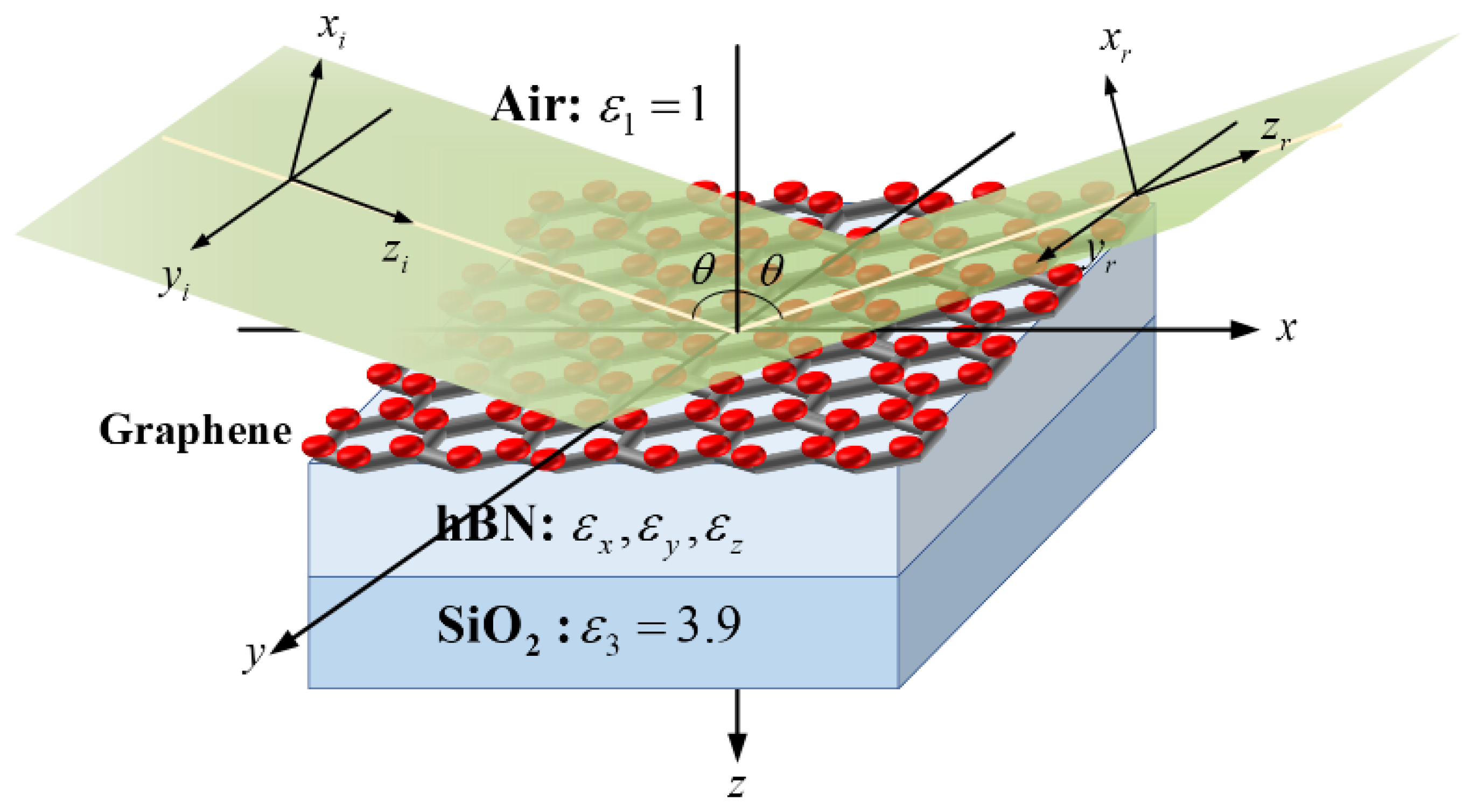
2. Theoretical Formulation
3. Results
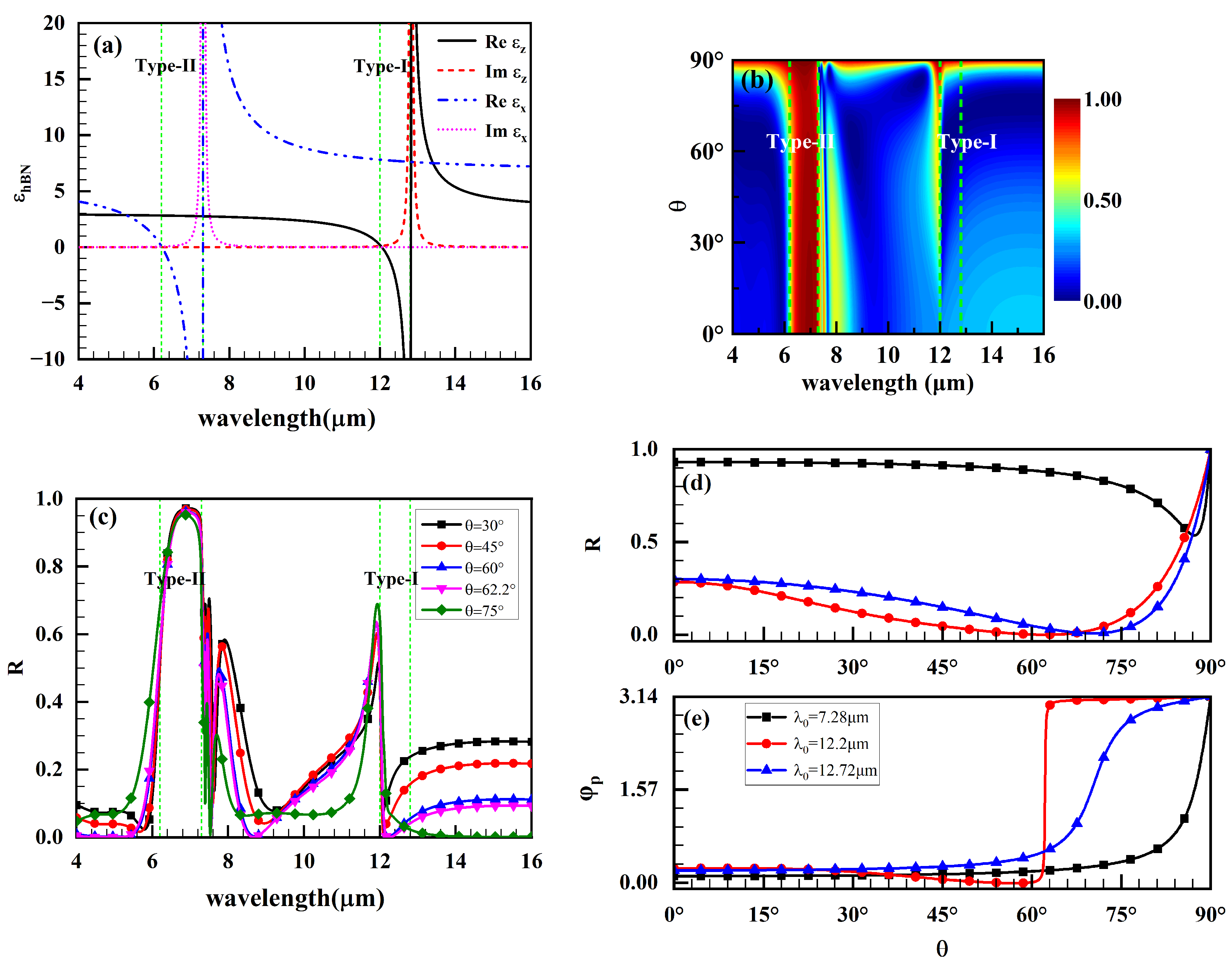
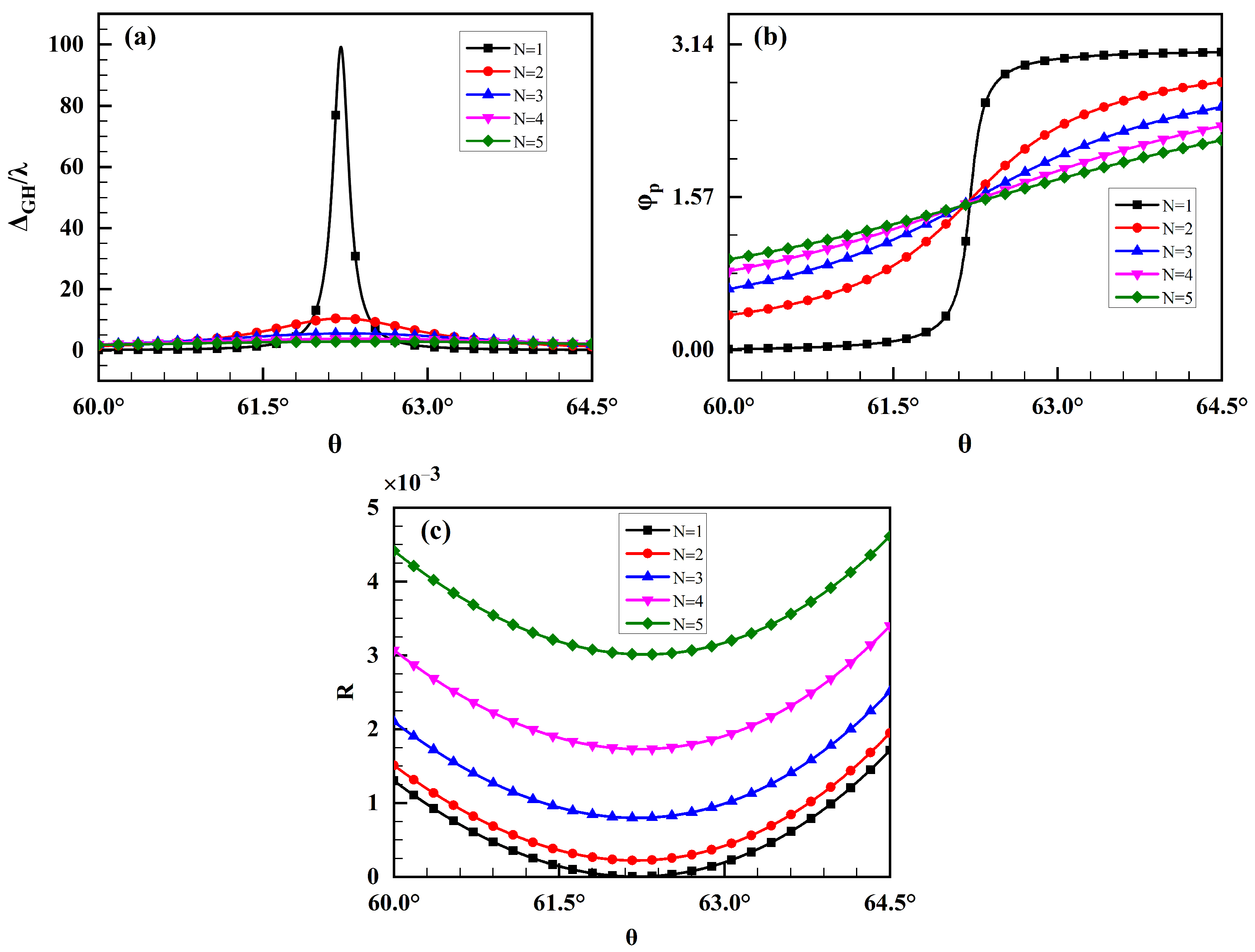
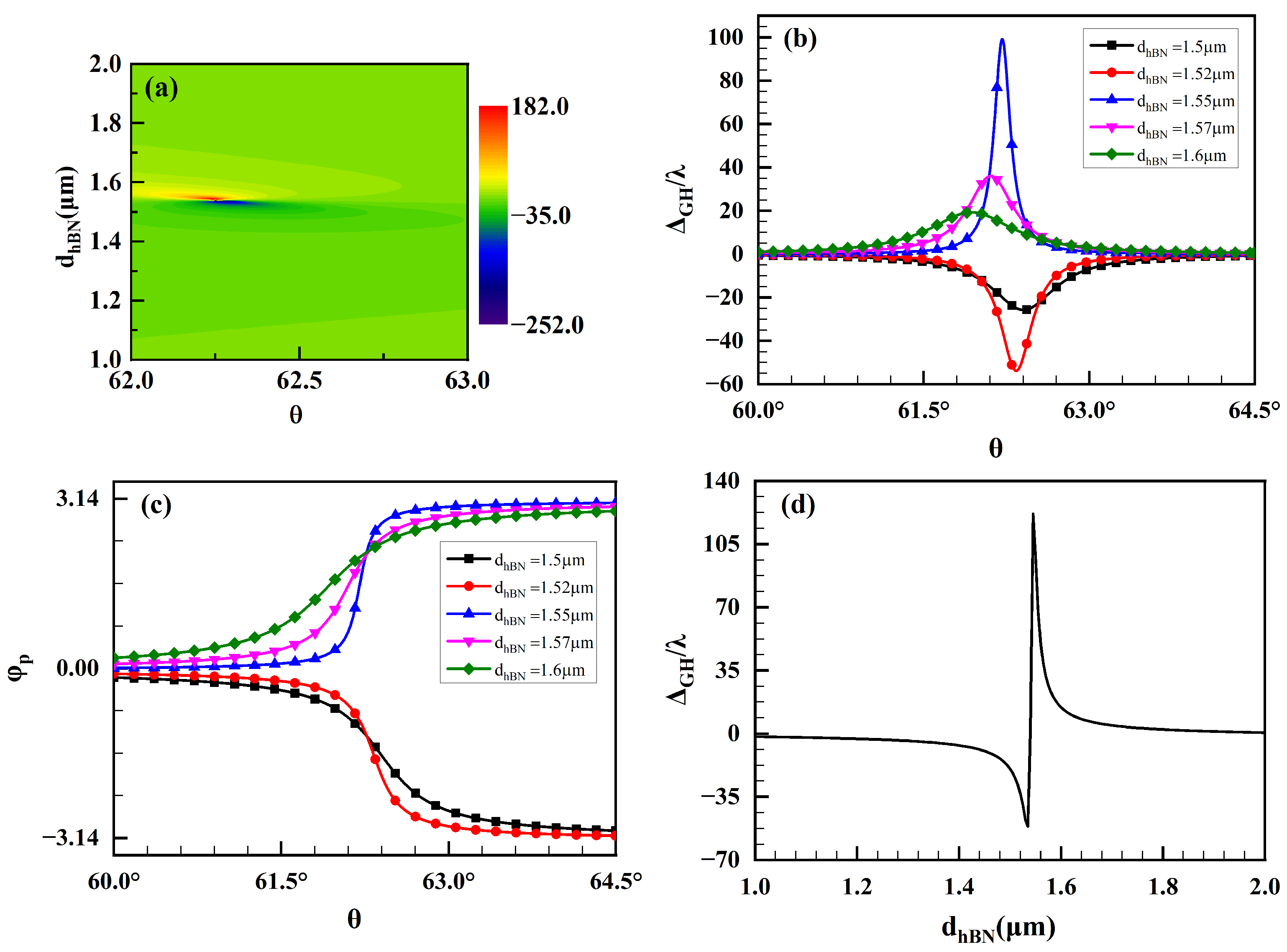
3.1. Effects of Graphene/hBN Heterostructure Parameters
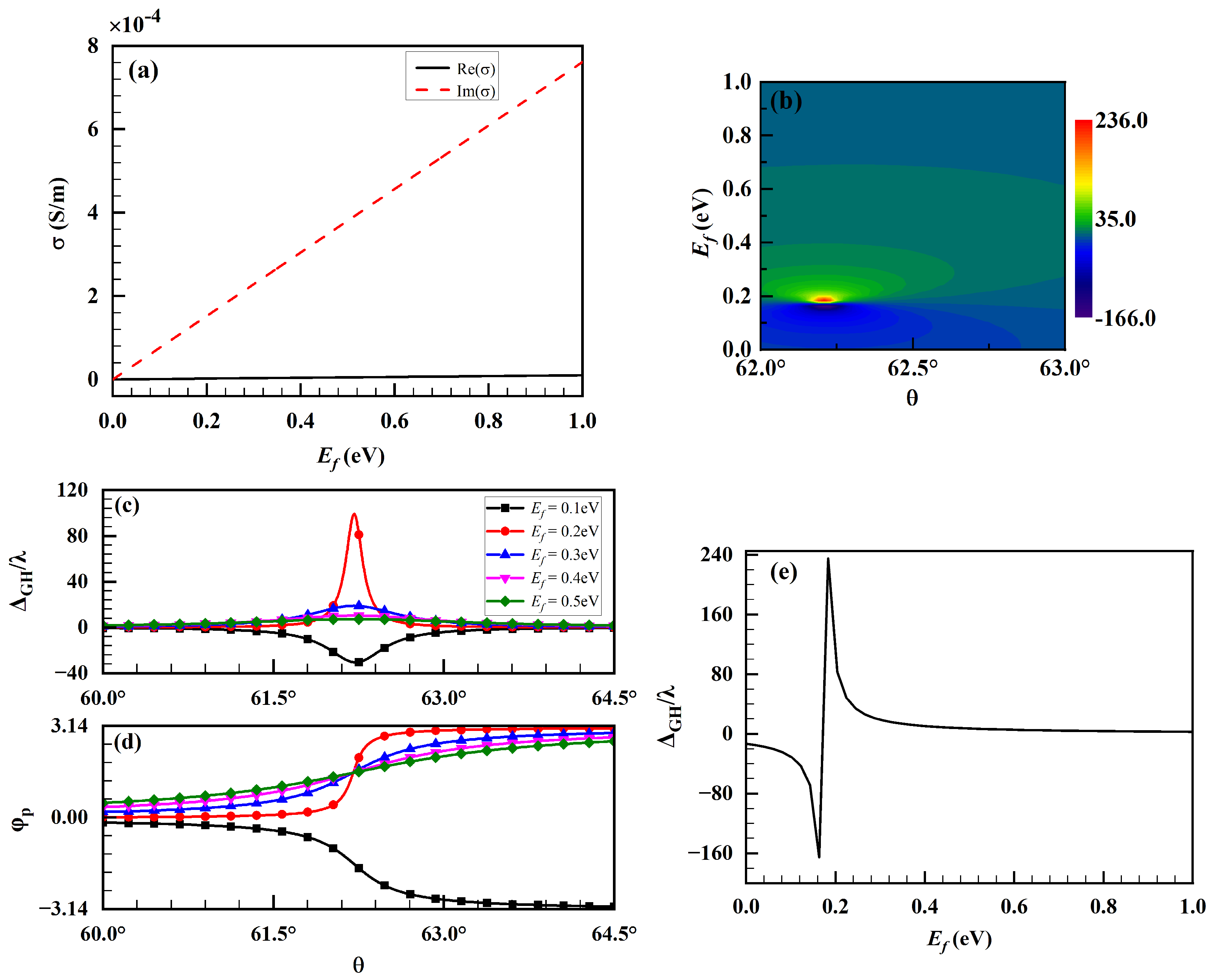
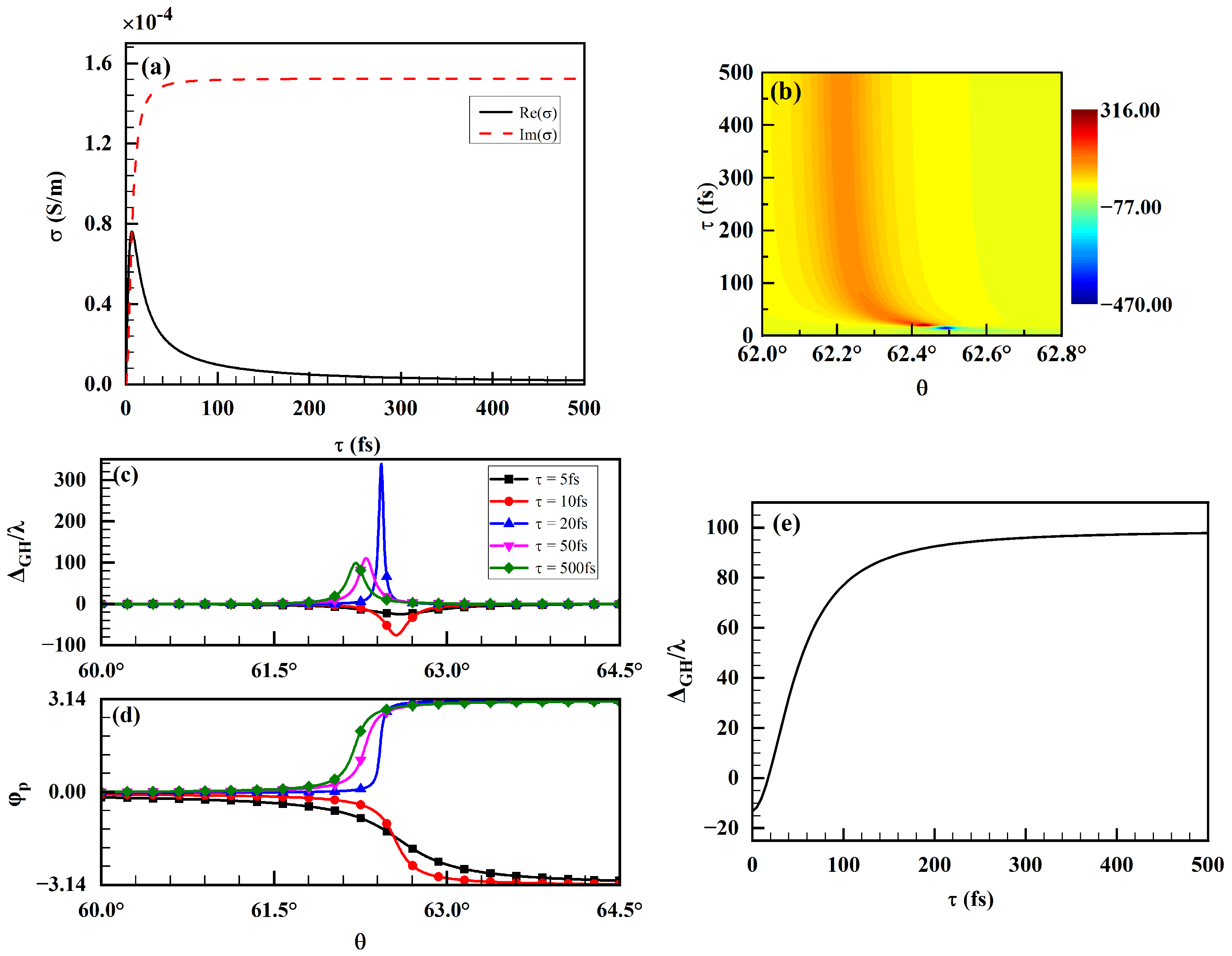
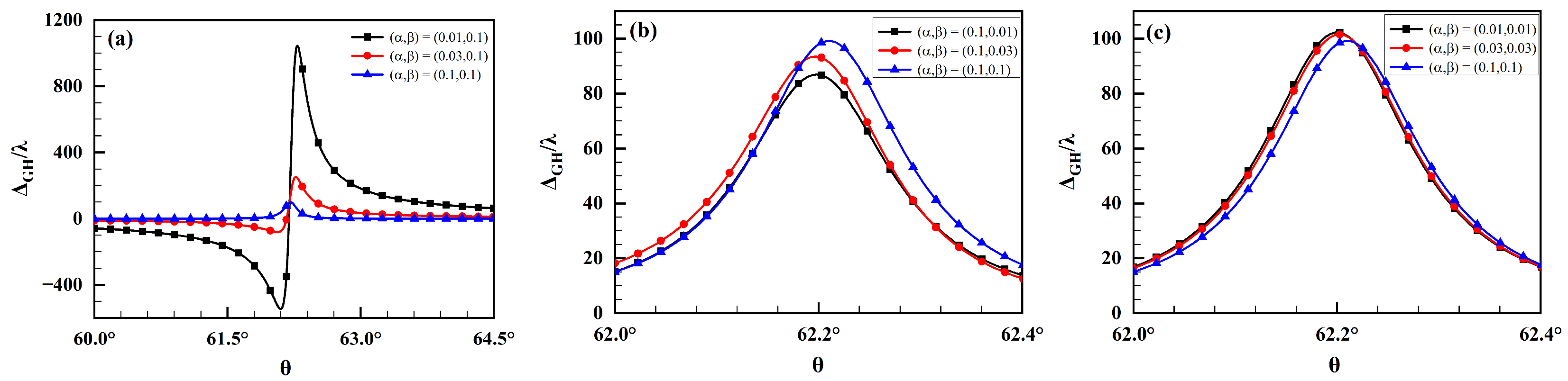
3.2. Effects of Airy Vortex Beam Parameters
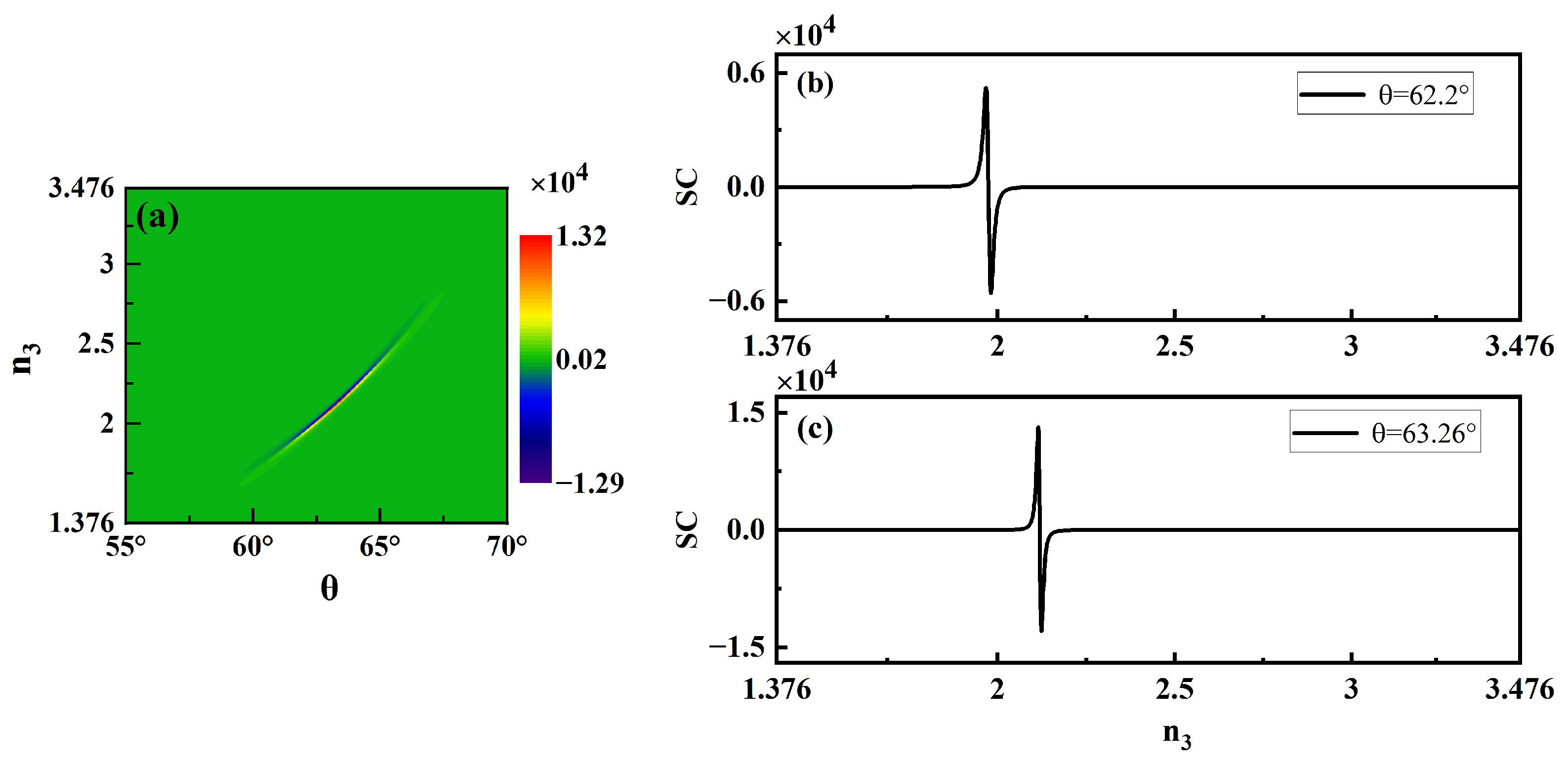
3.3. Spatial GH Shifts for Sensing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Efremidis, N.K.; Chen, Z.; Segev, M.; Christodoulides, D.N. Airy beams and accelerating waves: An overview of recent advances. Optica 2019, 6, 686–701. [Google Scholar] [CrossRef]
- Berry, M.V.; Balazs, N.L. Nonspreading wave packets. Am. J. Phys. 1979, 47, 264–267. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of accelerating Airy beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
- Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979–981. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Ballistic dynamics of Airy beams. Opt. Lett. 2008, 33, 207–209. [Google Scholar] [CrossRef]
- Broky, J.; Siviloglou, G.A.; Dogariu, A.; Christodoulides, D.N. Self-healing properties of optical Airy beams. Opt. Express 2008, 16, 12880–12891. [Google Scholar] [CrossRef]
- Gu, Y.; Gbur, G. Scintillation of Airy beam arrays in atmospheric turbulence. Opt. Lett. 2010, 35, 3456–3458. [Google Scholar] [CrossRef] [PubMed]
- Baumgartl, J.; Mazilu, M.; Dholakia, K. Optically mediated particle clearing using Airy wavepackets. Nat. Photonics 2008, 2, 675–678. [Google Scholar] [CrossRef]
- Zhang, P.; Prakash, J.; Zhang, Z.; Mills, M.S.; Efremidis, N.K.; Christodoulides, D.N.; Chen, Z. Trapping and guiding microparticles with morphing autofocusing Airy beams. Opt. Lett. 2011, 36, 2883–2885. [Google Scholar] [CrossRef]
- Suarez, R.A.B.; Neves, A.A.R.; Gesualdi, M.R.R. Optical trapping with non-diffracting Airy beams array using a holographic optical tweezers. Opt. Laser Technol. 2021, 135, 106678. [Google Scholar] [CrossRef]
- Polynkin, P.; Kolesik, M.; Moloney, J.V.; Siviloglou, G.A.; Christodoulides, D.N. Curved Plasma Channel Generation Using Ultraintense Airy Beams. Science 2009, 324, 229–232. [Google Scholar] [CrossRef] [PubMed]
- Polynkin, P.; Kolesik, M.; Moloney, J. Filamentation of femtosecond laser Airy beams in water. Phys. Rev. Lett. 2009, 103, 123902. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Fan, X.; Zang, W.; Tian, J. Vacuum electron acceleration driven by two crossed Airy beams. Opt. Lett. 2011, 36, 648–650. [Google Scholar] [CrossRef] [PubMed]
- Salandrino, A.; Christodoulides, D.N. Airy plasmon: A nondiffracting surface wave. Opt. Lett. 2010, 35, 2082–2084. [Google Scholar] [CrossRef]
- Minovich, A.; Klein, A.E.; Janunts, N.; Pertsch, T.; Neshev, D.N.; Kivshar, Y.S. Generation and Near-Field Imaging of Airy Surface Plasmons. Phys. Rev. Lett. 2011, 107, 116802. [Google Scholar] [CrossRef] [PubMed]
- Ng, J.; Lin, Z.; Chan, C.T. Theory of optical trapping by an optical vortex beam. Phys. Rev. Lett. 2010, 104, 103601. [Google Scholar] [CrossRef] [PubMed]
- Dholakia, K.; Čižmár, T. Shaping the future of manipulation. Nat. Photonics 2011, 5, 335–342. [Google Scholar] [CrossRef]
- Gibson, G.; Courtial, J.; Padgett, M.J. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 2004, 12, 5448–5456. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.-Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Molina-Terriza, G.; Torres, J.P.; Torner, L. Twisted photons. Nat. Phys. 2007, 3, 305–310. [Google Scholar] [CrossRef]
- Mazilu, M.; Baumgartl, J.; Cizmar, T.; Dholakia, K. Accelerating vortices in Airy beams. Proc. SPIE 2009, 7430, 74300C. [Google Scholar] [CrossRef]
- Dai, H.T.; Liu, Y.J.; Luo, D.; Sun, X.W. Propagation properties of an optical vortex carried by an Airy beam: Experimental implementation. Opt. Lett. 2011, 36, 1617–1619. [Google Scholar] [CrossRef] [PubMed]
- Suarez, R.A.B.; Neves, A.A.R.; Gesualdi, M.R.R. Generation and characterization of an array of Airy-vortex beams. Opt. Commun. 2020, 458, 124846. [Google Scholar] [CrossRef]
- Gao, M.; Wang, G.; Yang, X.; Liu, H.; Deng, D. Goos-Hänchen and Imbert-Fedorov shifts of off-axis Airy vortex beams. Opt. Express 2020, 28, 28916–28923. [Google Scholar] [CrossRef]
- Fang, Z.X.; Chen, Y.; Ren, Y.X.; Gong, L.; Wang, P. Interplay between topological phase and self-acceleration in a vortex symmetric Airy beam. Opt. Express 2018, 26, 7324–7335. [Google Scholar] [CrossRef] [PubMed]
- Casiraghi, C.; Hartschuh, A.; Lidorikis, E.; Qian, H.; Harutyunyan, H.; Gokus, T.; Novoselov, K.S.; Ferrari, A.C. Rayleigh Imaging of Graphene and Graphene Layers. Nano Lett. 2007, 7, 2711–2717. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef]
- Yankowitz, M.; Xue, J.; LeRoy, B.J. Graphene on hexagonal boron nitride. J. Phys. Condens. Matter 2014, 26, 303201. [Google Scholar] [CrossRef]
- Kumar, A.; Low, T.; Fung, K.H.; Avouris, P.; Fang, N.X. Tunable Light–Matter Interaction and the Role of Hyperbolicity in Graphene–hBN System. Nano Lett. 2015, 15, 3172–3180. [Google Scholar] [CrossRef] [PubMed]
- Dean, C.R.; Young, A.F.; Meric, I.; Lee, C.; Wang, L.; Sorgenfrei, S.; Watanabe, K.; Taniguchi, T.; Kim, P.; Shepard, K.L.; et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 2010, 5, 722–726. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.; Ma, Q.; Liu, M.K.; Andersen, T.; Fei, Z.; Goldflam, M.D.; Wagner, M.; Watanabe, K.; Taniguchi, T.; Thiemens, M.; et al. Graphene on hexagonal boron nitride as a tunable hyperbolic metamaterial. Nat. Nanotechnol. 2015, 10, 682–686. [Google Scholar] [CrossRef]
- Brar, V.W.; Jang, M.S.; Sherrott, M.; Kim, S.; Lopez, J.J.; Kim, L.B.; Choi, M.; Atwater, H. Hybrid Surface-Phonon-Plasmon Polariton Modes in Graphene/Monolayer h-BN Heterostructures. Nano Lett. 2014, 14, 3876–3880. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Zhang, Z.M. Enhanced Photon Tunneling by Surface Plasmon–Phonon Polaritons in Graphene/hBN Heterostructures. J. Heat Transf. 2016, 139, 022701. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, L.; Guo, J.; Dai, X.; Xiang, Y.; Wen, S. Tunable perfect absorption at infrared frequencies by a graphene-hBN hyper crystal. Opt. Express 2016, 24, 17103–17114. [Google Scholar] [CrossRef] [PubMed]
- Hajian, H.; Ghobadi, A.; Butun, B.; Ozbay, E. Tunable, omnidirectional, and nearly perfect resonant absorptions by a graphene-hBN-based hole array metamaterial. Opt. Express 2018, 26, 16940–16954. [Google Scholar] [CrossRef]
- Deng, G.; Song, X.; Dereshgi, S.A.; Xu, H.; Aydin, K. Tunable multi-wavelength absorption in mid-IR region based on a hybrid patterned graphene-hBN structure. Opt. Express 2019, 27, 23576–23584. [Google Scholar] [CrossRef]
- Zheng, Z.; Lu, F.; Dai, X. Tunable reflected group delay from the graphene/hBN heterostructure at infrared frequencies. Results Phys. 2019, 15, 102681. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Goos, V.F.; Hänchen, H. Ein neuer und fundamentaler Versuch zur Totalreflexion. Ann. Phys. 1947, 436, 333–346. [Google Scholar] [CrossRef]
- Fedorov, F.I. K teorii polnovo otrazenija. Dokl. Akad. Nauk SSSR 1955, 105, 465–467. [Google Scholar]
- Bliokh, K.Y.; Aiello, A. Goos-Hänchen and Imbert-Fedorov beam shifts: An overview. J. Opt. 2013, 15, 014001. [Google Scholar] [CrossRef]
- Aiello, A.; Woerdman, J.P. Theory of angular Goos-Hänchen shift near Brewster incidence. arXiv 2009, arXiv:0903.3730v2. [Google Scholar]
- Zhen, W.; Deng, D.; Guo, J. Goos-Hänchen shifts of Gaussian beams reflected from surfaces coated with cross-anisotropic metasurfaces. Opt. Laser Technol. 2021, 135, 106679. [Google Scholar] [CrossRef]
- Fan, G.; Ding, Y.; Guo, J.; Deng, D. Goos–Hänchen and Imbert–Fedorov shifts for rotational elliptical Gaussian beams impinging on graphene–substrate surfaces. Opt. Commun. 2023, 538, 129455. [Google Scholar] [CrossRef]
- Ornigotti, M.; Aiello, A. Goos–Hänchen and Imbert–Fedorov shifts for bounded wavepackets of light. J. Opt. 2013, 15, 014004. [Google Scholar] [CrossRef]
- Ou, J.; Jiang, Y.; Zhang, J.; He, Y. Reflection of Laguerre-Gaussian beams carrying orbital angular momentum: A full Taylor expanded solution. J. Opt. Soc. Am. A 2013, 30, 2561–2571. [Google Scholar] [CrossRef] [PubMed]
- Aiello, A. Goos–Hänchen and Imbert–Fedorov shifts: A novel perspective. New J. Phys. 2012, 14, 013058. [Google Scholar] [CrossRef]
- Prajapati, C.; Ranganathan, D. Goos-Hanchen and Imbert-Fedorov shifts for Hermite-Gauss beams. J. Opt. Soc. Am. A 2012, 29, 1377–1382. [Google Scholar] [CrossRef]
- Aiello, A.; Woerdman, J.P. Goos–Hänchen and Imbert–Fedorov shifts of a nondiffracting Bessel beam. Opt. Lett. 2011, 36, 543–545. [Google Scholar] [CrossRef]
- Ornigotti, M. Goos-Hänchen and Imbert-Fedorov shifts for Airy beams. Opt. Lett. 2018, 43, 1411–1414. [Google Scholar] [CrossRef]
- Gao, M.; Deng, D. Spatial Goos-Hänchen and Imbert-Fedorov shifts of rotational 2-D finite energy Airy beams. Opt. Express 2020, 28, 10531–10541. [Google Scholar] [CrossRef]
- Zhen, W.; Deng, D. Goos-Hänchen shifts for Airy beams impinging on graphene-substrate surfaces. Opt. Express 2020, 28, 24104–24114. [Google Scholar] [CrossRef] [PubMed]
- Zhai, C.; Zhang, S. Goos-Hänchen shift of an Airy beam reflected in an epsilon-near-zero metamaterial. Optik 2019, 184, 234–240. [Google Scholar] [CrossRef]
- He, J.; Yi, J.; He, S. Giant negative Goos-Hänchen shifts for a photonic crystal with a negative effective index. Opt. Express 2006, 14, 3024–3029. [Google Scholar] [CrossRef]
- Felbacq, D.; Moreau, A.; Smaâli, R. Goos-Hänchen effect in the gaps of photonic crystals. Opt. Lett. 2003, 28, 1633–1635. [Google Scholar] [CrossRef]
- Berman, P.R. Goos-Hanchen shift in negatively refractive media. Phys. Rev. E 2002, 66, 067603. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Chen, Z.; Li, Y.; Zhang, Z.; Zhuang, G.; Liu, J.; Meng, Y. Interference effect on Goos–Hänchen shifts of anisotropic medium interface. New J. Phys. 2023, 25, 123018. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, S.; Ding, Y.; Min, L.; Luo, Z. Precise control of positive and negative Goos-Hänchen shifts in graphene. Carbon 2019, 149, 604–608. [Google Scholar] [CrossRef]
- Yan, Y.; Zha, M.; Liu, J.; Tu, J.; Liu, Z. Tunable giant goos-hänchen shift in Au-ReS2-graphene heterostructure. Opt. Lett. 2024, 49, 3484–3487. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Chan, C.T.; Chen, H. Goos-Hänchen effect in epsilon-near-zero metamaterials. Sci. Rep. 2015, 5, 8681. [Google Scholar] [CrossRef]
- Villegas, D.; Lazcano, Z.; Arriaga, J.; Pérez-Álvarez, R.; de León-Pérez, F. Goos–Hänchen shift for coupled vibrational modes in a semiconductor structure. J. Phys. Condens. Matter 2024, 36, 325301. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, G.; Luo, M.; Chang, S.; Gao, S. Beam shifts controlled by orbital angular momentum in a guided-surface plasmon resonance structure with a four-level atomic medium. Opt. Express 2023, 31, 25253–25266. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Zhen, W.; Wang, G.; Deng, D.; Guo, J. Goos-Hänchen and Imbert-Fedorov shifts of reflected rotating elliptical Gaussian beams from surfaces coated with cross-anisotropic metasurfaces. Results Phys. 2021, 27, 104548. [Google Scholar] [CrossRef]
- Xue, T.; Li, Y.-B.; Song, H.-Y.; Wang, X.-G.; Zhang, Q.; Fu, S.-F.; Zhou, S.; Wang, X.-Z. Giant and controllable Goos–Hänchen shift of a reflective beam off a hyperbolic metasurface of polar crystals. Chin. Phys. B 2023, 33, 014207. [Google Scholar] [CrossRef]
- Töppel, F.; Ornigotti, M.; Aiello, A. Goos-Hänchen and Imbert-Fedorov shifts from a quantum-mechanical perspective. New J. Phys. 2013, 15, 113059. [Google Scholar] [CrossRef]
- Jayaswal, G.; Mistura, G.; Merano, M. Weak measurement of the Goos-Hänchen shift. Opt. Lett. 2013, 38, 1232–1234. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Sheng, L.; Ling, X. Photonic spin Hall effect enabled refractive index sensor using weak measurements. Sci. Rep. 2018, 8, 1221. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Hu, Z.; Pan, J.; Huang, T.; Luo, D. High-Sensitivity Goos-Hänchen Shifts Sensor Based on BlueP-TMDCs-Graphene Heterostructure. Sensors 2020, 20, 3605. [Google Scholar] [CrossRef]
- Zhou, X.; Ling, X.; Luo, H.; Wen, S. Identifying graphene layers via spin Hall effect of light. Appl. Phys. Lett. 2012, 101, 251602. [Google Scholar] [CrossRef]
- Chen, S.; Ling, X.; Shu, W.; Luo, H.; Wen, S. Precision Measurement of the Optical Conductivity of Atomically Thin Crystals via the Photonic Spin Hall Effect. Phys. Rev. Appl. 2020, 13, 014057. [Google Scholar] [CrossRef]
- Xu, D.; He, S.; Zhou, J.; Chen, S.; Wen, S.; Luo, H. Goos–Hänchen effect enabled optical differential operation and image edge detection. Appl. Phys. Lett. 2020, 116, 211103. [Google Scholar] [CrossRef]
- Chamorro-Posada, P.; Sanchez-Curto, J.; Aceves, A.B.; McDonald, G.S. Widely varying giant Goos-Hänchen shifts from Airy beams at nonlinear interfaces. Opt. Lett. 2014, 39, 1378–1381. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Chen, Z.; Li, Y.; Hao, S.; Zhang, Q.; Zhou, S.; Fu, S.; Wang, X. Large spatial shifts of a reflected Airy beam on the surface of hyperbolic crystals. J. Opt. Soc. Am. B 2023, 40, 1240. [Google Scholar] [CrossRef]
- Fan, Y.; Shen, N.-H.; Zhang, F.; Zhao, Q.; Wu, H.; Fu, Q.; Wei, Z.; Li, H.; Soukoulis, C.M. Graphene Plasmonics: A Platform for 2D Optics. Adv. Opt. Mater. 2019, 7, 1800537. [Google Scholar] [CrossRef]
- Fan, Y.; Shen, N.-H.; Zhang, F.; Wei, Z.; Li, H.; Zhao, Q.; Fu, Q.; Zhang, P.; Koschny, T.; Soukoulis, C.M. Electrically Tunable Goos–Hänchen Effect with Graphene in the Terahertz Regime. Adv. Opt. Mater. 2016, 4, 1824–1828. [Google Scholar] [CrossRef]
- Song, H.; Fu, S.; Zhang, Q.; Zhou, S.; Wang, X. Large spatial shifts of reflective beam at the surface of graphene/hBN metamaterials. Opt. Express 2021, 29, 19068–19083. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Lu, F.; Jiang, L.; Lin, W.; Zheng, Z. Tunable Goos-Hänchen Shift Surface Plasmon Resonance Sensor Based on Graphene-hBN Heterostructure. Biosensors 2021, 11, 201. [Google Scholar] [CrossRef]
- Zhao, Y.; Jin, G.; Zhou, S.; Zhang, Q.; Fu, S.F.; Wang, X.G.; Wang, X.Z. Giant goos-hänchen shift with heigh reflection base on guided mode resonance in trapezoidal hBN/dielectric metasurface. Phys. Scr. 2024, 99, 065540. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. Magneto-optical conductivity in graphene. J. Phys. Condens. Matter 2007, 19, 026222. [Google Scholar] [CrossRef]
- Yan, H.; Li, X.; Chandra, B.; Tulevski, G.; Wu, Y.; Freitag, M.; Zhu, W.; Avouris, P.; Xia, F. Tunable infrared plasmonic devices using graphene/insulator stacks. Nat. Nanotechnol. 2012, 7, 330–334. [Google Scholar] [CrossRef]
- Zhan, T.; Shi, X.; Dai, Y.; Liu, X.; Zi, J. Transfer matrix method for optics in graphene layers. J. Phys. Condens. Matter 2013, 25, 215301. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Ke, S.; Liu, Q.; Wang, B.; Lu, P. Giant Goos-Hänchen shifts in non-Hermitian dielectric multilayers incorporated with graphene. Opt. Express 2018, 26, 2817–2828. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Qu, T.; Li, Z.; Wu, Z. Spatial Goos–Hänchen Shifts of Airy Vortex Beams Impinging on Graphene/hBN Heterostructure. Photonics 2025, 12, 105. https://doi.org/10.3390/photonics12020105
Yang X, Qu T, Li Z, Wu Z. Spatial Goos–Hänchen Shifts of Airy Vortex Beams Impinging on Graphene/hBN Heterostructure. Photonics. 2025; 12(2):105. https://doi.org/10.3390/photonics12020105
Chicago/Turabian StyleYang, Xiaojin, Tan Qu, Zhengjun Li, and Zhensen Wu. 2025. "Spatial Goos–Hänchen Shifts of Airy Vortex Beams Impinging on Graphene/hBN Heterostructure" Photonics 12, no. 2: 105. https://doi.org/10.3390/photonics12020105
APA StyleYang, X., Qu, T., Li, Z., & Wu, Z. (2025). Spatial Goos–Hänchen Shifts of Airy Vortex Beams Impinging on Graphene/hBN Heterostructure. Photonics, 12(2), 105. https://doi.org/10.3390/photonics12020105





