Topological Phase Transition by Tuning Central Unit in C3 Symmetric Lattice of Terahertz Photonic Crystals
Abstract
1. Introduction
2. Design and Discussion
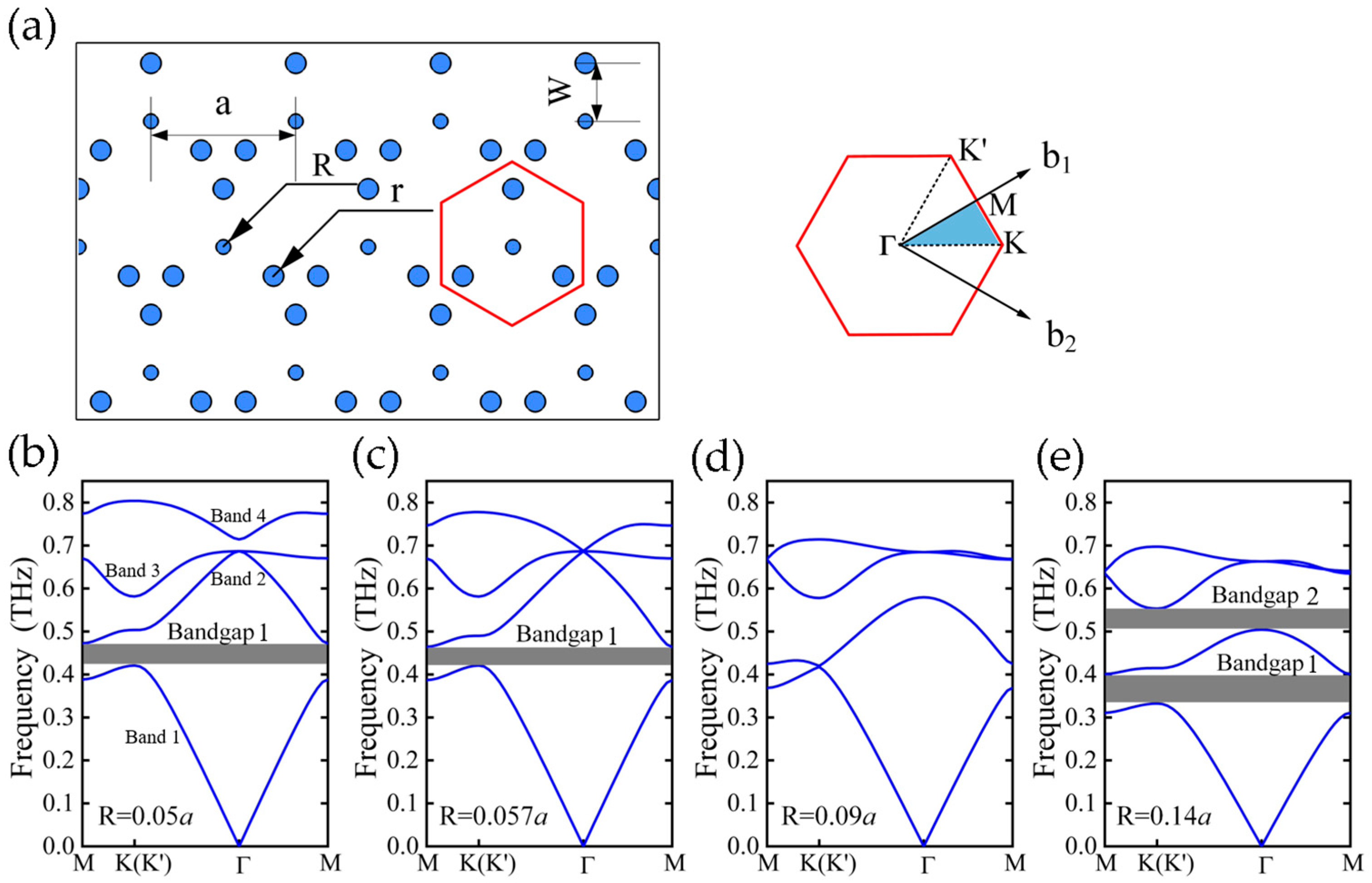
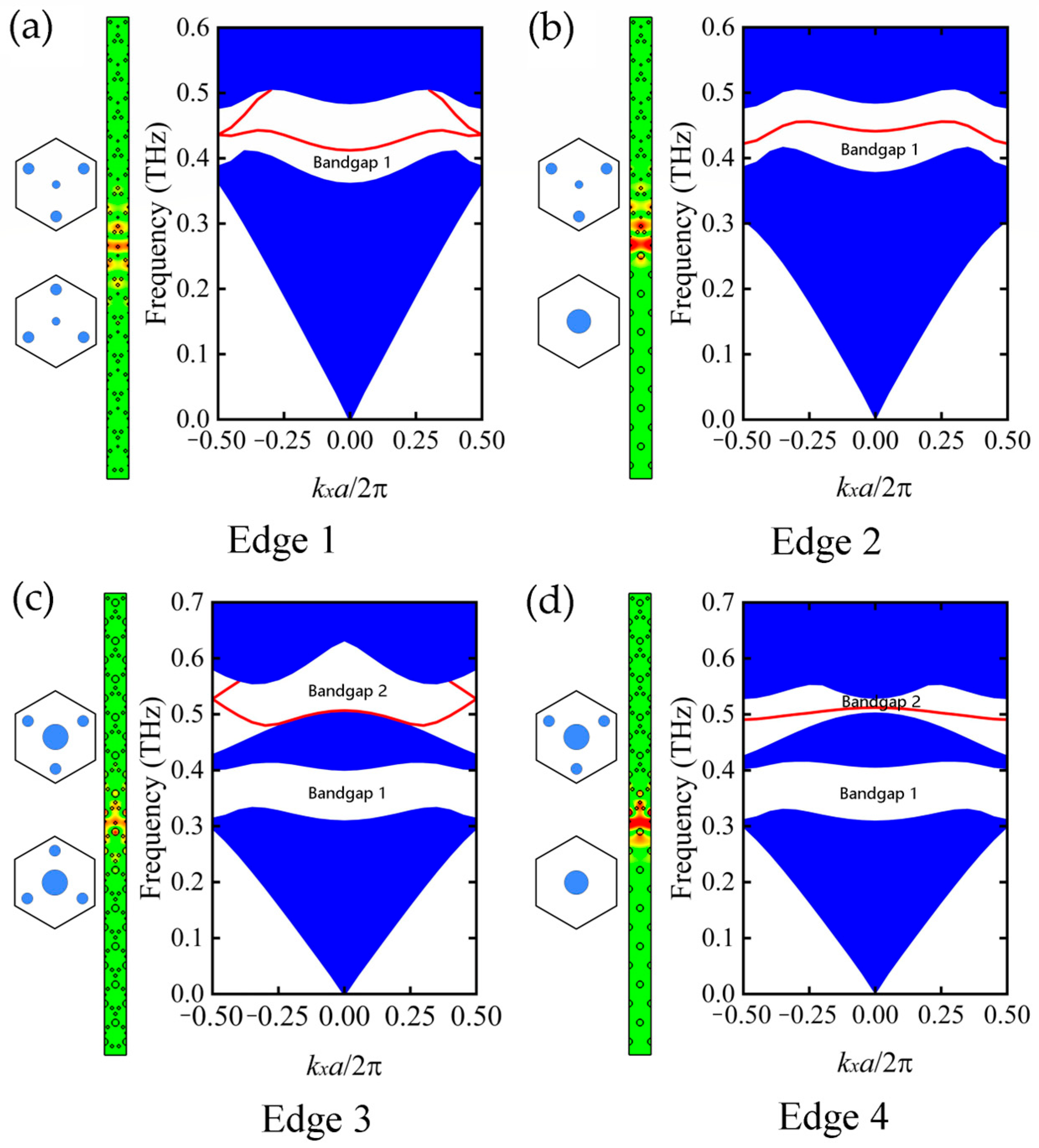
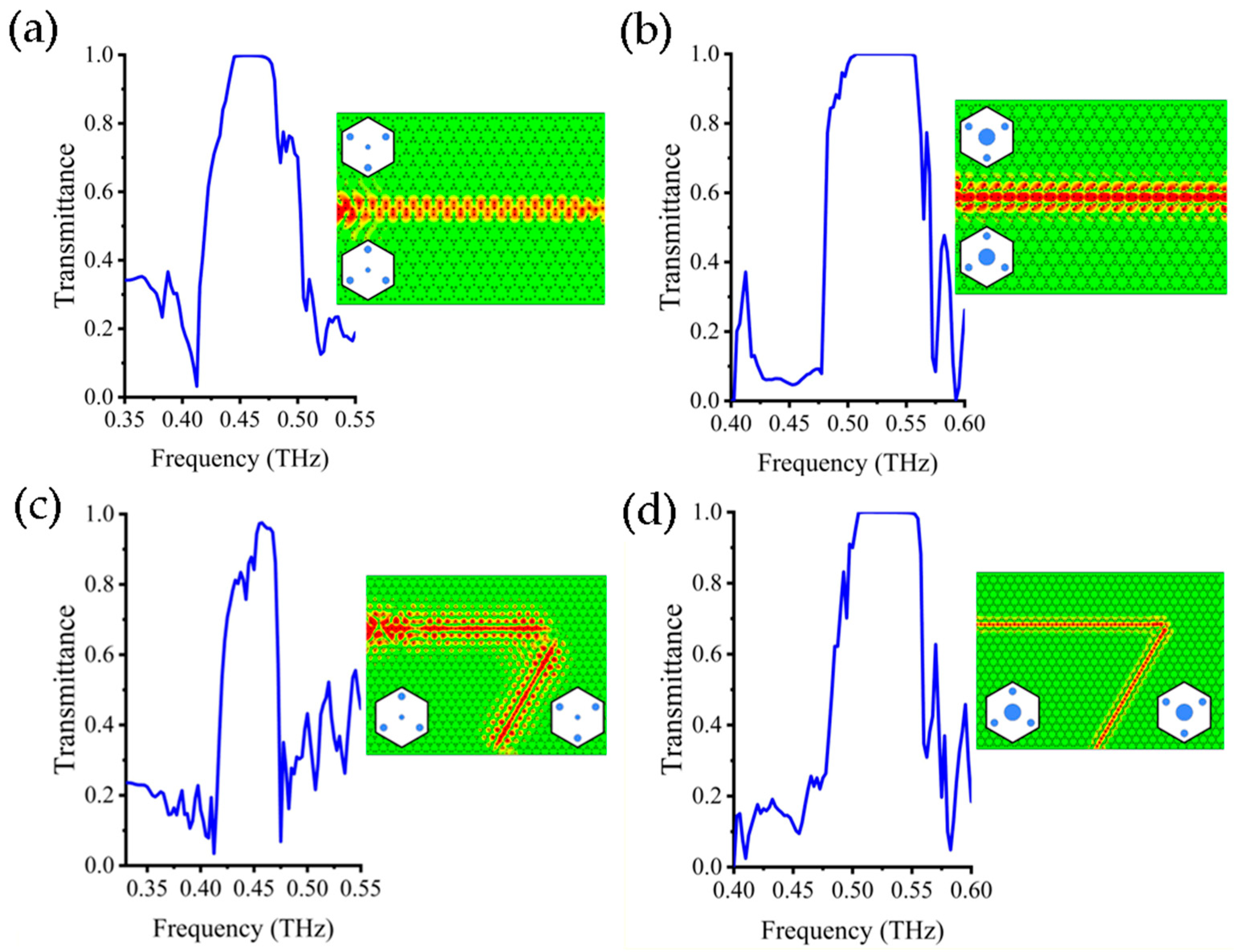
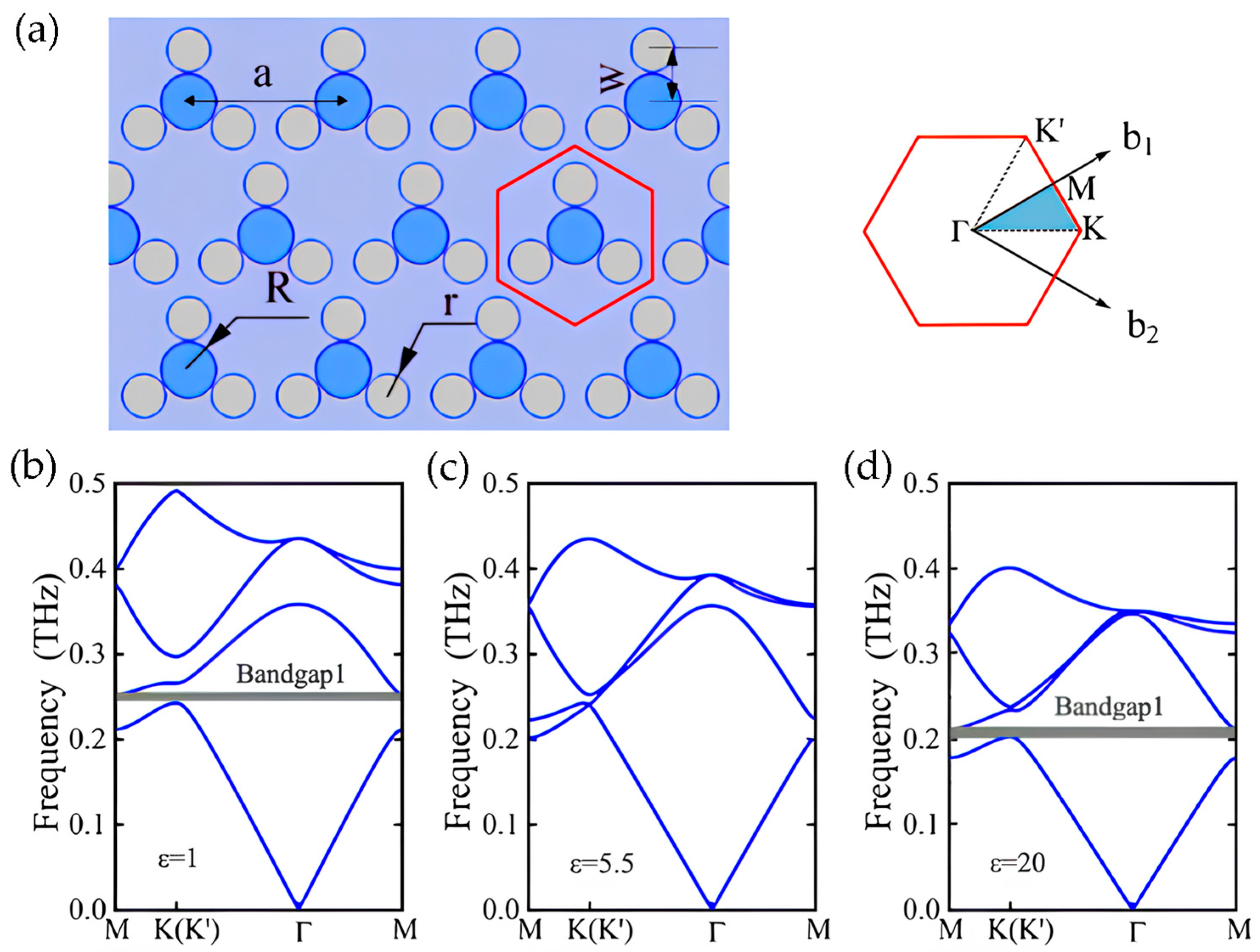
2.1. PTI with Rod-Type PhC
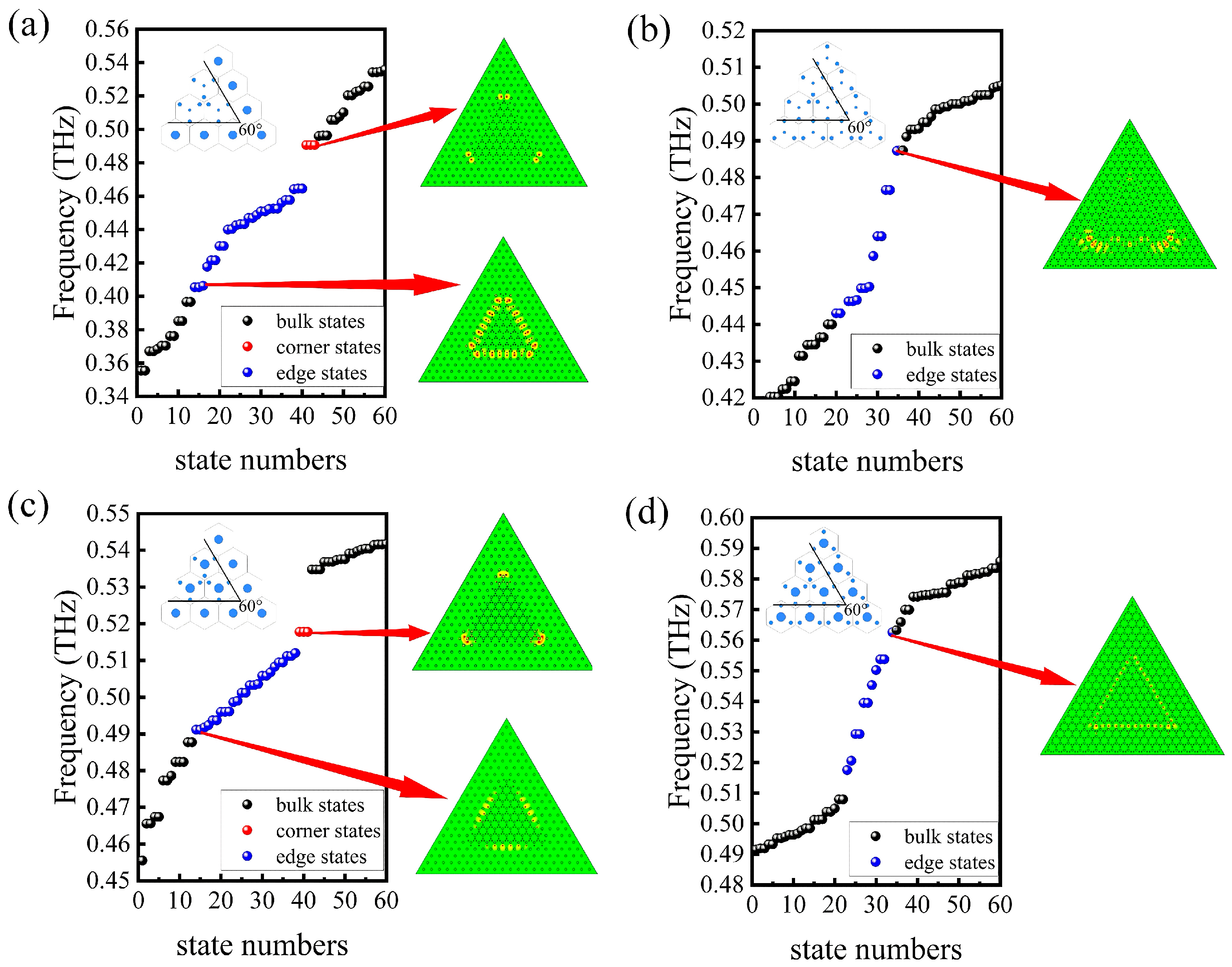
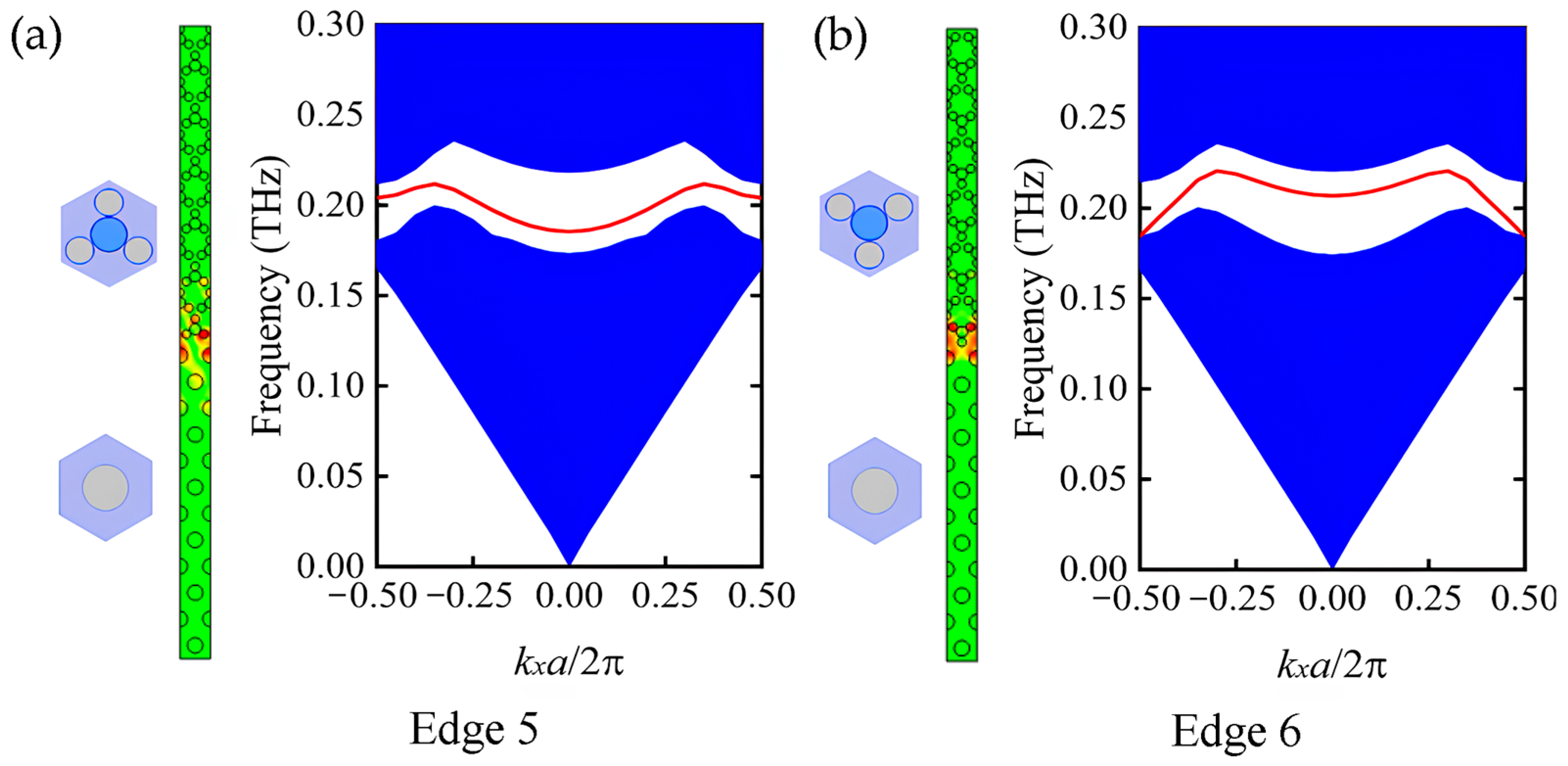
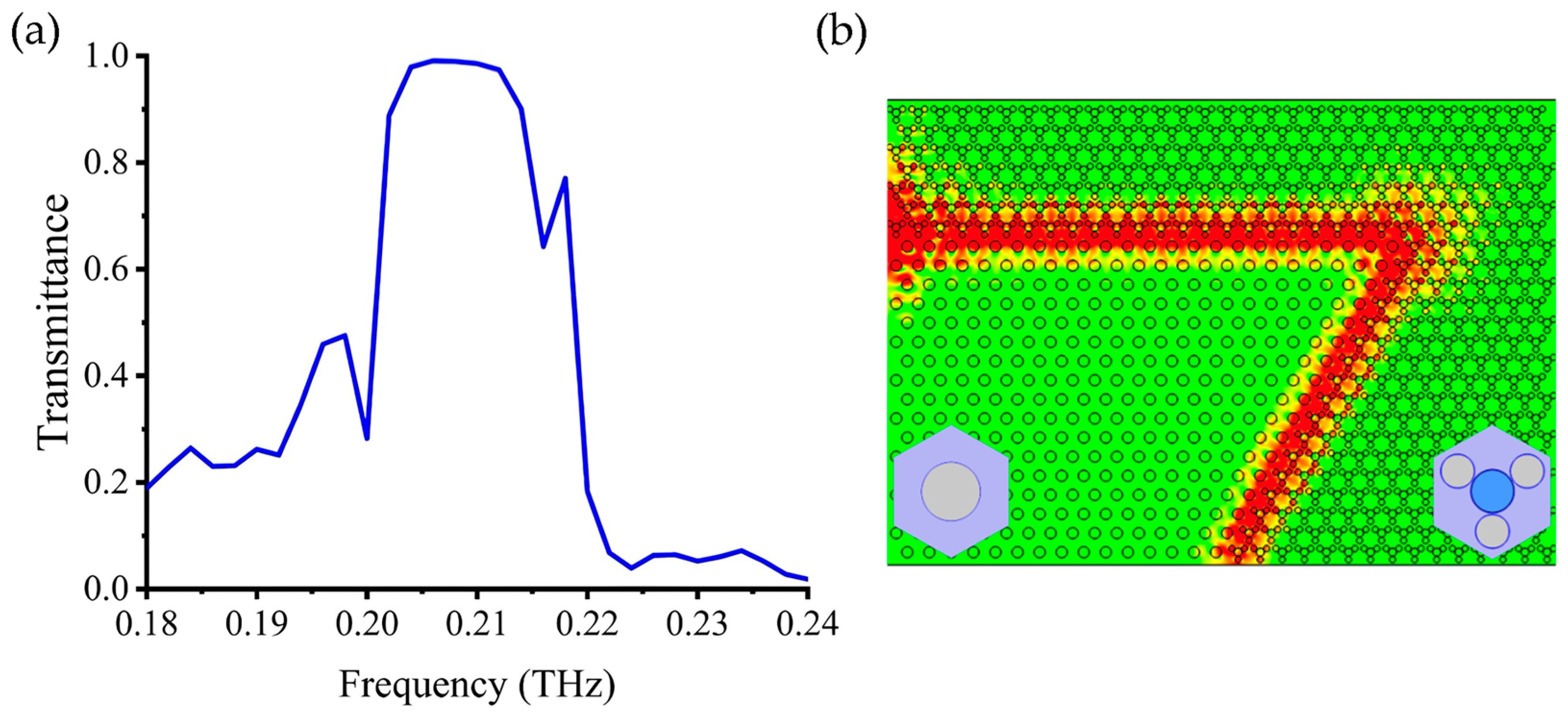
2.2. PTI with Hole-Type PhC
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Raghu, S.; Haldane, F.D.M. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 2008, 100, 013904. [Google Scholar] [CrossRef] [PubMed]
- Haldane, F.D.M.; Raghu, S. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 2008, 78, 033834. [Google Scholar]
- Wang, Z.; Chong, Y.D.; Joannopoulos, J.D.; Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 2009, 461, 772–775. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.H.; Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 2015, 114, 223901. [Google Scholar] [CrossRef]
- Chen, Z.G.; Mei, J.; Sun, X.C.; Zhang, X.; Zhao, J.; Wu, Y. Multiple topological phase transitions in a gyromagnetic photonic crystal. Phys. Rev. A 2017, 95, 043827. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Y.F.; Xu, T.; Wang, H.X.; Jiang, J.H.; Hu, X.; Hang, Z.H. Visualization of a unidirectional electromagnetic waveguide using topological photonics. Phys. Rev. Lett. 2018, 120, 217401. [Google Scholar] [CrossRef]
- Ren, Y.; Lin, H.; Zhou, R.; Shi, X.; Jin, J.; Liu, Y. A topological gap waveguide based on unidirectional locking of pseudo-spins. J. Appl. Phys. 2023, 2306, 15544. [Google Scholar] [CrossRef]
- Sui, W.; Zhang, Y.; Zhang, Z.; Zhang, H.; Shi, Q.; Lv, Z.; Yang, B. Pseudospin topological phase transition induced by rotation operation in two-dimensional dielectric photonic crystal with C6 symmetry. Opt. Commun. 2023, 527, 128972. [Google Scholar] [CrossRef]
- Borges-Silva, D.; Costa, C.H.O.; Bezerra, C.G. Robust topological edge states in C6 photonic crystals. Photonics 2023, 10, 961. [Google Scholar] [CrossRef]
- Borges-Silva, D.; Costa, C.H.; Bezerra, C.G. Topological phase transition and robust pseudospin interface states induced by angular perturbation in 2D topological photonic crystals. Sci. Rep. 2023, 13, 850. [Google Scholar] [CrossRef]
- Chen, M.L.; Jiang, L.J.; Lan, Z.; Sha, W.E. Coexistence of pseudospin- and valley-Hall-like edge states in a photonic crystal with C3v symmetry. Phys. Rev. Res. 2020, 2, 043148. [Google Scholar] [CrossRef]
- Chen, X.D.; Zhao, F.L.; Chen, M.; Dong, J.W. Valley-contrasting physics in all-dielectric photonic crystals: Orbital angular momentum and topological propagation. Phys. Rev. B 2017, 96, 020202. [Google Scholar] [CrossRef]
- Shalaev, M.I.; Walasik, W.; Tsukernik, A.; Xu, Y.; Litchinitser, N.M. Robust topologically protected transport in photonic crystals at telecommunication wavelengths. Nat. Nanotechnol. 2019, 14, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Xie, B.; Ren, W. Coexistence of chiral and antichiral edge states in photonic crystals. Laser Photonics Rev. 2024, 18, 2300764. [Google Scholar] [CrossRef]
- He, L.; Ren, Q.; You, J.W.; Sha, W.E.; Lan, Z.; Wu, L.; Zhang, Y.; Yao, J. Coexistence of slow light states and valley-polarized kink states in all-dielectric valley photonic crystals with triangular lattice. Opt. Laser Technol. 2023, 167, 109790. [Google Scholar] [CrossRef]
- Su, Y.; Qin, M.; Ouyang, M.; Lei, L.; He, L.; Wang, T.; Yu, T. Compact topological polarization beam splitter based on all-dielectric fishnet photonic crystals. Opt. Lett. 2023, 48, 3171–3174. [Google Scholar] [CrossRef]
- Li, W.; Chen, Q.; Sun, Y.; Han, S.; Liu, X.; Mei, Z.; Xu, X.; Fan, S.; Qian, Z.; Chen, H.; et al. Topologically enabled on-chip THz taper-free waveguides. Adv. Opt. Mater. 2023, 11, 2300764. [Google Scholar] [CrossRef]
- Wu, X.F.; Zhao, X.P. Robust valley transport of disordered topological waveguide in visible light waveband. Phys. Rev. B 2022, 105, 414132. [Google Scholar] [CrossRef]
- Xi, X.; Ye, K.P.; Wu, R.X. Topological photonic crystal of large valley Chern numbers. Photonics Res. 2020, 8, 1–7. [Google Scholar] [CrossRef]
- Parameswaran, S.A.; Yuan, W. Topological Insulators Turn a Corner. Physics 2017, 10, 132. [Google Scholar] [CrossRef]
- Schindler, F.; Cook, A.M.; Vergniory, M.G.; Wang, Z.; Parkin, S.S.; Bernevig, B.A.; Neupert, T. Higher-order topological insulators. Sci. Adv. 2018, 4, eaat0346. [Google Scholar] [CrossRef]
- Wu, S.; Jiang, B.; Liu, Y.; Jiang, J.H. All-dielectric photonic crystal with unconventional higher-order topology. Photonics Res. 2021, 9, 668–677. [Google Scholar] [CrossRef]
- Xu, Q.; Peng, Y.; Yan, B.; Shi, A.; Peng, P.; Xie, J.; Liu, J. Multiband topological states in the Penrose-triangle photonic crystals. Opt. Lett. 2022, 48, 101–104. [Google Scholar] [CrossRef]
- Kang-Hyok, O.; Kim, K.H. Multiband quadrupole topological photonic crystals with glide symmetries. Opt. Laser Technol. 2024, 168, 109901. [Google Scholar]
- Kang-Hyok, O.; Kim, K.H. Hexagonal photonic crystal with nontrivial quadrupole topology. Photonics Nanostruct. 2023, 54, 101118. [Google Scholar]
- Song, L.; Bongiovanni, D.; Hu, Z.C.; Wang, Z.T.; Xia, S.Q.; Tang, L.Q.; Song, D.H.; Morandotti, R.; Chen, Z.G. Observation of topologically distinct corner states in “bearded” photonic kagome lattices. Adv. Opt. Mater. 2024, 12, 2301614. [Google Scholar] [CrossRef]
- He, Y.H.; Gao, Y.F.; He, Y.; Qi, X.F.; Si, J.Q.; Yang, M.; Zhou, S.Y. Realization of edge and corner states in photonic crystals with kagome lattices through topological insulator generators. Opt. Laser Technol. 2023, 161, 109196. [Google Scholar] [CrossRef]
- Li, M.Y.; Zhirihin, D.; Gorlach, M.; Ni, X.; Filonov, D.; Slobozhanyuk, A.; Alù, A.; Khanikaev, A.B. Higher-order topological states in photonic kagome crystals with long-range interactions. Nat. Photonics 2020, 14, 89–94. [Google Scholar] [CrossRef]
- Xing, H.; Fan, J.; Lu, D.; Gao, Z.; Shum, P.P.; Cong, L. Terahertz metamaterials for free-space and on-chip applications: From active metadevices to topological photonic crystals. Adv. Devices Instrum. 2022, 2022, 9852503. [Google Scholar] [CrossRef]
- Kumar, A.; Gupta, M.; Pitchappa, P.; Wang, N.; Fujita, M.; Singh, R. Terahertz topological photonic integrated circuits for 6G and beyond: A Perspective. J. Appl. Phys. 2022, 132, 140901. [Google Scholar] [CrossRef]
- Gupta, M.; Kumar, A.; Singh, R. Electrically tunable topological notch filter for THz integrated photonics. Adv. Opt. Mater. 2023, 11, 2301051. [Google Scholar] [CrossRef]
- Tan, Y.J.; Wang, W.; Kumar, A.; Singh, R. Interfacial topological photonics: Broadband silicon waveguides for THz 6G communication and beyond. Opt. Express 2022, 30, 33035–33047. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Liang, F.; Han, J.; Zhao, D.; Wang, B.Z. Terahertz topological edge states and corner states in metallic photonic crystals. In Proceedings of the 2022 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Harbin, China, 12–15 August 2022. [Google Scholar]
- Tang, G.H.; Hong, Y.L.; Zhang, R.L.; Fan, R.H.; Ma, Z.L.; Wu, X.Y.; Wang, M. Adjustable topological corner states in terahertz valley photonic crystals. Phys. Rev. B 2023, 108, 205411. [Google Scholar] [CrossRef]
- Shen, Z.; Tan, Y.J.; Wang, W.; Tan, T.C.; Yan, R.; Zhang, L.; Singh, R. Interface Topology Driven Loss Minimization in Integrated Photonics: THz Ultrahigh-Q Cavities and Waveguides. Adv. Mater. 2025, 37, 2503460. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.; Gilbert, M.J.; Bernevig, B.A. Bulk topological invariants in noninteracting point group symmetric insulators. Phys. Rev. B 2012, 86, 115112. [Google Scholar] [CrossRef]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 2017, 96, 245115. [Google Scholar] [CrossRef]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Quantized electric multipole insulators. Science 2017, 357, 61–66. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Deng, K.; Song, S.; Liu, T.; Cai, J.; Zhang, L.; Fang, B. Topological Phase Transition by Tuning Central Unit in C3 Symmetric Lattice of Terahertz Photonic Crystals. Photonics 2025, 12, 1143. https://doi.org/10.3390/photonics12111143
Yan Z, Deng K, Song S, Liu T, Cai J, Zhang L, Fang B. Topological Phase Transition by Tuning Central Unit in C3 Symmetric Lattice of Terahertz Photonic Crystals. Photonics. 2025; 12(11):1143. https://doi.org/10.3390/photonics12111143
Chicago/Turabian StyleYan, Zhigang, Kangrong Deng, Shuangjie Song, Tingting Liu, Jinhui Cai, Le Zhang, and Bo Fang. 2025. "Topological Phase Transition by Tuning Central Unit in C3 Symmetric Lattice of Terahertz Photonic Crystals" Photonics 12, no. 11: 1143. https://doi.org/10.3390/photonics12111143
APA StyleYan, Z., Deng, K., Song, S., Liu, T., Cai, J., Zhang, L., & Fang, B. (2025). Topological Phase Transition by Tuning Central Unit in C3 Symmetric Lattice of Terahertz Photonic Crystals. Photonics, 12(11), 1143. https://doi.org/10.3390/photonics12111143




