A Pre-Measurement Device for Contour Measurement Path Planning of Complex Small Workpieces
Abstract
1. Introduction
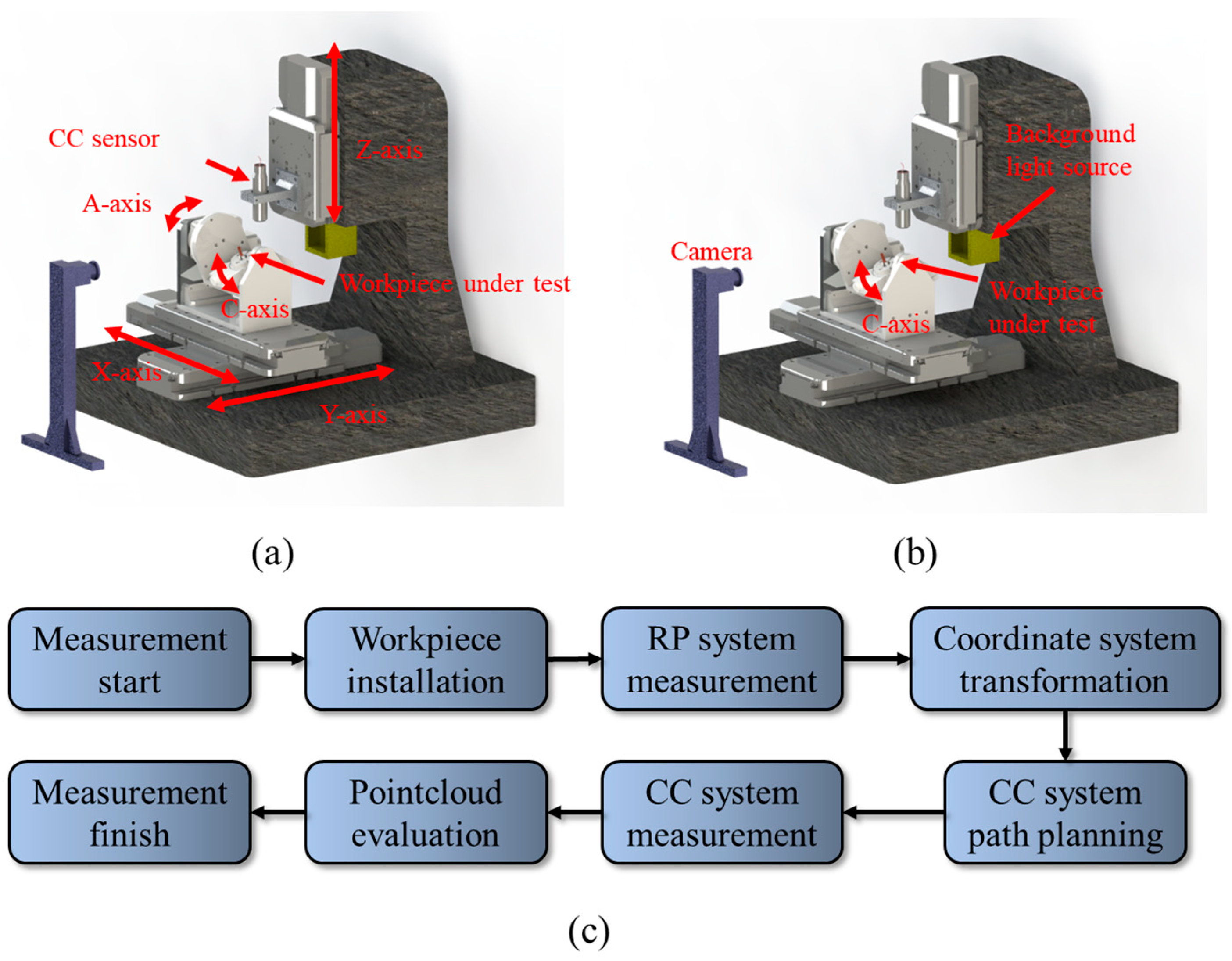
2. Measurement Scheme
3. Principle of the Pre-Measurement System
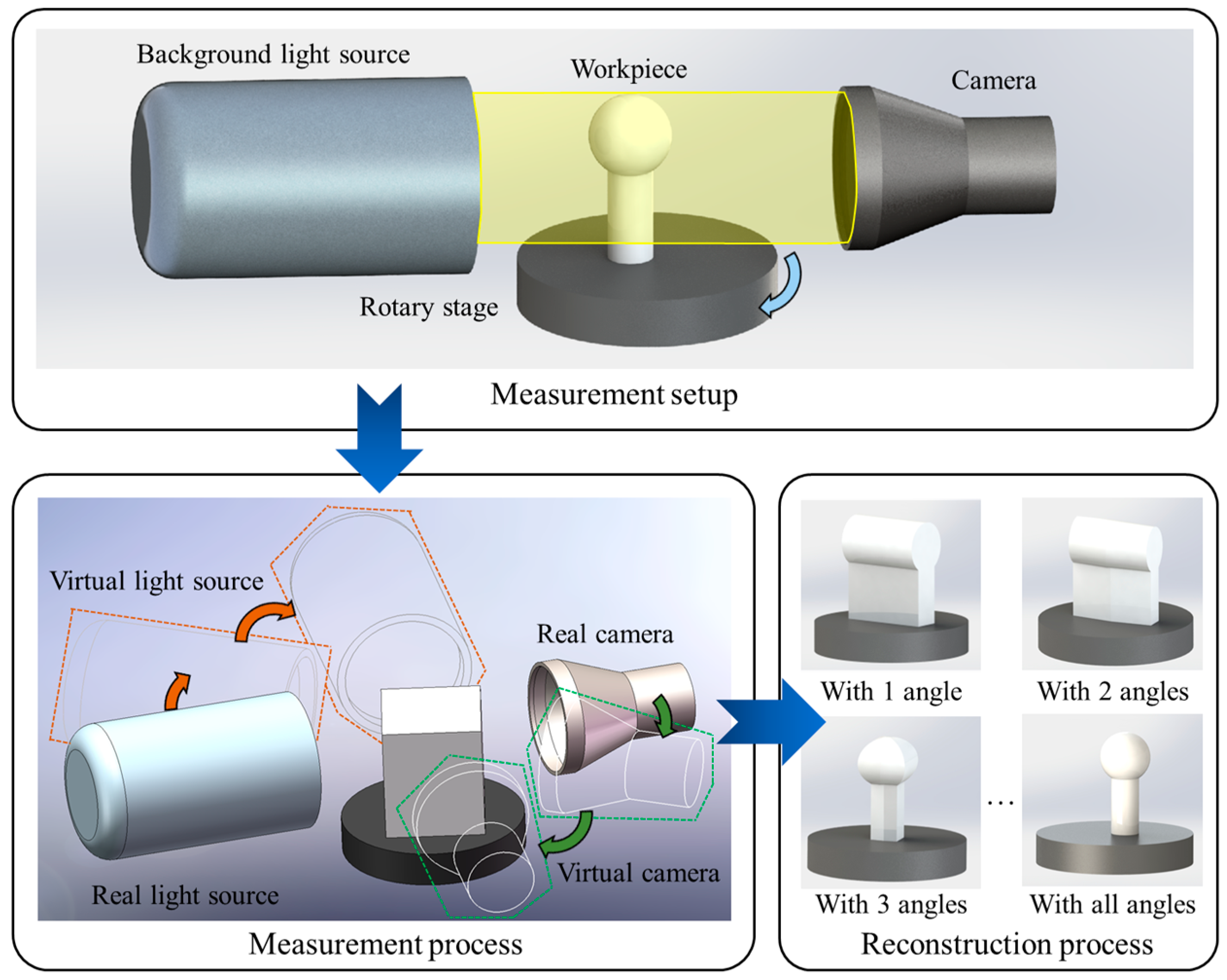
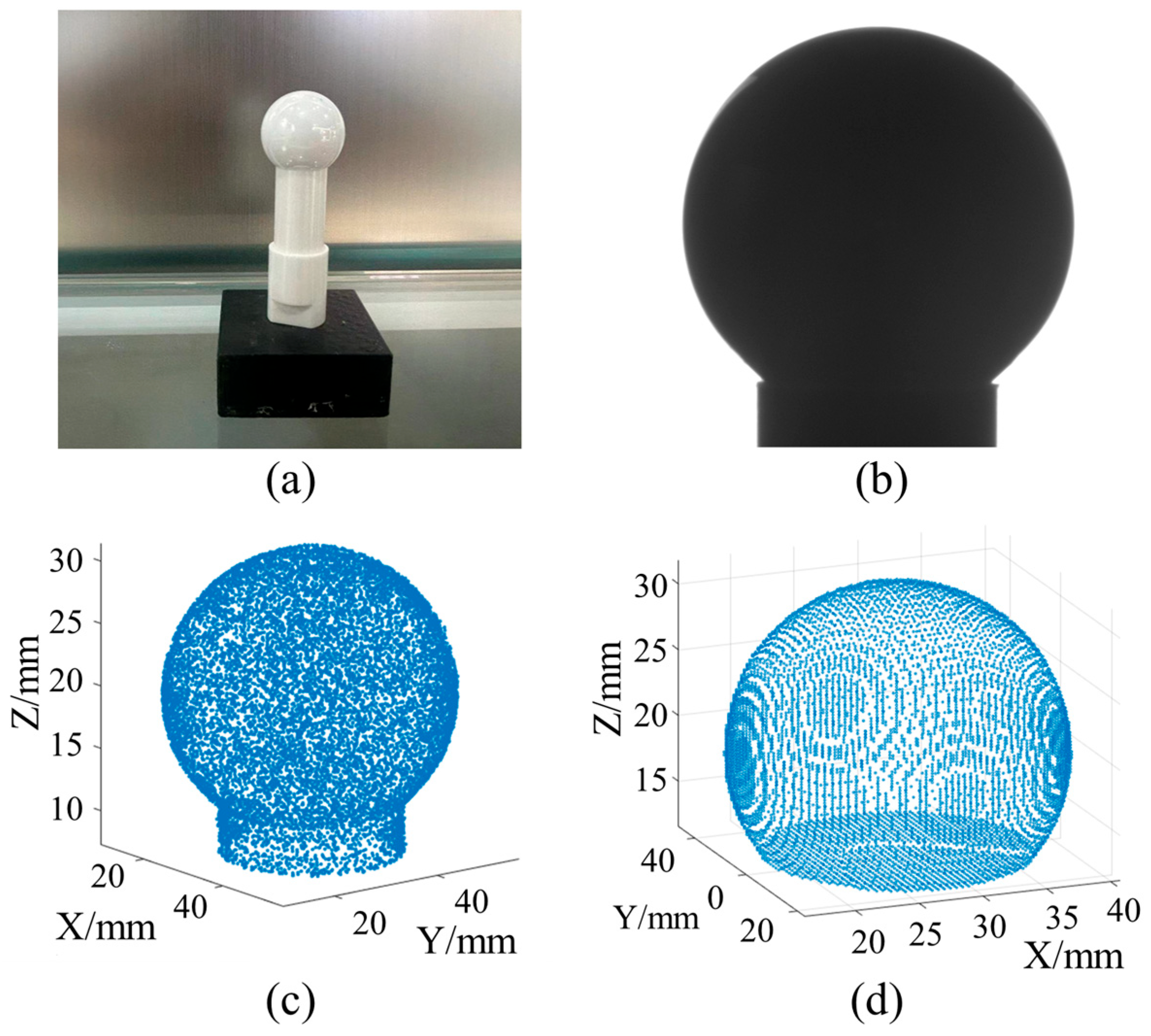
3.1. Measurement Process of the RP System
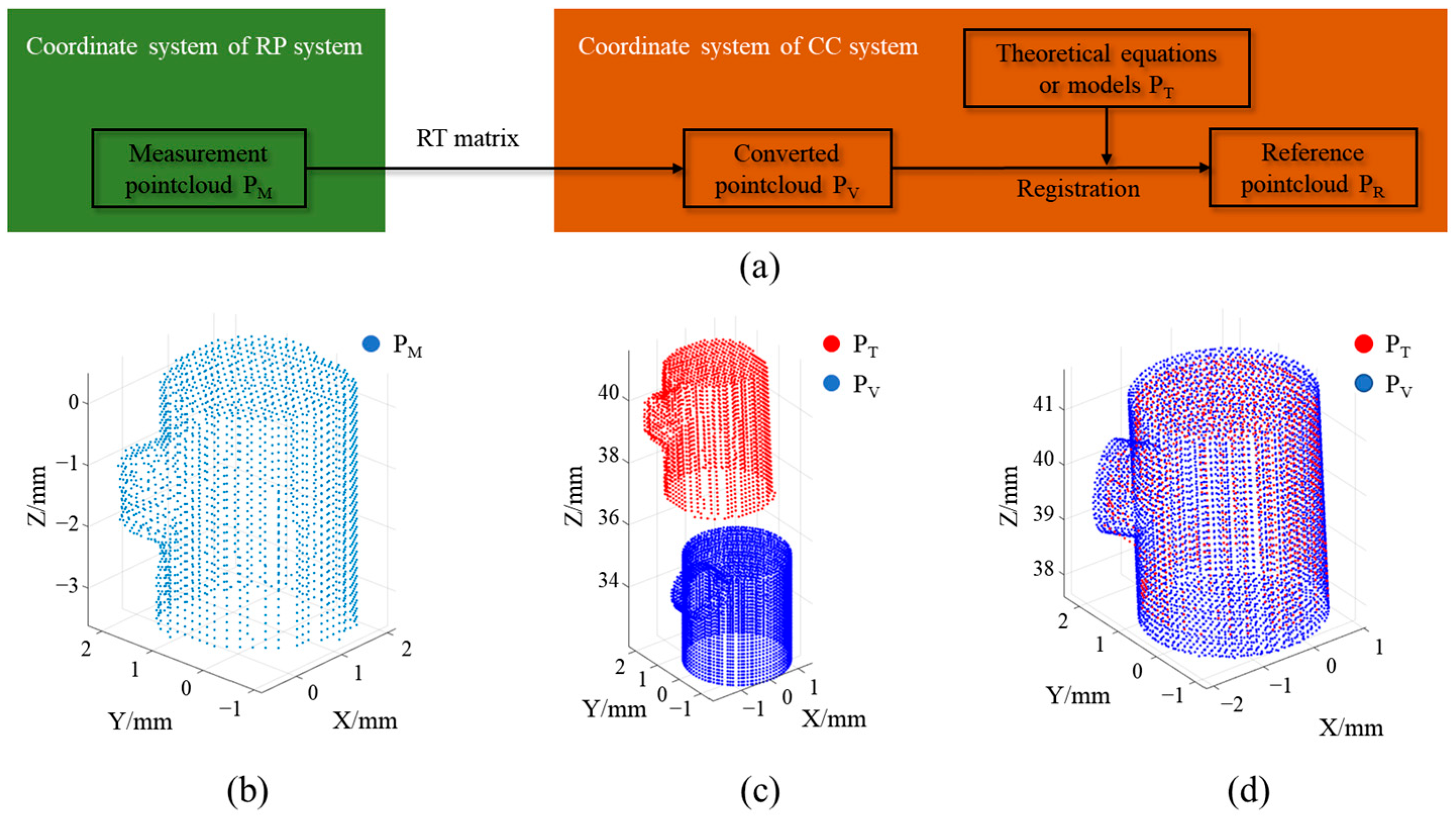
3.2. Calibration of the RP System
4. Pre-Measurement Results Guiding Path Planning of the CC System
4.1. Dual-System Coupling Process
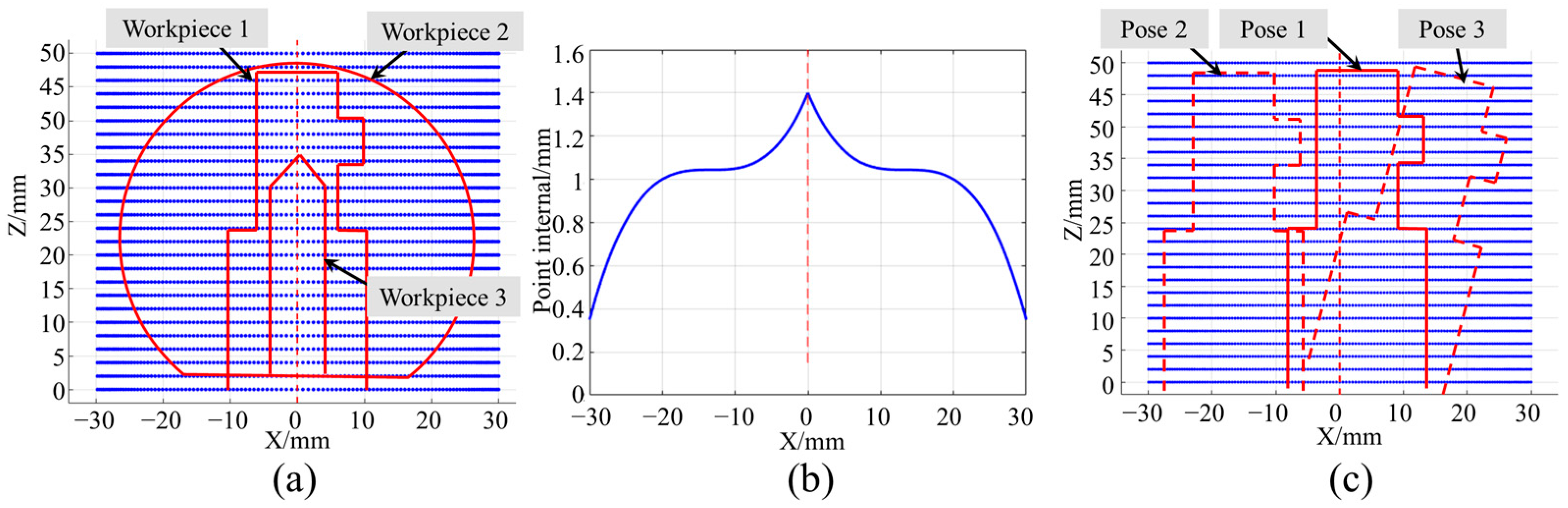
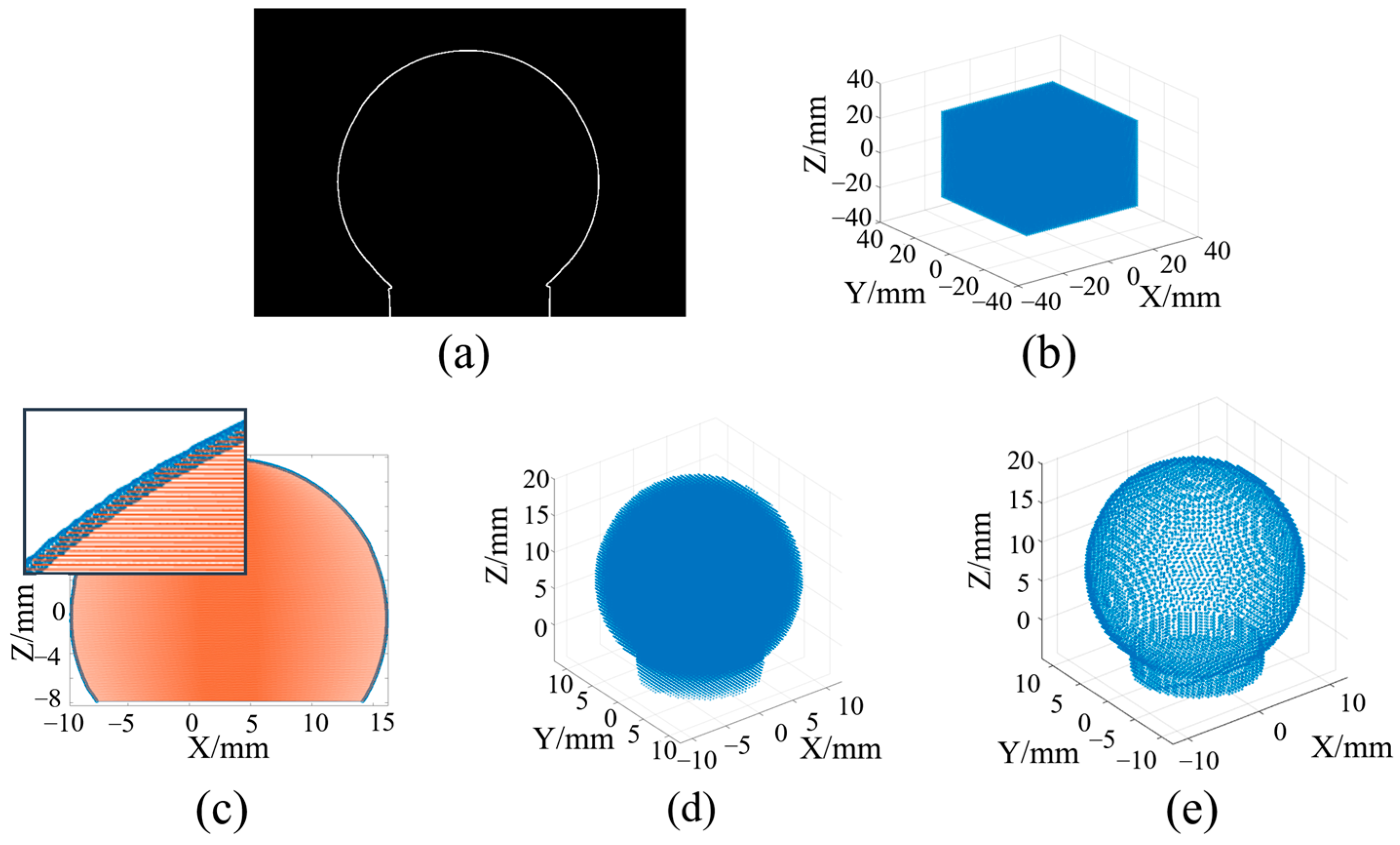
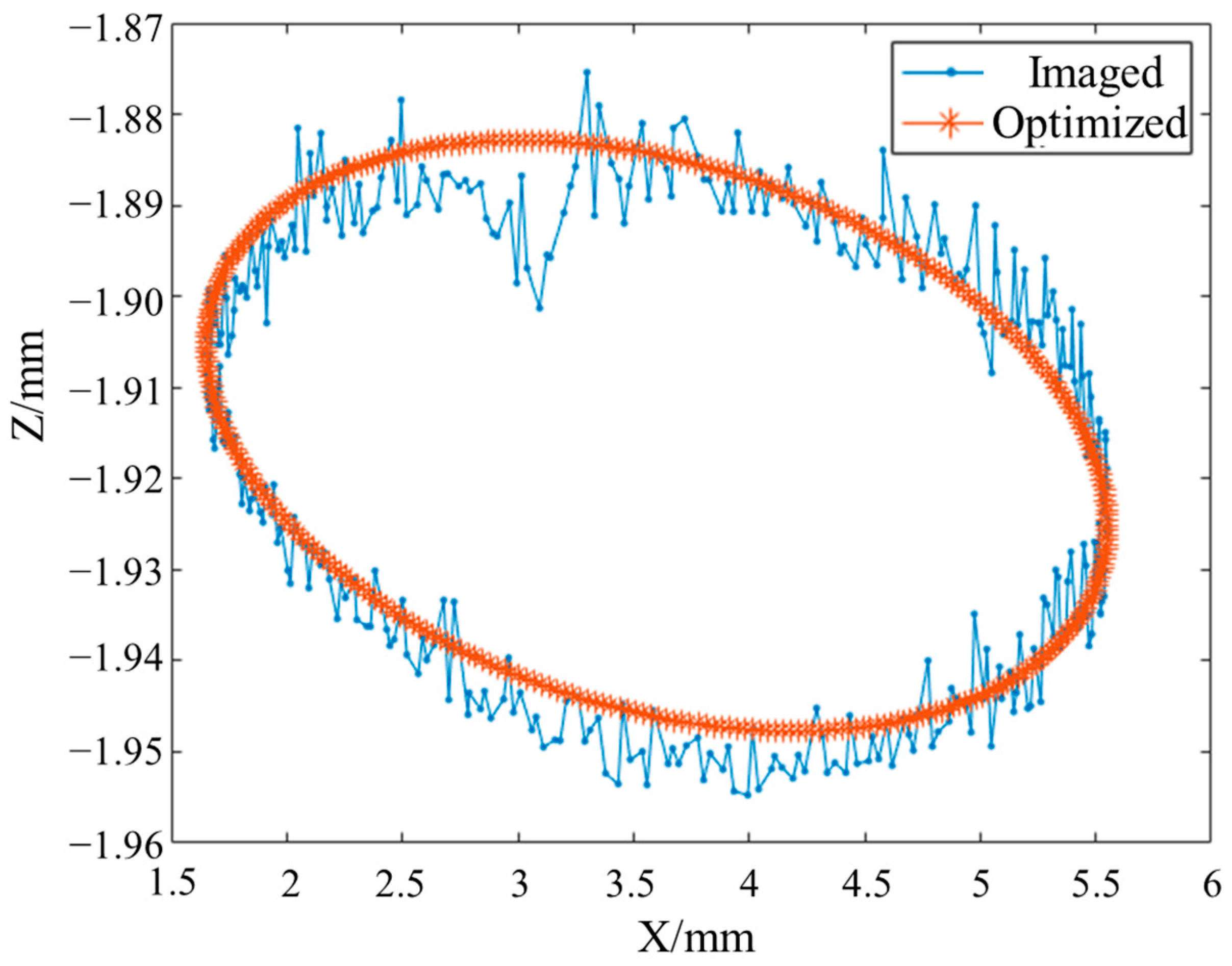
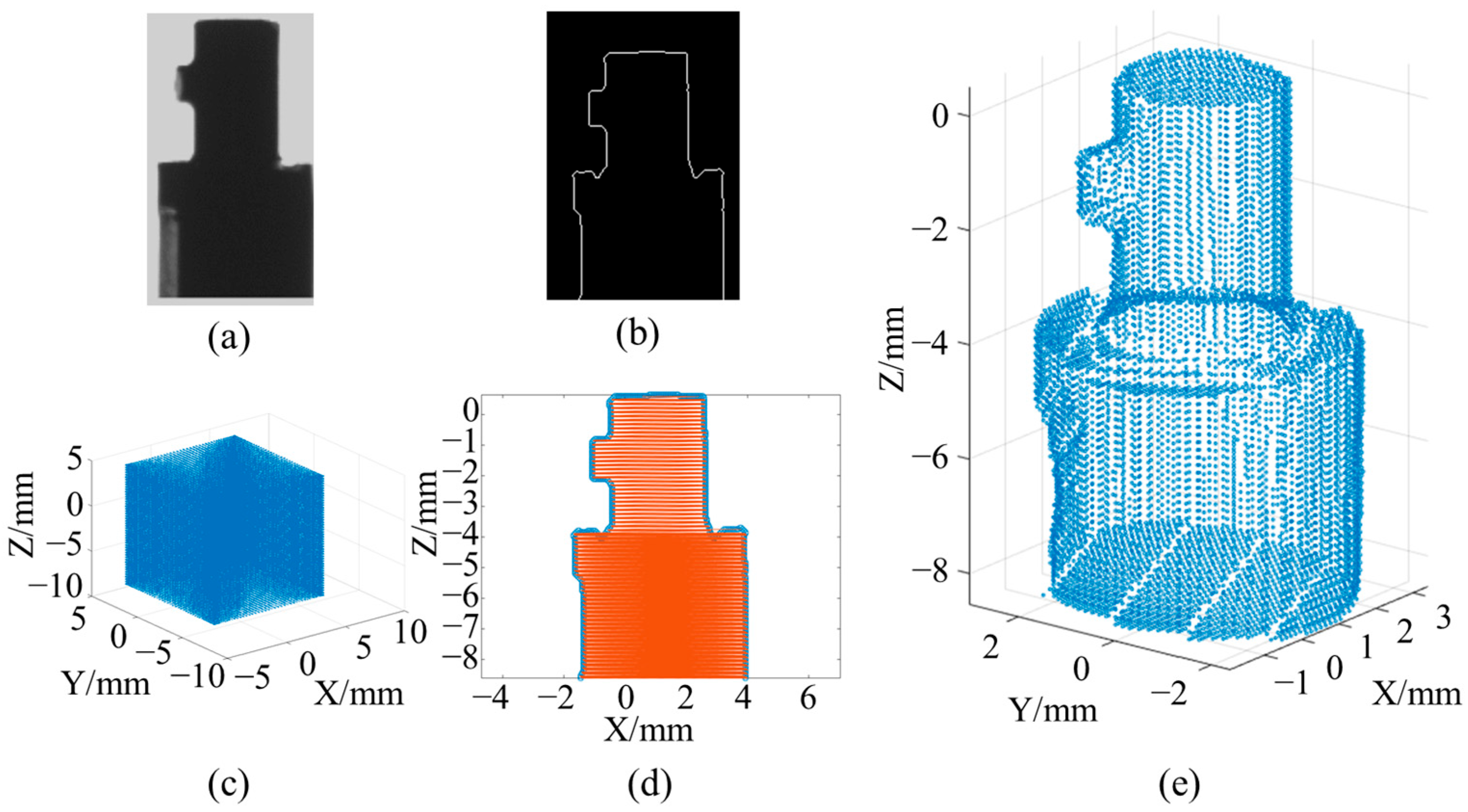
4.2. Measurement Path Planning of the CC System
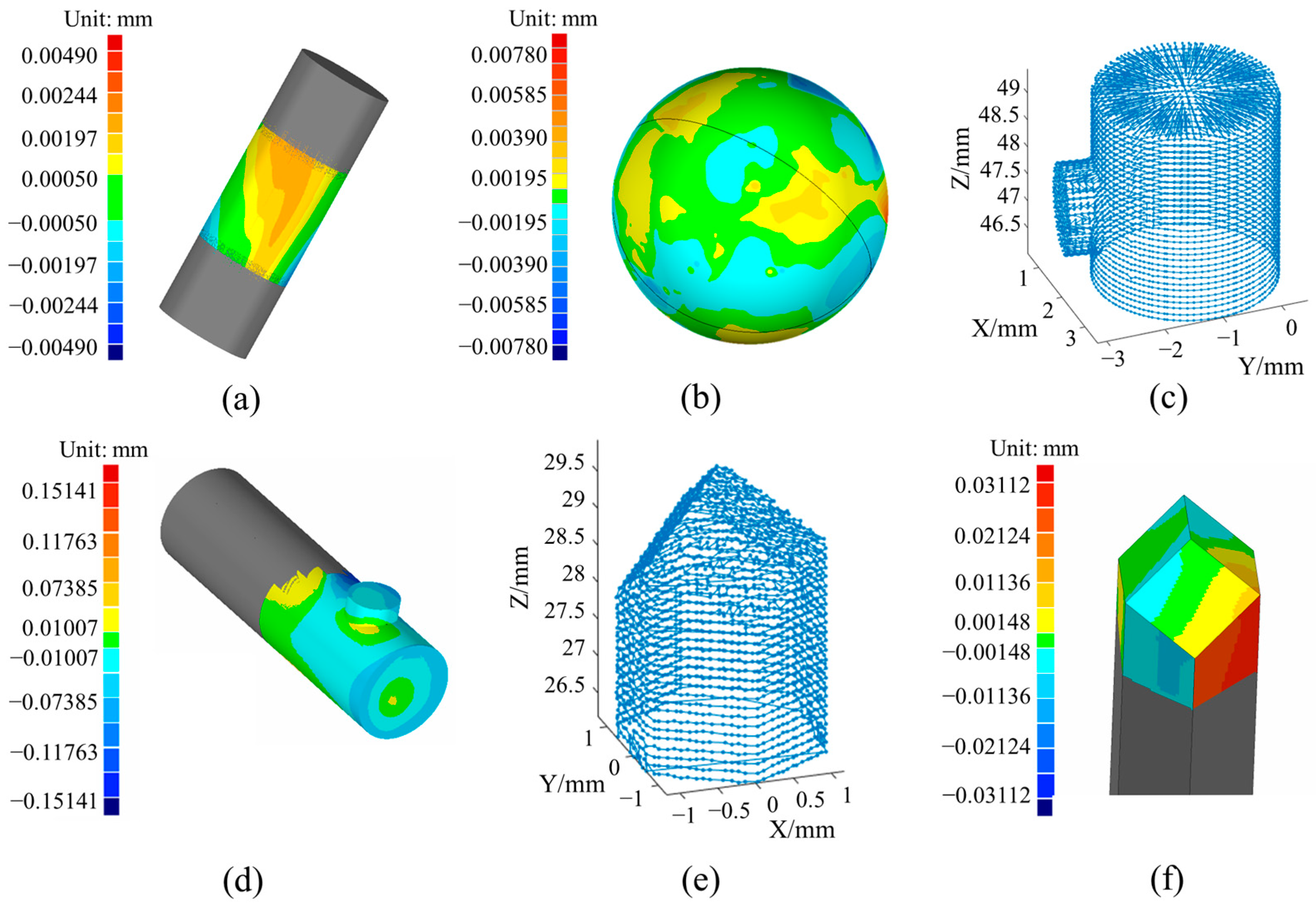
5. Results
6. Discussions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CSW | Complex small workpiece |
| RP | Reverse projection |
| CC | Chromatic confocal |
| PV | Peak to valley |
| 3D | Three-dimensional |
| 2D | Two-dimensional |
| CMM | Coordinate measuring machine |
| MDOF | Multi-degree-of-freedom |
| RT | Rotation-translation |
References
- Seo, J.H.; Lee, I.D.; Yoo, B. Effectiveness of rough initial scan for high-precision automatic 3D scanning. J. Comput. Des. Eng. 2021, 8, 1332–1354. [Google Scholar] [CrossRef]
- Catalucci, S.; Thompson, A.; Piano, S.; Branson, D.T., III; Leach, R. Optical metrology for digital manufacturing: A review. Int. J. Adv. Manuf. Technol. 2022, 120, 4271–4290. [Google Scholar] [CrossRef]
- Gao, J.; Lei, Y.; Xu, Z. Research on Micro-Triangular Pyramid Array-Based Fly-Cutting Technology Using the Orthogonal Test Method. Coatings 2024, 14, 806. [Google Scholar] [CrossRef]
- Hou, Q.; Yang, X.; Li, D.; Cheng, J.; Wang, S.; Xiao, J.; Li, W. Tribological performance of hydrophobic and micro/nano triangle textured rake face of cutting tools. Appl. Surf. Sci. 2022, 571, 151250. [Google Scholar] [CrossRef]
- Zhou, Q.; Zuo, J.; Kang, W.; Ren, M. High-Precision 3D Reconstruction in Complex Scenes via Implicit Surface Reconstruction Enhanced by Multi-Sensor Data Fusion. Sensors 2025, 25, 2820. [Google Scholar] [CrossRef]
- Zahwi, S.; Mekawi, A.M. Some effects of stylus force on scratching surfaces. Int. J. Mach. Tools Manuf. 2001, 41, 2011–2015. [Google Scholar] [CrossRef]
- Lee, D.-H. 3-Dimensional profile distortion measured by stylus type surface profilometer. Measurement 2013, 46, 803–814. [Google Scholar] [CrossRef]
- Schulz, M.; Elster, C. Traceable multiple sensor system for measuring curved surface profiles with high accuracy and high lateral resolution. Opt. Eng. 2006, 45, 060503. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, F.; Ma, S.; Dong, L. Review of surface profile measurement techniques based on optical interferometry. Opt. Lasers Eng. 2017, 93, 164–170. [Google Scholar] [CrossRef]
- Park, S.-Y.; Baek, J.; Moon, J. Hand-held 3D scanning based on coarse and fine registration of multiple range images. Mach. Vis. Appl. 2011, 22, 563–579. [Google Scholar] [CrossRef]
- Shaw, L.; Ettl, S.; Mehari, F.; Weckenmann, A.; Häusler, G. Automatic registration method for multisensor datasets adopted for dimensional measurements on cutting tools. Meas. Sci. Technol. 2013, 24, 045002. [Google Scholar] [CrossRef]
- Wu, C.; Yang, L.; Luo, Z.; Jiang, W. Linear laser scanning measurement method tracking by a binocular vision. Sensors 2022, 22, 3572. [Google Scholar] [CrossRef]
- Li, Z.; Liu, L.; Li, C.; Fang, C.; Miao, L.; Zhu, L.; Zhang, X. Complete topographic measurement of the monolithic multi-surface workpiece on a cylindrical cavity. Opt. Laser Technol. 2023, 161, 109222. [Google Scholar] [CrossRef]
- Sensofar. S neox Five Axis: Complete 3D Measurement Solution. Available online: https://www.sensofar.com/metrology/industry-research/sneox-fiveaxis (accessed on 24 October 2025).
- Werth StentCheck®—Multi-Sensor Systems for Stent Measurement. Available online: https://www.werth.de/en/products/machines/d/production-monitoring/device/stentcheckr.html (accessed on 24 October 2025).
- Fan, C.; Wang, H.; Cao, Z.; Chen, X.; Xu, L. Path Planning of Autonomous 3-D Scanning and Reconstruction for Robotic Multi-Model Perception System. Machines 2022, 11, 26. [Google Scholar] [CrossRef]
- Han, H.; Li, S.; Chen, J.; Lin, Q.; Chen, Q.; Wang, Z. Next View Planning Policy for Autonomous 3D Reconstruction of Unknown Environments. In Proceedings of the 2023 8th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 21–23 April 2023; pp. 766–771. [Google Scholar]
- Liu, Y.; Zhao, W.; Sun, R.; Yue, X. Optimal path planning for automated dimensional inspection of free-form surfaces. J. Manuf. Syst. 2020, 56, 84–92. [Google Scholar] [CrossRef]
- AMETEK Inc. LUPHOScan 260/420 HD. Available online: https://www.taylor-hobson.com/products/non-contact-3d-optical-profilers/luphos/luphoscan-260-420-hd (accessed on 24 October 2025).
- Henselmans, R.; Gubbels, G.; van Drunen, C.; van Venrooy, B.; Leijtens, J. NANOMEFOS non-contact measurement machine for aspheric and freeform optics. In Proceedings of the International Conference on Space Optics—ICSO 2010, Rhodes, Greece, 4–8 October 2010; pp. 495–500. [Google Scholar]
- Mahr GmbH. Mahr MarForm MFU 200. Available online: https://metrology.mahr.com/en-us/ (accessed on 24 October 2025).
- Xiao, S.; Li, C.; Fang, C.; Li, Z.; Zhang, X. Iterative line laser scanning for full profile of polyhedral freeform prism. Opt. Laser Technol. 2025, 181, 111712. [Google Scholar] [CrossRef]
- Lu, K.; Wang, W. A multi-sensor approach for rapid and precise digitization of free-form surface in reverse engineering. Int. J. Adv. Manuf. Technol. 2015, 79, 1983–1994. [Google Scholar] [CrossRef]
- Li, C.; Fang, C.; Zhang, X. Automated line scan profilometer based on the surface recognition method. Opt. Lasers Eng. 2024, 182, 108464. [Google Scholar] [CrossRef]
- Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef]
- Sun, Y.; Lu, L.; Wu, F.; Xiao, S.; Sha, J.; Zhang, L. Error analysis of a coordinate measuring machine with a 6-DOF industrial robot holding the probe. Actuators 2023, 12, 173. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, J.; Zhang, Q. Complete 3D measurement in reverse engineering using a multi-probe system. Int. J. Mach. Tools Manuf. 2005, 45, 1474–1486. [Google Scholar] [CrossRef]
- Fan, Y.; Liu, B.; Chen, P. Research on CT imaging method of complex shaped workpiece based on contour prior constraint. Chin. J. Electron. 2020, 48, 1976–1982. [Google Scholar]

| Systems | Parameters | Values |
|---|---|---|
| RP system | Camera resolution | 4096 × 2160 |
| Telecentric degree of lens | 0.1° | |
| Field of view | 40 mm × 40 mm × 30 mm | |
| CC system | Stroke of the X/Y/Z stages | 100 mm |
| Positioning accuracy of the X/Y/Z axes | 1.0 μm | |
| Angular range of the A/C stages | 180°/360° | |
| Angular positioning accuracy of the A/C axes | ±10″ | |
| Range of the CC sensor | 150 μm | |
| Allowable angle range of the sensor | ±45° |
| Times | Cylinder | Sphere | ||
|---|---|---|---|---|
| RP System | CC System | RP System | CC System | |
| 1 | 1.3 μm | 0.3 μm | 1.8 μm | 1.1 μm |
| 2 | 1.3 μm | 0.3 μm | 1.3 μm | −0.9 μm |
| 3 | 1.2 μm | 0.4 μm | −1.3 μm | −0.7 μm |
| 4 | −0.2 μm | 0.4 μm | 1.7 μm | 1.0 μm |
| 5 | −0.3 μm | 0.3 μm | 1.8 μm | 0.9 μm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Li, Z.; Zhang, X. A Pre-Measurement Device for Contour Measurement Path Planning of Complex Small Workpieces. Photonics 2025, 12, 1140. https://doi.org/10.3390/photonics12111140
Liu L, Li Z, Zhang X. A Pre-Measurement Device for Contour Measurement Path Planning of Complex Small Workpieces. Photonics. 2025; 12(11):1140. https://doi.org/10.3390/photonics12111140
Chicago/Turabian StyleLiu, Lei, Zexiao Li, and Xiaodong Zhang. 2025. "A Pre-Measurement Device for Contour Measurement Path Planning of Complex Small Workpieces" Photonics 12, no. 11: 1140. https://doi.org/10.3390/photonics12111140
APA StyleLiu, L., Li, Z., & Zhang, X. (2025). A Pre-Measurement Device for Contour Measurement Path Planning of Complex Small Workpieces. Photonics, 12(11), 1140. https://doi.org/10.3390/photonics12111140







