Experimental Study on the Scintillation Index of Vortex Beam Superposition States Perturbed by Linear Array Acoustic Sources in Atmospheric Environments

Abstract

Acoustic waves, as mechanical waves, can perturb atmospheric pressure during propagation, altering the refractive index and turbulence distribution. This study explores a method to mitigate the impact of atmospheric turbulence on optical wave transmission using a linear array acoustic source. We investigated the transmission characteristics of vortex beam superposition states under acoustic perturbation, examining the effects of different wave frequencies and propagation distances on the acoustic field distribution, scintillation index, and atmospheric refractive index structure constant. The results show that acoustic field distributions vary with frequency, and a stable acoustic field is achievable with proper configuration. The scintillation index and refractive index structure constant are influenced by both the acoustic wave propagation distance and sound pressure level. Furthermore, a higher sound pressure level of the source enhances the impact of the linear array acoustic waves on both the scintillation index and the atmospheric refractive index structure constant. This research presents a novel approach to improving optical wave transmission by mitigating atmospheric turbulence.

1. Introduction

Atmospheric turbulence, one of the primary challenges encountered by light waves during free-space propagation, has long been a central issue in application fields such as Free-Space Optical Communication (FSOC), laser radar, and remote sensing [1,2,3]. Atmospheric turbulence causes random spatial and temporal variations in the refractive index of the atmosphere, severely distorting the wavefront of light waves propagating through it [4]. These disturbances manifest in various forms [5,6,7], including beam wandering, beam spreading, degradation of spatial coherence, and intensity fluctuations, the latter commonly referred to as “scintillation.” Among these effects, the scintillation index is a critical factor that affects the performance and reliability of FSOC systems. It causes significant fluctuations in received signal power, increases the bit error rate, and may even disrupt communication links [8]. As a result, addressing the disturbances caused by atmospheric turbulence and exploring effective mitigation or compensation methods has become a key challenge in modern optics.

Vortex beams carrying Orbital Angular Momentum (OAM) have attracted widespread attention due to their unique phase structure [9,10,11]. Simultaneously, OAM multiplexing technology provides a new dimension for FSOC, demonstrating great potential for high-capacity optical communication [12,13,14]. However, studies have shown that the helical phase structure of a single OAM mode is easily disrupted during propagation through atmospheric turbulence, leading to crosstalk between modes and degradation of beam quality [15,16]. To explore more robust beam structures, researchers have begun to focus on the superposition states of vortex beams. These superposition states are formed by combining vortex fields with different topological charges, creating a more complex light field distribution. To some extent, this approach exhibits better directional stability or specific intensity distribution characteristics [17,18,19,20,21]. Nevertheless, the superposition state of vortex beams still undergoes phase distortion and intensity scintillation caused by atmospheric turbulence. Therefore, improving the transmission quality of vortex beam superposition states in complex atmospheric environments has become an important direction in current research.

Acoustic waves, as mechanical waves capable of modulating the physical properties of a medium, offer a new approach for the active control of atmospheric turbulence. When acoustic waves propagate through air, they generate periodic pressure variations and density fluctuations, thereby altering the refractive index distribution along the light propagation path and affecting the atmospheric refractive index structure constant [22,23,24,25]. For example, when a Gaussian laser beam interacts with ultrasound, it is modulated by the ultrasound, resulting in diffraction and refraction phenomena [26]. Ultrasound can effectively deflect ultrashort laser pulses in conventional air while maintaining excellent beam quality [27]. By controlling the frequency and acoustic pressure of the acoustic waves, controllable dynamic phase disturbances can be intentionally introduced into the optical path [28,29]. During transmission, the energy of acoustic waves also influences both the inner and outer scales of atmospheric turbulence, playing a role in regulating the atmospheric turbulence power spectrum model [30]. Furthermore, experimental studies have shown that coherent acoustic waves can significantly affect the drift and scintillation of Gaussian lasers [31,32]. Therefore, acoustic waves can serve as an active control method to study the impact of acoustic wave disturbances on beam characteristics. In recent years, initial results have been achieved in the application of acousto-optic interactions in atmospheric optics, but experimental research on the transmission characteristics of vortex beam superposition states under acoustic wave control has not yet been reported.

This paper presents experimental research on the transmission of vortex beam superposition states disturbed by linear array acoustic waves. First, the distribution of the acoustic field under different conditions is analyzed. Then, the impact of different acoustic field distributions on the scintillation index of vortex beam superposition states and the refractive index structure constant is explored.

2. Propagation Modeling of Vortex Beam Superposition States Under Linear Array Acoustic Sources Perturbation

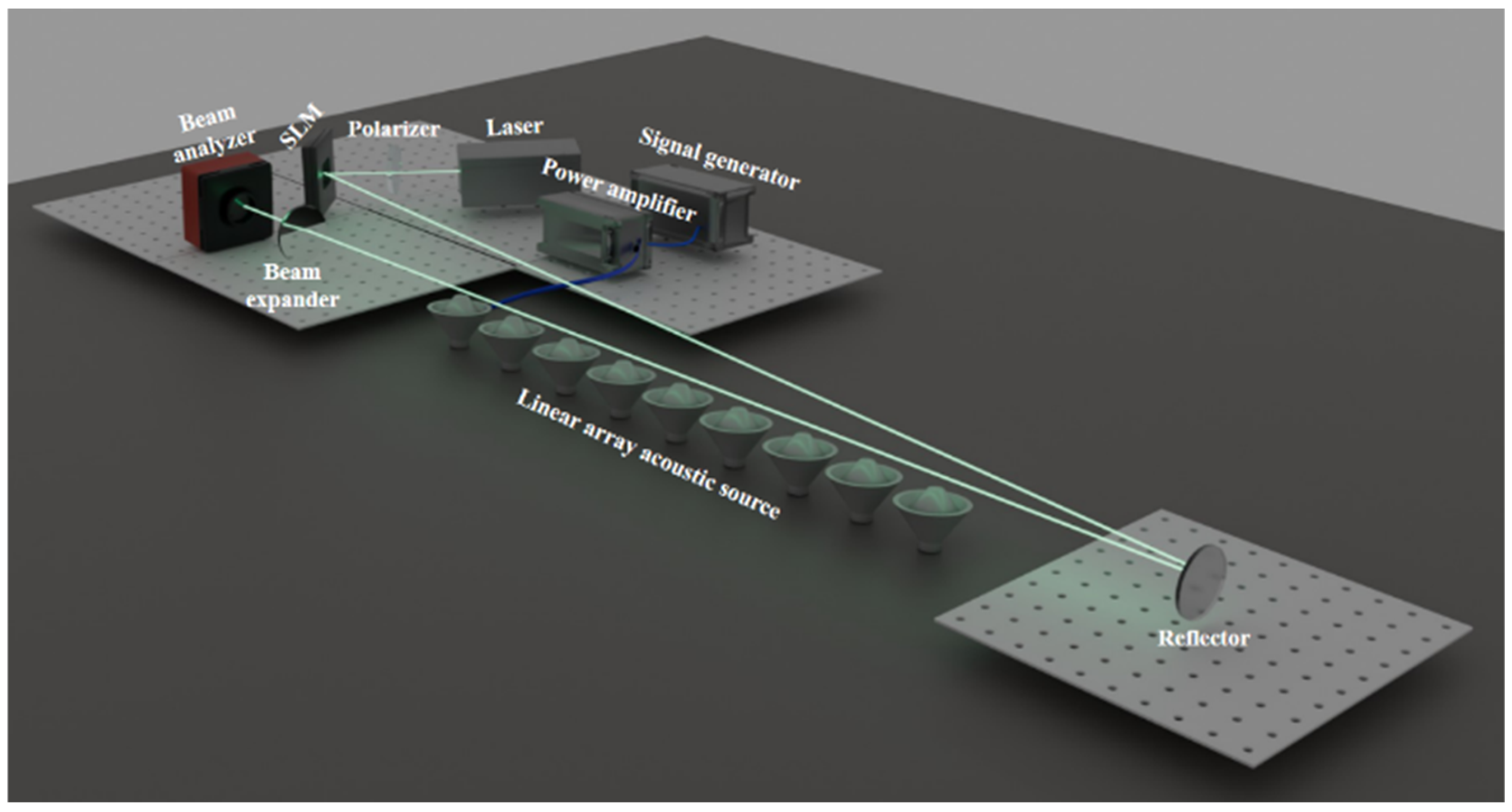
Figure 1 illustrates the experimental setup for the transmission of vortex beam superposition states with a linear array acoustic source disturbance. The main equipment and parameters used in the experiment are listed in

Table 1. Main equipment and parameters.

Equipment	Parameter
Laser	Wavelength: 532 nm, Output Power: 1~100 mW, Spatial Mode: TEM00, Beam diameter < 2 mm, Beam Divergence (full angle) < 1.5 mrad
Spatial light modulator	Reflective, 420~1100 nm, Resolution: $1920\times 1080$
Beam expander	Maximum incident beam diameter: 4 mm, Transmittance > 98.5%
Beam analyzer	Sensor: Sony IMX304 Gen2, Resolution: $4096\times 3000$, Receiving area: $14 \mathrm{mm}\times 10 \mathrm{mm}$
Power amplifier	Frequency response: 40 Hz~16 KHz, Maximum power: 600 W
Signal generator	Frequency range: 0~15 MHz
Acoustic source	Frequency response range: 55 Hz~20 KHz, Rated power: 8 W, Size: 4 inches, Rated Impedance: 8 Ω

. The experimental system primarily consists of two components: the optical and acoustic parts. For the optical wave, the Gaussian beam emitted by the laser is transformed into a vortex beam after passing through the collimator, polarizer, and spatial light modulator (which loads the vortex phase hologram). The beam is then reflected by a mirror, transmitted to the receiver, expanded by a beam expander, and detected by a beam analyzer. The beam analyzer sends the received light information to a computer for display and recording. For the acoustic wave, a fixed-frequency audio signal generated by a signal generator is amplified by a power amplifier and transmitted to the array acoustic source to generate coherent acoustic waves. The sound pressure level (SPL) generated by the acoustic source was measured and recorded using a digital acoustic level meter positioned 10 cm directly above the acoustic source.

As illustrated in Figure 1, the linear array acoustic source is positioned beneath the optical transmission path (due to the angle between the two optical paths after reflection, the linear array acoustic source is placed midway between the two optical paths), meaning that the acoustic wave transmission path is perpendicular to the optical transmission path. In this scenario, the parameters determining the acoustic field distribution of the linear array are the acoustic wave frequency and the acoustic wave transmission distance. In our previous study, we theoretically investigated the relationship between acoustic wave pressure and atmospheric turbulence. Since acoustic pressure alters atmospheric pressure, which is closely correlated with atmospheric turbulence, we proposed that different acoustic field distributions (corresponding to varying atmospheric turbulence intensities) could be constructed to examine their effects on optical wave propagation characteristics [33]. Therefore, to investigate the impact of the linear array acoustic source on the scintillation index of the vortex beam superposition state, it is essential to first examine the acoustic field distribution formed under different acoustic wave frequencies and transmission distances.

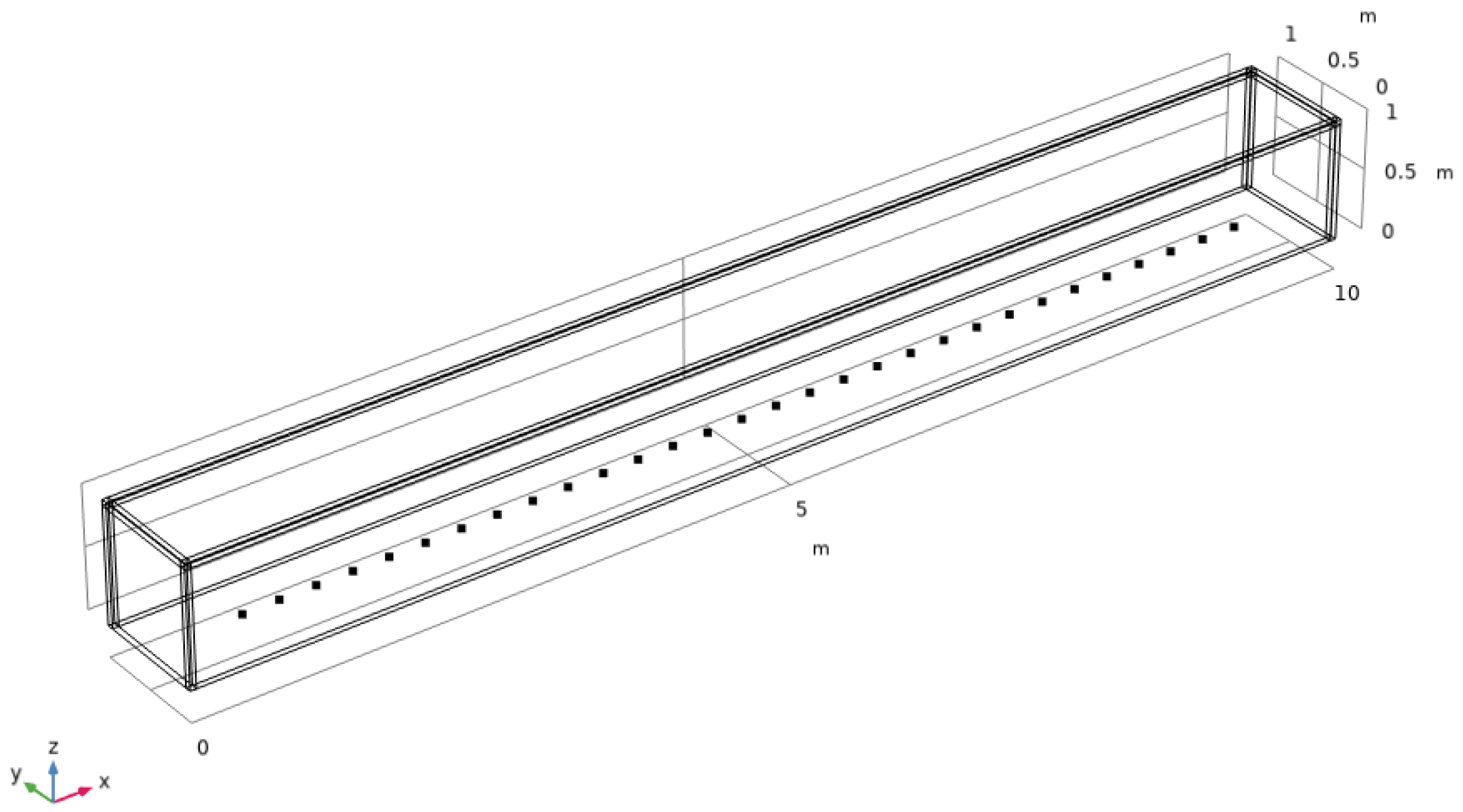
The linear array acoustic field was numerically simulated using COMSOL software 6.2, with the computational model shown in Figure 2. The model consists of a rectangular cuboid measuring 10 m in length, 1 m in width, and 1 m in height, filled with air. The boundary containing the linear array acoustic source was set as a hard acoustic field boundary. To simulate acoustic wave absorption as the waves propagate away from the source, all other boundaries were configured as Perfectly Matched Layers (PML) to represent open boundaries. The linear array acoustic source was positioned in the $x-y$ plane, comprising 30 individual acoustic sources emitting sinusoidal acoustic signals. Each individual source has a power of 5 W and a spacing of 0.3 m between adjacent sources.

According to the definition of acoustic pressure, it represents the difference between the actual atmospheric pressure with acoustic wave disturbance and the static atmospheric pressure without such disturbance [33]

$$p=p_i-p_h$$

(1)

where $p$ represents the acoustic pressure, $p_i$ denotes the actual atmospheric pressure under acoustic wave disturbance, and $p_h$ is the static atmospheric pressure without disturbance. This implies that when the acoustic pressure values in the acoustic field generated by the linear array are predominantly positive, the disturbed atmospheric pressure ($p_i$) exceeds the undisturbed pressure ($p_h$). Conversely, when the acoustic pressure values are mostly negative, the opposite holds true. Thus, different acoustic frequencies produce distinct acoustic field distributions, thereby exerting varying effects on local atmospheric pressure.

As indicated by literature [34], there is the following relationship between acoustic pressure and the atmospheric refractive index structure constant

$$C_{ns}^2={\alpha }^2{L}_0^{4/3}\left[-79\times {10}^{-6}{\displaystyle \frac{p_i}{T}}\left(-{\displaystyle \frac{\kappa }{p_i}}{\displaystyle \frac{\partial p_i}{\partial x}}\right)\right]$$

(2)

From Equation (2), the disturbed atmospheric pressure $p_i$ influences the atmospheric refractive index structure constant. As shown in Equation (1), $p_i$ changes under acoustic wave disturbances. Therefore, by constructing different acoustic wave distributions to achieve varying acoustic pressure values, it is possible to regulate the atmospheric refractive index structure constant using acoustic waves.

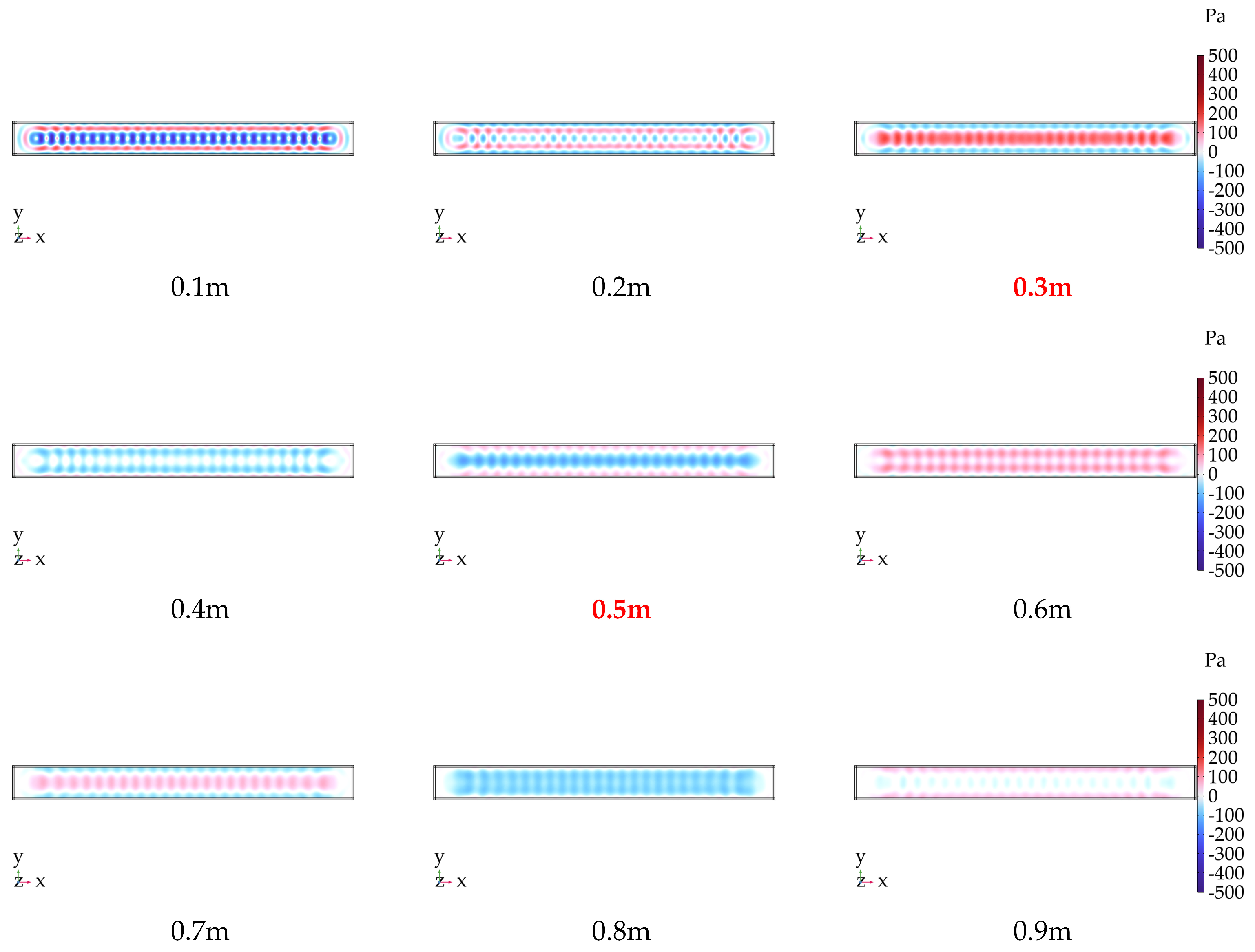
Figure 3 presents the simulated acoustic field distributions of the linear array under different acoustic frequencies. As shown in Figure 3, the acoustic pressure exhibits an oscillatory distribution pattern, with the oscillations becoming more densely packed as the frequency increases. At $f_s=1000 \mathrm{Hz}$, the acoustic pressure demonstrates a stratified distribution, yielding an optimal acoustic field configuration—where positive and negative pressure zones are uniformly distributed, resulting in stable atmospheric pressure modulation. Consequently, an acoustic frequency of $f_s=1000 \mathrm{Hz}$ was selected for subsequent experimental investigations.

Figure 4 illustrates the acoustic field distributions at different acoustic propagation distances when the acoustic wave frequency is $f_s=1000 \mathrm{Hz}$. As shown in Figure 4, when the propagation distances are $x=0.3 \mathrm{m}$, $x=0.6 \mathrm{m}$, and $x=0.7 \mathrm{m}$, the acoustic pressure values are predominantly positive (indicating that the atmospheric pressure under acoustic disturbance exceeds the ambient atmospheric pressure). Conversely, at propagation distances of $x=0.5 \mathrm{m}$ and $x=0.8 \mathrm{m}$, the acoustic pressure values are mostly negative (suggesting that the disturbed atmospheric pressure is lower than the ambient pressure). Taking into account the attenuation of acoustic waves during actual propagation, the propagation distances of $x=0.3 \mathrm{m}$ and $x=0.5 \mathrm{m}$ were selected for subsequent experimental investigations.

The scintillation index characterizes the intensity fluctuations of a laser beam propagating through atmospheric turbulence, which are induced by random variations in the refractive index of air. As a crucial parameter for evaluating the performance of laser communication systems, lidar, and other related applications, it serves as an important metric for system assessment. While conventional methods employ optical power meters to capture power fluctuations, the scintillation index can alternatively be calculated using a series of captured light intensity images [35],

$${\sigma }^2\left(z\right)={\displaystyle \frac{〈P^2\left(z\right)〉}{{〈P\left(z\right)〉}^2}}-1$$

(3)

$$P\left(z\right)={\displaystyle \iint I\left(a,b,z\right)\mathrm{d}a\mathrm{d}b}$$

(4)

where $P$ represents the light intensity value captured by the beam analyzer, $I$ is the power density, $a$ and $b$ denote the pixel coordinates of the intensity image, $z$ stands for the propagation distance, and $〈\cdot 〉$ indicates the statistical averaging parameter.

3. Experimental Methodology

3.1. Experimental Setup

Based on the acoustic field distribution simulation results obtained from COMSOL, we constructed an experimental setup for investigation, as shown in Figure 5. Figure 5 demonstrates the experimental study of vortex beam superposition state transmission under linear array acoustic perturbation in a real atmospheric environment, with an optical wave propagation distance of 20 m. Figure 5a shows the setup of the transmitter and receiver, where the transmitter includes the laser, polarizer, and spatial light modulator (SLM), while the receiver includes the beam expander and beam analyzer. Figure 5b shows the setup of the reflector, which includes the reflector itself. Figure 5c shows the complete transmission link setup, including the linear array acoustic source, signal generator, and power amplifier. The entire optical setup was mounted on a rigid optical breadboard placed on a stable platform to minimize mechanical vibrations. We compared the scintillation index with the acoustic source both on and off, while keeping all other experimental conditions constant. Since the optical setup, laser source, and detection system remained unchanged, any significant difference in scintillation can be attributed to the acoustic modulation of the atmospheric refractive index, rather than instrumental noise or system drift.

3.2. Acoustic and Optical Parameters

The linear array acoustic configuration consists of 30 acoustic sources spaced 0.3 m apart. During the acoustic perturbation experiments, each source operates at a frequency of 1000 Hz with a sound pressure level of 130 dB. An audio signal generator produces a fixed-frequency audio signal, which is amplified by a power amplifier and transmitted to the array of sound sources to generate coherent sound waves. The sound pressure level is recorded using a digital sound level meter. The laser source is a cylindrically symmetric Gaussian beam. In the experiment, the vortex beam superposition state was generated using an optical setup with SLM. The phase hologram loaded on SLM is calculated by [36,37].

$$E_{p_1,l_1,p_2,l_2}\left(r,\phi ,z\right)=E_{p_1,l_1}\left(r,\phi ,z\right)+E_{p_2,l_2}\left(r,\phi ,z\right)$$

(5)

$$\begin{array}{cc}\begin{array}{cc}\hfill E_{p_i,l_i}\left(r,\phi ,z=0\right)& =\sqrt{{\displaystyle \frac{2}{\pi \left(p_i+\left|l_i\right|\right)!}}}\times {\displaystyle \frac{1}{{\omega }_0}}{\left({\displaystyle \frac{\sqrt{2}r}{{\omega }_0}}\right)}^{\left|l_i\right|}\hfill \\ \hfill & \times \exp \left({\displaystyle \frac{-r^2}{{\omega }_0^2}}\right)L_{p_i}^{\left|l_i\right|}\left({\displaystyle \frac{2r^2}{{\omega }_0^2}}\right)\exp \left(i{l}_i\phi \right)\hfill \end{array}& i=1,2\hfill \end{array}$$

(6)

where $r$ is the radius in the cylindrical coordinate system, $\phi$ is the angle in the cylindrical coordinate system, $p_i$ is the vortex optical order, $l_i$ is the topological charge, ${\omega }_0$ is the beam waist, $L_{p_i}^{\left|l_i\right|}$ is the Laguerre polynomial. In this paper, the phase hologram parameters used for the vortex beam superposition state are specified as $p_1=p_2=0$, $l_1=1$ and $l_2=4$, ${\omega }_0=2 \mathrm{mm}$, Receiver area is $14 \mathrm{mm}\times 10 \mathrm{mm}$. 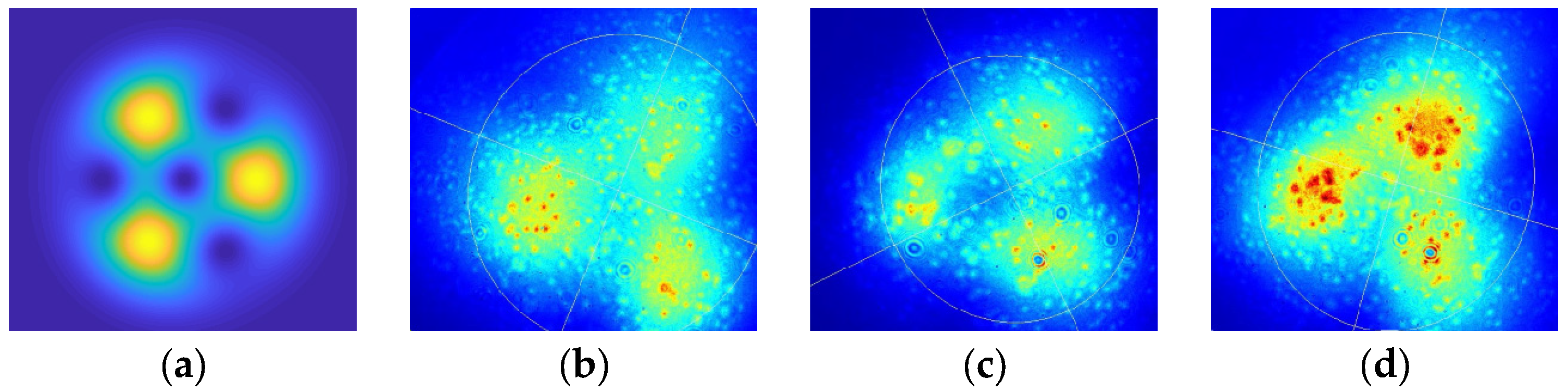The modal purity of the vortex beam superposition was verified using a modal purity check, and the results show that the superposition states generated by the hologram align with the theoretical expectations.

In this study, we assumed the weak-turbulence regime for applying the scintillation formula, which is valid for typical outdoor conditions with moderate turbulence. The camera aperture and beam geometry were designed to ensure weak-fluctuation conditions, allowing effective use of the scintillation formula. We also assumed plane waves in our analysis, as the short propagation distance and minimal beam divergence made this approximation valid. This simplified the analysis without affecting result accuracy. Additionally, the scintillation estimator is appropriate for vortex beam superposition states, as they exhibit intensity fluctuations similar to Gaussian beams under weak turbulence, with changes in the scintillation index primarily influenced by the beam structure rather than the complex phase profile.

3.3. Data Acquisition and Environmental Conditions

Prior to initiating the experiment, all equipment was preheated for 10–15 min to achieve thermal stabilization. The laser beam was precisely aligned, and system parameters were carefully adjusted and recorded. Throughout the experimental process, parameter recalibration was performed at 30 min intervals to ensure measurement stability during the entire duration of the experiment. To mitigate experimental errors and minimize the influence of inherent variations in the actual atmospheric environment on the experimental results, a cross-experimental methodology was employed. This approach involved conducting paired control experiments: one set without acoustic perturbation and another with acoustic perturbation.

For each experimental condition, ten independent trials were conducted. Images were captured in free-running mode using a 12-megapixel CMOS camera (resolution 4096 × 3000, UPOLabs, Xi’an, China) via a USB 3.0 interface. The camera exposure time was set to 100 ms, and the system operated stably with a frame interval of approximately 300 ms, corresponding to an average frame rate of 3.33 Hz. In each trial, images were acquired continuously for 5 min, yielding 1000 frames for subsequent statistical analysis. The intensity was integrated over the full frame for each image. The scintillation index, defined as the variance of the normalized intensity, was computed from these frames and showed convergence as the sample size increased.

All measurements were conducted outdoors, with the optical path positioned at heights of 0.3 m and 0.5 m above the acoustic source on the ground. Ambient temperature and wind speed were monitored during each trial. The temperature ranged from 30.2 °C to 32.4 °C, and wind speeds varied between 1.4 m/s and 2.8 m/s, indicating moderate atmospheric conditions without strong gusts.

4. Experimental Results and Analysis

Figure 6 shows the original density distribution of intensity, the density distribution of intensity without acoustic wave disturbance, and with acoustic wave disturbance. When vortex beam superposition states propagate through the atmosphere, they are affected by atmospheric turbulence. Under acoustic wave disturbance, at $x=0.3 \mathrm{m}$, the density distribution of intensity shows a more significant decay, indicating that atmospheric turbulence is enhanced by the acoustic wave. At $x=0.5 \mathrm{m}$, the decay is less pronounced, suggesting that the acoustic wave reduces the effect of atmospheric turbulence.

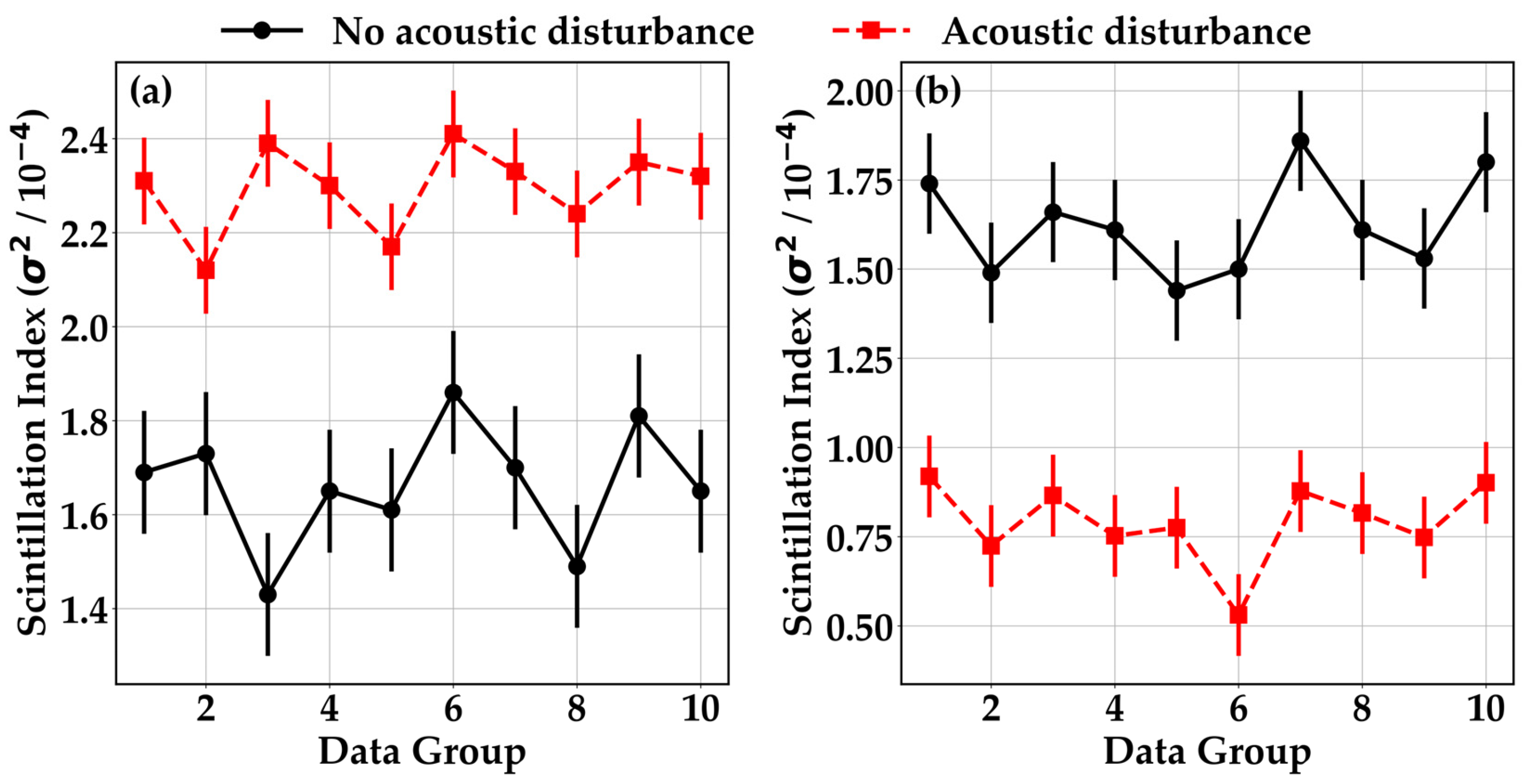
Figure 7 presents the variation in the scintillation index for vortex beam superposition states under the disturbance of a linear array acoustic source in an outdoor real atmospheric environment. The uncertainty in the scintillation index and the derived atmospheric refractive index structure constants was evaluated considering finite-sample statistics, background subtraction, and region-of-interest (ROI) selection. The finite-sample uncertainty was assessed by analyzing the variation across the 1000 frames collected per trial. Variations in background subtraction methods were considered, with minimal impact on the results. The ROI selection contributed a minor uncertainty, which was included in the overall analysis. Since detector noise was minimized by the control experiment design, it did not significantly affect the results. Confidence intervals were added to the experimental curves to reflect these uncertainties and provide a clearer picture of the experimental precision. As shown in Figure 7, the influence of the linear array acoustic source on the scintillation index of vortex beam superposition states varies depending on the distance between the acoustic source and the laser beam. When the acoustic wave propagation distance is 0.3 m, the scintillation index of the vortex beam superposition state is higher than that without acoustic wave disturbance. The scintillation index increased from a range of $1.43\times {10}^{-4}\sim 1.86\times {10}^{-4}$ to a range of $2.12\times {10}^{-4}\sim 2.41\times {10}^{-4}$. Conversely, when the acoustic wave propagation distance is 0.5 m, the scintillation index becomes lower than the undisturbed case. The scintillation index decreased from a range of $1.44\times {10}^{-4}\sim 1.86\times {10}^{-4}$ to a range of $5.3\times {10}^{-5}\sim 9.19\times {10}^{-5}$. This occurs because, at a propagation distance of 0.3 m, most of the acoustic pressure values are positive (indicating that the actual atmospheric pressure under acoustic disturbance is higher than the original atmospheric pressure), thereby enhancing the disturbance on the vortex beam superposition state and increasing the scintillation index. In contrast, the opposite effect is observed at a propagation distance of 0.5 m.

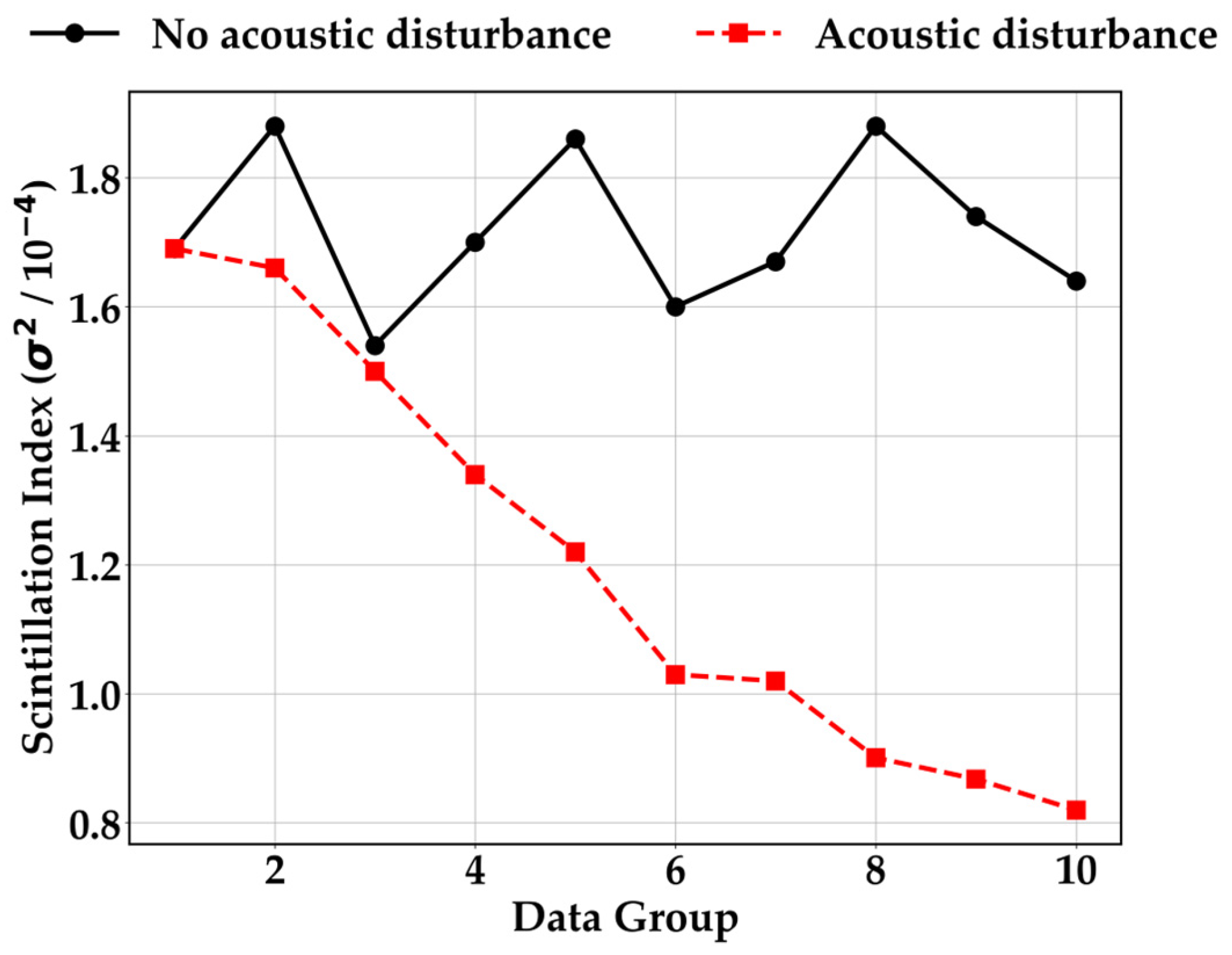
Figure 8 shows the variation curves of the scintillation index for vortex beam superposition states under different sound pressure levels. Here, only the case where the acoustic wave propagation distance is 0.5 m is presented. This is because, as demonstrated by the experimental results in Figure 6, the influence of linear array acoustic source on the scintillation index of vortex beam superposition states varies at different propagation distances—sometimes improving and sometimes deteriorating the performance. In practical applications, the primary concern is often how to enhance the transmission quality of vortex beams. Therefore, only the scenario with an acoustic wave propagation distance of 0.5 m is discussed here. From Figure 8, it can be observed that when the acoustic wave propagation distance is 0.5 m, the scintillation index of the vortex beam superposition state gradually decreases as the sound pressure levels increase. Under the disturbance of acoustic waves, the scintillation index decreases from $1.69\times {10}^{-4}$ to $8.2\times {10}^{-5}$ as the sound pressure level increases. Moreover, the higher the sound pressure levels, the stronger its impact on the scintillation index of the vortex beam superposition state.

As indicated in the literature, the scintillation index exhibits the following relationship with the atmospheric refractive index structure constants [38]:

$${\sigma }^2=1.23C_n^2{k}^{7/6}{z}^{11/6}$$

(7)

where $k$ is the optical wavenumber and $z$ is the propagation distance of the light wave. The atmospheric refractive index structure constants $C_n^2$ directly reflects the severity of the refractive index fluctuations caused by atmospheric turbulence. As the $C_n^2$ value increases, the severity of these fluctuations also increases, which in turn determines the amplitude and characteristics of the negative effects experienced by the laser beam as it passes through the turbulent atmosphere.

Based on Equation (7), the atmospheric refractive index structure constants can be expressed in terms of the scintillation index as:

$$C_n^2={\sigma }^2{\left(1.23k^{7/6}{z}^{11/6}\right)}^{-1}$$

(8)

Therefore, based on Equation (8), the atmospheric refractive index structure constants (i.e., atmospheric turbulence strength) under different experimental conditions can be calculated using the scintillation index experimental data obtained from Figure 7 and Figure 8.

Table 2. Atmospheric refractive index structure constants under fixed SPL conditions with and without acoustic wave disturbance.

SPL	Experimental Condition	$\mathbf{Min} {\mathit{\sigma }}^2$	$\mathbf{Max} {\mathit{\sigma }}^2$	$\mathbf{Min} {\mathit{C}}_{\mathit{n}}^2$	$\mathbf{Max} {\mathit{C}}_{\mathit{n}}^2$
Fixed SPL (x = 0.3 m)	No acoustic disturbance	$1.43\times {10}^{-4}$	$1.86\times {10}^{-4}$	$2.6868\times {10}^{-15}$	$3.4947\times {10}^{-15}$
	Acoustic disturbance	$2.12\times {10}^{-4}$	$2.41\times {10}^{-4}$	$3.9832\times {10}^{-15}$	$4.5280\times {10}^{-15}$
Fixed SPL (x = 0.5 m)	No acoustic disturbance	$1.44\times {10}^{-4}$	$1.86\times {10}^{-4}$	$2.7056\times {10}^{-15}$	$3.4947\times {10}^{-15}$
	Acoustic disturbance	$5.30\times {10}^{-5}$	$9.19\times {10}^{-5}$	$9.9579\times {10}^{-16}$	$1.7267\times {10}^{-15}$

and

Table 3. Atmospheric refractive index structure constants under variable SPL conditions.

SPL	Experimental Condition	${\mathit{\sigma }}^2$	${\mathit{C}}_{\mathit{n}}^2$
Variable SPL (x = 0.5 m)	$\mathrm{SPL}=85 \mathrm{dB}$	$1.69\times {10}^{-4}$	$3.1753\times {10}^{-15}$
	$\mathrm{SPL}=90 \mathrm{dB}$	$1.66\times {10}^{-4}$	$3.1189\times {10}^{-15}$
	$\mathrm{SPL}=95 \mathrm{dB}$	$1.50\times {10}^{-4}$	$2.8183\times {10}^{-15}$
	$\mathrm{SPL}=100 \mathrm{dB}$	$1.34\times {10}^{-4}$	$2.5177\times {10}^{-15}$
	$\mathrm{SPL}=105 \mathrm{dB}$	$1.22\times {10}^{-4}$	$2.2922\times {10}^{-15}$
	$\mathrm{SPL}=110 \mathrm{dB}$	$1.03\times {10}^{-4}$	$1.9352\times {10}^{-15}$
	$\mathrm{SPL}=115 \mathrm{dB}$	$1.02\times {10}^{-4}$	$1.9164\times {10}^{-15}$
	$\mathrm{SPL}=120 \mathrm{dB}$	$9.01\times {10}^{-5}$	$1.6928\times {10}^{-15}$
	$\mathrm{SPL}=125 \mathrm{dB}$	$8.68\times {10}^{-5}$	$1.6308\times {10}^{-15}$
	$\mathrm{SPL}=130 \mathrm{dB}$	$8.20\times {10}^{-5}$	$1.5407\times {10}^{-15}$

Note: SPL is the sound pressure level, ${\sigma }^2$ is the scintillation index, $C_n^2$ is the atmospheric refractive index structure constants.

present the calculated atmospheric refractive index structure constants under various experimental conditions in an outdoor real atmospheric environment. As shown in Table 2, when the distance between the acoustic source and laser beam is 0.3 m, the atmospheric refractive index structure constants ranges from $2.6868\times {10}^{-15}\sim 3.4947\times {10}^{-15}$ without acoustic disturbance, but increases to $3.9832\times {10}^{-15}\sim 4.5280\times {10}^{-15}$ with acoustic disturbance, indicating that the acoustic waves enhance atmospheric turbulence in this case. Conversely, when the distance is 0.5 m, the atmospheric refractive index structure constantly decreases from $2.7056\times {10}^{-15}\sim 3.4947\times {10}^{-15}$ to $9.9579\times {10}^{-16}\sim 1.7267\times {10}^{-15}$, demonstrating that the acoustic waves suppress turbulence under these conditions. Furthermore, as shown in Table 3, at an acoustic wave propagation distance of 0.5 m, both the scintillation index and atmospheric refractive index structure constants gradually decrease with increasing sound pressure level. This suggests that higher sound pressure levels result in stronger acoustic effects on both atmospheric turbulence and light wave propagation.

5. Conclusions

This paper presents an experimental study on the scintillation index of vortex beam superposition states under the influence of disturbances caused by linear array acoustic sources. Through simulation analysis, we investigated the distribution of acoustic fields generated by the array under different acoustic frequencies and propagation distances, and examined their effects on the scintillation index of vortex beam superposition states. The results show that varying acoustic frequencies and propagation distances result in distinct array acoustic field distributions, which lead to different perturbations in atmospheric pressure. When the acoustic frequency is 1000 Hz, a stratified acoustic pressure distribution emerges, leading to a relatively stable acoustic field. At a propagation distance of 0.3 m, the disturbance from the linear array acoustic source increases the scintillation index of vortex beam superposition states, with the atmospheric refractive index structure constant rising from $2.6868\times {10}^{-15}\sim 3.4947\times {10}^{-15}$ to $3.9832\times {10}^{-15}\sim 4.5280\times {10}^{-15}$, indicating an enhancement of atmospheric turbulence. In contrast, at a propagation distance of 0.5 m, the disturbance reduces the scintillation index, lowering the atmospheric refractive index structure constant from $2.7056\times {10}^{-15}\sim 3.4947\times {10}^{-15}$ to $9.9579\times {10}^{-16}\sim 1.7267\times {10}^{-15}$, suggesting a suppression effect on turbulence. Moreover, as the sound pressure level increases, the scintillation index of vortex beam superposition states decreases progressively, accompanied by a reduction in the atmospheric refractive index structure constant from $3.1753\times {10}^{-15}$ to $1.5407\times {10}^{-15}$. These findings confirm that higher sound pressure levels exert a stronger influence on both atmospheric turbulence and the scintillation characteristics of vortex beam superposition states. The results provide a solid experimental foundation for further studies on acousto-optic co-propagation, the development of acoustic-based methods for optical transmission control, and the mitigation of atmospheric turbulence-induced disturbances in light wave propagation.