Drastic Slowdown of EIT Dynamics by Doppler Broadening and Its Compensation in Room-Temperature Atomic Vapor
Abstract
1. Introduction
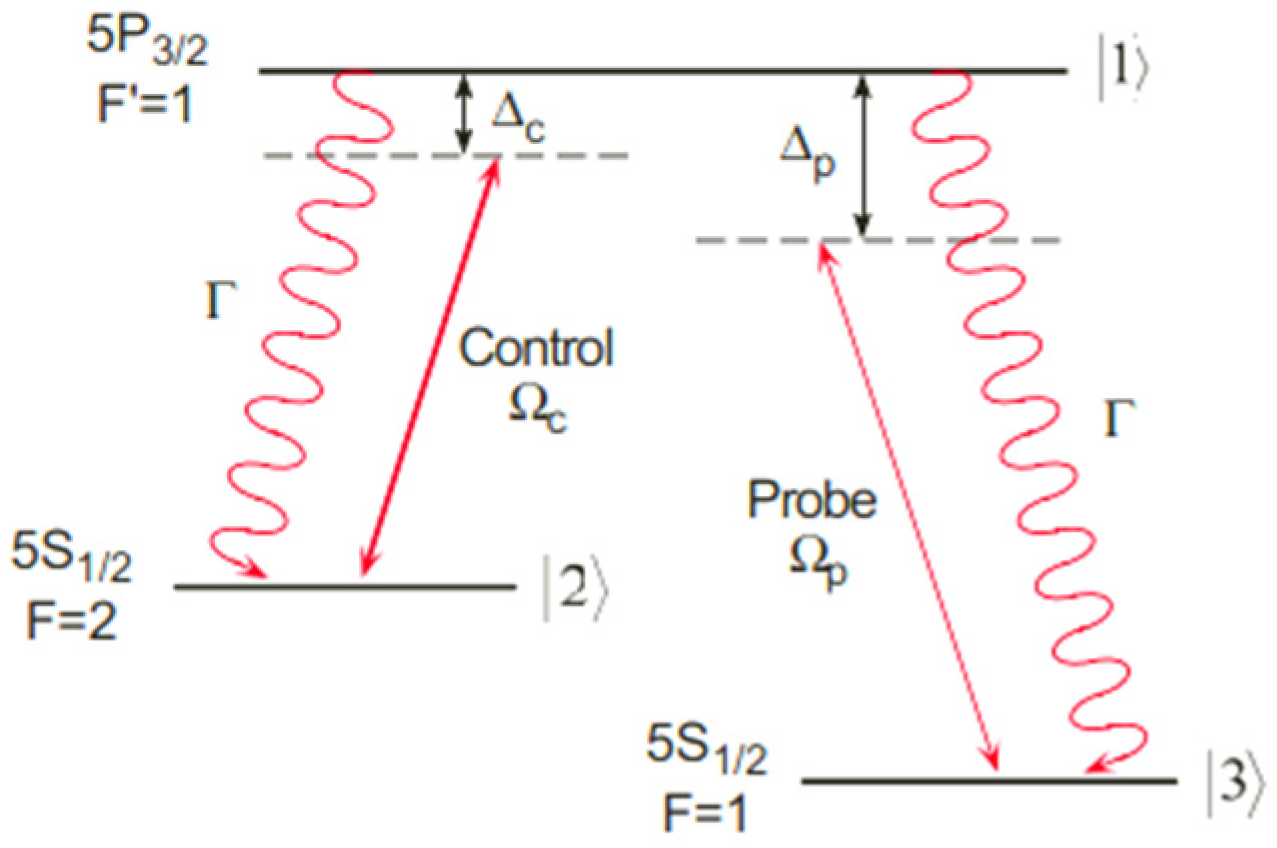
2. Theoretical Formulations
3. Results and Discussion
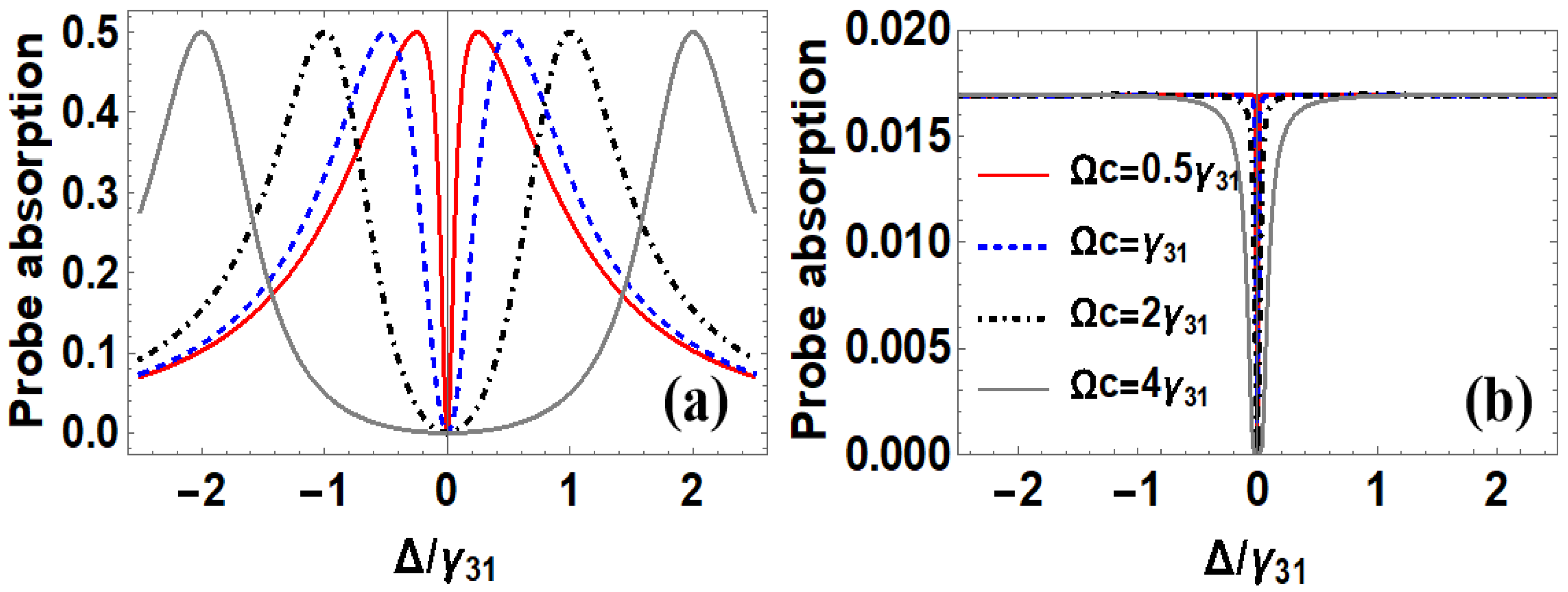
3.1. Absorption Spectra
3.2. Transient Optical Response
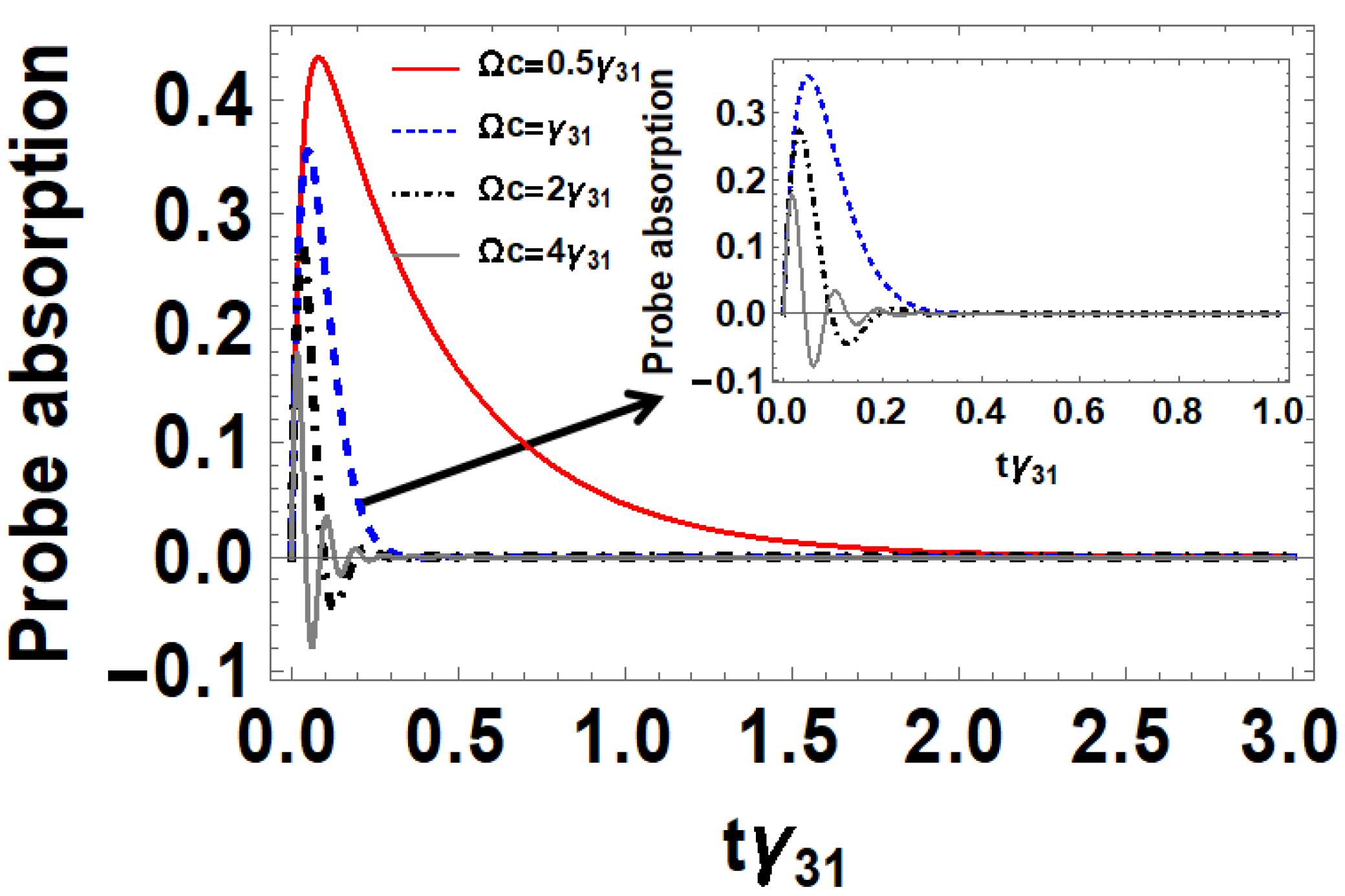
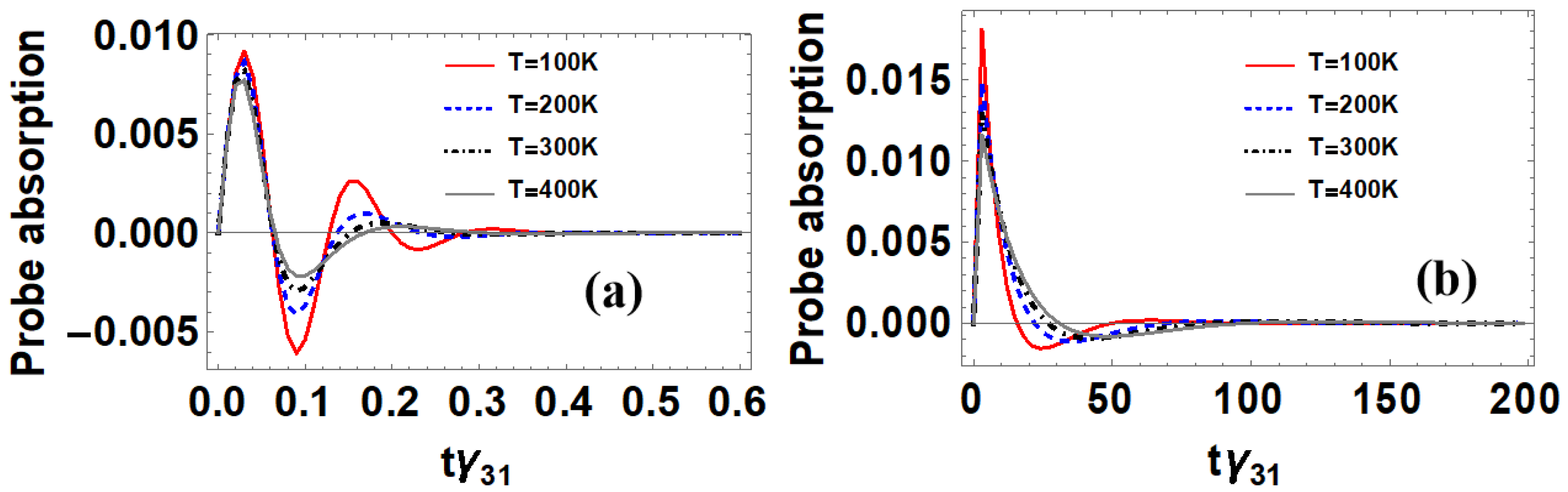
3.2.1. Atoms in Doppler-Free Medium
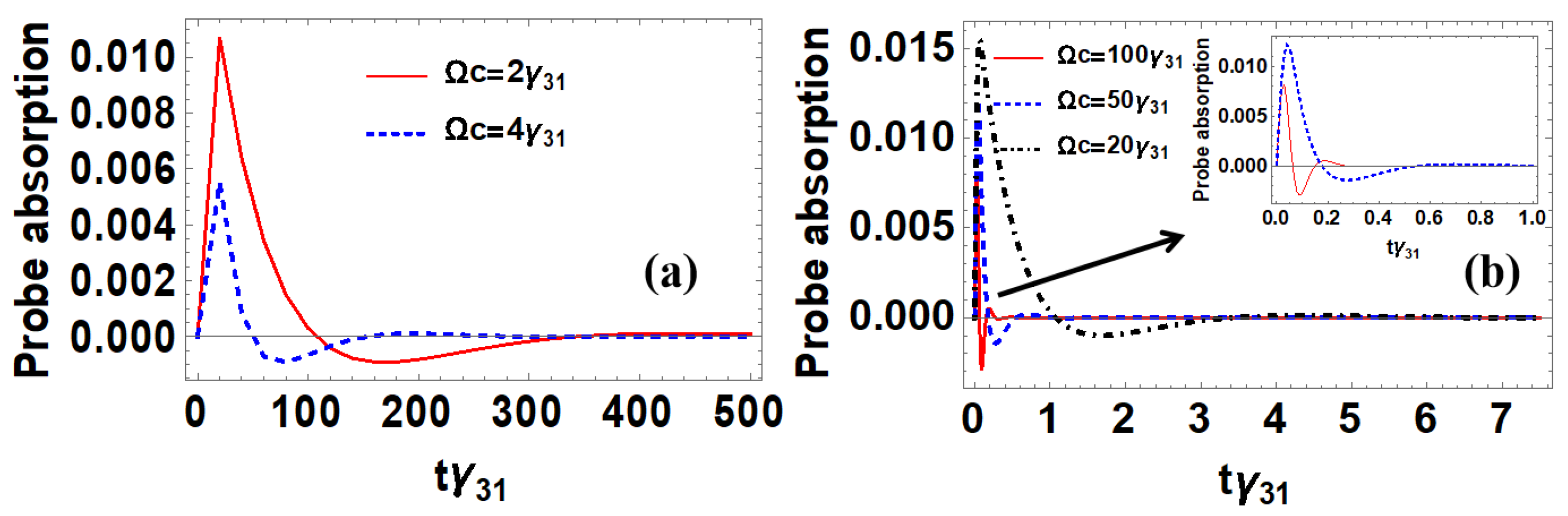
3.2.2. Atoms in Doppler Broadened Medium at Room Temperature
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harris, S.E.; Field, J.E.; Imamoğlu, A. Nonlinear optical processes using electromagnetically induced transparency. Phys. Rev. Lett. 1990, 64, 1107–1110. [Google Scholar] [CrossRef] [PubMed]
- Hau, L.V.; Harris, S.E.; Dutton, Z.; Behroozi, C.H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 1999, 397, 594–598. [Google Scholar] [CrossRef]
- Lvovsky, A.I.; Sanders, B.C.; Tittel, W. Optical quantum memory. Nat. Photon. 2009, 3, 706–714. [Google Scholar] [CrossRef]
- Dudin, Y.O.; Li, L.; Kuzmich, A. Light storage on the time scale of a minute. Phys. Rev. A 2013, 87, 031801. [Google Scholar] [CrossRef]
- Firstenberg, O.; Adams, C.S.; Hofferberth, S. Nonlinear quantum optics mediated by Rydberg interactions. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 152003. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Zhang, L.H.; Liu, Z.K.; Liu, B.; Zhang, Z.Y.; Guo, G.C.; Ding, D.S.; Shi, B.S. Highly Sensitive Measurement of a Megahertz rf Electric Field with a Rydberg-Atom Sensor. Phys. Rev. Appl. 2022, 18, 014033. [Google Scholar] [CrossRef]
- Heshami, K.; England, D.G.; Humphreys, P.C.; Bustard, P.J.; Acosta, V.M.; Nunn, J.; Sussman, B.J. Quantum memories: Emerging applications and recent advances. J. Mod. Opt. 2016, 63, 2005–2028. [Google Scholar] [CrossRef]
- Parigi, V.; D’Ambrosio, V.; Arnold, C.; Marrucci, L.; Sciarrino, F.; Laurat, J. Storage and retrieval of vector beams of light in a multiple-degree-of-freedom quantum memory. Nat. Commun. 2015, 6, 7706. [Google Scholar] [CrossRef]
- Gorshkov, A.V.; André, A.; Fleischhauer, M.; Sørensen, A.S.; Lukin, M.D. Universal Approach to Optimal Photon Storage in Atomic Media. Phys. Rev. Lett. 2007, 98, 123601. [Google Scholar] [CrossRef]
- Novikova, I.; Walsworth, R.L.; Xiao, Y. Electromagnetically induced transparency-based slow and stored light in warm atoms. Laser Photon. Rev. 2012, 6, 333–353. [Google Scholar] [CrossRef]
- England, D.G.; Fisher, K.A.G.; MacRae, A.M.; Bustard, P.J.; Heshami, K.; Sussman, B.J. Storage and Retrieval of THz-Bandwidth Single Photons Using a Room-Temperature Diamond Quantum Memory. Phys. Rev. Lett. 2015, 114, 053602. [Google Scholar] [CrossRef]
- Adams, C.S.; Pritchard, J.D.; Shaffer, J.P. Rydberg atom quantum technologies. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 012002. [Google Scholar] [CrossRef]
- Fan, H.Q.; Kagalwala, K.H.; Polyakov, S.V.; Migdall, A.L.; Goldschmidt, E.A. Electromagnetically induced transparency in inhomogeneously broadened solid media. Phys. Rev. A 2019, 99, 053821. [Google Scholar] [CrossRef]
- Dos Santos, F.C.D.; Martins, W.S.; Barreiro, S.; de Oliveira, R.A. Electromagnetically induced absorption free from power broadening. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 185002. [Google Scholar] [CrossRef]
- Mücke, M.; Figueroa, E.; Bochmann, J.; Hahn, C.; Murr, K.; Ritter, S.; Villas-Boas, C.J.; Rempe, G. Electromagnetically induced transparency with single atoms in a cavity. Nature 2010, 465, 755–758. [Google Scholar] [CrossRef]
- Heinze, G.; Hubrich, C.; Halfmann, T. Stopped Light and Image Storage by Electromagnetically Induced Transparency up to the Regime of One Minute. Phys. Rev. Lett. 2013, 111, 033601. [Google Scholar] [CrossRef] [PubMed]
- Berman, P.R.; Salomaa, R. Comparison between dressed-atom and bare-atom pictures in laser spectroscopy. Phys. Rev. A 1982, 25, 2667–2682. [Google Scholar] [CrossRef]
- Lu, N.; Berman, P.R. Transient probe spectra in a driven two-level atom. Phys. Rev. A 1987, 36, 3845. [Google Scholar] [CrossRef] [PubMed]
- Lu, N.; Berman, P.R.; Yodh, A.G.; Bai, Y.S.; Mossberg, T.W. Transient probe spectra in strongly driven atoms and their dependence on initial atomic conditions. Phys. Rev. A 1986, 33, 3956. [Google Scholar] [CrossRef] [PubMed]
- Harris, S.E.; Luo, Z. Preparation energy for electromagnetically induced transparency. Phys. Rev. A 1995, 52, R928–R931. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, M. Transient properties of an electromagnetically induced transparency in three-level atoms. Opt. Lett. 1995, 20, 1489. [Google Scholar] [CrossRef]
- Zhu, Y. Lasing without inversion in a @sV -type system: Transient and steady-state analysis. Phys. Rev. A 1996, 53, 2742. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y. Light amplification mechanisms in a coherently coupled atomic system. Phys. Rev. A 1997, 55, 4568. [Google Scholar] [CrossRef]
- Fang, L. An analytical model for transient evolution of EIT-AT spectrum with Rydberg atoms. Opt. Lett. 2025, 50, 1369. [Google Scholar] [CrossRef]
- Rotunno, A.P.; Robinson, A.K.; Prajapati, N. Inverse transform sampling for efficient Doppler-averaged spectroscopy simulations. AIP Adv. 2023, 13, 075218. [Google Scholar] [CrossRef]
- Artusio-Glimpse, A.; Simons, M.T.; Prajapati, N.; Holloway, C.L. Modern RF Measurements with Hot Atoms: A Technology Review of Rydberg Atom-Based Radio Frequency Field Sensors. IEEE Microw. Mag. 2022, 23, 44–56. [Google Scholar] [CrossRef]
- Leahy, C.; Hastings, J.T.; Wilt, P.M. Temperature dependence of Doppler-broadening in rubidium: An undergraduate experiment. Am. J. Phys. 1997, 65, 367–371. [Google Scholar] [CrossRef]
- Peters, T.; Wittrock, B.; Blatt, F.; Halfmann, T.; Yatsenko, L.P. Thermometry of ultracold atoms by electromagnetically induced transparency. Phys. Rev. A 2012, 85, 063416. [Google Scholar] [CrossRef]
- Javan, A.; Kocharovskaya, O.; Lee, H.; Scully, M.O. Narrowing of electromagnetically induced transparency resonance in a Doppler-broadened medium. Phys. Rev. A 2002, 66, 013805. [Google Scholar] [CrossRef]
- Finkelstein, R.; Lahad, O.; Michel, O.; Davidson, O.; Poem, E.; Firstenberg, O. Power narrowing: Counteracting Doppler broadening in two-color transitions. New J. Phys. 2019, 21, 103024. [Google Scholar] [CrossRef]
- Iftiquar, S.; Karve, G.; Natarajan, V. Subnatural linewidth for probe absorption in an electromagnetically-induced-transparency medium due to Doppler averaging. Phys. Rev. A 2008, 77, 063807. [Google Scholar] [CrossRef]
- Pack, M.V.; Camacho, R.M.; Howell, J.C. Electromagnetically induced transparency line shapes for large probe fields and optically thick media. Phys. Rev. A 2007, 76, 013801. [Google Scholar] [CrossRef]
- Meinert, F.; Basler, C.; Lambrecht, A.; Welte, S.; Helm, H. Quantitative analysis of the transient response of the refractive index to conditions of electromagnetically induced transparency. Phys. Rev. A 2012, 85, 013820. [Google Scholar] [CrossRef]
- Vemuri, G.; Agarwal, G.S.; Nageswara Rao, B.D. Sub-Doppler resolution in inhomogeneously broadened media using intense control fields. Phys. Rev. A 1996, 53, 2842. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Reynaud, S. Dressed-atom description of resonance fluorescence and absorption spectra of a multi-level atom in an intense laser beam. J. Phys. B 1977, 10, 365. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F. Drastic Slowdown of EIT Dynamics by Doppler Broadening and Its Compensation in Room-Temperature Atomic Vapor. Photonics 2025, 12, 1092. https://doi.org/10.3390/photonics12111092
Li F. Drastic Slowdown of EIT Dynamics by Doppler Broadening and Its Compensation in Room-Temperature Atomic Vapor. Photonics. 2025; 12(11):1092. https://doi.org/10.3390/photonics12111092
Chicago/Turabian StyleLi, Fang. 2025. "Drastic Slowdown of EIT Dynamics by Doppler Broadening and Its Compensation in Room-Temperature Atomic Vapor" Photonics 12, no. 11: 1092. https://doi.org/10.3390/photonics12111092
APA StyleLi, F. (2025). Drastic Slowdown of EIT Dynamics by Doppler Broadening and Its Compensation in Room-Temperature Atomic Vapor. Photonics, 12(11), 1092. https://doi.org/10.3390/photonics12111092




