A Low-Complexity Receiver-Side Lookup Table Equalization Method for High-Speed Short-Reach IM/DD Transmission Systems
Abstract
1. Introduction
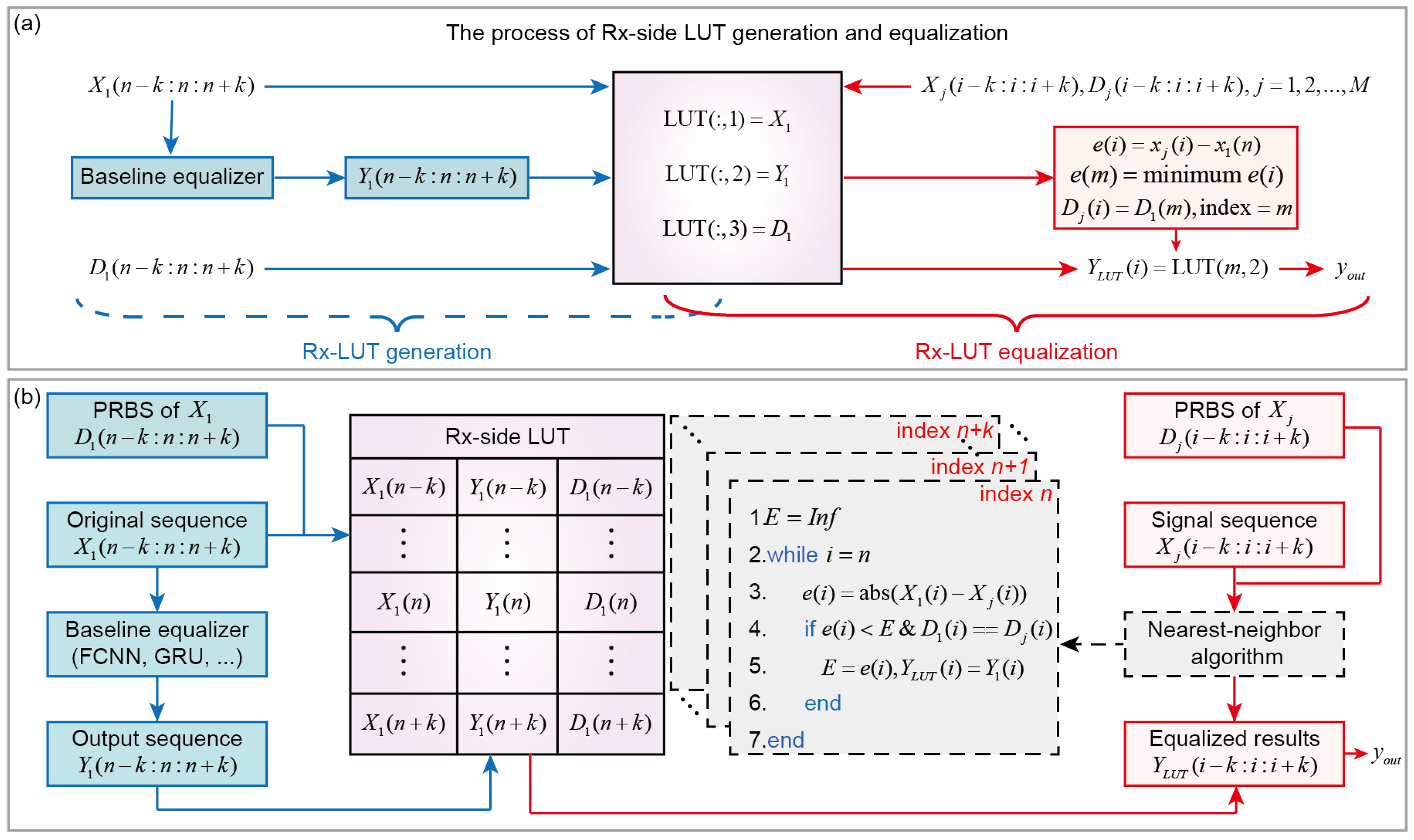
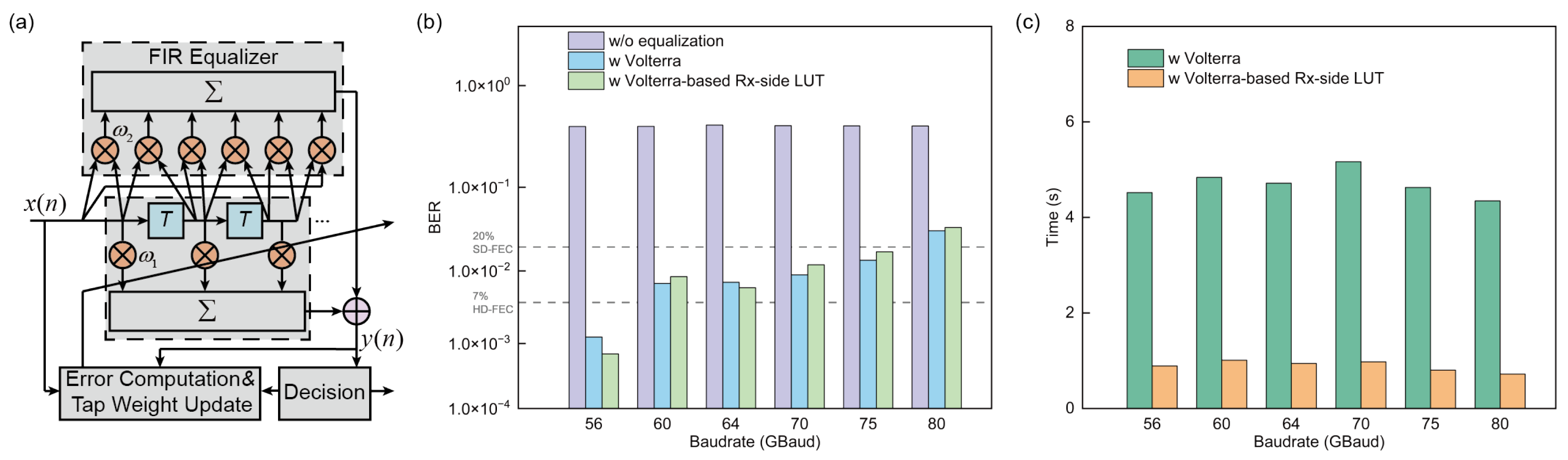
2. Working Principle of Rx-Side LUT Equalization
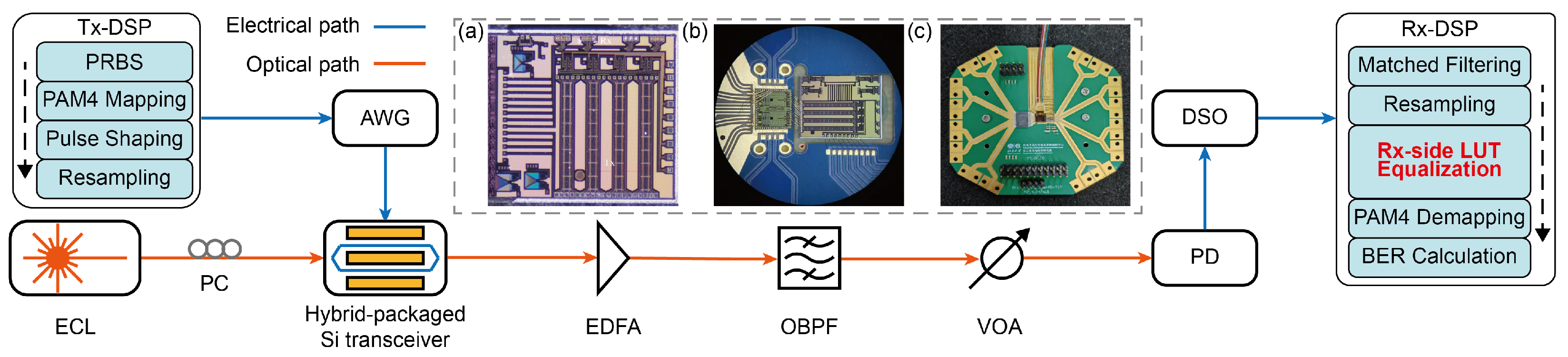
3. Experiment Setup
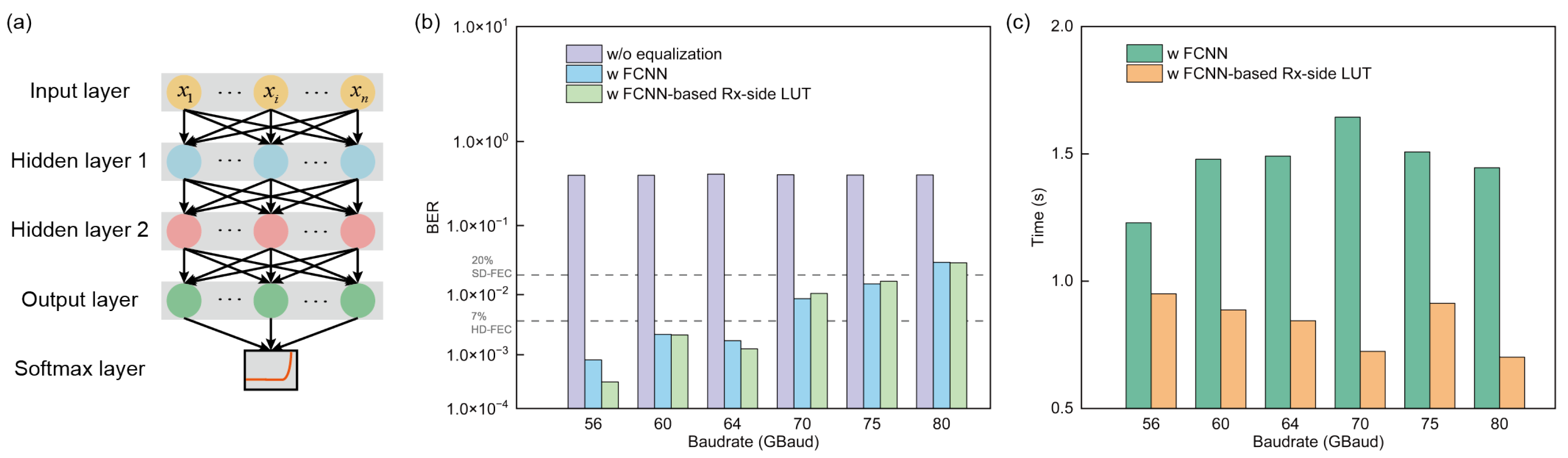
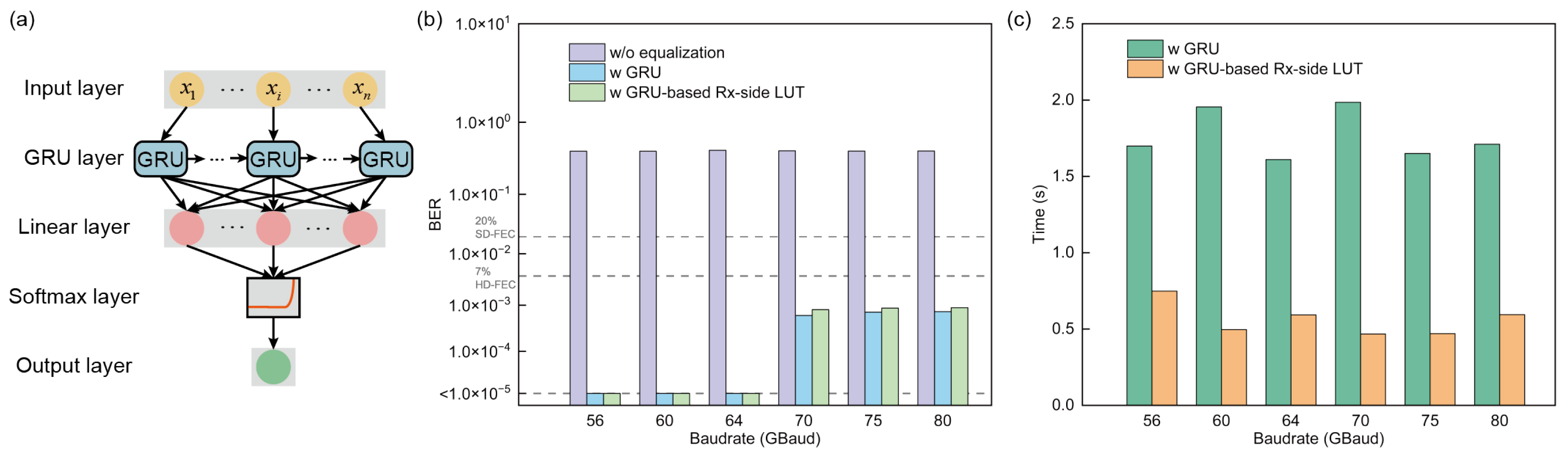
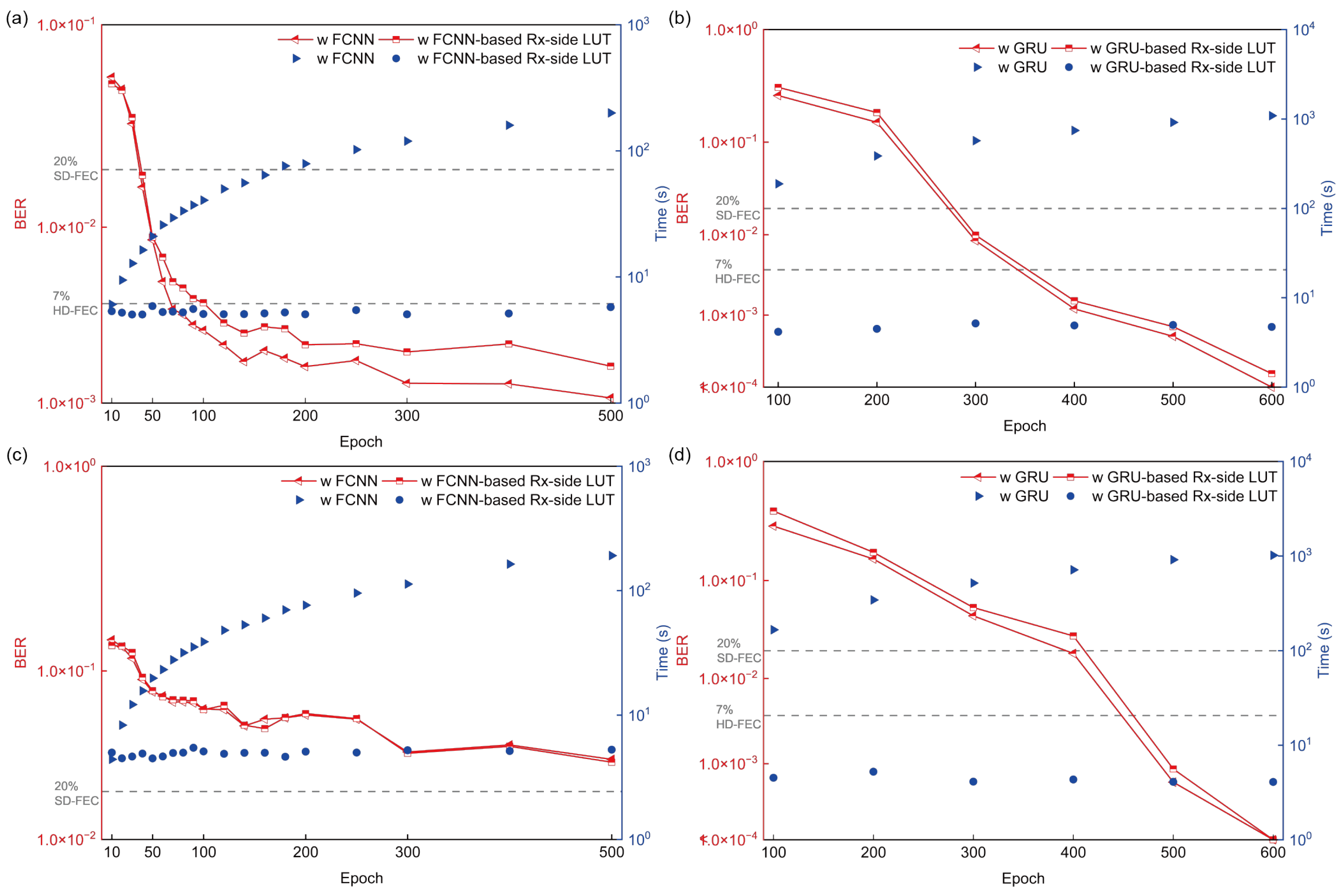
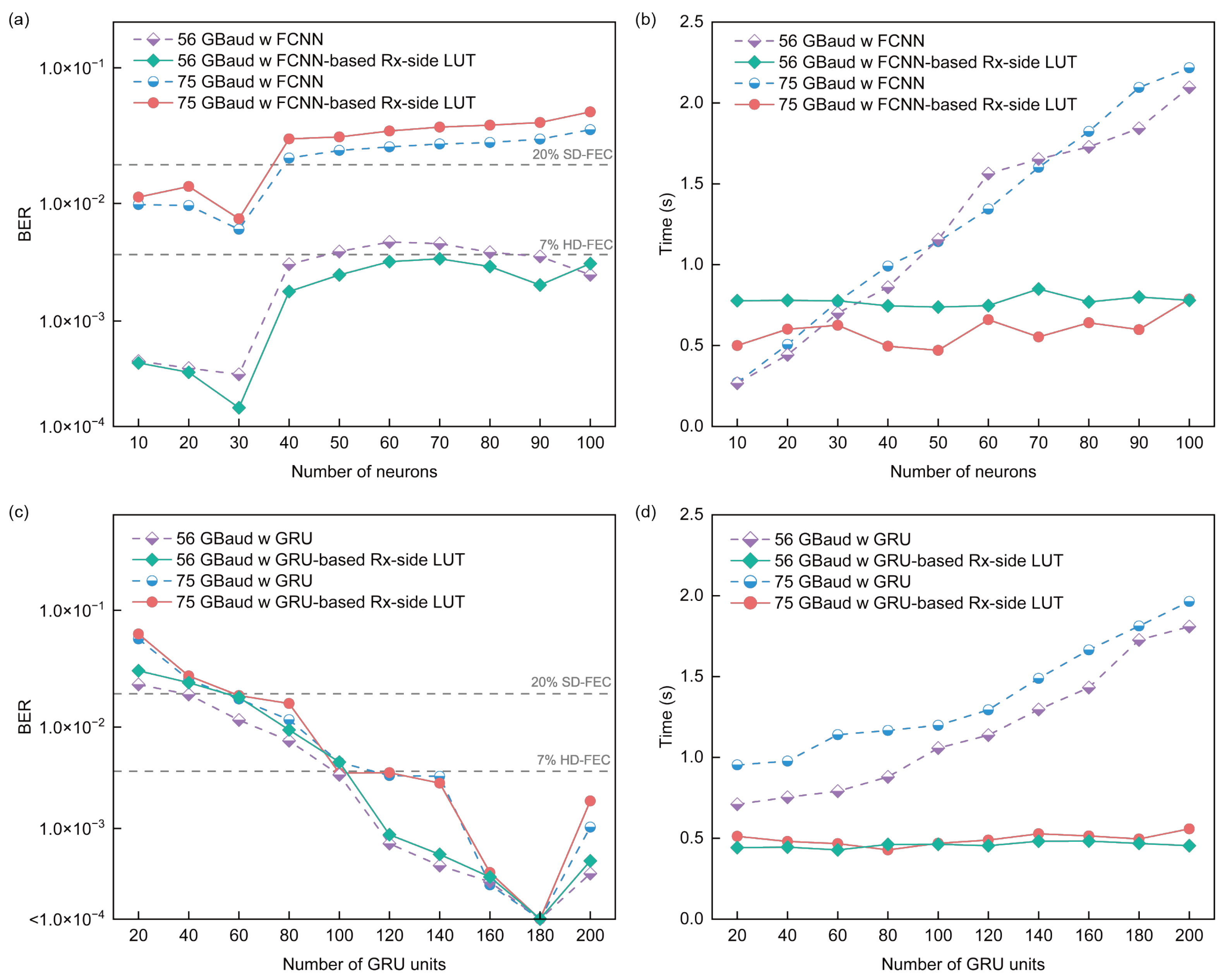
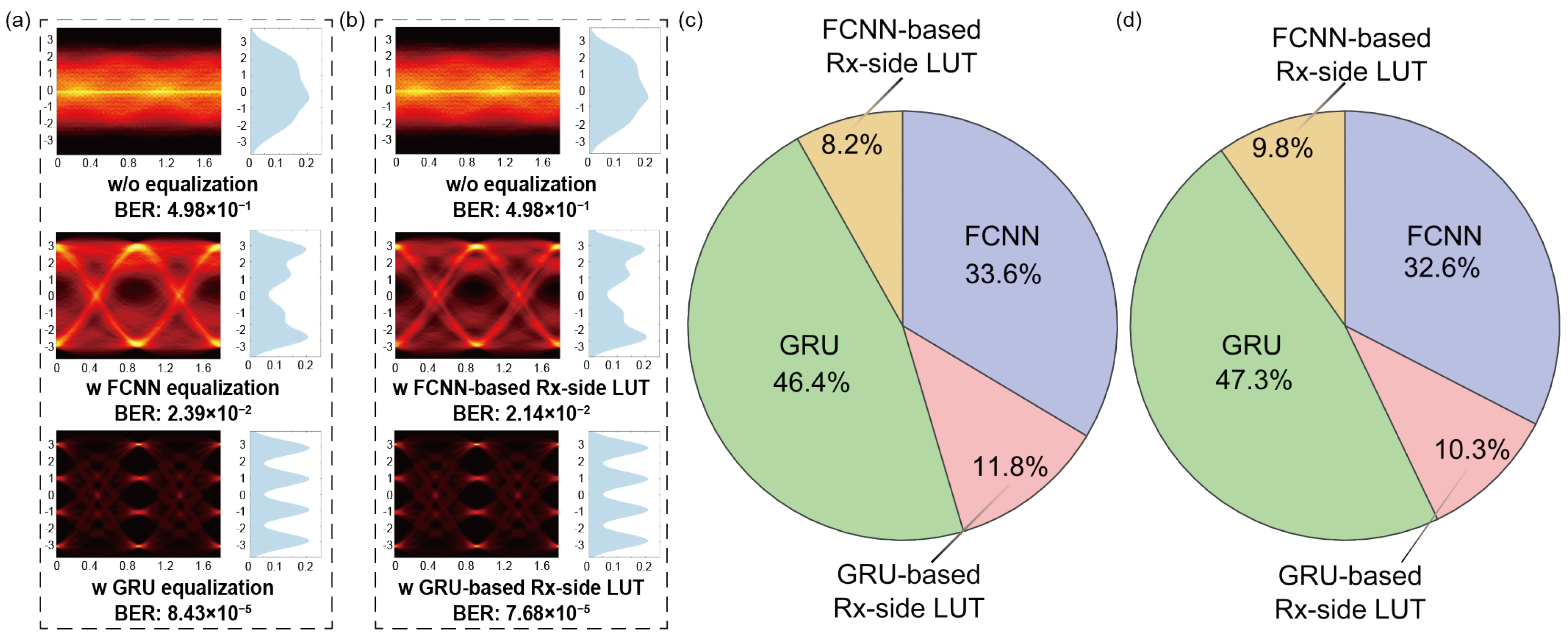
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, C.; Wang, H.; Shu, H.; Qin, J.; Wang, X. Latest Research Progress in Silicon-Based Modulators (Invited). Acta Opt. Sin. 2024, 44, 1513017. [Google Scholar] [CrossRef]
- Karar, A.S. Iterative Algorithm for Electronic Dispersion Compensation in IM/DD Systems. J. Light. Technol. 2020, 38, 698–704. [Google Scholar] [CrossRef]
- Zhong, K.; Zhou, X.; Huo, J.; Yu, C.; Lu, C.; Lau, A.P.T. Digital Signal Processing for Short-Reach Optical Communications: A Review of Current Technologies and Future Trends. J. Light. Technol. 2018, 36, 377–396. [Google Scholar] [CrossRef]
- Liu, X.; Chraplyvy, A.R.; Winzer, P.J.; Tkach, R.W.; Chandrasekhar, S. Phase-conjugated twin waves for communication beyond the Kerr nonlinearity limit. Nat. Photonics 2013, 7, 560–568. [Google Scholar] [CrossRef]
- Ros, F.D.; Gajda, A.; Silva, E.P.D.; Peczek, A.; Mai, A.; Petermann, K. Optical Phase Conjugation in a Silicon Waveguide With Lateral p-i-n Diode for Nonlinearity Compensation. J. Light. Technol. 2019, 37, 323–329. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Z.; Zhang, L.; Li, J.; Wu, H.; Li, Y.; Zeng, J.; Rao, Y. Phase-Sensitive Optical Time-Domain Reflectometry Assisted by Gated Raman Amplification. In Proceedings of the 2014 Asia Communications and Photonics Conference (ACP), Shanghai, China, 11–14 November 2014. [Google Scholar]
- Gao, S.; Li, Q.; Zhao, Y.; Wang, W.; Yao, G.; Yuan, W. MMI-Based Pseudo-Real-Value Silicon Photonic Neural Networks. In Proceedings of the 2024 Asia Communications and Photonics Conference (ACP) and International Conference on Information Photonics and Optical Communications (IPOC), Beijing, China, 2–5 November 2024. [Google Scholar]
- Li, Y.; Wang, B.; Xu, T.; Liu, S.; Xiao, Q.; Huang, C. Scalable and Energy-Efficient Photonic Neural Networks Through Convolution Compression. In Proceedings of the 2024 Asia Communications and Photonics Conference (ACP) and International Conference on Information Photonics and Optical Communications (IPOC), Beijing, China, 2–5 November 2024. [Google Scholar]
- Tseng, C.; Tseng, C.; Hwang, Y. Efficient DSP Equalization Algorithm and Architecture Designs for High Speed Serial Links. In Proceedings of the 2024 International Conference on Consumer Electronics-Taiwan (ICCE-Taiwan), Taichung, Taiwan, 9–11 July 2024. [Google Scholar]
- Chen, Y.; Tseng, C.; Lin, D. Optimizing Equalizations of FFE, CTLE, and DFE Jointly Through a Single Pulse Response. IEEE Trans. Signal Power Integr. 2025, 4, 88–95. [Google Scholar] [CrossRef]
- Peddanarappagari, K.V.; Brandt-Pearce, M. Volterra series approach for optimizing fiber-optic communications system designs. J. Light. Technol. 1998, 16, 2046–2055. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, J.; Zhou, G.; Lau, A.P.T.; Lu, C. C-Band 112-Gb/s PAM-4 Transmission over 50-km SSMF Using Absolute-Term Based Nonlinear FFE-DFE. In Proceedings of the 2021 Asia Communications and Photonics Conference (ACP), Shanghai, China, 24–27 October 2021. [Google Scholar]
- Chen, J.; Huang, Y.; Li, Y.; Li, H.; Li, Y.; Song, Y.; Zhang, Q.; Zhang, J. High-performance low-complexity Volterra decision feedback equalizer based on FPGA for C-Band PAM-4 transmission. Opt. Fiber Technol. 2021, 64, 1068–5200. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, W.; Zou, D.; Ni, W.; Luo, D.; Li, F. Real-Valued Neural Network Nonlinear Equalization for Long-Reach PONs Based on SSB Modulation. IEEE Photonics Technol. Lett. 2023, 35, 167–170. [Google Scholar] [CrossRef]
- Ji, Y.; Gu, R.; Yang, Z.; Li, J.; Li, H.; Zhang, M. Artificial intelligence-driven autonomous optical networks: 3S architecture and key technologies. Sci. China Inf. Sci. 2020, 63, 160301. [Google Scholar] [CrossRef]
- Niu, W.; Yinear, H.; Chi, N. Support vector machine based machine learning method for GS 8QAM constellation classification in seamless integrated fiber and visible light communication system. Sci. China Inf. Sci. 2019, 63, 202306. [Google Scholar] [CrossRef]
- Gou, P.; Yu, J. A nonlinear ANN equalizer with mini-batch gradient descent in 40Gbaud PAM-8 IM/DD system. Opt. Fiber Technol. 2018, 46, 113–117. [Google Scholar] [CrossRef]
- Chuang, C.; Wei, C.; Lin, T.; Chi, K.; Liu, L.; Shi, J. Employing Deep Neural Network for High Speed 4-PAM Optical Interconnect. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017. [Google Scholar]
- Dong, Y.; Shi, Y.; Zou, X.; Pan, W.; Yan, L. Comparison of neural network equalizers for IMDD optical transmission. In Proceedings of the 2024 Asia Communications and Photonics Conference (ACP) and International Conference on Information Photonics and Optical Communications (IPOC), Beijing, China, 2–5 November 2024. [Google Scholar]
- Lu, X.; Lu, C.; Yu, W.; Qiao, L.; Liang, S.; Lau, A.P.T.; Chi, N. Memory-controlled deep LSTM neural network post-equalizer used in high-speed PAM VLC system. Opt. Express 2019, 27, 7822–7833. [Google Scholar] [CrossRef]
- Li, C.; Chen, X.; Shi, Y. An Event Recognition Method for a ϕ-OTDR System Based on CNN-BiGRU Network Model with Attention. Photonics 2025, 12, 313. [Google Scholar] [CrossRef]
- Wang, K.; Wang, C.; Zhang, J.; Chen, Y.; Yu, J. Mitigation of SOA-Induced Nonlinearity with the Aid of Deep Learning Neural Networks. J. Light. Technol. 2022, 40, 979–986. [Google Scholar] [CrossRef]
- Xu, Z.; Ji, H.; Yang, Y.; Qiao, G.; Wu, Q.; Lu, W.; Liu, L.; Wang, S.; Liang, J.; Li, J.; et al. Quantization of Recurrent Neural Network for Low-Complexity High-Speed IM/DD System Equalization Based on Neuron Clustering. In Proceedings of the 2023 Asia Communications and Photonics Conference/2023 International Photonics and Optoelectronics Meetings (ACP/POEM), Wuhan, China, 4–7 November 2023. [Google Scholar]
- Freire, P.; Srivallapanondh, S.; Spinnler, B.; Napoli, A.; Costa, N.; Prilepsky, J.E.; Turitsyn, S.K. Computational complexity optimization of neural network-based equalizers in digital signal processing: A comprehensive approach. J. Light. Technol. 2024, 42, 4177–4201. [Google Scholar] [CrossRef]
- Nojehdeh, M.E.; Aksoy, L.; Altun, M. Efficient Hardware Implementation of Artificial Neural Networks Using Approximate Multiply-Accumulate Blocks. In Proceedings of the 2020 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Limassol, Cyprus, 6–8 July 2020. [Google Scholar]
- Freire, P.J.; Abode, D.; Prilepsky, J.E.; Costa, N.; Spinnler, B.; Napoli, A.; Turitsyn, S.K. Transfer Learning for Neural Networks-Based Equalizers in Coherent Optical Systems. J. Light. Technol. 2021, 39, 6733–6745. [Google Scholar] [CrossRef]
- Liu, B.; Bluemm, C.; Calabrò, S.; Li, B.; Schlichtmann, U. Area-Efficient Neural Network CD Equalizer for 4 × 200 Gb/s PAM4 CWDM4 Systems. In Proceedings of the 2023 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 5–9 March 2023. [Google Scholar]
- Du, X.; Ma, X.; Zeng, Z.; Zhang, R.; Xie, J. Transformer Fault Sample Equalization Method Based on Reduced Dimensional Generative Adversarial Networks. In Proceedings of the 2024 4th International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), Hangzhou, China, 5–7 July 2024. [Google Scholar]
- Zheng, J.; Wu, J.; Xu, S.; Du, S.; Li, Y. Disparity Distribution Equalization: An Effective Data Enhancement for Stereo Matching. In Proceedings of the 2024 6th International Conference on Pattern Analysis and Intelligent Systems (PAIS), El Oued, Algeria, 24–25 April 2024. [Google Scholar]
- Ren, X.; Liu, J.; Huang, X.; Zhang, Q.; Zhang, J.; Qiu, K. Meta-learning Accelerated Bi-LSTM for Fiber Nonlinearity Compensation. In Proceedings of the 2023 21st International Conference on Optical Communications and Networks (ICOCN), Qufu, China, 31 July–3 August 2023. [Google Scholar]
- Yadav, G.S.; Chuang, C.; Feng, K.; Chen, J.; Chen, Y. Computation efficient sparse DNN nonlinear equalization for IM/DD 112 Gbps PAM4 inter-data center optical interconnects. Opt. Lett. 2021, 46, 1999–2002. [Google Scholar] [CrossRef]
- Freire, P.J.; Napoli, A.; Spinnler, B.; Anderson, M.; Ron, D.A.; Schairer, W.; Bex, T.; Costa, N.; Turitsyn, S.K.; Prilepsky, J.E. Reducing Computational Complexity of Neural Networks in Optical Channel Equalization: From Concepts to Implementation. J. Light. Technol. 2023, 41, 4557–4581. [Google Scholar] [CrossRef]
- Toffola, L.; Pradel, M.; Gross, T.R. Performance problems you can fix: A dynamic analysis of memoization opportunities. Acm Sigplan Not. 2015, 50, 607–622. [Google Scholar] [CrossRef]
- Mohaidat, T.; Khalil, K. A Survey on Neural Network Hardware Accelerators. IEEE Trans. Artif. Intell. 2024, 5, 3801–3822. [Google Scholar] [CrossRef]
- Huang, Y.; Cheng, Y.; Bapna, A.; Firat, O.; Chen, M.X.; Chen, D.; Lee, H.; Ngiam, J.; Le, Q.V.; Wu, Y.; et al. GPipe: Efficient Training of Giant Neural Networks using Pipeline Parallelism. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Yu, J.; Wei, Y. Digital Signal Processing for High-Speed THz Communications. Chin. J. Electron. 2022, 31, 534–546. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, Z.; Zhu, Y.; Ji, T.; Ji, H.; Yang, Y.; Liang, J.; Cheng, C.; Qiao, G.; He, Z.; et al. Beyond 200-Gb/s O-band intensity modulation and direct detection optics with joint look-up-table-based predistortion and digital resolution enhancement for low-cost data center interconnects. Adv. Photonics Nexus 2024, 3, 036007. [Google Scholar] [CrossRef]
- Zhang, J.; Gou, P.; Kong, M.; Fang, K.; Xiao, J.; Zhang, Q.; Xin, X.; Yu, J. PAM-8 IM/DD transmission based on modified lookup table nonlinear predistortion. IEEE Photonics J. 2018, 10, 7903709. [Google Scholar] [CrossRef]
- Lu, J.; Sun, Y.; Qin, J.; Tan, J.; Wang, Q.; Shi, J.; Chen, L.; Li, Y.; Sun, J. Receiver-side Lookup-Table-Assisted Equalization for PAM4 IM/DD Transmission Systems. In Proceedings of the 2024 Asia Communications and Photonics Conference (ACP) and International Conference on Information Photonics and Optical Communications (IPOC), Beijing, China, 2–5 November 2024. [Google Scholar]
- Xie, F.; Huang, X.; Liu, S.; Tang, D.; Wang, Z.; Qiao, Y. Multiplication-Free Equalization Schemes for 244-Gbps PAM-4 Transmission. In Proceedings of the 2024 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 24–28 March 2024. [Google Scholar]
- Sang, B.; Zhou, W.; Tan, Y.; Kong, M.; Wang, C.; Wang, M.; Zhao, L.; Zhang, J.; Yu, J. Low Complexity Neural Network Equalization Based on Multi-Symbol Output Technique for 200+ Gbps IM/DD Short Reach Optical System. J. Light. Technol. 2022, 40, 2890–2900. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Wang, X.; Xu, H.; Li, C.; Xin, X. Bi-directional gated recurrent unit neural network based nonlinear equalizer for coherent optical communication system. Opt. Express 2021, 29, 5923–5932. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Ming, J.; Song, J.; He, H.; Mu, Y.; Wen, Y.; Li, Z.; Wang, R.; Tian, B.; Dong, Z.; et al. Complexity Reduced MLSE Equalization Assisted with Pattern-Integrated LUT for Bandwidth Efficient PAM-4 IM/DD Interconnection. J. Light. Technol. 2025, 43, 8181–8190. [Google Scholar] [CrossRef]
- Han, C.; Zheng, Z.; Shu, H.; Jin, M.; Qin, J.; Chen, R.; Tao, Y.; Shen, B.; Bai, B.; Yang, F.; et al. Slow-light silicon modulator with 110-GHz bandwidth. Sci. Adv. 2023, 9, 5339. [Google Scholar] [CrossRef]
- Hu, S.; Zheng, T.; Bian, C.; Yang, X.; Sun, X.; Zhu, Z.; Gou, Y.; Meng, Y.; Zhang, J.; Ge, J.; et al. FPGA Implementation for 24.576-Gbit/s Optical PAM4 Signal Transmission with MLP-Based Digital Pre-Distortion. Sensors 2024, 24, 7872. [Google Scholar] [CrossRef]



| Equalization | Execution Time (s) | Percentage of Time Reduction (%) |
|---|---|---|
| CNN | 0.328710 | - |
| CNN-based Rx-side LUT | 0.193491 | 41.1 |
| Transformer | 0.351095 | - |
| Transformer-based Rx-side LUT | 0.226950 | 35.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Sun, Y.; Qin, J.; Han, C.; Shi, J.; Chen, L.; Shi, J.; Zheng, J.; Jiang, S.; Zhang, C.; et al. A Low-Complexity Receiver-Side Lookup Table Equalization Method for High-Speed Short-Reach IM/DD Transmission Systems. Photonics 2025, 12, 1091. https://doi.org/10.3390/photonics12111091
Lu J, Sun Y, Qin J, Han C, Shi J, Chen L, Shi J, Zheng J, Jiang S, Zhang C, et al. A Low-Complexity Receiver-Side Lookup Table Equalization Method for High-Speed Short-Reach IM/DD Transmission Systems. Photonics. 2025; 12(11):1091. https://doi.org/10.3390/photonics12111091
Chicago/Turabian StyleLu, Junde, Yu Sun, Jun Qin, Changhao Han, Jie Shi, Lanling Chen, Jianyu Shi, Jiaxin Zheng, Shuo Jiang, Chi Zhang, and et al. 2025. "A Low-Complexity Receiver-Side Lookup Table Equalization Method for High-Speed Short-Reach IM/DD Transmission Systems" Photonics 12, no. 11: 1091. https://doi.org/10.3390/photonics12111091
APA StyleLu, J., Sun, Y., Qin, J., Han, C., Shi, J., Chen, L., Shi, J., Zheng, J., Jiang, S., Zhang, C., Yang, Y., Li, Y., Sun, J., & Lu, G.-W. (2025). A Low-Complexity Receiver-Side Lookup Table Equalization Method for High-Speed Short-Reach IM/DD Transmission Systems. Photonics, 12(11), 1091. https://doi.org/10.3390/photonics12111091





