Fano Resonances in Location-Dependent Terahertz Stub Waveguide
Abstract
1. Introduction
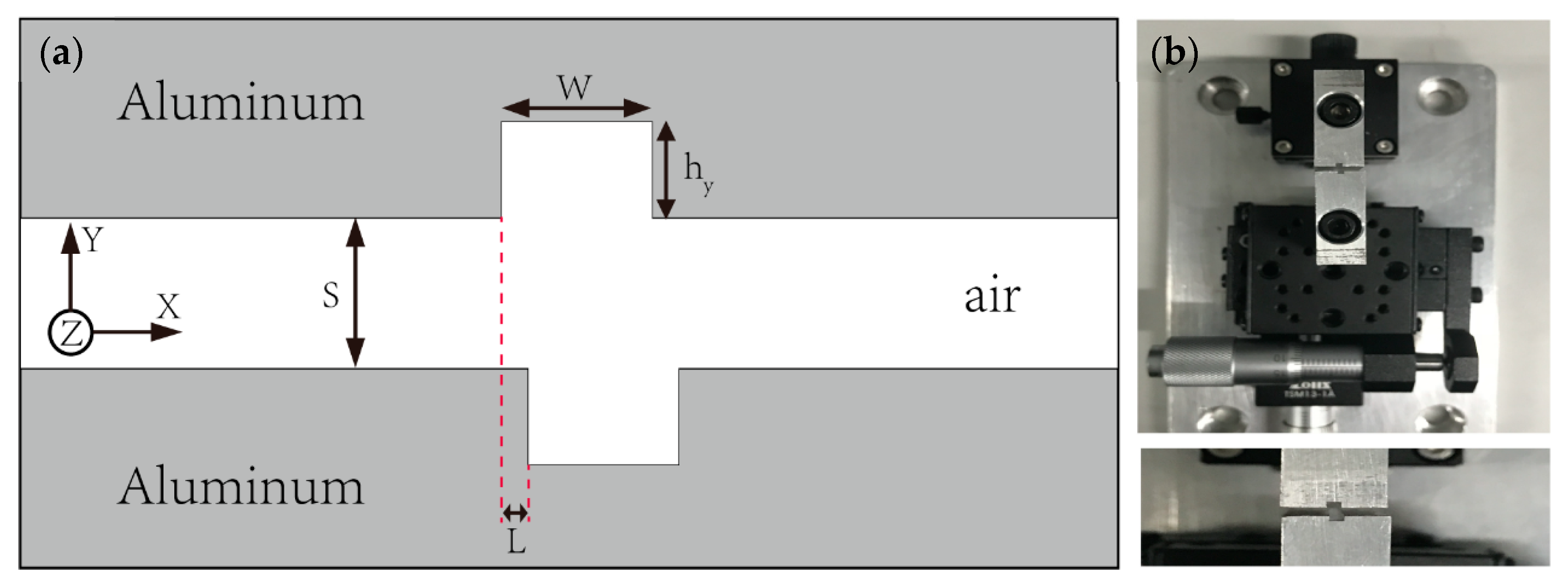
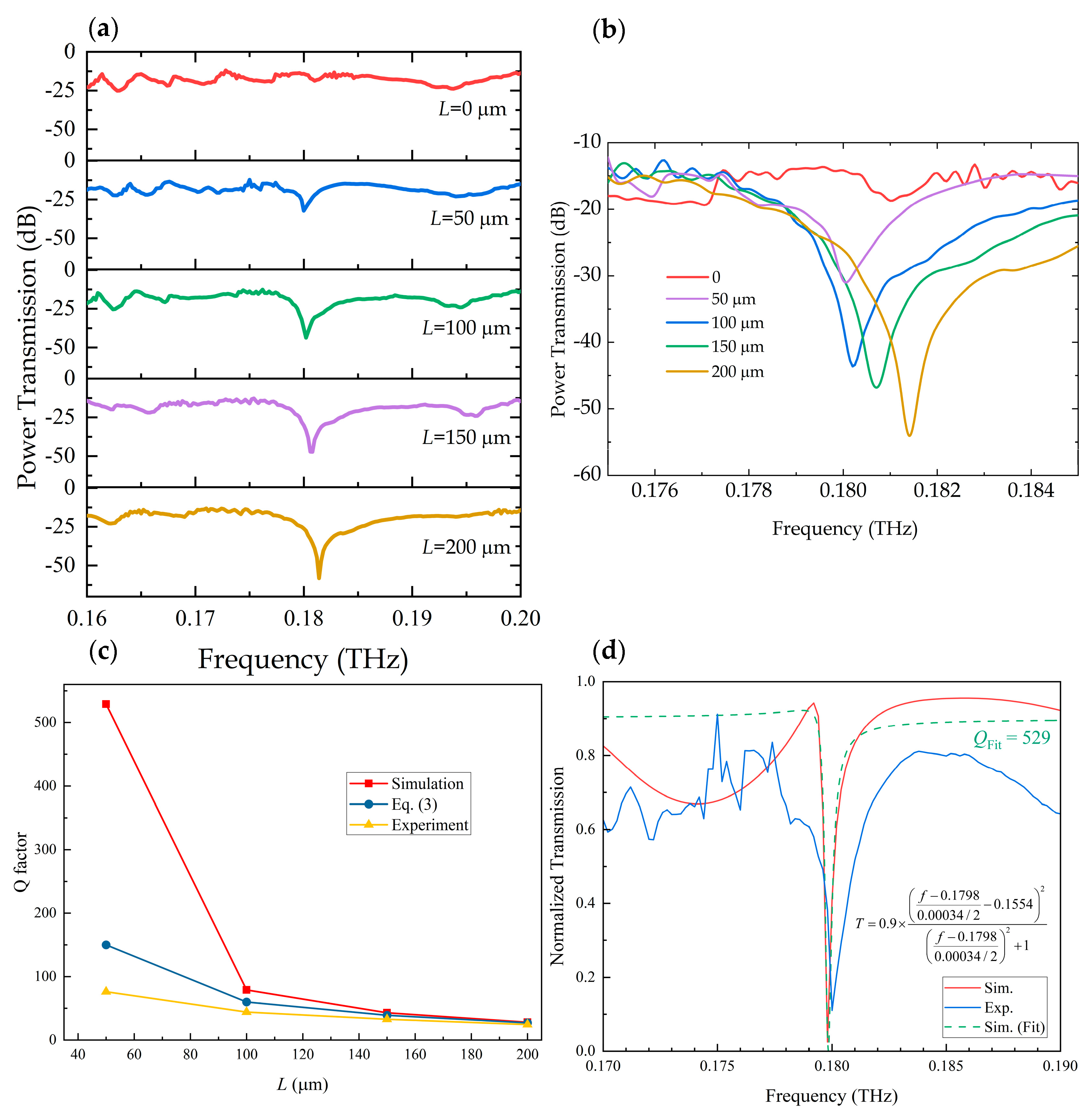
2. Theory and Simulations
3. Experiments
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fano, U. Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 2010, 9, 707–715. [Google Scholar] [CrossRef]
- Christ, A.; Tikhodeev, S.G.; Gippius, N.A.; Kuhl, J.; Giessen, H. Waveguide-Plasmon Polaritons: Strong Coupling of Photonic and Electronic Resonances in a Metallic Photonic Crystal Slab. Phys. Rev. Lett. 2003, 91, 183901. [Google Scholar] [CrossRef]
- Bingham, A.L.; Grischkowsky, D. Terahertz two-dimensional high-Q photonic crystal waveguide cavities. Opt. Lett. 2008, 33, 348–350. [Google Scholar] [CrossRef]
- Fedotov, V.A.; Rose, M.; Prosvirnin, S.L.; Papasimakis, N.; Zheludev, N.I. Sharp trapped-mode resonances in planar metamaterials with a broken structural symmetry. Phys. Rev. Lett. 2007, 99, 147401. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Rockstuhl, C.; Lederer, F.; Zhang, W. Coupling between a dark and a bright eigenmode in a terahertz metamaterial. Phys. Rev. B 2009, 79, 085111. [Google Scholar] [CrossRef]
- Singh, R.; Naib, I.A.I.A.; Yang, Y.; Chowdhury, D.R.; Cao, W.; Rockstuhl, C.; Ozaki, T.; Morandotti, R.; Zhang, W. Observing metamaterial induced transparency in individual Fano resonators with broken symmetry. Appl. Phys. Lett. 2011, 99, 201107. [Google Scholar] [CrossRef]
- Chen, L.; Xu, N.; Singh, L.; Cui, T.; Singh, R.; Zhu, Y.; Zhang, W. Defect-Induced Fano Resonances in Corrugated Plasmonic Metamaterials. Adv. Opt. Mater. 2017, 5, 1600960. [Google Scholar] [CrossRef]
- Chen, L.; Wei, Y.M.; Zang, X.F.; Zhu, Y.M.; Zhuang, S.L. Excitation of dark multipolar plasmonic resonances at terahertz frequencies. Sci. Rep. 2016, 6, 22027. [Google Scholar] [CrossRef]
- Genet, C.; van Exter, M.P.; Woerdman, J.P. Fano-type interpretation of red shifts and red tails in hole array transmission spectra. Opt. Commun. 2003, 225, 331–336. [Google Scholar] [CrossRef]
- García-Vidal, F.J.; Martín-Moreno, L.; Ebbesen, T.W.; Kuipers, L. Light passing through subwavelength apertures. Rev. Mod. Phys. 2010, 82, 729. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, Y.M.; Zang, X.F.; Cai, B.; Li, Z.; Xie, L.; Zhuang, S.L. Mode splitting transmission effect of surface wave excitation through a metal hole array. Light Sci. Appl. 2013, 2, e60. [Google Scholar] [CrossRef]
- Fan, J.A.; Wu, C.; Bao, K.; Bao, J.; Bardhan, R.; Halas, N.J.; Manoharan, V.N.; Nordlander, P.; Shvets, G.; Capasso, F. Self-assembled plasmonic nanoparticle clusters. Science 2010, 328, 1135. [Google Scholar] [CrossRef]
- Chuntonov, L.; Haran, G. Trimeric plasmonic molecules: The role of symmetry. Nano Lett. 2011, 11, 2440–2445. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Flach, S.; Kivshar, Y.S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257–2298. [Google Scholar] [CrossRef]
- Hayashi, S.; Nesterenko, D.V.; Rahmouni, A.; Sekkat, Z. Observation of Fano line shapes arising from coupling between surface plasmon polariton and waveguide modes. Appl. Phys. Lett. 2016, 108, 051101. [Google Scholar] [CrossRef]
- Sekkat, Z.; Hayashi, S.; Nesterenko, D.V.; Rahmouni, A.; Refki, S.; Ishitobi, H.; Inouye, Y.; Kawata, S. Plasmonic coupled modes in metal-dielectric multilayer structures: Fano resonance and giant field enhancement. Opt. Express 2016, 24, 20080. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, S.; Nesterenko, D.V.; Rahmouni, A.; Sekkat, Z. Polarization effects in light-tunable Fano resonance in metal-dielectric multilayer structures. Phys. Rev. B 2017, 95, 165402. [Google Scholar] [CrossRef]
- Qi, J.; Chen, Z.; Chen, J.; Li, Y.; Qiang, W.; Xu, J.; Sun, Q. Independently tunable double Fano resonances in asymmetric MIM waveguide structure. Opt. Express 2014, 22, 14688. [Google Scholar] [CrossRef]
- Yang, J.; Song, X.; Yang, S.; Luna, C.; Li, Y. Independently controllable multiple Fano resonances in side-coupled MDM structure and its applications for sensing and wavelength demultiplexing. J. Phys. D Appl. Phys. 2017, 50, 325107. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Jiao, R.; Wang, L.; Duan, G.; Yu, L. Fano resonances based on multimode and degenerate mode interference in plasmonic resonator system. Opt. Express 2017, 25, 3525. [Google Scholar] [CrossRef]
- Chen, L.; Song, Y.; Lim, D.C.Y.; Zhu, Y.; Zhuang, S.; Singh, R. Biochemical sensing with terahertz microfluidics: Recent progress and future prospects. Trends Anal. Chem. 2025, 193, 118416. [Google Scholar] [CrossRef]
- Lyu, J.; Huang, L.; Chen, L.; Zhu, Y.; Zhuang, S. Review on the terahertz metasensor: From featureless refractive index sensing to molecular identification. Photonics Res. 2024, 12, 194–217. [Google Scholar] [CrossRef]
- Ma, S.; Fan, Y.; Chen, L.; Zhao, C.; Sun, J.; Wang, F.; Lei, D.; Chen, S.; Wang, P.; Zhu, Y.; et al. Electrically controlled real-time terahertz microladder integrated with VO2 patches for broadband holographic encryption. Adv. Photonics 2025, 7, 066003. [Google Scholar] [CrossRef]
- Gao, J.; Wang, X.; Chen, Y.; Chen, T.; Qi, Y.; Yang, H.; Zheng, X. Multiple Fano resonances by MIM waveguide coupling whispering gallery mode resonator and application in Refractive index sensing. Phys. Scr. 2024, 99, 055554. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, S.; Cao, H. Fano Resonant Sensing in MIM Waveguide Structures Based on Multiple Circular Split-Ring Resonant Cavities. Micromachines 2025, 16, 183. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Tian, J.; Yang, R. Study of Fano resonance and its application in MIM waveguide using a k-shaped resonator. Opt Quant. Electron. 2023, 55, 75. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Chen, J.; Rohimah, S.; Tian, H.; Wang, J. Independently tunable triple Fano resonances based on MIM waveguide structure with a semi-ring cavity and its sensing characteristics. Opt. Express 2021, 29, 20829–20838. [Google Scholar] [CrossRef]
- Mendis, R.; Grischkowsky, D. Undistorted guided wave propagation of sub-picosecond THz pulses. Opt. Lett. 2001, 26, 846–848. [Google Scholar] [CrossRef]
- Mendis, R.; Mittleman, D.M. An investigation of the lowest-order transverse-electric (TE1) mode of the parallel-plate waveguide for THz pulse propagation. J. Opt. Soc. Am. B 2009, 26, A6–A13. [Google Scholar] [CrossRef]
- Reichel, K.S.; Iwaszczuk, K.; Jepsen, P.U.; Mendis, R.; Mittleman, D.M. In situ spectroscopic characterization of a terahertz resonant cavity. Optica 2014, 1, 272–275. [Google Scholar] [CrossRef]
- Deibel, J.A.; Escarra, M.; Berndsen, N.; Wang, K.; Mittleman, D.M. Finite-Element Method Simulations of Guided Wave Phenomena at Terahertz Frequencies. Proc. IEEE 2007, 95, 1624–1640. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric Metasurfaces with High-Q Resonances Governed by Bound States in the Continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef]
- Li, S.; Zhou, C.; Liu, T.; Xiao, S. Symmetry-protected bound states in the continuum supported by all-dielectric metasurfaces. Phys. Rev. A 2019, 100, 063803. [Google Scholar] [CrossRef]
- Zhou, C.; Zhou, M.; Fu, Z.; He, H.; Deng, Z.L.; Xiang, H.; Chen, X.; Lu, W.; Li, G.; Han, D. Ultrahigh-Q Quasi-BICs via Precision-Controlled Asymmetry in Dielectric Metasurfaces. Nano Lett. 2025, 25, 5916–5924. [Google Scholar] [CrossRef] [PubMed]
- Lim, W.X.; Manjappa, M.; Pitchappa, P.; Singh, R. Shaping High Q Planar Fano Resonant Metamaterials toward Futuristic Technologies. Adv. Opt. Mater. 2018, 6, 1800502. [Google Scholar] [CrossRef]
- Available online: https://www.hasco-inc.com/content/Waveguide/Waveguide_Straight_Sections/HWSS05-1.0-ER_Waveguide_WR-5_1-Inch_Straight_Section_140_to_220_GHz_Datasheet.pdf (accessed on 27 October 2025).
- Tanaka, T.; Akazawa, M.; Sano, E.; Tanaka, M.; Miyamaru, F.; Hangyo, M. Transmission Characteristics through Two-Dimensional Periodic Hole Arrays Perforated in Perfect Conductors. Jpn. J. Appl. Phys. 2006, 45, 4058. [Google Scholar] [CrossRef]
- Wang, B.X.; Duan, G.Y.; Lv, W.Z.; Tao, Y.; Xiong, H.; Zhang, D.Q.; Yang, G.F.; Shu, F.Z. Design and experimental realization of triple-band electromagnetically induced transparency terahertz metamaterials employing two big-bright modes for sensing applications. Nanoscale 2023, 15, 18435–18446. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Ma, S.; Li, H.; Wang, Y.; Zhang, D.; Chen, L.; Zhu, Y. Fano Resonances in Location-Dependent Terahertz Stub Waveguide. Photonics 2025, 12, 1088. https://doi.org/10.3390/photonics12111088
Li Y, Ma S, Li H, Wang Y, Zhang D, Chen L, Zhu Y. Fano Resonances in Location-Dependent Terahertz Stub Waveguide. Photonics. 2025; 12(11):1088. https://doi.org/10.3390/photonics12111088
Chicago/Turabian StyleLi, Yanrui, Shuxiang Ma, Hongguang Li, Yuanbo Wang, Deng Zhang, Lin Chen, and Yiming Zhu. 2025. "Fano Resonances in Location-Dependent Terahertz Stub Waveguide" Photonics 12, no. 11: 1088. https://doi.org/10.3390/photonics12111088
APA StyleLi, Y., Ma, S., Li, H., Wang, Y., Zhang, D., Chen, L., & Zhu, Y. (2025). Fano Resonances in Location-Dependent Terahertz Stub Waveguide. Photonics, 12(11), 1088. https://doi.org/10.3390/photonics12111088






