Tunable Filtering via Lossy Mode Resonance in Integrated Photonics
Abstract
1. Introduction
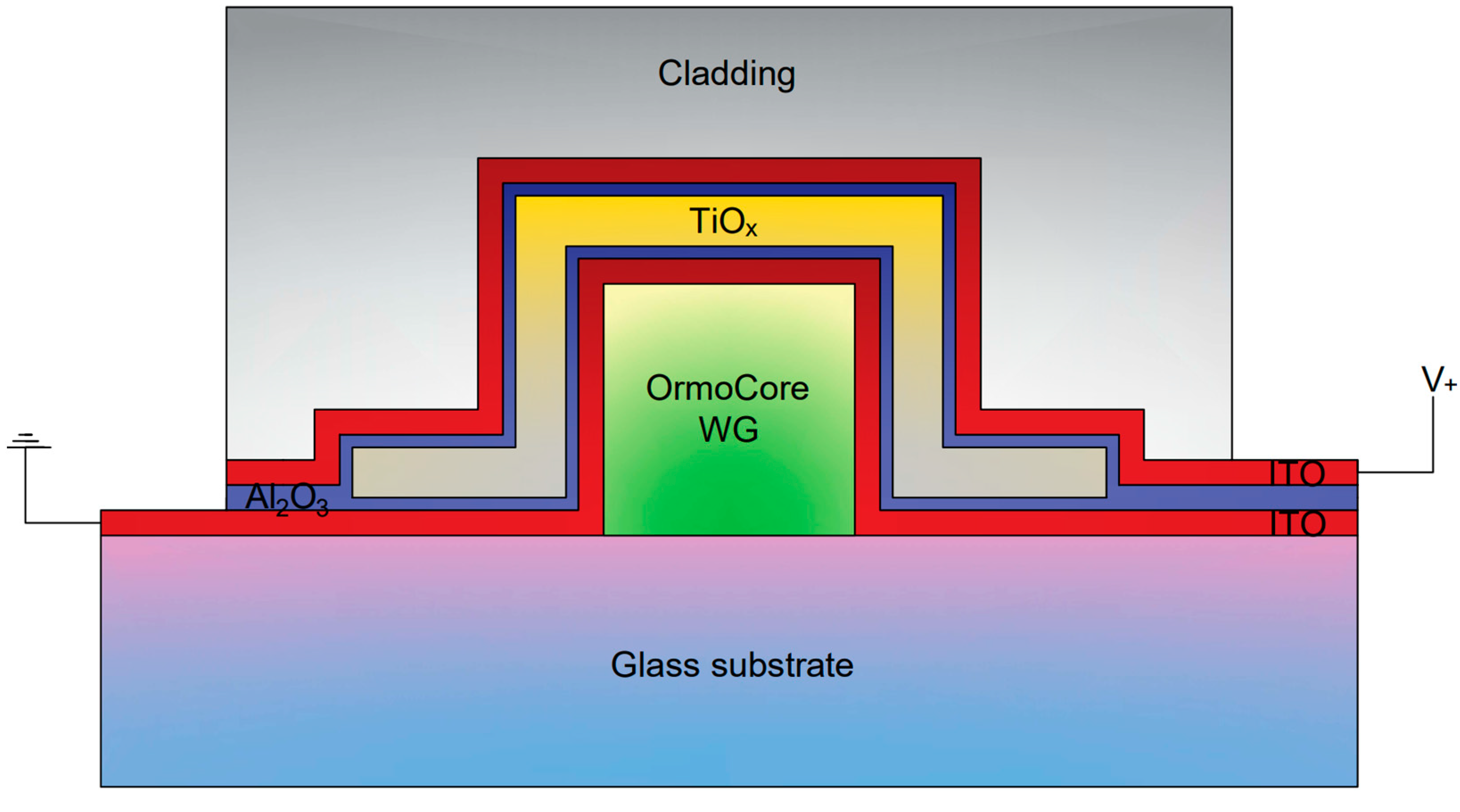
2. Materials and Methods
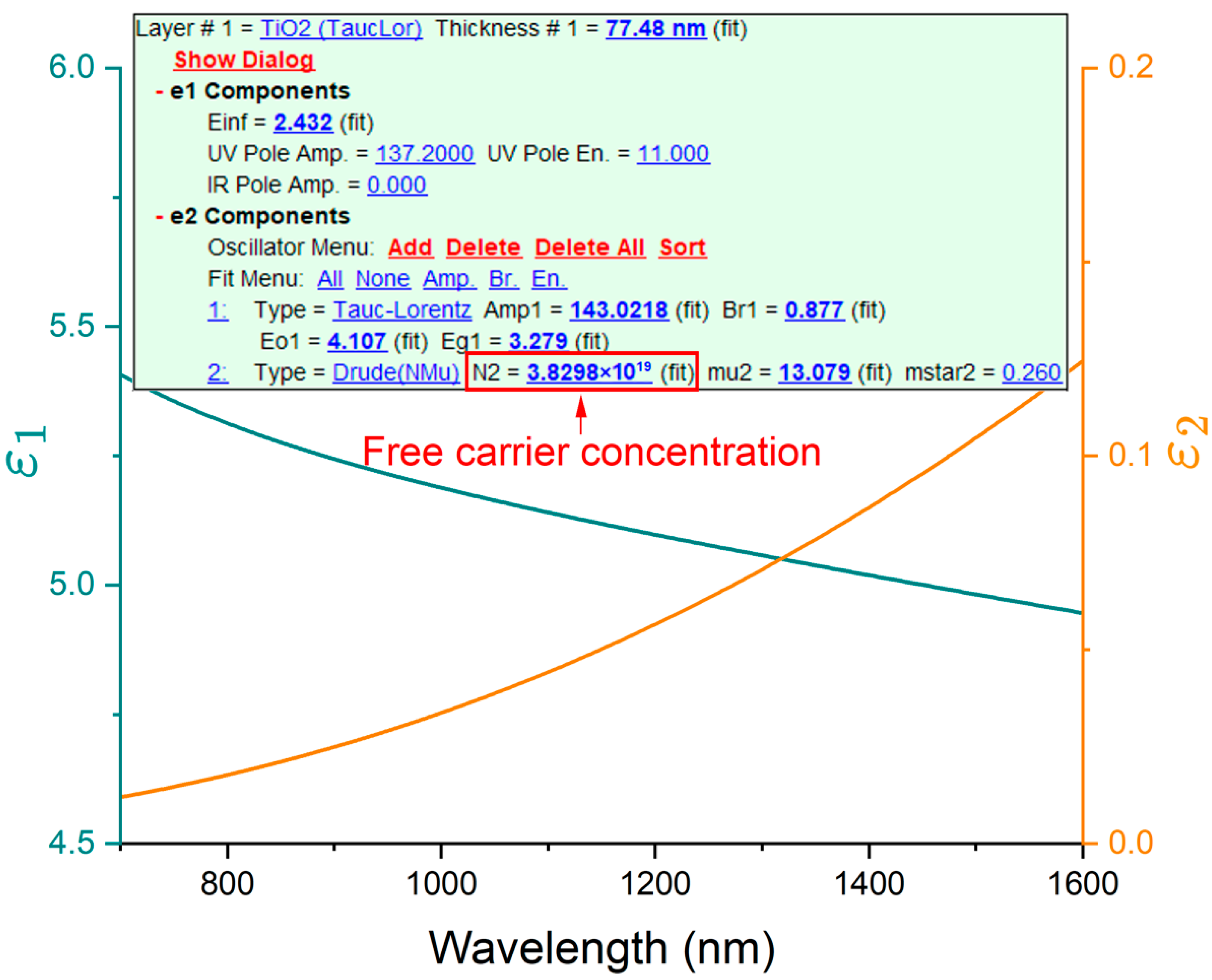
2.1. Materials Fabrication and Characterization
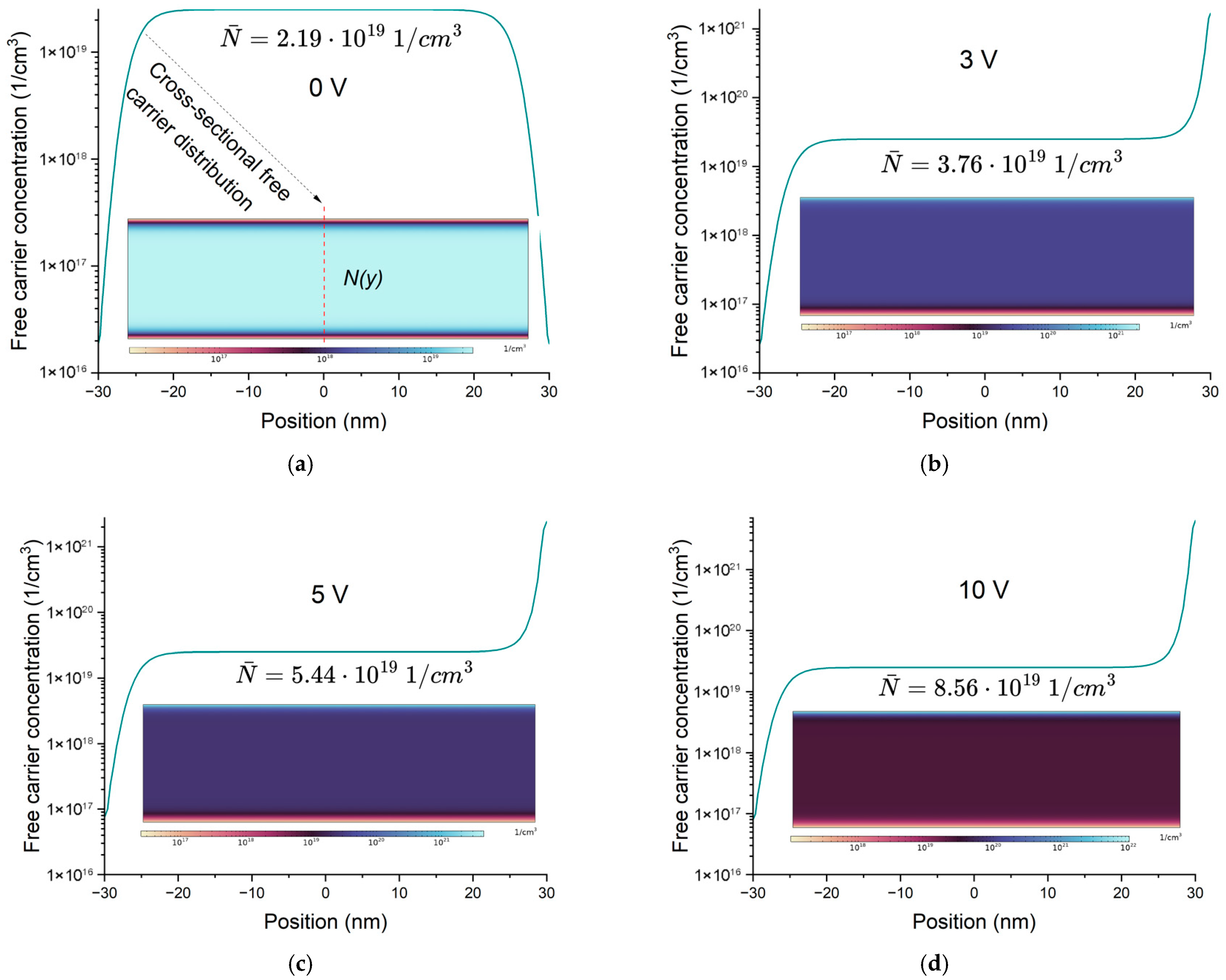
2.2. Device Simulations
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Q.; Zhao, W.M. A Comprehensive Review of Lossy Mode Resonance-Based Fiber Optic Sensors. Opt. Lasers Eng. 2018, 100, 47–60. [Google Scholar] [CrossRef]
- Sánchez, P.; Zamarreño, C.R.; Arregui, F.J.; Matías, I.R. LMR-Based Optical Fiber Refractometers for Oil Degradation Sensing Applications in Synthetic Lubricant Oils. J. Light. Technol. 2016, 34, 4537–4542. [Google Scholar] [CrossRef]
- Zamarreño, C.R.; Hernáez, M.; Del Villar, I.; Matías, I.R.; Arregui, F.J. Optical Fiber PH Sensor Based on Lossy-Mode Resonances by Means of Thin Polymeric Coatings. Sens. Actuators B Chem. 2011, 155, 290–297. [Google Scholar] [CrossRef]
- Zamarreño, C.R.; Hernaez, M.; Del Villar, I.; Matias, I.R.; Arregui, F.J. Tunable Humidity Sensor Based on ITO-Coated Optical Fiber. Sens. Actuators B Chem. 2010, 146, 414–417. [Google Scholar] [CrossRef]
- Elosúa, C.; Vidondo, I.; Arregui, F.J.; Bariain, C.; Luquin, A.; Laguna, M.; Matías, I.R. Lossy Mode Resonance Optical Fiber Sensor to Detect Organic Vapors. Sens. Actuators B Chem. 2013, 187, 65–71. [Google Scholar] [CrossRef]
- Letko, E.; Bundulis, A.; Vanags, E.; Mozolevskis, G. Lossy Mode Resonance in Photonic Integrated Circuits. Opt. Lasers Eng. 2024, 181, 108387. [Google Scholar] [CrossRef]
- Zhao, W.M.; Wang, Q. Analytical Solutions to Fundamental Questions for Lossy Mode Resonance. Laser Photon Rev. 2023, 17, 2200554. [Google Scholar] [CrossRef]
- Arregui, F.J.; Del Villar, I.; Corres, J.M.; Goicoechea, J.; Carlos, R.; Elosua, C.; Hernaez, M.; Rivero, P.J.; Socorro, A.B.; Sanchez, P.; et al. Fiber-Optic Lossy Mode Resonance Sensors. Procedia Eng. 2014, 87, 3–8. [Google Scholar] [CrossRef]
- Refractometer, F.; Sudas, D.P.; Zakharov, L.Y.; Jitov, V.A.; Golant, K.M. Silicon Oxynitride Thin Film Coating to Lossy Mode Resonance. Sensors 2022, 22, 3665. [Google Scholar] [CrossRef] [PubMed]
- Vos, M.; Grande, P.L. Simple Model Dielectric Functions for Insulators. J. Phys. Chem. Solids 2017, 104, 192–197. [Google Scholar] [CrossRef]
- Śmietana, M.; Burnat, D.; Curda, P.; Janaszek, B.; Kieliszczyk, M.; Sezemsky, P.; Koba, M.; Stranak, V.; Szczepański, P. Electro-Optically Modulated Lossy-Mode Resonance—A New Approach for Label-Free Sensing. ACS Photonics 2024, 11, 2061–2069. [Google Scholar] [CrossRef]
- Letko, E.; Bundulis, A.; Mozolevskis, G. Theoretical Development of Polymer-Based Integrated Lossy-Mode Resonance Sensor for Photonic Integrated Circuits. Photonics 2022, 9, 764. [Google Scholar] [CrossRef]
- Zuo, H.; Yu, S.; Gu, T.; Hu, J. Low Loss, Flexible Single-Mode Polymer Photonics. Opt. Express 2019, 27, 11152. [Google Scholar] [CrossRef]
- Girschikofsky, M.; Rosenberger, M.; Förthner, M.; Rommel, M.; Frey, L.; Hellmann, R. Waveguide Bragg Gratings in Ormocer®s for Temperature Sensing. Sensors 2017, 17, 2459. [Google Scholar] [CrossRef]
- Madani, A.; Azarinia, H.; Latifi, H. Design and Fabrication of a Polymer Micro Ring Resonator with Novel Optical Material at Add/Drop Geometry Using Laser Beam Direct Write Lithography Technique. Optik 2013, 124, 1746–1748. [Google Scholar] [CrossRef]
- Liang, Y.; Zhao, M.; Wu, Z.; Morthier, G. Bimodal Waveguide Interferometer RI Sensor Fabricated on Low-Cost Polymer Platform. IEEE Photonics J. 2019, 11, 6801108. [Google Scholar] [CrossRef]
- Julian, M.N.; Williams, C.; Borg, S.; Bartram, S.; Kim, H.J. Reversible Optical Tuning of GeSbTe Phase-Change Metasurface Spectral Filters for Mid-Wave Infrared Imaging. Optica 2020, 7, 746. [Google Scholar] [CrossRef]
- Gökbulut, B. A Hybrid Photonic-Plasmonic Resonator Based on a Partially Encapsulated 1D Photonic Crystal Waveguide and a Plasmonic Nanoparticle. Heliyon 2022, 8, e12346. [Google Scholar] [CrossRef]
- Ciminelli, C.; Dell’Olio, F.; Brunetti, G.; Conteduca, D.; Armenise, M.N. New Microwave Photonic Filter Based on a Ring Resonator Including a Photonic Crystal Structure. In Proceedings of the 19th International Conference on Transparent Optical Networks, Girona, Spain, 2–6 July 2017; pp. 3–6. [Google Scholar] [CrossRef]
- Cheng, W.; Lin, D.; Wang, P.; Shi, S.; Lu, M.; Wang, J.; Guo, C.; Chen, Y.; Cang, Z.; Tian, Z.; et al. Tunable Bandpass Microwave Photonic Filter with Largely Reconfigurable Bandwidth and Steep Shape Factor Based on Cascaded Silicon Nitride Micro-Ring Resonators. Opt. Express 2023, 31, 25648. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Perron, D.; Aurangozeb, F.; Jiang, Z.; Hossain, M.; Van, V. Silicon Photonic Vernier Cascaded Microring Filter for Broadband Tunability. IEEE Photonics Technol. Lett. 2019, 31, 1503–1506. [Google Scholar] [CrossRef]
- Khattou, S.; Rezzouk, Y.; Amrani, M.; El Ghafiani, M.; El Boudouti, E.H.; Talbi, A.; Djafari-Rouhani, B. Friedrich-Wintgen Bound States in the Continuum in a Photonic and Plasmonic T -Shaped Cavity: Application to Filtering and Sensing. Phys. Rev. Appl. 2023, 20, 1. [Google Scholar] [CrossRef]
- Wei, B.; Chen, H.; Hua, W.; Chen, M.; Ding, X.; Li, C. Formation Mechanism and Photoelectric Properties of Al2O3 Film Based on Atomic Layer Deposition. Appl. Surf. Sci. 2022, 572, 151419. [Google Scholar] [CrossRef]
- Niedziałkowski, P.; Białobrzeska, W.; Burnat, D.; Sezemsky, P.; Stranak, V.; Wulff, H.; Ossowski, T.; Bogdanowicz, R.; Koba, M.; Śmietana, M. Electrochemical Performance of Indium-Tin-Oxide-Coated Lossy-Mode Resonance Optical Fiber Sensor. Sens. Actuators B Chem. 2019, 301, 127043. [Google Scholar] [CrossRef]
- Letko, E.; Bundulis, A.; Mozolevskis, G. Lossy Mode Resonance Sensors Based on Planar Waveguides: Theoretical and Experimental Comparison. IEEE Photonics J. 2024, 16, 6800107. [Google Scholar] [CrossRef]
- Walker, J.M.; Akbar, S.A.; Morris, P.A. Synergistic Effects in Gas Sensing Semiconducting Oxide Nano-Heterostructures: A Review. Sens. Actuators B Chem. 2019, 286, 624–640. [Google Scholar] [CrossRef]
- Von Blanckenhagen, B.; Tonova, D.; Ullmann, J. Application of the Tauc-Lorentz Formulation to the Interband Absorption of Optical Coating Materials. Appl. Opt. 2002, 41, 3137–3141. [Google Scholar] [CrossRef]
- Tan, W.C.; Koughia, K.; Singh, J.; Kasap, S.O. Fundamental Optical Properties of Materials I. In Optical Properties of Condensed Matter and Applications; Wiley: Hoboken, NJ, USA, 2006; pp. 1–25. [Google Scholar] [CrossRef]
- Fuentes, O.; Del Villar, I.; Corres, J.M.; Matias, I.R. Lossy Mode Resonance Sensors Based on Lateral Light Incidence in Nanocoated Planar Waveguides. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Justice, P.; Marshman, E.; Singh, C. Student Understanding of Fermi Energy, the Fermi-Dirac Distribution and Total Electronic Energy of a Free Electron Gas. Eur. J. Phys. 2020, 41, 015704. [Google Scholar] [CrossRef]
- Bulyarskiy, S.V.; Koiva, D.A.; Belov, V.S.; Zenova, E.V.; Rudakov, G.A.; Gusarov, G.G. Titanium Oxide Thin Films Stoichiometric Composition Dependence on the Oxygen Flow at Magnetron Sputtering. Thin Solid. Film. 2022, 741, 138991. [Google Scholar] [CrossRef]
- Tekin, S.B.; Almalki, S.; Finch, H.; Vezzoli, A.; O’Brien, L.; Dhanak, V.R.; Hall, S.; Mitrovic, I.Z. Electron Affinity of Metal Oxide Thin Films of TiO2, ZnO, and NiO and Their Applicability in 28.3 THz Rectenna Devices. J. Appl. Phys. 2023, 134, 084503. [Google Scholar] [CrossRef]
- Choi, J.H.; Kim, J.W.; Oh, T.S. Dielectric Properties and Leakage Current Characteristics of Al2O3 Thin Films with Thickness Variation. Mater. Res. Soc. Symp.-Proc. 2001, 666, 1–6. [Google Scholar] [CrossRef]
- Nehate, S.D.; Prakash, A.; Mani, P.D.; Sundaram, K.B. Work Function Extraction of Indium Tin Oxide Films from MOSFET Devices. ECS J. Solid. State Sci. Technol. 2018, 7, 87–90. [Google Scholar] [CrossRef]
- Zhang, Z.; Yates, J.T. Band Bending in Semiconductors: Chemical and Physical Consequences at Surfaces and Interfaces. Chem. Rev. 2012, 112, 5520–5551. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, H. Electronic Transport and Interface Properties of FeOCl-Type Monolayer SnNCl for Flexible Nanodevices. Surf. Interfaces 2025, 65, 106524. [Google Scholar] [CrossRef]
- Liu, X.; Kang, J.H.; Yuan, H.; Park, J.; Kim, S.J.; Cui, Y.; Hwang, H.Y.; Brongersma, M.L. Electrical Tuning of a Quantum Plasmonic Resonance. Nat. Nanotechnol. 2017, 12, 866–870. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, J.; Zhao, H. Surface Plasmon Polariton Excitation by Electrostatic Modulation and Phase Grating in Indium-Tin-Oxide Coated Lithium Niobate Slabs. J. Appl. Phys. 2015, 118, 063102. [Google Scholar] [CrossRef]
- Li, J.; Yao, H.; Deng, J.; Hu, Z.; Zhao, Z.; Ma, X.; Chen, K. Electro-Optic Tunable Optical Filter Based on Long-Period Waveguide Grating in Lithium Niobate on Insulator with Absorption Ribbons. Opt. Express 2023, 31, 30658. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Zhu, H.; Hu, Y.; Yang, F.; Zang, Z.; Ou, J.; Han, H.; Ruan, S.; Han, P.; Xiang, B. Electro-Optic Tunable Bragg Grating Filters on Hybrid Silicon and Lithium Niobate Thin Films. Opt. Express 2024, 32, 46335. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, J.; Hu, X.; Gong, Q. Electro-Optic Tunable Multi-Channel Filter in Two-Dimensional Ferroelectric Photonic Crystals. J. Opt. 2010, 12, 075202. [Google Scholar] [CrossRef]
- Yu, J.; Ruan, Z.; Xue, Y.; Wang, H.; Gan, R.; Gao, T.; Guo, C.; Chen, K.; Ou, X.; Liu, L. Tunable and Stable Micro-Ring Resonator Based on Thin-Film Lithium Tantalate. APL Photonics 2024, 9, 036115. [Google Scholar] [CrossRef]




| Material | Physical Parameter | Value | Reference |
|---|---|---|---|
| TiOx | 40 | [31] | |
| 3.3 V | [32] | ||
| 3.9 V | [32] | ||
| Al2O3 | 9 | [33] | |
| Thickness | 2 nm | ||
| ITO | 4.6 V | [34] |
| Configuration | Tuning Efficiency, nm/V | FWHM, nm | FOM, V−1 |
|---|---|---|---|
| 2 nm Al2O3, 30 nm ITO, 40 nm TiOx | 3.2 | 144 | 0.022 |
| 2 nm Al2O3, 20 nm ITO, 60 nm TiOx | 4.0 | 130 | 0.031 |
| 2 nm Al2O3, 20 nm ITO, 100 nm TiOx | 2.0 | 98 | 0.020 |
| 2 nm Al2O3, 20 nm ITO, 150 nm TiOx | 1.6 | 71 | 0.023 |
| Technology | Tuning Efficiency, nm/V | FWHM, nm | FOM, V−1 |
|---|---|---|---|
| Long-period grating filter [39] | 0.34 | 5.0 | 0.068 |
| Bragg grating filter [40] | 0.016 | 0.30 | 0.053 |
| Photonic crystal-based filter [41] | 0.55 | 24 | 0.023 |
| Microring-based filter [42] | 0.0019 | 0.0050 | 0.38 |
| LMR-based filter | 4.0 | 130 | 0.031 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Letko, E. Tunable Filtering via Lossy Mode Resonance in Integrated Photonics. Photonics 2025, 12, 1086. https://doi.org/10.3390/photonics12111086
Letko E. Tunable Filtering via Lossy Mode Resonance in Integrated Photonics. Photonics. 2025; 12(11):1086. https://doi.org/10.3390/photonics12111086
Chicago/Turabian StyleLetko, Edvins. 2025. "Tunable Filtering via Lossy Mode Resonance in Integrated Photonics" Photonics 12, no. 11: 1086. https://doi.org/10.3390/photonics12111086
APA StyleLetko, E. (2025). Tunable Filtering via Lossy Mode Resonance in Integrated Photonics. Photonics, 12(11), 1086. https://doi.org/10.3390/photonics12111086





