A Unified OFDM-ISAC Signal Generation Architecture in W-Band via Photonics-Aided Frequency Multiplication and Phase Noise Mitigation

Abstract

This work proposes a photonics-aided W-band integrated sensing and communication (ISAC) system using photonics-aided frequency multiplication to suppress phase noise. Conventional dual-laser architectures suffer from phase noise accumulation, degrading both communication reliability and sensing resolution. To address this, we integrate photonics-aided frequency multiplication with orthogonal frequency-division multiplexing (OFDM), enabling a unified signal structure that simultaneously encodes communication data and radar waveforms without redundant resource allocation. Theoretical analysis reveals phase noise cancellation through coherent beating of symmetrically filtered sidebands in the photodetector (PD). Results demonstrate concurrent delivery of probability shaping (PS)-256QAM OFDM signals with a symbol error rate below 4.2 × 10⁻² and radar sensing with a 13.6 dB peak-to-sidelobe ratio (PSLR). Under a 1 MHz laser linewidth, the system achieves a 3.2 dB PSLR improvement over conventional methods, validating its potential for high-performance ISAC in beyond-5G networks.

1. Introduction

These days, one can witness ISAC emerging as a pivotal enabler for 6G networks [1,2]. As a result, achieving high-frequency (W/D-band), ultra-bandwidth, and low-noise signal transmission alongside high-precision sensing has become a critical research frontier. Compared to sub-6 GHz bands, the W-band (75–110 GHz) offers unique advantages, including ultra-wide contiguous spectral resources (>10 GHz bandwidth) and short wavelength properties, enabling terabit-per-second (Tbit/s) communication rates and sub-centimeter radar resolution [3]. However, conventional electronic solutions face severe challenges with W-band, such as inefficient high-frequency devices exacerbating phase noise, limited instantaneous bandwidth restricting ranging resolution, and complex RF chains escalating power consumption and system costs.

Photonics-aided techniques have enabled breakthroughs in W-band ISAC by leveraging optical-domain signal generation to overcome electronic limitations in high-frequency broadband signal generation [3,4,5,6,7,8,9]. Recent studies integrated OFDM [10,11], NOMA [12,13], and LFM [14] signals to achieve multi-user communication and multi-target detection. While homogeneous OFDM-based schemes have improved spectral efficiency (e.g., achieving a 47.06 Gbit/s net rate with 0.96 cm ranging resolution [10]) and enabled millimeter-level ranging via symbol-domain matched filtering [11], challenges persist. Heterogeneous signal multiplexing suffers from fragmented resource allocation, while photonics-aided systems face phase noise limitations and hardware complexity.

Innovations like self-coherent detection [15] and self-interference cancellation [16] partially addressed noise and interference, yet simplified architectures remain critical for practical deployment.

In this work, we propose a method for generating W-band integrated sensing and communication signals based on photonics-aided frequency multiplication. This method effectively mitigates the impact of optical phase noise, and theoretical derivations are provided. Results show that the proposed system, utilizing OFDM signals as ISAC signals, achieves a 15 GHz bandwidth transmission of ps-256QAM signals with a bit error rate (BER) of 3.97 × 10⁻², which is below the soft-decision threshold. Furthermore, in terms of sensing, the system maintains an effective PSLR under high phase noise conditions. The inverse synthetic aperture radar (ISAR) imaging performance of the system under high phase noise is also validated.

The remainder of this paper is structured as follows: Section 2 establishes the system model and theoretical foundation for phase noise cancellation; Section 3 describes the simulation setup and optical frequency comb generation; Section 4 analyzes communication performance through BER, error vector magnitude (EVM) and signal-to-noise ratio (SNR) metrics; Section 5 evaluates sensing performance using PSLR and ISAR imaging; finally, Section 6 concludes the work and suggests future research directions.

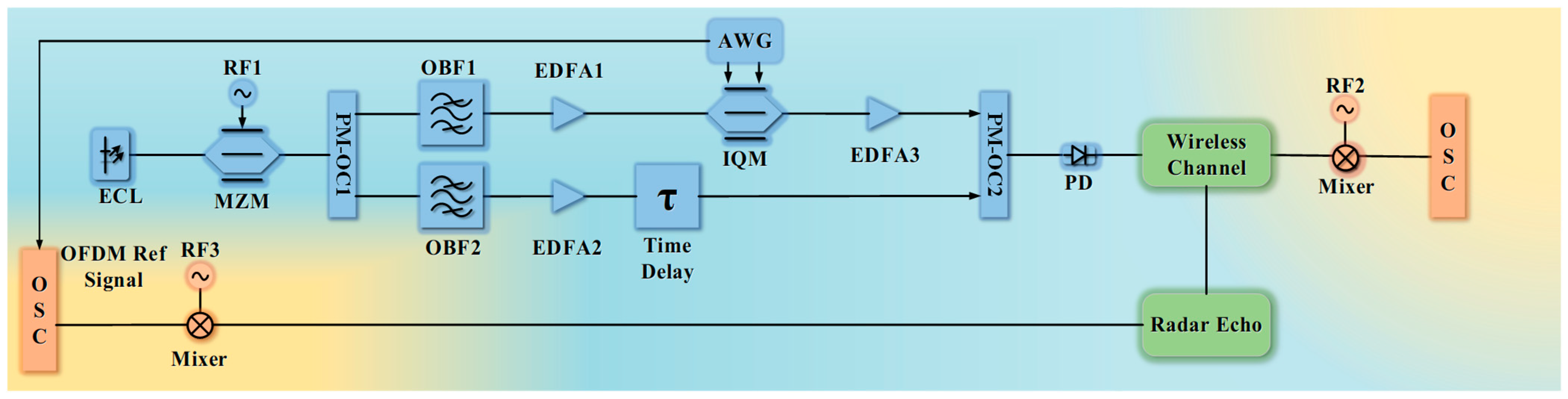
2. System Model

We propose a W-band OFDM ISAC system employing photonics-aided frequency multiplication, with system performance validated through VPI. The system schematic of the proposed photonics-aided W-band ISAC system is illustrated in Figure 1. The architecture comprises a unified transmitter that generates a dual-sideband optical signal through photonic frequency multiplication. The key innovation lies in the coherent combining of the +k-th and −k-th order sidebands for inherent phase noise cancellation.

The generated W-band signal is radiated into free space via a transmit antenna. The reflected echo signals from potential targets are captured by a receive antenna. These echoes are then downconverted to an intermediate frequency (IF) by mixing with a local oscillator. Finally, the IF signal is digitized and processed by offline digital signal processing (DSP) algorithms for target detection and ISAR imaging.

The optical signal generated by a laser can be expressed as:

$$E(t)=E\exp (2\pi f_{c}t+\phi )$$

(1)

where $E$ denotes the amplitude of the optical signal, $f_c$ the optical carrier frequency, and $\phi$ the phase noise of the optical signal.

The process of generating high-frequency signals via the conventional photonics-aided dual-laser system can be mathematically represented as [13]:

$$E(t)=E_1{S}_{OFDM}\exp [j(2\pi f_{c1}t+{\phi }_1(t))]+E_2\exp [j(2\pi f_{c2}t+{\phi }_2(t))]$$

(2)

where $S_{OFDM}$ is a baseband signal. This method makes the phase noise of the optical signals mix together, resulting in amplified phase noise aliasing. The detected signal is expressed as:

$$I(t)=K\Re \left\{S_{OFDM}\exp \left[j(2\pi (f_{c1}-f_{c2})t+({\phi }_1(t)-{\phi }_2(t)))\right]\right\}$$

(3)

where $\Re (•)$ means the real part of the signals and $K$ is the response factor of PD. This kind of carrier with two-phase noise reduces the SNR for communication and deteriorates sensing resolution, necessitating advanced algorithmic compensation to restore system performance.

Let the RF driving signal be:

$$E_{RF1}=E_{RF}\cos (2\pi f_{RF}t)$$

(4)

where $f_{RF}$ denotes the RF signal frequency and $E_{RF}$ is the amplitude of the RF signal. After RF modulation, the output optical signal from the Mach–Zehnder modulator (MZM) can be expressed as:

$$E_{MZM}(t)=E_1\exp (j2\pi f_{c}t+j\phi )\cos \left[\pi {\displaystyle \frac{E_{RF}\cos (2\pi f_{RF}t)}{V\pi }}+\pi {\displaystyle \frac{V_{DC}}{V_{\pi }}}\right]$$

(5)

where $V_{\pi }$ is the MZM half-wave voltage and $V_{DC}$ denotes the DC bias voltage. Using Jacobi–Anger expansion, Equation (5) can be expanded as:

$$\begin{array}{cc}\hfill E_{MZM}(t)& ={\displaystyle \frac{1}{2}}{E}_1\exp (j2\pi f_{c}t+j\phi )\left\{\exp [j\beta \cos (2\pi f_{RF})+j\gamma ]+\exp [-j\beta \cos (2\pi f_{RF})-j\gamma ]\right\}\hfill \\ & =E_1\cos (\gamma ){\displaystyle \sum _{m=-\infty }^{\infty }{(-1)}^m{J}_{2m}(\beta )\exp \left(j2m\cdot 2\pi f_{RF}t+j2\pi f_{c}t+j2\phi \right)}\hfill \\ & -E_1\sin (\gamma ){\displaystyle \sum _{m=-\infty }^{\infty }{(-1)}^m{J}_{2m+1}(\beta )\exp \left(j(2m+1)\cdot 2\pi f_{RF}t+j2\pi f_{c}t+j2\phi \right)}\hfill \end{array}$$

(6)

where $J_n(x)$ denotes the nth order Bessel function of the first kind, $\gamma =\pi V_{DC}/V_{\pi }$ the phase induced by the DC bias voltage of the Mach–Zehnder modulator (MZM), and $\beta =E_{RF}/V\pi$ the modulation depth. By setting $V_{DC}=V_{\pi }/2$, the even-order optical carriers are suppressed with $\cos (\gamma )=0$ and $\sin (\gamma )=1$, and thus Equation (6) can be simplified to:

$$E_{MZM}(t)=-E_1{\displaystyle \sum _{m=-\infty }^{\infty }{(-1)}^m{J}_{2m+1}(\beta )\exp \left[j2\pi f_{c}t+j(2m+1)\cdot 2\pi f_{RF}t+j2\phi \right]}$$

(7)

by controlling the operating range of the optical filter, the $\pm k$-th order sideband ($k=2m+1,m=0,1,\dots ,n$) of the MZM output signal required for photon beat frequency generation can be obtained. Due to the property of the Bessel function of the first kind $J_n(x)={(-1)}^n{J}_n(x)$, Equation (7) can be simplified to:

$$\begin{array}{l}{E}_k(t)={(-1)}^{k-{\displaystyle \frac{3}{2}}}{E}_1{J}_k(\beta )\exp [j2\pi f_{c}t+jk\cdot 2\pi f_{RF}t+j2\phi ]\\ E_{-k}(t)={(-1)}^{-k-{\displaystyle \frac{3}{2}}}{E}_1{J}_k(\beta )\exp [j2\pi f_{c}t-jk\cdot 2\pi f_{RF}t+j2\phi ]\end{array}$$

(8)

where $E_k(t)$ has been selected as the optical carrier. OFDM signal $S_{OFDM}$ is modulated onto an optical carrier $f_c+k\cdot f_{RF}$ through the IQ-MZM, which can be expressed as:

$$E_{IQM}=A_1{S}_{OFDM}\exp [j2\pi f_{c}t+jk\cdot 2\pi f_{RF}t+j2\phi ]$$

(9)

after the coupling of a polarization-maintaining optical coupler (PM-OC), the coupled signal can be expressed as:

$$\begin{array}{cc}\hfill E_{PMOC2}& =A_1{S}_{OFDM}\exp [j2\pi f_{c}t+jk\cdot 2\pi f_{RF}t+j2\phi ]\hfill \\ & +A_2\exp [j2\pi f_{c}t-jk\cdot 2\pi f_{RF}t+j2\phi ]\hfill \end{array}$$

(10)

where $A_1={(-1)}^{k-{\displaystyle \frac{3}{2}}}{E}_1{J}_k(\beta )$ and $A_2={(-1)}^{-k-{\displaystyle \frac{3}{2}}}{E}_1{J}_k(\beta )$. After photoelectric conversion, the electrical signal output by the PD can be expressed as:

$$\begin{array}{cc}\hfill I_{PD}(t)& =\mu {\left|E_{PMOC2}\right|}^2=\mu E_{PMOC2}\cdot E_{PMOC2}^{*}\hfill \\ & =\mu \left\{A_1^2{S}_{OFDM}^2+A_2^2+A_1{A}_2{S}_{OFDM}\left[\exp (j2k\cdot 2\pi f_{RF}t)+\exp (-j2k\cdot 2\pi f_{RF}t)\right]\right\}\hfill \\ & =\mu \left\{A_1^2{S}_{OFDM}^2+A_2^2+2A_1{A}_2{S}_{OFDM}\cos (2k\cdot 2\pi f_{RF}t)\right\}\hfill \end{array}$$

(11)

where $\mu$ is the PD responsivity. The first two terms in Equation (11)—the baseband signal and DC signal—will be filtered out by the W-band devices. The third term is the photonics-aided low-phase-noise W-band OFDM ISAC signal. It can be observed that by applying an appropriate time delay to $E_{-k}(t)$ to synchronize its phase noise with that of $E_k(t)$ the output signal can achieve significant phase noise suppression.

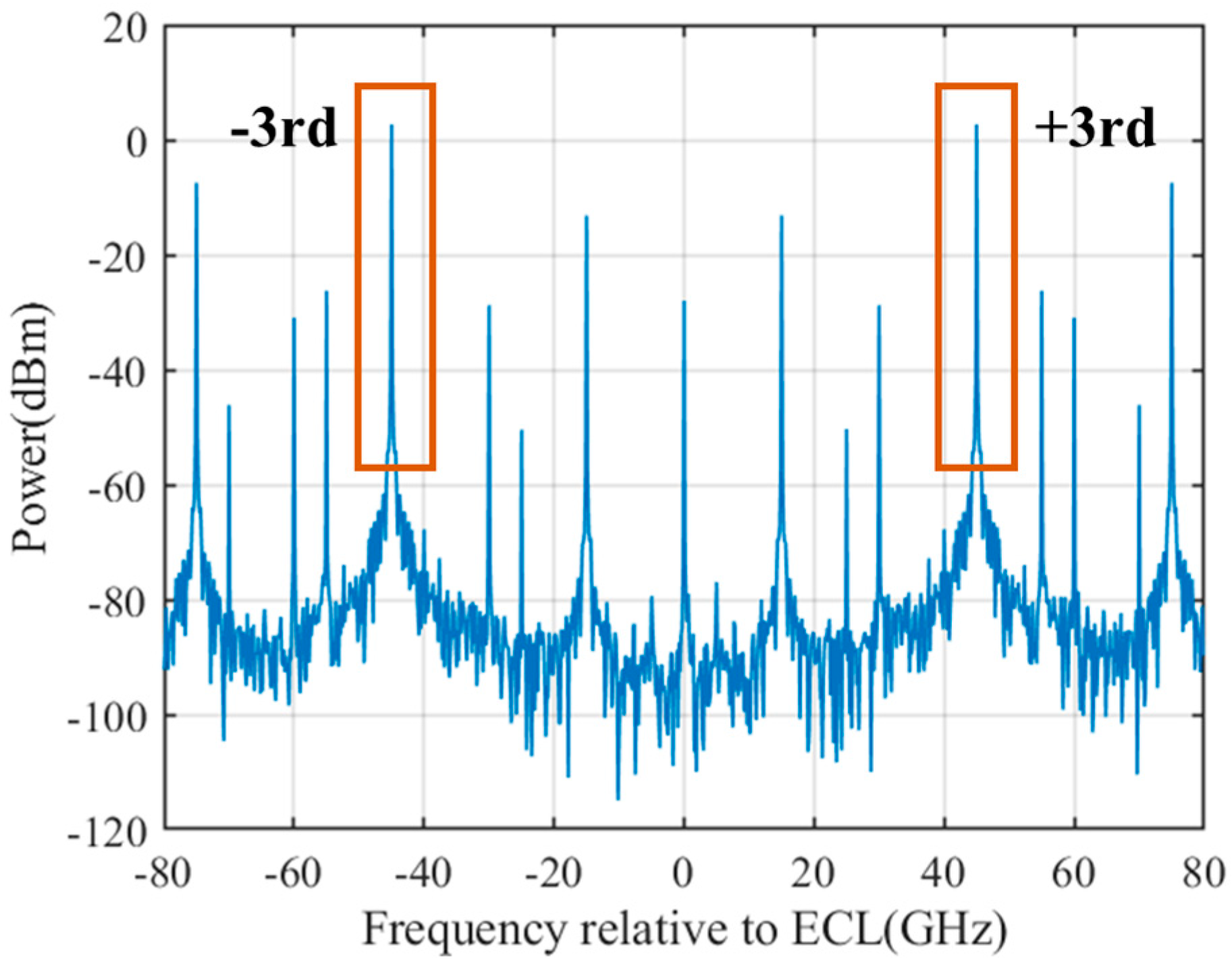
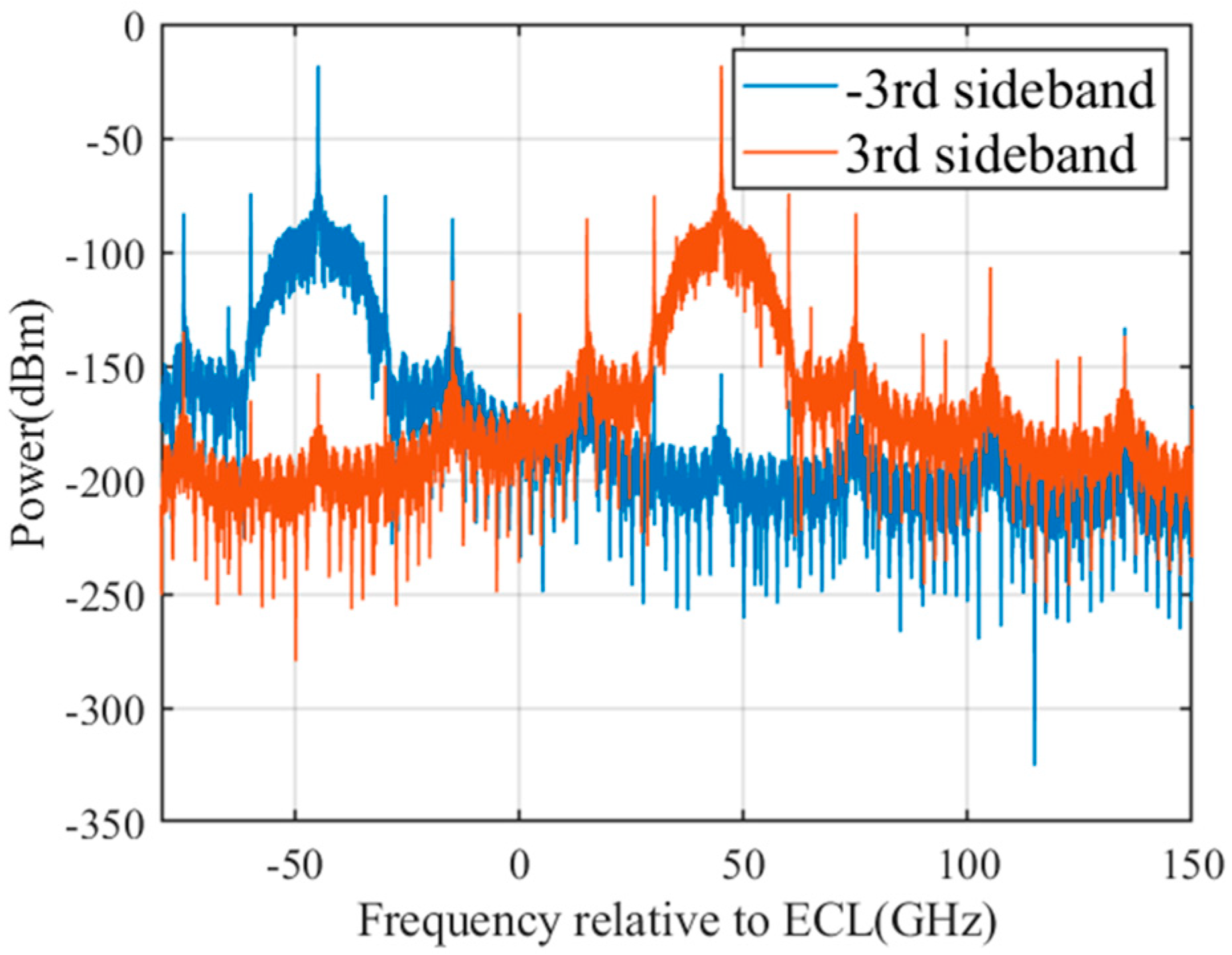
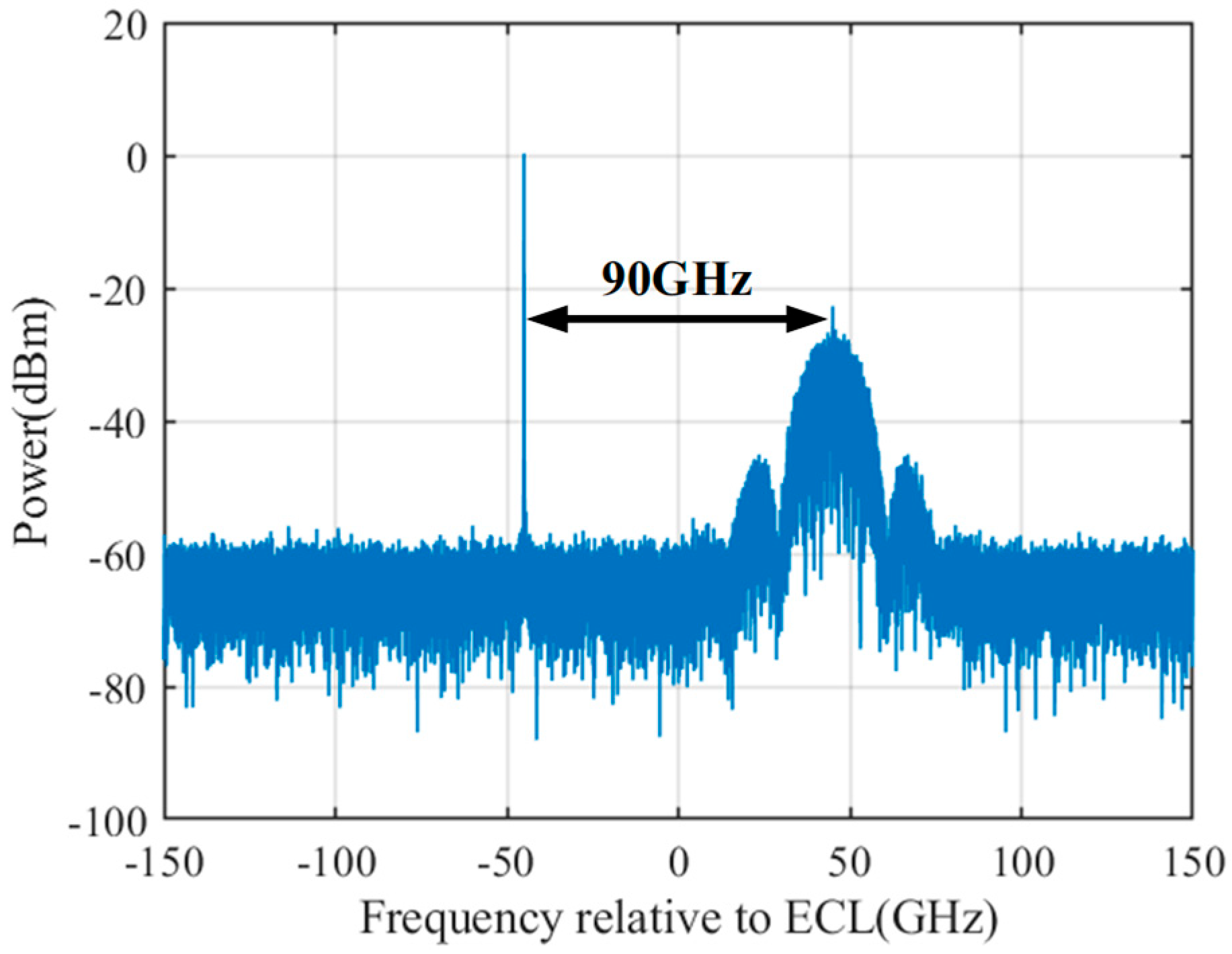
3. Simulation of the Proposed System

The structure of the proposed photonics-aided low-phase-noise W-band ISAC system is shown in Figure 1. The external cavity laser (ECL) generates an optical signal of 10 dBm and 193.1 THz, with its linewidth tunable, which is fed into the MZM and modulated by the RF source. The half-wave voltage of the MZM is 5 V, and the bias voltage is 2.5 V, while the MZM operates exactly at the quadrature point. The RF source (RF1) operates at 15 GHz.

The frequency of the modulated optical frequency comb signal is depicted in Figure 2. As demonstrated, by selecting an appropriate driving voltage, the positive and negative third-order sidebands of the signal emerge as the dominant components, while the even-order signals exhibit varying degrees of suppression.

To extract the ±3rd-order optical sidebands, the MZM output is split into two paths via the PM-OC and sent to optical bandpass filters OBF1 and OBF2. The center frequency of OBF1 is 193.145 THz, and that of OBF2 is 193.055 THz. Both filters feature a 30 dB rejection ratio and a 3 dB bandwidth of 30 GHz. The filtered optical spectra are shown in Figure 3. After filtering, the ±3rd-order sidebands stand out with a PSLR of 57 dB.

The filtered optical signals are amplified by two erbium-doped fiber amplifiers (EDFA) with a 24 dB gain each. An arbitrary waveform generator (AWG) produces 16 GBaud OFDM signals, which are modulated onto the +3rd-order sideband optical carrier at 193.145 THz through the IQ-MZM. The IQ-MZM output is further amplified by EDFA3 with a 9 dB gain to ensure its optical power matches that of the −3rd-order sideband at 193.055 THz. The optical spectrum of the two optical signals after PMOC is shown in Figure 4.

After photoelectric conversion, the two optical signals with a frequency difference of 90 GHz are converted into a millimeter-wave signal at 90 GHz carrier frequency with 16 GHz bandwidth, which enters free space. The communication signal is downconverted by RF2 with a frequency of 75 GHz, and then captured by the OSC, and the BER is calculated after processing through offline DSP algorithms. The sensed signal, after being reflected and delayed, is downconverted by the RF source RF3, which also operates at 75 GHz, and processed by offline sensing algorithms.

4. Communication Performance Analysis

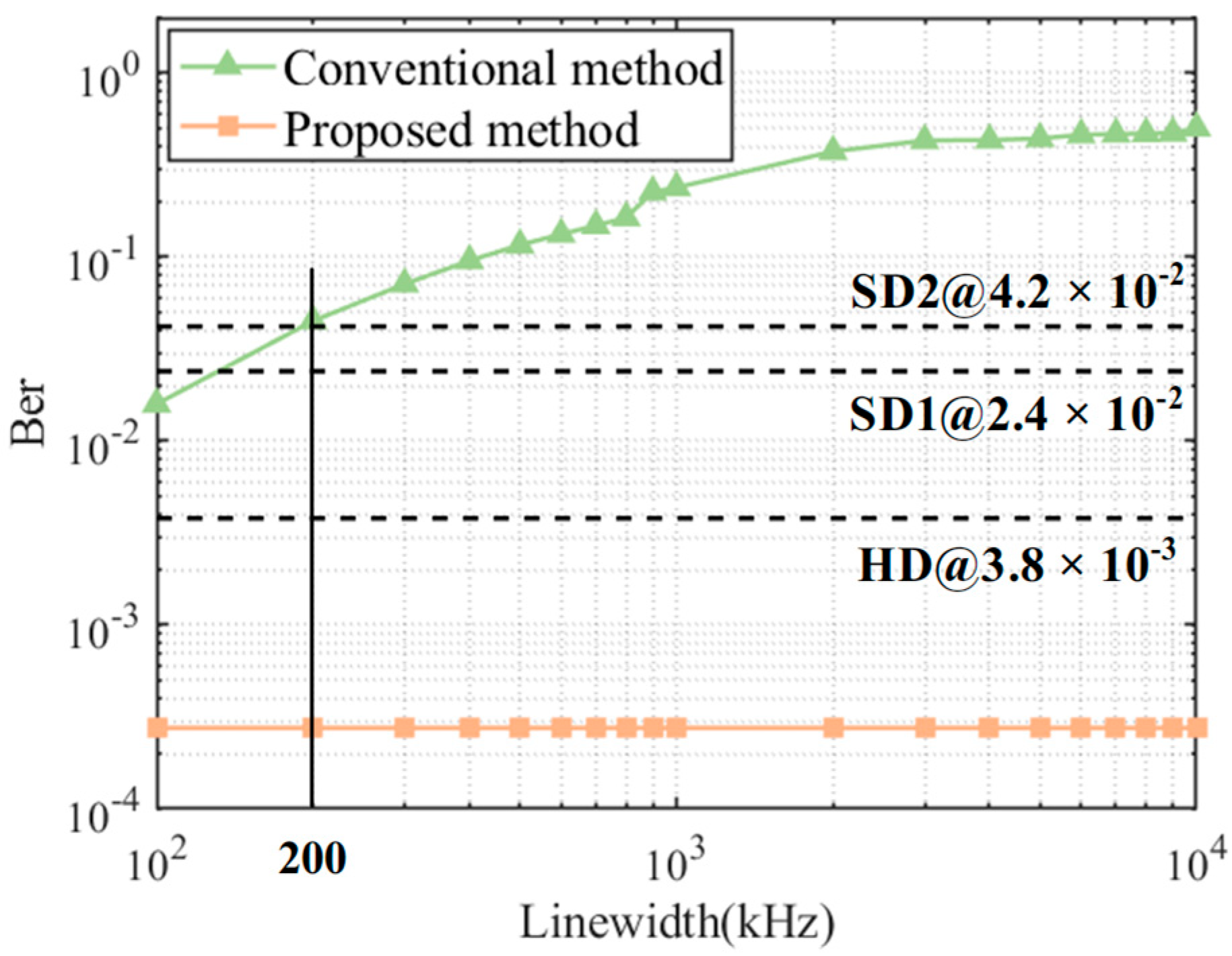
4.1. BER Performance Comparison

In the simulations, the signal format was configured with an FFT size of 4096 and a cyclic prefix (CP) length of 128. To better align with practical channel conditions, subcarriers near the zero-frequency region were intentionally excluded to mitigate DC offset impairment. Consequently, 4000 subcarriers were actively employed as carriers for both communication and sensing functions.

Pilot tones were inserted every 64 subcarriers to facilitate accurate channel estimation. It is noteworthy that all communication signals, including these pilot tones, were simultaneously utilized for sensing purposes. This approach leverages pulse compression techniques, enabling holistic utilization of all available time–frequency resources to enhance sensing performance without compromising communication functionality.

Results have compared the BER performance at varying laser linewidths. The signal baud rate is set to 16 GBaud. Figure 5 shows variation curves of BER versus laser linewidth for 16QAM signals transmitted through both the conventional dual-laser system and the proposed system. When the laser linewidth is 100 kHz, the bit error rate of the dual-laser system falls below the soft decision threshold with 20% overhead (SD1@2.4 × 10⁻²); when it exceeds 100 kHz, the BER surpasses the 25% overhead soft-decision threshold (SD2@4.2 × 10⁻²). The dual-laser system requires additional overhead for effective signal transmission. In contrast, the proposed low-phase-noise system has a BER lower than the hard-decision threshold (HD@3.8 × 10⁻³) across all tested laser linewidths, demonstrating its immunity to source phase noise and stable communication capability.

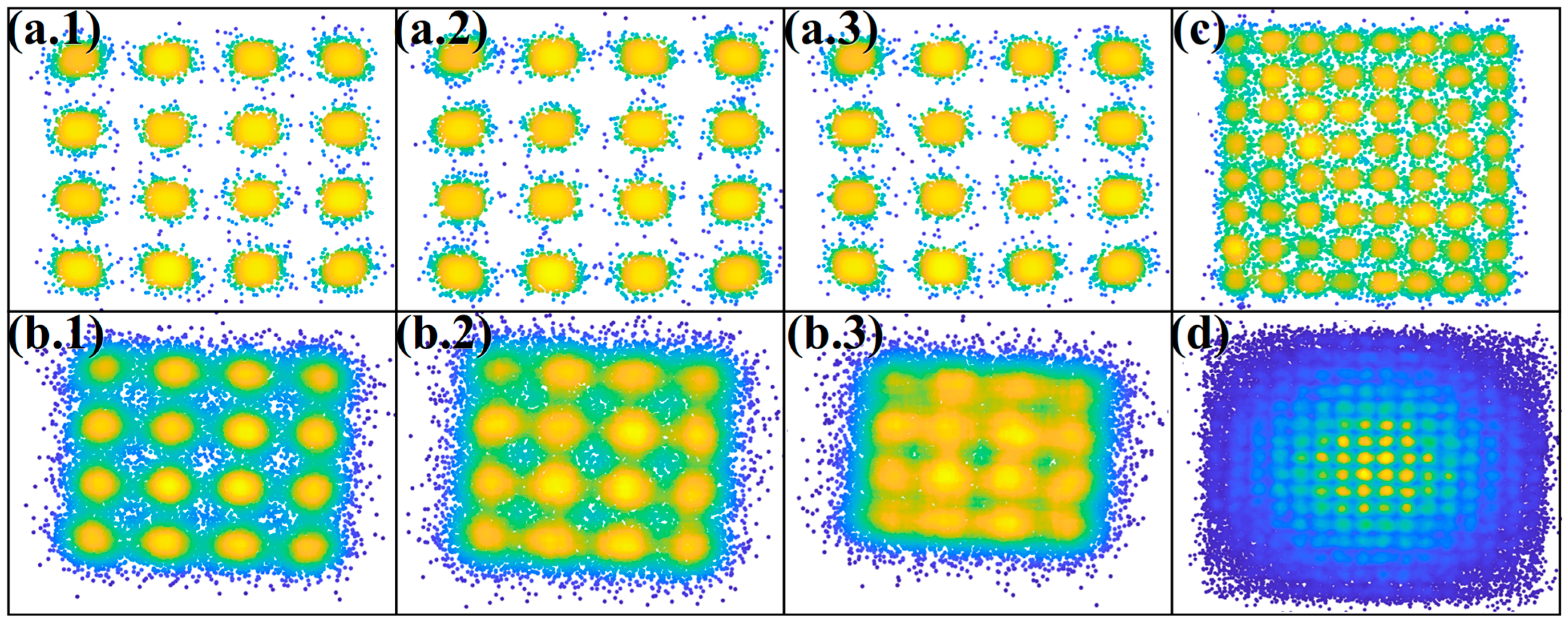
4.2. Constellation Diagram Comparison

Figure 6 presents constellation diagrams of 16QAM signals. Figure 6(a.1–a.3) show results for the proposed frequency multiplication system at laser linewidths of 100 kHz, 1 MHz, and 10 MHz, respectively. Since the phase noise of the signal is eliminated during optical-electrical conversion, the 16QAM signal constellation diagrams remain clear with few scattered points, approaching a zero-bit error rate, even with lasers of different linewidths. This result demonstrates that the proposed system can effectively eliminate the phase noise caused by the laser linewidth.

Figure 6(b.1–b.3) displays results for a conventional photonics-aided millimeter-wave system at 100 kHz, 200 kHz, and 300 kHz linewidths. Phase noise degrades OFDM orthogonality, causing increased scattering and rotational distortion. At a 300 kHz linewidth, constellation points become indistinguishable, revealing limited phase noise tolerance.

To verify its transmission capability of high-order QAM signals, 64QAM and PS-256QAM signals are transmitted in the system with a laser linewidth of 1 MHz. The PS scheme can fully utilize the communication capabilities of the signal. The PS technique generates QAM signals that follow a Maxwell-Boltzmann (MB) distribution, which maximizes the achievable information entropy under an average power constraint, thereby effectively improving the system’s communication rate. For a PS-QAM signal format, if the constellation symbol set is denoted as $\chi$, the probability of generating a constellation point $x\in \chi$ satisfies the MB distribution [17]:

$$P_{\chi }(x)={\displaystyle \frac{e^{-v{\left|x\right|}^2}}{{\displaystyle {\sum }_{x^{\prime }\in \chi }{e}^{-v{\left|x^{\prime }\right|}^2}}}}$$

(12)

Figure 6c serves as the 64QAM constellation diagram with BER of 1.28 × 10⁻² (below the soft decision threshold SD1@2.4 × 10⁻²). Figure 6d presents the PS-256QAM probability distribution function (information entropy = 7.5488) and the demodulated constellation diagram (BER = 3.97 × 10⁻², below SD2@4.2 × 10⁻²). These results confirm reliable high-order modulation transmission without phase noise impact.

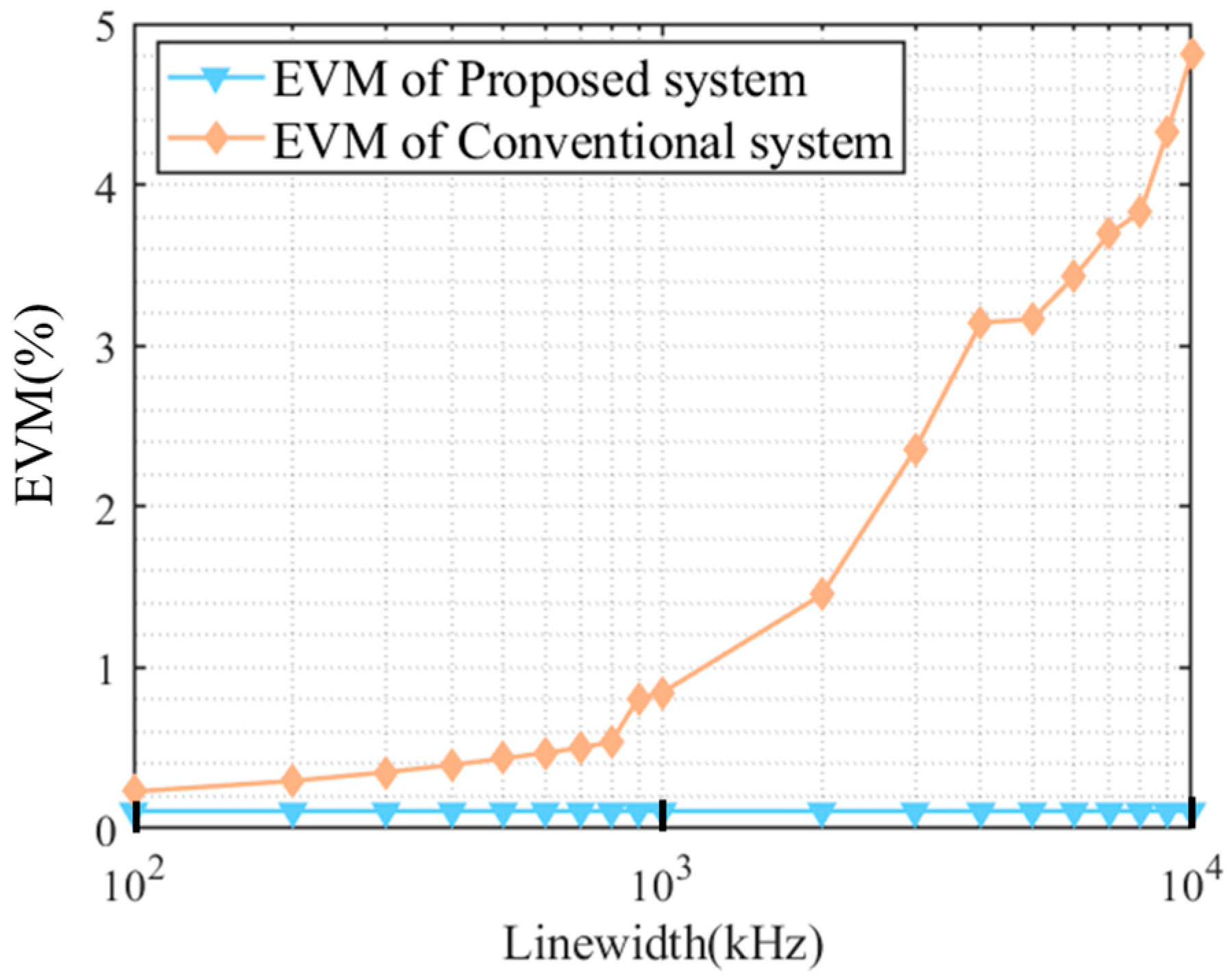
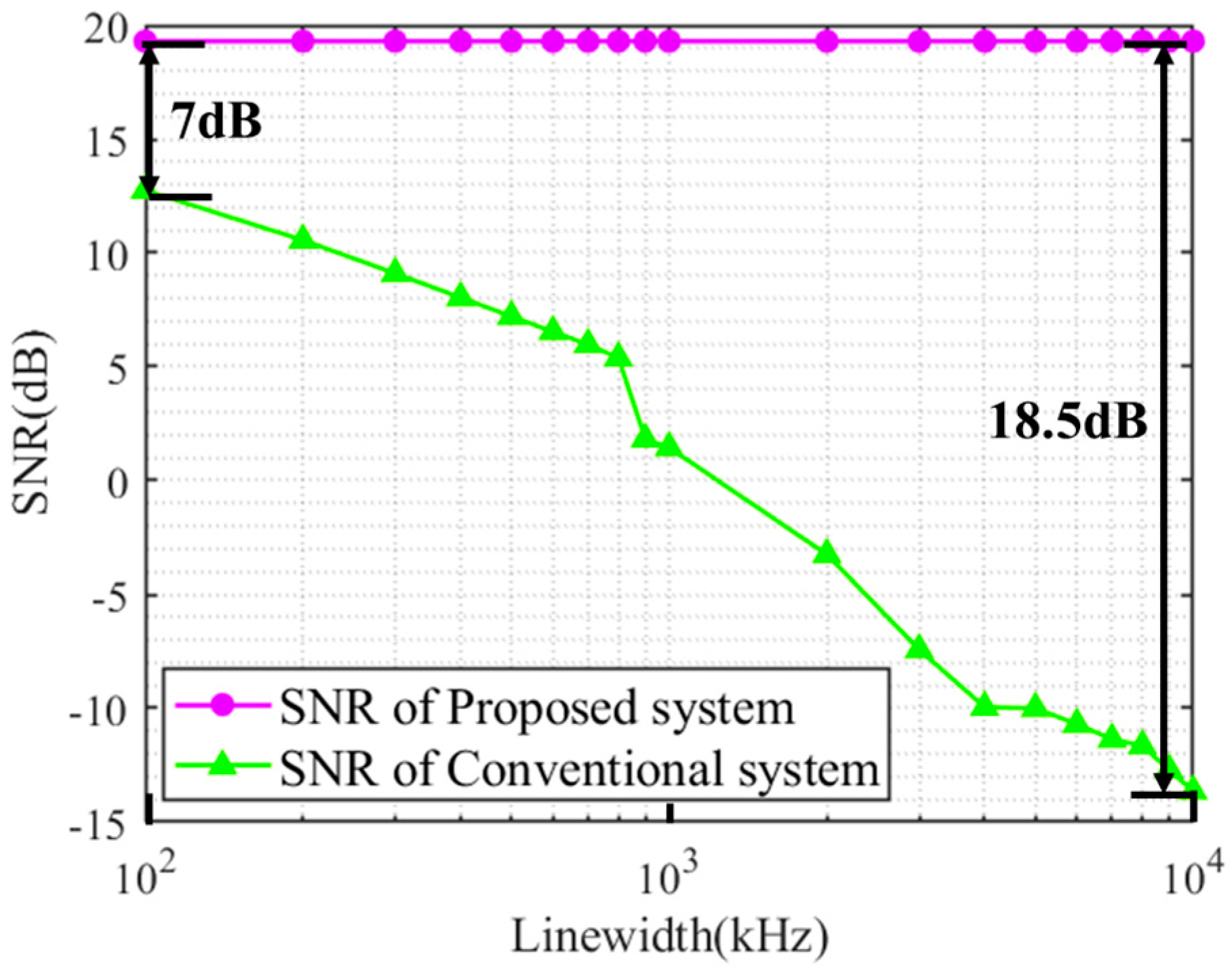
4.3. EVM and SNR Performance Comparison

To quantitatively evaluate the phase noise suppression capability of the proposed architecture, comprehensive simulation measurements of EVM and SNR were conducted across a laser linewidth range from 100 kHz to 10 MHz. As shown in Figure 7 and Figure 8, the SNR of the conventional dual-laser system deteriorates significantly while EVM increases markedly with increasing laser linewidth. In stark contrast, the proposed system maintains stable SNR and EVM performance regardless of linewidth variations. Specifically, it achieves significant SNR improvements of 7 dB and 18.5 dB compared to the conventional approach at 100 kHz and 1 MHz laser linewidths, respectively.

The performance degradation observed in traditional systems stems from the cumulative effect of irrelevant phase noise during optical heterodyning reception. This cumulative effect induces two critical impairments: inter-carrier interference (ICI) that disrupts the orthogonality of frequency-division multiplexed subcarriers, and constellation rotation that causes symbol detection distortion. As illustrated in the constellation diagram of Figure 6, these effects become increasingly pronounced with widening laser linewidth, ultimately limiting achievable data rates and communication reliability. These quantitative metrics collectively validate the inherent phase noise cancellation mechanism achieved through symmetric sideband coherent beat generation, which effectively eliminates the impact of laser phase noise during optical detection.

5. Sensing Performance Analysis

To validate the sensing potential of the proposed system, the echo time delay is set to 20 ns (equivalent to a target distance of 3 m from the transceiver). The PSLR is adopted as the key performance metric. Figure 9 shows the variation curves of the PSLR versus laser linewidth for single-target detection in the two systems. The laser linewidth varies from 100 kHz to 10 MHz.

As shown in Figure 9, the traditional dual-laser system exhibits significant degradation in sensing performance as the laser linewidth increases. The PSLR deteriorates from 13.6 dB at a 100 kHz linewidth (consistent with theoretical predictions) to 10 dB at a 10 MHz linewidth, indicating reduced target detection capability. In contrast, the proposed system maintains a stable PSLR of 13.6 dB—the theoretical value—regardless of laser linewidth variation, achieving a 3.2 dB improvement over the conventional system at a 1 MHz linewidth.

This performance degradation primarily stems from phase noise accumulation during optical heterodyning, which disrupts the critical coherence properties essential for precise pulse compression in continuous-wave radar operation. Accumulated phase noise not only elevates sidelobe levels but also weakens phase coherence in echo signal processing, ultimately compromising target distinguishability and resolution.

To achieve high-resolution ISAR imaging, this system employs a signal processing workflow based on two-dimensional fast Fourier transform (2D-FFT). Specifically, it first performs FFT processing on the fast-time dimension data to generate a high-resolution range image, thereby resolving target reflection characteristics at different ranges. Building upon this, it then applies FFT operations to the slow-time dimension (azimuth dimension) data within each range cell to extract target Doppler characteristics, ultimately forming a two-dimensional Doppler image.

As demonstrated by the ISAR imaging results in Figure 10, the conventional system fails to effectively suppress sidelobes under high phase noise conditions, generating significant interference in multi-target environments. These findings collectively validate that the optoelectronic conversion phase noise cancellation mechanism, achieved through symmetric sideband coherent beat generation, effectively preserves the critical correlation properties essential for high-resolution sensing.

To further evaluate the sensing performance of the system under varying phase noise conditions, we simulated single-target imaging and investigated the impact of different laser linewidths on detection performance. Figure 10(a.1–a.3) displays the range Doppler 2D images of the proposed system at laser linewidths of 100 kHz, 10 MHz, and 50 MHz. The imaging results remain unaffected by laser linewidth variations, consistently exhibiting a standard star-like point distribution. By optimizing the signal time delay, the phase noise of the dual optical signals is synchronized and mutually canceled during photonic beating, effectively suppressing phase noise-induced degradation caused by laser linewidth. The performance across laser linewidths aligns with the invariant PSLR shown in Figure 9.

In contrast, Figure 10(b.1–b.3) presents the range Doppler 2D images of the conventional system at the same linewidths. As the laser linewidth increases, signal coherence deteriorates, resulting in elevated noise power, reduced target-background contrast, and degraded PSLR in the range Doppler images. It is further verified that the proposed system has a huge performance advantage over the conventional system in terms of the OFDM signal-based sensing function.

6. Conclusions

This work demonstrates a photonics-aided frequency multiplication architecture for W-band ISAC systems that fundamentally addresses phase noise challenges in high-frequency integrated sensing and communication. By exploiting coherent beating of symmetrically filtered ±k-th order optical sidebands, the proposed system achieves inherent phase noise cancellation during photoelectric conversion, eliminating the performance degradation caused by laser linewidth broadening. Theoretical analysis and results in VPI validate its dual advantages: (1) for communications, the architecture supports stable transmission of 16-GBaud PS-256QAM OFDM signals with a BER of 3.97 × 10⁻² under 1 MHz laser linewidth, outperforming conventional dual-laser systems by 18.5 dB in SNR and enabling entropy-efficient modulation (7.5488 bits/symbol); (2) for sensing, it maintains a consistent 13.6 dB PSLR in radar detection regardless of laser phase noise fluctuations—a 3.2 dB improvement over traditional methods at 1 MHz linewidth. The unified OFDM waveform structure further eliminates redundant resource allocation between communication and sensing functions, achieving 90 GHz carrier generation with 15 GHz instantaneous bandwidth through photonic frequency multiplication. This architecture overcomes critical limitations in electronic-based W-band systems, including phase noise accumulation and fragmented spectrum utilization. The results suggest promising applications in 5G beyond networks requiring simultaneous Tbit/s data rates and millimeter-precision sensing, particularly for dynamic environments like autonomous vehicles and smart factories. Future work will focus on experimental validation of multi-target ISAR imaging and hardware simplification for cost-effective deployment.

The proposed photonics-aided W-band ISAC system, leveraging its large bandwidth and low power consumption, shows particular promise for UAV-enabled low-altitude economy scenarios. This architecture effectively supports simultaneous high-resolution sensing and high-speed communications, making it suitable for applications such as aerial monitoring, real-time swarm coordination, and navigation in urban environments. Its efficient performance aligns well with next-generation autonomous aerial systems, while its phase noise suppression ensures reliable operation under dynamic conditions.

In combination with advanced beamforming and maneuver strategies—such as those discussed in [18] by Lyu et al. for UAV-enabled ISAC—this photonic integration offers a scalable and power-efficient solution toward future aerial ISAC applications, paving the way for more sophisticated and coordinated operations in congested spectral environments.