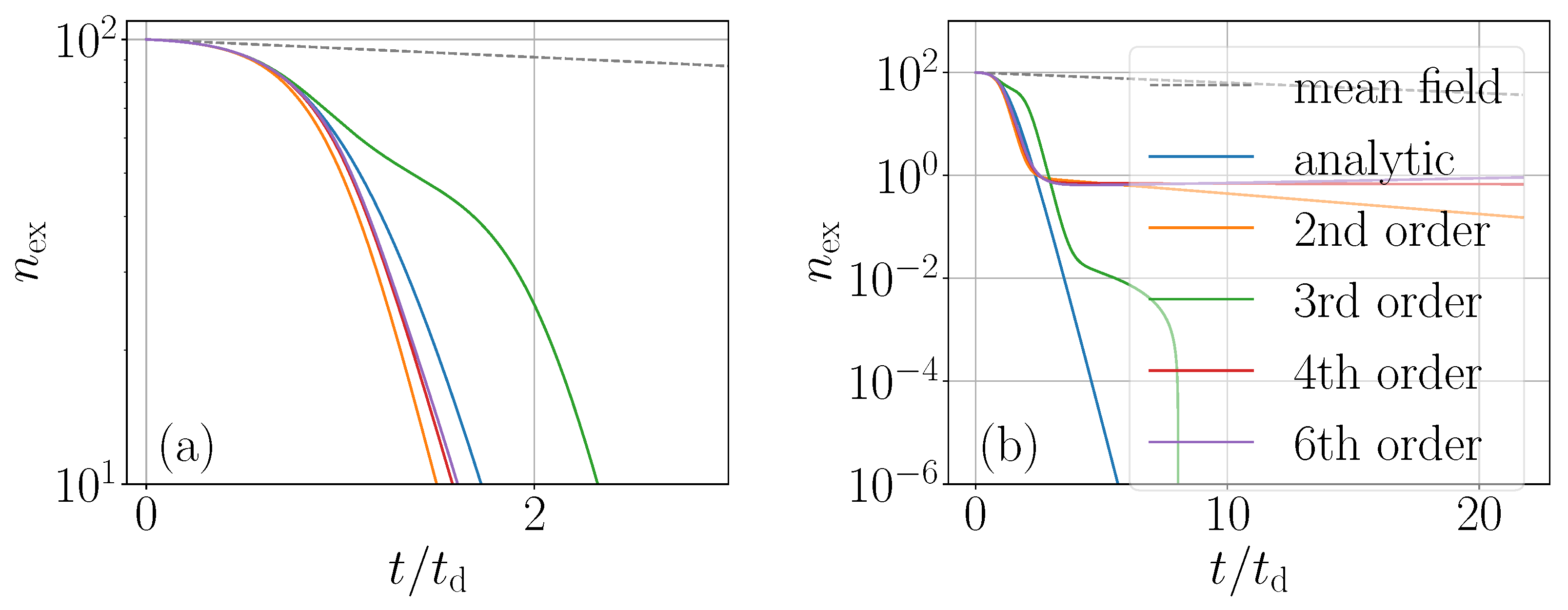Benchmarking the Cumulant Expansion Method Using Dicke Superradiance

Abstract

Collective superradiant decay of a tightly packed inverted quantum emitter ensemble is among the most intensely studied phenomena in quantum optics. Since the seminal work of Dicke more than half a century ago, a plethora of theoretical calculations in quantum many-body physics have followed. Widespread experimental efforts range from the microwave to the X-ray regime. Nevertheless, accurate calculations of the time dynamics of the superradiant emission pulse still remain a challenging task requiring approximate methods for large ensembles. Here, we benchmark the cumulant expansion method for describing collective superradiant decay against a newly found exact solution. The application of two variants of the cumulant expansion exhibits reliable convergence of time and magnitude of the maximum emission power with increasing truncation order. The long-term population evolution is only correctly captured for low emitter numbers, where an individual spin-based cumulant expansion proves more reliable than the collective spin-based variant. Surprisingly, odd orders show unphysical behavior. At sufficiently high spin numbers, both chosen cumulant methods agree, but still fail to reliably converge to the numerically exact result. Generally, on longer time scales the expansions substantially overestimate the remaining population. While numerically fast and efficient, cumulant expansion methods need to be treated with sufficient caution when used for long-time evolution or reliably finding steady states.

1. Introduction

Quantum many-body problems rarely allow for full analytical solutions and are typically also prohibitively difficult to solve numerically. A plethora of expansion methods has thus been developed to study them approximately [1]. In particular, when convergence to their classical counterparts is expected in the large-number limit, the first quantum corrections to appear are of central interest. Beyond a first order expansion [2], the quantum cumulant expansion is one of the most widely used methods for studying the influence of quantum correlations in many-body physics [3]. It has proven very successful in studies of photon statistics and quantum correlations in various light sources, beginning with the first successful model description of a laser and even non-classical light sources such as few-photon emitters [4]. Despite its success in solving concrete practical problems, hardly any detailed studies of its convergence when applying higher-order expansions exist [5]. Mostly, second-order calculations, which include pair correlations, have proven sufficient. Systematic numerical studies in this direction are often hampered by a lack of analytically solvable, nonlinear, and nontrivial many-body dynamics models, in which convergence could be studied thoroughly and quantitatively.

Luckily, many decades after the prediction of superradiance [6,7,8] and clear experimental evidence [9], a tractable analytical solution for the seminal problem of free space Dicke superradiance has been recently put forward [10,11]. This new analytic form of the solution beyond the single spin quantum Rabi model [12] allows us to obtain highly accurate solutions for very large atom numbers, way beyond any direct numerical solution of the master equation. As high-order correlations build up during the time evolution of superradiant decay, this gives an ideal reference frame for a systematic test of the cumulant expansion for high quantum emitter numbers.

Recent experiments in free-space atomic arrays and waveguided platforms have heightened the interest in collective light–matter effects relevant to (driven) superradiance. In this context, cumulant (cluster) expansions provide a microscopically based yet tractable framework for modeling higher-order correlations. Recent experimental works [13,14,15,16,17,18] employed cumulant-based expansions to theoretically model driven superradiant dynamics. This experimental progress further motivates our work of benchmarking cumulant truncations against the exact master equation numerics. Here we can use the established quantum cumulant approach [19] to generate high-order expansions and study the convergence of key quantities, such as the peak emitted power or the time of maximum emission, as well as higher-order photon correlations. While no quantum entanglement builds up in pure superradiant decay [20], a closely related recent study exhibited the buildup of dipole correlations, particularly in the early phase of superradiance [21]. This shows the need for higher-order corrections beyond a field expansion, which misses all correlations. The early time phase correlation buildup starting from a random first emission event typically leads to a significant variance of the time when the intensity maximum occurs, if one unravels the evolution in single wavefunction trajectories [22]. Alternative approaches to modeling collective light–matter dynamics include phase-space techniques such as the truncated Wigner approximation [23], stochastic wavefunction/quantum-trajectory (MCWF) simulations [24], exact diagonalization for small ensembles, and tensor-network/MPS methods [25] that are most effective in (quasi) 1D or weakly entangled regimes. Cumulant (cluster) expansions occupy a complementary niche: they retain operator correlations up to a chosen order, exploit permutation symmetry when present, and scale favorably with system size, yielding analytic insight and computationally efficient predictions for early-time, low-order observables.

Interestingly, while most of the individual stochastic trajectories exhibit highly nonclassical, entangled intermediate states [26], this property is completely washed out by ensemble averaging. Efforts to reproduce the vanishing trajectory-averaged entanglement using a stochastic unraveling thus prove numerically very intensive. The buildup of spin correlations, however, appears automatically when evaluating the second-order cumulant as introduced below. A comparison of the exact result with the predictions of a truncated cumulant expansion can then reveal the importance of even higher-order correlations.

This work is organized as follows: After introducing the Dicke model and the resulting master equation in both the individual and collective bases, we define and present the two corresponding forms of the cumulant expansion in the two operator basis sets. As the first test, we study the convergence of a cumulant expansion of the collective Spin operators to the exact results for increasing expansion order. For smaller numbers of atoms, we then study the convergence properties of an individual spin-based expansion, which becomes exact once the expansion order reaches the number of spins. We then compare the two expansion methods for larger ensembles, followed by a more detailed analysis of how the error scales with the number of atoms and the expansion order for both methods.

2. Theoretical Description

2.1. Quantum Master Equation

The Dicke superradiance problem involves finding the density operator $\rho$ which satisfies the following master equation in Lindblad form (in an interaction picture where the trivial action of the free Hamiltonian is removed):

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}}\rho \left(t\right)& =\mathsf{\Gamma }\sum _{n,m=1}^N\left[{\sigma }_n\rho {\sigma }_m^{†}-{\displaystyle \frac{1}{2}}\left({\sigma }_n^{†}{\sigma }_m\rho -\rho {\sigma }_n^{†}{\sigma }_m\right)\right]\hfill \\ \hfill & =\mathsf{\Gamma }\left[S\rho S^{†}-{\displaystyle \frac{1}{2}}\left(S^{†}S\rho -\rho S^{†}S\right)\right],\hfill \end{array}$$

(1)

where ${\sigma }_n=|e_n\rangle \langle g_n|$ is the jump operator for emitter n and $S={\sum }_n{\sigma }_n$ is the symmetric jump operator in the Dicke basis [7]. Note that besides the number of emitters N, we are left with only one parameter $\mathsf{\Gamma }$, the spontaneous decay rate of a single two-level emitter, which simply sets the time scale.

We will calculate the averaged total emitted power and excited state population, given by (setting $\hslash =1$)

$$P_{\mathrm{out}}=\mathsf{\Gamma }\sum _{n,m=1}^N\langle {\sigma }_n^{†}{\sigma }_m\rangle =\mathsf{\Gamma }\langle S^{†}S\rangle ,n_{\mathrm{ex}}=\sum _{n=1}^N\langle {\sigma }_n^{ee}\rangle ,$$

(2)

as a figure of merit using both the full master equation in the symmetric Dicke subspace and using the cumulant expansion method, explained below. The total excited state population $n_{\mathrm{ex}}$ in Equation (2) tracks how much population resides in the excited state during the dissipative time evolution.

2.2. Equations of Motion for Expectation Values of Operators

Let us further define a general operator $\mathcal{O}$ with expectation value $\langle \mathcal{O}\rangle \left(t\right)=\mathrm{Tr}\{\mathcal{O}\rho (t\left)\right\}$. Then, its dynamics are given by

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}\langle \mathcal{O}\rangle =\mathsf{\Gamma }\sum _{n,m=1}^N〈{\sigma }_n^{†}\mathcal{O}{\sigma }_m-{\displaystyle \frac{1}{2}}\{{\sigma }_n^{†}{\sigma }_m,\mathcal{O}\}〉.\end{array}$$

(3)

Throughout this work, we assume that the system is initialized in the uncorrelated product state $|{\psi }_0\rangle ={\prod }_{n=1}^N|e_n\rangle$, and using Equation (3), we start noticing that $\langle {\sigma }_n\rangle =0$, $\langle {\sigma }_n{\sigma }_m^{ee}\rangle =0$, $\langle {\sigma }_n^{†}{\sigma }_m^{†}{\sigma }_k\rangle =0$ (for $n\ne m\ne k$) and so forth, namely terms ${\sigma }_a^{†}{\sigma }_b$ have to appear simultaneously. We are interested in the time evolution of the system operators, which leads to a coupled set of equations with increasing order in the operator correlations, namely

$$\{\langle {\sigma }_n^{ee}\rangle ,\langle {\sigma }_n^{†}{\sigma }_m\rangle ,\langle {\sigma }_n^{ee}{\sigma }_m^{ee}\rangle ,\langle {\sigma }_n^{†}{\sigma }_m{\sigma }_k^{ee}\rangle ,\langle {\sigma }_n^{ee}{\sigma }_m^{ee}{\sigma }_k^{ee}\rangle ,\dots \},$$

(4)

where $n\ne m\ne k$. The computational complexity of the coupled set of equations scales polynomially with correlation order r as $\sim \mathcal{O}\left(N^r\right)$. In order to obtain a closed set of equations and render the system numerically tractable, the correlations have to be truncated, which can be done systematically using the cumulant expansion method [27], explained in the next section.

3. Cumulant Expansion Method

In order to stop the hierarchy of equations above from expanding and close the system of equations, we need to apply a systematic cumulant expansion on the operator averages. The cumulant (cluster) expansion rewrites moments of spin operators in terms of operator correlators (“cumulants”), which quantify correlations beyond products of lower-order moments. Truncating at order k (i.e., setting all cumulants of order $>k$ to zero) closes the equations of motion for cumulants up to that order: $k=1$ is first order (mean field); $k=2$ retains pair correlations and already captures the collective build-up underlying the superradiant pulse; higher k include three- and four-body effects but may become numerically challenging and, if pushed too far, can yield unphysical behavior [1]. The approximation is most reliable when correlations remain moderate or approximately Gaussian (early times, large N, near-symmetric states), while accuracy degrades for long-time/steady-state properties and high-order observables. We employ both individual-operator and collective-spin formulations: the former resolves site-to-site structure, the latter exploits permutation symmetry in the Dicke limit. In the following sections we compare each truncation directly to the exact dynamics based on the master equation and quantify errors.

In order to obtain a closed set of equations, only correlations up to a certain order are considered, while all higher-order correlations are expanded in terms of lower orders. This approximation can be computed in a systematic fashion, using the cumulant expansion. The joint cumulant of an M$\mathrm{th}$-order correlation $\langle {\widehat{\mathcal{O}}}_1\dots {\widehat{\mathcal{O}}}_M\rangle$ can be expressed as an alternate sum of products of their expectation values and is compactly written as [27]

$$\kappa ({\widehat{\mathcal{O}}}_1,\dots ,{\widehat{\mathcal{O}}}_M)=\sum _P\left(\right|P|-1)!{(-1)}^{\left|P\right|-1}\prod _{B\in P}〈\prod _{i\in B}{\widehat{\mathcal{O}}}_i〉$$

(5)

where P runs through the list of all partitions of $\{1,\dots ,M\}$, B runs through the list of all blocks of the partition P and $\left|P\right|$ is the number of parts in the partition. An approximation can be made by setting $\kappa ({\widehat{\mathcal{O}}}_1,\dots ,{\widehat{\mathcal{O}}}_M)=0$, which allows to express $\langle {\widehat{\mathcal{O}}}_1\dots {\widehat{\mathcal{O}}}_M\rangle$ with correlations of order $M-1$ and lower. For instance, the expansion of expectation values involving three operators reads

$$\begin{array}{cc}\hfill \langle {\widehat{\mathcal{O}}}_1{\widehat{\mathcal{O}}}_2{\widehat{\mathcal{O}}}_3\rangle & \approx \langle {\widehat{\mathcal{O}}}_1\rangle \langle {\widehat{\mathcal{O}}}_2{\widehat{\mathcal{O}}}_3\rangle +\langle {\widehat{\mathcal{O}}}_2\rangle \langle {\widehat{\mathcal{O}}}_1{\widehat{\mathcal{O}}}_3\rangle \hfill \\ \hfill & +\langle {\widehat{\mathcal{O}}}_3\rangle \langle {\widehat{\mathcal{O}}}_1{\widehat{\mathcal{O}}}_2\rangle -2\langle {\widehat{\mathcal{O}}}_1\rangle \langle {\widehat{\mathcal{O}}}_2\rangle \langle {\widehat{\mathcal{O}}}_3\rangle .\hfill \end{array}$$

(6)

This introduces some error, as all higher-order correlations are neglected. In the following sections, we will quantitatively analyze this error based on the truncation order and number of emitters.

4. Benchmarking Cumulant Expansion Convergence

Let us now proceed to test the accuracy and convergence of the cumulant expansion approximation with the exact master equation using superradiant decay as a benchmark. We note, that the primary goal is to test the convergence of higher order cumulant orders with exact numerics in the context of strongly correlated systems, and not provide accurate predictions of Dicke superradiance. In this section we test this for increasing cumulant expansion orders, i.e., setting the $M\mathrm{th}$-order cumulant to zero for increasing M.

Before going into details, however, let’s note that in the chosen Dicke limit [8] of all atoms well within a cubic wavelength and neglecting dipolar energy shifts, there is actually only a single interesting physical parameter, namely the total atom number N entering the exact dynamics. The other free parameter $\mathsf{\Gamma }$ is the single-atom decay rate (proportional to the square of the dipole moment), which only fixes the overall time scale. It does not change the results in any other way. Of course, for any finite extent or nonspherical shape of the cloud as well as for any imperfect excitation of the ensemble, many more details of the geometry will enter [28]. While these corrections will somewhat change the actual numbers, we will ignore them here for the sake of clarity of the arguments.

4.1. Time Evolution

Let us start with a comparison of the predicted time evolution of the full ensemble and use key quantities as the total remaining excited state population as well as the momentarily emitted power in Equation (2) for benchmarking the cumulant expansion versus the full density matrix evolution. In a first step, we choose only two representative system sizes from small $(N=4)$ to large $(N=100)$. In a further step below, we will then compare characteristic quantities as the time and magnitude of the maximal emitted power, as key average properties to characterize the reliability of the approximations over many orders of magnitude of atom numbers.

In Figure 1 we depict the population decay of an average-sized ensemble of $N=100$ emitters in units of the analytically predicted time of maximal emission power, $t_d$. On the left, we show the evolution till the time where $90\%$ of the atoms have decayed, comparing different expansion orders. Note that $t_d=lnN/\left(N\mathsf{\Gamma }\right)$ is the delayed time, when the superradiant peak emission approximatiely occurs [8] and plot the time evolution in units of $t_d$. We only find a quantitatively good agreement for times before maximum emission. Strong deviation from the exact results appears in particular for odd orders at later times. Let us add here that the first expansion fails from the beginning, as it simply reproduces individual (exponential) decay with no buildup of collective dynamics. This is shown in the straight uppermost dashed line. We see that in this time range, even orders slowly converge to the exact result, already diverging by about 10% for the prediction of the time when only 10% of the initial population is left in the ensemble.

For longer times, where the remaining population has decayed to less than one percent, the cumulant expansion simply fails to correctly reproduce the decay process. Somewhat surprisingly, no convergence towards the exact dynamics appears even for higher-order calculations. The predicted decay curves from the truncated expansion generally exhibit a rather nonphysical long-lived population fraction.

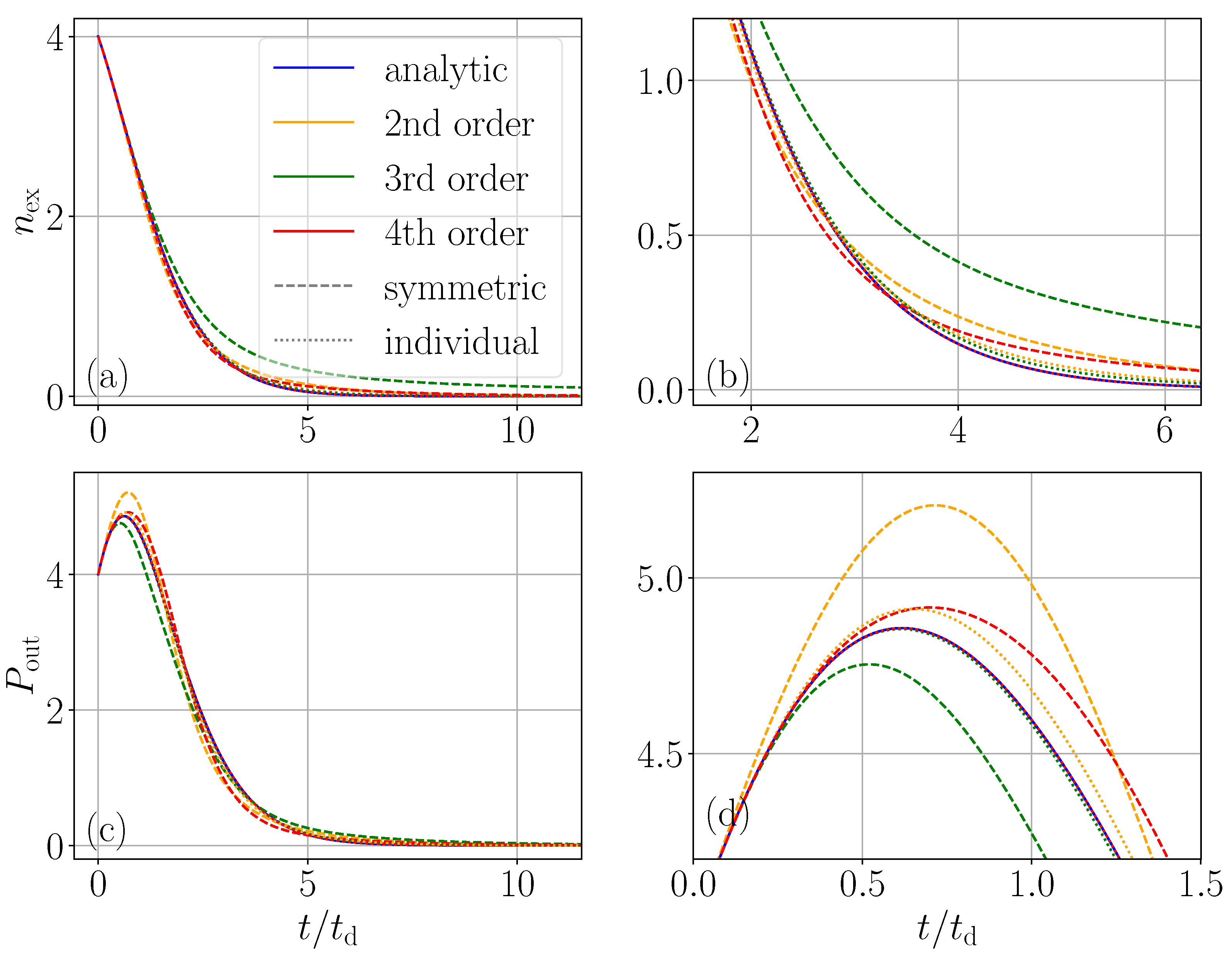
It is well known that the cumulant expansion approximation of interacting spins becomes exact when the order reaches the number of spins [27]. Hence, in the next step, we look at the small number of only four spins to study the cumulant convergence as shown in Figure 2. Indeed, the fourth order represented by exactly the same set of coupled equations used above for the case of $N=100$ now behaves indistinguishably from the exact result based on solving the full master equation. Again, as above, the third-order expansion exhibits a worse agreement than the second order. Interestingly, the individual spin-based expansion here converges very well and way better than the symmetric collective approach.

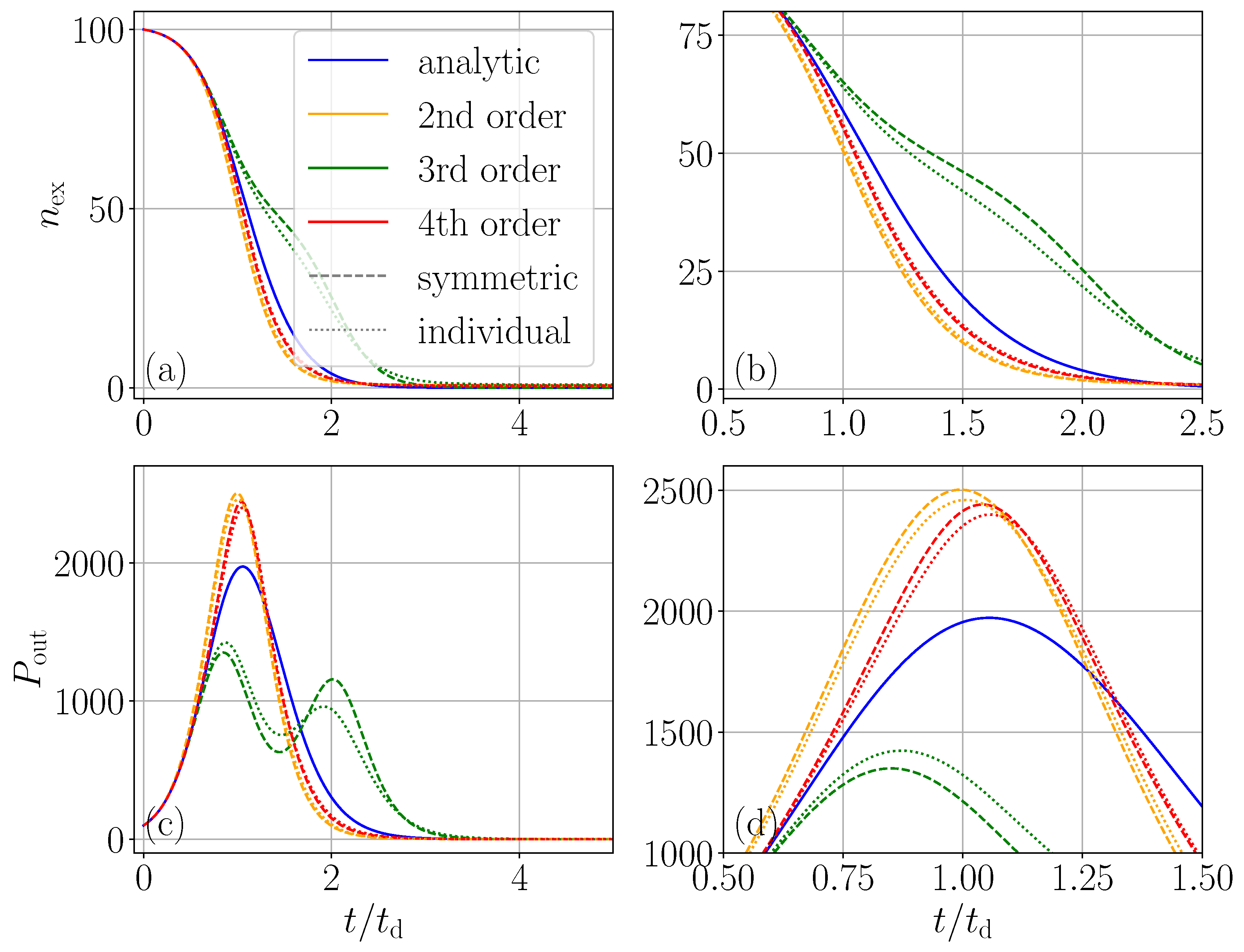
As we will see below in more detail, the convergence difference between individual and collective spin cumulants strongly reduces with sample size, but while the two methods converge to each other, they still significantly deviate from the exact numerical result. In Figure 3 we highlight this for the case of $N=100$ emitters. While the two approaches only differ on a few percent level at a later time, there are even qualitative deviations from the exact dynamics. In particular, we see a clearly nonphysical double peak structure in the emission power depicted on the lower left for the third-order cumulant expansion. On the lower left (zoomed plot), we see a better agreement of the various approaches, at least until the time of maximum emission. It remains a bit unclear to us where this curious behavior originates, but it seems to be related to the crossing of the equator in the Bloch sphere, where dynamics change from synchronization to dephasing of the individual spins. Geometrically on the Bloch sphere, inhomogeneous frequency shifts (e.g., disorder- or dipole-interaction-induced) generate azimuthal phase diffusion of individual spins; the collective transverse magnetization $\langle S^{†}\rangle$ then dephases as the enclosed phase area grows, diminishing the macroscopic dipole that drives superradiance. This “phase–area” picture is standard in cooperative emission and explains how dephasing suppresses cooperativity [8,29]. This might lead to erroneous three-spin correlations, which need non-trivial four-spin correlations as correction factors. Overall, it is a strong reminder that the cumulant expansion beyond second order needs to be taken with great care.

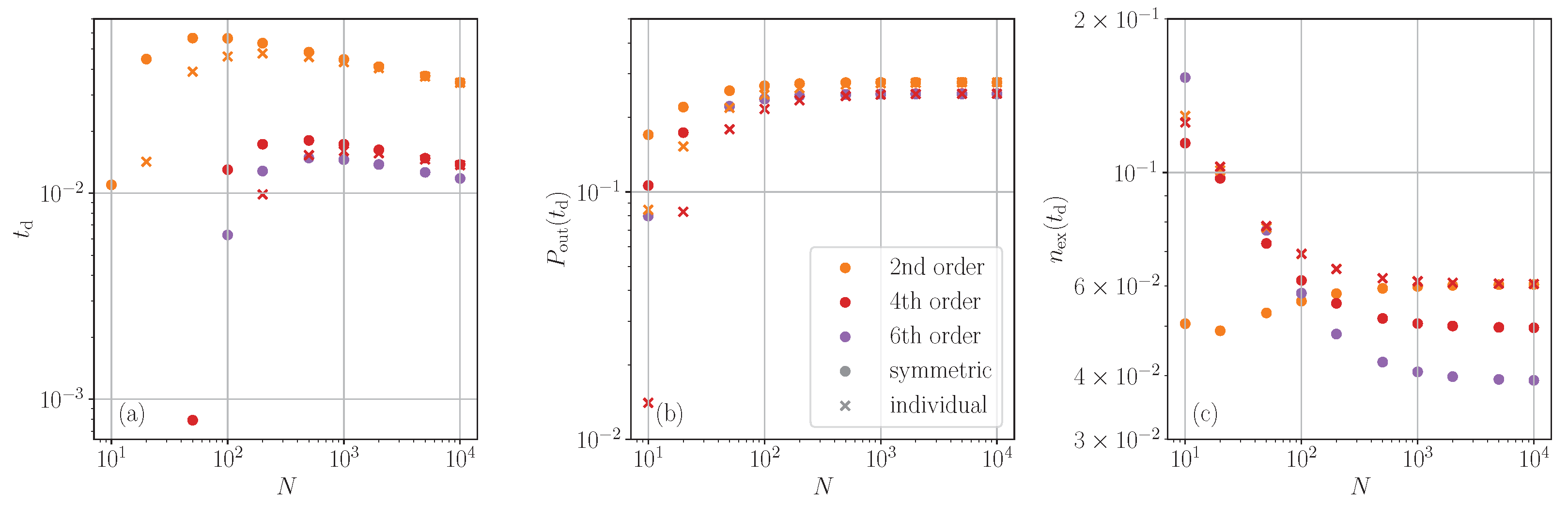
4.2. Peak Emission Time and Power

After highlighting some key properties of the time evolution, we now come to a more systematic quantitative analysis of the system size scaling. For this, we choose two central observables in the dynamics, namely time and power of the maximum emission peak. This allows us to compare the quantitative accuracy of various orders of our two cumulant approaches (individual or collective spin basis) as a function of system size N. In Figure 4 on the left, we plot the relative deviation of the predicted time of maximum emission from the exact value. It appears promising that already the second order cumulant expansion yields results accurate to better than 5%, which somewhat slowly improves with emitter number. The fourth order is more accurate and converges towards a 1% error for large ensembles. Again, the individual operator-based expansions behave consistently superior, particularly for smaller N.

The prediction for maximal power shown in the middle is somewhat less accurate and converges only to the few percent level for large N. Surprisingly, higher-order corrections do not substantially improve the prediction.

Looking at the remaining upper state population at maximum emission time plotted in the right panel of Figure 4, we find a similar percent level accuracy. However, in this case, we find significant improvement for larger ensembles, and a higher-order expansion significantly improves the prediction. As already seen in the time evolution plots in Figure 1, Figure 2 and Figure 3, the third order turns out to be very unreliable even at this rather short evolution time. Again, a second-order expansion using individual operators turns out to be a fairly good and reliable approximation over all system sizes.

In summary, we see that the quality and usefulness of the cumulant expansions strongly depend on the targeted observable and deteriorate for longer time scales. In general, going beyond the second order is hardly worth the effort, as some minor improvements come with a much more complex set of equations to solve. On the other hand, several important quantities, such as intensity correlations or spectra, require higher-order observables anyway. The rather poor long-time behaviors also hint that steady state calculations can be rather problematic, even if one finds a numerical solution of the nonlinear coupled set of equations.

5. Conclusions

It is well known that for the perfectly inverted initial state, i.e., all emitters in the excited state, in the Dicke model, a first cumulant expansion completely fails, as no coherence dipole–dipole correlations are accounted for [30]. Here, we have demonstrated that a second-order cumulant expansion produces a fairly reliable approximation to the full superradiant decay, in particular, for higher atom numbers and up to intermediate timescales. Surprisingly, higher-order expansions generally only lead to minor improvements even in the best case. Actually, the third expansion often exhibits physically incorrect oscillatory solutions on intermediate timescales [1]. Interestingly, two possible variants of the cumulant expansion, based either on individual atomic spin operators or, alternatively, on the collective spin basis, lead to different predictions beyond first-order cumulant expansion. For not too large numbers, the first case of using a many-particle cumulant expansion leads to significantly higher accuracy and even converges to the exact result when the order approaches the particle number. Fortunately, the differences between the two basis models vanish in the large N limit. Future work will involve systematic benchmarks of equal-time spin–spin quantum correlations of higher orders and in particular two-time/intensity correlations $g^{\left(2\right)}\left(0\right)$, important to characterize the correlated emission process [31]. In summary, we find that a cumulant expansion to second order can capture a large part of the deviation from classical to quantum dynamics, while the usefulness of higher-order expansions is rather limited. In particular, due to the much larger number of equations to be solved, the extra effort barely pays off. Of course, fourth-order expansions are still required to obtain higher-order correlation functions such as the $g^2\left(0\right)$-function for intensity correlations. These results, however, should be interpreted with caution.